Radiobiological Meta-Analysis of the Response of Prostate Cancer to High-Dose-Rate Brachytherapy: Investigation of the Reduction in Control for Extreme Hypofractionation
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
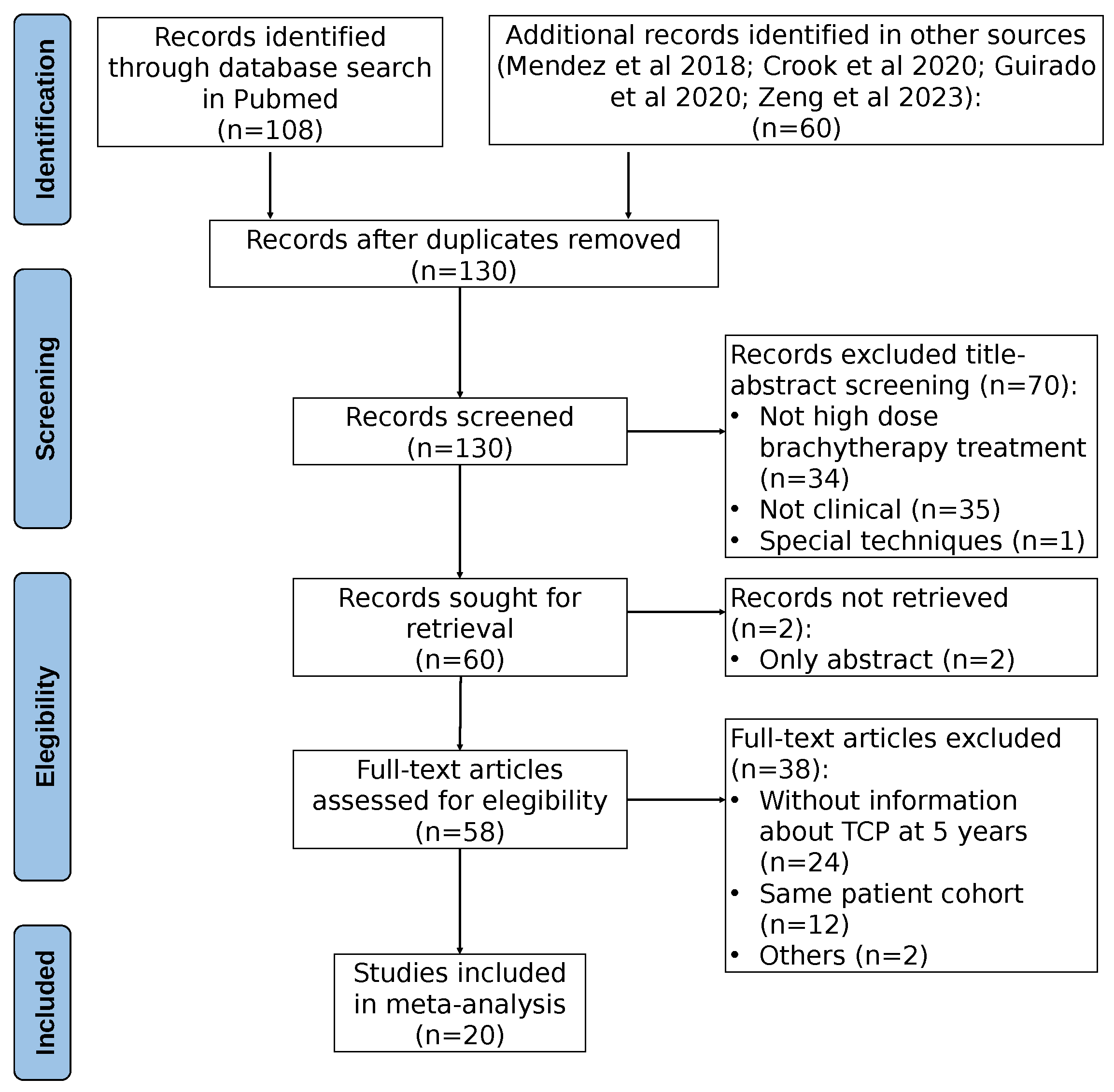
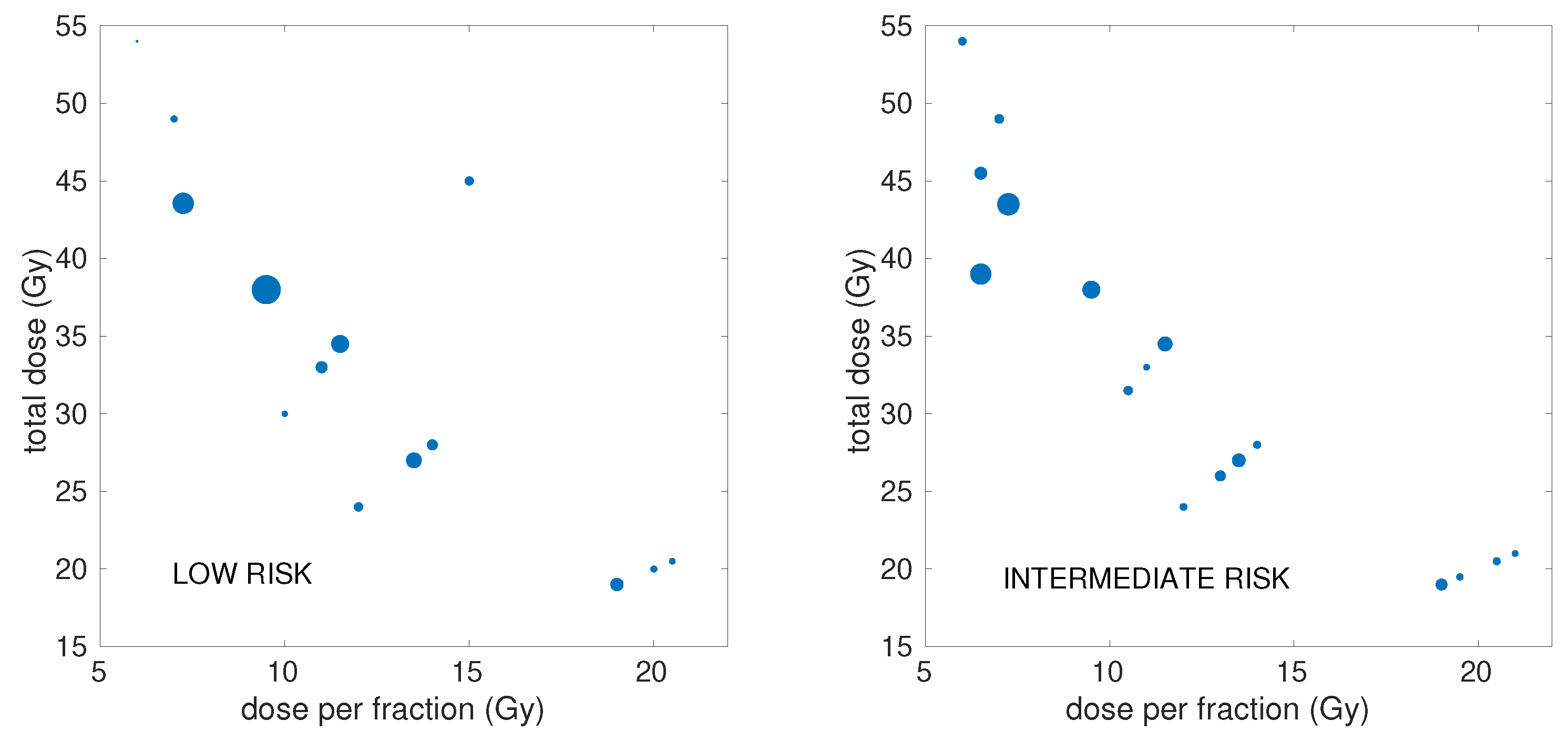
2.1. Clinical Dataset
2.2. Radiobiological Modeling
2.2.1. Models
- The LQL model: This model [20] includes a moderation of the quadratic term of the LQ model with increasing dose, which is controlled by the parameter :
- Stavrev’s model of reoxygenation: this model [43] relies on the LQ model, but with time-dependent and parameters to account for reoxygenation during treatment:with parameters b and controlling the evolution of and . This results in a time-dependent ratio, which, due to the quadratic dependence of , increases with time.
2.2.2. Incomplete Repair
2.2.3. Overall Surviving Fraction and Proliferation
2.2.4. Tumor Control Probability and EQD2
2.3. Statistical Methods
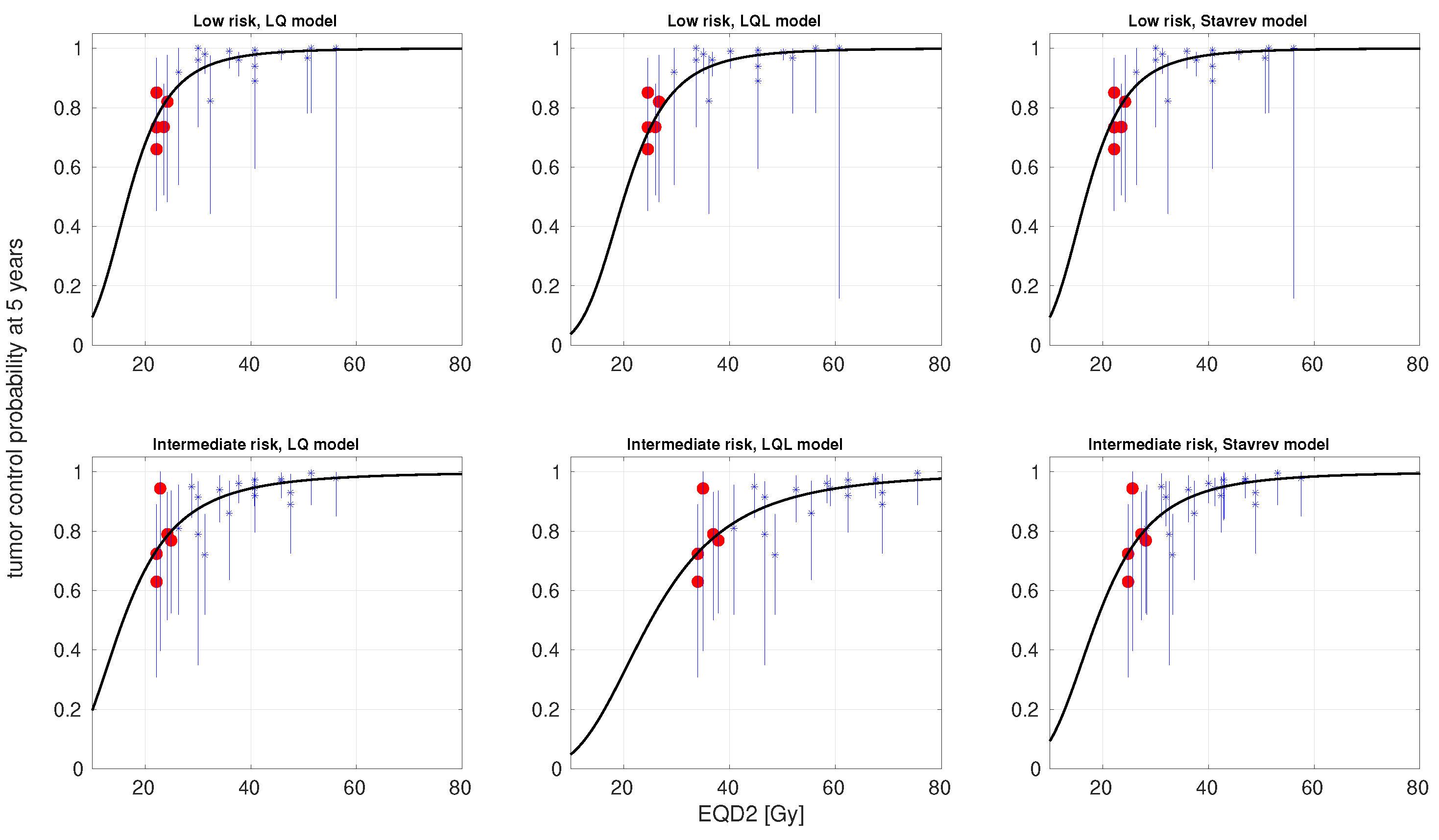
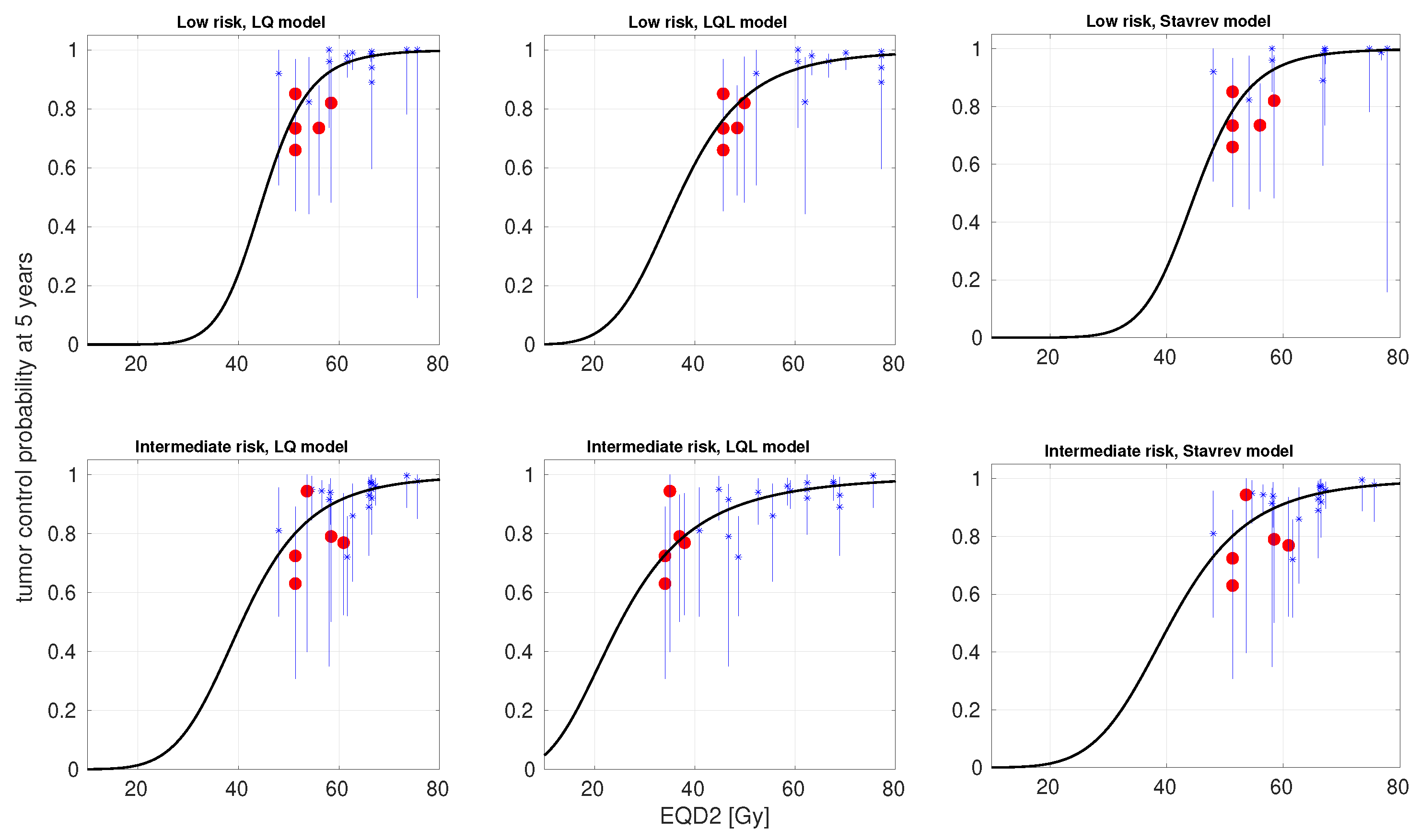
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sekhoacha, M.; Riet, K.; Motloung, P.; Gumenku, L.; Adegoke, A.; Mashele, S. Prostate Cancer Review: Genetics, Diagnosis, Treatment Options, and Alternative Approaches. Molecules 2022, 27, 5730. [Google Scholar] [CrossRef] [PubMed]
- Arcangeli, G.; Saracino, B.; Arcangeli, S.; Gomellini, S.; Petrongari, M.G.; Sanguineti, G.; Strigari, L. Moderate Hypofractionation in High-Risk, Organ-Confined Prostate Cancer: Final Results of a Phase III Randomized Trial. J. Clin. Oncol. 2017, 35, 1891–1897. [Google Scholar] [CrossRef] [PubMed]
- Bryant, C.M.; Henderson, R.H.; Nichols, R.C.; Mendenhall, W.M.; Hoppe, B.S.; Vargas, C.E.; Daniels, T.B.; Choo, C.R.; Parikh, R.R.; Giap, H.; et al. Consensus Statement on Proton Therapy for Prostate Cancer. Int. J. Part. Ther. 2021, 8, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.Y.; Fan, K.H. Proton therapy for prostate cancer: Current state and future perspectives. Br. J. Radiol. 2022, 95, 20210670. [Google Scholar] [CrossRef]
- Stish, B.J.; Davis, B.J.; Mynderse, L.A.; McLaren, R.H.; Deufel, C.L.; Choo, R. Low dose rate prostate brachytherapy. Transl. Androl. Urol. 2018, 7, 341–356. [Google Scholar] [CrossRef]
- Mendez, L.C.; Morton, G.C. High dose-rate brachytherapy in the treatment of prostate cancer. Transl. Androl. Urol. 2018, 7, 357–370. [Google Scholar] [CrossRef]
- Crook, J.; Marbán, M.; Batchelar, D. HDR Prostate Brachytherapy. Semin. Radiat. Oncol. 2020, 30, 49–60. [Google Scholar] [CrossRef]
- Miralbell, R.; Roberts, S.A.; Zubizarreta, E.; Hendry, J.H. Dose-fractionation sensitivity of prostate cancer deduced from radiotherapy outcomes of 5,969 patients in seven international institutional datasets: α/β = 1.4 (0.9–2.2) Gy. Int. J. Radiat. Oncol. Biol. Phys. 2012, 82, e17–e24. [Google Scholar] [CrossRef]
- Fowler, J.F. The radiobiology of prostate cancer including new aspects of fractionated radiotherapy. Acta Oncol. 2005, 44, 265–276. [Google Scholar] [CrossRef]
- Bentzen, S.M.; Ritter, M.A. The alpha/beta ratio for prostate cancer: What is it, really? Radiother. Oncol. 2005, 76, 1–3. [Google Scholar] [CrossRef]
- Nahum, A.E.; Movsas, B.; Horwitz, E.M.; Stobbe, C.C.; Chapman, J.D. Incorporating clinical measurements of hypoxia into tumor local control modeling of prostate cancer: Implications for the alpha/beta ratio. Int. J. Radiat. Oncol. Biol. Phys. 2003, 57, 391–401. [Google Scholar] [CrossRef] [PubMed]
- Hannan, R.; Tumati, V.; Xie, X.J.; Cho, L.C.; Kavanagh, B.D.; Brindle, J.; Raben, D.; Nanda, A.; Cooley, S.; Kim, D.W.N.; et al. Stereotactic body radiation therapy for low and intermediate risk prostate cancer-Results from a multi-institutional clinical trial. Eur. J. Cancer 2016, 59, 142–151. [Google Scholar] [CrossRef] [PubMed]
- Datta, N.R.; Stutz, E.; Rogers, S.; Bodis, S. Clinical estimation of α/β values for prostate cancer from isoeffective phase III randomized trials with moderately hypofractionated radiotherapy. Acta Oncol. 2018, 57, 883–894. [Google Scholar] [CrossRef] [PubMed]
- Vogelius, I.R.; Bentzen, S.M. Diminishing Returns From Ultrahypofractionated Radiation Therapy for Prostate Cancer. Int. J. Radiat. Oncol. Biol. Phys. 2020, 107, 299–304. [Google Scholar] [CrossRef]
- Pardo-Montero, J.; González-Crespo, I.; Gómez-Caamaño, A.; Gago-Arias, A. Radiobiological Meta-Analysis of the Response of Prostate Cancer to Different Fractionations: Evaluation of the Linear-Quadratic Response at Large Doses and the Effect of Risk and ADT. Cancers 2023, 15, 3659. [Google Scholar] [CrossRef]
- Guirado, D.; Ruiz-Arrebola, S.; Tornero-López, A.M.; de la Vega, J.M.; Prada, P.J.; Lallena, A.M. A radiobiological study of the schemes with a low number of fractions in high-dose-rate brachytherapy as monotherapy for prostate cancer. J. Contemp. Brachyther. 2020, 12, 193–200. [Google Scholar] [CrossRef]
- Kirkpatrick, J.P.; Meyer, J.J.; Marks, L.B. The linear-quadratic model is inappropriate to model high dose per fraction effects in radiosurgery. Semin. Radiat. Oncol. 2008, 18, 240–243. [Google Scholar] [CrossRef]
- Wang, J.Z.; Huang, Z.; Lo, S.S.; Yuh, W.T.C.; Mayr, N.A. A generalized linear-quadratic model for radiosurgery, stereotactic body radiation therapy, and high-dose rate brachytherapy. Sci. Transl. Med. 2010, 2, 39ra48. [Google Scholar] [CrossRef]
- Song, C.W.; Lee, Y.J.; Griffin, R.J.; Park, I.; Koonce, N.A.; Hui, S.; Kim, M.S.; Dusenbery, K.E.; Sperduto, P.W.; Cho, L.C. Indirect Tumor Cell Death After High-Dose Hypofractionated Irradiation: Implications for Stereotactic Body Radiation Therapy and Stereotactic Radiation Surgery. Int. J. Radiat. Oncol. Biol. Phys. 2015, 93, 166–172. [Google Scholar] [CrossRef]
- Guerrero, M.; Li, X.A. Extending the linear-quadratic model for large fraction doses pertinent to stereotactic radiotherapy. Phys. Med. Biol. 2004, 49, 4825–4835. [Google Scholar] [CrossRef]
- Zeng, H.; Dai, J.; Cao, D.; Wang, M.; Zhao, J.; Zeng, Y.; Xu, N.; Xie, Y.; Liu, H.; Zeng, H.; et al. Safety and efficacy associated with single-fraction high-dose-rate brachytherapy in localized prostate cancer: A systematic review and meta-analysis. Strahlenther. Und Onkol. 2023, 199, 525–535. [Google Scholar] [CrossRef] [PubMed]
- Hauswald, H.; Kamrava, M.R.; Fallon, J.M.; Wang, P.C.; Park, S.J.; Van, T.; Borja, L.; Steinberg, M.L.; Demanes, D.J. High-Dose-Rate Monotherapy for Localized Prostate Cancer: 10-Year Results. Int. J. Radiat. Oncol. Biol. Phys. 2016, 94, 667–674. [Google Scholar] [CrossRef] [PubMed]
- Barkati, M.; Williams, S.G.; Foroudi, F.; Tai, K.H.; Chander, S.; van Dyk, S.; See, A.; Duchesne, G.M. High-dose-rate brachytherapy as a monotherapy for favorable-risk prostate cancer: A Phase II trial. Int. J. Radiat. Oncol. Biol. Phys. 2012, 82, 1889–1896. [Google Scholar] [CrossRef] [PubMed]
- Strouthos, I.; Tselis, N.; Chatzikonstantinou, G.; Butt, S.; Baltas, D.; Bon, D.; Milickovic, N.; Zamboglou, N. High dose rate brachytherapy as monotherapy for localised prostate cancer. Radiother. Oncol. 2018, 126, 270–277. [Google Scholar] [CrossRef]
- Kukiełka, A.M.; Dąbrowski, T.; Walasek, T.; Olchawa, A.; Kudzia, R.; Dybek, D. High-dose-rate brachytherapy as a monotherapy for prostate cancer–Single-institution results of the extreme fractionation regimen. Brachytherapy 2015, 14, 359–365. [Google Scholar] [CrossRef]
- Jawad, M.S.; Dilworth, J.T.; Gustafson, G.S.; Ye, H.; Wallace, M.; Martinez, A.; Chen, P.Y.; Krauss, D.J. Outcomes Associated With 3 Treatment Schedules of High-Dose-Rate Brachytherapy Monotherapy for Favorable-Risk Prostate Cancer. Int. J. Radiat. Oncol. Biol. Phys. 2016, 94, 657–666. [Google Scholar] [CrossRef]
- Prada, P.J.; Cardenal, J.; Blanco, A.G.; Anchuelo, J.; Ferri, M.; Fernández, G.; Arrojo, E.; Vázquez, A.; Pacheco, M.; Fernández, J. High-dose-rate interstitial brachytherapy as monotherapy in one fraction for the treatment of favorable stage prostate cancer: Toxicity and long-term biochemical results. Radiother. Oncol. 2016, 119, 411–416. [Google Scholar] [CrossRef]
- Behmueller, M.; Tselis, N.; Zamboglou, N.; Zoga, E.; Baltas, D.; Rödel, C.; Chatzikonstantinou, G. High-Dose-Rate Brachytherapy as Monotherapy for Low- and Intermediate-Risk Prostate Cancer. Oncological Outcomes After a Median 15-Year Follow-Up. Front. Oncol. 2021, 11, 770959. [Google Scholar] [CrossRef]
- Johansson, B.; Olsén, J.S.; Karlsson, L.; Lundin, E.; Lennernäs, B. High-dose-rate brachytherapy as monotherapy for low- and intermediate-risk prostate cancer: Long-term experience of Swedish single-center. J. Contemp. Brachyther. 2021, 13, 245–253. [Google Scholar] [CrossRef]
- Tselis, N.; Tunn, U.W.; Chatzikonstantinou, G.; Milickovic, N.; Baltas, D.; Ratka, M.; Zamboglou, N. High dose rate brachytherapy as monotherapy for localised prostate cancer: A hypofractionated two-implant approach in 351 consecutive patients. Radiat. Oncol. 2013, 8, 115. [Google Scholar] [CrossRef]
- Nagore, G.; Moreno-Olmedo, E.; Suárez-Gironzini, V.; Aakki, L.; Ramos-García, L.; Gómez, E.; García, A.; Beltrán, L.; Gómez-Iturriaga, A. Long-term outcomes of ultra-hypofractionated 2 fractions single day HDR brachytherapy in localized prostate cancer. Radiother. Oncol. 2023, 186, 109807. [Google Scholar] [CrossRef] [PubMed]
- Yamazaki, H.; Masui, K.; Suzuki, G.; Nakamura, S.; Yoshida, K.; Kotsuma, T.; Tanaka, E.; Otani, K.; Yoshioka, Y.; Ogawa, K. Comparison of three moderate fractionated schedules employed in high-dose-rate brachytherapy monotherapy for clinically localized prostate cancer. Radiother. Oncol. 2018, 129, 370–376. [Google Scholar] [CrossRef] [PubMed]
- Prada, P.J.; Ferri, M.; Cardenal, J.; Blanco, A.G.; Anchuelo, J.; Díaz de Cerio, I.; Vázquez, A.; Pacheco, M.; Raba, I.; Ruiz, S. High-dose-rate interstitial brachytherapy as monotherapy in one fraction of 20.5 Gy for the treatment of localized prostate cancer: Toxicity and 6-year biochemical results. Brachytherapy 2018, 17, 845–851. [Google Scholar] [CrossRef] [PubMed]
- Hannoun-Levi, J.M.; Chand-Fouche, M.E.; Pace-Loscos, T.; Gautier, M.; Gal, J.; Schiappa, R.; Pujol, N. Single fraction of HDR brachytherapy for prostate cancer: Results of the SiFEPI phase II prospective trial. Clin. Transl. Radiat. Oncol. 2022, 37, 64–70. [Google Scholar] [CrossRef]
- Siddiqui, Z.A.; Gustafson, G.S.; Ye, H.; Martinez, A.A.; Mitchell, B.; Sebastian, E.; Limbacher, A.; Krauss, D.J. Five-Year Outcomes of a Single-Institution Prospective Trial of 19-Gy Single-Fraction High-Dose-Rate Brachytherapy for Low- and Intermediate-Risk Prostate Cancer. Int. J. Radiat. Oncol. Biol. Phys. 2019, 104, 1038–1044. [Google Scholar] [CrossRef]
- Yoshioka, Y.; Suzuki, O.; Isohashi, F.; Seo, Y.; Okubo, H.; Yamaguchi, H.; Oda, M.; Otani, Y.; Sumida, I.; Uemura, M.; et al. High-Dose-Rate Brachytherapy as Monotherapy for Intermediate- and High-Risk Prostate Cancer: Clinical Results for a Median 8-Year Follow-Up. Int. J. Radiat. Oncol. Biol. Phys. 2016, 94, 675–682. [Google Scholar] [CrossRef]
- Rogers, C.L.; Alder, S.C.; Rogers, R.L.; Hopkins, S.A.; Platt, M.L.; Childs, L.C.; Crouch, R.H.; Hansen, R.S.; Hayes, J.K. High dose brachytherapy as monotherapy for intermediate risk prostate cancer. J. Urol. 2012, 187, 109–116. [Google Scholar] [CrossRef]
- Patel, S.; Demanes, D.J.; Ragab, O.; Zhang, M.; Veruttipong, D.; Nguyen, K.; Park, S.J.; Marks, L.; Pantuck, A.; Steinberg, M.; et al. High-dose-rate brachytherapy monotherapy without androgen deprivation therapy for intermediate-risk prostate cancer. Brachytherapy 2017, 16, 299–305. [Google Scholar] [CrossRef]
- Hoskin, P.; Rojas, A.; Ostler, P.; Hughes, R.; Alonzi, R.; Lowe, G. Single-dose high-dose-rate brachytherapy compared to two and three fractions for locally advanced prostate cancer. Radiother. Oncol. 2017, 124, 56–60. [Google Scholar] [CrossRef]
- Salari, K.; Hazy, A.J.; Ye, H.; Sebastian, E.; Limbacher, A.; Johnson, M.; Mitchell, B.; Thompson, A.B.; Seymour, Z.A.; Nandalur, S.R.; et al. 21 Gy single fraction prostate HDR brachytherapy: 5-year results of a single institution prospective pilot study. Brachytherapy 2024, 23, 321–328. [Google Scholar] [CrossRef]
- Hudson, J.M.; Loblaw, A.; McGuffin, M.; Chung, H.T.; Tseng, C.L.; Helou, J.; Cheung, P.; Szumacher, E.; Liu, S.; Zhang, L.; et al. Prostate high dose-rate brachytherapy as monotherapy for low and intermediate-risk prostate cancer: Efficacy results from a randomized phase II clinical trial of one fraction of 19 Gy or two fractions of 13.5 Gy: A 9-year update. Radiother. Oncol. 2024, 198, 110381. [Google Scholar] [CrossRef] [PubMed]
- Fowler, J.F. The linear-quadratic formula and progress in fractionated radiotherapy. Br. J. Radiol. 1989, 62, 679–694. [Google Scholar] [CrossRef] [PubMed]
- Stavrev, P.; Stavreva, N.; Genova, B.; Ruggieri, R.; Alongi, F.; Nahum, A.E.; Pressyanov, D. The Impact of Different Timing Schedules on Prostate HDR-Mono-Brachytherapy. A TCP Modeling Investigation. Cancers 2021, 13, 4899. [Google Scholar] [CrossRef] [PubMed]
- Wakisaka, Y.; Yagi, M.; Sumida, I.; Takashina, M.; Ogawa, K.; Koizumi, M. Impact of time-related factors on biologically accurate radiotherapy treatment planning. Radiat. Oncol. 2018, 13, 30. [Google Scholar] [CrossRef]
- Bentzen, S.M.; Tucker, S.L. Quantifying the position and steepness of radiation dose-response curves. Int. J. Radiat. Biol. 1997, 71, 531–542. [Google Scholar] [CrossRef]
- Huang, H.T.; Brand, D.H.; Fenwick, J.D.; Hawkins, M.A. ImmunoChemoradiation for Non-Small Cell Lung Cancer: A Meta-Analysis of Factors Influencing Survival Benefit in Combination Trials. Int. J. Radiat. Oncol. Biol. Phys. 2024, 120, 409–421. [Google Scholar] [CrossRef]
- Royston, P. Profile Likelihood for Estimation and Confidence Intervals. Stata J. 2007, 7, 376–387. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Nickers, P.; Hermesse, J.; Deneufbourg, J.M.; Vanbelle, S.; Lartigau, E. Which α/β ratio and half-time of repair are useful for predicting outcomes in prostate cancer? Radiother. Oncol. 2010, 97, 462–466. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. (Eds.) Model Selection and Multimodel Inference; Springer: New York, NY, USA, 2004. [Google Scholar] [CrossRef]
- Kuperman, V.Y.; Lubich, L.M. Effect of reoxygenation on hypofractionated radiotherapy of prostate cancer. Med. Phys. 2020, 47, 5383–5391. [Google Scholar] [CrossRef] [PubMed]
- Jeong, J.; Shoghi, K.; Deasy, J. Modelling the interplay between hypoxia and proliferation in radiotherapy tumour response. Phys. Med. Biol. 2013, 58, 4897–4919. [Google Scholar] [CrossRef] [PubMed]
- Zilli, T.; Franzese, C.; Guckenberger, M.; Giaj-Levra, N.; Mach, N.; Koutsouvelis, N.; Achard, V.; Mcdonald, A.; Alongi, F.; Scorsetti, M.; et al. ONE SHOT—Single shot radiotherapy for localized prostate cancer: 18-month results of a single arm, multicenter phase I/II trial. Radiother. Oncol. 2024, 194, 110181. [Google Scholar] [CrossRef] [PubMed]
- Kuperman, V.Y.; Lubich, L.M. Impact of target dose inhomogeneity on BED and EUD in lung SBRT. Phys. Med. Biol. 2021, 66, 01NT02. [Google Scholar] [CrossRef]
| Risk | Model | Parameters | Statistics | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| α/β [Gy] | λ′ [Gy day−1] | [day] | δ [Gy−1] | ϕ | b [h−2] | [h] | [Gy] | γ50 | −log(L) | Δ | |||
| LR | LQ | 100 * | 0 * | - | - | - | - | - | 16.83 | 1.09 | 36.71 | 87.41 | - |
| LQL | 17.6 | 0.63 | 32.49 | 0.2 | - | - | - | 20.13 | 1.16 | 35.98 | 89.97 | −2.56 | |
| 100 * | 0 * | - | - | 0 * | 0 * | - | 16.83 | 1.09 | 36.71 | 96.03 | −8.62 | ||
| 97.6 | 0.24 | 29.18 | - | - | - | 0 * | 17.02 | 1.09 | 36.46 | 90.91 | −3.5 | ||
| 4.6 | 1.17 | 35.06 | 0.24 | - | - | 0.05 | 26.89 | 1.28 | 35.80 | 94.22 | −6.81 | ||
| 93.0 | 1.03 | 37.64 | - | 0.12 | 0.05 | 17.44 | 1.11 | 36.37 | 100.73 | −13.32 | |||
| IR | LQ | 100 * | 0 * | - | - | - | - | - | 15.85 | 0.76 | 43.44 | 100.40 | - |
| LQL | 1 * | 0 * | - | 0.53 | - | - | - | 25.12 | 0.81 | 43.08 | 103.41 | −3.01 | |
| 53.9 | 0.11 | 0.15 | - | 0.58 | - | 18.87 | 0.90 | 43.33 | 108.12 | −7.72 | |||
| 100 * | 0 * | - | - | - | - | 0 * | 15.84 | 0.76 | 43.44 | 104.12 | −3.72 | ||
| 1.3 | 0 * | - | 0.54 | - | - | 0 * | 23.69 | 0.80 | 43.09 | 107.64 | −7.24 | ||
| 100 * | 0 * | - | - | 0 * | 0 * | 0 * | 15.85 | 0.76 | 43.44 | 113.16 | −12.76 | ||
| Risk | Model | Parameters | Statistics | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| α/β [Gy] | λ′ [Gy day−1] | [day] | δ [Gy−1] | ϕ | b [h−2] | [h] | [Gy] | γ50 | −log(L) | Δ | |||
| LR | LQ | 8 * | 1 | 35.02 | - | - | - | - | 44.96 | 2.45 | 41.65 | 97.30 | - |
| LQL | 1 * | 1.33 | 27.00 | 0.31 | - | - | - | 36.71 | 1.34 | 35.63 | 89.25 | 8.05 | |
| 8 * | 1 | 35.02 | - | 0 * | 0 * | - | 44.96 | 2.45 | 41.65 | 105.91 | −8.61 | ||
| 8 * | 0.27 | 28.18 | - | - | - | 1.59 | 46.00 | 2.42 | 41.08 | 100.16 | −2.86 | ||
| 1.9 | 0.44 | 29.11 | 0.38 | - | - | 0.26 | 28.93 | 1.27 | 36.03 | 94.68 | 2.62 | ||
| 8 * | 0.50 | 29.91 | - | 0.05 | 0.05 | 44.61 | 2.35 | 41.67 | 111.34 | −14.04 | |||
| IR | LQ | 8 * | 0 * | - | - | - | - | - | 40.66 | 1.50 | 52.21 | 117.95 | - |
| LQL | 1 * | 0 * | - | 0.53 | - | - | - | 25.15 | 0.81 | 43.08 | 103.41 | 14.54 | |
| 8 * | 0 * | 0.15 | - | 0 * | 0 * | - | 40.67 | 1.50 | 52.21 | 125.89 | −7.94 | ||
| 8 * | 0 * | - | - | - | - | 4.00 | 41.59 | 1.27 | 45.86 | 108.96 | 8.99 | ||
| 1.28 | 1.51 | 47.65 | 0.45 | - | - | 1.47 | 26.65 | 0.82 | 42.89 | 107.25 | 10.7 | ||
| 5.25 | 0.09 | 44.12 | - | 0.11 | 4.23 | 44.00 | 1.34 | 45.52 | 117.32 | 0.63 | |||
| Risk | Model | Parameters | ||||||
|---|---|---|---|---|---|---|---|---|
| α/β [Gy] | λ′ [Gy day−1] | [day] | δ [Gy−1] | [h] | [Gy] | γ50 | ||
| LR | LQ | [6.7, 8 *] | [0 *, 2 *] | [0, 42 *] | - | - | [40.1, 49.5] | [1.76, 3.12] |
| LQL | [1 *, 8 *] | [0 *, 2 *] | [0, 42 *] | [0.07, 1 *] | - | [12.6, 59.6] | [0.77, 2.14] | |
| [6.2, 8 *] | [0 *, 2 *] | [0, 42 *] | - | [0 *, 3.69] | [38.9, 50.8] | [1.43, 3.04] | ||
| IR | LQ | [7.2, 8 *] | [0 *, 2 *] | [0, 42 *] | - | - | [32.8, 45.1] | [0.97, 2.04] |
| LQL | [1 *, 8 *] | [0 *, 2 *] | [0, 42 *] | [0.06, 1 *] | - | [10.4, 49.4] | [0.50, 1.40] | |
| [5.8, 8 *] | [0 *, 2 *] | [0, 42 *] | - | [2.03, 6 *] | [31.6, 51.1] | [0.72, 1.91] | ||
| Strategy 1 (1 Gy ≤ ≤ 100 Gy) | Strategy 2 (1 Gy ≤ ≤ 8 Gy) | |||
|---|---|---|---|---|
| LR - LQ | IR - LQ | LR - LQL | IR - LQL | |
| [Gy] | 90.11 ± 16.70 | 97.29 ± 11.95 | 2.22 ± 1.10 | 1.17 ± 0.80 |
| [Gy ] | 0.20 ± 0.36 | 0.01 ± 0.04 | 0.93 ± 0.55 | 0.01 ± 0.05 |
| [day] | 13.29 ± 15.33 | 0.00 ± 0.00 | 26.69 ± 8.33 | 0.01 ± 0.05 |
| [Gy] | 17.43 ± 1.52 | 16.06 ± 1.01 | 30.49 ± 6.06 | 24.93 ± 3.41 |
| 1.12 ± 0.01 | 0.78 ± 0.05 | 1.29 ± 0.15 | 0.81 ± 0.05 | |
| [] | - | - | 0.36 ± 0.16 | 0.56 ± 0.13 |
| [range] | [−3.53, −2.51] | [−3.58, −1.52] | [4.99, 11.12] | [7.91, 17.31] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kölmel, E.G.; Pombar, M.; Pardo-Montero, J. Radiobiological Meta-Analysis of the Response of Prostate Cancer to High-Dose-Rate Brachytherapy: Investigation of the Reduction in Control for Extreme Hypofractionation. Cancers 2025, 17, 1338. https://doi.org/10.3390/cancers17081338
Kölmel EG, Pombar M, Pardo-Montero J. Radiobiological Meta-Analysis of the Response of Prostate Cancer to High-Dose-Rate Brachytherapy: Investigation of the Reduction in Control for Extreme Hypofractionation. Cancers. 2025; 17(8):1338. https://doi.org/10.3390/cancers17081338
Chicago/Turabian StyleKölmel, Eva G., Miguel Pombar, and Juan Pardo-Montero. 2025. "Radiobiological Meta-Analysis of the Response of Prostate Cancer to High-Dose-Rate Brachytherapy: Investigation of the Reduction in Control for Extreme Hypofractionation" Cancers 17, no. 8: 1338. https://doi.org/10.3390/cancers17081338
APA StyleKölmel, E. G., Pombar, M., & Pardo-Montero, J. (2025). Radiobiological Meta-Analysis of the Response of Prostate Cancer to High-Dose-Rate Brachytherapy: Investigation of the Reduction in Control for Extreme Hypofractionation. Cancers, 17(8), 1338. https://doi.org/10.3390/cancers17081338







