Optimal Design of a Synchronous Reluctance Motor Using a Genetic Topology Algorithm
Abstract
:1. Introduction
2. Design Method
2.1. Preprocess
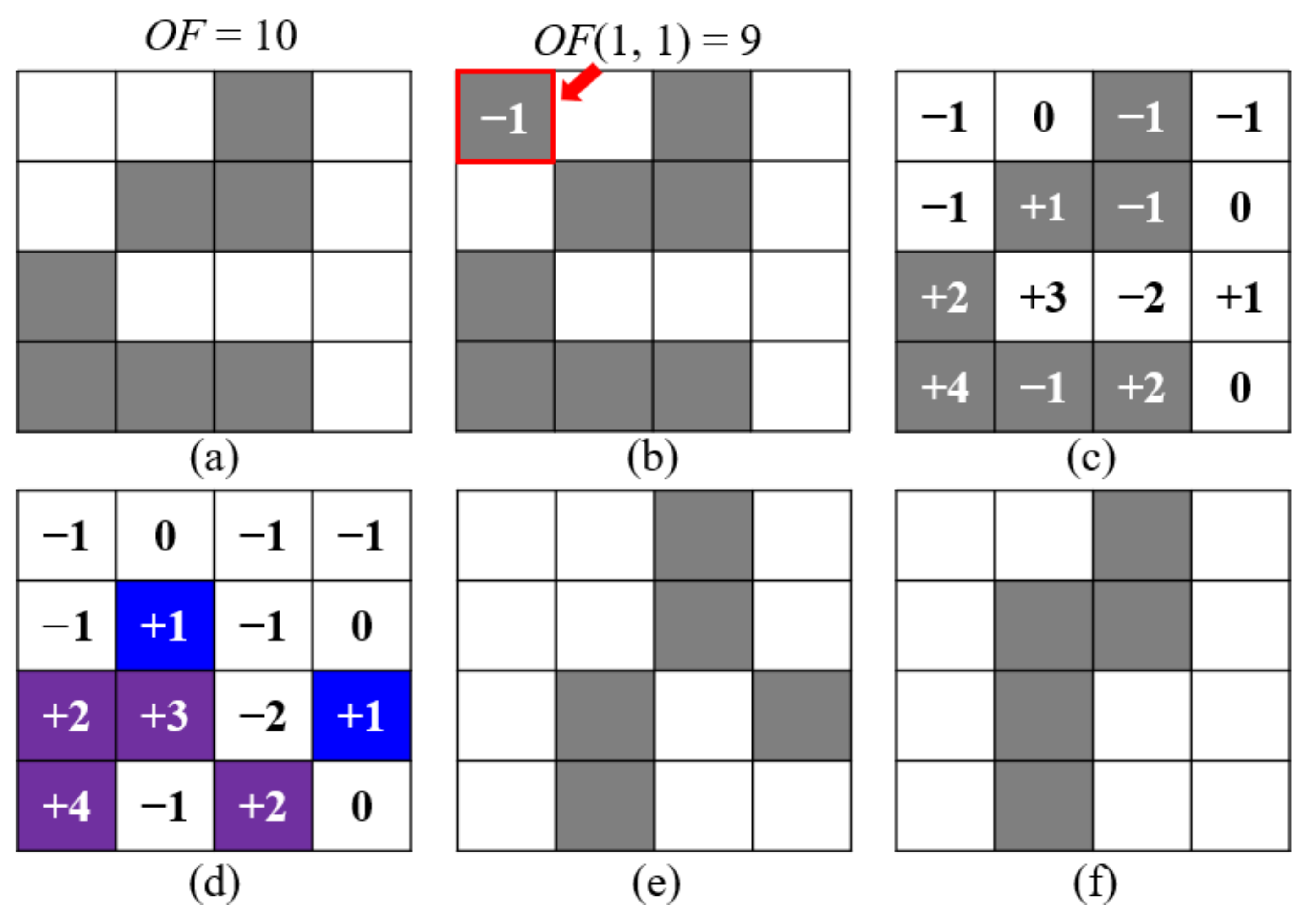
2.2. Genetic Algorithm
2.3. ON-OFF Method
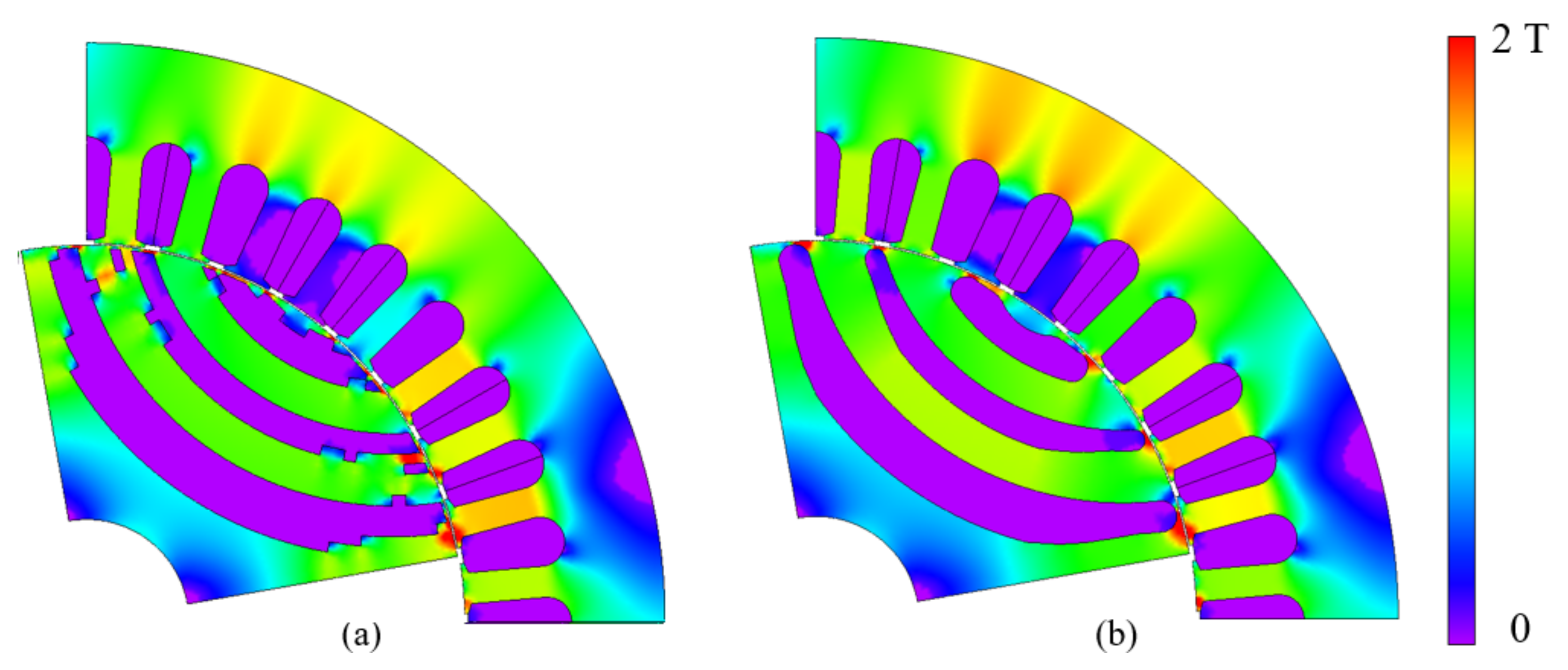
3. Postprocess
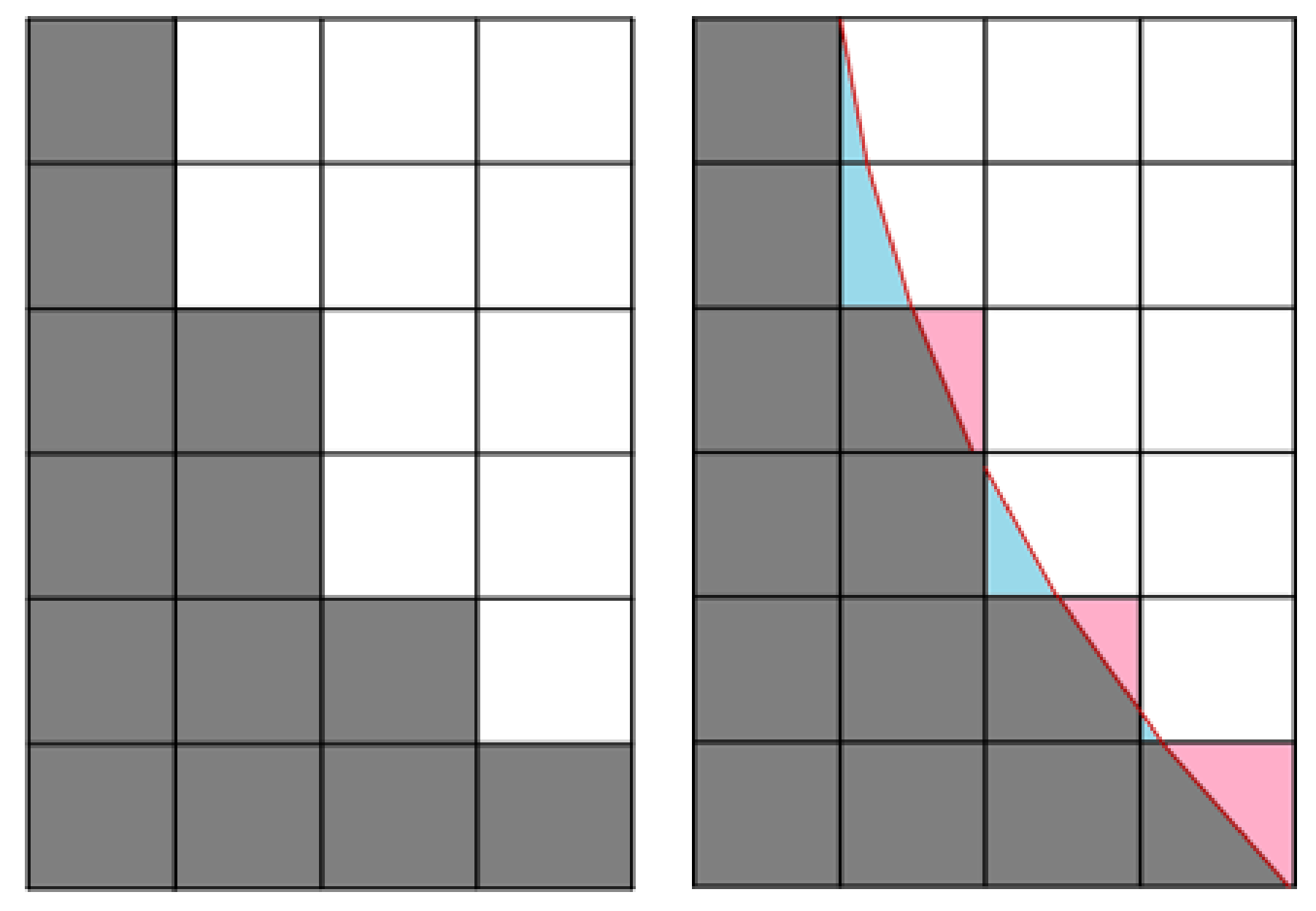
3.1. Smoothing
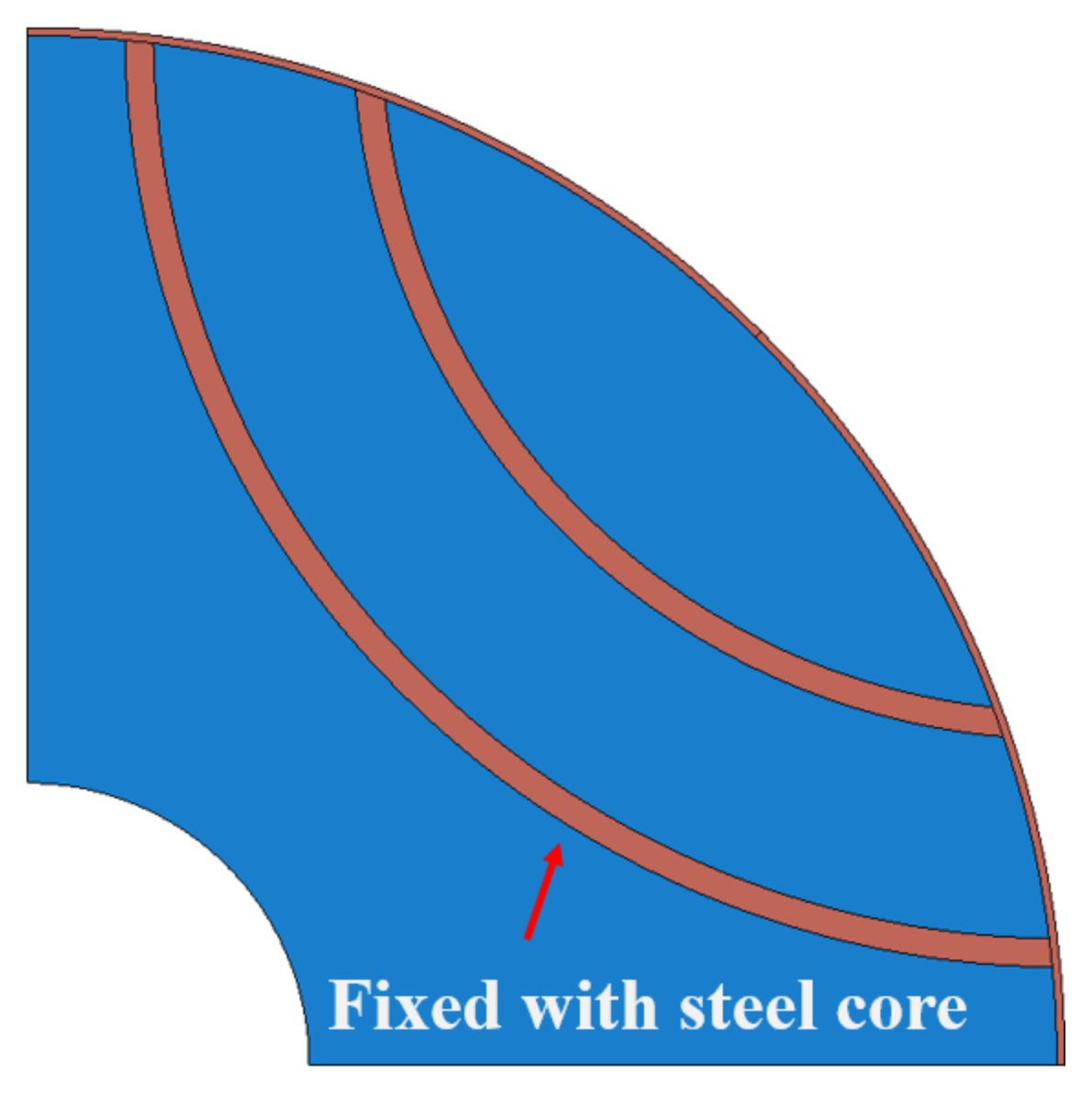
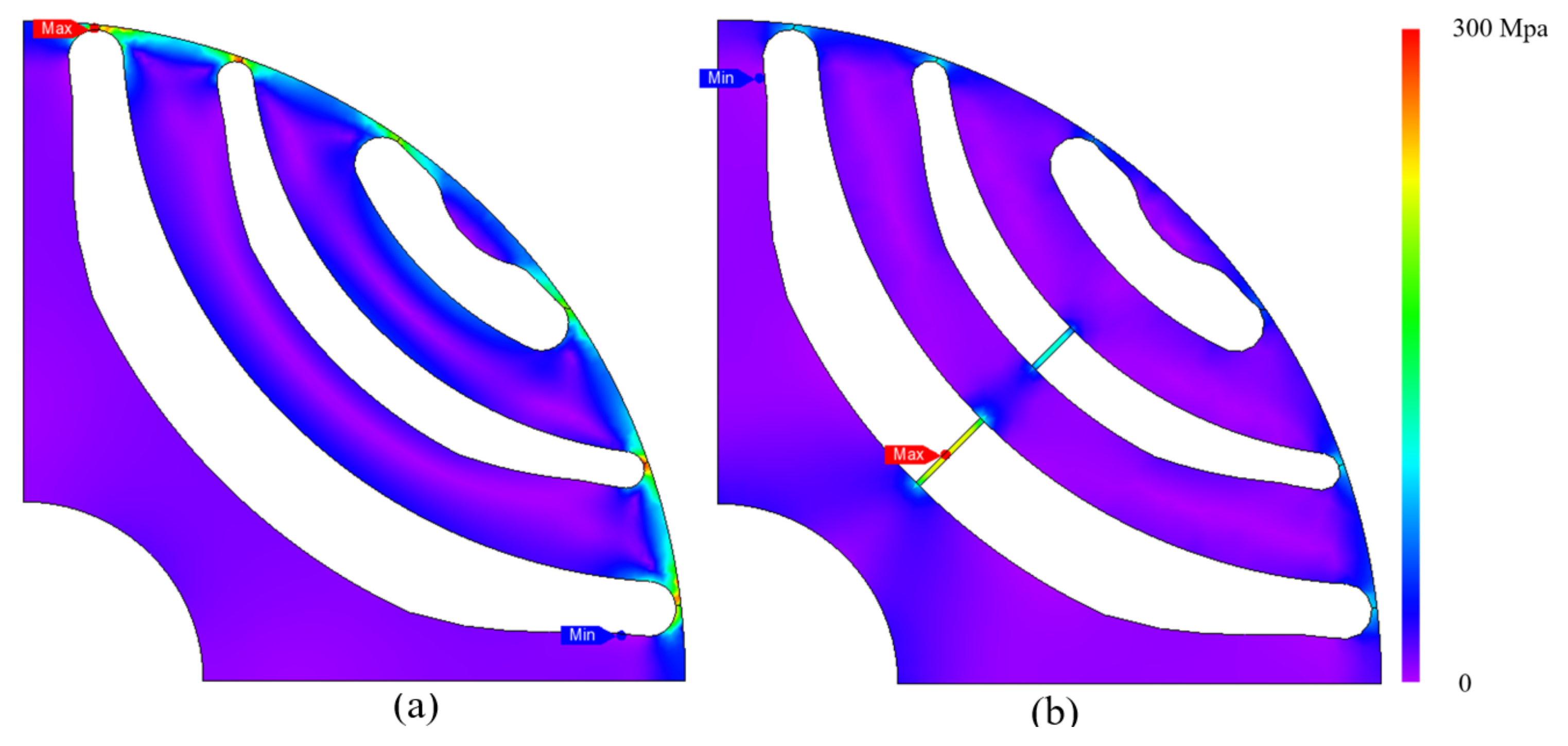
3.2. Stress Analysis
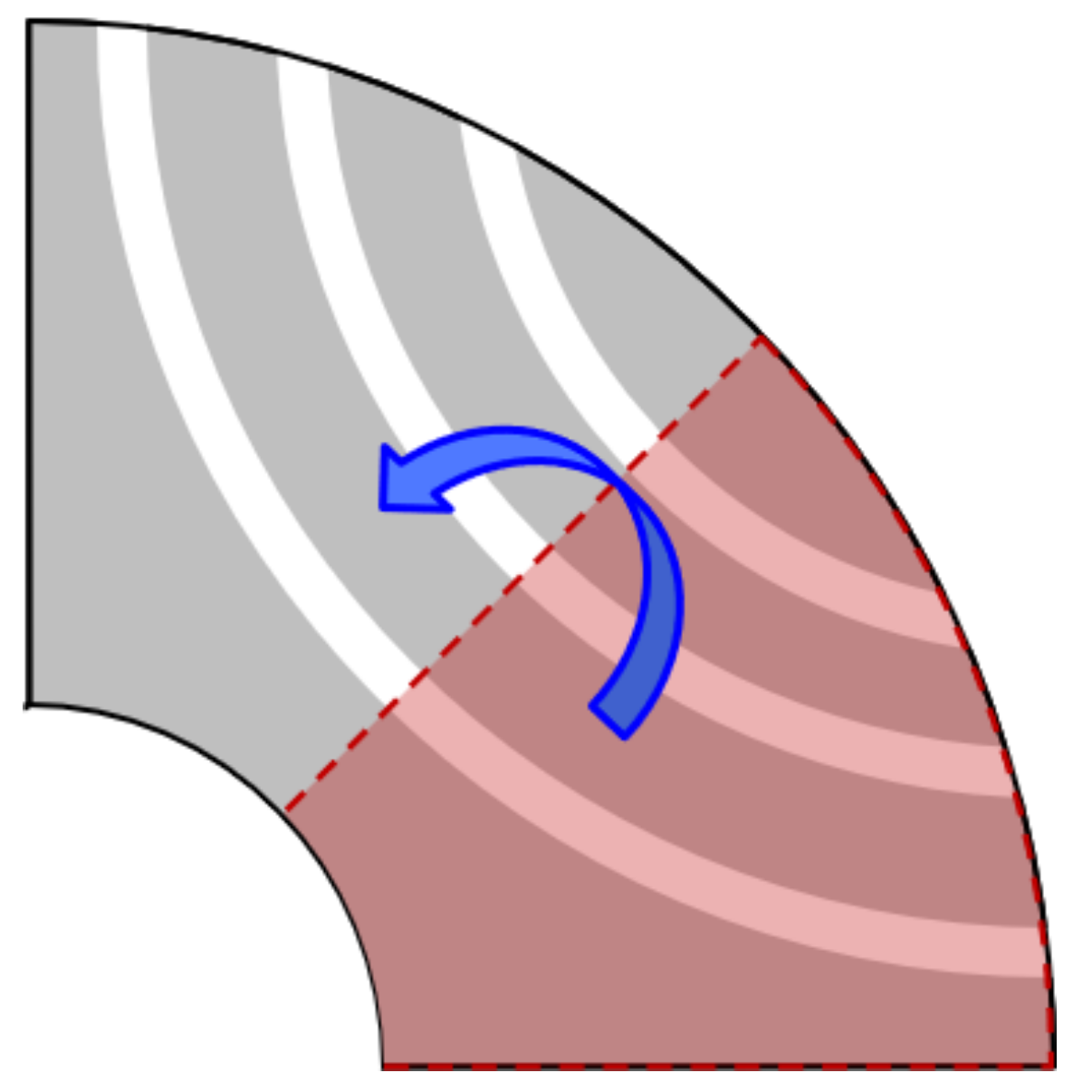
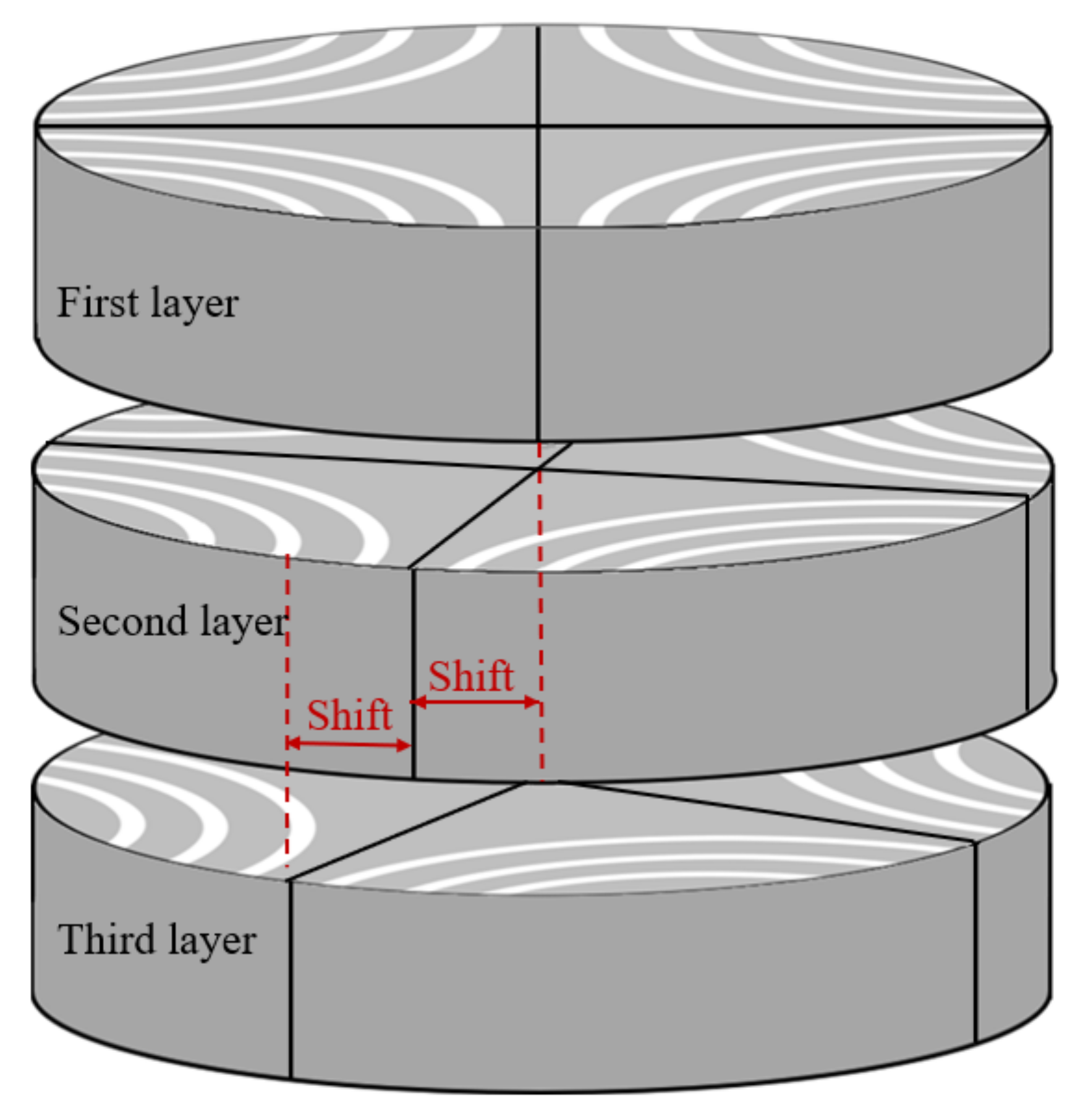
3.3. Skew
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- De Martin, M.; Luise, F.; Pieri, S.; Tessarolo, A.; Poloni, C. Numerical multi-objective optimization of a squirrel cage induction motor for industrial application. In Proceedings of the 2015 International Aegean Conference on Electrical Machines & Power Electronics (ACEMP), Side, Turkey, 2–4 September 2015. [Google Scholar]
- Li, H.; Curiac, R.S. Designing More Efficient Large Industrial Induction Motors by Utilizing the Advantages of Adjustable-Speed Drives. IEEE Trans. Ind. Appl. 2010, 46, 1805–1809. [Google Scholar] [CrossRef]
- Staton, D.; Boglietti, A.; Cavagnino, A. Solving the More Difficult Aspects of Electric Motor Thermal Analysis in Small and Medium Size Industrial Induction Motors. IEEE Trans. Energy Convers. 2005, 20, 3. [Google Scholar] [CrossRef] [Green Version]
- Jeong, S.-W. Optimal Design of IE4 Super Premium Efficiency Synchronous Reluctance Motor for Industrial Application. Master’s Thesis, Department Electrical and Information Engineering, Seoul University, Seoul, Korea, 2020. [Google Scholar]
- Park, J.H.; Seo, J.H.; Cha, C.-H.; Lee, J. Characteristics Analysis of 15kW Industrial Machine using Synchronous Reluctance Motor for High Efficiency. In Proceedings of the 2013 International Conference on Electrical Machines and Systems (ICEMS), Piscataway, NJ, USA, 26–29 October 2013. [Google Scholar]
- Weigel, T. Control of Synchronous Reluctance Motors without Encoder for Industrial Applications. In Proceedings of the 2016 6th International Electric Drives Production Conference, Nuremberg, Germany, 30 November–1 December 2016. [Google Scholar]
- ABB. High Output Synchronous Reluctance Motor and Drive Package. Optimized Cost of Ownership for Pump and Fan Applications; ABB: Zurich, Switzerland, 2013. [Google Scholar]
- Lopez, C.; Michalski, T.; Espinosa, A.; Romeral, L. Rotor of Synchronous Reluctance Motor Optimization by Means Reluctance Network and Genetic Algorithm. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Laussane, Switzerland, 4–7 September 2016. [Google Scholar]
- Cupertino, F.; Pellegrino, G.; Gerada, C. Design of Synchronous Reluctance Motors with Multi-objective Optimization Algorithms. IEEE Trans. Ind. Appl. 2014, 50, 6. [Google Scholar] [CrossRef] [Green Version]
- Kang, Y.-R.; Son, J.-C.; Lim, D.-K. Optimal Design of IPMSM for Fuel Cell Electric Vehicles Using Autotuning Elliptical Niching Genetic Algorithm. IEEE Access 2020, 8, 117405–117412. [Google Scholar] [CrossRef]
- Lee, T.H.; Kang, Y.R.; Son, J.C.; Lim, D.K. Optimized Design of Permanent Magnet Assisted Synchronous Reluctance Motor Using Oriented Auto-tuning Niching Algorithm. J. Electr. Eng. Technol 2021, 16, 1495–1503. [Google Scholar] [CrossRef]
- Okamoto, Y.; Hoshino, R.; Wakao, S.; Tsuburaya, T. Improvement of Torque Characteristics for a Synchronous Reluctance Motor Using MMA-based Topology Optimization Method. IEEE Trans. Magn. 2017, 54, 1–4. [Google Scholar] [CrossRef]
- Otomo, Y.; Igarashi, H. Topology Optimization Using Gabor Filter: Application to Synchronous Reluctance Motor. IEEE Trans. Magn. 2021, 57, 6. [Google Scholar] [CrossRef]
- Sato, S.; Sato, T.; Igarashi, H. Topology Optimization of Synchronous Reluctance Motor Using Normalized Gaussian Network. IEEE Trans. Magn. 2015, 51, 3. [Google Scholar] [CrossRef] [Green Version]
- Hidaka, Y.; Igarashi, H. Topology Optimization of Synchronous Reluctance Motors Considering Localized Magnetic Degradation Caused by Punching. IEEE Trans. Magn. 2017, 53, 6. [Google Scholar] [CrossRef]
- Lipo, T.A.; Miller, T.J.; Vagati, A.; Boldea, I.; Malesani, L.; Fukao, T. Synchronous Reluctance Drives. In Proceedings of the IEEE IAS Annual Meeting, Denver, CO, USA, 2–6 October 1994. [Google Scholar]
- Vagati, A. The Synchronous Reluctance Solution: A New Alternative in AC Drives, 1994. In Proceedings of the 20th International Conference of IEEE Industrial Electronics, Bologna, Italy, 5–9 September 1994; Volume 1, pp. 1–13. [Google Scholar]
- Bianchi, N.; Bolognani, S.; Carraro, E.; Castiello, M.; Fornasiero, E. Electric Vehicle Traction Based on Synchronous Reluctance Motors. IEEE Trans. Ind. Appl. 2016, 52, 4762–4769. [Google Scholar] [CrossRef]
- Diao, X.; Zhu, H.; Qin, Y.; Hua, Y. Torque Ripple Minimization for Bearingless Synchronous Reluctance Motor. IEEE Trans. Appl. Supercond. 2018, 28, 3. [Google Scholar] [CrossRef]
- Ding, H.; Zhu, H.; Hua, Y. Optimization Design of Bearingless Synchronous Reluctance Motor. IEEE Trans. Appl. Supercond. 2018, 28, 1–5. [Google Scholar] [CrossRef]
- Ishikawa, T.; Nakayama, K.; Kurita, N.; Dawson, F.P. Optimization of Rotor Topology in PM Synchronous Motors by Genetic Algorithm Considering Cluster of Materials and Cleaning Procedure. IEEE Trans. Magn. 2014, 50, 2. [Google Scholar] [CrossRef]
- Dilettoso, E.; Salerno, N. A Self-Adaptive Niching Genetic Algorithm for Multimodal Optimization of Electromagnetic Devices. IEEE Trans. Magn. 2006, 42, 2006. [Google Scholar] [CrossRef]
- Maruyama, T.; Igarashi, H. An Effective Robust Optimization Based on Genetic Algorithm. IEEE Trans. Magn. 2008, 44, 990–993. [Google Scholar] [CrossRef] [Green Version]
- Cohoon, J.P.; Paris, W. Genetic Placement. In Proceedings of the IEEE International Conference on Computer-Aided Design, Port Chester, NY, USA, 7 October 1985; pp. 422–425. [Google Scholar]
- Im, C.H.; Jung, H.-K.; Kim, Y.J. Hybrid Genetic Algorithm for Electromagnetic Topology Optimization. IEEE Trans. Magn. 2003, 39, 5. [Google Scholar]
- Ocak, O.; Aydin, M. An Innovative Semi-FEA Based, Variable Magnet-Step-Skew to Minimize Cogging Torque and Torque Pulsations in Permanent Magnet Synchronous Motors. IEEE Access 2020, 8, 210775–210783. [Google Scholar] [CrossRef]








| Requirement | Value |
|---|---|
| Rated power (kW) | 15 |
| Rated torque (Nm) | 80 |
| Rated/maximum speed (RPM) | 1800/5400 |
| Lowest efficiency limit (%) Safety factor | 94.1 1.2 |
| Parameter | Value |
|---|---|
| Number of poles | 4 |
| Number of slots | 36 |
| Stator outer/inner diameter (mm) | 260/170 |
| Rotor outer/inner diameter (mm) | 169.2/46 |
| Air gap (mm) | 0.8 |
| Stacking length (mm) | 205 |
| Coil occupancy rate (%) | 0.47 |
| Material of core | 50JN290 |
| Step | Tave (Nm) | Tripple (%) |
|---|---|---|
| 0(GA) | 61.19 | 94.93 |
| 1 | 81.98 | 102.5 |
| 2 | 85.27 | 33.76 |
| 3 | 85.82 | 35.86 |
| 4 | 88.87 | 22.59 |
| Model | Tave (Nm) | Tripple (%) | Ploss (W) | Efficiency (%) |
|---|---|---|---|---|
| Sample | 86.71 | 116.54 | 598.3 | 96.47 |
| GA | 61.19 | 94.93 | 593.5 | 95.11 |
| ON-OFF | 88.87 | 22.59 | 611.5 | 96.48 |
| Smoothing | 88.97 | 20.58 | 607.7 | 96.50 |
| Center post | 87.87 | 22.13 | 606.8 | 96.47 |
| Skew | 81.45 | 11.01 | 601.8 | 96.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, T.-H.; Lee, J.-H.; Yi, K.-P.; Lim, D.-K. Optimal Design of a Synchronous Reluctance Motor Using a Genetic Topology Algorithm. Processes 2021, 9, 1778. https://doi.org/10.3390/pr9101778
Lee T-H, Lee J-H, Yi K-P, Lim D-K. Optimal Design of a Synchronous Reluctance Motor Using a Genetic Topology Algorithm. Processes. 2021; 9(10):1778. https://doi.org/10.3390/pr9101778
Chicago/Turabian StyleLee, Tae-Hee, Jin-Hwan Lee, Kyung-Pyo Yi, and Dong-Kuk Lim. 2021. "Optimal Design of a Synchronous Reluctance Motor Using a Genetic Topology Algorithm" Processes 9, no. 10: 1778. https://doi.org/10.3390/pr9101778





