The Uncertainty Principle and the Minimal Space–Time Length Element
Abstract
1. Introduction, General Relativity, Quantum Mechanics and the Problem of a Minimal Length
2. The Uncertainty Principle
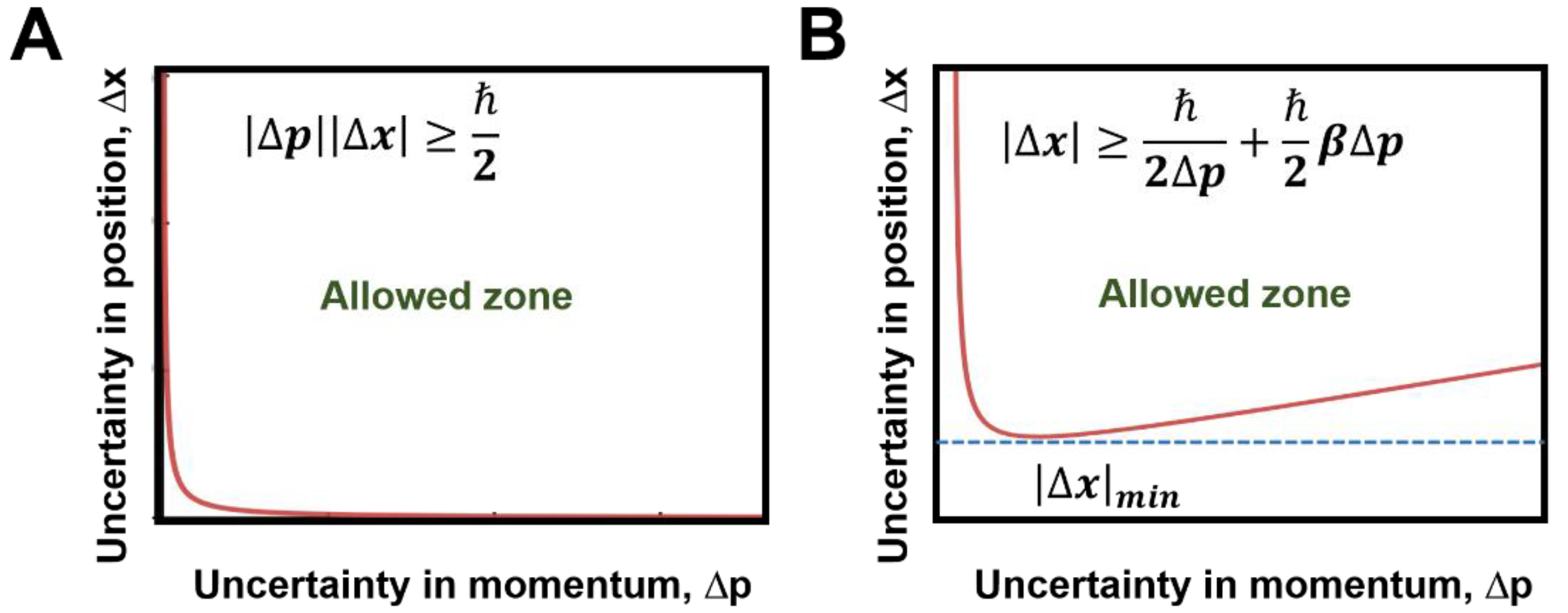
3. Generalized Uncertainty Principle (GUP) and Its Modifications
4. Relativistic Formulations of GUP
5. Covariant Reformulation of the Classical Uncertainty Principle
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aharony, O.; Gubser, S.S.; Maldacena, J.; Ooguri, H.; Oz, Y. Large N field theories, string theory and gravity. Phys. Rep. 2000, 323, 183–386. [Google Scholar] [CrossRef]
- Moreno Casares, P.A. A review on Loop Quantum Gravity. arXiv 2018, arXiv:1808.01252. [Google Scholar] [CrossRef]
- Einstein, A. Grundlage der allgemeinen Relativitätstheorie. Ann. der Phys. 1916, 354, 769–822. [Google Scholar] [CrossRef]
- Einstein, A. The foundations of the general theory of relativity In The Collected Papers of Albert Einstein, Volume 6: The Berlin Years: Writings, 1914–1917. (English Translation Supplement); Klein, M.J., Kox, A.J., Schulman, R., Eds.; Princeton University Pres: Princeton, NJ, USA, 1997; pp. 160–200. Available online: https://einsteinpapers.press.princeton.edu/vol6-trans/158 (accessed on 20 September 2022).
- Ashtekar, A.; Lewandoski, J. Background Independent Quantum Gravity: A Status Report. Class. Quant. Grav. 2004, 21, R53–R152. [Google Scholar] [CrossRef]
- Carcassi, G.; Maccone, L.; Aidala, C.A. The four postulates of quantum mechanics are three. Phys. Rev. Lett. 2021, 126, 110402. [Google Scholar] [CrossRef] [PubMed]
- Nottale, L.; Celerier, M.N. Derivation of the postulates of quantum mechanics from the first principles of scale relativity. J. Phys. A 2007, 40, 14471–14498. [Google Scholar] [CrossRef]
- Connes, A.; Kreimer, D. Renormalization in quantum field theory and the Riemann-Hilbert problem I: The Hopf algebra structure of graphs and the main theorem. Commun. Math. Phys. 2000, 210, 249–273. [Google Scholar] [CrossRef]
- Hossenfelder, S. Minimal length scale scenarios for quantum gravity. Living Rev. Rel. 2013, 16, 2. [Google Scholar] [CrossRef] [PubMed]
- Heisenberg, W. Über die in der Theorie der Elementarteilchen auftretende universelle Länge. Ann. Phys. 1938, 32, 20–33. [Google Scholar] [CrossRef]
- Snyder, H.S. Quantized space-time. Phys. Rev. 1947, 71, 38–41. [Google Scholar] [CrossRef]
- Peres, A.; Rosen, N. Quantum limitations on the measurement of gravitational fields. Phys. Rev. 1960, 118, 335–336. [Google Scholar] [CrossRef]
- Bronstein, M. Republication of: Quantum theory of weak graviational fields. Gen. Relativ. Gravit. 2012, 44, 267–283. [Google Scholar] [CrossRef]
- Alden Mead, C. Possible connection between gravitation and fundamental length. Phys. Rev. 1964, 135, B849–B862. [Google Scholar] [CrossRef]
- Gross, D.J.; Mende, P.F. String theory beyond the Planck scale. Nucl. Phys. B. 1988, 303, 407–454. [Google Scholar] [CrossRef]
- Amati, D.; Ciafaloni, M.; Veneziano, G. Superstring collisions at the Planckian energies. Phys. Lett. B 1987, 198, 81–88. [Google Scholar] [CrossRef]
- Amati, D.; Ciafaloni, M.; Veneziano, G. Classical and quantum gravity effects from Planckian energy superstring collisions. Int. J. Mod. Phys. A 1988, 3, 1615–1661. [Google Scholar] [CrossRef]
- Majid, S.; Ruegg, H. Bicrossproduct structure of k-Poincare group and non-commutative geometry. Phys. Lett. B 1994, 334, 348–354. [Google Scholar] [CrossRef]
- Kempf, A.; Mangano, G.; Mann, R.B. Hilbert space representation of the minimal length uncertainty relation. Phys. Rev. D 1995, 52, 1108. [Google Scholar] [CrossRef]
- Kempf, A. Uncertainty relation in quantum mechanics with quantum group symmetry. J. Math. Phys. 1993, 35, 4483–4496. [Google Scholar] [CrossRef]
- Kempf, A. Quantum groups and quantum field theory with nonzero minimal uncertainties in positions and momenta. Czech. J. Phys. 1994, 44, 1041–1048. [Google Scholar] [CrossRef]
- Heisenberg, W. Über den anschaulichen inhalt der quantentheoretischen Kinematik und Mechanik. Z. Physik 1927, 43, 172–198. [Google Scholar] [CrossRef]
- Kennard, E.H. Zur Quantenmechanik einfacher Bewegungstypen. Z. Phys. 1927, 44, 326–352. [Google Scholar] [CrossRef]
- Mandelshtam, L.I.; Tamm, I.E. The uncertainty relation between energy and time in nonrelativistic quantum mechanics. J.Phys. (USSR) 1945, 9, 249–254, Reprinted in Tamm, I.E. Selected Papers; Bolotovskii, B.M., Frenkel, V.Y., Peierls, R., Eds.; Springer: Berlin/Heidelberg, Germany, 1991; pp. 115–123.. [Google Scholar] [CrossRef]
- Das, S.; Vanegas, E.C. Phenomenological implications of the generalized uncertainty principle. Can. J. Phys. 2009, 87, 233–240. [Google Scholar] [CrossRef]
- Gine, J. Hawking effect and Unruh effect from the uncertainty principle. EPL (Europhys. Lett.) 2018, 121, 10001. [Google Scholar] [CrossRef]
- Ozawa, M. Heisenberg’s original derivation of the uncertainty principle and its universally valid reformulations. Curr. Sci. 2015, 109, 2006–2016. [Google Scholar] [CrossRef]
- Sassoli de Bianchi, M. The observer effect. Found. Sci. 2013, 18, 213–242. [Google Scholar] [CrossRef]
- Werner, R.F.; Farrely, T. Uncertainty from Heisenberg to today. Found. Phys. 2019, 49, 460–491. [Google Scholar] [CrossRef]
- Riggs, P.J. What is the uncertainty principle of non-relativistic quantum mechanics? Eur. J. Phys. 2018, 39, 035409. [Google Scholar] [CrossRef]
- Susskind, L.; Uglum, J. String physics and black holes. Nucl. Phys. B. Proc. Suppl. 1996, 45, 115–134. [Google Scholar] [CrossRef]
- Rovelli, C. Loop Quantum Gravity. Living Rev. Rel. 2008, 11, 5. [Google Scholar] [CrossRef] [PubMed]
- Helesfai, G.; Bene, G. A numerical study of spectral properties of the area operator y loop quatum gravity. arXiv 2003, arXiv:gr-qc/0306124. [Google Scholar] [CrossRef]
- Ashtekar, A.; Lewandoski, J. Quantum theory of geometry. I: Area operators. Class. Quant. Grav. 1997, 14, A55–A82. [Google Scholar] [CrossRef]
- Brunnemann, J.; Rideout, D. Properties of the volume operators in loop quantum gravity I: Results. Class. Quant. Grav. 2008, 25, 065001. [Google Scholar] [CrossRef]
- Magueijo, J.; Smolin, L. String theories with deformed energy momentum relations, and a possible non-tachyonic bosonic string. Phys. Rev. D 2005, 71, 026010. [Google Scholar] [CrossRef]
- Arnowitt, R.; Deser, S.; Misner, C. Dynamical structure and definition of energy in general relativity. Phys. Rev. 1959, 116, 1322–1330. [Google Scholar] [CrossRef]
- Capozziello, S.; Lambiase, G.; Scarpetta, G. Generalized uncertainty principle from quantum geometry. Int. J. Theor. Phys. 2000, 39, 15–22. [Google Scholar] [CrossRef]
- Garay, L.J. Quantum gravity and minimum length. Int. J. Mod. Phys. 1995, 10, 145–166. [Google Scholar] [CrossRef]
- Amelino-Camelia, G. Doubly-special relativity: Facts, myths and some key open issues. Symmetry 2010, 2, 230. [Google Scholar] [CrossRef]
- Guida, R.; Konishi, K. On the short distance behaviour of string theories. Mod. Phys. Lett. 1991, 6, 1487–1503. [Google Scholar] [CrossRef]
- Konishi, K.; Paffuti, G.; Provero, P. Minimum physical length and the generalized uncertainty principle in string theory. Phys. Lett. B 1990, 234, 276–284. [Google Scholar] [CrossRef]
- Yonega, T. On the interpretation of minimal length in string theories. Mod. Phys. Lett. A 1989, 4, 1587–1595. [Google Scholar] [CrossRef]
- Amati, D.; Ciafaloni, M.; Veneziano, G. Can spacetime be probed below the string size? Phys. Lett. B 1989, 216, 41–47. [Google Scholar] [CrossRef]
- Maggiore, M. The algebraic structure of the generalized uncertainty principle. Phys. Lett. B 1993, 319, 83–86. [Google Scholar] [CrossRef]
- Veneziano, G. A stringy nature needs just two constants. Europhys. Lett. 1986, 2, 199–204. [Google Scholar] [CrossRef]
- Dzhunushaliev, V.; Folomeev, V.; Kleihaus, B.; Kunz, J. Modified gravity from the quantum part of the metric. Eur. Phys. J. C 2014, 74, 1–4. [Google Scholar] [CrossRef]
- Lorentz, H.A. Electromagnetic phenomena in a system moving with any velocity smaller than that of light. Proc. Royal Acad. Amsterdam. 1904, 6, 809–831, Reprinted in Lorentz, H.A. Collected Papers. Volume 5; Zeeman, P., Fokker, A., Eds.; Springer Science+Business Media: Dordrecht, The Netherlands, 1937; pp. 172–197.. [Google Scholar]
- Einstein, A. Zur Elektrodynamik bewegter Körper. Ann. Phys. 1905, 322, 891–921. [Google Scholar] [CrossRef]
- Einstein, A. On the electrodynamics of moving bodies. In The Collected Papers of Albert Einstein, Volume 2: The Swiss Years: Writings, 1900-1909 (English Translation Supplement); Renn, J., Schulmann, R., Eds.; Princeton University Press: Princeton, NJ, USA, 1990; pp. 275–310. Available online: https://einsteinpapers.press.princeton.edu/vol2-doc/311 (accessed on 20 September 2022).
- Dzierzak, P.; Jezierski, J.; Malkiewicz, P.; Piechocki, W. The minimum length problem of loop quantum cosmology. Acta Phys. Polon. B 2010, 41, 717–726. Available online: https://www.actaphys.uj.edu.pl/R/41/3 (accessed on 20 September 2022).
- Todorinov, V.; Bosso, P.; Das, S. Relativistic generalized uncertainty principle. Ann. Phys. 2019, 405, 92–100. [Google Scholar] [CrossRef]
- Kempf, A. Non-pointlike particles in harmonic oscillators. J. Phys. A Math. Gen. 1997, 30, 2093–2102. [Google Scholar] [CrossRef]
- Quesne, C.; Tkachuk, V.M. Lorentz-covariant deformed algebra with minimal length. Czech. J. Phys. 2006, 56, 1269–1274. [Google Scholar] [CrossRef]
- Moshinsky, M.; Szczepaniak, A. The Dirac oscillator. J. Phys. A Math. Gen. 1989, 22, L817–L819. [Google Scholar] [CrossRef]
- Singh, R.; Kothawala, D. Covariant formulation of Generalised Uncertainty Principle. Phys. Rev. D 2022, 105, L101501. [Google Scholar] [CrossRef]
- Bacry, H.; Levy-Leblond, J.M. Possible kinematics. J. Math. Phys. 1968, 9, 1605–1614. [Google Scholar] [CrossRef]
- Aldrovandi, R.; Pereira, J.G. De Sitter Relativity: A new road to quantum gravity? Found. Phys. 2009, 39, 1–19. [Google Scholar] [CrossRef]
- Aldrovandi, R.; Beltran Almeida, J.P.; Pereira, J.G. de Sitter special relativity. Class. Quant. Grav. 2007, 24, 1385–1404. [Google Scholar] [CrossRef]
- Licata, I.; Chiatti, L. Archaic universe and cosmological model:”big-bang” as nucleation by vacuum. Int. J. Theor. Phys. 2010, 49, 2379–2402. [Google Scholar] [CrossRef]
- Escors, D.; Kochan, G. Constraints on general relativity geodesics by a covariant geometric uncertainty principle. Physics 2021, 3, 790–798. [Google Scholar] [CrossRef]
- Escors, D.; Kochan, G. Covariant space-time line elements in the Friedmann-Lemaitre-Robertson-Walker geometry. Axioms 2022, 11, 310. [Google Scholar] [CrossRef]
- Lachieze-Rey, M.; Luminet, J.P. Cosmic tolopogy. Phys. Rep. 1995, 254, 135–214. [Google Scholar] [CrossRef]
- Mueller, T.; Grave, F. Catalogue of spacetimes. arXiv 2010, arXiv:0904.4184. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. [Planck Collaboration] Planck 2018 results: VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Schwarzschild, K. Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie. Sitzungsber. Preuss. Akad. Wiss. Berl. Math. Phys. 1916, 1916, 189–196. Available online: https://www.jp-petit.org/Schwarzschild-1916-exterior-de.pdf (accessed on 20 September 2022).
- Schwarzschild, K. “Golden Oldie”: On the gravitational field of a mass point according to Einstein’s theory. Gen. Relat. Gravit. 2003, 35, 951–959. [Google Scholar] [CrossRef]
- Teukolsky, S.A. The Kerr metric. Class. Quantum Grav. 2015, 32, 124006. [Google Scholar] [CrossRef]
- Townsend, P.K. Black holes. arXiv 1997, arXiv:gr-qc/9707012. [Google Scholar] [CrossRef]
- Dai, X. The black hole paradoxes and possible solutions. J. Phys. Conf. Ser. 2020, 1634, 012088. [Google Scholar] [CrossRef]
- Mathur, S.D. The Fuzzball proposal for black holes: An elementary review. Fortsch. Phys. 2005, 53, 793–827. [Google Scholar] [CrossRef]
- Rovelli, C.; Vidotto, F. Planck stars. Int. J. Mod. Phys. D 2014, 23, 1442026. [Google Scholar] [CrossRef]
- Rovelli, C.; Wilson-Ewing, E. Why are the effective equations of loop quantum cosmology so accurate? Phys. Rev. D 2014, 90, 023538. [Google Scholar] [CrossRef]
- Burderi, L.; Sanna, A.; Di Salvo, T.; Amati, L.; Amelino-Camelia, G.; Branchesi, M.; Capozziello, S.; Coccia, E.; Colpi, M.; Costa, E.; et al. GrailQuest: Hunting for atoms of space and time hidden in the wrinkle of space-time. arXiv 2020, arXiv:1911.02154. [Google Scholar] [CrossRef]
- Ellis, J.; Konoplich, R.; Mavromatos, N.E.; Nguyen, L.; Sakharov, A.S.; Sarkisyan-Grinbaum, E.K. Robust constraint on Lorentz violation using Fermi-LAT gamma-ray burst data. Phys. Rev. D 2019, 99, 083009. [Google Scholar] [CrossRef]
- Wei, J.J.; Wu, X.F. A Further Test of Lorentz violation from the rest-frame spectral Lags of gamma-ray bursts. Astrophys. J. 2017, 851, 127. [Google Scholar] [CrossRef]
- Laurent, P.; Götz, D.; Binétruy, P.; Covino, S.; Fernandez-Soto, A. Constraints on Lorentz Invariance Violation using INTEGRAL/IBIS observations of GRB041219A. Phys. Rev. D 2011, 83, 121301. [Google Scholar] [CrossRef]
- Maccione, L.; Liberati, S.; Celotti, A.; Krik, J.G.; Ubertini, P. Gamma-ray polarization constraints on Planck scale violations of special relativity. Phys. Rev. D 2008, 78, 103003. [Google Scholar] [CrossRef]
- Jacobson, T.; Liberati, S.; Mattingly, D. Lorentz violation at high energy: Concepts, phenomena and astrophysical constraints. Annals Phys. 2006, 321, 150–196. [Google Scholar] [CrossRef]
- Anderson, E. The problem of time in quantum gravity. Ann. d. Physik 2012, 524, 757–786. [Google Scholar] [CrossRef]
- Vucetich, H. Testing Loretnz invariance violation in quantum gravity theories. arXiv 2005, arXiv:gr-qc/0502093. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; D´Amico, N.; Rosati, G.; Loret, N. In-vacuo-dispersion features for GRB neutrinos and photons. Nat. Astron. 2017, 1, 0139. [Google Scholar] [CrossRef]
- Xu, H.; Ma, B.-Q. Light speed variation from gamma-ray bursts. Astropart. Phys. 2016, 82, 72–76. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Escors, D.; Kochan, G. The Uncertainty Principle and the Minimal Space–Time Length Element. Physics 2022, 4, 1230-1240. https://doi.org/10.3390/physics4040079
Escors D, Kochan G. The Uncertainty Principle and the Minimal Space–Time Length Element. Physics. 2022; 4(4):1230-1240. https://doi.org/10.3390/physics4040079
Chicago/Turabian StyleEscors, David, and Grazyna Kochan. 2022. "The Uncertainty Principle and the Minimal Space–Time Length Element" Physics 4, no. 4: 1230-1240. https://doi.org/10.3390/physics4040079
APA StyleEscors, D., & Kochan, G. (2022). The Uncertainty Principle and the Minimal Space–Time Length Element. Physics, 4(4), 1230-1240. https://doi.org/10.3390/physics4040079




