1. Introduction
The Hamilton–Jacobi equation is an alternative formulation of classical mechanics, equivalent to other formulations, such as Lagrangian and Hamiltonian mechanics [
1,
2]. The Hamilton–Jacobi equation is particularly useful in identifying conserved quantities for mechanical systems, which may be possible even when the mechanical problem itself cannot be solved completely.
The Hamilton–Jacobi equation has been extensively studied in the case of symplectic Hamiltonian systems, more specifically, for Hamiltonian functions
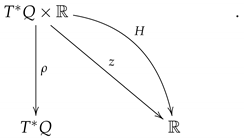
H defined in the cotangent bundle
of the configuration space
Q. The Hamiltonian vector field is obtained by the equation
where
is the canonical symplectic form on
. As we know, bundle coordinates
are also Darboux coordinates so that
has the local form
The Hamilton–Jacobi problem consists in finding a function
such that
for some
. The above, Equation (
1), is called the Hamilton–Jacobi equation for
H. Of course, one easily see that (
1) can be written as follows:
which opens the possibility to consider general 1-forms on
Q (considered as sections of the cotangent bundle
).
Recently, the observation that given such a section
permits to relate
with its projection
via
onto
Q, in the sense that
and
are
-related if and only if (
2) holds, provided that
be closed (or, equivalently, its image be a Lagrangian submanifold of
) has opened the possibility to discuss the Hamilton–Jacobi problem in many other scenarios [
3,
4,
5,
6]: nonholonomic systems, multisymplectic field theories, and time-dependent mechanics, among others.
In Reference [
7], we have started the extension of the Hamilton–Jacobi theory for contact Hamiltonian systems (also see Reference [
8]). Let us recall that a contact Hamilton system is defined by a Hamiltonian function on a contact manifold, in our case, the extended cotangent bundle
equipped with the canonical contact form
, where
z is a global coordinate in
and
the Liouville form on
, with the obvious identifications.
Contact Hamiltonian systems are widely used in many fields of Physics, such as thermodynamics, dissipative systems, cosmology, and even in Biology (the so-called neurogeometry). The corresponding Hamilton equations were obtained in 1930 by G. Herglotz [
9] using a variational principle that extends the usual one of Hamilton, but they can be alternatively derived using contact geometry.
The goal of this paper is to continue the study of the Hamilton–Jacobi problem in the contact context, using the two vector fields associated to the Hamiltonian H:
the Hamiltonian vector field:
the evolution vector field:
We notice that the Hamilton–Jacobi problem has been treated by other authors [
10,
11], who establish a relationship between the Herglotz variational principle and the Hamilton–Jacobi equation, although their interests are analytical rather than geometrical.
The content of the paper is as follows.
Section 2 is devoted to introducing the main ingredients of contact manifolds and contact Hamiltonian systems, as well as the interpretation of a contact manifold as a Jacobi structure. In
Section 3, we discuss the different types of submanifolds of a contact manifold.
Section 4 is the main part of the paper; there, we discuss the Hamilton–Jacobi problem for a contact Hamiltonian vector field, as well as for the corresponding evolution vector field. The results are more involved than in the case of symplectic Hamiltonian systems due to the different possibilities that may occur. In
Section 5, we study the relations of the Hamilton–Jacobi problem for a contact Hamiltonian systems and its symplectification. Finally, some examples are discussed in
Section 6.
2. Contact Hamiltonian Systems
2.1. Contact Manifolds
Consider a contact manifold [
12,
13,
14,
15,
16,
17]
with contact form
; this means that
, and
M has odd dimension
. Then, there exists a unique vector field
(called Reeb vector field) such that
There is a Darboux theorem for contact manifolds (see References [
18,
19]) so that, around each point in
M, one can find local coordinates (called Darboux coordinates)
such that
and we have
The contact structure defines an isomorphism between tangent vectors and covectors. For each
,
Similarly, we obtain a vector bundle isomorphism
over
M.
We will also denote by the corresponding isomorphism of -modules between vector fields and 1-forms over M; ♯ will denote the inverse of .
Therefore, we have that
so that, in this sense,
is the dual object of
.
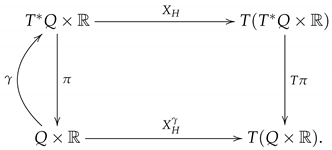
For a Hamiltonian function
H on
M, we define the Hamiltonian vector field
by
In Darboux coordinates, we get this local expression:
Therefore, an integral curve
of
satisfies the contact Hamilton equations
In addition to the Hamiltonian vector field
associated to a Hamiltonian function
H, there is another relevant vector field, called
evolution vector field defined by
so that it reads in local coordinates as follows:
Consequently, the integral curves of
satisfy the differential equations
Remark 1. The evolution vector field plays a relevant role in the geometric description of thermodynamics (see References [20,21]). Given a contact
dimensional manifold
, we can consider the following distributions on
M, that we will call
vertical and
horizontal distribution, respectively:
We have a Whitney sum decomposition
and, at each point
:
We will denote by and the projections onto these subspaces. We notice that and , and that is non-degenerate, and is generated by the Reeb vector field .
Definition 1. - 1.
A diffeomorphism between two contact manifolds is a contactomorphism
if - 2.
A diffeomorphism is a conformal contactomorphism
if there exists a nowhere zero function such that - 3.
A vector field is an infinitesimal contactomorphism (respectively, infinitesimal conformal contactomorphism) if its flow consists of contactomorphisms (respectively, conformal contactomorphisms).
Therefore, we have
Proposition 1. - 1.
A vector field X is an infinitesimal contactomorphism if and only if - 2.
X is an infinitesimal conformal contactomorphism if and only if there exists such that In this case, we say that is an infinitesimal conformal contactomorphism.
If
is a
-dimensional contact manifold and takes Darboux coordinates
, then
where
and are dual basis.
2.2. Contact Manifolds as Jacobi Structures
Definition 2. A Jacobi manifold [19,22,23] is a triple , where Λ is a bivector field (a skew-symmetric contravariant 2-tensor field), and is a vector field, so that the following identities are satisfied:where is the Schouten–Nijenhuis bracket. Given a Jacobi manifold
, we define the
Jacobi bracket:
where
This bracket is bilinear, antisymmetric, and satisfies the Jacobi identity. Furthermore, it fulfills the weak Leibniz rule:
That is,
is a local Lie algebra in the sense of Kirillov.
Conversely, given a local Lie algebra , we can find a Jacobi structure on M such that the Jacobi bracket coincides with the algebra bracket.
Remark 2. The weak Leibniz rule is equivalent to this identity: Given a contact manifold
, we can define the associated Jacobi structure
by
where
. For an arbitrary function
f on
M, we can prove that the Hamiltonian vector field
with respect to the contact structure
coincides with the one defined by its associated Jacobi structure, say:
where
is the vector bundle morphism from tangent covectors to tangent vectors defined by
, i.e.,
for all covectors
and
.
3. Submanifolds
As in the case of symplectic manifolds, we can consider several interesting types of submanifolds of a contact manifold
. To define them, we will use the following notion of
complement for contact structures [
13]:
Let
be a contact manifold and
. Let
be a linear subspace. We define the
contact complement of
where
is the annihilator.
We extend this definition for distributions by taking the complement pointwise in each tangent space.
Here, is the associated 2-tensor according to the previous section.
Definition 3. Let be a submanifold. We say that N is:
Isotropic if .
Coisotropic if .
Legendrian or Legendre if .
The coisotropic condition can be written in local coordinates as follows.
Let be a k-dimensional manifold given locally by the zero set of functions , with .
Therefore, N is coisotropic if and only if, for all .
According to (
11), we conclude that
N is coisotropic if and only if
for all
.
Using the above results, one can easily prove the following characterization of a Legendrian submanifold.
Proposition 2. Let be a contact manifold of dimension . A submanifold N of M is Legendrian if and only if it is a maximal integral manifold of (and then it has dimension n).
Consider a function
, and let
the canonical contact structure on
. Here,
is the canonical projection, and
is the canonical Liouville form on
. In bundle coordinates
, we have
so that
are Darboux coordinates.
We denote by
the 1-jet of
f, say:
Then, one immediately checks that is a Legendrian submanifold of . Moreover, we have:
Proposition 3. A section of the canonical projection is a Legendrian submanifold of if and only if γ is locally the 1-jet of a function .
Remark 3. The above result is the natural extension of the well-known fact that a section α of the cotangent bundle is a Lagrangian submanifold with respect to the canonical symplectic structure on if and only if α is a closed 1-form (and, hence, locally exact).
5. Symplectification of the Hamilton–Jacobi Equation
5.1. Homogeneous Hamiltonian Systems and Contact Systems
There is a close relationship between homogeneous symplectic and contact systems; see, for example, References [
24,
25]. Here, we briefly recall some facts about the symplectification of cotangent bundles.
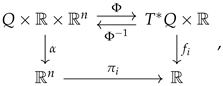
For any manifold M, a function is said to be homogeneous if, for any , we have for any . In this situation, the function F can be projected to the projective bundle over M obtained by projectivization of every cotangent space. We are interested in the case that , with natural coordinates on . We note that this definition can be generalized to any vector bundle.
Let
be an homogeneous Hamiltonian function on
. Locally, we have that
, for all
. Equivalently, one can write
for
, where
,
is well defined.
With the above changes, we have identified the manifold as the projective bundle of the cotangent bundle , taking out the points at infinity, that is, the subset defined by .
Following Reference [
25],
Section 4.1, the map
sends the Hamiltonian symplectic system
onto the Hamiltonian contact system
, where
and
are the canonical symplectic and contact forms, respectively. Observe that the natural coordinates of
, denoted by
, correspond to the homogeneous coordinates in the projective bundle. In fact, the map
is projectivization up to a minus sign, i.e., the map that sends each point in the fibers of
to the line that passes through it and the origin.
The map satisfies and .
It can be shown that
provides a bijection between conformal contactomorphisms and homogeneous symplectomorphisms. Moreover,
maps homogeneous Lagrangian submanifolds
onto Legendrian submanifolds
. Indeed, if
is homogeneous, then
is Legendrian if and only if
is Lagrangian. Moreover, the Hamilton equations for
are transformed into the Hamilton equations for
H, i.e.,
. See References [
25,
26] for more details on this topic.
We also remark that this construction is symplectomorphic to the symplectification defined in Reference [
24], which is given by
where
t is the (global) coordinate of the second
factor. The “symplectified” Hamiltonian is
so that both dynamics are
-related. That is,
is such that
where
is the projection onto the first two factors.
The following map provides the symplectomorphism
that is,
. This map is a symplectomorphism that maps
onto
. Moreover, it is a fiber bundle automorphism over
(see the diagram below):
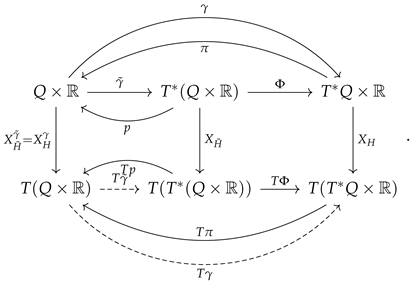
5.2. Relations for the Hamiltonian Vector Field
Now, we will establish a relationship between solutions to the Hamilton–Jacobi problem in both scenarios. Suppose that
is a solution of the symplectic Hamilton–Jacobi equation, i.e.,
is Lagrangian and
or, equivalently
where
is the projected vector field and
the canonical projection. We want to use the solution
of the Hamilton–Jacobi problem in the symplectification (which we will often refer to as “symplectic solution”) to obtain a section that is a solution in the contact setting (“contact solution”, for simplicity). We assume
and take
. In local coordinates:
We can summarize the situation in the following commutative diagram:
We note that the projected vector fields and coincide. The dashed lines of (respectively, ) commute if and only if is a symplectic solution (respectively, is a contact solution) of the Hamilton–Jacobi problem.
Lemma 1. Let H be a Hamiltonian and its symplectified version. Assume . Then, is a symplectic solution, or, equivalently, and are -related if and only if and are γ-related.
Proof. Assume that and are -related. Then, by the commutativity of the diagram (51), we see that and are -related.
Conversely, assume that
and
are
-related. Let
, and let
We note that is the inverse of along the submanifold . In particular, . Looking at the diagram (51), this implies that and are -related. □
Lemma 2. Assume that the image of is Lagrangian. Then, the image of γ is coisotropic, and the images of are Lagrangian if and only if for some function .
Conversely, if the image of γ is coisotropic and the images of are Lagrangian, then we can choose so that the image of is coisotropic. Indeed, it is given by either , where g is a solution to the PDE Proof. Let
be such that its image is Lagrangian. That is,
. Splitting the part in
Q and in
, we see that this is equivalent to
Now,
. By Theorem 2, it is necessary that
and
. We compute
hence, the images of
are Lagrangian, and the image of
is coisotropic if and only if
is proportional to
.
Conversely, assume that
satisfies
and
. We must find
so that (
54) are satisfied. Since
, we have that (
54) are equivalent to
A solution for
on the first equation above clearly solves the second one. Since we look for nonvanishing
, we let
so that is just
and, if we let
this equation can be written as
and we note that this vector fields commute, indeed,
If this PDE has local solutions, operating with the equations above, one has,
This condition is clearly necessary, and it is also sufficient by (Thm. 19.27) [
27]. We have that
□
Combining the last two results, we obtain a correspondence between symplectic and contact solutions to the Hamilton–Jacobi problem.
Theorem 7. Let H be a Hamiltonian, and its symplectified version. Then, is a solution of the symplectic Hamilton–Jacobi problem for , if and only if is a solution of the contact Hamilton–Jacobi problem for H and for some function .
Conversely, given a contact solution γ of the Hamilton–Jacobi equation, there exists a symplectic solutions such that , where g is a solution to the PDE The Alternative Approach
For each
z, we have sections
of the form
, being
. We know that
is a solution of the contact Hamilton–Jacobi problem if and only if
is Legendrian, and
The condition that
is Legendrian is equivalent to
where we write
, which, by definition of
and using that
is Lagrangian, reads
therefore,
, with
functions depending only on the
. This can be summarized as follows:
Theorem 8. Suppose is a solution of the symplectified Hamilton–Jacobi problem. Then,is a solution of the contact Hamilton–Jacobi problem if and only if 5.3. Relations for the Evolution Vector Field
We now consider the evolution field
. First, note that
so that we cannot simply expect to project the vector field as before. In fact, one can easily prove that, under the assumption that the symplectified Hamiltonian is of the form
then the associated vector field
such that
will never verify
We will now see that, despite this apparent obstruction, one can still establish some relations. Let
be a solution of the symplectified problem and define the section
. This will be a solution of the associated Hamilton–Jacobi problem for the evolution field if and only if
is Legendrian, and
The Legendrian condition is equivalent to
or, using that
is Lagrangian, such as in the previous section,
On the other hand, we know that
is a solution of the symplectic problem, and, therefore,
, which, by definition, means
with
C constant. Since
), using the previous equation, we obtain:
Then, the condition
reads
which occurs if and only if, at every point
, we have:
The functional form found for
tells us that it is either non-zero at every point or it vanishes everywhere. If it does not vanish (everywhere), we claim that the second equation must be true. Indeed, suppose the first two equations do not hold. Then, the third equation must be true not just at a given point but in an open neighborhood, and we would have
where
are arbitrary functions. Using, again, that
is Lagrangian, we could write
which would imply that
h depends also on
z. Therefore, if
, then the second equation is true at every point. Using that
is Lagrangian, we see this is equivalent to
. Therefore, we find:
Theorem 9. Let be a solution of the symplectified problem with , where , and consider the sectionThen, γ is a solution of the contact problem for the evolution field if and only if one of the two following conditions is fulfilled: - 1.
,
- 2.
.
6. Examples
6.1. Particle with Linear Dissipation
Consider the Hamiltonian
H:
where
is a constant. The extended phase space is
.
The Hamiltonian and evolution vector field are given by
Assume that
is a section of the canonical projection
, that is,
We assume that
is a Legendrian submanifold of
as in
Section 4.2.2; then,
and
and
are
-related if and only if
for a constant
. Then, the Hamilton–Jacobi equation becomes
or, equivalently,
which is a non-linear ordinary differential equation.
6.2. Application to Thermodynamic Systems
We consider thermodynamic systems in the so-called
energy representation. Hence, the
thermodynamic phase space, representing the extensive variables, is the manifold
, equipped with its canonical contact form
The local coordinates on the configuration manifold Q are , where U is the internal energy, and ’s denote the rest of extensive variables. Other variables, such as the entropy, may be chosen instead of the internal energy, by means of a Legendre transformation.
The state of a thermodynamic system always lies on the equilibrium submanifold , which is a Legendrian submanifold. The pair is a thermodynamic system. The equations (locally) defining are called the state equations of the system.
On a thermodynamic system , one can consider the dynamics generated by a Hamiltonian vector field associated to a Hamiltonian H. If this dynamics represents quasistatic processes, meaning that, at every time the system is in equilibrium, that is, its evolution states remain in the submanifold , it is required for the contact Hamiltonian vector field to be tangent to . This happens if and only if H vanishes on .
Using Hamilton–Jacobi theory, one sees that a section satisfied if and only if and are -related.
The Classical Ideal Gas
A detailed description of this example can be found in References [
28,
29]; we summarize here the main ingredients.
The classical ideal gas is described by the following variables.
U: internal energy,
T: temperature,
S: entropy,
P: pressure,
V: volume,
: chemical potential,
N: mole number.
Thus, the thermodynamic phase space is
, and the contact 1-form is
The Hamiltonian function is
where
R is the constant of ideal gases. The Reeb vector field is
.
The Hamiltonian and evolution vector fields are just
The Hamiltonian vector field here represents an isochoric and isothermal process on the ideal gas.
Assume that
is the section locally given by
we know that
is a Legendrian submanifold of
if and only if,
The Hamilton–Jacobi equation is
for some
. That is,
This is a first order linear PDE, whose solution is given by
with
an arbitrary function. The case
, which is the one relevant for the thermodynamic interpretation, is given by
7. Conclusions
In this paper, we construct a Hamilton–Jacobi theory for contact Hamiltonian systems, which completes, in several respects, some first approximations in previous papers. Let us consider the two main vector fields associated with a given Hamiltonian, which give rise to two distinct dynamics. On the one hand, the usual Hamiltonian vector field, , and, on the other hand, the so-called evolution field, . The latter plays an essential role in the study of thermodynamic systems. For both cases, the corresponding Hamilton–Jacobi equations are obtained (two for each dynamics, four in total), characterizing them with the characteristics that their solutions provide coisotropic, Lagrangian, or Legendrian submanifolds. These characterizations have allowed in the case of symplectic mechanics to obtain new results in the study of the properties of the Hamilton–Jacobi equation.
We also study an alternative formulation, using the so-called symplectification of a contact structure, thus relating our results to those known in that case, although the problem we encounter is that we must deal with homogeneous Hamiltonians (which does not occur in a contact context). Finally, we consider two examples to illustrate the results obtained.
We are confident that these results can be applied in different areas, such as cosmology or thermodynamics, to name just a few. Among the tasks we intend to address is the detailed study of the discrete Hamilton–Jacobi equation and the identification of generating functions that allow us to use the general theory to integrate the dissipative equations generated by the Hamiltonian.