The Lie Algebraic Approach for Determining Pricing for Trade Account Options
Abstract
:1. Introduction
2. Symmetry Analysis
3. Options for a Trade Account
4. Utilizing Symmetry Analysis for the Pricing Problem
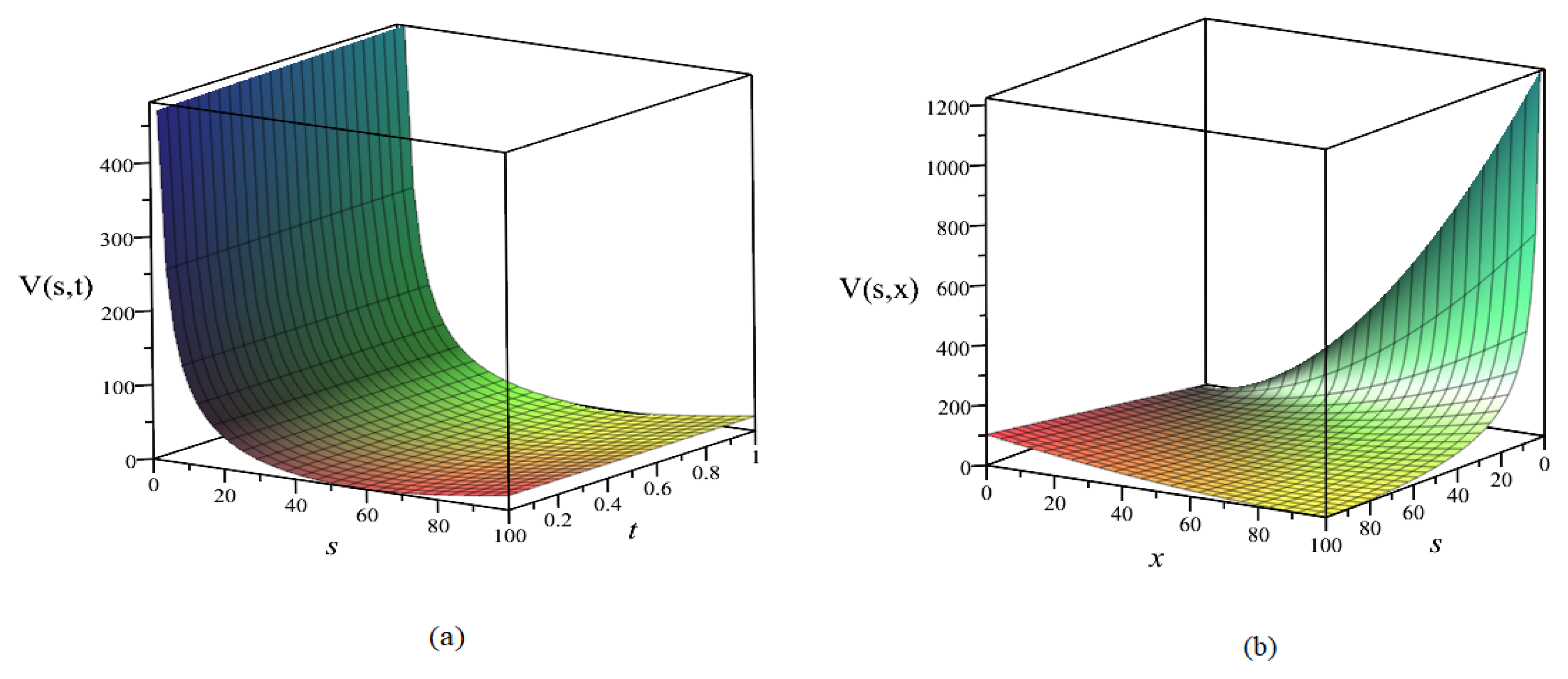
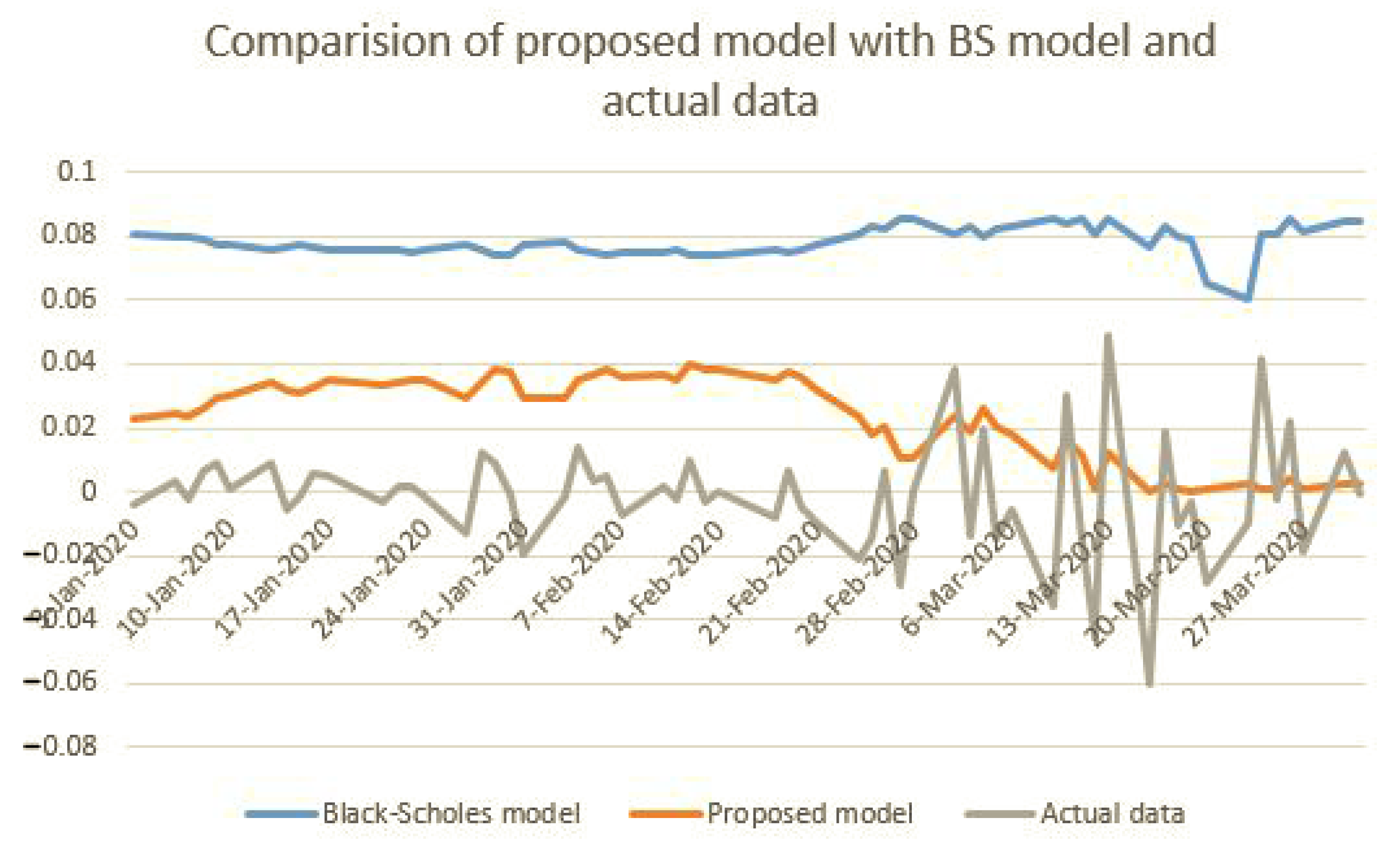
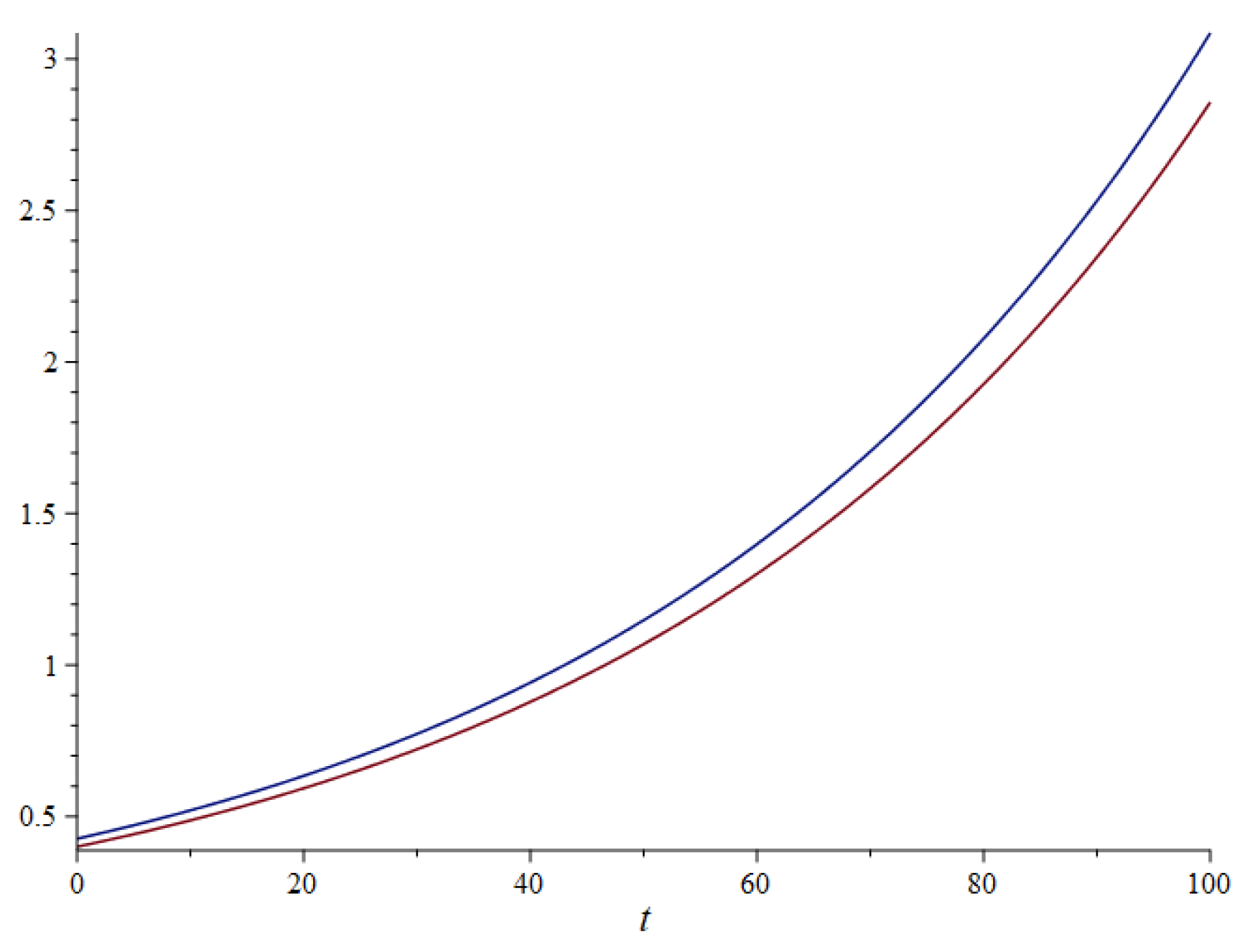
5. Numerical Example
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Merton, R.C. Theory of rational option pricing. Bell J. Econ. Manag. Sci. 1973, 4, 141–183. [Google Scholar] [CrossRef] [Green Version]
- Shreve, S.E.; Večeř, J. Options on a traded account: Vacation calls, vacation puts and passport options. Financ. Stoch. 2000, 4, 255–274. [Google Scholar] [CrossRef]
- Vecer, J.; Kampen, J.; Navratil, R. Options on a traded account: Symmetric treatment of the underlying assets. Quant. Financ. 2020, 20, 37–47. [Google Scholar] [CrossRef]
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef] [Green Version]
- Cox, J.C.; Ross, S.A.; Rubinstein, M. Option pricing: A simplified approach. J. Financ. Econ. 1979, 7, 229–263. [Google Scholar] [CrossRef]
- Hyer, T.; Lipton-Lifschitz, A.; Pugachevsky, D. Passport to success: Unveiling a new class of options that offer principal protection to actively managed funds. Risk Lond. Risk Mag. Ltd. 1997, 10, 127–132. [Google Scholar]
- Vecer, J. A new PDE approach for pricing arithmetic average Asian options. J. Comput. Financ. 2001, 4, 105–113. [Google Scholar] [CrossRef] [Green Version]
- Malloch, H., Jr. The Valuation of Options on Traded Accounts: Continuous and Discrete Time Models. Ph.D. Thesis, University of Sydney, Sydney, Australia, 1 August 2010. [Google Scholar]
- Andersen, L.; Andreasen, J.; Brotherton-Ratcliffe, R. The passport option. J. Comput. Financ. 1998, 1, 15–36. [Google Scholar] [CrossRef]
- Gazizov, R.K.; Ibragimov, N.H. Lie symmetry analysis of differential equations in finance. Nonlinear Dyn. 1998, 17, 387–407. [Google Scholar] [CrossRef]
- Guillaume, T. On the multidimensional Black–Scholes partial differential equation. Ann. Oper. Res. 2019, 281, 229–251. [Google Scholar] [CrossRef]
- Taylor, S.; Glasgow, S. A novel reduction of the simple Asian option and Lie-group invariant solutions. Int. J. Theor. Appl. Financ. 2009, 12, 1197–1212. [Google Scholar] [CrossRef] [Green Version]
- Caister, N.C.; O’hara, J.G.; Govinder, K.S. Solving the Asian option PDE using Lie symmetry methods. Int. J. Theor. Appl. Financ. 2010, 13, 1265–1277. [Google Scholar] [CrossRef]
- Geman, H.; Yor, M. Bessel processes, Asian options, and perpetuities. Math. Financ. 1993, 3, 349–375. [Google Scholar] [CrossRef]
- Sinkala, W. On the generation of arbitrage-free stock price models using Lie symmetry analysis. Comput. Math. Appl. 2016, 72, 1386–1393. [Google Scholar] [CrossRef] [Green Version]
- Jagannathan, R. A Linear Regression Approach for Determining Option Pricing for Currency-Rate Diffusion Model with Dependent Stochastic Volatility, Stochastic Interest Rate, and Return Processes. J. Math. Financ. 2018, 8, 161–177. [Google Scholar] [CrossRef] [Green Version]
- Paliathanasis, A.; Krishnakumar, K.; Tamizhmani, K.; Leach, P.G. Lie symmetry analysis of the Black-Scholes-Merton Model for European options with stochastic volatility. Mathematics 2016, 4, 28. [Google Scholar] [CrossRef] [Green Version]
- Lie, S. On integration of a class of linear partial differential equations by means of definite integrals. Crc Handb. Lie Group Anal. Differ. Equ. 1881, 2, 473–508. [Google Scholar]
- Baumann, G. MathLie a program of doing symmetry analysis. Math. Comput. Simul. 1998, 48, 205–223. [Google Scholar] [CrossRef]
- Ovsjannikov, L.V. Group Properties of Differential Equations; Siberian Section of the Academy of Science of USSR: Novosibirsk, Russia, 1962. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2000; Volume 107. [Google Scholar]
- Charnes, J.M. Using simulation for option pricing. In Proceedings of the 2000 Winter Simulation Conference Proceedings (Cat. No. 00CH37165), Orlando, FL, USA, 10–13 December 2000; pp. 151–157. [Google Scholar]
- Kou, S.G. A jump-diffusion model for option pricing. Manag. Sci. 2002, 48, 1086–1101. [Google Scholar] [CrossRef] [Green Version]
- Kou, S.G.; Wang, H. Option pricing under a double exponential jump diffusion model. Manag. Sci. 2004, 50, 1178–1192. [Google Scholar] [CrossRef] [Green Version]
- Chalikias, M.; Lalou, P.; Skordoulis, M. Customer Exposure to Sellers, Probabilistic Optimization and Profit Research. Mathematics 2019, 7, 621. [Google Scholar] [CrossRef] [Green Version]
- Newton, D.P.; Paxson, D.A.; Widdicks, M. Real R&D options 1. Int. J. Manag. Rev. 2004, 5, 113–130. [Google Scholar]
- Kalantonis, P.; Schoina, S.; Missiakoulis, S.; Zopounidis, C. The impact of the disclosed R & D expenditure on the value relevance of the accounting information: Evidence from Greek listed firms. Mathematics 2020, 8, 730. [Google Scholar]
- Kortge, G.D.; Okonkwo, P.A. Perceived value approach to pricing. Ind. Mark. Manag. 1993, 22, 133–140. [Google Scholar] [CrossRef]
- Husted, B.W. Risk management, real options, corporate social responsibility. J. Bus. Ethics 2005, 60, 175–183. [Google Scholar] [CrossRef]
- Popescu, C.R.G.; Popescu, G.N. An exploratory study based on a questionnaire concerning green and sustainable finance, corporate social responsibility, and performance: Evidence from the Romanian business environment. J. Risk Financ. Manag. 2019, 12, 162. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Li, W.; Zhang, Y. Family Control, Political Connection, and Corporate Green Governance. Sustainability 2020, 12, 7068. [Google Scholar] [CrossRef]
- Mamais, K.; Karvelas, K. Feeling good, as a guide to performance: The impact of economic sentiment in financial market performance for Germany. Appl. Econ. 2020, 52, 4529–4541. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tseng, S.-H.; Nguyen, T.S.; Wang, R.-C. The Lie Algebraic Approach for Determining Pricing for Trade Account Options. Mathematics 2021, 9, 279. https://doi.org/10.3390/math9030279
Tseng S-H, Nguyen TS, Wang R-C. The Lie Algebraic Approach for Determining Pricing for Trade Account Options. Mathematics. 2021; 9(3):279. https://doi.org/10.3390/math9030279
Chicago/Turabian StyleTseng, Shih-Hsien, Tien Son Nguyen, and Ruei-Ci Wang. 2021. "The Lie Algebraic Approach for Determining Pricing for Trade Account Options" Mathematics 9, no. 3: 279. https://doi.org/10.3390/math9030279
APA StyleTseng, S.-H., Nguyen, T. S., & Wang, R.-C. (2021). The Lie Algebraic Approach for Determining Pricing for Trade Account Options. Mathematics, 9(3), 279. https://doi.org/10.3390/math9030279






