Mathematical Model and FPGA Realization of a Multi-Stable Chaotic Dynamical System with a Closed Butterfly-Like Curve of Equilibrium Points
Abstract
:1. Introduction
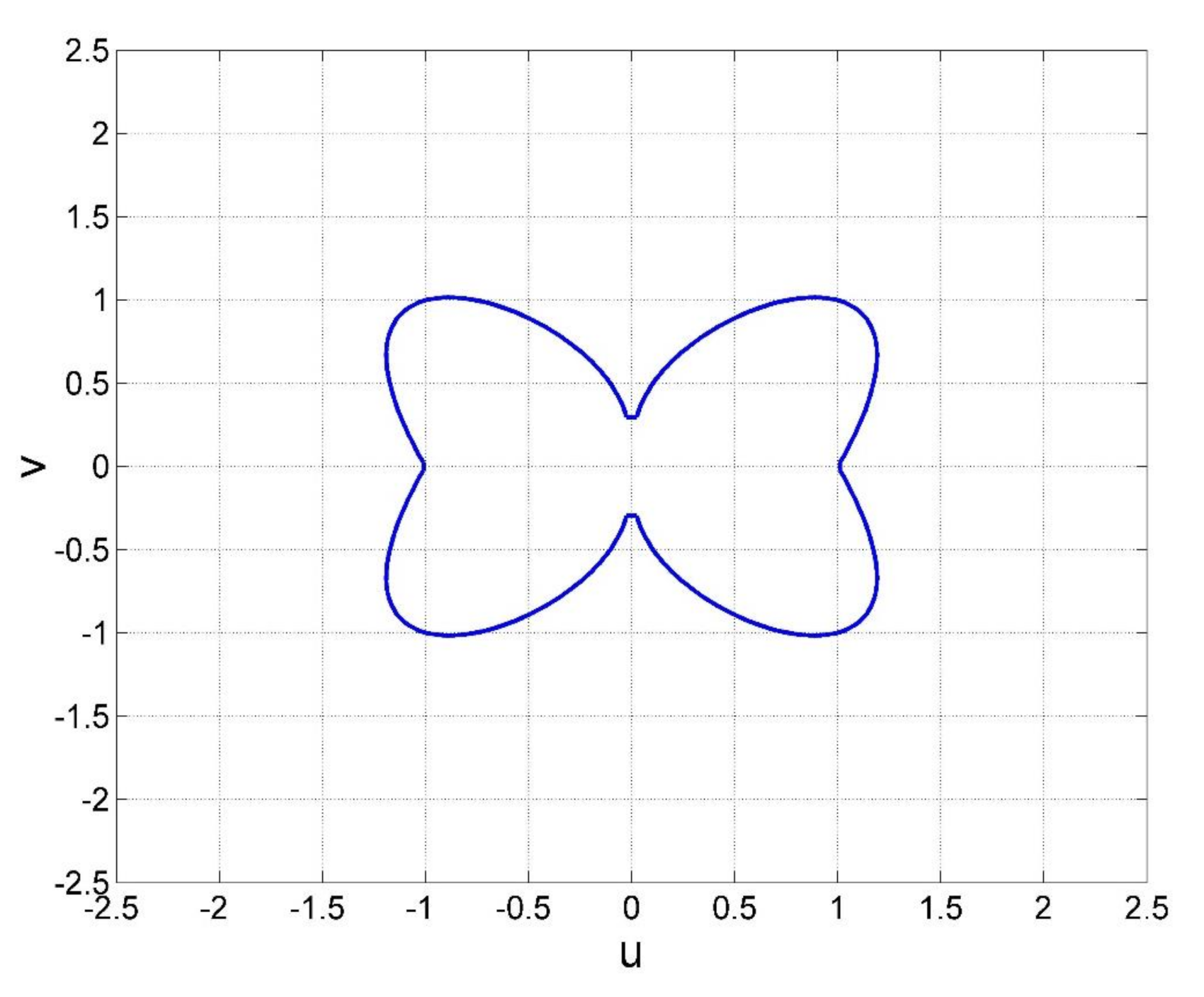
2. Mathematical Model of a Chaotic System with a Butterfly-Like Curve of Balance Points
3. Dynamic Study of the Chaotic System with Butterfly-Molded Curve of Balance Points
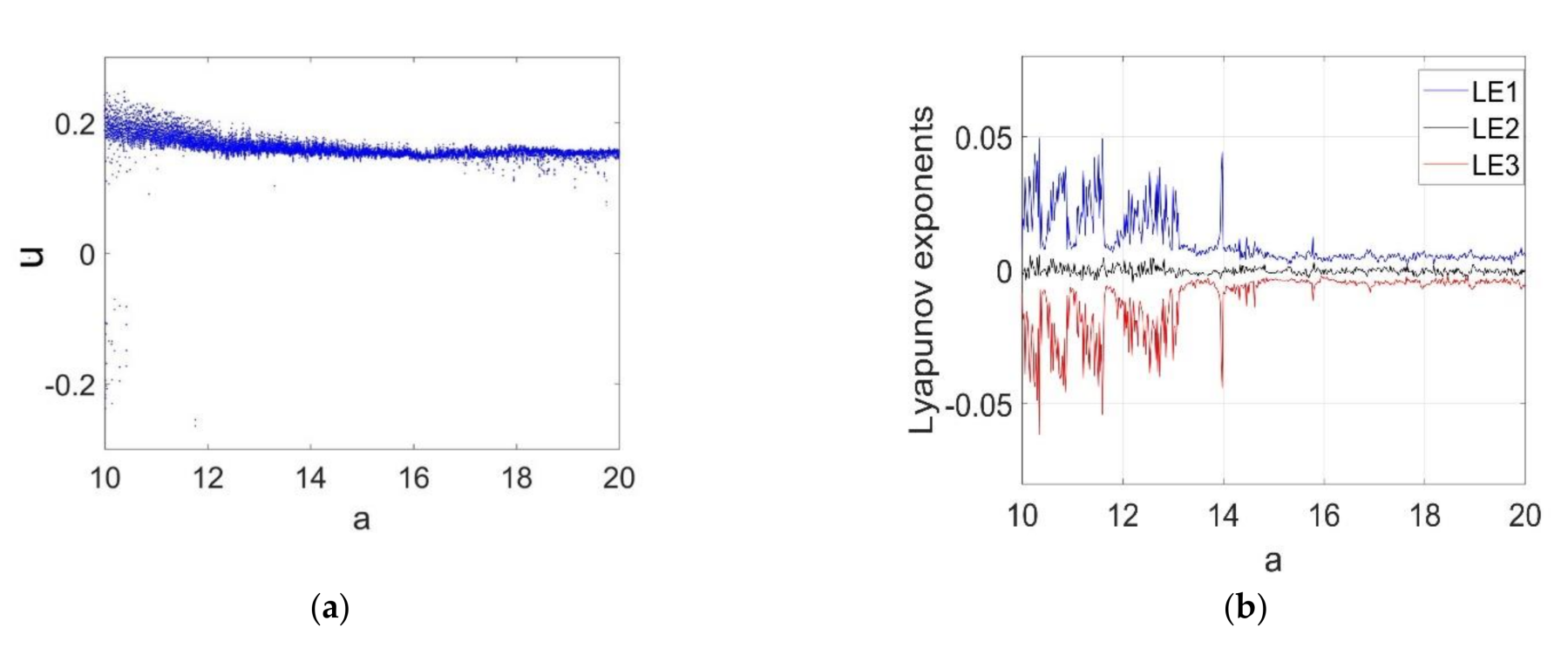
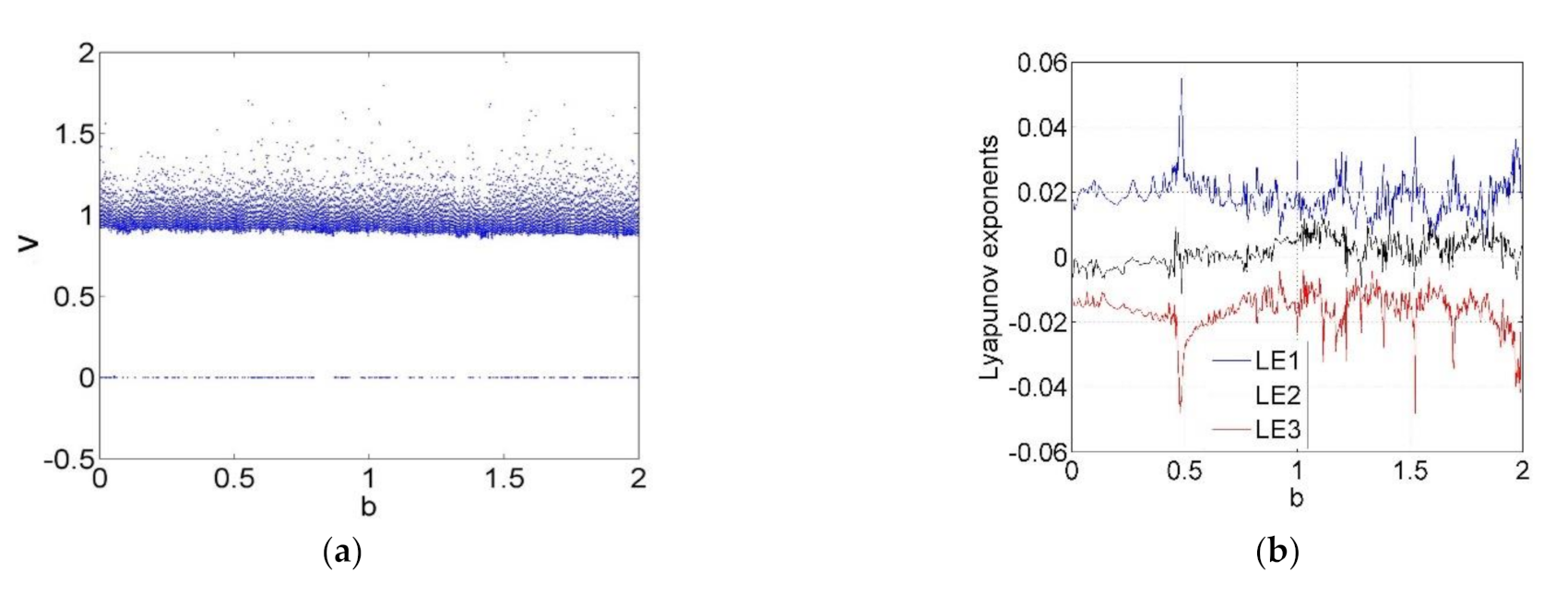
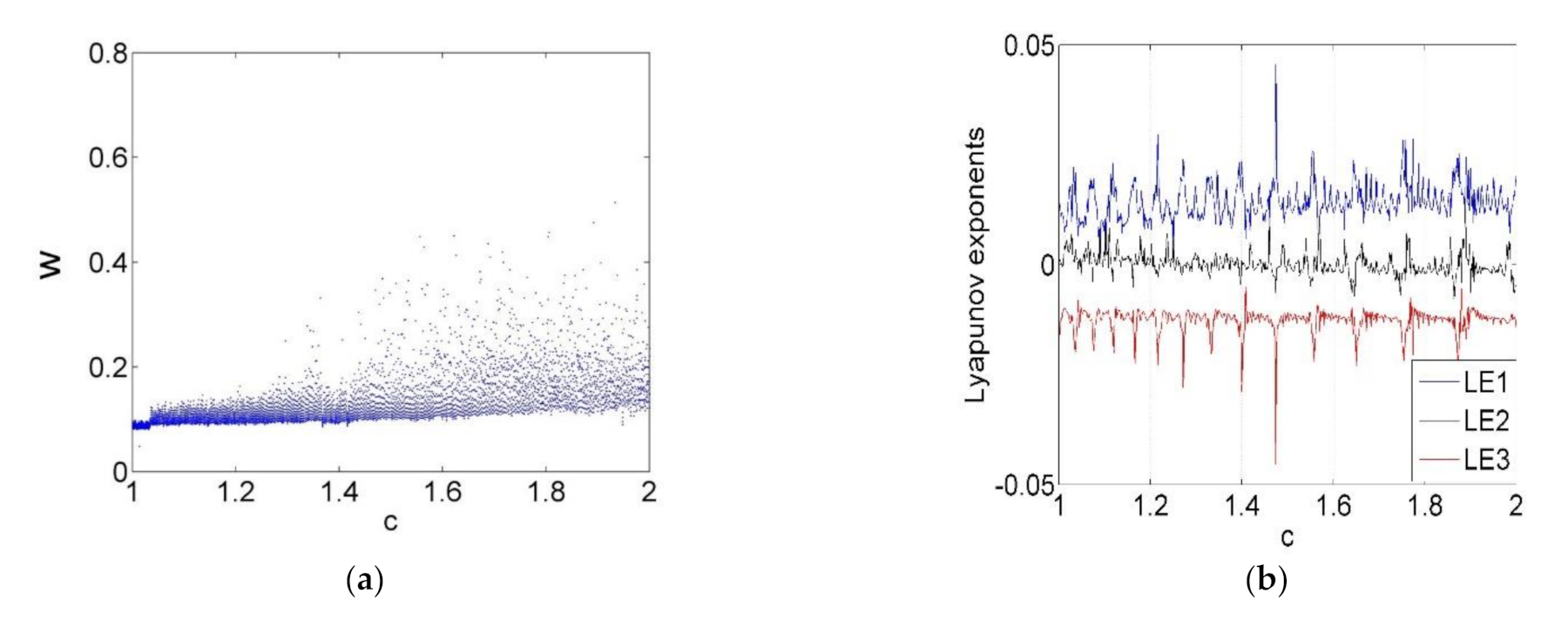
3.1. Bifurcation Study
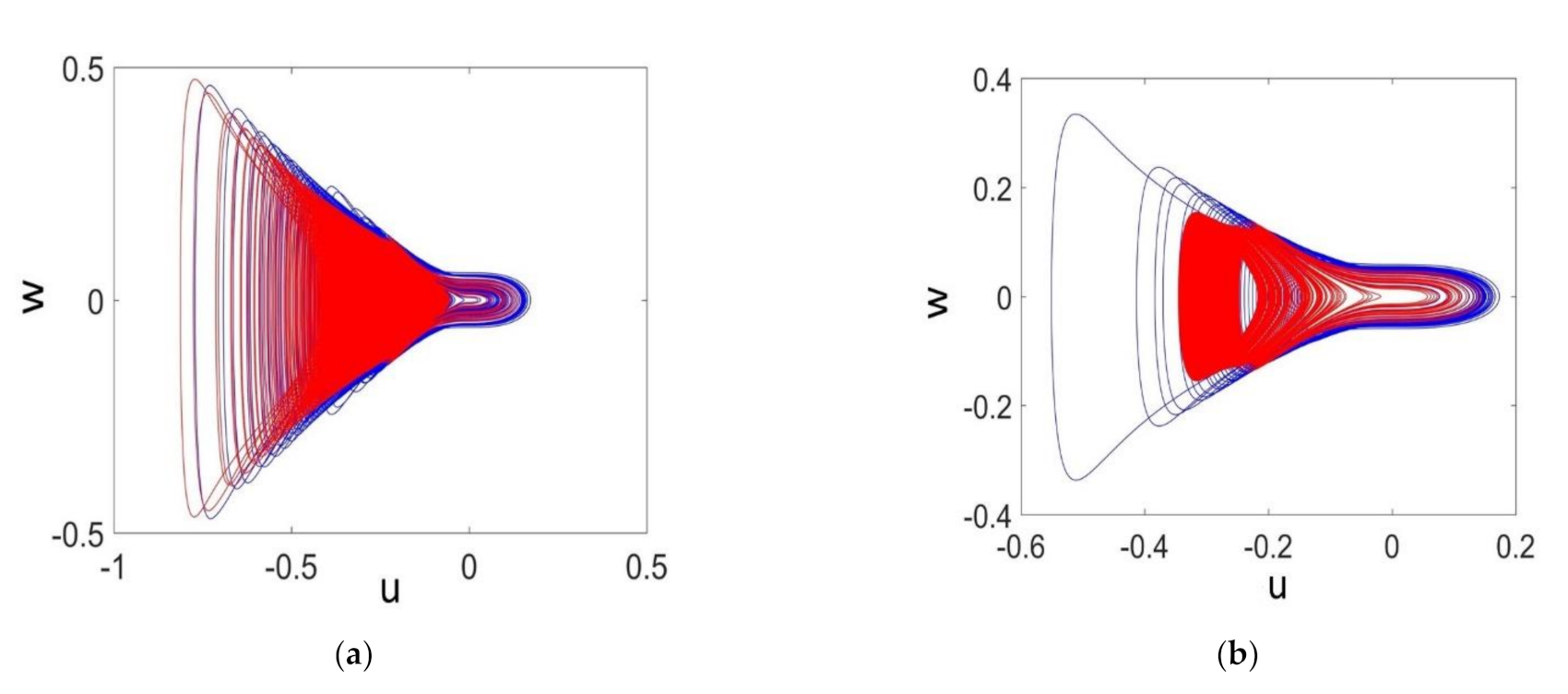
3.2. Multi-Stability
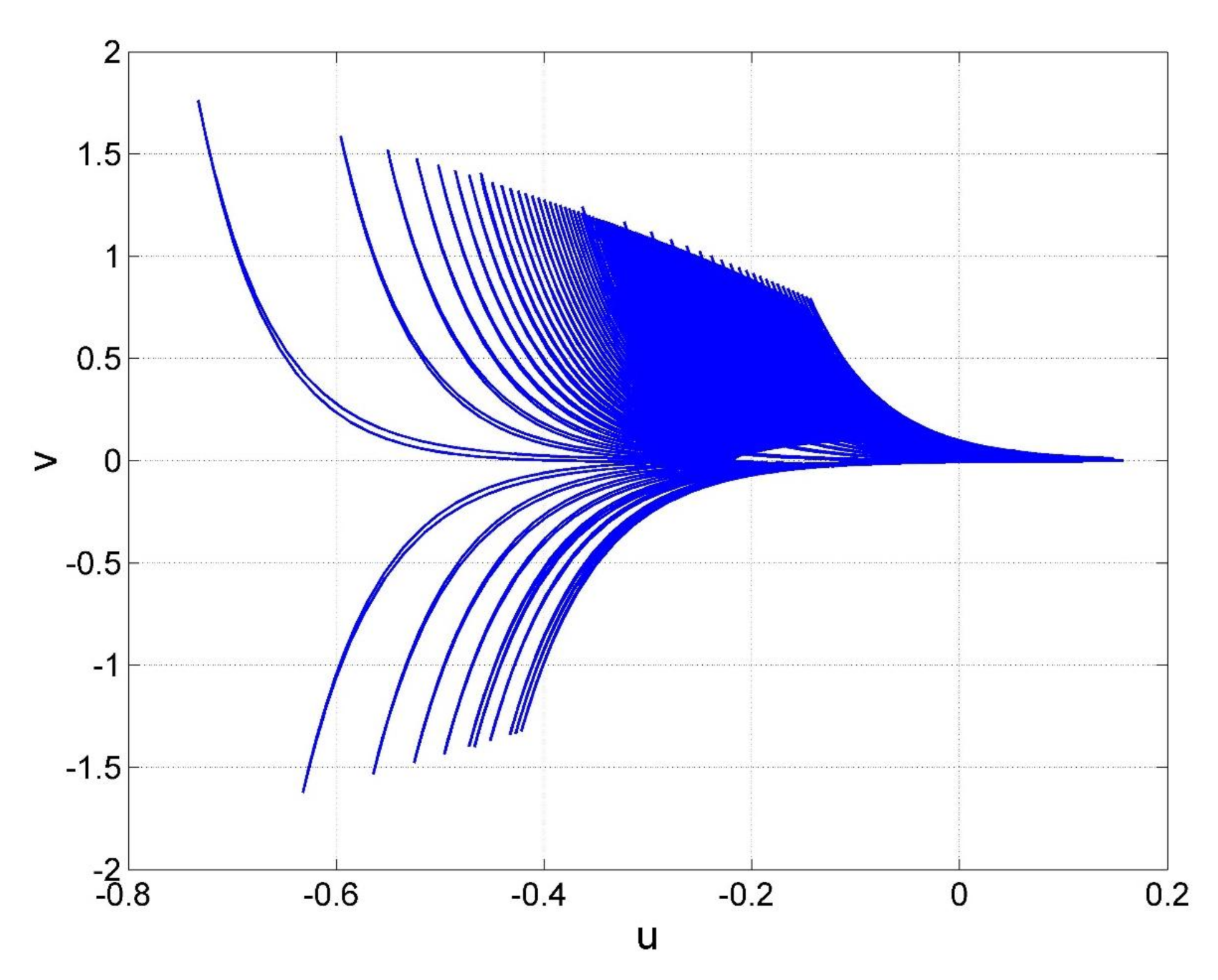
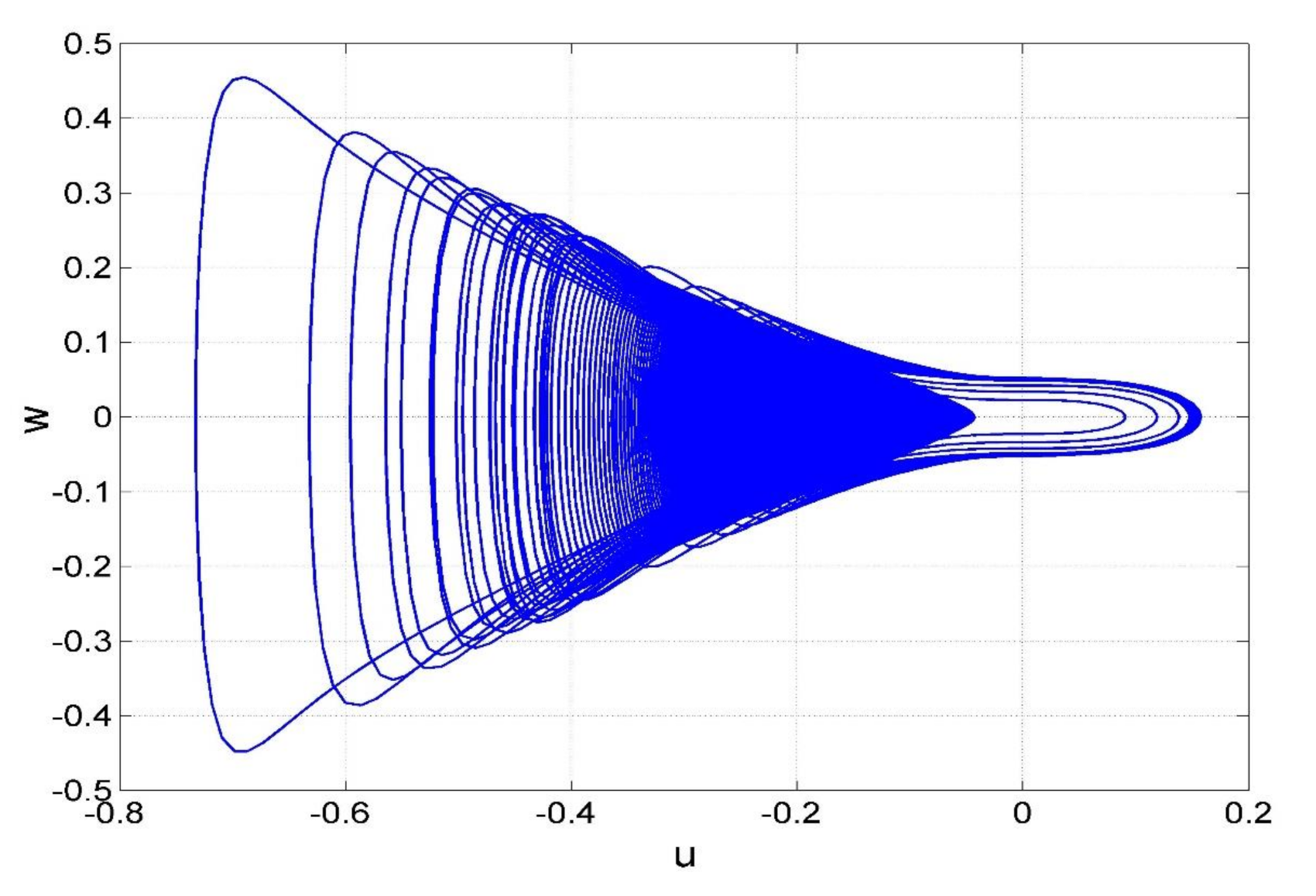
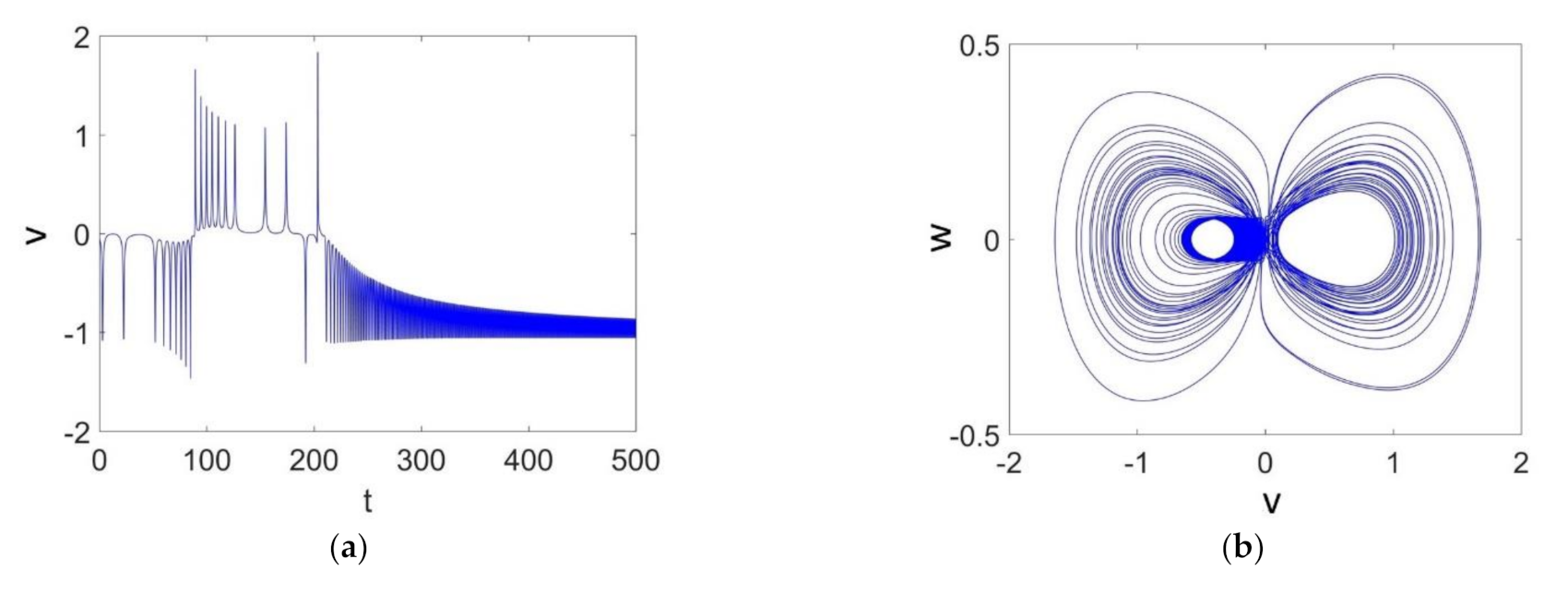
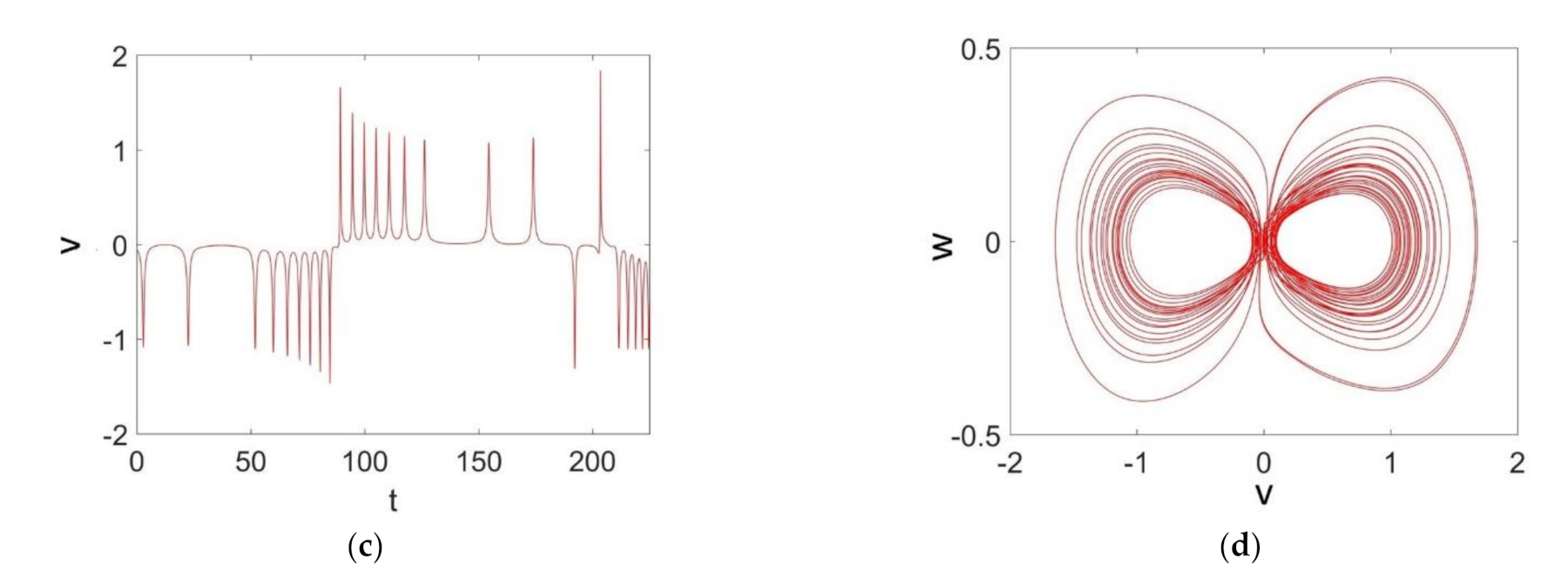
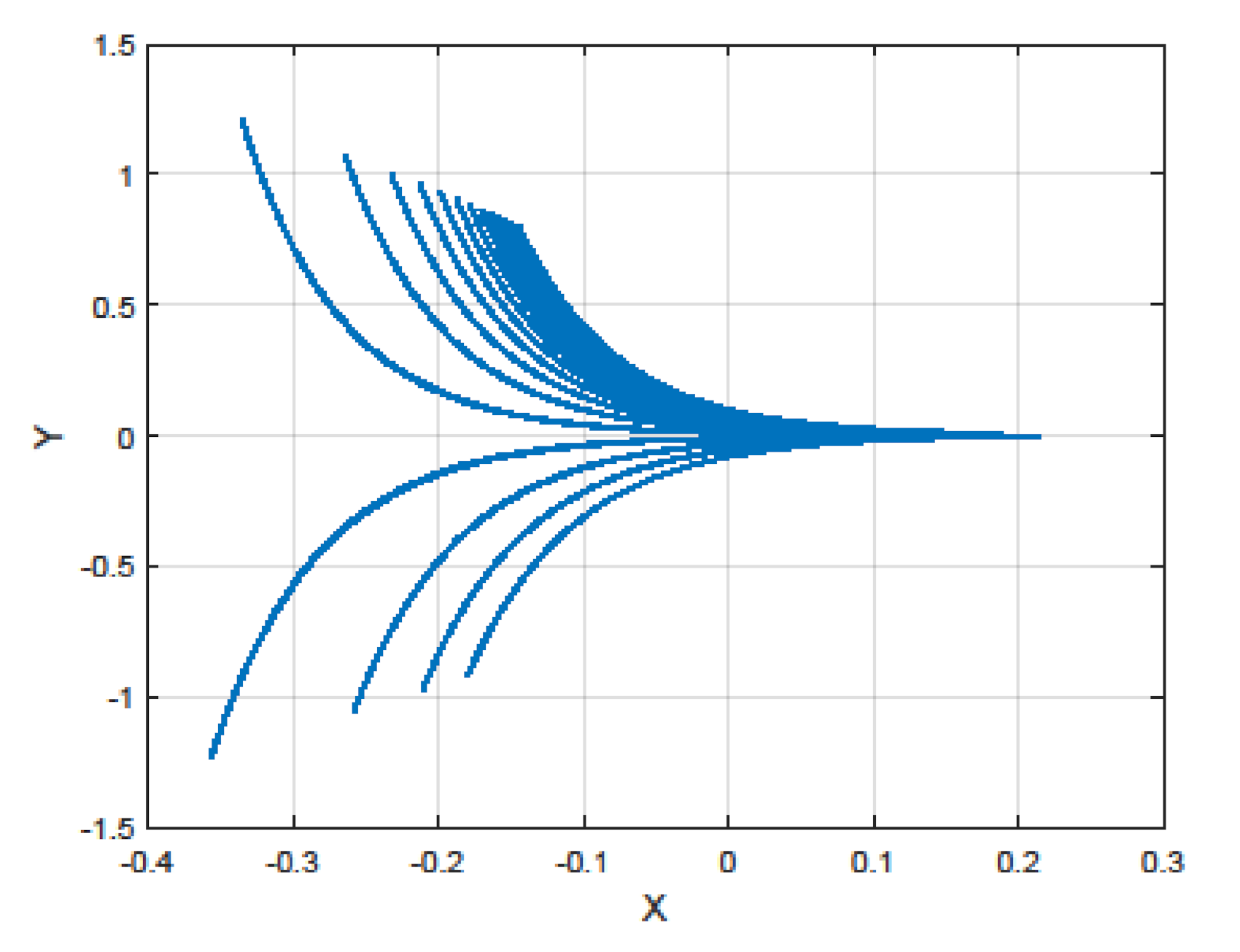
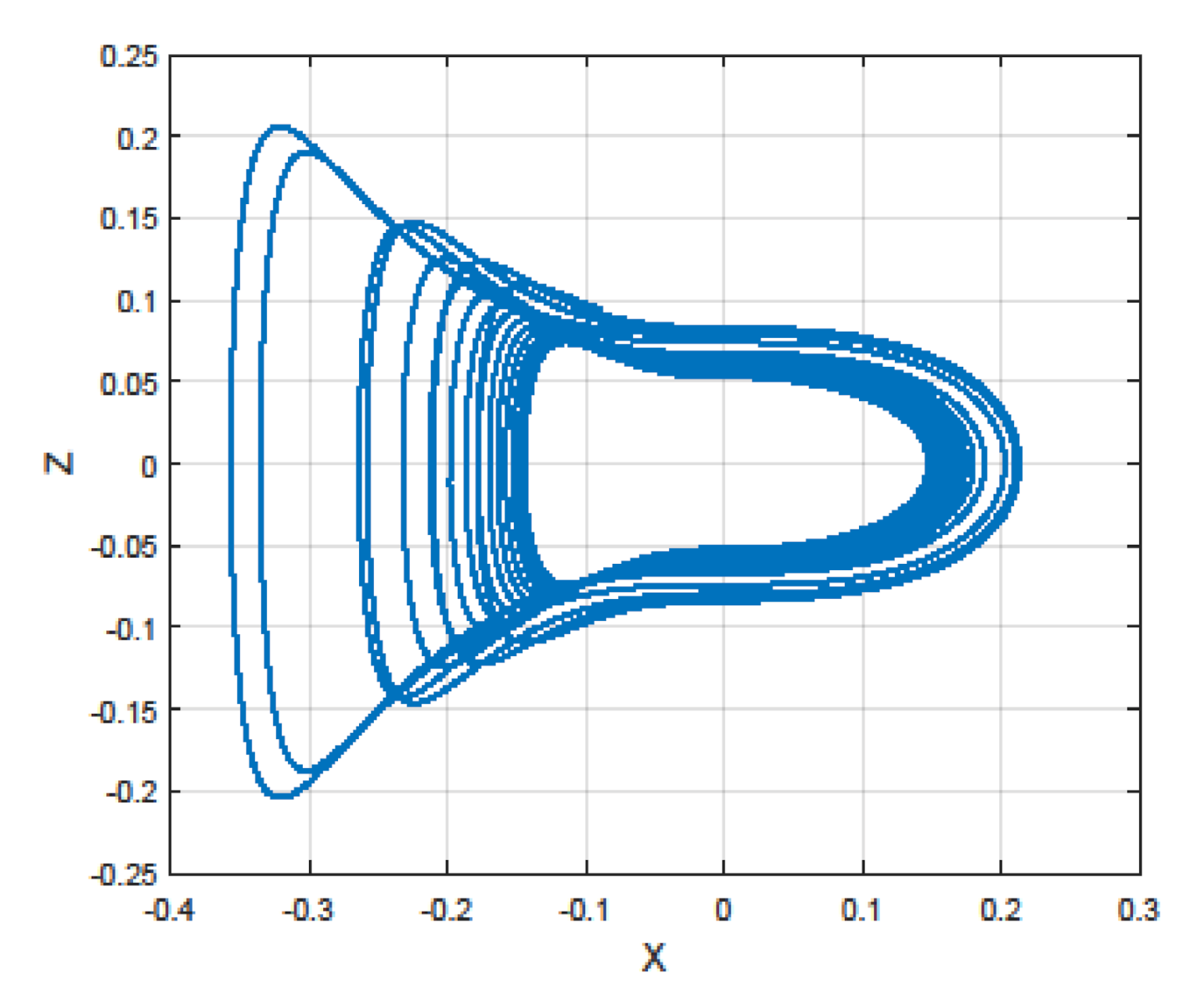
3.3. Transient Chaos
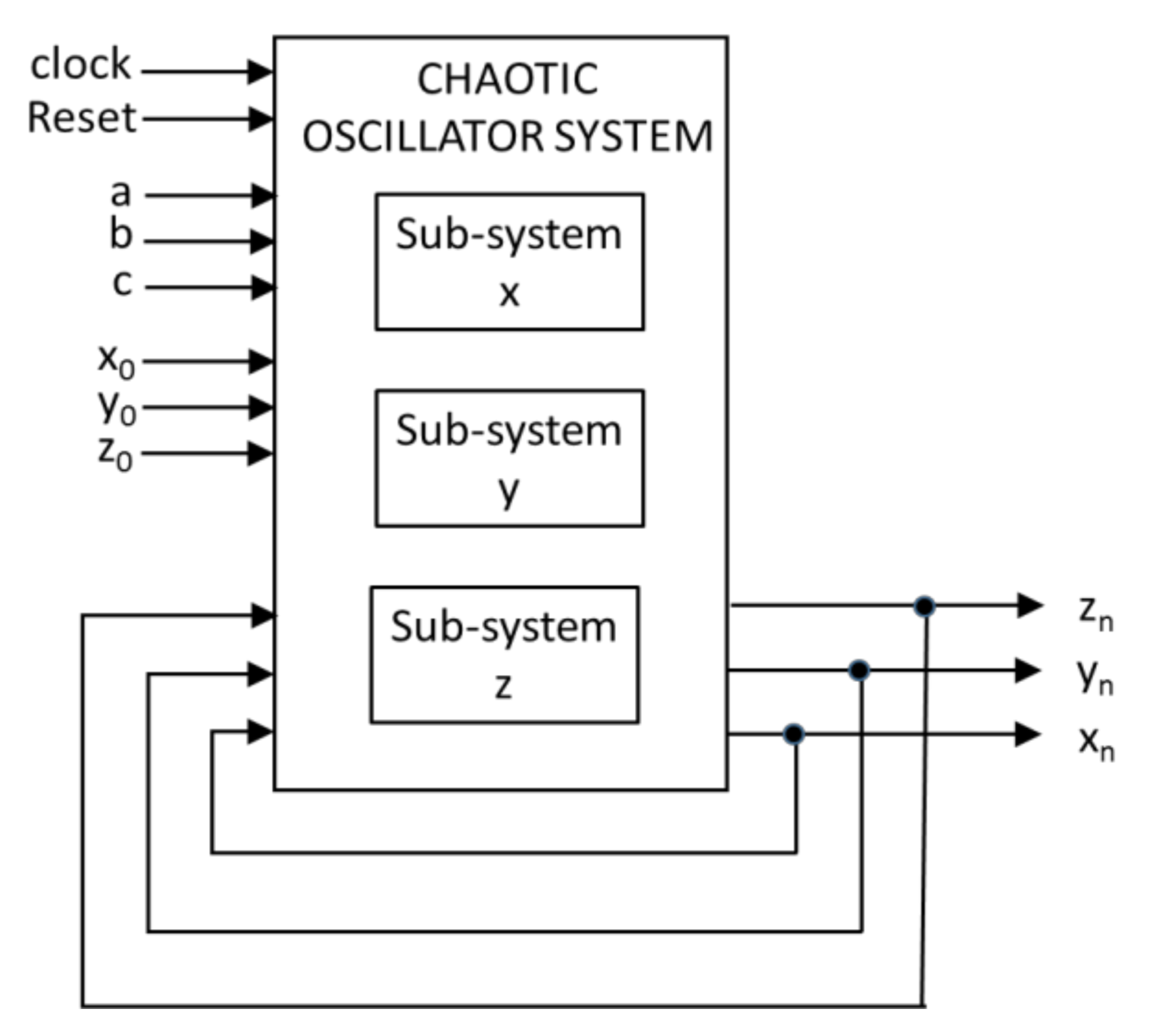
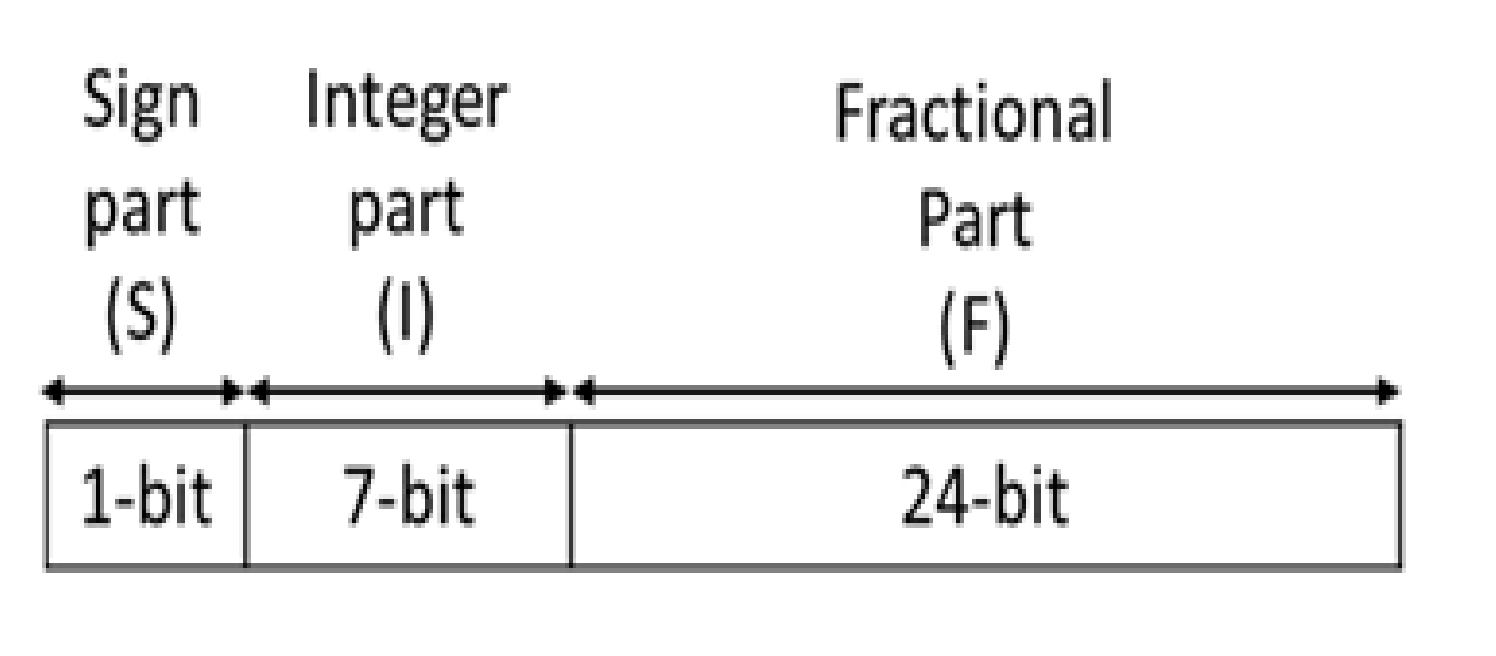
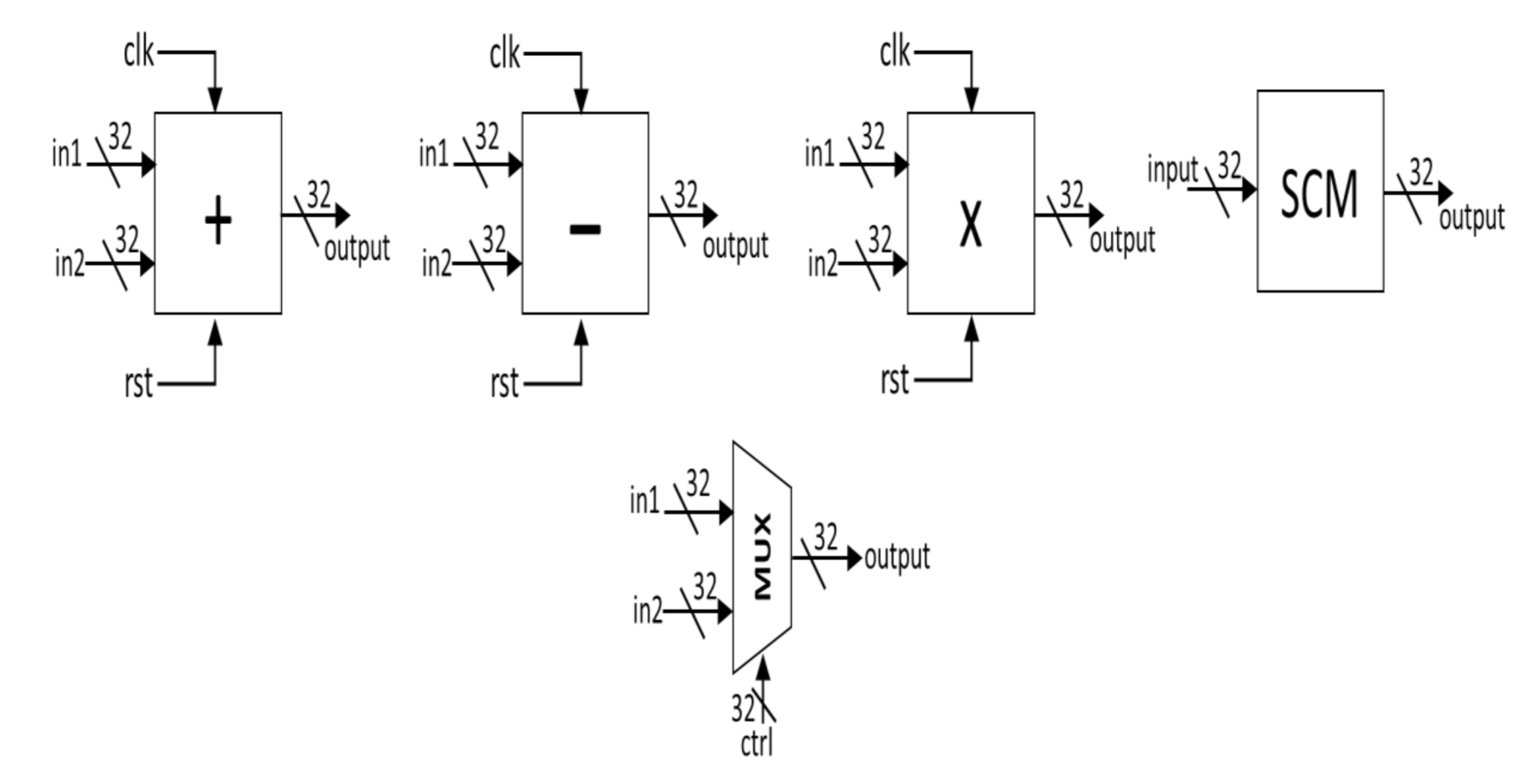
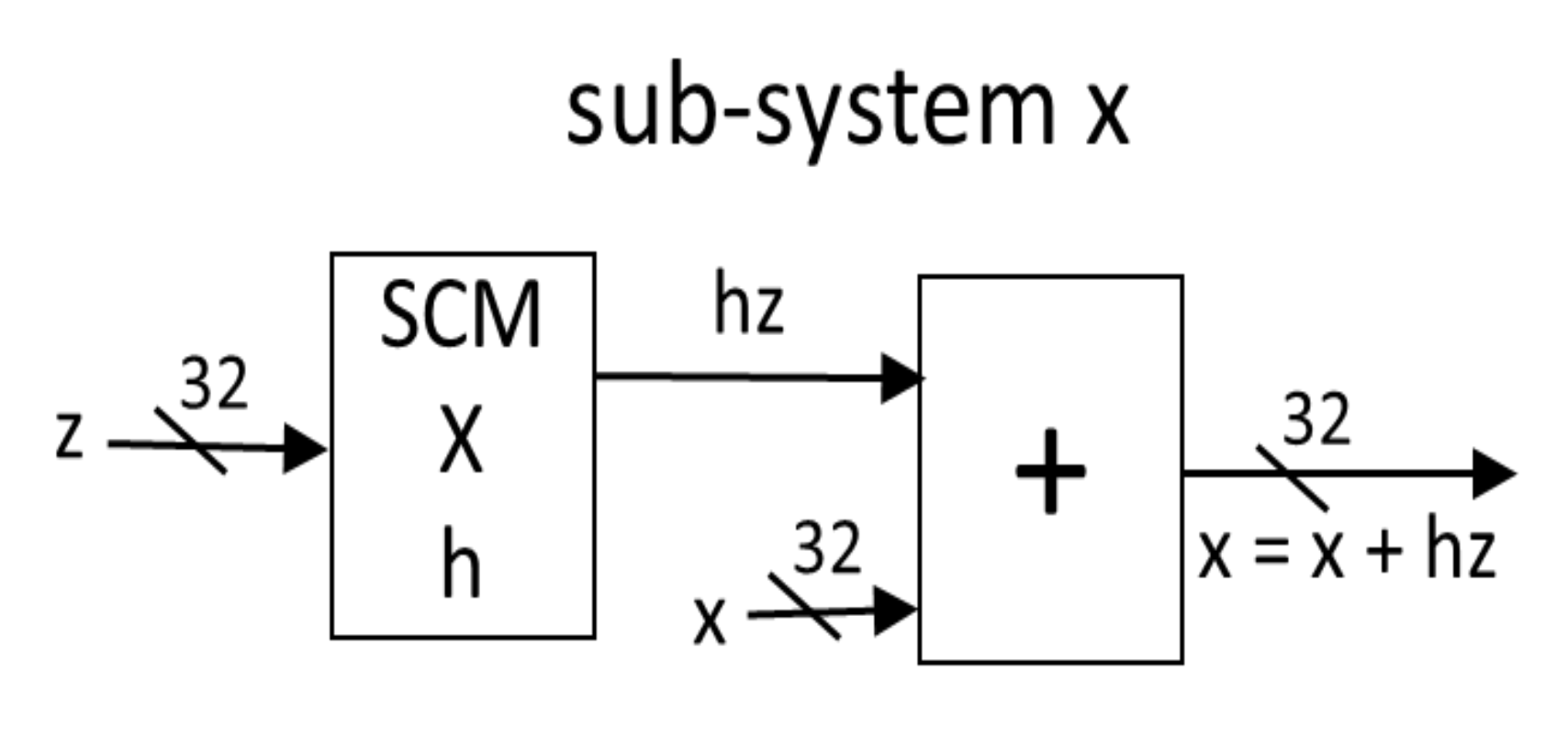
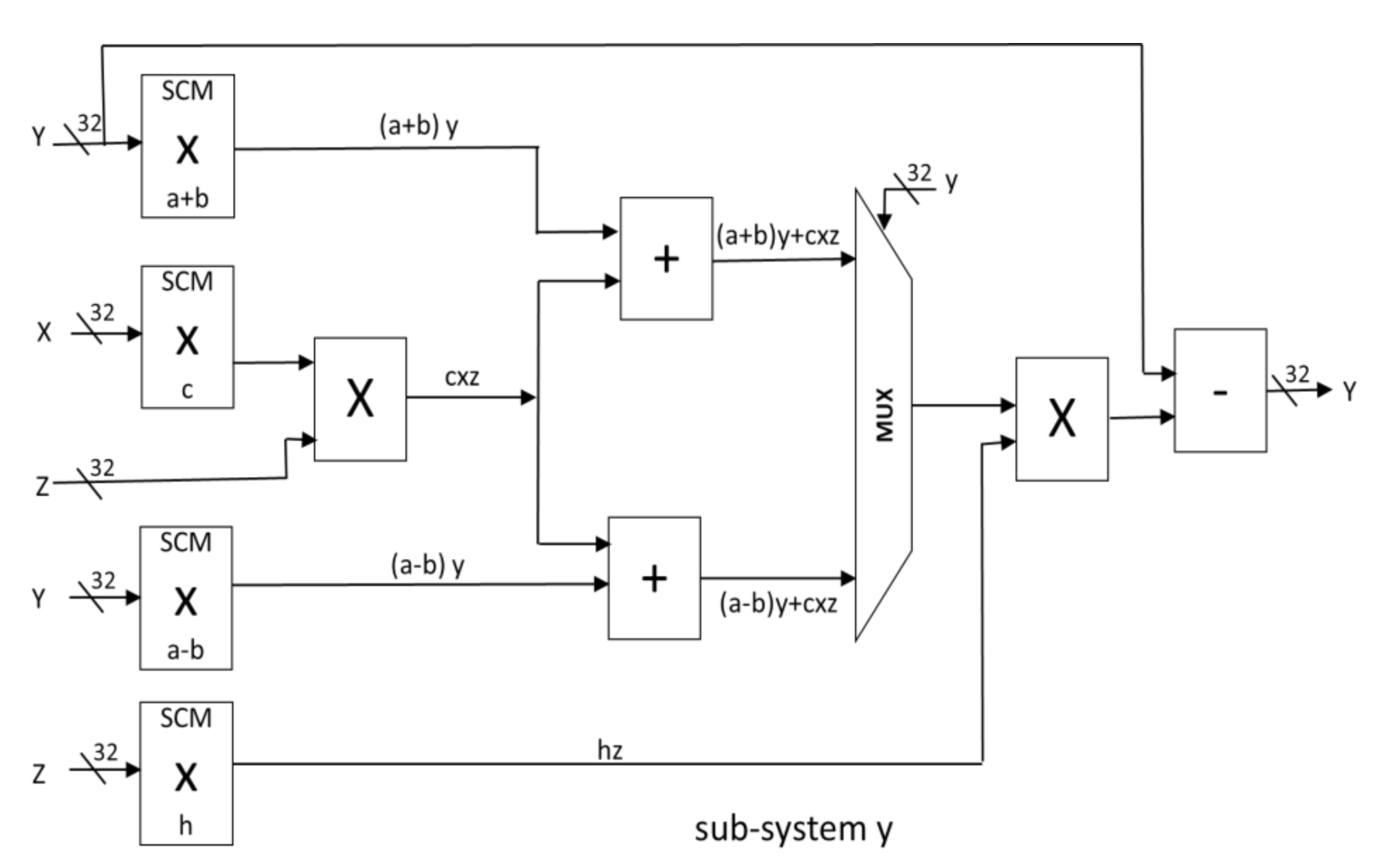
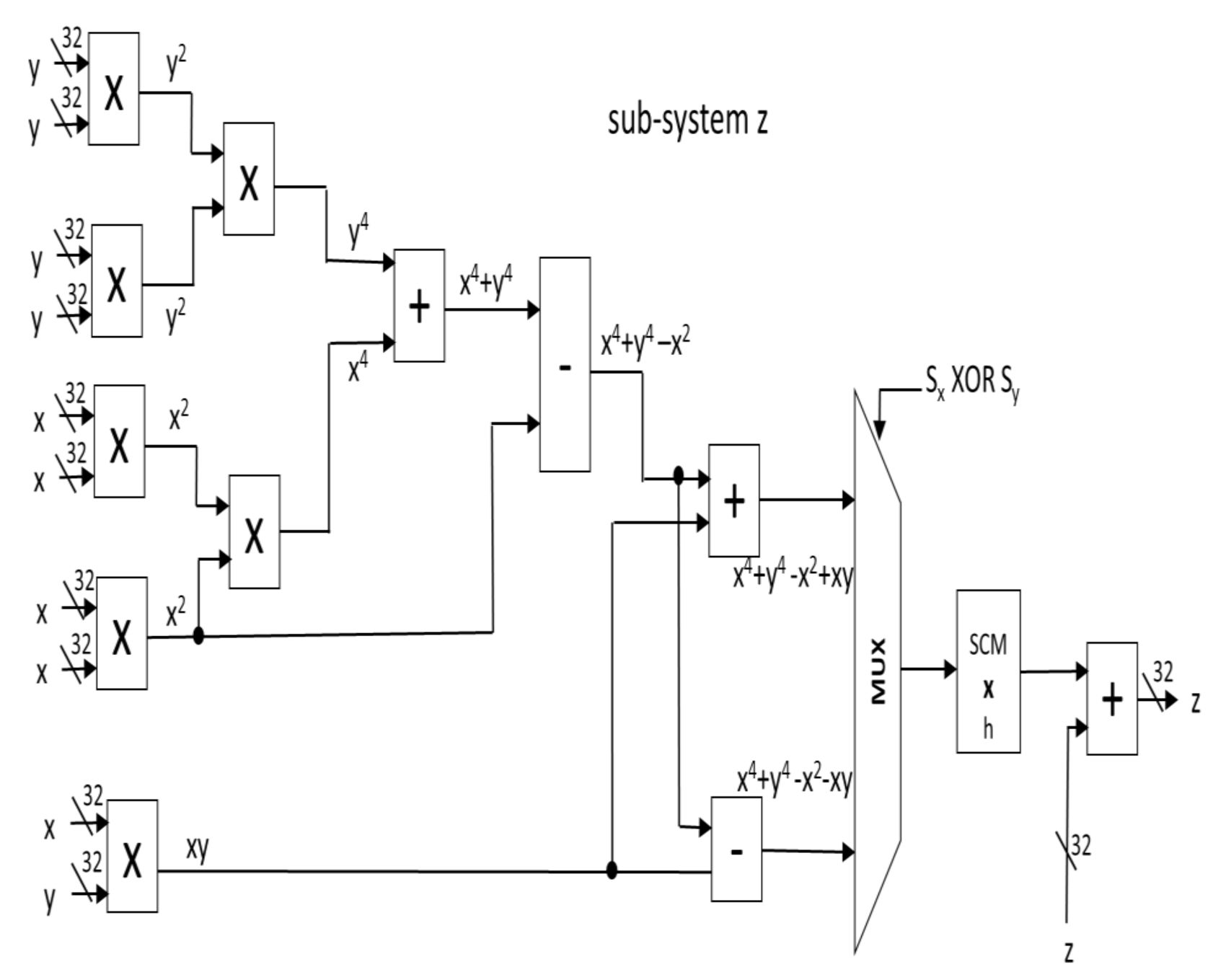
4. FPGA Realization of the Chaotic Dynamical System with a Butterfly-Like Curve of Balance Points
| Algorithm 1 Python code for the new discrete-time chaotic system (9) |
| Input: Initial states x0, y0, and z0. System parameters a, b, and c. Output: xn, yn, and zn j = 1 step = 500,000 x = x0 y = y0z = z0 while j < step do xn.insert(j, x + h ∗ z) yn.insert(j, y + h ∗ (z ∗ (−a ∗ y − b ∗ abs(y) − c ∗ x ∗ z)) zn.insert(j, z + h ∗ (pow(x,4) + pow(y,4) −abs(x) ∗ abs(y) − pow(x,2))) x = xn[j] y = yn[j] z = zn[j] j = j + 1 end |
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, H.; Liu, Z.; Tanougast, C.; Liu, F.; Blondel, W. A novel chaos based optical cryptosystem for multiple images using DNA-blend and gyrator transform. Opt. Lasers Eng. 2021, 138, 106448. [Google Scholar] [CrossRef]
- Zhang, Y. A new unified image encryption algorithm based on a lifting transformation and chaos. Inf. Sci. 2021, 547, 307–327. [Google Scholar] [CrossRef]
- Hua, Z.; Zhu, Z.; Yi, S.; Zhang, Z.; Huang, H. Cross-plane colour image encryption using a two-dimensional logistic tent modular map. Inf. Sci. 2021, 546, 1063–1083. [Google Scholar] [CrossRef]
- Samimi, M.; Majidi, M.H.; Khorashadizadeh, S. Secure communication based on chaos synchronization using brain emotional learning. AEU Int. J. Electron. Commun. 2020, 127, 153424. [Google Scholar] [CrossRef]
- Abbasi, A.A.; Mazinani, M.; Hosseini, R. Chaotic evolutionary-based image encryption using RNA codons and amino acid truth table. Opt. Laser Technol. 2020, 132, 106465. [Google Scholar] [CrossRef]
- Alemami, Y.; Mohamed, M.A.; Atiewi, S.; Mamat, M. Speech encryption by multiple chaotic maps with fast Fourier transform. Int. J. Electr. Comput. Eng. 2020, 10, 5658–5664. [Google Scholar] [CrossRef]
- Bazzi, S.; Sternad, D. Human control of complex objects: Towards more dexterous robots. Adv. Robot. Robt. 2020, 34, 1137–1155. [Google Scholar] [CrossRef]
- Fonseca, L.M.; Savi, M.A. Nonlinear dynamics of an autonomous robot with deformable origami wheels. Int. J. Non-Linear Mech. 2020, 125, 103533. [Google Scholar] [CrossRef]
- Yaghoubi, Z.; Zarabadipour, H. Hybrid neural-network control of mobile robot system via anti-control of chaos. Mech. Syst. Control 2020, 48, 239–248. [Google Scholar] [CrossRef]
- Liu, S.; Jiang, N.; Zhao, A.; Zhang, Y.; Qiu, K. Chaos synchronization and communication in global semiconductor laser network with coupling time delay signature concealment. Appl. Opt. 2020, 59, 6788–6795. [Google Scholar] [CrossRef]
- Schenkendorff, R.; Xie, X.; Krewer, U. An efficient polynomial chaos expansion strategy for active fault identification of chemical processes. Comput. Chem. Eng. 2019, 122, 228–237. [Google Scholar] [CrossRef]
- Xiu, C.; Zhou, R.; Liu, Y. New chaotic memristive cellular neural network and its application in secure communication system. Chaos Solitons Fract. 2020, 141, 110316. [Google Scholar] [CrossRef]
- Yildirim, M.; Kacar, F. Chaotic circuit with OTA based memristor on image cryptology. AEU Int. J. Electron. Commun. 2020, 127, 153424. [Google Scholar] [CrossRef]
- Caldarola, F.; Pantano, P.; Bilotta, E. Computation of supertrack functions for Chua’s oscillator and for Chua’s circuit with memristor. Commun. Nonlinear Sci. Numer. Simul. 2021, 94, 105568. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Pano-Azucena, A.D.; Guillén-Fernández, O.; Silva-Juárez, A. Analog/Digital Implementation of Fractional Order Chaotic Circuits and Applications; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Ding, P.F.; Feng, X.Y.; Wu, C.M. Novel two-directional grid multi-scroll chaotic attractors based on the jerk system. Chin. Phys. B 2020, 29, 108202. [Google Scholar] [CrossRef]
- Huang, Y. A five-dimensional grid multi-wing butterfly chaotic system and its circuit simulation. J. Phys. Conf. Ser. 2020, 1575, 012217. [Google Scholar] [CrossRef]
- Wang, F.; Zhu, B.; Wang, K.; Zhao, M.; Zhao, L.; Yu, J. Physical layer encryption in DMT based on digital multi-scroll chaotic system. IEEE Photonics Technol. Lett. 2020, 32, 1303–1306. [Google Scholar] [CrossRef]
- Mathale, D.; Doungmo Goufo, E.F.; Khumalo, M. Coexistence of multi-scroll chaotic attractors for fractional systems with exponential law and non-singular kernel. Chaos Solitons Fract. 2020, 139, 110021. [Google Scholar] [CrossRef]
- Liu, S.; Wei, Y.; Liu, J.; Chen, S.; Zhang, G. Multi-scroll chaotic system model and its cryptographic application. Int. J. Bifurc. Chaos 2020, 30, 2050186. [Google Scholar] [CrossRef]
- Nag Chowdhury, S.; Ghosh, D. Hidden attractors: A new chaotic system without equilibria. Eur. Phys. J. Spec. Top. 2020, 229, 1299–1308. [Google Scholar] [CrossRef]
- Singh, P.P.; Roy, B.K. A novel chaotic system without equilibria, with parachute and thumb shapes of Poincare map and its projective synchronisation. Eur. Phys. J. Spec. Top. 2020, 229, 1265–1278. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kamdem Kuate, P.D. Modelling and circuit realisation of a new no-equilibrium chaotic system with hidden attractor and coexisting attractors. Electron. Lett. 2020, 56, 1044–1046. [Google Scholar] [CrossRef]
- Pham, V.T.; Vaidyanathan, S.; Volos, C.; Kapitaniak, T. Nonlinear Dynamical Systems with Self-Excited and Hidden Attractors; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Vaidyanathan, S.; Sambas, A.; Lien, C.H.; Idowu, B.A. A new chaotic dynamical system with a hyperbolic curve of rest points, its complete synchronisation via integral sliding mode control and circuit design. Int. J. Model. Identif. Control 2019, 33, 198–207. [Google Scholar] [CrossRef]
- Sambas, A.; Sukono; Vaidyanathan, S.; Hidayat, Y.; Zhang, S.; Gundara, G.; Mohamed, M.A. Dynamic analysis and synchronization of a new chaotic system with a circle equilibrium and two perpendicular lines of equilibrium points. J. Adv. Res. Dyn. Control Syst. 2020, 12, 573–584. [Google Scholar]
- Sambas, A.; Sukono; Zhang, S.; Vaidyanathan, S.; Hidayat, Y.; Mujiarto. Electronic circuit design of a novel chaotic system with apple-shaped curve equilibrium and multiple coexisting attractors. J. Phys. Conf. Ser. 2020, 1477, 022015. [Google Scholar]
- Vaidyanathan, S.; Sambas, A.; Mamat, M. A new chaotic system with axe-shaped equilibrium, its circuit implementation and adaptive synchronization. Arch. Control Sci. 2018, 28, 443–462. [Google Scholar]
- Mamat, M.; Vaidyanathan, S.; Sambas, A.; Mohamed, M.A.; Sampath, S.; Sanjaya, W.S.M. A new 3-D chaotic system with conch-shaped equilibrium curve and its circuit implementation. Int. J. Eng. Tech. 2018, 7, 1410–1414. [Google Scholar] [CrossRef]
- Sambas, A.; Vaidyanathan, S.; Tlelo-Cuautle, E.; Abd-El-Atty, B.; El-Latif, A.A.A.; Guillen-Fernandez, O.; Sukono; Hidayat, Y.; Gundara, G. A 3-D multi-stable system with a peanut-shaped equilibrium curve: Circuit design, FPGA realization, and an application to image encryption. IEEE Access 2020, 8, 137116–137132. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, Y. A simple jerk-like system without equilibrium: Asymmetric coexisting hidden attractors, bursting oscillation and double full Feigenbaum remerging trees. Chaos Solitons Fract. 2019, 120, 25–40. [Google Scholar] [CrossRef]
- Zhang, S.; Zheng, J.; Wang, X.; Zeng, Z.; He, S. Initial offset boosting coexisting attractors in memristive multi double-scroll Hopfield neural network. Nonlinear Dyn. 2020. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, G.; Kuznetsov, N.V.; Bao, H. Hidden attractors and multistability in a modified Chua’s circuit. Commun. Nonlinear Sci. Numer. Simul. 2021, 92, 105494. [Google Scholar] [CrossRef]
- Sabarathinam, S.; Thamilmaran, K. Transient chaos in a globally coupled system of nearly conservative Hamiltonian Duffing oscillators. Chaos Solitons Fract. 2015, 73, 129–140. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, Y.; Li, Z.; Wang, M.; Xiong, L. Generating one to four-wing hidden attractors in a novel 4D no-equilibrium chaotic system with extreme multistability. Chaos 2018, 28, 013113. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Wang, X.; Zeng, Z. A simple no-equilibrium chaotic system with only one signum function for generating multidirectional variable hidden attractors and its hardware implementation. Chaos 2020, 30, 053129. [Google Scholar] [CrossRef] [PubMed]
- Bonny, T. Chaotic or hyper-chaotic oscillator? Numerical solution, circuit design, MATLAB HDL-coder implementation, VHDL code, security analysis, and FPGA realization. Circuits Syst. Signal Process. 2020. [Google Scholar] [CrossRef]
- Bonny, T.; Nasir, Q. Clock glitch fault injection attack on an FPGA-based non-autonomous chaotic oscillator. Nonlinear Dyn. 2019, 96, 2087–2101. [Google Scholar] [CrossRef]
- Bonny, T.; Al Debsi, R.; Majzoub, S.; Elwakil, A.S. Hardware optimized FPGA implementations of high-speed true random bit generators based on switching-type chaotic oscillators. Circuits Syst. Signal Process. 2019, 38, 1342–1359. [Google Scholar] [CrossRef]
- Bonny, T.; Elwakil, A.S. FPGA realizations of high-speed switching-type chaotic oscillators using compact VHDL codes. Nonlinear Dyn. 2018, 93, 819–833. [Google Scholar] [CrossRef]
- Tuna, M. A novel secure chaos-based pseudo random number generator based on ANN-based chaotic and ring oscillator: Design and its FPGA implementation. Analog Integr. Circuits Signal Process. 2020, 105, 167–181. [Google Scholar] [CrossRef]
- Saber, M.; Hagras, E.A.A. Parallel multi-layer selector S-Box based on Lorenz chaotic system with FPGA implementation. Indones. J. Electr. Eng. Comput. Sci. 2020, 19, 784–792. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov Exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef] [Green Version]
- Cencini, M.; Cecconi, F.; Vulpiani, A. Chaos from Simple Models to Complex Systems; World Scientific: Singapore, 2010. [Google Scholar]
- Chapra, S.; Canale, R. Numerical Methods for Engineers; McGraw-Hill: New York, NY, USA, 2014. [Google Scholar]



| Chaotic System | The Curve of Balance Points |
|---|---|
| Vaidyanathan et al. [25] | Hyperbola |
| Sambas et al. [26] | Circle |
| Sambas et al. [27] | Apple |
| Vaidyanathan et al. [28] | Axe |
| Mamat et al. [29] | Conch |
| Sambas et al. [30] | Peanut |
| Resources | Available | Sub-System X | Sub-System Y | Sub-System Z | Complete System |
|---|---|---|---|---|---|
| Use (%) | Use (%) | Use (%) | Use (%) | ||
| FF | 106,400 | 107 (0.10%) | 172 (0.16%) | 209 (0.2%) | 390 (0.37%) |
| LUT | 53,200 | 137 (0.26%) | 877 (1.65%) | 434 (0.82%) | 1295 (2.43%) |
| I/O | 200 | 99 (49.5%) | 99 (49.5%) | 99 (49.5%) | 99 (49.5%) |
| DSP48 | 220 | 0 (0%) | 8 (3.64%) | 20 (9.09%) | 28 12.73%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sambas, A.; Vaidyanathan, S.; Bonny, T.; Zhang, S.; Sukono; Hidayat, Y.; Gundara, G.; Mamat, M. Mathematical Model and FPGA Realization of a Multi-Stable Chaotic Dynamical System with a Closed Butterfly-Like Curve of Equilibrium Points. Appl. Sci. 2021, 11, 788. https://doi.org/10.3390/app11020788
Sambas A, Vaidyanathan S, Bonny T, Zhang S, Sukono, Hidayat Y, Gundara G, Mamat M. Mathematical Model and FPGA Realization of a Multi-Stable Chaotic Dynamical System with a Closed Butterfly-Like Curve of Equilibrium Points. Applied Sciences. 2021; 11(2):788. https://doi.org/10.3390/app11020788
Chicago/Turabian StyleSambas, Aceng, Sundarapandian Vaidyanathan, Talal Bonny, Sen Zhang, Sukono, Yuyun Hidayat, Gugun Gundara, and Mustafa Mamat. 2021. "Mathematical Model and FPGA Realization of a Multi-Stable Chaotic Dynamical System with a Closed Butterfly-Like Curve of Equilibrium Points" Applied Sciences 11, no. 2: 788. https://doi.org/10.3390/app11020788





