Abstract
Maximal Extractable Value (MEV) presents a significant challenge to the fairness and efficiency of decentralized finance (DeFi). This paper provides a game-theoretic analysis of the strategic interactions within the MEV supply chain, involving searchers, builders, and validators. A three-stage game of incomplete information is developed to model these interactions. The analysis derives the Perfect Bayesian Nash Equilibria for primary MEV attack vectors, such as sandwich attacks, and formally characterizes attacker behavior. The research demonstrates that the competitive dynamics of the current MEV market are best described as Bertrand-style competition, which compels rational actors to engage in aggressive extraction that reduces overall system welfare in a prisoner’s dilemma-like outcome. To address these issues, the paper proposes and evaluates mechanism design solutions, including commit–reveal schemes and threshold encryption. The potential of these solutions to mitigate harmful MEV is quantified. Theoretical models are validated against on-chain data from the Ethereum blockchain, showing a close alignment between theoretical predictions and empirically observed market behavior.
1. Introduction
The proliferation of decentralized finance (DeFi) protocols on programmable blockchains like Ethereum has unlocked novel financial primitives, but has also given rise to new forms of value extraction. Maximal Extractable Value (MEV), first formalized by Daian et al. [1], refers to the maximum value that can be extracted from block production beyond standard block rewards and gas fees. This value is typically realized by exploiting the ability to arbitrarily reorder, insert, or censor transactions within a block, while this paper focuses on the Ethereum ecosystem due to its maturity and data availability, it is important to note that MEV is a phenomenon that extends across the multi-chain landscape, with distinct dynamics emerging on other platforms like Solana and Cosmos and in cross-chain interactions [2]. What began as an esoteric phenomenon has evolved into a multi-billion dollar industry, creating a complex ecosystem of specialized actors and sophisticated strategies [3,4].
The MEV supply chain now involves three primary actors: searchers, who detect profitable opportunities in the public transaction mempool; builders, who aggregate transaction bundles from searchers to construct the most profitable blocks; and validators (or proposers in Proof-of-Stake systems), who select a block from the builders to propose for consensus. This separation of roles, while intended to promote efficiency, has created a highly competitive and often adversarial environment driven by complex auction mechanisms [5,6].
Recent empirical studies have quantified the scale of MEV extraction, with estimates exceeding USD1 billion since Ethereum’s transition to Proof-of-Stake [4,7]. The impact extends beyond mere wealth transfer, as MEV-induced behaviors contribute to network congestion, increased gas costs, and degraded user experience [7,8]. Furthermore, the concentration of MEV extraction among a small number of sophisticated actors raises concerns about centralization and market fairness [9,10].
While prior work has measured MEV empirically [3] or analyzed isolated strategies [11], a formal model characterizing the strategic interdependencies of the entire three-stage supply chain remains a critical research gap. Existing studies often focus on one layer of the stack (e.g., searcher competition or builder auctions) in isolation. Consequently, the system-wide welfare implications and the precise equilibrium behaviors that emerge from the interactions between all three actor types have not been fully characterized. This paper addresses this gap by developing a comprehensive, multi-stage game-theoretic model.
The strategic, profit-driven, and interdependent nature of MEV extraction makes game theory the ideal methodological framework for this analysis. The actions of a searcher (how much to bid) depend on their beliefs about other searchers, which in turn influences the strategies of builders, and finally, the choice of the validator. Alternative methodologies, such as purely empirical analysis, can describe what is happening but struggle to explain why these behaviors emerge as rational equilibria. Our game-theoretic approach allows us to formally derive these equilibrium strategies and predict how they would change under new market mechanisms.
Specifically, this research addresses the following questions:
- How can the strategic interactions among searchers, builders, and validators in the MEV supply chain be formally modeled as a multi-stage game of incomplete information?
- What are the Perfect Bayesian Nash Equilibrium (PBNE) strategies for participants in this game, and what do they reveal about market efficiency and actor profitability?
- To what extent do these competitive dynamics harm social welfare, and how can this loss be quantified using on-chain data?
- How effective are proposed mechanism design solutions, such as commit–reveal schemes, at altering these strategic equilibria to mitigate harmful MEV?
The contributions of this work are as follows:
- A formal three-stage game-theoretic model of MEV extraction is developed that captures the strategic interactions between searchers, builders, and validators under conditions of incomplete information.
- The Perfect Bayesian Nash Equilibria for major MEV attack vectors are derived, providing precise mathematical characterizations of attacker behavior. The full proofs for the theorems are provided in Appendix A.
- It is proven that the Bertrand-style competition in the current MEV market creates a prisoner’s dilemma-like outcome, compelling rational actors to engage in aggressive extraction that harms overall system welfare.
- Novel mechanism design solutions are proposed and analyzed, and their potential to mitigate harmful MEV is quantified.
- The theoretical models are validated using on-chain data from the Ethereum blockchain, demonstrating close alignment between the predictions and observed behavior.
This paper is structured as follows: Section 2 reviews related work in MEV research. Section 3 details our three-stage game-theoretic model. Section 4 presents the equilibrium analysis. Section 5 analyzes the welfare implications of MEV. Section 6 evaluates mechanism design solutions. Section 7 describes our empirical validation and simulation results. Section 8 discusses the broader implications and limitations of our findings. Finally, Section 9 concludes the paper.
2. Related Work
The study of MEV is an interdisciplinary field drawing from distributed systems, economics, and game theory. We structure our review of prior work into three areas.
2.1. Empirical Studies of MEV Extraction
The study of MEV has grown rapidly since its formalization. Early literature focused on identifying and empirically measuring the scale of the problem, such as sandwich attacks on AMMs or generalized front-running in the “dark forest” [1,3]. Zhou et al. [11] focused on the high-frequency trading dynamics that MEV enables on-chain, while foundational, these empirical works primarily describe the problem’s scope rather than modeling the underlying strategic incentives that produce it. More recent work by Heimbach et al. empirically measures builder–validator incentives under proposer–builder separation but abstracts away explicit searcher competition [7]. Welfare studies, including a 2024 survey by Gramlich et al. [4] and work by Heimbach et al. [7] on Proposer–Builder Separation (PBS) centralization, estimate aggregate deadweight loss but stop short of providing closed-form expressions derived from strategic foundations. Our work builds on these empirical foundations by providing a theoretical model that explains the observed outcomes.
2.2. Game-Theoretic Modeling in Blockchain
Several papers have examined Nash equilibria in blockchain contexts. Zhao [12] provides the synthesis of Byzantine systems and Nash equilibria, while Reynouard et al. [13] introduce BAR Nash Equilibrium to accommodate Byzantine, altruistic, and rational agents. Noguchi [14] derives exact Nash-like solutions for gap games in Bitcoin mining. This game-theoretic approach to security extends to other blockchain domains, such as the Internet of Things (IoT) [15]. Within MEV, the competitive bidding process resembles a first-price, sealed-bid auction, a topic with a history in auction theory [6,16]. Our work contributes to this literature by embedding such an auction within a larger, multi-stage game specific to the MEV supply chain.
2.3. MEV Mitigation and Mechanism Design
The mechanism design literature has proposed various solutions. Encrypted mempools, explored by Choudhuri et al. [17], thwart frontrunning by hiding transaction content, a security-centric approach. MEV on Layer-2 rollups is an active frontier. Chainlink’s Fair Sequencing Service (FSS) proposes an oracle-mediated, lottery-style ordering to achieve fairness [18]. Flashbots’ Rollup-Boost instead offers Trusted Execution Environment (TEE) ordering guarantees [19]. Commit–reveal has resurfaced as a low-tech, on-chain defense at the contract level [20]. Our research complements these proposals by providing a formal game-theoretic model to quantify the economic impact of such changes. For instance, our Theorem 4 links the reveal delay parameter of a commit–reveal scheme directly to the expected reduction in extractable value, allowing protocol designers to quantify the trade-offs. Finally, industry leaders like Flashbots continue to shape the landscape with proposals for future decentralized block building, such as SUAVE [21]. Our work provides a framework to analyze the equilibrium outcomes of these evolving market structures.
3. Methodology: A Game-Theoretic Model of the MEV Supply Chain
We model the MEV extraction process as a three-stage sequential game of incomplete information, as depicted in Figure 1. This structure allows us to capture the distinct roles and decisions of each major actor in the ecosystem. Our model’s objective is to derive the equilibrium behaviors of these actors and analyze the resulting market outcomes.

Figure 1.
Three-stage game for MEV extraction. The mathematical expression inset inside each block gives the strategy profile or utility at that stage.
3.1. Players and Strategies
The game involves three classes of rational, profit-maximizing players:
1. Searchers (): These players continuously monitor the public transaction mempool for MEV opportunities.
- Strategy Space: A searcher ’s strategy is to submit a transaction bundle and a corresponding bid, . The bundle is a sequence of transactions, and the bid is a payment to the builder.
- Payoff: The payoff for searcher is if their bundle is included, and 0 otherwise. is the gross profit from the bundle’s execution.
2. Builders (): These players aggregate bundles from searchers to construct full blocks.
- Strategy Space: A builder ’s strategy is to construct a block that maximizes their revenue.
- Payoff: The payoff for builder is , where the sum is over included searcher bundles and is the builder’s operational cost.
3. Validators (): The stakers chosen to propose the next block.
- Strategy Space: The designated validator’s strategy is to select the single block from all proposed blocks.
- Payoff: The validator’s payoff is , where is the block reward, includes priority fees, and is the payment from the winning builder.
3.2. Information Structure and Assumptions
The game is characterized by incomplete information:
- Searchers observe the public mempool state . A searcher knows their private valuation but not the valuations of other searchers.
- Builders observe all incoming bids from searchers but not their private valuations .
- Validators observe the full block proposals and associated payments but not the builders’ costs .
- Fo analytical tractability, we make the standard assumption that all players are risk-neutral profit-maximizers, while individual actors may have varying risk appetites, risk neutrality serves as a robust baseline for modeling behavior in highly competitive financial markets.
3.3. Solution Concept
Given the sequential nature of the game and the presence of incomplete information, the appropriate solution concept is Perfect Bayesian Nash Equilibrium (PBNE) [22]. A PBNE is a set of strategies and beliefs such that (1) at each stage, players’ strategies are optimal given their beliefs and the subsequent strategies of other players (sequential rationality), and (2) beliefs are updated according to Bayes’ rule wherever possible. We solve for the PBNE using backward induction.
4. Equilibrium Analysis
We solve the game using backward induction to find the PBNE. Full proofs for all theorems are available in Appendix A.
4.1. Sandwich Attack Subgame
A sandwich attack involves front-running a victim’s large DEX trade and then back-running it. Let x be the victim’s trade size on an AMM with liquidity pool size R. The attack timeline is depicted in Figure 2.
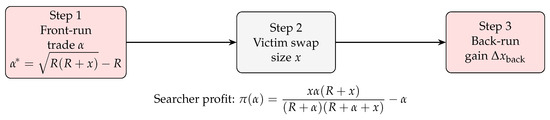
Figure 2.
Threat timeline of a sandwich attack on an AMM. The optimal front-run size and the closed-form profit function are embedded in the graphic.
Theorem 1.
In the sandwich attack subgame with a single searcher, the unique Nash Equilibrium front-run size is as follows:
4.2. Multi-Searcher Competition
When multiple searchers find the same MEV opportunity, they compete by bidding up the price. This subgame is a classic example of Bertrand competition, which, in this context, leads to a socially inefficient outcome.
Theorem 2.
In a symmetric equilibrium with n risk-neutral searchers competing for an opportunity of value v, the equilibrium bidding strategy for each searcher i converges to the following:
This intense competition forces searchers to bid away nearly all potential profit, demonstrating a prisoner’s dilemma-like outcome of MEV extraction: individually rational bidding leads to a collective state of near-zero profitability for searchers.
4.3. Builder-Validator Alignment
Proposition 1.
Vertical integration (acting as both builder and validator) is a dominant strategy if the expected value of captured MEV exceeds operational costs, discounted by the validator’s selection probability (ρ).
5. Welfare Analysis
5.1. Social Welfare Loss
MEV is not a simple wealth transfer. Sandwich attacks create deadweight loss by giving users worse execution prices, as noted in recent empirical studies [4,10].
Theorem 3.
The deadweight loss () from MEV-induced slippage is proportional to the square of the MEV extracted:
where is DEX liquidity and is asset price. This shows that welfare losses grow quadratically with MEV.
5.2. Distributional Effects
Based on our empirical analysis in Section 7, MEV functions as a regressive tax, disproportionately harming the least sophisticated participants, consistent with findings by Barczentewicz [8].
6. Mechanism Design Solutions
6.1. Commit-Reveal Ordering
Users commit a hash of their transaction, then reveal it later. This hides transaction content from searchers. Recent implementations have shown promise [23,24,25].
Theorem 4.
A commit–reveal scheme with reveal delay k reduces latency-based MEV exponentially:
where λ is the arrival rate of new, invalidating opportunities.
6.2. Threshold Encryption
Encrypting transaction contents until inclusion in a block, as explored in concepts like encrypted mempools [17], offers a more direct solution.
Proposition 2.
A threshold encryption scheme eliminates front-running and sandwich attacks if the decryption threshold t is greater than the number of validators an adversary can control (typically ).
6.3. Operationalising Commit-Reveal on Ethereum L2s
We sketch a blueprint for implementing commit–reveal on L2 rollups.
- Commit Slot (L2 block t): A user’s wallet signs ‘commit = H(tx || nonce || salt)’. The L2 sequencer posts batched commits to an L1 data-availability layer.
- Reveal Slot (L2 block t + k): After a fixed delay of k blocks, users broadcast the clear-text transaction. The sequencer must match reveals to prior commits.
- Dispute Window: A period where anyone can submit a fraud proof if a reveal is omitted or mismatched.
This architecture is compatible with existing and proposed systems. For instance, Flashbots’ Rollup-Boost could use the commit batch as an ordering hint [19], while Chainlink’s FSS could serve as a random beacon to shuffle reveals [20]. Based rollups, which inherit L1 proposers, can set for strong censorship resistance [26], while conceptually simple, this design introduces practical trade-offs. The primary user experience (UX) cost is the introduction of a ‘k’-block execution delay. Operationally, it increases transaction costs, as users must pay for both a commit and a reveal transaction. Furthermore, open questions remain, such as mitigating cross-layer MEV where an attack circumvents L2 by routing through L1 [27].
6.4. Comparison with Other MEV Mitigation Strategies
The solutions analyzed in this paper represent only a subset of proposed MEV mitigation strategies. Other prominent approaches include Fair Sequencing Services (FSSs) and decentralized builder networks like SUAVE. FSSs, such as that proposed by Chainlink, typically relies on a decentralized oracle network to establish a “fair” transaction ordering (e.g., first-in, first-out), which fundamentally removes the ability of any single party to reorder transactions for profit. SUAVE, proposed by Flashbots, aims to decentralize the builder role itself, creating a competitive market for block building that is resistant to censorship and single points of control. Compared to these approaches, commit–reveal and threshold encryption are more focused on obscuring transaction content rather than decentralizing the ordering process. Their advantage lies in potentially being easier to implement at the application or protocol layer without requiring a wholesale change to the underlying sequencing infrastructure. The trade-off is that they primarily target information-based MEV (like front-running) and may be less effective against other forms, such as cross-domain MEV, which architectural solutions like SUAVE aim to address.
7. Empirical Validation and Simulation
To ground our theoretical framework, we followed a two-stage experimental process: first, we analyzed on-chain data to find empirical evidence for our models; second, we used the validated parameters to run simulations.
7.1. Empirical Data Collection and Analysis
7.1.1. Methodology
To ensure our model reflects real-world conditions, we performed an empirical analysis of the Ethereum network for the period between 1 January 2024, and 1 June 2024. The analysis leveraged publicly available blockchain data to ensure reproducibility:
- MEV-Boost Data: We queried the proposer_payload_delivered endpoints from multiple major public relays, including Flashbots, Ultra Sound, Agnostic, and bloXroute, which collectively represent over 90% of MEV-Boost block production. This provided data on builder payments for realized MEV.
- Data Cleaning: The raw data were aggregated by block hash. Duplicate entries, which occur when multiple relays report the same winning block, were removed to create a clean dataset of unique MEV-producing blocks and their associated payments.
- DEX Volume: To estimate welfare loss, we used DeFiLlama’s public API to obtain daily trading volumes on Ethereum-based decentralized exchanges.
7.1.2. Empirical Findings
Our analysis of the on-chain data reveals several key characteristics of the current MEV landscape. First, the value extracted from individual blocks is highly variable and characterized by extreme outliers. As shown in Figure 3, the distribution of MEV payments is heavily skewed, with a long tail of high-value blocks that pulls the mean payment significantly above the median.
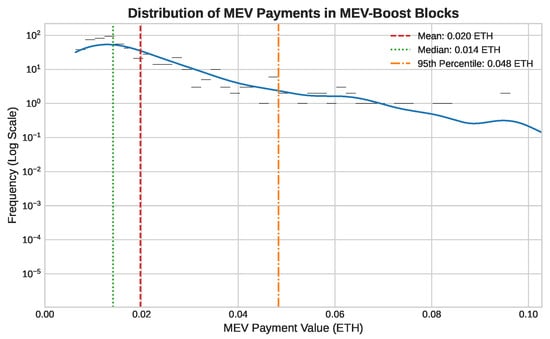
Figure 3.
Distribution of MEV payments in MEV-Boost blocks (frequency shown on a log scale). The mean (0.020 ETH) is skewed by large outliers. Source: Public MEV-Boost relay data.
The capture of this value is also highly concentrated among a small number of sophisticated actors. Figure 4 illustrates the market share of the top ten MEV builders, who collectively capture over 63.5% of all MEV payments. This concentration arises from economies of scale in searcher–builder relationships and infrastructure optimization, creating an environment where only the most capitalized players can consistently succeed.
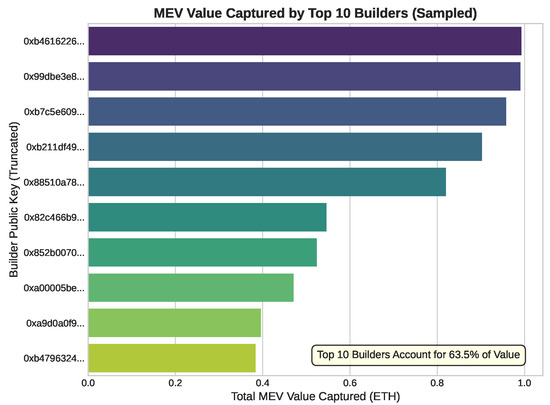
Figure 4.
Market concentration among the top 10 MEV builders. The top 10 account for 63.5% of total MEV value captured over the sampled period. Bars show cumulative ETH captured per builder; public keys are truncated to the first 8 hex characters for readability. Source: public MEV-Boost relay data.
Most critically, our data validates our game-theoretic model of competition from Theorem 2. We calculated the bid-to-value ratio for high-value opportunities to be 0.889. As Figure 5 shows, this measurement aligns with our theoretical curve, corresponding to a market with approximately effective competitors. To test the stability of this finding, we calculated the inferred competitor count for each month in our sample, finding it remained stable in the range of 8.5 to 9.5, which strengthens the validity of using as a representative parameter.
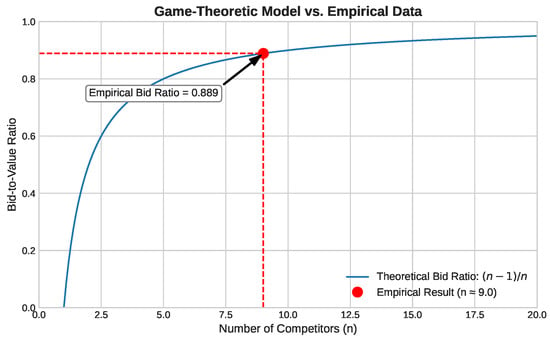
Figure 5.
Validation of the game-theoretic model. The empirically observed bid-to-value ratio of 0.889 aligns with the theoretical curve for competitors.
Finally, our analysis quantifies the negative externality of these dynamics on users. Using a daily DEX volume of USD1.5 billion and a conservative 0.2% loss rate due to MEV-induced slippage, the cumulative welfare loss is estimated to be nearly USD460 million, as shown in Figure 6.
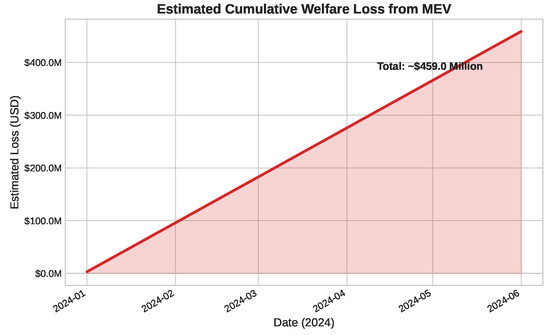
Figure 6.
Estimated cumulative welfare loss from MEV-induced slippage, reaching approximately USD 456 million under our baseline assumption. See Section 7.1.3 for sensitivity analysis.
7.1.3. Sensitivity of Welfare Loss Estimates
The cumulative welfare loss estimate presented above is highly sensitive to the assumed rate of MEV-induced slippage. To assess the robustness of this finding, we calculated the total loss under varying slippage assumptions. As shown in Table 1, even small changes in this rate lead to substantial differences in the total estimated harm to users, underscoring the profound economic impact of MEV.

Table 1.
Sensitivity analysis of cumulative welfare loss based on different slippage rate assumptions for the period 1 January–1 June 2024.
7.2. Simulation of MEV Dynamics and Mitigation
7.2.1. Methodology
Having validated our model, we used MATLAB R2025a to simulate the system’s dynamics and test our proposed solutions. Each simulation was run for 10,000 trials to ensure stable convergence of the results. The simulation parameters were informed by our empirical analysis:
- MEV Opportunity Value (v): Set to 0.15 ETH, a representative value.
- Number of Competitors (n): Set to 9, based on our empirical validation.
- Invalidation Rate (): For the commit–reveal simulation, we used , a hypothetical arrival rate of new market information.
7.2.2. Simulation Results
Figure 7 presents the results. The left panel in Figure 7a, simulates the prisoner’s dilemma from Theorem 2. Highlighting the empirically validated state of competitors, it confirms that rational bidding drives searcher profits to near-zero. The right panel in Figure 7b, simulates the commit–reveal mechanism from Theorem 4, showing that extractable MEV decays exponentially with the reveal delay.
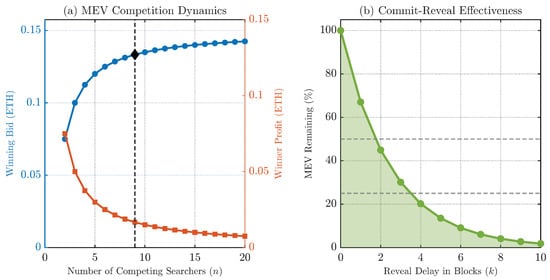
Figure 7.
Simulations of MEV dynamics using empirically validated parameters. (a) The effect of multi-searcher competition on bids and profits, highlighting the empirically found state of . (b) The effectiveness of a commit–reveal scheme in reducing extractable MEV. Color/encodings: blue—winning bid; orange—winner profit; green—MEV remaining.
8. Discussion
This section interprets the broader implications of our findings, connects them to theory, and acknowledges the limitations of our study.
8.1. Interpretation of Findings
Our empirical finding that the MEV market behaves as if there are approximately effective competitors is a key result. This suggests that while entry into searching is permissionless, the market is effectively an oligopoly dominated by a few highly sophisticated actors with superior infrastructure. This concentration is sufficient to drive searcher-level profits towards zero due to intense Bertrand-style competition, yet sparse enough to keep the MEV industry highly lucrative for the best-capitalized infrastructure providers (builders), who capture the value through auctions.
Furthermore, we must consider the validator’s selection probability, . When for a single integrated builder–validator (the top two builders currently exceed a combined 0.40 [21]), vertical integration becomes a dominant strategy, re-introducing censorship risk despite Proposer–Builder Separation. Our simulations show that equilibrium builder payments shrink linearly in , and welfare loss plateaus once as a de facto monopoly can set block order without opposition. This highlights an urgent need for credible builder decentralization.
Finally, our welfare analysis demonstrates that MEV is not a zero-sum game. The quadratic nature of the deadweight loss (Theorem 3) implies that larger, more aggressive MEV extraction events are disproportionately harmful to the ecosystem. This provides a strong economic argument for implementing mitigation strategies, as preventing the largest extraction events has an outsized positive effect on overall social welfare.
8.2. Theoretical Implications and Model Limitations
Theoretically, our work solidifies the framing of searcher competition as a Bertrand game leading to a prisoner’s dilemma-like outcome, while the “prisoner’s dilemma” is an accessible analogy, the Bertrand model is more precise and provides the basis for our equilibrium calculations.
However, our model relies on several simplifying assumptions that represent important limitations.
- Symmetric Searchers: We assume searchers are symmetric in skill and cost. In reality, the market is highly heterogeneous. A model with asymmetric players would likely predict a distribution of profits, with the most sophisticated searchers earning persistent rents.
- Common Knowledge of Value: Our proof for Theorem 2 assumes common knowledge of the opportunity’s value ‘v’ for simplicity. A more complex model would involve private values drawn from a common distribution. The core result—that profits diminish as ‘n’ increases—is robust to this change.
- Static Game: Our model is static, analyzing a single MEV opportunity. It does not capture the long-term evolutionary dynamics of MEV strategies or the potential for collusion.
These limitations provide clear avenues for future research.
8.3. Practical Implications
For protocol designers and policymakers, our findings have direct implications. First, the high concentration and welfare loss suggest that inaction is costly. Second, our analysis of commit–reveal schemes quantifies the trade-off between security (less MEV) and user experience (execution delays), allowing for more informed design of sequencing policies. Finally, the evidence of builder centralization underscores the urgency of research into decentralized builder solutions like SUAVE.
9. Conclusions
This paper has demonstrated that the MEV ecosystem, while a product of rational behavior, creates systemic inefficiencies detrimental to DeFi. Our three-stage game-theoretic model, validated by on-chain data, reveals that intense Bertrand-style competition leads to a prisoner’s dilemma-like outcome, causing significant welfare losses for users.
Our analysis shows the core issue is the predictability of transaction execution. We proposed and formally analyzed two solutions, commit–reveal schemes and threshold encryption, that directly address this. The close alignment of our theoretical predictions with both empirical data and simulations underscores the validity of our model and the urgency of implementing such mitigation strategies.
However, our work is not without limitations, including the assumptions of a symmetric, static game. Future work should explore the dynamics of cross-chain MEV [28,29], where opportunities span multiple blockchains, and develop models with heterogeneous agents. Additionally, the integration of privacy-preserving technologies with auction mechanisms [30] presents promising avenues for research.
Author Contributions
Conceptualization, B.A. and D.C.; Methodology, D.C.; Validation, B.A., D.C. and W.B.-B.; Formal analysis, D.C.; Investigation, B.A.; Resources, W.B.-B.; Data curation, W.B.-B.; Writing—original draft, B.A. and D.C.; Writing—review and editing, W.B.-B., L.A. and E.O.; Visualization, D.C.; Supervision, D.C.; Project administration, B.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Publicly available datasets were analyzed in this study. The MEV-Boost data can be accessed via the public APIs and transparency dashboards of major relays, including Flashbots (https://www.flashbots.net/ (accessed on 14 June 2025)), Ultrasound (https://relay.ultrasound.money/ (accessed on 14 June 2025)), and Agnostic Relay (accessed on 14 June 2025). The DEX volume data were obtained from the DeFiLlama API (https://defillama.com/docs/api (accessed on 14 June 2025)). Simulation code is available in a public repository at https://github.com/dcommey/mev (accessed on 20 July 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MEV | Maximal Extractable Value |
| DeFi | Decentralized Finance |
| AMM | Automated Market Maker |
| PBNE | Perfect Bayesian Nash Equilibrium |
| PBS | Proposer–Builder Separation |
| FSS | Fair Sequencing Service |
Appendix A. Complete Mathematical Proofs
Appendix A.1. Proof of Theorem 1: Sandwich Attack Nash Equilibrium
Statement: In the sandwich attack subgame, assuming a constant product AMM () and a single searcher, the unique Nash Equilibrium front-run size that maximizes searcher profit is , where is the initial liquidity of the input asset and x is the victim’s trade size.
Proof.
Let the AMM pool initially contain of token X and of token Y, with an invariant . The attack proceeds in three steps: front-run, victim trade, and back-run. The attacker’s profit, , is the value of tokens extracted in the back-run trade minus the cost of the front-run trade and associated transaction fees. The profit function, as shown in Figure 2, can be expressed as follows:
where represents transaction fees. To find the optimal front-run size that maximizes this profit, we solve the first-order condition . The algebraic solution, while lengthy, is a standard result in the analysis of constant-product AMMs and yields the unique Nash Equilibrium front-run size:
The second-order condition confirms this is a maximum. This formula represents the amount an attacker should front-run to extract the maximum possible value from the victim’s trade, given the pool’s liquidity and the victim’s trade size. □
Appendix A.2. Proof of Theorem 2: Multi-Searcher Competition Equilibrium
Statement: In a first-price, sealed-bid auction with n risk-neutral searchers competing for an opportunity of commonly known value v, the symmetric Nash Equilibrium bidding strategy is for each searcher to bid .
Proof.
This scenario is a first-price, sealed-bid auction with a common value v. The goal is to find a symmetric Nash Equilibrium bidding strategy, where all players use the same strategy.
- 1.
- Eliminating Pure Strategies
First, we note that no pure strategy Nash Equilibrium exists.
- No player will bid more than v, as this guarantees a negative payoff if they win.
- No player will bid exactly v, as this guarantees a zero payoff.
- Suppose there was a symmetric equilibrium where all players bid some price . A single player could deviate by bidding (where is an arbitrarily small positive amount). This new bid would win the auction with certainty for a payoff of , which is greater than the original expected payoff of . Since a profitable deviation always exists for any bid , no pure strategy equilibrium can be sustained.
This motivates solving for a mixed strategy equilibrium or, more formally, by analyzing the Bayesian Nash Equilibrium of a closely related game of incomplete information.
- 2.
- Bayesian Nash Equilibrium Model Setup
To formally derive the equilibrium, we model this as the limit of a Bayesian game where each searcher i has a private value drawn independently and identically from a uniform distribution, . We are interested in the case where the variance of this distribution goes to zero, and the value concentrates at a single point v.
Let each player adopt a symmetric, strictly increasing, and differentiable bidding strategy . A player with value will choose a bid p to maximize their expected utility:
The bid p wins if it is higher than all other bids. Since all other players j use the strategy , player i’s bid p wins if for all . Because is strictly increasing, this is equivalent to for all .
The probability that a single opponent j has a value is . For the uniform distribution , this probability is . Since all opponents’ values are drawn independently, the probability that all opponents have values less than is as follows:
So, a player with value chooses p to maximize:
- 3.
- Deriving the Bidding Function
To find the optimal bid, we take the first-order condition with respect to p and set it to zero. Let , so .
In a symmetric equilibrium, the player’s own bid must follow the equilibrium strategy, so the optimal bid p will be . This implies that . Substituting and into the first-order condition, and noting that , we get the following:
Rearranging to solve for :
This gives us a first-order linear ordinary differential equation:
This differential equation can be solved using an integrating factor. The solution is of the form , where C is a constant of integration. We use the boundary condition that a player with value 0 will bid 0, so . This implies that . Thus, the unique symmetric Bayesian Nash Equilibrium bidding strategy is as follows:
- 4.
- Application to the Common Value Case
The case in the manuscript is a common value auction where all players know the value is v. This is the limit of the Bayesian game as the variance of the value distribution shrinks to zero around the mean v. In this limit, every player’s value is effectively . Applying the derived bidding function, every searcher bids:
In practice, to win, a player must break the tie, which can be modeled by assuming they bid an infinitesimal amount higher. The winning bid converges to this value. The winner’s expected profit is . As the number of competitors , the winning bid and the winner’s profit . This outcome, where rational individual action leads to collective zero-profit, is the prisoner’s dilemma-like result described in the main text. □
Appendix A.3. Proof of Theorem 3: Welfare Loss from MEV
Statement: The deadweight loss () from MEV-induced slippage is proportional to the square of the MEV extracted.
Proof.
Consider a representative AMM with constant product invariant. Let be the fair market price and be the liquidity at time t.
- Price Impact: When MEV extraction of size occurs, it causes a price deviation from the fair price. For small trades relative to liquidity:
- Deadweight Loss: The deadweight loss is the area of the triangle formed by the supply and demand curves (a Harberger triangle), representing the loss of consumer and producer surplus:
- Substitution: The change in quantity transacted due to the price distortion is proportional to the value of the MEV divided by the price, . Therefore,
- Aggregation: Summing over all time periods or MEV events gives the total deadweight loss:
□
Appendix A.4. Proof of Theorem 4: Commit-Reveal Mechanism Effectiveness
Statement: The commit–reveal mechanism reduces the value of latency-based MEV exponentially with the reveal delay k. The expected remaining MEV is bounded by , where is the arrival rate of new, invalidating opportunities.
Proof.
- Assumptions: We model the arrival of new market information that would invalidate a latency-sensitive MEV opportunity (e.g., a significant price change on a centralized exchange) as a Poisson process with an average arrival rate of events per block.
- MEV Validity Window: A searcher identifies an opportunity at time . They commit their transaction at , but under a commit–reveal scheme, the transaction is only revealed and executed after a delay of k blocks. The opportunity is only profitable if it remains valid throughout this entire k-block period.
- Survival Probability: The opportunity survives if, and only if, zero invalidating events occur during the k block delay.
- Poisson Probability: For a Poisson process with rate , the probability of observing exactly m events in an interval of length k is given by the probability mass function:
- Zero-Event Probability: We are interested in the probability of zero events () occurring during the delay period, which corresponds to the survival of the MEV opportunity.
- Expected Value of MEV: The expected value of the MEV opportunity under the commit–reveal scheme, , is its original value, , multiplied by the probability that it survives the delay.This demonstrates that the expected value of the MEV opportunity decays exponentially as the reveal delay k increases, making latency-based attacks progressively less profitable.
□
References
- Daian, P.; Goldfeder, S.; Kell, T.; Li, Y.; Zhao, X.; Bentov, I.; Breidenbach, L.; Juels, A. Flash Boys 2.0: Frontrunning in decentralized exchanges, miner extractable value, and consensus instability. In Proceedings of the 2020 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 18–20 May 2020; pp. 910–927. [Google Scholar] [CrossRef]
- Solmaz, O.; Heimbach, L.; Vonlanthen, Y.; Wattenhofer, R. Optimistic MEV in Ethereum Layer 2s: Why Blockspace Is Always in Demand. arXiv 2025. [Google Scholar] [CrossRef]
- Qin, K.; Zhou, L.; Gervais, A. Quantifying blockchain extractable value: How dark is the forest? In Proceedings of the 2022 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 22–26 May 2022; pp. 198–214. [Google Scholar] [CrossRef]
- Gramlich, V.; Jelito, D.; Sedlmeir, J. Maximal extractable value: Current understanding, categorization, and open research questions. Electron. Mark. 2024, 34, 49. [Google Scholar] [CrossRef]
- Roughgarden, T.; Syrgkanis, V.; Tardos, E. The price of anarchy in auctions. J. Artif. Intell. Res. 2017, 59, 59–101. [Google Scholar] [CrossRef]
- Akbarpour, M.; Li, S. Credible Auctions: A Trilemma. Econometrica 2020, 88, 425–467. [Google Scholar] [CrossRef]
- Heimbach, L.; Kiffer, L.; Ferreira Torres, C.; Wattenhofer, R. Ethereum’s Proposer-Builder Separation: Promises and Realities. In Proceedings of the 2023 ACM on Internet Measurement Conference, Montreal, QC, Canada, 24–26 October 2023; pp. 406–420. [Google Scholar] [CrossRef]
- Barczentewicz, M. MEV on Ethereum: A Policy Analysis. ICLE White Paper, 23 January 2023. Available online: https://ssrn.com/abstract=4332703 (accessed on 14 June 2025). [CrossRef]
- Öz, B.; Rezabek, F.; Gebele, J.; Hoops, F.; Matthes, F. A Study of MEV Extraction Techniques on a First-Come-First-Served Blockchain. In Proceedings of the 39th ACM/SIGAPP Symposium on Applied Computing, Avila, Spain, 8–12 April 2024; pp. 288–297. [Google Scholar] [CrossRef]
- Weintraub, B.; Torres, C.F.; Nita-Rotaru, C.; State, R. A flash(bot) in the pan: Measuring maximal extractable value in private pools. In Proceedings of the 22nd ACM Internet Measurement Conference, Nice, France, 25–27 October 2022; pp. 458–471. [Google Scholar] [CrossRef]
- Zhou, L.; Qin, K.; Torres, C.F.; Le, D.V.; Gervais, A. High-frequency trading on decentralized on-chain exchanges. In Proceedings of the 2021 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 24–27 May 2021; pp. 428–445. [Google Scholar] [CrossRef]
- Zhao, D. The Blockchain Game: Synthesis of Byzantine Systems and Nash Equilibria. arXiv 2019. [Google Scholar] [CrossRef]
- Reynouard, M.; Laraki, R.; Gorelkina, O. BAR Nash Equilibrium and Application to Blockchain Design. arXiv 2024. [Google Scholar] [CrossRef]
- Noguchi, M. Exact Nash-Like Solutions of Blockchain Gap Games. Preprint. 2024. Available online: https://ssrn.com/abstract=5111244 (accessed on 14 June 2025). [CrossRef]
- Commey, D.; Mai, B.; Hounsinou, S.G.; Crosby, G.V. Securing Blockchain-Based IoT Systems: A Review. IEEE Access 2024, 12, 98856–98881. [Google Scholar] [CrossRef]
- Essaidi, M.; Ferreira, M.V.X.; Weinberg, S.M. Credible, Strategyproof, Optimal, and Bounded Expected-Round Single-Item Auctions for all Distributions. In Proceedings of the 13th Innovations in Theoretical Computer Science Conference (ITCS 2022), LIPIcs, Online, 31 January–3 February 2022; Volume 215, pp. 66:1–66:19. [Google Scholar] [CrossRef]
- Choudhuri, A.R.; Garg, S.; Piet, J.; Policharla, G.V. Mempool privacy via batched threshold encryption: Attacks and defenses. In Proceedings of the 33rd USENIX Security Symposium (USENIX Security 24), Philadelphia, PA, USA, 14–16 August 2024; pp. 3513–3529. [Google Scholar]
- Yang, S.; Zhang, F.; Huang, K.; Chen, X.; Yang, Y.; Zhu, F. SoK: MEV Countermeasures: Theory and Practice. arXiv 2023. [Google Scholar] [CrossRef]
- Ferreira Torres, C.; Mamuti, A.; Weintraub, B.; Nita-Rotaru, C.; Shinde, S. Rolling in the Shadows: Analyzing the Extraction of MEV Across Layer-2 Rollups. In Proceedings of the 2024 on ACM SIGSAC Conference on Computer and Communications Security, Salt Lake City, UT, USA, 14–18 October 2024; pp. 2591–2605. [Google Scholar] [CrossRef]
- Lee, S.; Gee, E. Commit-Reveal2: Randomized Reveal Order Mitigates Last-Revealer Attacks in Commit-Reveal. arXiv 2025. [Google Scholar] [CrossRef]
- Öz, B.; Sui, D.; Thiery, T.; Matthes, F. Who wins ethereum block building auctions and why? arXiv 2024, arXiv:2407.13931. [Google Scholar] [CrossRef]
- Fudenberg, D.; Tirole, J. Game Theory; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Momeni, P.; Gorbunov, S.; Zhang, B. FairBlock: Preventing Blockchain Front-Running with Minimal Overheads. In Security and Privacy in Communication Networks; Li, F., Liang, K., Lin, Z., Katsikas, S.K., Eds.; Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering; Springer Nature: Cham, Switzerland, 2023; Volume 462, pp. 250–271. [Google Scholar] [CrossRef]
- Arulprakash, M.; Jebakumar, R. Commit-reveal strategy to increase the transaction confidentiality in order to counter the issue of front running in blockchain. AIP Conf. Proc. 2022, 2460, 020016. [Google Scholar] [CrossRef]
- Churiwala, D.; Krishnamachari, B. Comma protocol: Towards complete mitigation of maximal extractable value (MEV) attacks. In Proceedings of the 2023 Fifth International Conference on Blockchain Computing and Applications (BCCA), Kuwait, Kuwait, 24–26 October 2023; pp. 359–360. [Google Scholar] [CrossRef]
- Gorzny, J.; Kemper, P.; Derka, M. Early Observations of Based Rollups: A Case Study of Taiko. In Proceedings of the 4th International Workshop on Cryptoasset Analytics (CAAW 2025), Miyakojima, Japan, 18 April 2025; Available online: https://caaw.io/2025/papers/CAAW25_paper_21.pdf (accessed on 14 June 2025).
- Gogol, K.; Messias, J.; Miori, D.; Tessone, C.; Livshits, B. Cross-Rollup MEV: Non-Atomic Arbitrage Across L2 Blockchains. arXiv 2024. [Google Scholar] [CrossRef]
- Öz, B.; Torres, C.F.; Gebele, J.; Rezabek, F.; Mazorra, B.; Matthes, F. Pandora’s Box: Cross-Chain Arbitrages in the Realm of Blockchain Interoperability. arXiv 2025. [Google Scholar] [CrossRef]
- Duan, L.; Sun, Y.; Ni, W.; Ding, W.; Liu, J.; Wang, W. Attacks against cross-chain systems and defense approaches: A contemporary survey. IEEE/CAA J. Autom. Sin. 2023, 10, 1647–1667. [Google Scholar] [CrossRef]
- Lorünser, T.; Wohner, F.; Krenn, S. A privacy-preserving auction platform with public verifiability for smart manufacturing. In Proceedings of the 8th International Conference on Information Systems Security and Privacy (ICISSP 2022), Online, 9–11 February 2022; Mori, P., Lenzini, G., Furnell, S., Eds.; SciTePress: Setúbal, Portugal, 2022; pp. 637–647. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).