Large-Eddy Simulation of the Flow Past a Circular Cylinder at Re = 130,000: Effects of Numerical Platforms and Single- and Double-Precision Arithmetic
Abstract
:1. Introduction
- Further verify and validate large-eddy simulation for the turbulent separated flows at practical Reynolds numbers.
- Review the available experimental data and compare the LES results obtained by the Ansys Fluent and OpenFOAM platforms.
- Evaluate the accuracy of LES using coarse and medium-sized computational grids (10–25 million cells).
- Investigate the LES results computed with single-precision arithmetic.
- Apply stability theory and Lyapunov metrics to analyze the turbulent separated flows as dynamic systems.
2. Problem Statement, Computational Grids, and Brief Aspects of Mathematical Modeling and Numerical Methods
Computational Grids
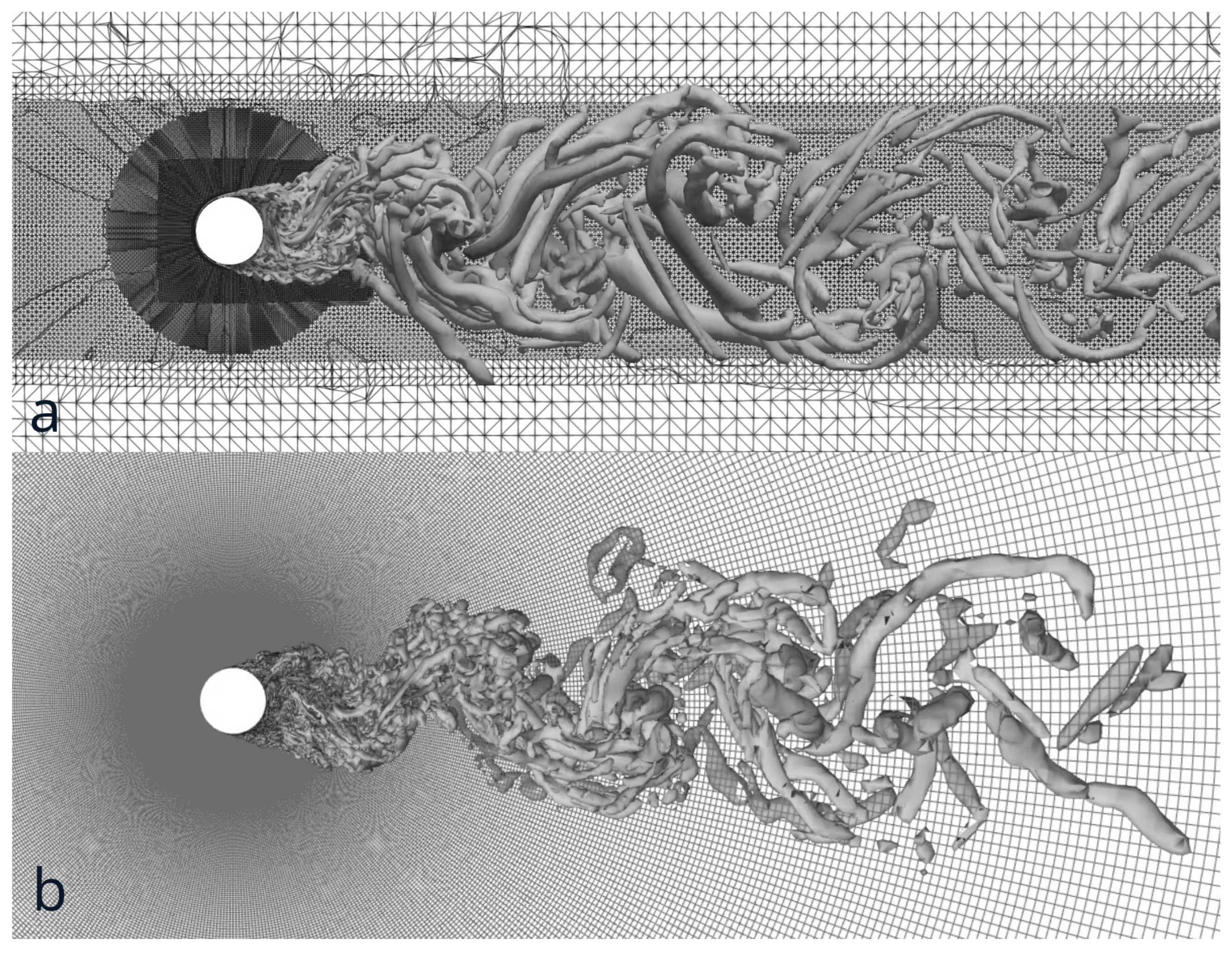
- Unstructured, hexahedral with different levels of adaptation (Figure 1b–d; used here and below the abbreviation HM). The computational domain is defined as a rectangular parallelepiped with dimensions in the x, y, and z directions, respectively. As a starting point, the computational block was divided into nodes. Next, the grid was successively adapted in three iterations with a coefficient of in the regions from to , to , and to . The cylindrical region with a radius of , located in the center of the Cartesian coordinates, was adapted at the next level with the same coefficient. The last iteration was applied to a rectangular region with dimensions to and from to . Grid adaptation at all levels completely covered the computational region in the spanwise direction. Thus, the circumferential grid resolution of the cylinder is , and along the span, (). For the adequate resolution of the boundary layer on the surface of the cylinder, a viscous sub-grid was added with a minimum dimensionless cell height, , an expansion factor of , and a total number of layers of 40, respectively. The total grid size is cells.
- Curvilinear, orthogonal O-type (Figure 1e–g; used here and below the abbreviation OM) with a dimension of ( cells) in the x, y, and z directions, respectively. The length of the computational domain in the streamwise direction is , and in the spanwise direction, . The grid nodes are radially relaxed from the cylinder toward the outflow boundary with the dimensionless height of the first cell being and an expansion coefficient in the radial direction of .
3. Brief Aspects of Mathematical Modeling and Numerical Simulations
4. Results
4.1. Instantaneous Flow Field
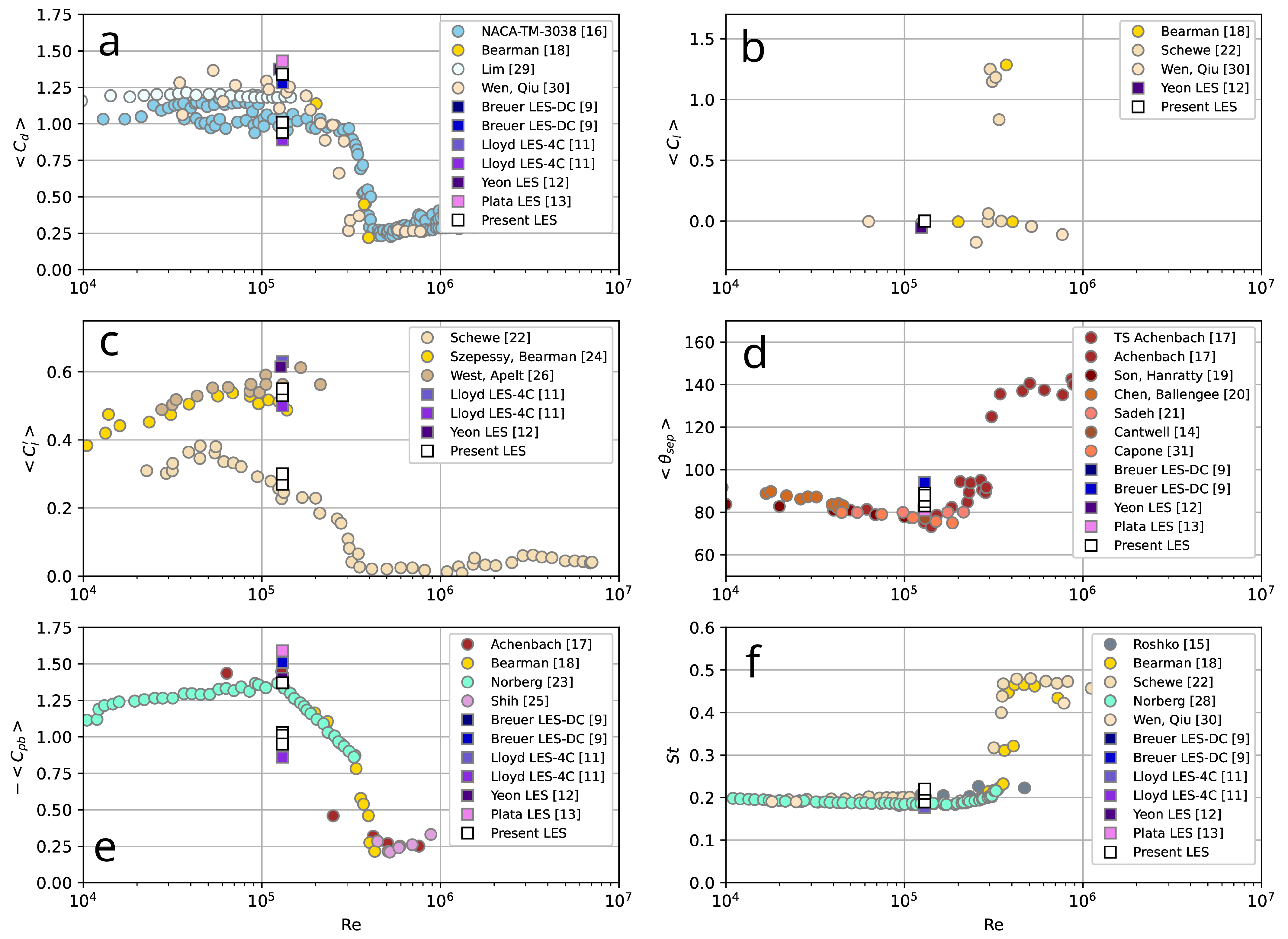
4.2. Integral Parameters
4.3. First- and Second-Order Statistics
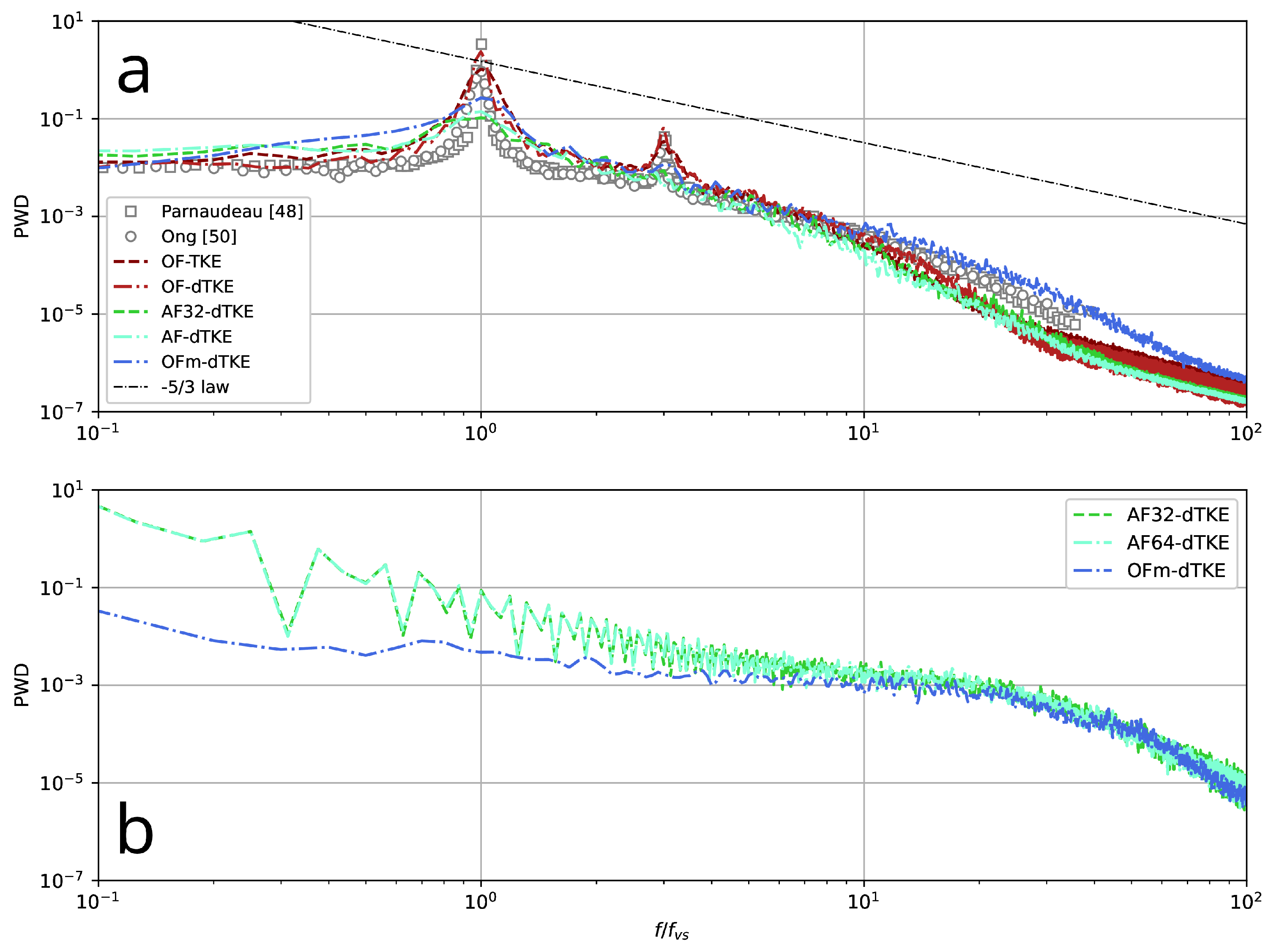
4.4. One-Dimensional Energy Spectra
4.5. Lyapunov Metric
5. Discussion
- Further validation and verification of LES for the external aerodynamics and turbulent separated flows. Previously, the turbulent flows over circular ( [1,2,3] and = 20,000 [4]), semi-circular ( = 50,000 [7]), and triangular ( = 45,000 [5,6]) cylinders were studied in detail. The differential sub-grid scale k-model (with constants and ) and its dynamic modification were tested. In the present work, the Reynolds number was increased by almost an order of magnitude to = 130,000. Also, in addition to OF, numerical simulations was extended to use the commercial CFD code AF.
- Investigation of LES and related numerical methods using single-precision arithmetic, which is also due to several factors. The most important is the possibility of the more efficient use of computational resources: on the one hand, numerical methods using SP arithmetic use less RAM and, as a rule, provide a small performance gain (≈10–20%) when using classical CPUs. On the other hand, they allow for achieving significant acceleration on graphics accelerators, which are usually optimized for single-precision calculations, as well as on hybrid CPU–GPU systems.As mentioned above, OF provides the ability to perform simulations using mixed-precision arithmetic, SPDP. To test it, another special run (OFm-dTKE) was performed using the O-type grid. In this case, the problem was set up as closely as possible to match the AF32-dTKE and AF64-dTKE runs. On the one hand, the predicted integral flow characteristics (Table 2) converge with a small variation to the data obtained by AF32-dTKE and AF64-dTKE, which indicates the reasonable consistency of the two numerical platforms. On the other hand, the numerical method implemented in OF, even for the SPDP case, has a smaller numerical diffusion, which is clearly seen in Figure 13, where the one-dimensional energy spectra are compared. Numerical dissipation is clearly visible for the AF32-dTKE and AF64-dTKE runs. It should be noted that it was not possible to obtain a final physical solution using OF with single-precision arithmetic (similarly to Brogi et al. [32]). Most likely, this is due to the fact that the linear algebra algorithms implemented in OF are more sensitive to high-frequency perturbations due to round-off errors. It is also worth emphasizing that in the present work, the dynamic differential sub-grid scale model for the kinetic energy was used, which is strictly dissipative under the condition that the turbulent viscosity is positive [35], i.e., it makes a certain contribution to the suppression of high-frequency oscillations, which, together with the algebraic multigrid method implemented in AF, allows for the effective simulation of the turbulent flows with single precision.
- Qualitative and quantitative testing of LES implemented in two numerical platforms, AF and OF, using coarse and medium-sized computational grids (10–25 M cells) for the Reynolds number of practical interest ( = 130,000). Curved, orthogonal O-type (OM) and unstructured, hexahedral (HM) meshes, with several levels of computational adaptation, are used.
- The overall performance of the computing system, which is usually limited by the execution time (the time per step per grid node, which is now effectively fixed, since the processor clock rate does not increase) and the number of effective MPI nodes, which depends on the problem size and the network communication rate. Parallel efficiency is also usually limited to about of the theoretical one in the case when pressure-based algorithms are used and the stability condition () is imposed by the computational grid and the boundary layer resolution ();
- The final period of time integration (the total number of time integration steps), consisting of the interval required to obtain a statistically converged flow field (reaching the self-oscillatory regime, on the order of several ) and the time segment required to get time-averaged data (usually several tens of ).
Critical Remark on the Grid Dependence
6. Conclusions
- The present LES (finite-volume method and the dynamic k-equation sub-grid scale model) successfully reproduced the complex physics of the turbulent flow over a circular cylinder, including the Kelvin–Helmholtz and Benard/von Kármán instabilities, the laminar–turbulent transition, development of vortex cores, their downstream convection, and vortex dynamics in the wake.
- In general, satisfactory agreement between LES results obtained using Ansys Fluent and OpenFOAM and experimental data was observed. Discrepancies between them can be attributed to the specifics of numerical simulations (e.g., various computational grids, convective schemes, sub-grid scale models, algorithms, and methods to solve the Navier–Stokes equations) and the techniques used for collecting physical measurements. The location of the laminar–turbulent transition, which is very sensitive to the turbulence intensity of the incoming flow, is critically important.
- The present LES results showed that it is possible to capture complex flow physics for this particular Reynolds number using medium-sized computational grids (up to 25 million cells) generated by different refinement strategies (O-type versus unstructured).
- Differences between LES results computed using single- and double-precision arithmetic implemented in Ansys Fluent were negligible for all integral, local, and spectral characteristics of the turbulent flow. A special run using the concept of mixed-precision arithmetic implemented in OpenFOAM showed satisfactory convergence with the results predicted by Ansys Fluent, indicating a significant degree of consistency between these numerical platforms.
- It is worth noting that an attempt to use OpenFOAM with single-precision arithmetic to predict this turbulent flow failed. It seems that the linear algebra solvers implemented in OpenFOAM are more sensitive to round-off errors and related high-frequency noise.
- Lyapunov stability theory and its metrics were applied to analyze the large-eddy simulation technique using single-precision arithmetic. The numerical methodology using single-precision arithmetic was shown to be stable by Lyapunov.
- Under some considerations, LES solutions can be treated as dynamical systems. Their time evolution can be visualized by reconstructed attractors, which can be bounded by simple ellipsoids in three-dimensional space.
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AF | Ansys Fluent |
| AMG | Algebraic Multigrid Method |
| BDF | Backward Differencing Formula |
| CDS | Central Differencing Scheme |
| CFD | Computational Fluid Dynamics |
| CPU | Central Processing Unit |
| CWT | Continuous Wavelet Transform |
| DP | Double-Precision |
| FFT | Fast Fourier Transform |
| FVM | Finite Volume Method |
| GAMG | Geometric Multigrid Method |
| GPU | Graphics Processing Unit |
| HPC | High-Performance Computing |
| LES | Large-Eddy Simulation |
| KH | Kelvin–Helmholtz Instability |
| OF | OpenFOAM |
| Probability Density Distribution | |
| RAM | Random-Access Memory |
| SOU | Second-Order Upwind Scheme |
| SP | Single-Precision |
| SPDP | Mixed-Precision |
| TKE | Turbulence Kinetic Energy |
References
- Lysenko, D.A.; Ertesvåg, I.S.; Rian, K.E. Large-eddy simulation of the flow over a circular cylinder at Reynolds number 3900 using the OpenFOAM toolbox. Flow Turbul. Combust. 2012, 89, 491–518. [Google Scholar] [CrossRef]
- Lysenko, D.A.; Ertesvåg, I.S.; Rian, K.E. Towards simulation of far-field aerodynamic sound from a circular cylinder using OpenFOAM. Int. J. Aeroacoust. 2014, 13, 141–168. [Google Scholar] [CrossRef]
- Lysenko, D.A. Free stream turbulence intensity effects on the flow over a circular cylinder at Re = 3900: Bifurcation, attractors and Lyapunov metric. Ocean Eng. 2023, 287, 115787. [Google Scholar] [CrossRef]
- Lysenko, D.A.; Ertesvåg, I.S.; Rian, K.E. Large-eddy simulation of the flow over a circular cylinder at Reynolds number 2 × 104. Flow Turbul. Combust. 2014, 92, 673–698. [Google Scholar] [CrossRef]
- Lysenko, D.A.; Ertesvåg, I.S. Reynolds-Averaged, Scale-Adaptive and Large-Eddy Simulations of Premixed Bluff-Body Combustion Using the Eddy Dissipation Concept. Flow Turbul. Combust. 2018, 100, 721–768. [Google Scholar] [CrossRef]
- Lysenko, D.A.; Ertesvåg, I.S. Assessment of algebraic subgrid scale models for the flow over a triangular cylinder at Re = 45,000. Ocean Eng. 2021, 222, 108559. [Google Scholar] [CrossRef]
- Lysenko, D.A.; Donskov, M.; Ertesvåg, I.S. Large-eddy simulations of the flow over a semi-circular cylinder at Re = 50,000. Comput. Fluids 2021, 228, 10505. [Google Scholar] [CrossRef]
- Lysenko, D.A.; Donskov, M.; Ertesvåg, I.S. Large-eddy simulations of the flow past a bluff-body with active flow control based on trapped vortex cells at Re = 50,000. Ocean Eng. 2023, 280, 114496. [Google Scholar] [CrossRef]
- Breuer, M. A challenging test case for large eddy simulation: High Reynolds number circular cylinder flow. Int. J. Heat Fluid Flow 2000, 21, 648–654. [Google Scholar] [CrossRef]
- Cao, Y.; Tamura, T. Numerical investigations into effects of three-dimensional wake patterns on unsteady aerodynamic characteristics of a circular cylinder at Re = 1.3 × 105. J. Fluids Struct. 2015, 59, 351–369. [Google Scholar] [CrossRef]
- Lloyd, T.P.; James, M. Large eddy simulations of a circular cylinder at Reynolds numbers surrounding the drag crisis. Appl. Ocean. Res. 2016, 59, 676–686. [Google Scholar] [CrossRef]
- Yeon, S.M.; Yang, J.; Stern, F. Large-eddy simulation of the flow past a circular cylinder at sub- to super-critical Reynolds numbers. Appl. Ocean. Res. 2016, 59, 663–675. [Google Scholar] [CrossRef]
- Plata, M.; Lamballais, E.; Naddei, F. On the performance of a high-order multiscale DG approach to LES at increasing Reynolds number. Comput. Fluids 2019, 194, 104306. [Google Scholar] [CrossRef]
- Cantwell, B.; Coles, D. An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder. J. Fluid Mech. 1983, 136, 321–374. [Google Scholar] [CrossRef]
- Roshko, A. On the Drag and Shedding Frequency of Two-Dimensional Bluff Bodies; NACA-TN-3169; National Advisory Committee for Aeronautics: Washington, DC, USA, 1953. [Google Scholar]
- Delany, K.; Sorensen, N.E. Low-Speed Drag of Cylinders of Various Shapes; NACA-TM-3038; NASA: Washington, DC, USA, 1956. [Google Scholar]
- Achenbach, E. Distribution of local pressure and skin friction around a circular cylinder in cross-flow up to Re = 5 × 106. J. Fluid Mech. 1968, 34, 625–639. [Google Scholar] [CrossRef]
- Bearman, P.W. On vortex shedding from a circular cylinder in the critical Reynolds number regime. J. Fluid Mech. 1969, 37, 577–585. [Google Scholar] [CrossRef]
- Son, J.; Hanratty, T. Velocity gradients at the wall for flow around a cylinder at Reynolds numbers from 5 × 103 to 105. J. Fluid Mech. 1969, 35, 353–368. [Google Scholar] [CrossRef]
- Chen, C.F.; Ballengee, D.B. Vortex shedding from circular cylinders in an oscillating freestream. AIAA J. 1971, 9, 340–342. [Google Scholar] [CrossRef]
- Sadeh, W.Z.; Saharon, D.B. Turbulence Effect on Crossflow Around a Circular Cylinder at Subcritical Reynolds Numbers; NASA-CR-3622; National Advisory Committee for Aeronautics: Washington, DC, USA, 1982. [Google Scholar]
- Schewe, G. On the force fluctuations acting on a circular cylinder in crossflow from subcritical up to transcritical Reynolds numbers. J. Fluid Mech. 1983, 133, 265–285. [Google Scholar] [CrossRef]
- Norberg, C. Effects of Reynolds Number and a Low Intensity Freestream Turbulence on the Flow Around a Circular Cylinder; Publication No. 87/2; Chalmers University of Technology: Göteborg, Sweden, 1987. [Google Scholar]
- Szepessy, S.; Bearman, P.W. Aspect ratio and end plate effects on vortex shedding from a circular cylinder. J. Fluid Mech. 1992, 234, 191–217. [Google Scholar] [CrossRef]
- Shih, W.C.L.; Wang, C.; Coles, D.; Roshko, A. Experiments on flow past rough circular cylinders at large Reynolds numbers. J. Wind Eng. Ind. Aerodyn. 1993, 49, 351–368. [Google Scholar] [CrossRef]
- West, G.S.; Apelt, C.J. Measurements of fluctuating pressures and forces on a circular cylinder in the Reynolds number range 104 to 2.5 × 105. J. Fluids Struct. 1993, 7, 227–244. [Google Scholar] [CrossRef]
- Norberg, C. Flow around rectangular cylinders: Pressure forces and wake frequencies. J. Wind Eng. Ind. Aerodyn. 1993, 49, 187–196. [Google Scholar] [CrossRef]
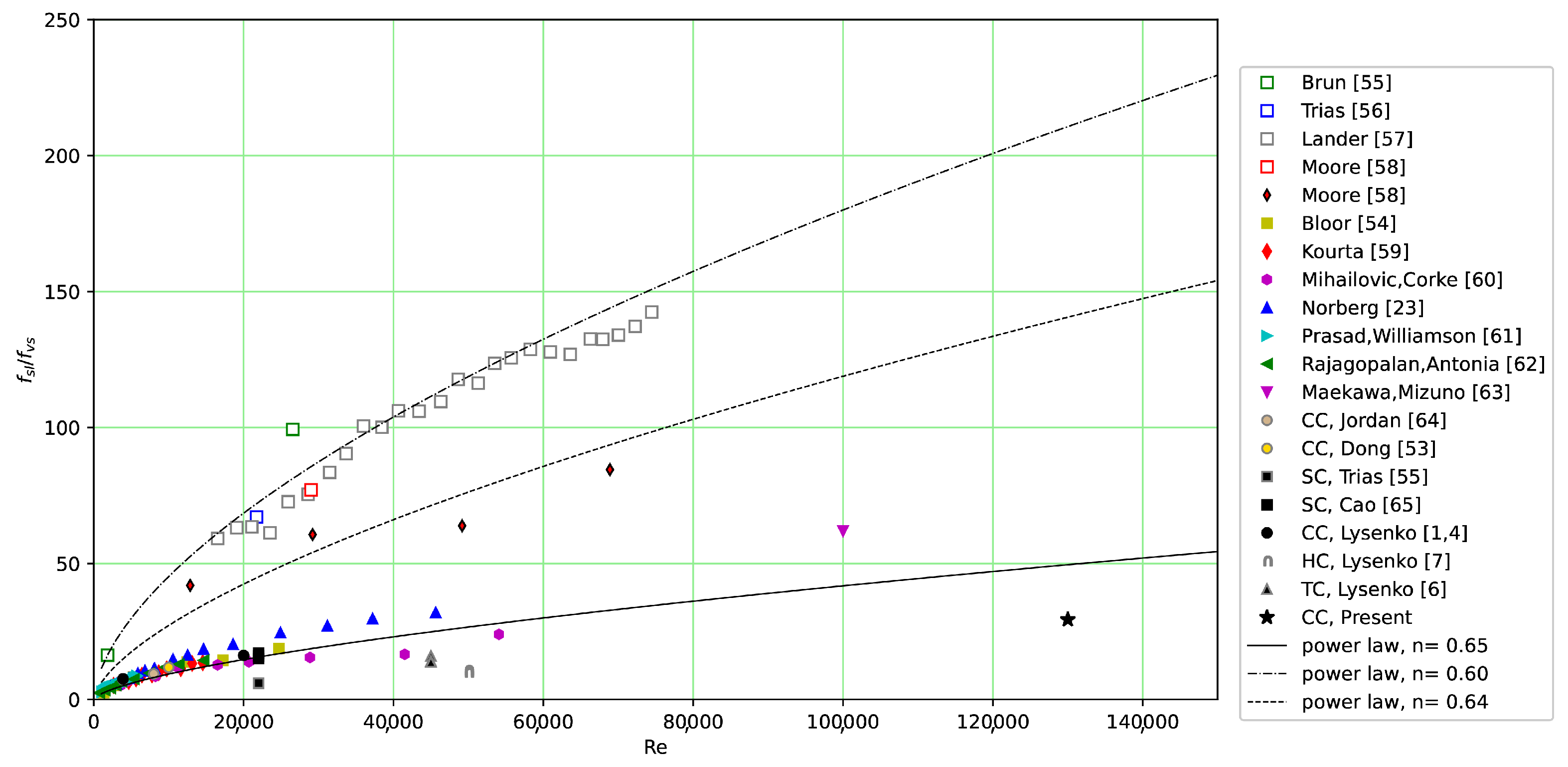
- Norberg, C. Flow around a circular cylinder: Aspects of fluctuating lift. J. Fluids Struct. 2001, 15, 459–469. [Google Scholar] [CrossRef]
- Lim, H.-C.; Lee, S.-J. Flow control of circular cylinders with longitudinal grooved surfaces. AIAA J. 2002, 40, 2027–2036. [Google Scholar] [CrossRef]
- Wen, P.; Qiu, W. Numerical studies of VIV of a smooth cylinder. In Proceedings of the 27th ITTC Workshop on Wave Run-Up and Vortex Shedding, Nantes, France, 17–18 October 2013. [Google Scholar]
- Capone, A.; Klein, C.; Felice, F.D.; Miozzi, M. Phenomenology of a flow around a circular cylinder at sub-critical and critical Reynolds numbers. Phys. Fluids 2016, 28, 074101. [Google Scholar] [CrossRef]
- Brogi, F.; Bnà, S.; Boga, G.; Amati, G.; Esposti Ongaro, T.; Cerminara, M. On floating point precision in computational fluid dynamics using OpenFOAM. Future Gener. Comput. Syst. 2024, 152, 1–16. [Google Scholar] [CrossRef]
- Karypis, G.; Kumar, V. Multilevel k-way partitioning scheme for irregular graphs. J. Parallel Dist. Comput. 1998, 48, 96–129. [Google Scholar] [CrossRef]
- Chevalier, C.; Pellegrini, F. PT-Scotch: A tool for efficient parallel graph ordering. Parallel Comput. 2008, 34, 318–331. [Google Scholar] [CrossRef]
- Geurts, B. Elements of Direct and Large-Eddy Simulation; R.T. Edwards: Philadelphia, PA, USA, 2004. [Google Scholar]
- Garnier, E.; Adams, N.; Sagaut, P. Large Eddy Simulation for Compressible Flows; Springer: New York, NY, USA, 2009. [Google Scholar]
- Schumann, U. Subgrid scale model for finite difference simulations of turbulent flows in plane channels and annuli. J. Comput. Phys. 1975, 18, 376–404. [Google Scholar] [CrossRef]
- Horiuti, K. Large eddy simulation of turbulent channel flow by one-equation modeling. J. Phys. Soc. Jpn. 1985, 54, 2855–2865. [Google Scholar] [CrossRef]
- Yoshizawa, A. Statistical theory for compressible shear flows, with the application to subgrid modelling. Phys. Fluids 1986, 29, 1416–1429. [Google Scholar] [CrossRef]
- Sagaut, P. Large Eddy Simulation for Incompressible Flows, 3rd ed.; Springer: Berlin, Germany, 2006. [Google Scholar]
- ANSYS FLUENT 2021SRb—Theory Guide; Technical Report; Ansys Inc.: Canonsburg, PA, USA, 2021.
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. J. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Issa, R. Solution of the implicitly discretized fluid flow equations by operator splitting. J. Comput Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Hutchinson, B.; Raithby, G. A multigrid method based on the additive correction strategy. J. Numer. Heat Transfer 1986, 9, 511–537. [Google Scholar]
- Wesseling, P.; Oosterlee, C.W. Geometric multigrid with applications to computational fluid dynamics. Comput. Appl. Math. 2001, 128, 311–334. [Google Scholar] [CrossRef]
- Welch, P. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef]
- Kravchenko, A.; Moin, P. Numerical studies of flow over a circular cylinder at Re = 3900. Phys. Fluids 2000, 12, 403–417. [Google Scholar] [CrossRef]
- Parnaudeau, P.; Carlier, J.; Heitz, D.; Lamballais, E. Experimental and numerical studies of the flow over a circular cylinder at Reynolds number 3900. Phys. Fluids 2008, 20, 085101. [Google Scholar] [CrossRef]
- Prasad, A.; Williamson, C.H.K. Three-dimensional effects in turbulent bluff-body wakes. J. Fluid Mech. 1997, 343, 235–265. [Google Scholar] [CrossRef]
- Ong, L.; Wallace, J. The velocity field of the turbulent very near wake of a circular cylinder. Exp. Fluids 1996, 20, 441–453. [Google Scholar] [CrossRef]
- Ma, X.; Karamanos, G.-S.; Karniadakis, G.E. Dynamics and low-dimensionality of a turbulent near wake. J. Fluid Mech. 2000, 410, 29–65. [Google Scholar] [CrossRef]
- Shanbhogue, S.J.; Husain, S.; Lieuwen, T. Lean blowoff of bluff body stabilized flames: Scaling and dynamics. Prog. Energy Combust. Sci. 2009, 35, 98–120. [Google Scholar] [CrossRef]
- Dong, S.; Karniadakis, G.E.; Ekmekci, A.; Rockwell, D. A combined direct numerical simulation particle image velocimetry study of the turbulent air wake. J. Fluid Mech. 2006, 569, 185–207. [Google Scholar] [CrossRef]
- Bloor, M. The transition to turbulence in the wake of a circular cylinder. J. Fluid Mech. 1964, 19, 290–304. [Google Scholar] [CrossRef]
- Brun, C.; Aubrun, S.; Goossens, T.; Ravier, P. Coherent structures and their frequency signature in the separated shear layer on the sides of a square cylinder. Flow Turbul. Combust. 2008, 81, 97–114. [Google Scholar] [CrossRef]
- Trias, F.X.; Gorobets, A.; Oliva, A. Turbulent flow around a square cylinder at Reynolds number 22,000: A DNS study. Comput. Fluids 2015, 123, 87–98. [Google Scholar] [CrossRef]
- Lander, D.C.; Moore, D.M.; Letchford, C.W.; Amitay, M. Scaling of square-prism shear layers. J. Fluid Mech. 2018, 849, 1096–1119. [Google Scholar] [CrossRef]
- Moore, D.M.; Letchford, C.W.; Amitay, M. Energetic scales in a bluff body shear layer. J. Fluid Mech. 2019, 875, 543–575. [Google Scholar] [CrossRef]
- Kourta, A.; Boisson, H.; Chassing, P.; Ha Minh, H. Non-linear interactions and the transition to turbulence in the wake of a circular cylinder. J. Fluid Mech. 1987, 181, 41–161. [Google Scholar] [CrossRef]
- Mihailovic, J.; Corke, T.C. Three-dimensional instability of the shear layer over a circular cylinder. Phys. Fluids 2019, 9, 3250–3257. [Google Scholar] [CrossRef]
- Prasad, A.; Williamson, C.H.K. The instability of the shear layer separating from a bluff body. J. Fluid Mech. 1997, 333, 375–402. [Google Scholar] [CrossRef]
- Rajagopalan, S.; Antonia, R.A. Flow around a circular cylinder - structure of the near wake shear layer. Exp. Fluids 2005, 38, 393–402. [Google Scholar] [CrossRef]
- Maekawa, T.; Mizuno, S. Flow around the separation point and in the near wake of a circular cylinder. Phys. Fluids 1967, 10, 184–186. [Google Scholar] [CrossRef]
- Jordan, S. Investigation of the cylinder separated shear-layer physics by large-eddy simulation. Int. J. Heat Fluid Flow 2002, 23, 1–12. [Google Scholar] [CrossRef]
- Cao, Y.; Tamura, T. Large-eddy simulations of flow past a square cylinder using structured and unstructured grids. Comput. Fluids 2016, 137, 36–54. [Google Scholar] [CrossRef]
- Nastac, G.; Labahn, J.W.; Magri, L.; Ihme, M. Lyapunov exponent as a metric for assessing the dynamic content and predictability of large-eddy simulations. Phys. Rev. Fluids 2017, 2, 094606. [Google Scholar] [CrossRef]
- Oseledets, V.I. Multiplicative ergodic theorem. Characteristic Lyapunov exponents of dynamical systems. Tr. Mosk. Mat. Obs. 1968, 19, 179–210. [Google Scholar]
- Lyapunov, A.M. The general problem of the stability of motion. Int. J. Control 1992, 55, 521–790. [Google Scholar] [CrossRef]
- Ruelle, D.; Takens, F. On the nature of turbulence. Commun. Math Phys. 1971, 23, 343–344. [Google Scholar] [CrossRef]
- Alberti, T.; Daviaud, F.; Donner, R.V.; Dubrulle, B.; Faranda, D.; Lucarini, V. Chameleon attractors in a turbulent flow. Chaos Solitons Fractals 2023, 168, 113195. [Google Scholar] [CrossRef]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Springer: Berlin/Heidelberg, Germany, 1981; Volume 898, pp. 366–381. [Google Scholar]
- Sharma, P.; Chung, W.T.; Akoush, B.; Ihme, M. A Review of Physics-Informed Machine Learning in Fluid Mechanics. Energies 2023, 16, 2343. [Google Scholar] [CrossRef]
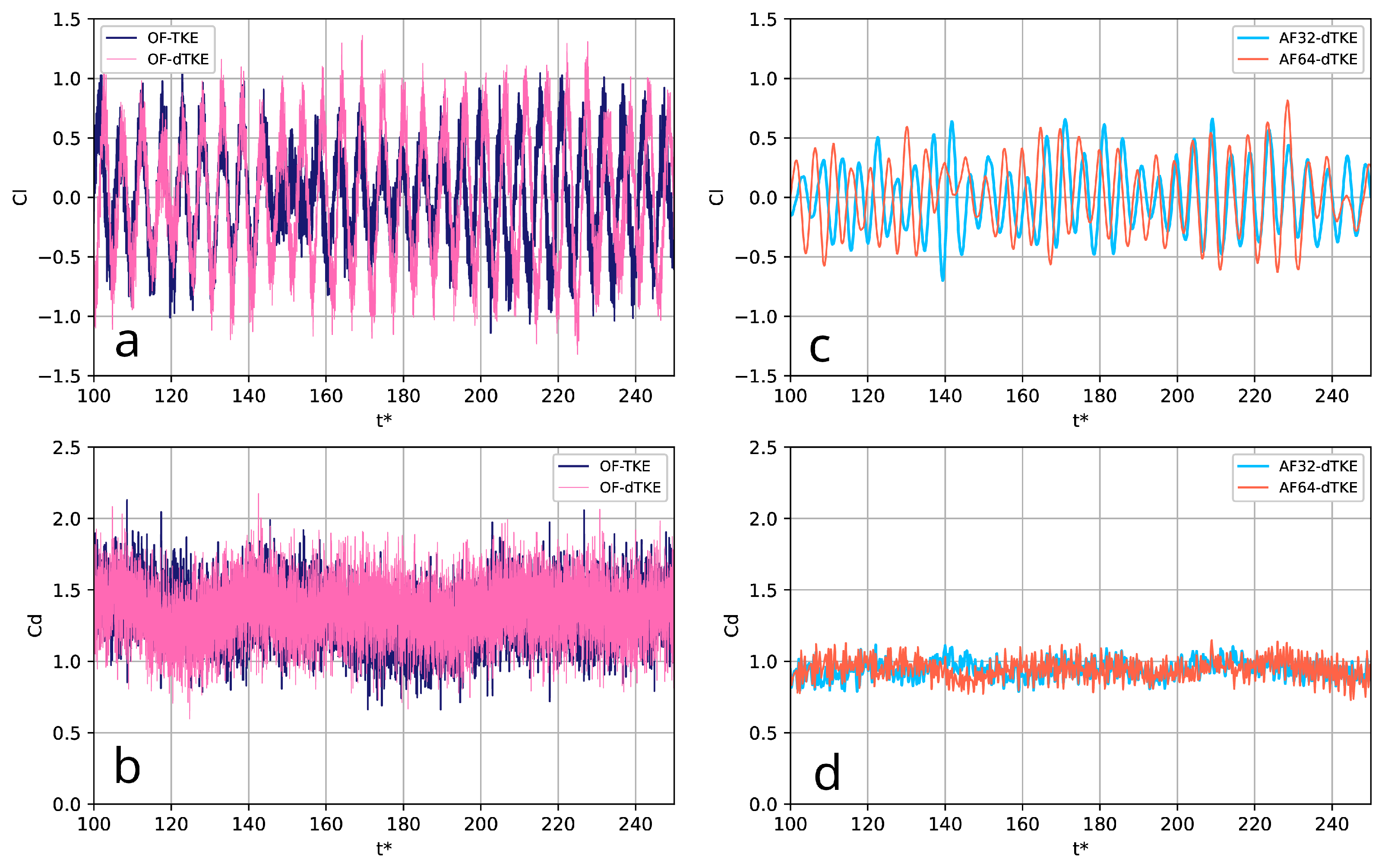
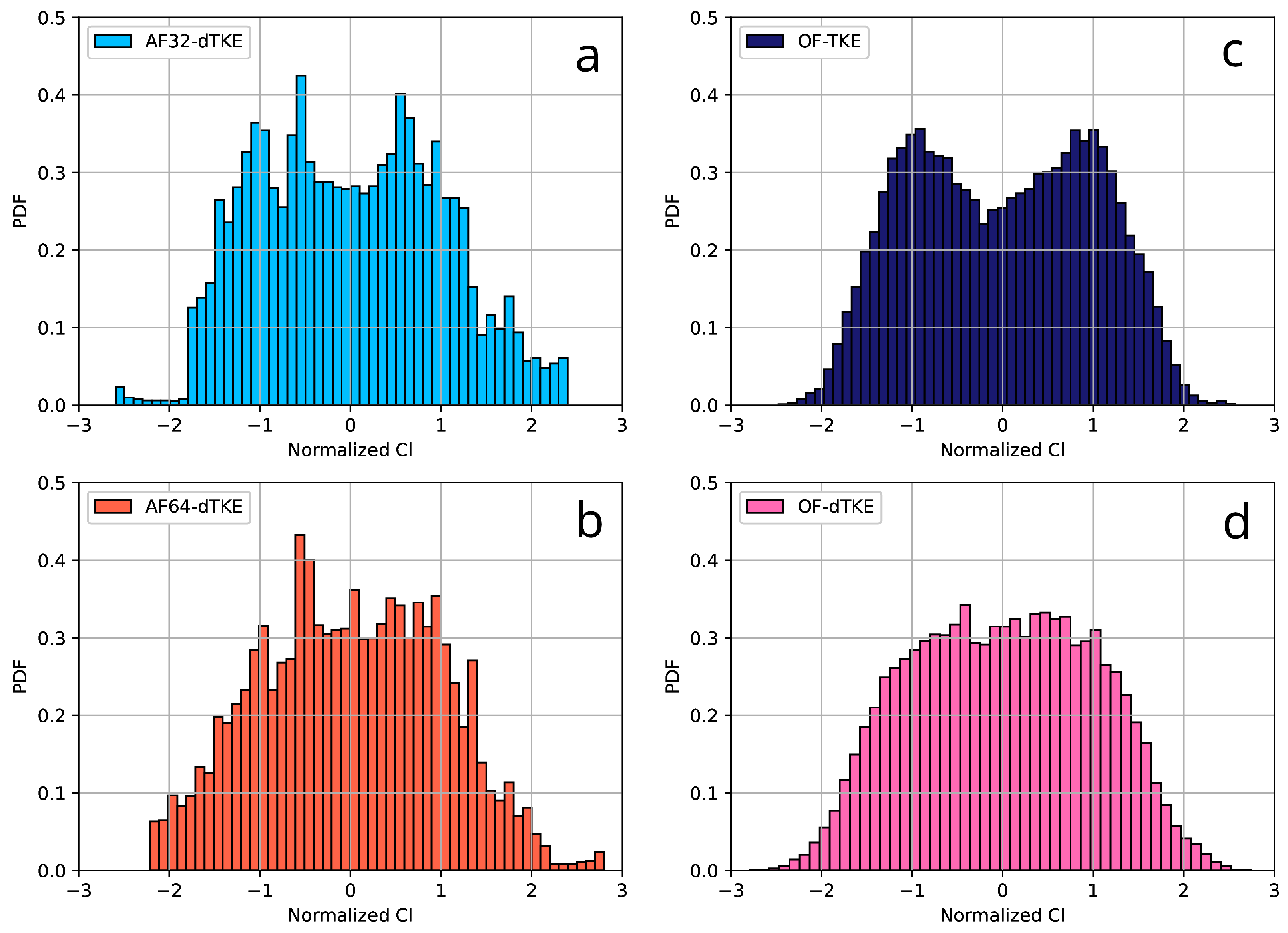

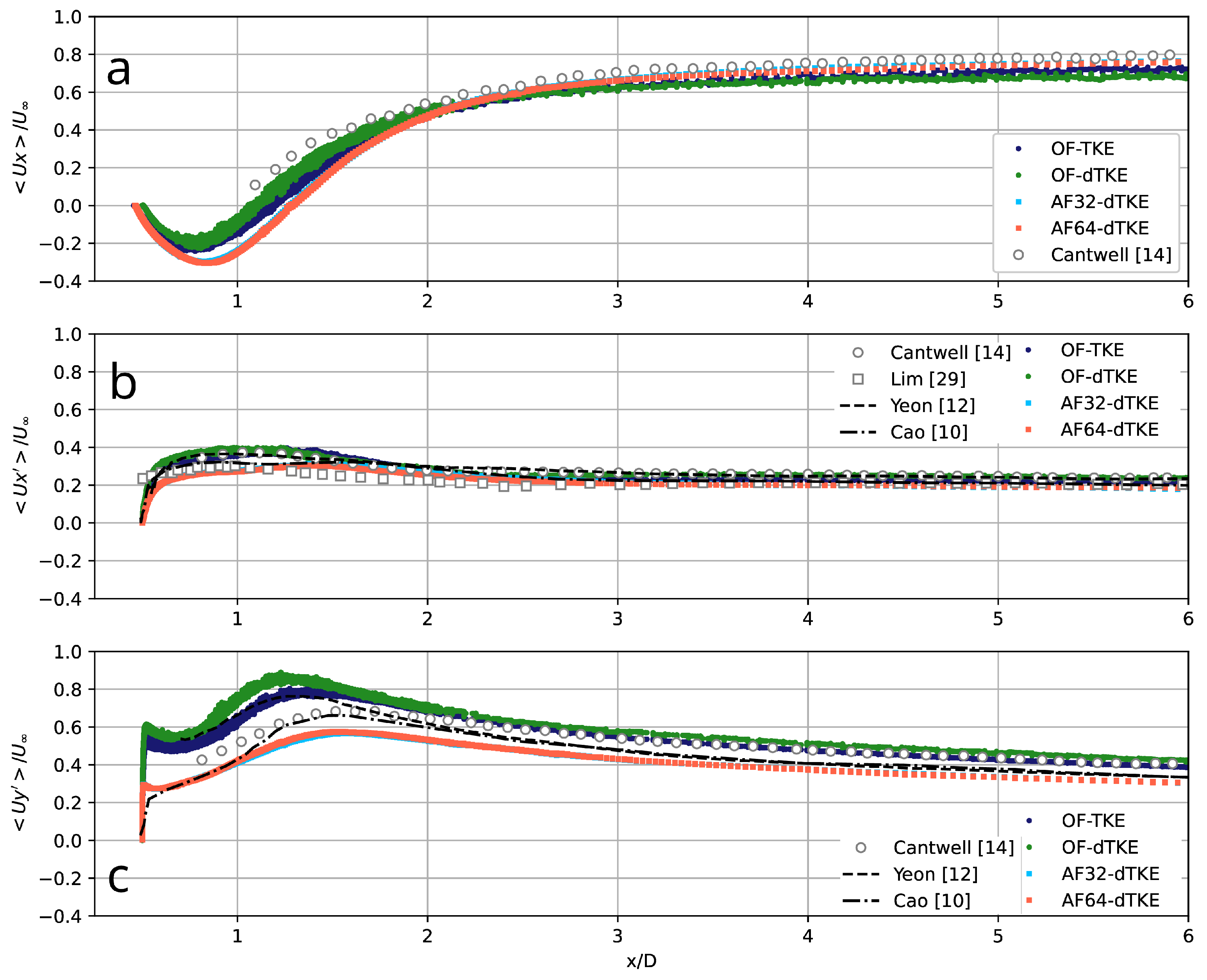

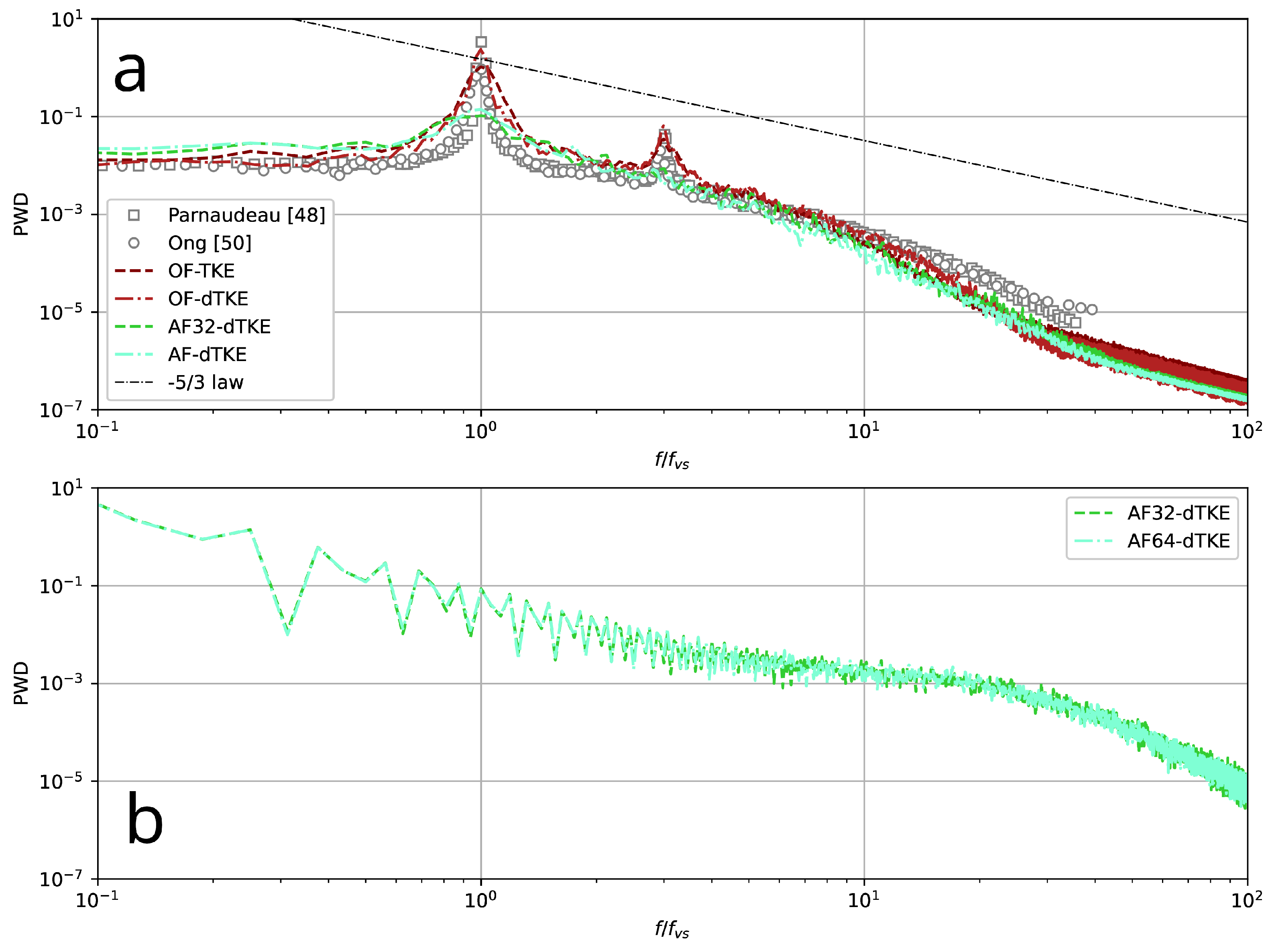


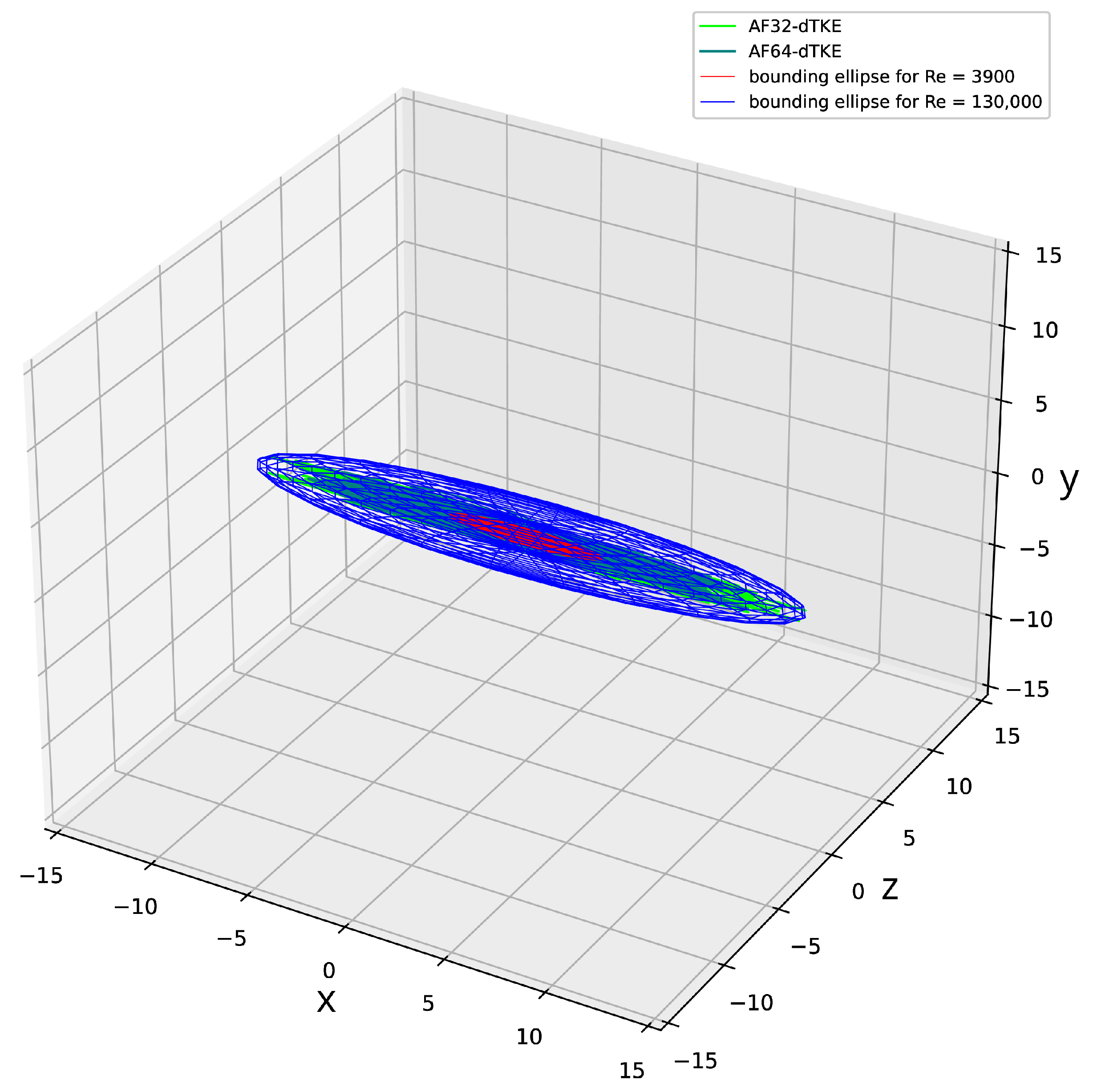

| Run | CFD Code | Precision | Mesh | TM |
|---|---|---|---|---|
| OF-TKE | OF | DP | HM | TKE |
| OF-dTKE | OF | DP | HM | dTKE |
| OFm-dTKE | OF | SPDP | OM | dTKE |
| AF32-dTKE | AF | SP | OM | dTKE |
| AF64-dTKE | AF | DP | OM | dTKE |
| T-AF32-dTKE | AF | SP | HMT | dTKE |
| T-AF64-dTKE | AF | DP | HMT | dTKE |
| Source | Method | ||||||
|---|---|---|---|---|---|---|---|
| Achenbach [17] | HWA | 1.19 | 1.25 | 78 | |||
| Cantwell & Coles [14] | HWA | 1.24 | 0.52 | 0.179 | 1.21 | 0.4–0.5 | 77 |
| Schewe [22] | HWA | 1.17 | 0.25 | 0.20 | |||
| Norberg [27] | 0.49 | 0.185 | |||||
| Lim & Lee [29] | HWA | 1.2 | 0.185 | 1.15 | |||
| Breuer (DC) [9] | LES | 1.28 | 0.22 | 1.51 | 0.46 | 94 | |
| Breuer (D3) [9] | LES | 1.37 | 0.21 | 1.6 | 0.42 | 91 | |
| Cao & Tamura [10] | LES | 1.16 | 0.3 | 0.2 | |||
| Lloyd & James (4C) [11] | LES | 1.00 | 0.63 | 0.177 | 1.01 | ||
| Lloyd & James (4F) [11] | LES | 0.89 | 0.5 | 0.203 | 0.86 | ||
| Yeon et al. [12] | LES | 1.37 | 0.62 | 0.2 | 1.64 | 0.63 | 81 |
| Plata et al. [13] | LES | 1.43 | 0.19 | 1.59 | 0.5 | ||
| Present work | |||||||
| LES | 1.33 | 0.41 | 0.19 | 1.36 | 0.55 | 83° | |
| LES | 1.34 | 0.53 | 0.19 | 1.37 | 0.58 | 83° | |
| LES | 0.98 | 0.55 | 0.18 | 1.03 | 0.62 | 89° | |
| LES | 0.94 | 0.28 | 0.21 | 1.01 | 0.68 | 85° | |
| LES | 0.94 | 0.27 | 0.21 | 1.01 | 0.68 | 85° | |
| LES | 1.01 | 0.30 | 0.22 | 0.95 | 0.67 | 89° | |
| LES | 1.01 | 0.31 | 0.22 | 0.95 | 0.67 | 89° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lysenko, D.A. Large-Eddy Simulation of the Flow Past a Circular Cylinder at Re = 130,000: Effects of Numerical Platforms and Single- and Double-Precision Arithmetic. Fluids 2025, 10, 4. https://doi.org/10.3390/fluids10010004
Lysenko DA. Large-Eddy Simulation of the Flow Past a Circular Cylinder at Re = 130,000: Effects of Numerical Platforms and Single- and Double-Precision Arithmetic. Fluids. 2025; 10(1):4. https://doi.org/10.3390/fluids10010004
Chicago/Turabian StyleLysenko, Dmitry A. 2025. "Large-Eddy Simulation of the Flow Past a Circular Cylinder at Re = 130,000: Effects of Numerical Platforms and Single- and Double-Precision Arithmetic" Fluids 10, no. 1: 4. https://doi.org/10.3390/fluids10010004
APA StyleLysenko, D. A. (2025). Large-Eddy Simulation of the Flow Past a Circular Cylinder at Re = 130,000: Effects of Numerical Platforms and Single- and Double-Precision Arithmetic. Fluids, 10(1), 4. https://doi.org/10.3390/fluids10010004






