Fault-Tolerant Time-Varying Formation Trajectory Tracking Control for Multi-Agent Systems with Time Delays and Semi-Markov Switching Topologies
Abstract
1. Introduction
2. Preliminaries and Problem Formulation
2.1. Graph Theory
2.2. Problem Formulation
2.3. Failure Distribution Model
2.4. Augmented System Model
- (1)
- If , the MAS can achieve control with the arbitrary initial value for
- (2)
- If , the tracking performance variable is poised to satisfy the following requirement under the condition of zero initial values:
- (3)
- If , the tracking performance variable can reach the below requirement under the condition of nonzero initial values:where is a pregiven accommodative matrix.
3. Main Results
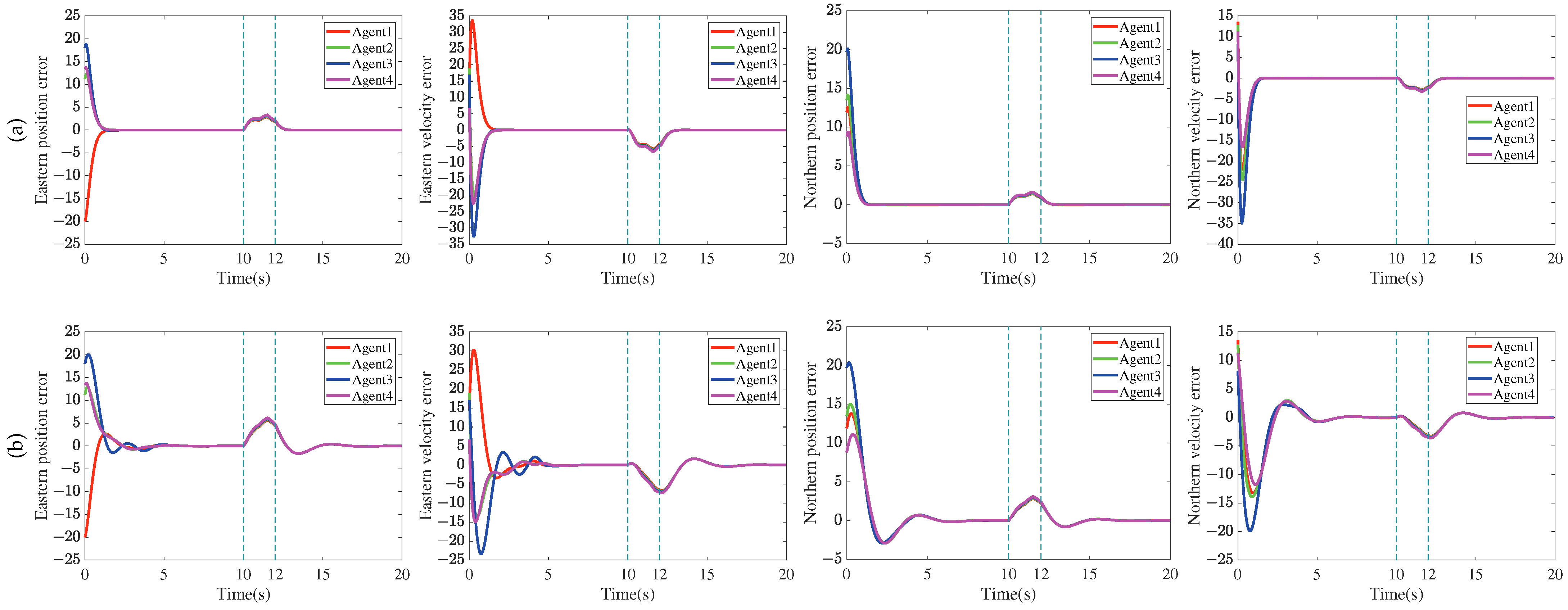
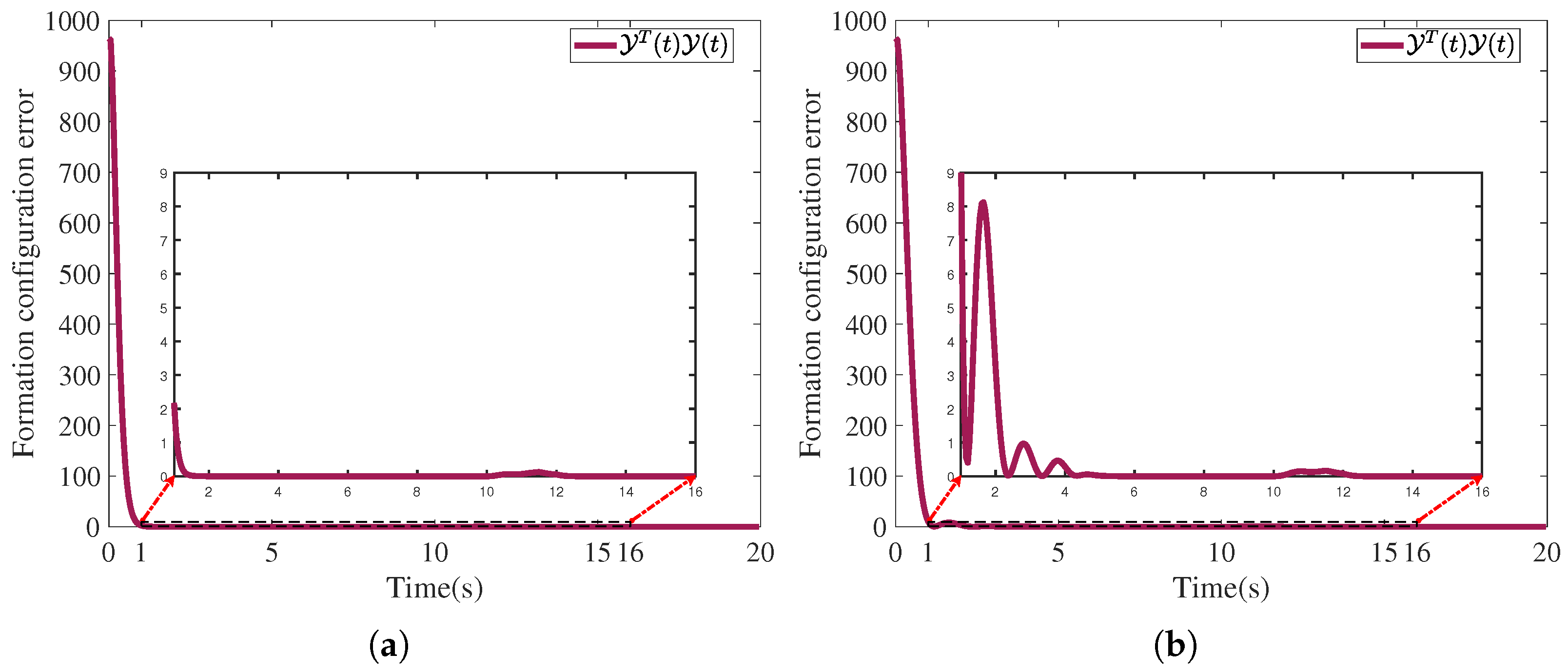
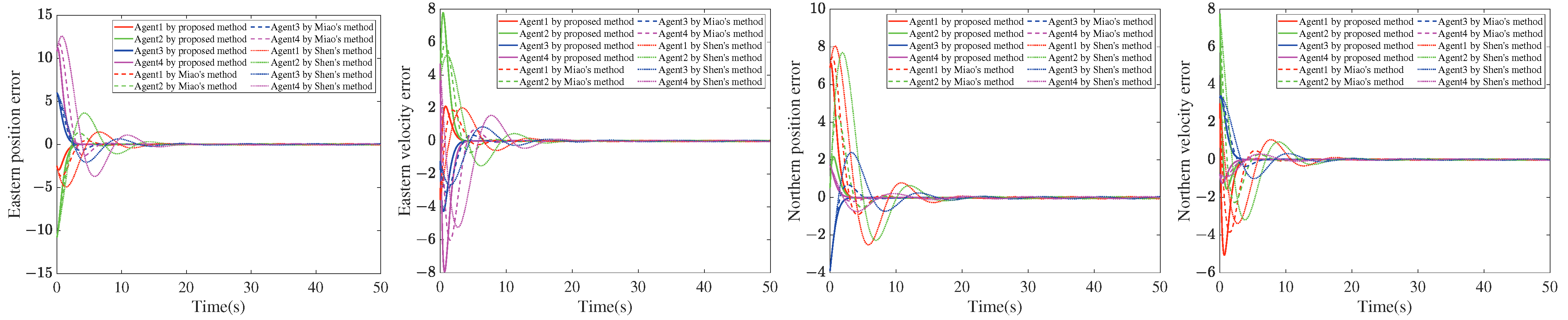
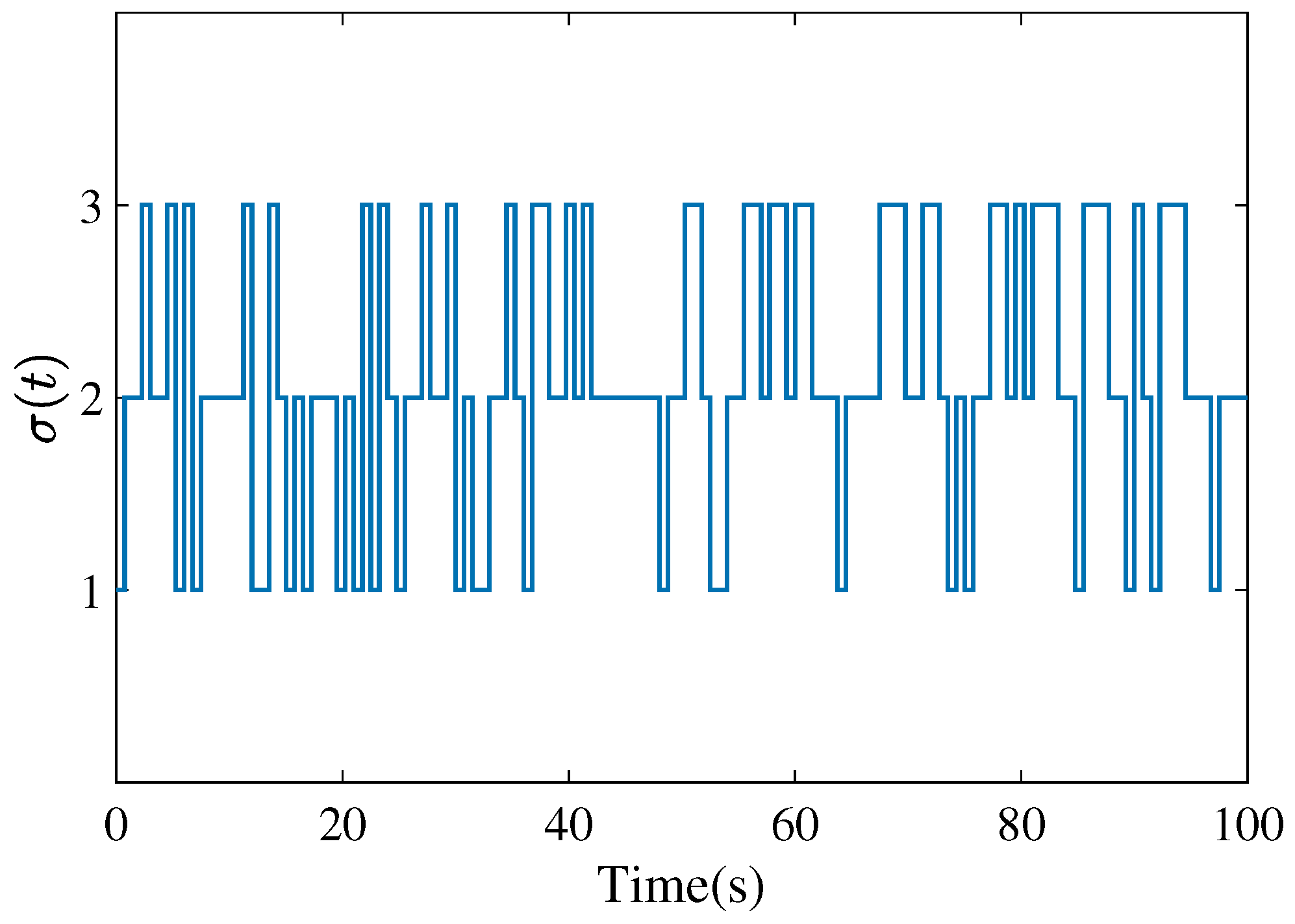
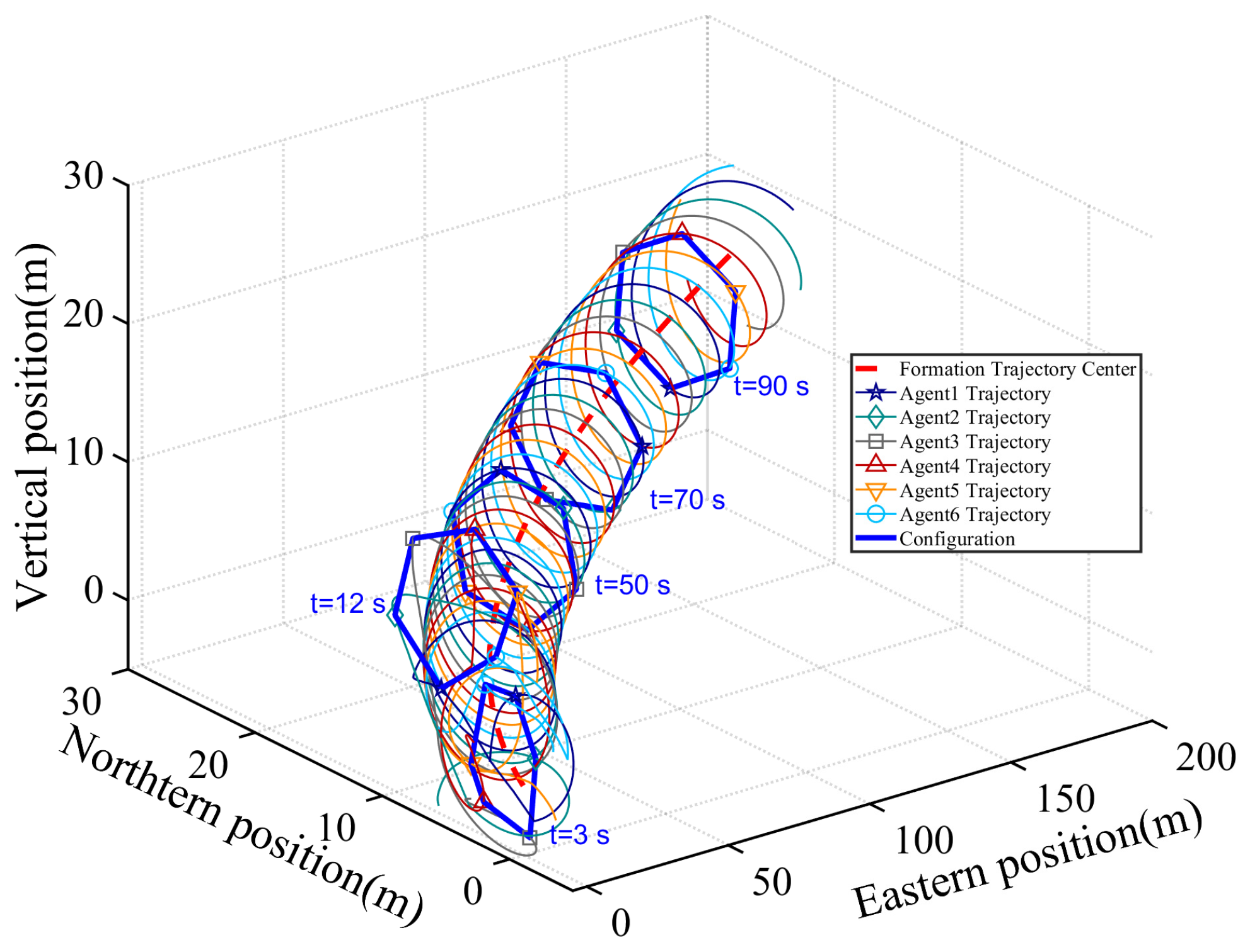
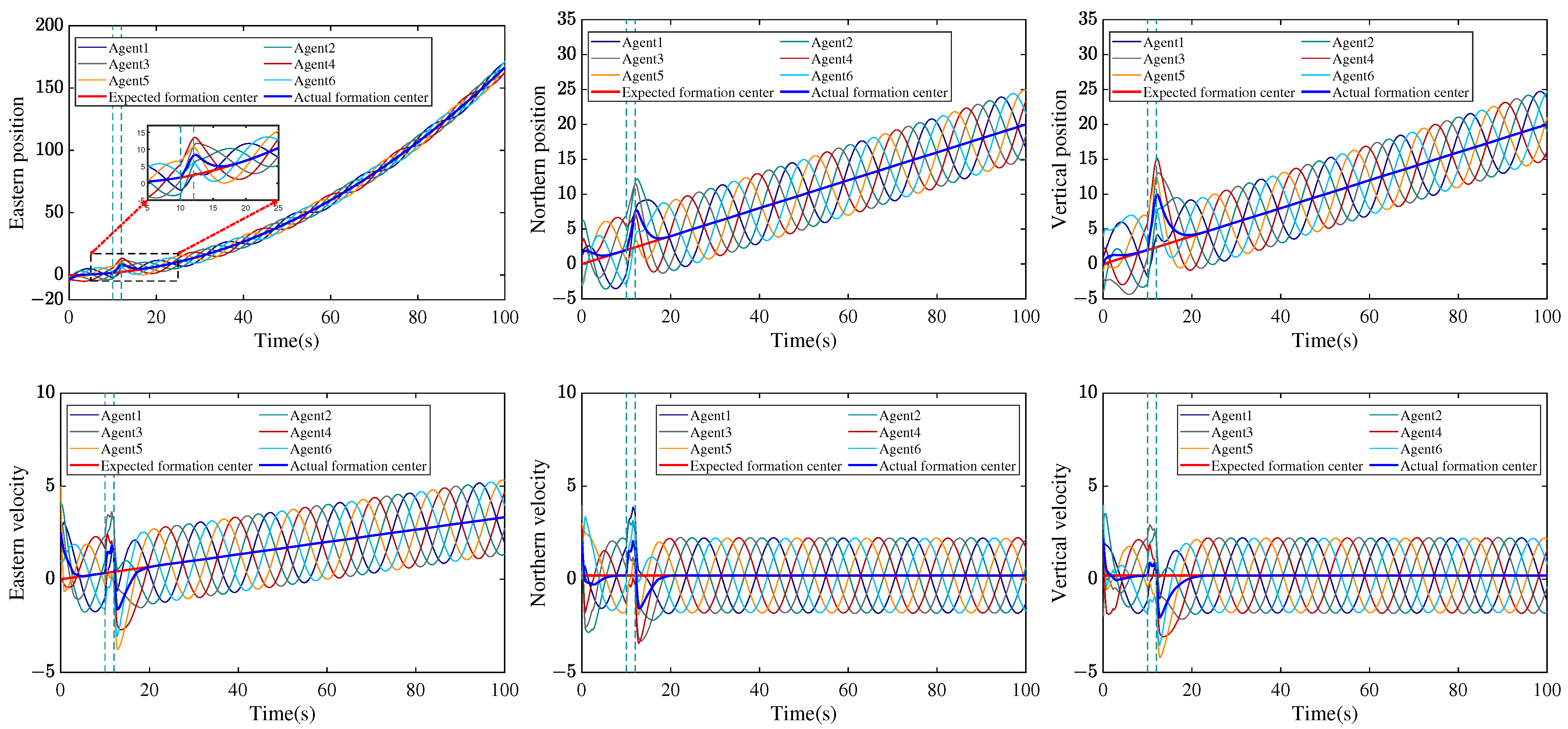
4. Simulation Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
Appendix A
References
- Yu, Y.; Chen, J.; Zheng, Z.; Yuan, J. Distributed Finite-Time ESO-Based Consensus Control for Multiple Fixed-Wing UAVs Subjected to External Disturbances. Drones 2024, 8, 260. [Google Scholar] [CrossRef]
- Yang, Y.; He, Y. Containment Control for Second-Order Multi-Agent Systems with Time-Varying Delays via Variable-Augmented-Based Free-Weighting Matrices. J. Franklin Inst. 2024, 361, 106816. [Google Scholar] [CrossRef]
- Cheng, H.; Huang, J. Adaptive Robust Bearing-Based Formation Control for Multi-Agent Systems. Automatica 2024, 162, 111509. [Google Scholar] [CrossRef]
- Huang, Y.; Fang, W.; Chen, Z.; Li, Y.; Yang, C. Flocking of Multiagent Systems with Nonuniform and Nonconvex Input Constraints. IEEE Trans. Autom. Control 2023, 68, 4329–4335. [Google Scholar] [CrossRef]
- Xiao, H.; Li, Z.; Philip Chen, C.L. Formation Control of Leader–Follower Mobile Robots’ Systems Using Model Predictive Control Based on Neural-Dynamic Optimization. IEEE Trans. Ind. Electron. 2016, 63, 5752–5762. [Google Scholar] [CrossRef]
- Gu, N.; Wang, D.; Peng, Z.; Liu, L. Distributed Containment Maneuvering of Uncertain Under-Actuated Unmanned Surface Vehicles Guided by Multiple Virtual Leaders with a Formation. Ocean Eng. 2019, 187, 105996. [Google Scholar] [CrossRef]
- Lin, J.; Hwang, K.; Wang, Y. A Simple Scheme for Formation Control Based on Weighted Behavior Learning. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1033–1044. [Google Scholar] [CrossRef]
- Koru, A.T.; Ramírez, A.; Sarsılmaz, S.B.; Sipahi, R.; Yucelen, T.; Dogan, K.M. Containment Control of Multi-Human Multi-Agent Systems Under Time Delays. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 3344–3356. [Google Scholar] [CrossRef]
- Kang, Y.; Luo, D.; Xin, B.; Cheng, J.; Yang, T.; Zhou, S. Robust Leaderless Time-Varying Formation Control for Nonlinear Unmanned Aerial Vehicle Swarm System with Communication Delays. IEEE Trans. Cybern. 2023, 53, 5692–5705. [Google Scholar] [CrossRef] [PubMed]
- Shahbazi, B.; Malekzadeh, M.; Koofigar, H.R. Robust Constrained Attitude Control of Spacecraft Formation Flying in the Presence of Disturbances. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2534–2543. [Google Scholar] [CrossRef]
- Cheng, J.; Kang, Y.; Xin, B.; Zhang, Q.; Mao, K.; Zhou, S. Time-Varying Trajectory Tracking Formation H∞ Control for Multiagent Systems with Communication Delays and External Disturbances. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 4311–4323. [Google Scholar] [CrossRef]
- Xu, Z.; Li, Y.; Zhan, X.; Yan, H.; Han, Y. Time-Varying Formation of Uncertain Nonlinear Multi-Agent Systems via Adaptive Feedback Control Approach with Event-Triggered Impulsive Estimator. Appl. Math. Comput. 2024, 475, 128707. [Google Scholar] [CrossRef]
- Guo, H.; Meng, M.; Feng, G. Lyapunov-Based Output Containment Control of Heterogeneous Multi-Agent Systems with Markovian Switching Topologies and Distributed Delays. IEEE/CAA J. Autom. Sin. 2023, 10, 1421–1433. [Google Scholar] [CrossRef]
- Li, M.; Deng, F. Necessary and Sufficient Conditions for Consensus of Continuous-Time Multiagent Systems with Markovian Switching Topologies and Communication Noises. IEEE Trans. Cybern. 2020, 50, 3264–3270. [Google Scholar] [CrossRef]
- Ma, L.; Wang, Z.; Han, Q.; Liu, Y. Consensus Control of Stochastic Multi-Agent Systems: A Survey. Sci. China Inf. Sci. 2017, 60, 120201. [Google Scholar] [CrossRef]
- Mu, X.; Hu, Z. Stability Analysis for Semi-Markovian Switched Singular Stochastic Systems. Automatica 2020, 118, 109014. [Google Scholar] [CrossRef]
- Dai, J.; Guo, G. Event-Triggered Leader-Following Consensus for Multi-Agent Systems with Semi-Markov Switching Topologies. Inform. Sci. 2018, 459, 290–301. [Google Scholar] [CrossRef]
- Liang, H.; Zhang, L.; Sun, Y.; Huang, T. Containment Control of Semi-Markovian Multiagent Systems with Switching Topologies. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3889–3899. [Google Scholar] [CrossRef]
- He, M.; Mu, J.; Mu, X. H∞ Leader-Following Consensus of Nonlinear Multi-Agent Systems under Semi-Markovian Switching Topologies with Partially Unknown Transition Rates. Inform. Sci. 2020, 513, 168–179. [Google Scholar] [CrossRef]
- Su, L.; Qi, Y.; Shen, H. Event-Based Fault-Tolerant H∞ Synchronization for Inertial Neural Networks via a Semi-Markov Jump Approach. J. Franklin Inst. 2023, 360, 11829. [Google Scholar] [CrossRef]
- Li, K.; Ding, S.X.; Zheng, W.X.; Hua, C.C. Global Distributed Fault-Tolerant Consensus Control of Nonlinear Delayed Multiagent Systems with Hybrid Faults. IEEE Trans. Autom. Control 2024, 69, 1967–1974. [Google Scholar] [CrossRef]
- Niederlinski, A. A Heuristic Approach to the Design of Linear Multivariable Interacting Control Systems. Automatica 1971, 7, 691–701. [Google Scholar] [CrossRef]
- Hu, H.; Liu, L.; Wang, Y.; Cheng, Z.; Luo, Q. Active Fault-Tolerant Attitude Tracking Control with Adaptive Gain for Spacecrafts. Aerosp. Sci. Technol. 2020, 98, 105706. [Google Scholar] [CrossRef]
- Ke, C.; Cai, K.Y.; Quan, Q. Uniform Passive Fault-Tolerant Control of a Quadcopter with One, Two, or Three Rotor Failure. IEEE Trans. Rob. 2023, 39, 4297–4311. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, H.; Wan, Y. Data-Driven Fault-Tolerant Formation Control for Nonlinear Quadrotors under Multiple Simultaneous Actuator Faults. Syst. Control Lett. 2021, 158, 105063. [Google Scholar] [CrossRef]
- Guo, X.; Wei, G.; Ding, D. Fault-Tolerant Consensus Control for Discrete-Time Multi-Agent Systems: A Distributed Adaptive Sliding-Mode Scheme. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 2515–2519. [Google Scholar] [CrossRef]
- Ruan, Z.; Yang, Q.; Ge, S.S.; Sun, Y. Adaptive Fuzzy Fault Tolerant Control of Uncertain MIMO Nonlinear Systems with Output Constraints and Unknown Control Directions. IEEE Trans. Fuzzy Syst. 2022, 30, 1224–1238. [Google Scholar] [CrossRef]
- Yin, S.; Gao, H.; Qiu, J.; Kaynak, O. Adaptive Fault-Tolerant Control for Nonlinear System with Unknown Control Directions Based on Fuzzy Approximation. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1909–1918. [Google Scholar] [CrossRef]
- Miao, K.; Li, J.; Chen, Y.; Xu, S. Finite-Time Fault-Tolerant Consensus for Leader-Following Multi-Agent Systems with Semi-Markov Switching Topologies. Int. J. Control 2022, 97, 373–386. [Google Scholar] [CrossRef]
- Zhou, Y.; Chang, X.; Park, J.H. Quantized Asynchronous Filtering for Fuzzy Semi-Markov Switching Systems with Multiple Stochastic Delays Under Deception Attacks. IEEE Trans. Fuzzy Syst. 2024, 32, 2378–2389. [Google Scholar] [CrossRef]
- Zhou, T.; Liu, C.; Wang, W. Nonfragile Robust H∞ Containment Control for Multi-Agent Systems with a Time-Varying Delay. J. Franklin Inst. 2024, 361, 106732. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R. Consensus Seeking in Multiagent Systems under Dynamically Changing Interaction Topologies. IEEE Trans. Autom. Control 2005, 50, 655–661. [Google Scholar] [CrossRef]
- Yang, R.; Liu, L.; Feng, G. Leader-Following Output Consensus of Heterogeneous Uncertain Linear Multiagent Systems with Dynamic Event-Triggered Strategy. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1626–1637. [Google Scholar] [CrossRef]
- Dong, X.; Yu, B.; Shi, Z.; Zhong, Y. Time-Varying Formation Control for Unmanned Aerial Vehicles: Theories and Applications. IEEE Trans. Control Syst. Technol. 2015, 23, 340–348. [Google Scholar] [CrossRef]
- Wang, A.; Fei, M.; Song, Y. A Novel Scalable and Reliable Control for DC Microgrids with Varying Number of Agents. IEEE Trans. Cybern. 2024, 54, 4962–4972. [Google Scholar] [CrossRef]
- Peng, X.; He, Y. Consensus of Multiagent Systems with Time-Varying Delays and Switching Topologies Based on Delay-Product-Type Functionals. IEEE Trans. Cybern. 2024, 54, 101–110. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Zhong, Q.; Wang, Y.; Shi, K.; Zhong, S. Nonfragile Memory-Based PD-Like Sampled-Data Consensus Control for Nonlinear Multiagent Systems with Time-Varying Communication Delays. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 4370–4380. [Google Scholar] [CrossRef]
- Cao, Y.; Lam, J. Robust H∞ Control of Uncertain Markovian Jump Systems with Time-Delay. IEEE Trans. Autom. Control 2000, 45, 77–83. [Google Scholar] [CrossRef]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; Studies in Applied and Numerical Mathematics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1994. [Google Scholar] [CrossRef]
- Chen, J.; Park, J.H.; Xu, S.; Zhang, B. A Survey of Inequality Techniques for Stability Analysis of Time-Delay Systems. Int. J. Robust Nonlinear Control 2022, 32, 6412–6440. [Google Scholar] [CrossRef]
- Park, P.; Ko, J.W.; Jeong, C. Reciprocally Convex Approach to Stability of Systems with Time-Varying Delays. Automatica 2011, 47, 235–238. [Google Scholar] [CrossRef]
- Yang, G.; Wang, J.L. Non-Fragile H∞ Control for Linear Systems with Multiplicative Controller Gain Variations. Automatica 2001, 37, 727–737. [Google Scholar] [CrossRef]
- Shen, H.; Park, J.H.; Wu, Z.G.; Zhang, Z. Finite-Time H∞ Synchronization for Complex Networks with Semi-Markov Jump Topology. Commun. Nonlinear Sci. Numer. Simul. 2015, 24, 40–51. [Google Scholar] [CrossRef]
- Shen, H.; Wang, Y.; Xia, J.; Park, J.H.; Wang, Z. Fault-Tolerant Leader-Following Consensus for Multi-Agent Systems Subject to Semi-Markov Switching Topologies: An Event-Triggered Control Scheme. Nonlinear Anal. Hybrid Syst 2019, 34, 92–107. [Google Scholar] [CrossRef]
- Balandin, D.V.; Kogan, M.M. LMI-Based H∞-Optimal Control with Transients. Int. J. Control 2010, 83, 1664–1673. [Google Scholar] [CrossRef]



| Reference | TVCDs | EDs 1 | UPs 2 | SMSTs | AFs 3 |
|---|---|---|---|---|---|
| [9] | ✗ | ✔ | ✗ | ✗ | ✗ |
| [11] | ✔ | ✔ | ✗ | ✗ | ✔ |
| [12] | ✗ | ✗ | ✔ | ✗ | ✗ |
| [16] | ✗ | ✗ | ✗ | ✔ | ✗ |
| [19] | ✗ | ✔ | ✗ | ✔ | ✗ |
| [20] | ✗ | ✗ | ✗ | ✔ | ✔ |
| [27] | ✗ | ✔ | ✔ | ✗ | ✔ |
| ‡4 | ✔ | ✔ | ✔ | ✔ | ✔ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Miao, K.; He, Z.; Zhang, H.; Niu, Y. Fault-Tolerant Time-Varying Formation Trajectory Tracking Control for Multi-Agent Systems with Time Delays and Semi-Markov Switching Topologies. Drones 2024, 8, 778. https://doi.org/10.3390/drones8120778
Yu H, Miao K, He Z, Zhang H, Niu Y. Fault-Tolerant Time-Varying Formation Trajectory Tracking Control for Multi-Agent Systems with Time Delays and Semi-Markov Switching Topologies. Drones. 2024; 8(12):778. https://doi.org/10.3390/drones8120778
Chicago/Turabian StyleYu, Huangzhi, Kunzhong Miao, Zhiqing He, Hong Zhang, and Yifeng Niu. 2024. "Fault-Tolerant Time-Varying Formation Trajectory Tracking Control for Multi-Agent Systems with Time Delays and Semi-Markov Switching Topologies" Drones 8, no. 12: 778. https://doi.org/10.3390/drones8120778
APA StyleYu, H., Miao, K., He, Z., Zhang, H., & Niu, Y. (2024). Fault-Tolerant Time-Varying Formation Trajectory Tracking Control for Multi-Agent Systems with Time Delays and Semi-Markov Switching Topologies. Drones, 8(12), 778. https://doi.org/10.3390/drones8120778








