Heuristic Optimization-Based Trajectory Planning for UAV Swarms in Urban Target Strike Operations
Abstract
1. Introduction
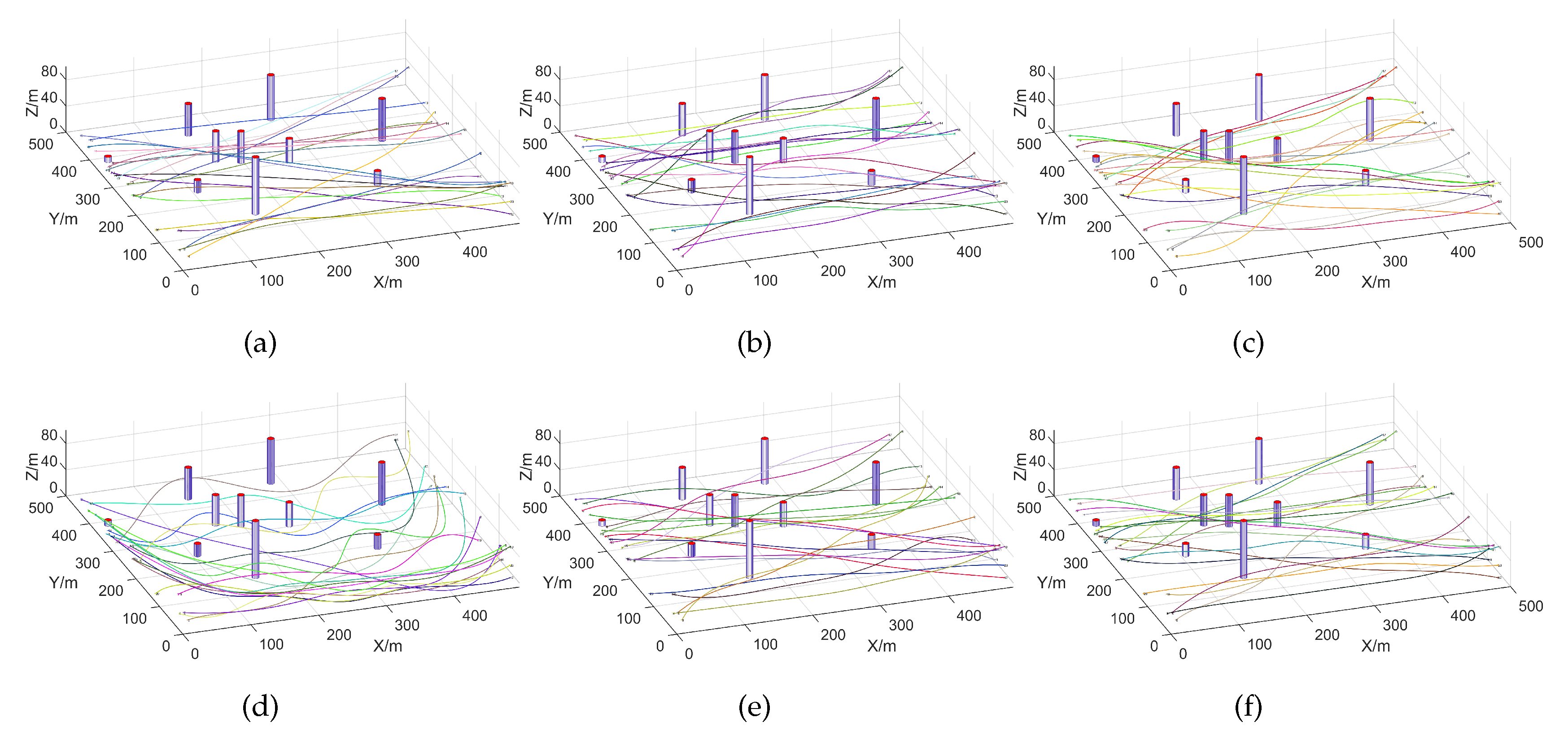
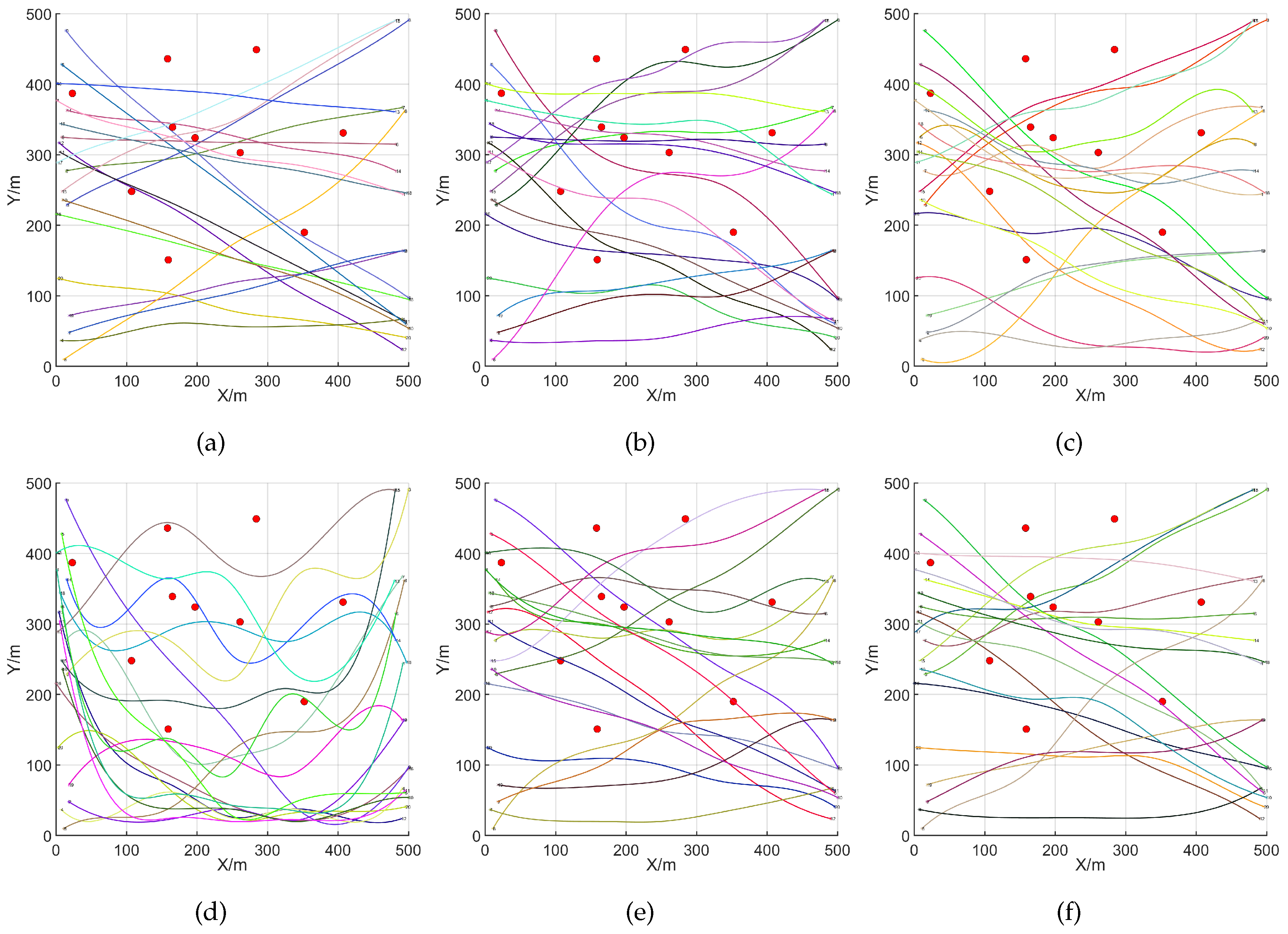
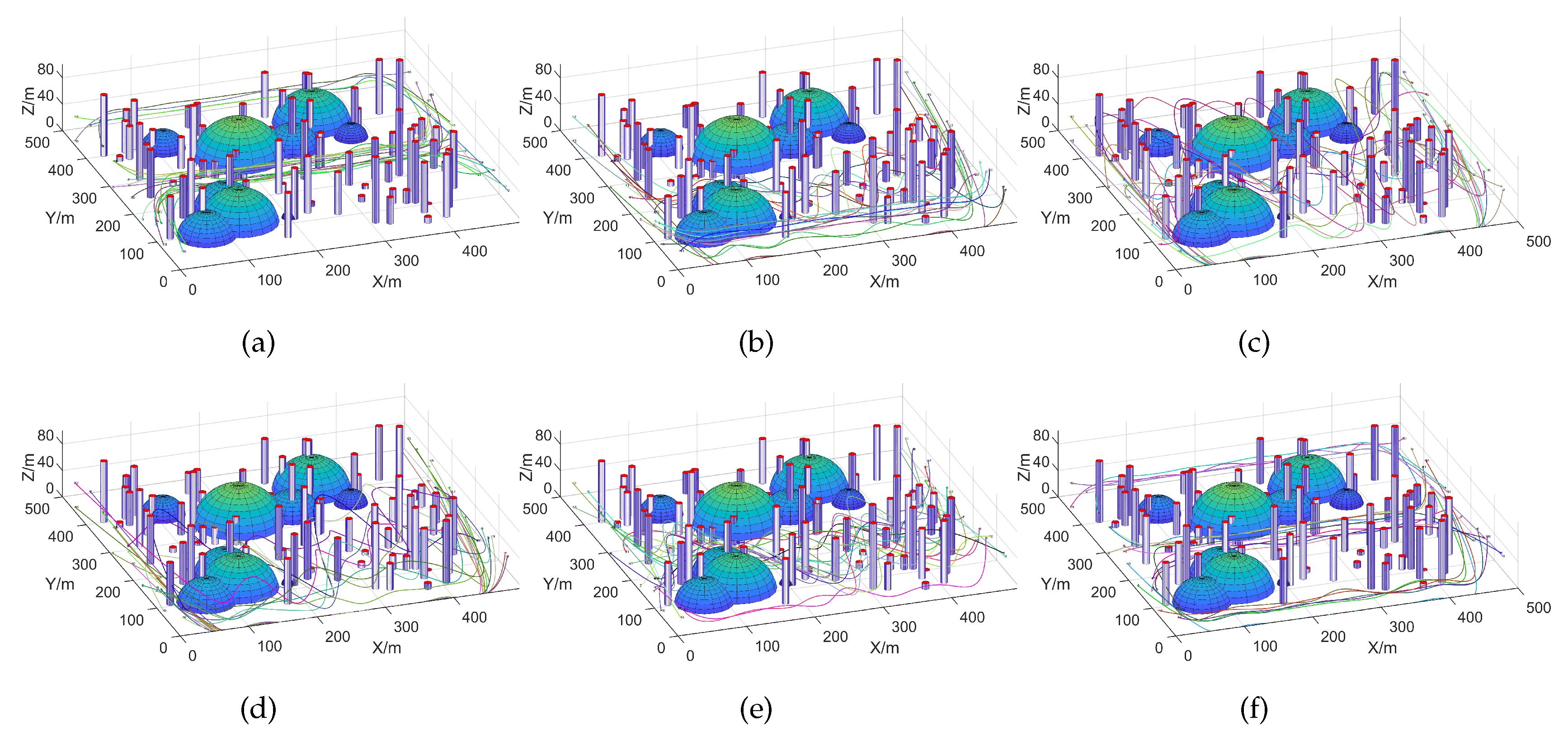
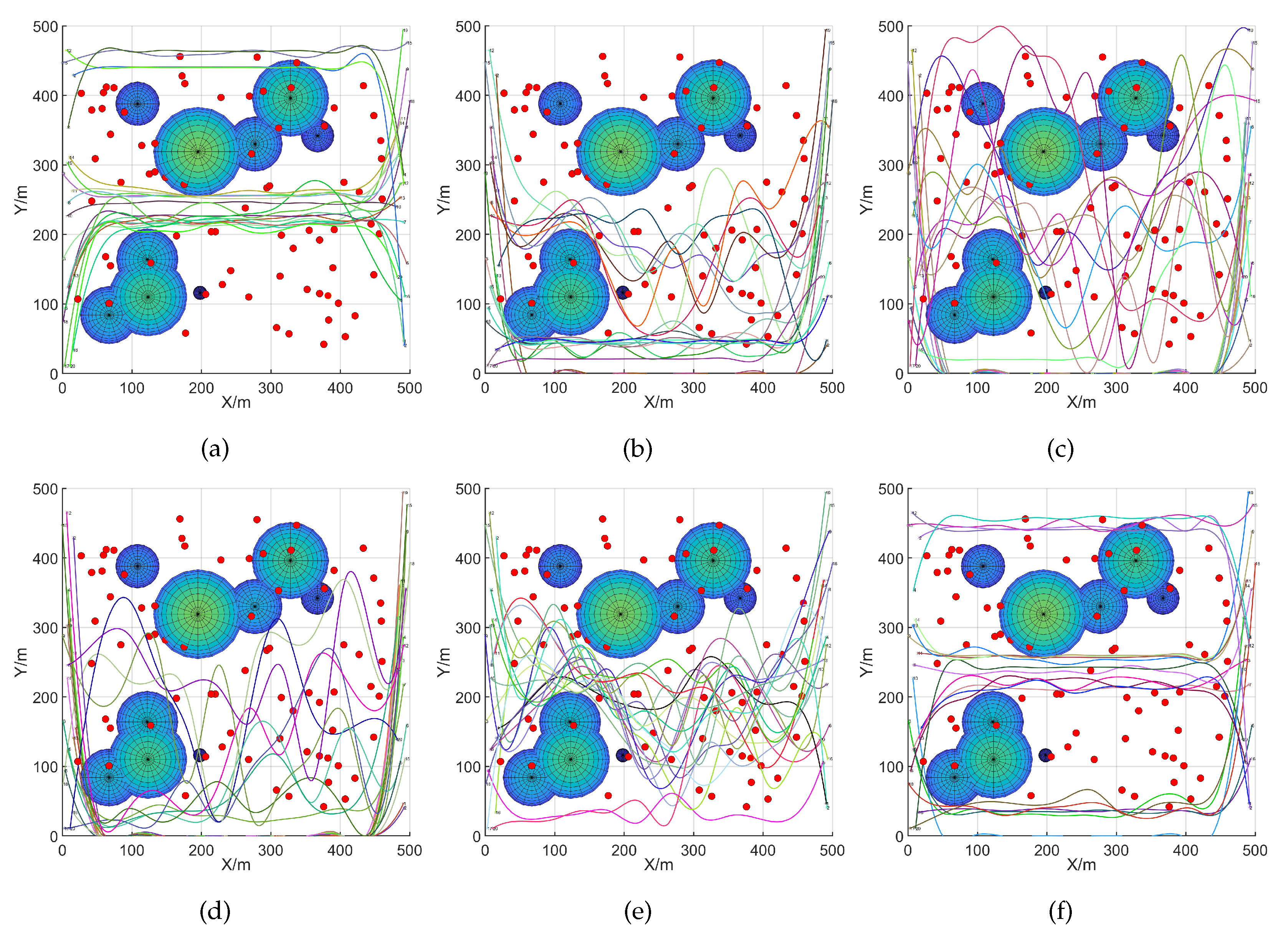
- To validate the advantages of the proposed method, this paper thoroughly considers two scenarios: invincible defense in a sparse environment, and enemy defense in a dense environment. Additionally, a model is designed that reflects real urban environments and establishes constraints and trajectory optimization cost functions that meet the needs of UAV flight. This approach accurately replicates the target strike situations of UAVs in urban settings, thereby enhancing the reliability and scientific validity of the proposed method.
- The proposed Electric Eel Foraging Optimization Algorithm (EEFO) simulates the movement and detection mechanisms of electric eels through mathematical modeling to enhance the adaptability of UAVs in complex environments. It introduces a multilevel decision mechanism for target selection and strike path optimization on both the global and local levels, improving the flexibility of task adjustment. Additionally, EEFO considers dynamic changes by adjusting strategies through real-time feedback, optimizing target recognition, path planning, and coordinated target strikes, thereby enhancing its robustness and interference resistance.
2. Related Works
3. System Model and Problem Formulation
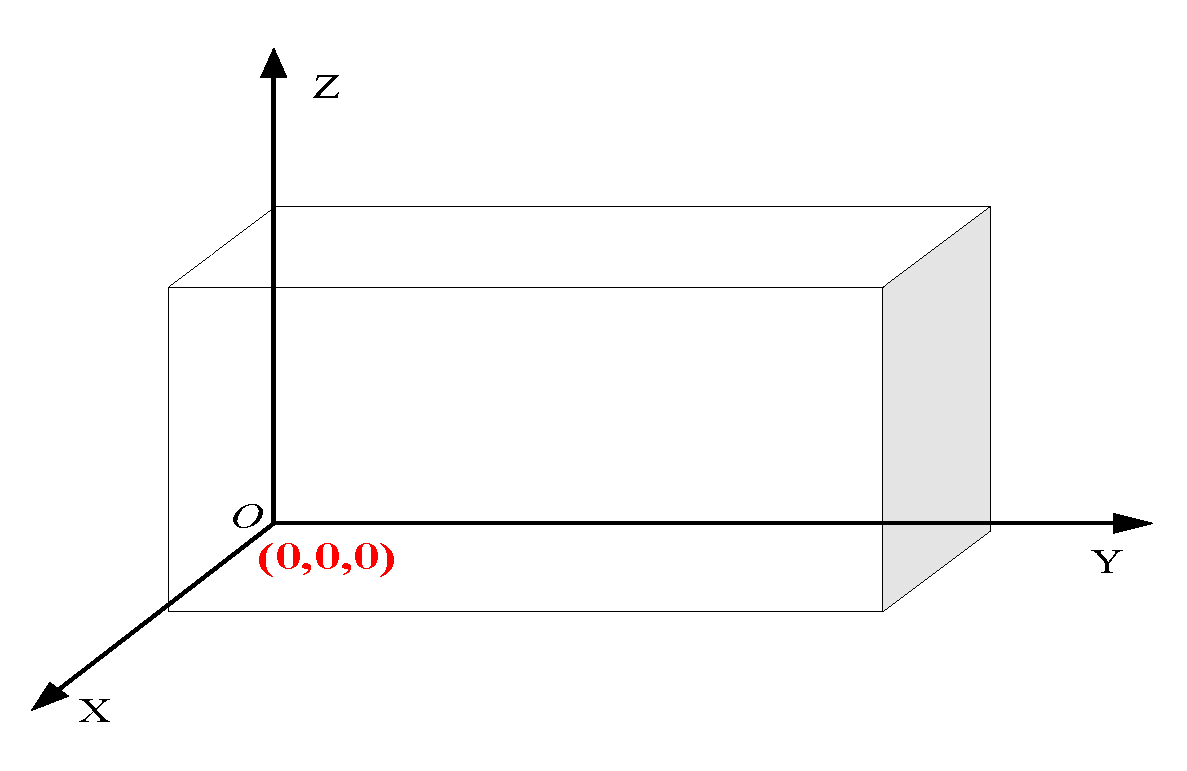
3.1. Urban Building Modeling
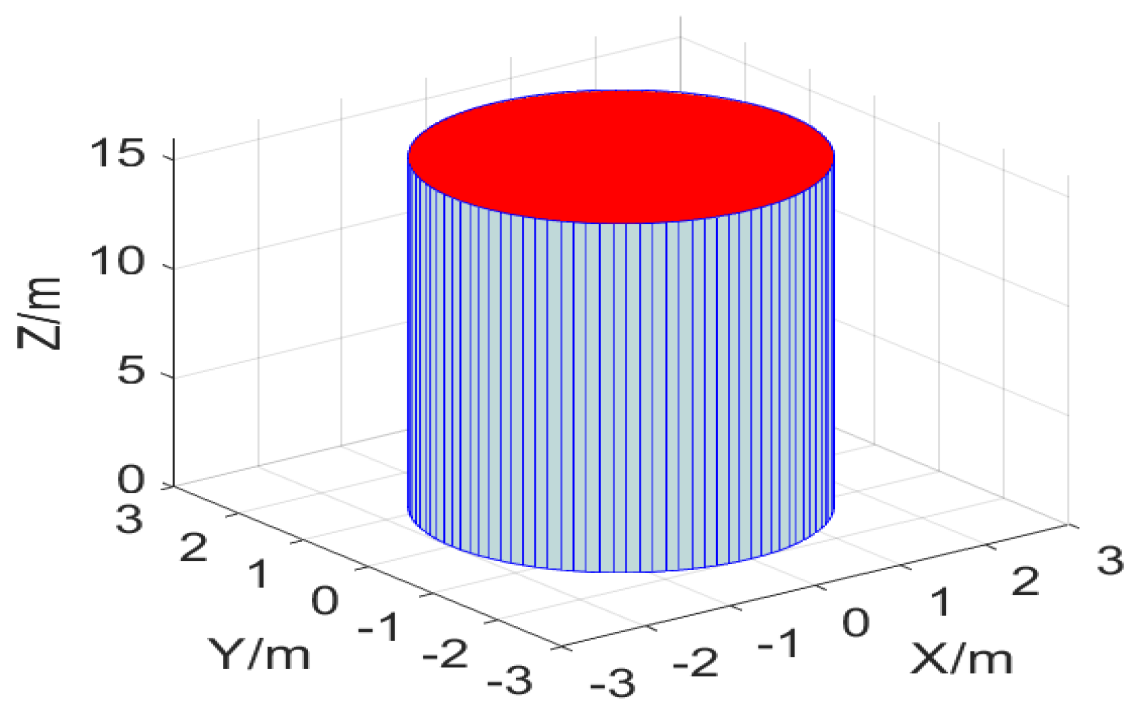
3.2. Threat Area Modeling
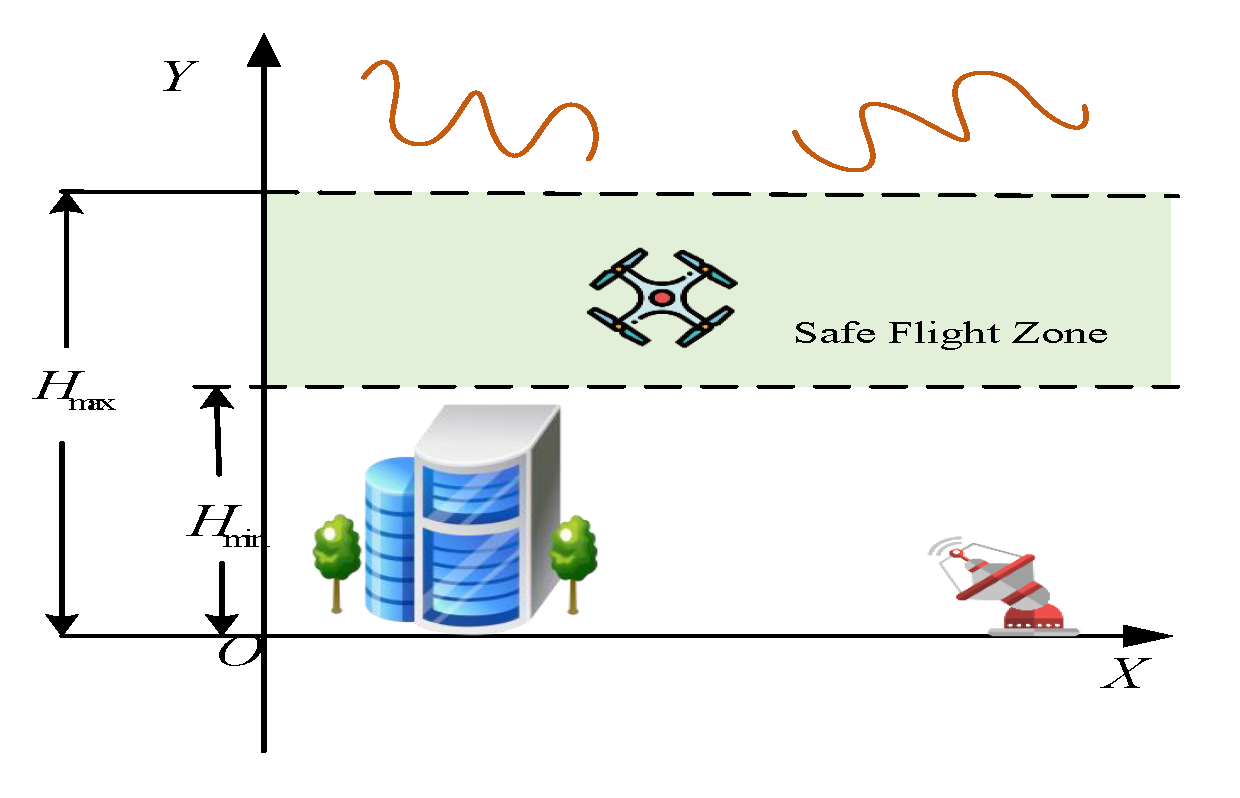
3.3. UAV Trajectory Constraints
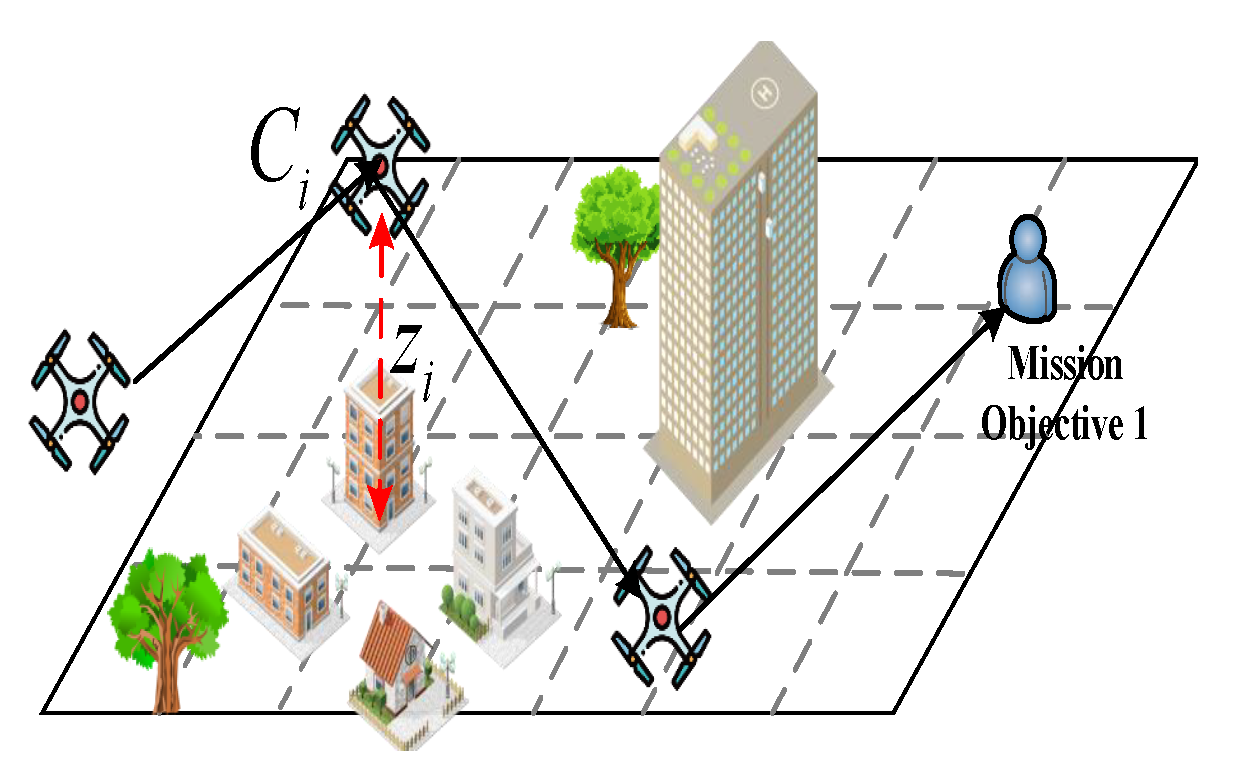
3.4. UAV Trajectory Cost Function
3.5. Cubic B-Spline Smoothing
4. Electric Eel Foraging Optimization Algorithm
4.1. Algorithm Principle
4.2. Algorithm Complexity
| Algorithm 1 Electric Eel Foraging Optimization (EEFO) |
| Input: Starting point coordinates, building coordinates and heights, threat area coordinates, and ranges. Output: Randomly generate the path for each eel within the feasible space, calculate the fitness for each eel, and let be the optimal solution. 1: while the termination condition is not met do 2: for each eel do 3: Calculate the energy factor E. 4: for each time slot t do if then 5: Update position according to interaction behavior 6: Calculate individual fitness 7: else if then 8: Calculate the resting area 9: Update position according to resting behavior 10: Calculate individual fitness 11: else if then 12: Update position according to migration behavior 13: else 14: Calculate the hunting area 15: Update position according to hunting behavior 16: end if 17: end for 18: Update the position of each eel 19: Update the optimal solution 20: end for 21: eturn the optimal solution 22: end while |
5. Experimental Simulation and Analysis
5.1. UAV Path Planning with the EEFO Algorithm in Sparse Environments Under Undefended Conditions
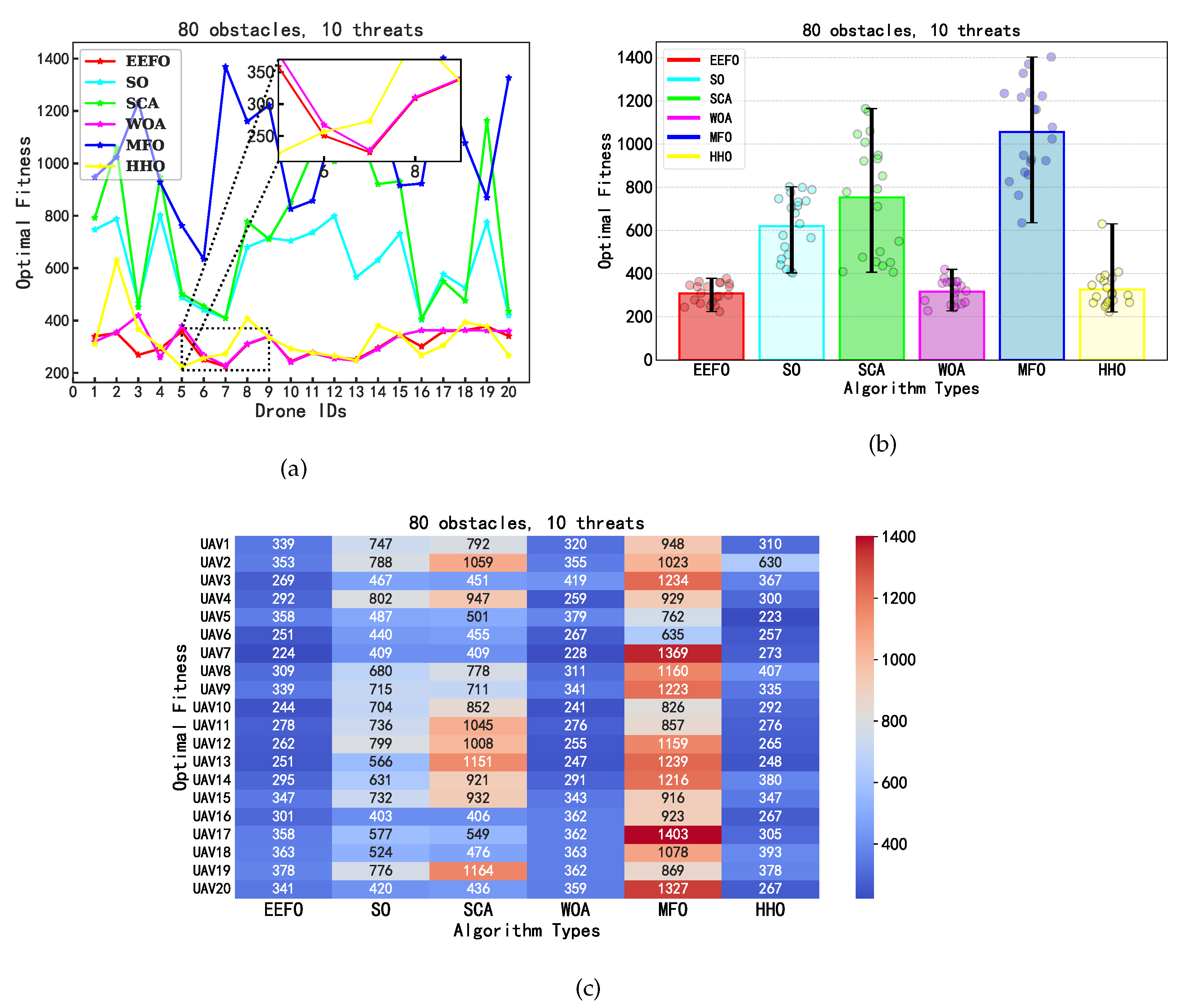
5.2. UAV Path Planning with the EEFO Algorithm in Dense Environments Under Defended Conditions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nwaogu, J.M.; Yang, Y.; Chan, A.P.; Chi, H.l. Application of drones in the architecture, engineering, and construction (AEC) industry. Autom. Constr. 2023, 150, 104827. [Google Scholar] [CrossRef]
- Mei, X.; Miao, F.; Wang, W.; Wu, H.; Han, B.; Wu, Z.; Chen, X.; Xian, J.; Zhang, Y.; Zang, Y. Enhanced Target Localization in the Internet of Underwater Things through Quantum-Behaved Metaheuristic Optimization with Multi-Strategy Integration. J. Mar. Sci. Eng. 2024, 12, 1024. [Google Scholar] [CrossRef]
- Miao, F.; Li, H.; Yan, G.; Mei, X.; Wu, Z.; Zhao, W.; Liu, T.; Zhang, H. Optimizing UAV Path Planning in Maritime Emergency Transportation: A Novel Multi-Strategy White Shark Optimizer. J. Mar. Sci. Eng. 2024, 12, 1207. [Google Scholar] [CrossRef]
- Franke, F.; Schwab, M.; Burger, U.; Hühne, C. An analytical model to determine the impact force of drone strikes. CEAS Aeronaut. J. 2022, 13, 69–84. [Google Scholar] [CrossRef]
- Mei, X.; Han, D.; Saeed, N.; Wu, H.; Han, B.; Li, K.C. Localization in underwater Acoustic IoT networks: Dealing with perturbed anchors and stratification. IEEE Internet Things J. 2024, 11, 17757–17769. [Google Scholar] [CrossRef]
- Mei, X.; Han, D.; Saeed, N.; Wu, H.; Ma, T.; Xian, J. Range difference-based target localization under stratification effect and NLOS bias in UWSNs. IEEE Wirel. Commun. Lett. 2022, 11, 2080–2084. [Google Scholar] [CrossRef]
- Beloev, I.H. A review on current and emerging application possibilities for unmanned aerial vehicles. Acta Technol. Agric. 2016, 19, 70–76. [Google Scholar] [CrossRef]
- Peng, Q.; Wu, H.; Xue, R. Review of dynamic task allocation methods for UAV swarms oriented to ground targets. Complex Syst. Model. Simul. 2021, 1, 163–175. [Google Scholar] [CrossRef]
- Xia, Z.; Du, J.; Wang, J.; Jiang, C.; Ren, Y.; Li, G.; Han, Z. Multi-agent reinforcement learning aided intelligent UAV swarm for target tracking. IEEE Trans. Veh. Technol. 2021, 71, 931–945. [Google Scholar] [CrossRef]
- Deng, H.; Huang, J.; Liu, Q.; Zhao, T.; Zhou, C.; Gao, J. A distributed collaborative allocation method of reconnaissance and strike tasks for heterogeneous UAVs. Drones 2023, 7, 138. [Google Scholar] [CrossRef]
- Mei, X.; Han, D.; Chen, Y.; Wu, H.; Ma, T. Target localization using information fusion in WSNs-based Marine search and rescue. Alex. Eng. J. 2023, 68, 227–238. [Google Scholar] [CrossRef]
- Kouroshnezhad, S.; Peiravi, A.; Haghighi, M.S.; Jolfaei, A. Energy-efficient drone trajectory planning for the localization of 6G-enabled IoT devices. IEEE Internet Things J. 2020, 8, 5202–5210. [Google Scholar] [CrossRef]
- Lu, Z.; Jia, Z.; Wu, Q.; Han, Z. Joint Trajectory Planning and Communication Design for Multiple UAVs in Intelligent Collaborative Air-Ground Communication Systems. IEEE Internet Things J. 2024, 11, 31053–31067. [Google Scholar] [CrossRef]
- Lu, Z.; Wu, G.; Zhou, F.; Wu, Q. Intelligently Joint Task Assignment and Trajectory Planning for UAV Cluster with Limited Communication. IEEE Trans. Veh. Technol. 2024, 73, 13122–13137. [Google Scholar] [CrossRef]
- Rabta, B.; Wankmüller, C.; Reiner, G. A drone fleet model for last-mile distribution in disaster relief operations. Int. J. Disaster Risk Reduct. 2018, 28, 107–112. [Google Scholar] [CrossRef]
- Muñoz, J.; López, B.; Quevedo, F.; Monje, C.A.; Garrido, S.; Moreno, L.E. Multi UAV coverage path planning in urban environments. Sensors 2021, 21, 7365. [Google Scholar] [CrossRef]
- Wu, J.; Wang, H.; Li, N.; Yao, P.; Huang, Y.; Yang, H. Path planning for solar-powered UAV in urban environment. Neurocomputing 2018, 275, 2055–2065. [Google Scholar] [CrossRef]
- Hu, X.; Pang, B.; Dai, F.; Low, K.H. Risk assessment model for UAV cost-effective path planning in urban environments. IEEE Access 2020, 8, 150162–150173. [Google Scholar] [CrossRef]
- Lin, Y.; Saripalli, S. Sampling-based path planning for UAV collision avoidance. IEEE Trans. Intell. Transp. Syst. 2017, 18, 3179–3192. [Google Scholar] [CrossRef]
- Wang, X.; Gursoy, M.C.; Erpek, T.; Sagduyu, Y.E. Learning-based UAV path planning for data collection with integrated collision avoidance. IEEE Internet Things J. 2022, 9, 16663–16676. [Google Scholar] [CrossRef]
- Alzakari, S.A.; Izci, D.; Ekinci, S.; Alhussan, A.A.; Hashim, F.A. A new control scheme for temperature adjustment of electric furnaces using a novel modified electric eel foraging optimizer. AIMS Math. 2024, 9, 13410–13438. [Google Scholar] [CrossRef]
- Linh, N.T.; Phong, D.H.T. Optimize power generation of thermal generating sources in solving the green energies-based economic load dispatch using Electric Eel Foraging Optimization. World J. Adv. Eng. Technol. Sci. 2024, 11, 368–378. [Google Scholar]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Seyala, N.; Abdullah, S.N. Cluster analysis on longitudinal data of patients with kidney dialysis using a smoothing cubic B-spline model. Int. J. Math. Stat. Comput. Sci. 2024, 2, 85–95. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z.; Fan, H.; Zhang, J.; Mirjalili, S.; Khodadadi, N.; Cao, Q. Electric eel foraging optimization: A new bio-inspired optimizer for engineering applications. Expert Syst. Appl. 2024, 238, 122200. [Google Scholar] [CrossRef]
- Javanmardi, S.; Sakellari, G.; Shojafar, M.; Caruso, A. Why it does not work? Metaheuristic task allocation approaches in Fog-enabled Internet of Drones. Simul. Model. Pract. Theory 2024, 133, 102913. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A novel meta-heuristic optimization algorithm. Knowl.-Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Zhong, C.; Li, G.; Meng, Z. Beluga whale optimization: A novel nature-inspired metaheuristic algorithm. Knowl.-Based Syst. 2022, 251, 109215. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Mirjalili, S.; Soleimanian Gharehchopogh, F.; Oliva, D. A critical review of moth-flame optimization algorithm and its variants: Structural reviewing, performance evaluation, and statistical analysis. Arch. Comput. Methods Eng. 2024, 31, 2177–2225. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Saha, A.K.; Ezugwu, A.E.; Agushaka, J.O.; Abuhaija, B.; Alsoud, A.R.; Abualigah, L. Moth flame optimization: Theory, modifications, hybridizations, and applications. Arch. Comput. Methods Eng. 2023, 30, 391–426. [Google Scholar] [CrossRef]




| Algorithm | Performance |
|---|---|
| Adaptive Path Re-Planning (APREP) | Limited response to sudden threats or extreme weather. |
| Insufficient robustness in unpredictable environments. | |
| Multi-Objective Hybrid Path Planning (MOHPP) | Computationally intensive with large UAV swarms or obstacles. |
| Challenges with real-time responsiveness. | |
| Risk-Aware Path Planning | Relies on accurate, up-to-date environmental data, which may not always be available. |
| Limited effectiveness in dynamic urban environments with rapidly changing conditions. | |
| Collaborative Obstacle Avoidance | Focuses on narrow passage environments, less suited for complex, three-dimensional urban settings. |
| Uncertain effectiveness in large-scale, dynamic urban environments. | |
| Electric Eel Foraging Optimization Algorithm (EEFO) | Simulates electric eel behavior to improve UAV adaptability and swarm coordination in complex, dynamic environments. |
| Adjusts planning and strategies dynamically based on real-time feedback, optimizing target recognition and obstacle avoidance. | |
| Optimizes strike paths and enhances targeting accuracy through adaptive planning and coordination. |
| Parameter Name | Unit | Simulation Value |
|---|---|---|
| Planning space size | m | 500 × 500 |
| Starting point position | m | (20, 10, 20) |
| Target point position | m | (410, 380, 30) |
| Population size | - | 30 |
| Maximum flight range constraint | m | 100, 0 |
| UAV flight height constraint | m | (0, 50) |
| Flight cost weight | - | 0.4 |
| Height change cost weight | - | 0.4 |
| Turning angle change weight | - | 0.2 |
| Number of iterations | - | 50 |
| Scene Name | Number of Buildings | Number of Threat Areas |
|---|---|---|
| Invincible Defense | 10 | 0 |
| Hostile Defense | 80 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fei, C.; Lu, Z.; Jiang, W. Heuristic Optimization-Based Trajectory Planning for UAV Swarms in Urban Target Strike Operations. Drones 2024, 8, 777. https://doi.org/10.3390/drones8120777
Fei C, Lu Z, Jiang W. Heuristic Optimization-Based Trajectory Planning for UAV Swarms in Urban Target Strike Operations. Drones. 2024; 8(12):777. https://doi.org/10.3390/drones8120777
Chicago/Turabian StyleFei, Chen, Zhuo Lu, and Weiwei Jiang. 2024. "Heuristic Optimization-Based Trajectory Planning for UAV Swarms in Urban Target Strike Operations" Drones 8, no. 12: 777. https://doi.org/10.3390/drones8120777
APA StyleFei, C., Lu, Z., & Jiang, W. (2024). Heuristic Optimization-Based Trajectory Planning for UAV Swarms in Urban Target Strike Operations. Drones, 8(12), 777. https://doi.org/10.3390/drones8120777







