Previous Article in Journal
Identification and Characterization of the Delta-12 Fatty Acid Desaturase from Euglena gracilis
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Bioresources and Bioproducts
Volume 1
Issue 2
10.3390/bioresourbioprod1020009
bioresourbioprod-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Eucalyptus nitens Wood of Spanish Origin as Timber Bioproduct: Fiber Saturation Point and Dimensional Variations

by
Óscar González-Prieto
*,
David Casais Goimil
and
Luis Ortiz Torres
Hydro-Forestry Geomodeling Research Group, School of Forestry Engineering, University of Vigo, 36005 Pontevedra, Spain
*
Author to whom correspondence should be addressed.
Bioresour. Bioprod. 2025, 1(2), 9; https://doi.org/10.3390/bioresourbioprod1020009
Submission received: 19 November 2025 / Revised: 10 December 2025 / Accepted: 16 December 2025 / Published: 18 December 2025
Browse Figures
Versions Notes

Abstract

Wood is a primary bioproduct widely utilized as timber in construction and carpentry. Characterization of its properties, particularly moisture response, is essential for industrial performance. The Fiber Saturation Point (FSP) influences the dimensional stability and efficiency of industrial processes such as drying. This study determines the maximum dimensional variation and the FSP of Eucalyptus nitens solid wood from plantations in Northwestern Spain, studying 354 specimens of 20 × 20 × 50 mm. Mean and median values were calculated considering and omitting outliers. Additionally, a graphical FSP value was obtained by applying the statistical theory of the center of gravity, defined as the intersection of lines derived from the two-dimensional data distribution. For maximum dimensional variation, the analysis yielded mean values of 5.2% [±1.53] and 11.2% [±2.84] and medians of 4.8% and 10.4%, in radial and tangential directions, respectively. The mean FSP was 29.9% [±7.95], the median 28.9%, and the graphical estimate 30.8%. Establishing the FSP defines the critical moisture threshold at which significant changes in physical and mechanical properties, as well as dimensional alterations, occur in this bioresource, particularly for its use as a bioproduct in carpentry and construction or for industrial wood drying.

1. Introduction

Wood is considered a bioproduct, as it comes from a renewable bioresource (trees) and can be transformed into a wide range of products with a lower environmental impact compared to fossil or mineral alternatives. Eucalyptus plantations in different parts of the world have gained importance by providing raw biomaterial with short growth periods and wood properties suitable for industry. Eucalyptus nitens (shining gum) has been successfully introduced through new plantations using reforestation in different parts of the world, such as Australia, Chile, South Africa, and Europe, but mainly in Northern Spain and Portugal [1]. For this reason, it has consolidated a strategic position in the forest landscape of Northern Spain, especially in the region of Galicia, and has been introduced at higher altitudes (reaching 1200 m) and cold climates due to its greater tolerance of frost periods compared to other eucalyptus species [2]. In some cases, it has served as a substitute for other species or has been used in combination with E. globulus. The productivity potential of E. nitens plantations is considerable, with studies reporting high Mean Annual Increments (MAIs) [3], which suggests an abundant source of bioresources [4]. There is some uncertainty about the exact surface area of this species, although the review of the Galician Forestry Plan [2] includes approximately 40,000 ha, with an estimated increase of 70,000 ha in the coming years. This is not a negligible quantity, considering that, for example, in Chile, there are already more than 120,000 ha [5], with an increasing interest in its use as bioproducts (e.g., solid wood). The raw material potential for the sawmill industry is high, but the properties of this newly introduced species need to be analyzed. This species is primarily utilized for pulp, wood panels, and biomass-based bioenergy, given its suitability for Short-Rotation Energy Crops (SRWCs) [6], yet it remains largely excluded from high-value structural timber applications despite its favorable mechanical properties and comparatively lower bending strength reduction [7] above the FSP.
One of the most relevant aspects of solid wood properties is its hygroscopicity as the inherent capacity to interact with environmental humidity and temperature conditions, yielding or absorbing moisture content (MC), until an EMC is reached [8]. The FSP is the point below which wood dimensions change and is theoretically settled at 30% of MC [8] for all wood species, although it can vary among species. Therefore, the FSP in wood can be defined as the MC at which the cell walls are completely saturated with water and there is no capillary water in the cell lumen or free spaces [8,9]. Moreover, the FSP has also been introduced as the MC below which cells are saturated with impregnation water, with no free water in their cavities, and the mechanical properties increase and the dimensions vary [10]. In more recent works [11,12], it has been defined as the MC below which the physical and mechanical properties of wood begin to increase, for example, with an increase in the strength and stiffness of wood [13,14,15]. Also, it represents the threshold where dimensional instability begins, and shrinkage and swelling of wood only occur within the hygroscopic range below this point. This phenomenon initiates the volumetric shrinkage of wood and is the main cause of the risks of warping, cracking, collapse, and splitting during the drying process and service use. Furthermore, the FSP is the threshold that regulates the impact on mechanical properties [7] and determines the target MC that sawn timber must reach to be suitable for structural or high-precision applications [16]. The determination of this value is also useful for forced wood-drying processes, since E. nitens could develop tensions and deformations in drying below this point [17], including collapse, a phenomenon that results from an abnormal contraction close to this point and is caused by capillary forces that arise when free water is removed [18].
Classical extrapolations, property transition analyses, and advanced techniques constitute the principal methods for determining the FSP [11,19,20]. Extrapolation methods plot adsorption isotherms to unit relative vapor pressure (100% relative humidity) [21] or extrapolate differential heat of wetting to zero heat evolved [11]. Other methods for the accurate estimation of FSP include the use of the Shrinkage Intersection Point (SIP), obtained by extrapolating from shrinkage curves, and the development of empirical mathematical models based on linear regression that correlate physical properties with MC [22,23]. Transition point methods identify the break point in the relationship between MC and logarithmic material properties, such as strength/compression properties or electrical conductivity [21]. Dimensional/volumetric methods extrapolate volumetric shrinkage versus MC to zero shrinkage (Shrinkage Intersection Point) or experimentally determine the MC at which wood dimensions initiate change during drying [21]. Cell Wall Saturation (CWS) or bound water can be derived from bulk volumetric properties/densities or measured using double-weighing techniques [11]. Other advanced/modeling techniques employ specialized methods like Differential Scanning Calorimetry (DSC), Nuclear Magnetic Resonance (NMR), or the application of sorption models such as the Hailwood–Horrobin (HH) equation [11,24]. Additionally, graphical analysis of drying rate curves (using LOWESS smoothing) can locate the FSP transition between the second and third drying phases [22]. Of these methods, the most common and simplest one makes use of the linear relationship between dimensional change (shrinkage or swelling) and the change in MC from anhydrous to saturated state.
Several authors [8,12,24] established the general average FSP value of between 28% and 30% of MC for all woods, and some even between values of 13 and 70% depending on the method of determination used [11,15]. Specific analyses of different woods, such as beech and certain African tropical woods [25], as well as acacia wood [26] or even woods from the Malaysian region [21], show that significant differences can exist with respect to these general values. Tropical heartwoods generally exhibit FSP values lower than European species, with some taxa registering minimum values around 17% (e.g., African padouk and Ipe), correlating inversely with basic wood density. Concurrently, studies on Acacia melanoxylon yielded a mean FSP of 24.7%, where inter-tree variability accounted for a significant portion (43%) of the total random variance. Furthermore, lesser-known timbers displayed an extensive FSP continuum, documented to range significantly from 17% to 33%. This pronounced heteroscedasticity necessitates that industrial drying protocols prohibit the co-mingling of timbers with substantially divergent FSP thresholds (e.g., 17.2% vs. 33.3%) to mitigate the genesis of catastrophic seasoning defects. For these reasons, it is important to study and understand this value in different woods, as a limit for the dimensional changes and for the significant variations in various physical and mechanical properties, which is especially relevant for species susceptible to collapse during drying, when wood bioproducts are manufactured [17].
Another relevant and inherent property of wood is its anisotropy, showing dimensional and property variations depending on the main fiber direction. Thus, it is important to differentiate between the three main cutting directions in wood [8]: radial direction (parallel to the wood rays and perpendicular to the growth rings); tangential direction (tangent to the growth rings); and longitudinal direction (follows the length of the tree trunk). In this study, two main directions were considered: radial and tangential. The longitudinal direction could be ignored due to its small and practically irrelevant values, unless pieces of large longitudinal sizes are involved [27]. Several works have studied dimensional variations in different wood species, especially those of high industrial interest, such as beech and certain African tropical woods [25], or Malaysian woods [21].
Making use of the inherent hygroscopicity of wood, which creates an affinity for the exchange of water molecules with the surrounding environment (liquid water or water vapor present in the air) until the EMC is reached, it is possible to achieve the desired dimensional variations in each of the specimens by controlling the changes in the ambient humidity and temperature or even reach maximum variation values by immersion in liquid water.
Among the various methods identified to determine the FSP, this study selected the approach applied to several wood species [28,29,30,31] based on the assessment of volumetric variation and moisture content from the saturated to the anhydrous state. This is a simple method based exclusively on dimensional variations in wood by total immersion in liquid water and desorption of its MC in an oven.
Freshly sawn green wood that had not undergone a previous drying process was used, thus avoiding possible modification or hygroscopic fatigue in the wood cells when they are subjected to high temperatures to reduce their MC [32]. According to previous work with E. nitens [22,23,33,34], some physical and mechanical properties change around the FSP limit. Even with the change in the slope of the drying curve fitting regression corresponding to the transition from the second to the third drying phase, the piece reached the experimental FSP between 26.2% and 27.0% and theoretical values of 26.8% and 28.8%, without distinguishing between radial and tangential directions [22]. The most important challenges for the use of E. nitens as structural timber are growth stresses and the collapse phenomenon [23]; therefore, knowledge of the FSP helps to establish the beginning of these phenomena.
The objectives of this study were to determine the MC and the maximum linear variations in the radial and tangential directions from the saturated state to an anhydrous state using a simple methodology and fixing the measurement points with nails and, from these data, to determine the FSP by mathematical calculations and the use of graphical analysis.

2. Materials and Methods

2.1. Raw Material and Measurement

Twelve green sawn boards were randomly selected from twelve 18-year-old trees from the north of the province of Lugo (Spain) and sawn in a local industrial sawmill with purely radial and tangential faces (largest width dimension), depending on whether the growth rings were tangent or perpendicular to the surface. When the growth ring strikes the surface to be measured at an angle below 45°, they are considered tangential, and when the growth ring strikes the surface to be measured at an angle above 45°, they are considered radial [35]. The samples used had an average density of 558.2 [±71.69] kg/m3 with 13.2% of MC.

2.2. Experimental Method

The methodology used in the preparation of the specimens and measurements was established by IRAM 9543 [36] and DIN 52184 [37] standards. These methods were used due to their simplicity in execution compared to other methods that require sophisticated mechanisms and tools. Roughly pre-cut samples were stored under standard climate conditions until equilibrium was reached. Subsequently, a total of 354 specimens of 20 × 20 × 50 mm were elaborated and measured. These samples were prepared according to the DIN 52184 standard [37] and stored under normal climate conditions (20 °C and 65% relative humidity) until a constant weight was achieved, i.e., when the weight of the samples changed by no more than 0.1% at 24 h intervals compared to the previous weighing. This weight stability criterion was also followed in the subsequent drying process. To facilitate consecutive measurements at the same points and avoid unwanted variations due to changes in measurement points, four metal nails were inserted into each of the specimens using a pre-drilled hole and separated by 40 mm (Figure 1a–c), following the guidelines of IRAM 9543 [36] and previous works [26,38]. More than 2300 measurements were taken at different MC levels of the wood. The moisture content was determined by the gravimetric method using a dry-oven.
The dimension between the two nails and the weight of the specimens were determined at three different MCs: at “normal conditions” when the specimens were stabilized under an air temperature and humidity of 20 °C and 65%, respectively; at a “saturated state”, after immersion in distilled water to overcome the FSP; and finally, at an “anhydrous state” before total drying in a labor oven. A balance and a caliper were used with an accuracy of 0.01 g and 0.01 mm, respectively. The immersion was carried out in distilled water at room temperature (20 °C) for 96 h. Before measuring them in a saturated state, the surface water was allowed to drain from the specimens onto laboratory paper. Before reaching the maximal dimension, the samples were dried until an anhydrous state was achieved. Drying was carried out in a naturally ventilated drying oven, increasing the temperature in three stages (to 50, to 80, and finally to 103 ± 3 °C) at 24 h intervals. This procedure was followed to avoid the loss of volatile components, which, at elevated temperatures, can alter the mass of the anhydrous sample [37]. After drying, specimens were cooled in a desiccator with a drying agent to prevent moisture absorption, and mass and dimension (between the nails) were measured.

2.3. Calculations and Analytical Tools of Analyzed Properties

The maximum dimensional variation from the saturated state to the anhydrous state were calculated with Equation (1) according to the DIN 52184 standard [37], where αmax is the maximum variation from the saturated state to the anhydrous state, lw (in mm) is the dimension in the saturated state, and l0 (in mm) is the dimension in the anhydrous state.
α m a x = l w − l 0 l 0 × 100   ( % )
The dimensional variation under normal conditions was determined according to Equation (2), following the DIN 52184 standard [37], where lnormal conditions (in mm) is the dimension in the equilibrium state in the chamber and l0 (in mm) is the dimension in the anhydrous state.
α n o r m a l   c o n d i t i o n s = l n o r m a l   c o n d i t i o n s − l 0 l 0 × 100   ( % )
To determine the FSP, numerical calculations were used on the one hand, employing mean and median values, and, on the other hand, graphical interpretation was used afterwards, representing the individual results.
A numerical methodology, according to previous references [8,26,31], was used with Equation (3), employing mean and median values of the population, where αmax is the maximum variation from the saturated state to the anhydrous state, αnormal conditions (in %) is the variation from the saturated to the equilibrium state in the chamber, and Hnormal conditions (in %) is the EMC reached by the specimen in the chamber.
F S P   % =   α m a x ∝ n o r m a l   c o n d i t i o n s H n o r m a l   c o n d i t i o n s  
The EMC reached by the specimens was determined using the Equation (4), according to DIN 52184 [38], where Ph (in g) is the weight determined by the weight in this state and P0 (in g) is the anhydrous weight used with the minimum reference.
E M C   % = P h − P 0 P 0 × 100
The graphical methodology represented the two-dimensional data distribution and, based on the statistical theory of the center of gravity [39], the FSP was determined as the value of the intersection between the straight lines of the results in the saturated and normal states.
Descriptive statistical analyses and graphical representations were carried out using Microsoft Excel and Sigmaplot 11.0. Normality and similarity analysis were performed with Statgraphics Centurion XV software, version 15.2. Anomalous data analysis was also performed [40], considering any value outside the interval (Q1 − 1.5 R, Q3 + 1.5 R) as an anomalous value, where Q1 is the first quartile, Q3 is the third quartile, and R = Q3 − Q1.

3. Results and Discussion

The study utilized a hybrid approach, combining dimensional measurement [11,14,28] (Equation (3)) with a graphical analysis rooted in the statistical theory of the center of gravity. This methodology serves as an alternative to that employed in previous investigations involving E. nitens [22], wherein the authors leveraged the change in the slope of the drying rate curve (using LOWESS smoothing) to ascertain the experimental FSP, which delineates the transition from the second to the third drying phase. Table 1 summarizes the mean and standard deviation values for the radial and tangential results obtained after performing the calculations with the previously described equations, without rejecting the data considered anomalous.
According to the results obtained, the MC under normal conditions was between 9.9 and 14%, and saturated mean values exceeded 100%. The total dimensional variation was 5.2% for the radial specimens and 11.2% for the tangential specimens. A slight increase in variability was observed in the tangential measurements compared to the radial measurements, possibly influenced by incipient deformations observed in some tangential specimens in their saturated and anhydrous states. The acquired results corroborate the pronounced anisotropic characteristic of E. nitens [23].
Figure 2 represents all the FSP values obtained by mathematical calculation (Equation (3)), for both the tangential and radial specimens.
Due to the slight dispersion found, especially in the values of the tangential specimens, the anomalous data were evaluated. Some anomalous values were detected with excessive deviation from the mean value (Figure 3). Anomalous values generally come from measurement errors or from specimens that, in addition to having dimensional variations, have deformations and loss of geometry.
Table 2 summarizes the mean and standard deviation values for the radial and tangential results obtained after performing the calculations with the previously described equations and excluding the anomalous values.
According to these results and using a Student’s t-test to analyze the statistical similarity or differences between means, no significant differences were identified among the values of all the results and excluding the anomalous values.
Once the analysis with the mean values was carried out, the analysis with the median values was performed to increase statistical rigor. The median was selected as a complementary statistical measure due to its resilience against extreme values, which are not uncommon in wood property assessments. Table 3 summarizes the median values for the radial and tangential results obtained after performing the calculations with the previously described equations.
Figure 4 shows the median FSP value obtained by mathematical calculation and establishes the interval for anomalous data described above. Using the median values reduces the influence of anomalous values, as it represents a central position. The FSP value thus obtained is 28.9%. These values obtained with the median are slightly lower than the mean values and are close to the mean values of maximum dimensional variation in both the radial and tangential directions obtained in previous works [34], which compared the properties of various eucalyptus trees from New Zealand, including E. nitens, obtaining radial and tangential variations of approximately 3.6% and 10.8%.
The elevated values of tangential variation (average 11.2% and median 10.4%) relative to radial variation concur with findings reported by authors who document similar results of high anisotropy in E. nitens [23], reporting tangential contractions of up to 14.1% and an anisotropy index of Ctg/Crd ≈ 2.08.
Finally, the results are graphically represented. Figure 5 shows the intersection value of the lines containing the centers of gravity of the measurements in the saturated state and in the normal state. The intersection of the regression lines in a two-dimensional data distribution is congruent with the center of gravity, or the arithmetic means.
Anisotropy influences the large difference between the numerically calculated radial and tangential FSP (Equation (3)) and could explain why the value of the center of gravity (30.8%) could be considered the most representative.
A previous exploratory study to characterize the drying rate of E. nitens boards (36 mm thick) [17], which used linear regression models and LOWESS smoothing to identify the change in slope of the drying curve, obtained experimental FSP values of 27.0% with a drying condition of 40 °C (with a theoretical value of 28.8% calculated based on ambient drying temperature [41]) and 26.2% with a condition of 55 °C (with a theoretical value of 26.8%) [41]. It may be suggested that the drying temperature or the specific methodology employed (dimensional versus drying kinetics) exerts an influence on the reported outcome. Studies using the Shrinkage Intersection Point (PIC) [23] have shown shrinkage rates of 28.1% to 33.5% in the radial direction and 28.6% to 34.0% in the axial direction. Furthermore, both FSP values are very close to the 30% established in previous studies [42,43] and are similar to eucalyptus trees with similar densities [44,45]. E. nitens is usually assumed to have a shrinkage rate of 30% [42]. It may be suggested that the drying temperature or the specific methodology employed (dimensional versus drying kinetics) exerts an influence on the reported outcome [14,21].

4. Conclusions

The quantification of maximum linear dimensional variations and the FSP with E. nitens was successfully achieved through a hybrid methodological approach that combined numerical computations with graphical analysis, utilizing dimensional variation and MC data spanning from saturated to anhydrous states.
The results were determined by mean and median values, with the latter providing the most appropriate representation. These median values established the maximum radial dimensional variation at 4.8% and the maximum tangential variation at 10.4%. The FSP was consistently defined across analytical methods. The overall mean FSP calculated mathematically was 29.9%. The graphical method, which utilized the intersection point of the lines containing the centers of gravity of the two-dimensional data distribution, yielded an FSP of 30.8%. This foundational data is indispensable for defining the requisite target MC for processing E. nitens as a high-precision or structural timber bioproduct, thereby enabling the strategic transition of this resource from lower-value applications (pulp and bioenergy) to higher-value structural uses in Northwestern Spain.
Future research should explore the influence of anatomical features on moisture dynamics and dimensional behavior. Advanced imaging and modeling techniques could refine FSP determination. Additionally, evaluating engineered wood products will support their structural valorization in sustainable construction.

Author Contributions

Conceptualization, Ó.G.-P.; methodology, Ó.G.-P., D.C.G. and L.O.T.; validation, Ó.G.-P. and L.O.T.; formal analysis, Ó.G.-P. and L.O.T.; investigation, Ó.G.-P. and D.C.G.; resources, Ó.G.-P.; writing—original draft preparation, Ó.G.-P.; writing—review and editing, Ó.G.-P., D.C.G. and L.O.T.; supervision, Ó.G.-P.; funding acquisition, Ó.G.-P. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author. The raw data supporting the conclusions of this article will be made available by the authors on request.

Acknowledgments

The authors would like to thank the FINSA company for providing the wood to carry out the study.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Hamilton, M.G.; Blackburn, D.P.; McGavin, R.L.; Baillères, H.; Vega, M.; Potts, B.M. Factors affecting log traits and green rotary-peeled veneer recovery from temperate eucalypt plantations. Ann. For. Sci. 2015, 72, 357–365. [Google Scholar] [CrossRef]
  2. Consellería Medio Rural. Xunta de Galicia. Law 140/2021, of September 30. First Revision of the Galicia Forestry Plan 2021–2040, Towards Carbon Neutrality. Revisión de Plan Forestal de Galicia. 2021. Available online: https://mediorural.xunta.gal/sites/default/files/temas/forestal/plan-forestal/PFG-DEFINITIVO_castelan.pdf (accessed on 29 July 2025). (In Spanish).
  3. Muñoz Saez, F. Evaluation of Silvicultural Practices in Eucalyptus nitens Deane & Maiden Plantations (Evaluación de Prácticas Silvícolas en Plantaciones de Eucalyptus nitens Deane & Maiden Maiden). Ph.D. Thesis, University of Granada, Granada, Spain, 2006. Available online: https://www.educacion.gob.es/teseo/imprimirFichaConsulta.do?idFicha=130037 (accessed on 15 April 2025). (In Spanish).
  4. González-García, M.; Hevia, A.; Majada, J.; Rubiera, F.; Barrio-Anta, M. Nutritional, carbon and energy evaluation of Eucalyptus nitens short rotation bioenergy plantations in northwestern Spain. iForest-Biogeosciences For. 2015, 9, 303–310. [Google Scholar] [CrossRef]
  5. Ananías, R.; Sepúlveda-Villarroel, V.; Pérez-Peña, N.; Torres-Mella, J.; Salvo-Sepúlveda, L.; Casti-llo-Ulloa, D.; Salinas-Lira, C. Radio Frequency Vacuum Drying of Eucalyptus nitens Juvenile Wood. BioResources 2020, 15, 4886–4897. [Google Scholar] [CrossRef]
  6. González-García, M. Modeling the Biomass Production of Eucalyptus nitens (Deane & Maiden) Maiden in Short Rotation for Energy Crop (Modelización de la Producción de Biomasa de Eucalyptus nitens (Deane & Maiden) Maiden en Corta Rotación para Cultivo Energético). Ph.D. Thesis, University of Oviedo, Oviedo, Sapin, 2015. Available online: http://hdl.handle.net/10651/33202 (accessed on 22 July 2025).
  7. Cheng, Y.; Nolan, G.; Holloway, D.; Kaur, J.; Lee, M.; Chan, A. Flexural characteristics of Eucalyptus nitens timber with high moisture content. Bioresources 2021, 16, 2921–2936. [Google Scholar] [CrossRef]
  8. Kollmann, F.F.P.; Côté, W.A. Principles of Wood Science and Technology: I, Solid Wood; Springer-Verlag: Berlin/Heidelberg, Germany, 1968; 592p, ISBN 9783642879302. Available online: https://www.springer.com/gp/book/9783642879302 (accessed on 28 October 2024).
  9. Dinwoodie, J.M. Timber: Its Nature and Behavior, 2nd ed.; Taylor & Francis Group: Abingdon, UK, 2000. [Google Scholar] [CrossRef]
  10. Tiemann, H.D. Effect of Moisture Upon the Strength and Stiffness of Wood; U.S. Department of Agriculture, Forest Service: Washington, DC, USA, 1906; 144p. Available online: http://hdl.handle.net/2027/hvd.32044102823747 (accessed on 15 April 2025).
  11. Babiak, M.; Kúdela, J. A contribution to the definition of the fiber saturation point. Wood Sci. Technol. 1995, 29, 217–226. [Google Scholar] [CrossRef]
  12. Glass, S.V.; Zelinka, S.L. Moisture relations and physical properties of wood. In Wood Handbook: Wood as an Engineering Material; Centennial Edition; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2010; Chapter 4. Available online: https://research.fs.usda.gov/treesearch/62243 (accessed on 15 April 2025).
  13. Passarini, L.; Malveau, C.; Hernandez, R.E. Water state study of wood structure of four hardwoods below fiber saturation point with nuclear magnetic resonance. Wood Fiber Sci. 2014, 46, 480–488. Available online: https://wfs.swst.org/index.php/wfs/article/view/915/915 (accessed on 28 April 2025).
  14. Almeida, G.; Hernandez, R.E. Influence of the pore structure of wood on moisture desorption at high relative humidities. Wood Mat. Sci. Eng. 2007, 2, 33–44. [Google Scholar] [CrossRef]
  15. Almeida, G.; Hernandez, R.E. Changes in physical properties of tropical and temperate hardwoods below and above the fiber saturation point. Wood Sci. Technol. 2006, 40, 599–613. [Google Scholar] [CrossRef]
  16. Ross, J.R. Wood Handbook: Wood as an Engineering Material; General Technical Report FPL-GTR-190; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2010; Volume 1, 509p. [CrossRef]
  17. Ananías, R.A.; Sepúlveda-Villarroel, V.; Pérez-Peña, N.; Leandro-Zuñiga, L.; Salvo-Sepúlveda, L.; Salinas-Lira, C.; Cloutier, A.; Elustondo, D.M. Collapse of Eucalyptus nitens wood after drying depending on the radial location within the stem. Dry. Technol. 2014, 32, 1699–1705. [Google Scholar] [CrossRef]
  18. Chafe, S.C.; Barnacle, J.E.; Hunter, A.J.; Ilic, J.; Northway, R.L.; Rozsa, A.N. Collapse: An Introduction; CSIRO Division of Forest Products: Melbourne, VIC, Australia, 1992; p. 9. ISBN 9780643054417. Available online: https://books.google.es/books?id=SYzdAAAACAAJ (accessed on 18 January 2025).
  19. Berry, S.L.; Roderick, M.L. Plant–water relations and the fibre saturation point. New Phytol. 2005, 168, 25–37. [Google Scholar] [CrossRef]
  20. Fredriksson, M.; Thybring, E.E.; Zelinka, S.L.; Glass, S.V. The fiber saturation point: Does it mean what you think it means? Cellulose 2025, 32, 2901–2918. [Google Scholar] [CrossRef]
  21. Sahri, H.; Jusoh, Z.; Ashaari, Z.; Apin, L. Fibre Saturation Point of Lesser-Known Timbers from Sabah. Pertanika J. Trop. Agric. Sci. 1998, 21, 67–71. [Google Scholar]
  22. Montero, C.; Rozas, C. Exploratory study for the characterization of the wood drying rate of Eucalyptus nitens timber, applying multiple regression models—Estudio exploratorio para la caracterización de la tasa de secado de la madera de Eucalyptus nitens, aplicando modelos de regresión multiple. Sci. For. 2019, 47, 105–113. [Google Scholar] [CrossRef]
  23. Ananias, R.A.; Díaz, C.; Leandro, L. Preliminary study of shrinkage and collapse in Eucalyptus nitens—Estudio preliminar de la contracción y el colapso en Eucalyptus nitens. Maderas-Cienc. Tecnol. 2009, 11, 251–260. [Google Scholar] [CrossRef]
  24. García Esteban, L. La Madera y Su Tecnología: Aserrado, Chapa, Tableros Contrachapados, Tableros de Partículas y de Fibras, Tableros OSB y LVL, Madera Laminada, Carpintería, Corte y Aspiración; Mundi-Prensa: Madrid, Spain, 2002; 336p, ISBN 9788484760368. Available online: https://books.google.es/books?id=NfQxAAAACAAJ (accessed on 15 April 2025).
  25. Jankowska, A.; Kozakiewicz, P. Determination of fibre saturation point of selected tropical wood species using different methods. Drewno 2016, 59, 89–97. [Google Scholar] [CrossRef]
  26. Igartúa, D.V.; Monteoliva, S.; Piter, J.C. Estudio de algunas propiedades físicas de la madera de Acacia melanoxylon en Argentina. Maderas-Cienc. Tecnol. 2009, 11, 3–18. [Google Scholar] [CrossRef]
  27. González-Prieto, O.; Medina, G. Mermas longitudinales en tarimas de exterior (deckings). Boletín Inf. Técnica AITIM 2011, 276, 42–44. [Google Scholar]
  28. Stamm, A.J. Review of nine methods for determining the fiber saturation points of wood and wood products. Wood Sci. 1971, 4, 114–128. [Google Scholar]
  29. Almeida, G. Influence of wood structure on moisture desorption and changes in its properties above the fiber saturation point. In Proceedings of the SWST 48th Annual Convention, Québec City, QC, Canada, 19 June 2005; Available online: http://www.swst.org/wp/meetings/AM05/almeida.pdf (accessed on 15 April 2025).
  30. Hernández, R.E.; Bizoň, M. Changes in shrinkage and tangential compression strength of sugar maple below and above the fiber saturation point. Wood Fiber Sci. 2007, 26, 360–369. [Google Scholar]
  31. Siau, J.F. Wood: Influence of Moisture on Physical Properties; Virginia Polytechnic Institute and State University: Blacksburg, VA, USA, 1995; 227p, ISBN 9780962218101. Available online: https://books.google.es/books?id=fErxAAAAMAAJ (accessed on 8 February 2025).
  32. Fernández-Golfín Seco, J.I.; Conde García, M. Manual Técnico de Secado de la Madera; AITIM: Madrid, Spain, 2007. [Google Scholar]
  33. Opazo-Vega, A.; Rosales-Garcés, V.; Oyarzo-Vera, C. Non-Destructive assessment of the dynamic elasticity modulus of Eucalyptus nitens timber boards. Materials 2021, 14, 269. [Google Scholar] [CrossRef]
  34. McKinley, R.B.; Shelbourne, C.J.A.; Low, C.B.; Penellum, B.; Kimberley, M.O. Wood properties of young Eucalyptus nitens, E. globulus, and E. maidenii in Northland, New Zealand. NZJ For. Sci. 2002, 32, 334–356. [Google Scholar]
  35. García Esteban, L.; Guindeo Casasús, A.; Peraza Oramas, C.; De Palacios, P. La Madera y su Tecnología; AITIM: Madrid, Spain, 2002; ISBN 9788484760368. [Google Scholar]
  36. IRAM 9543; Método de Determinación de las Contracciones Totales, Radial y Tangencial y el Punto de Saturación de las Fibras. Instituto Argentino de Racionalización de Materiales: Buenos Aires, Argentina, 1966. Available online: https://catalogo.iram.org.ar/#/normas/detalles/7169 (accessed on 14 November 2024).
  37. DIN 52184; Testing of Wood; Determination of Swelling and Shrinkage. German Institute for Standardisation: Berlin, Germany, 1979. Available online: https://www.din.de/de/mitwirken/normenausschuesse/nhm/wdc-beuth:din21:625145 (accessed on 14 November 2024).
  38. Calvo, C.F.; Cotrina, A.D.; Cuffré, A.G.; Piter, J.C.; Stefani, P.M.; Torrán, E.A. Radial and axial variation of swelling, anisotropy and density in Argentinean Eucalyptus Grandis. Maderas-Cienc. Tecnol. 2006, 8, 159–168. [Google Scholar] [CrossRef]
  39. Ruiz, G. El concepto estadístico de centro de gravedad. Números. Rev. Didáct. Mat. 2003, 53, 43–53. [Google Scholar]
  40. García, N.A. Elementos de Bioestadística. In Colección Manual UEX, 3rd ed.; Universidad de Extremadura, Servicio de Publicaciones: Cáceres, Spain, 2011; Volume 79, p. 29. ISBN 978-84-694-9432-5. Available online: https://dialnet.unirioja.es/servlet/libro?codigo=678354 (accessed on 17 March 2025). (In Spanish)
  41. Keey, R.; Langrish, T.; Walker, J. Kiln-Drying of Lumber; Springer Verlag: Berlin/Heidelberg, Germany, 2000; 289p. [Google Scholar] [CrossRef]
  42. Dawson, B.S.W.; Pearson, H.; Kimberley, M.O.; Davy, B.; Dickson, A.R. Effect of supercritical CO2 treatment and kiln drying on collapse in Eucalyptus nitens wood. Eur. J. Wood Wood Prod. 2020, 78, 209–217. [Google Scholar] [CrossRef]
  43. Chen, X.; Cheng, Y.; Chan, A.; Holloway, D.; Nolan, G. Anisotropic Tensile Characterisation of Eucalyptus nitens Timber above Its Fibre Saturation Point, and Its Application. Polymers 2022, 14, 2390. [Google Scholar] [CrossRef] [PubMed]
  44. Redman, A.L.; Bailleres, H.; Turner, I.; Perre, P. Characterisation of wood–water relationships and transverse anatomy and their relationship to drying degrade. Wood Sci. Technol. 2016, 50, 739–757. [Google Scholar] [CrossRef]
  45. Haslett, A.N. Properties and utilisation of exotic speciality timbers grown in New Zealand. Part VI: Eastern blue gums and stringy barks. Eucalyptus botryoides Sm. Eucalyptus saligna Sm. Eucalyptus globoidea Blakey. Eucalyptus muellerana Howitt. Eucalyptus pilularis Sm. FRI Bull. 1990, 119, 21. [Google Scholar]
Bioresourbioprod 01 00009 g001
Figure 1. Group of specimens at the time of pre-drilling. Insertion of metal nails (a) with nails detailed inside the blue box. Diagram of the measurement of variation in the radial (b) and tangential (c) directions.
Figure 1. Group of specimens at the time of pre-drilling. Insertion of metal nails (a) with nails detailed inside the blue box. Diagram of the measurement of variation in the radial (b) and tangential (c) directions.
Bioresourbioprod 01 00009 g001
Bioresourbioprod 01 00009 g002
Figure 2. Representation of FSP values obtained by mathematical calculation considering anomalous values. The dash lines indicate the FSP abscissa value of the radial and tangential mean values (black) and the mean value of all specimens (red).
Figure 2. Representation of FSP values obtained by mathematical calculation considering anomalous values. The dash lines indicate the FSP abscissa value of the radial and tangential mean values (black) and the mean value of all specimens (red).
Bioresourbioprod 01 00009 g002
Bioresourbioprod 01 00009 g003
Figure 3. (a,b) show all radial and tangential values, without ruling out the values considered anomalous; (c,d) show the values that were analyzed after removing those considered anomalous, located outside the range marked by the solid red line. The circles indicate calculated values. The dashed line indicates the position of the mean value relative to the abscissa values.
Figure 3. (a,b) show all radial and tangential values, without ruling out the values considered anomalous; (c,d) show the values that were analyzed after removing those considered anomalous, located outside the range marked by the solid red line. The circles indicate calculated values. The dashed line indicates the position of the mean value relative to the abscissa values.
Bioresourbioprod 01 00009 g003
Bioresourbioprod 01 00009 g004
Figure 4. Median values were identified once anomalous data were eliminated. The dash line indicates the FSP value on the abscissa values, both the median of the radial and tangential values, as well as the median value of all the data.
Figure 4. Median values were identified once anomalous data were eliminated. The dash line indicates the FSP value on the abscissa values, both the median of the radial and tangential values, as well as the median value of all the data.
Bioresourbioprod 01 00009 g004
Bioresourbioprod 01 00009 g005
Figure 5. Intersection value of the lines containing the centers of gravity. The black cross symbols indicate the centers of gravity used (x and y values). The red cross symbol indicates the intersection of the two lines; -dotted line that through by (x = 0, y = 0) and (x = 13.21 %, y = 3.35 %), and - dashed line, as parallel to the x-axis, and through the coordinate (x = 115.76 %, y = 7.79 %).
Figure 5. Intersection value of the lines containing the centers of gravity. The black cross symbols indicate the centers of gravity used (x and y values). The red cross symbol indicates the intersection of the two lines; -dotted line that through by (x = 0, y = 0) and (x = 13.21 %, y = 3.35 %), and - dashed line, as parallel to the x-axis, and through the coordinate (x = 115.76 %, y = 7.79 %).
Bioresourbioprod 01 00009 g005
Table 1. Radial and tangential mean and standard deviation without rejecting the data considered anomalous.
Table 1. Radial and tangential mean and standard deviation without rejecting the data considered anomalous.
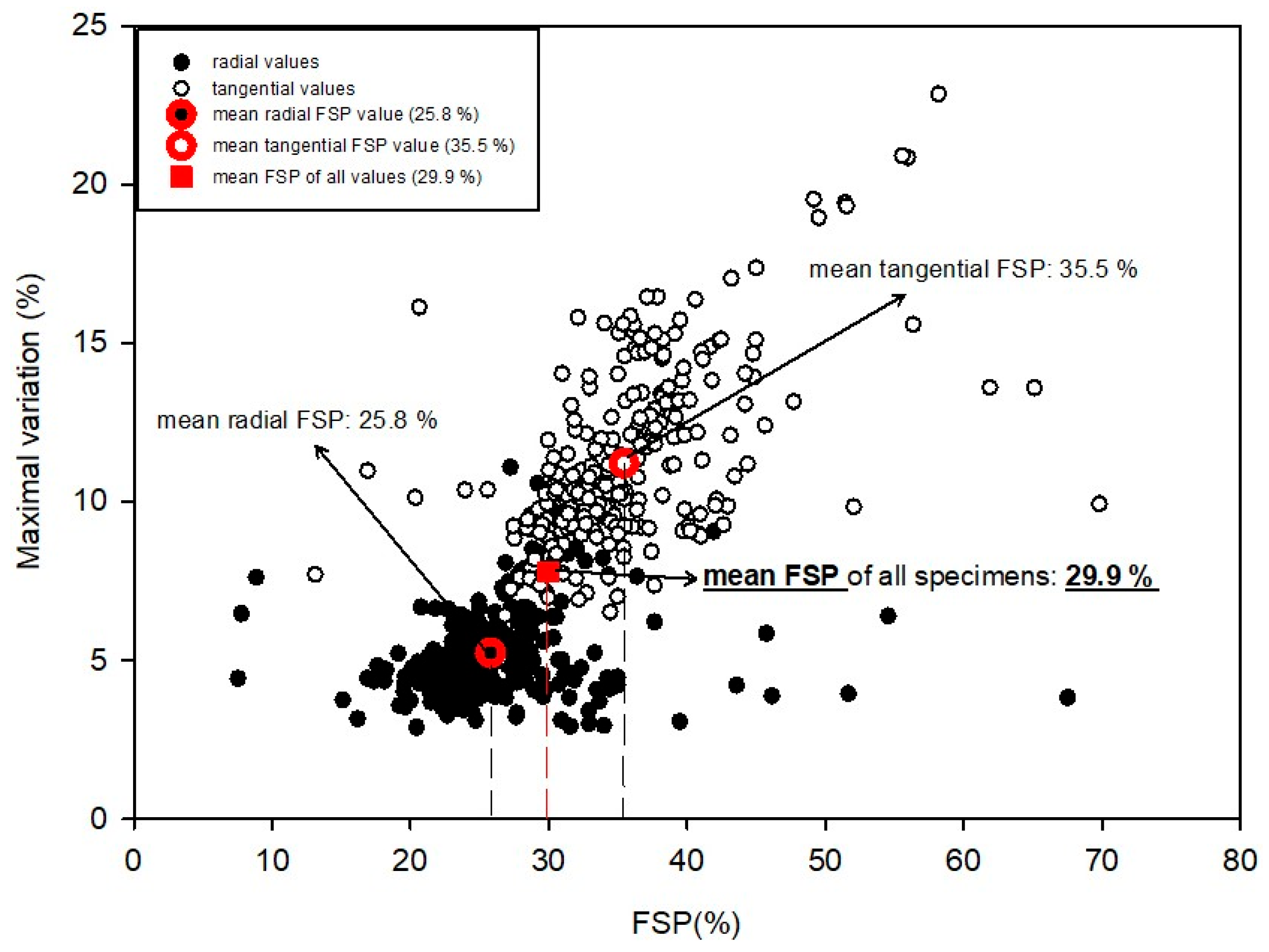
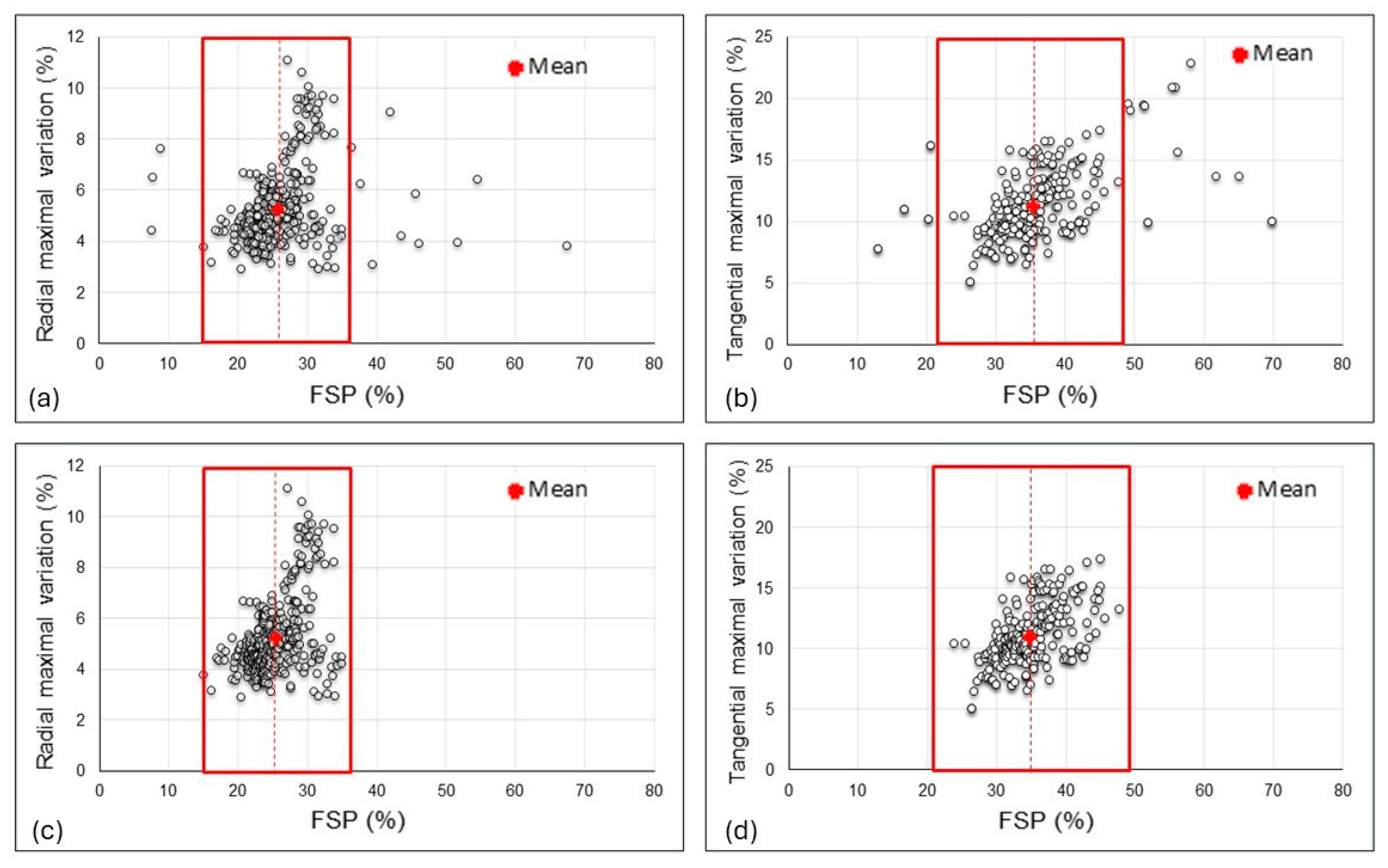
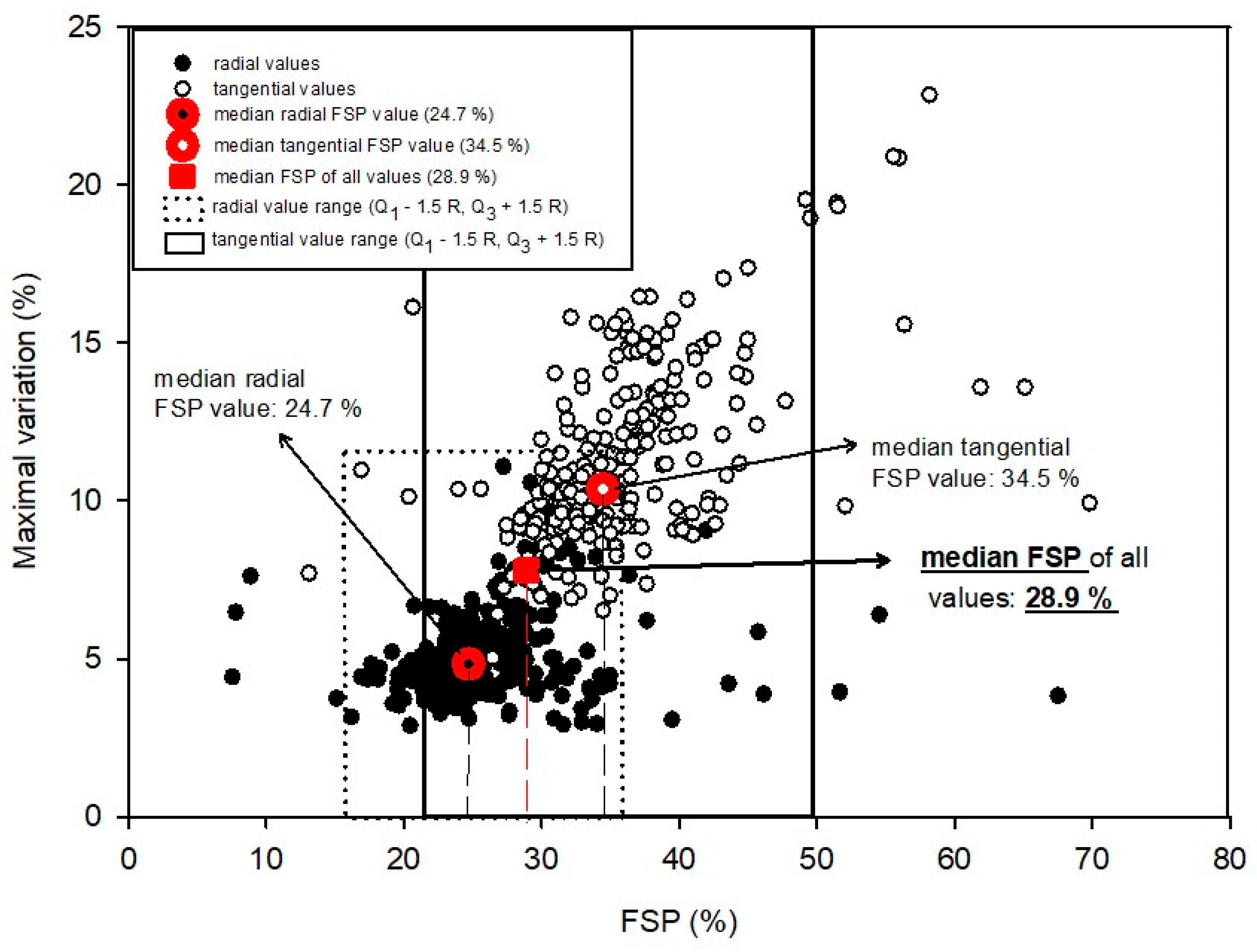
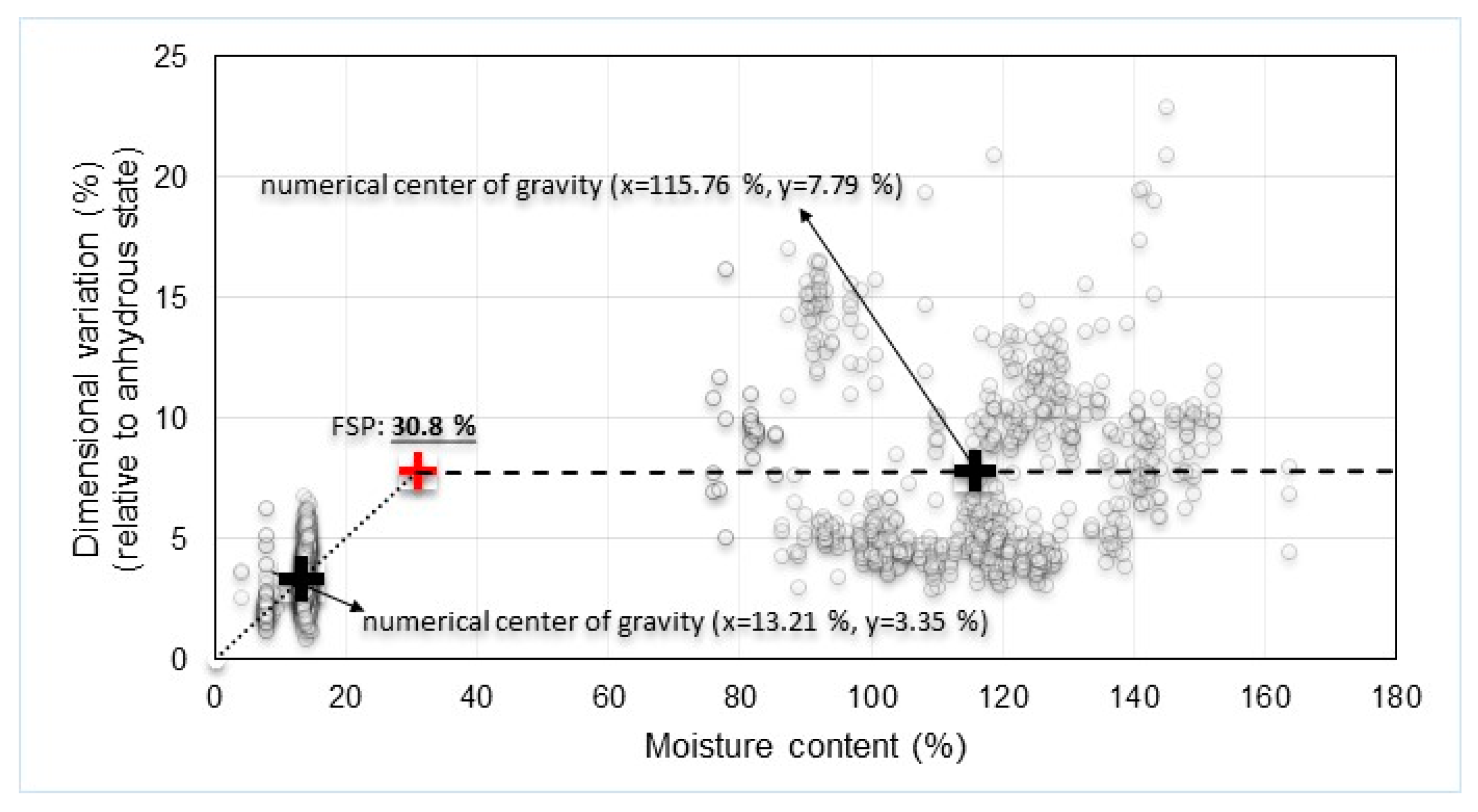
Mean Values with Anomalous DataEquationRadial DirectionTangential Direction
Total variation, saturated * to anhydrous ** (%)15.2 [±1.53]11.2 [±2.84]
Saturated MC (%) 4116.0 [±15.08]115.5 [±23.34]
Normal conditions *** to anhydrous ** state variation (%)22.8 [±0.70]4.0 [±1.27]
Normal conditions *** MC (%)413.8 [±0.96]12.5 [±2.63]
Average FSP325.8 [±5.46]35.5 [±7.38]
Average FSP of all values 29.9 [±7.95]
* immersion in distilled water for 96 h; ** after drying in an oven; *** specimens stabilized under 20 °C and 65% humidity.
Table 2. Radial and tangential mean and standard deviation rejecting the data considered anomalous.
Table 2. Radial and tangential mean and standard deviation rejecting the data considered anomalous.
Mean Values Without Anomalous DataEquationRadial DirectionTangential Direction
Total variation, saturated * to anhydrous ** (%)15.2 ± [1.52]10.9 ± [2.42]
Saturated MC (%)4115.8 ± [14.86]116.5 ± [22.58]
Normal conditions *** to anhydrous ** state variation (%)22.9 ± [0.67]4.0 ± [1.22]
Normal conditions *** MC (%)413.9 ± [0.36]12.7 ± [2.50]
Average FSP325.3 ± [3.61]34.8 ± [4.35]
Average FSP of all values 29.3 ± [6.10]
* immersion in distilled water for 96 h; ** after drying in an oven; *** specimens stabilized under 20 °C and 65% humidity.
Table 3. Results obtained with the median data.
Table 3. Results obtained with the median data.
Values of Median DataEquationRadial DirectionTangential Direction
Total variation, saturated * to anhydrous ** (%)14.810.4
Saturated MC (%)4116.8121.4
Normal conditions *** to anhydrous ** state variation (%)22.84.3
Normal conditions *** MC (%)413.913.9
Average FSP324.734.5
Average FSP of all values 28.9
* immersion in distilled water for 96 h; ** after drying in an oven; *** specimens stabilized under 20 °C and 65% humidity.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

González-Prieto, Ó.; Casais Goimil, D.; Ortiz Torres, L. Eucalyptus nitens Wood of Spanish Origin as Timber Bioproduct: Fiber Saturation Point and Dimensional Variations. Bioresour. Bioprod. 2025, 1, 9. https://doi.org/10.3390/bioresourbioprod1020009

AMA Style

González-Prieto Ó, Casais Goimil D, Ortiz Torres L. Eucalyptus nitens Wood of Spanish Origin as Timber Bioproduct: Fiber Saturation Point and Dimensional Variations. Bioresources and Bioproducts. 2025; 1(2):9. https://doi.org/10.3390/bioresourbioprod1020009

Chicago/Turabian Style

González-Prieto, Óscar, David Casais Goimil, and Luis Ortiz Torres. 2025. "Eucalyptus nitens Wood of Spanish Origin as Timber Bioproduct: Fiber Saturation Point and Dimensional Variations" Bioresources and Bioproducts 1, no. 2: 9. https://doi.org/10.3390/bioresourbioprod1020009

APA Style

González-Prieto, Ó., Casais Goimil, D., & Ortiz Torres, L. (2025). Eucalyptus nitens Wood of Spanish Origin as Timber Bioproduct: Fiber Saturation Point and Dimensional Variations. Bioresources and Bioproducts, 1(2), 9. https://doi.org/10.3390/bioresourbioprod1020009

Article Metrics

Back to TopTop