Fast Conversion of Molecular Diagrams into Plausible Crystal Structures Using Graph-Based Force Fields
Abstract
1. Introduction
2. Materials and Methods
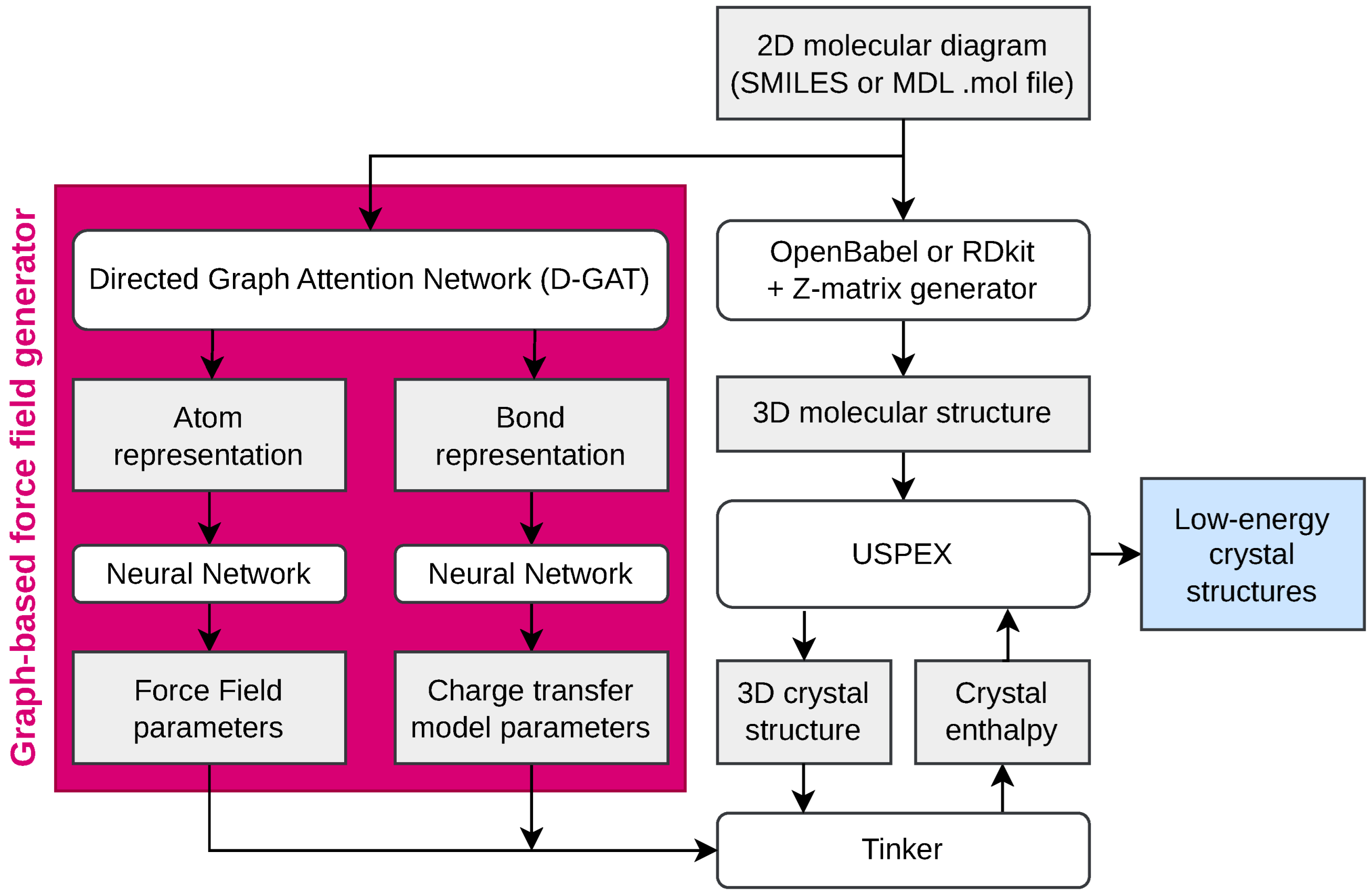
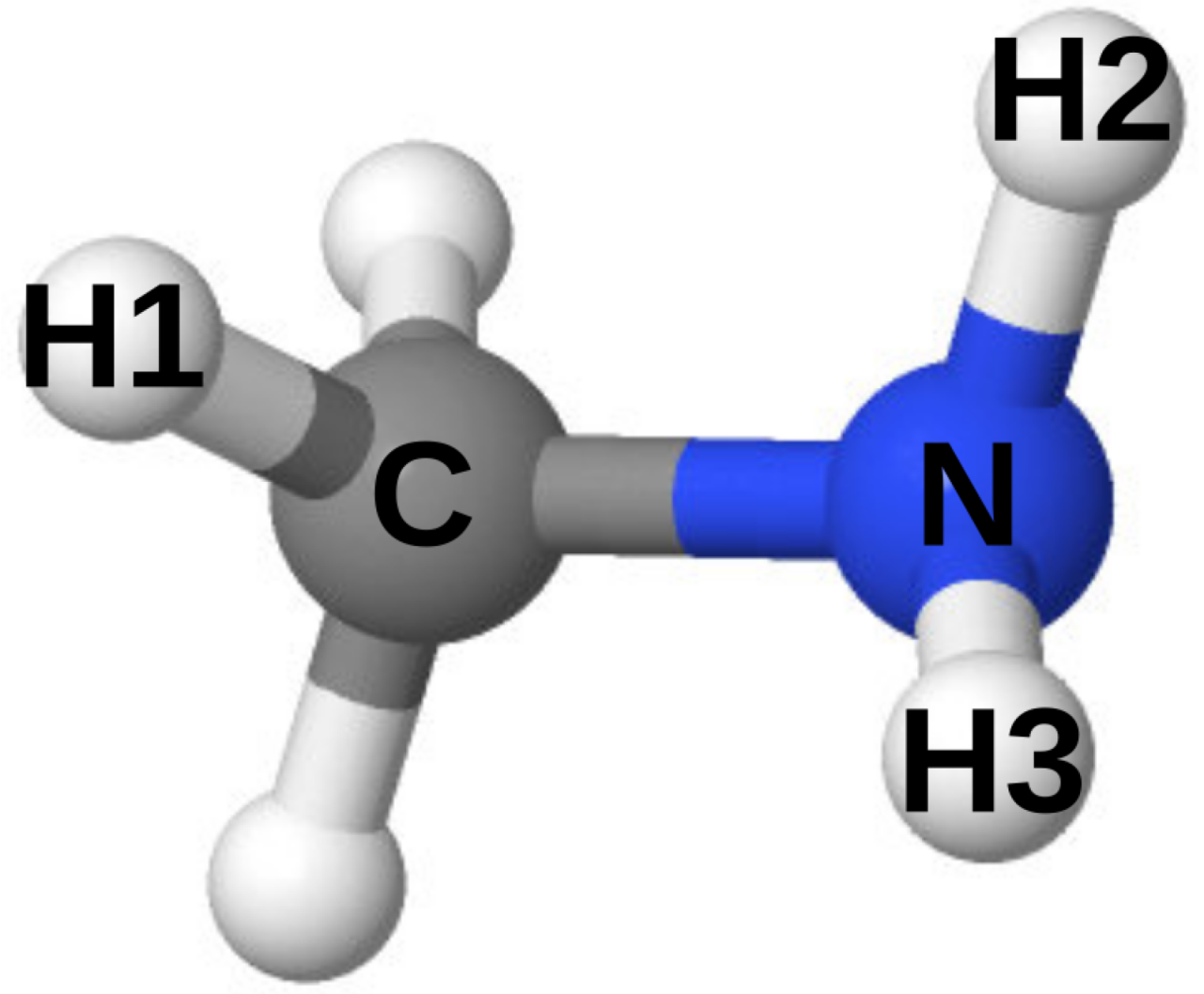
2.1. Graph-Based Force Field Generator
2.2. Tinker Simulation Engine
2.3. USPEX Genetic Algorithm for Crystal Structure Generation
2.4. Python Implementation: mol2crystal.py
3. Results
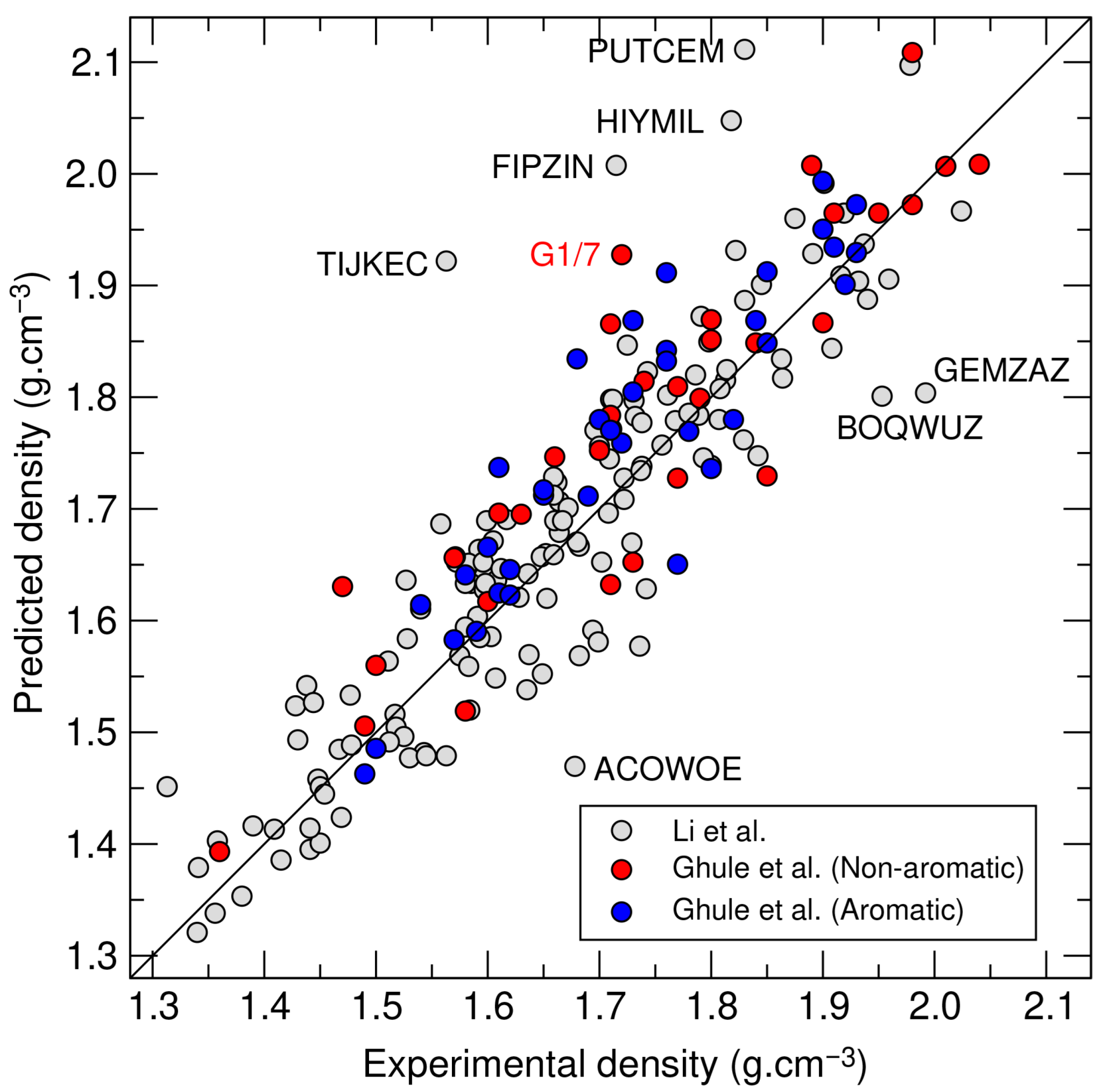
3.1. Relaxed Experimental Structures
3.2. Predicted Crystal Structures
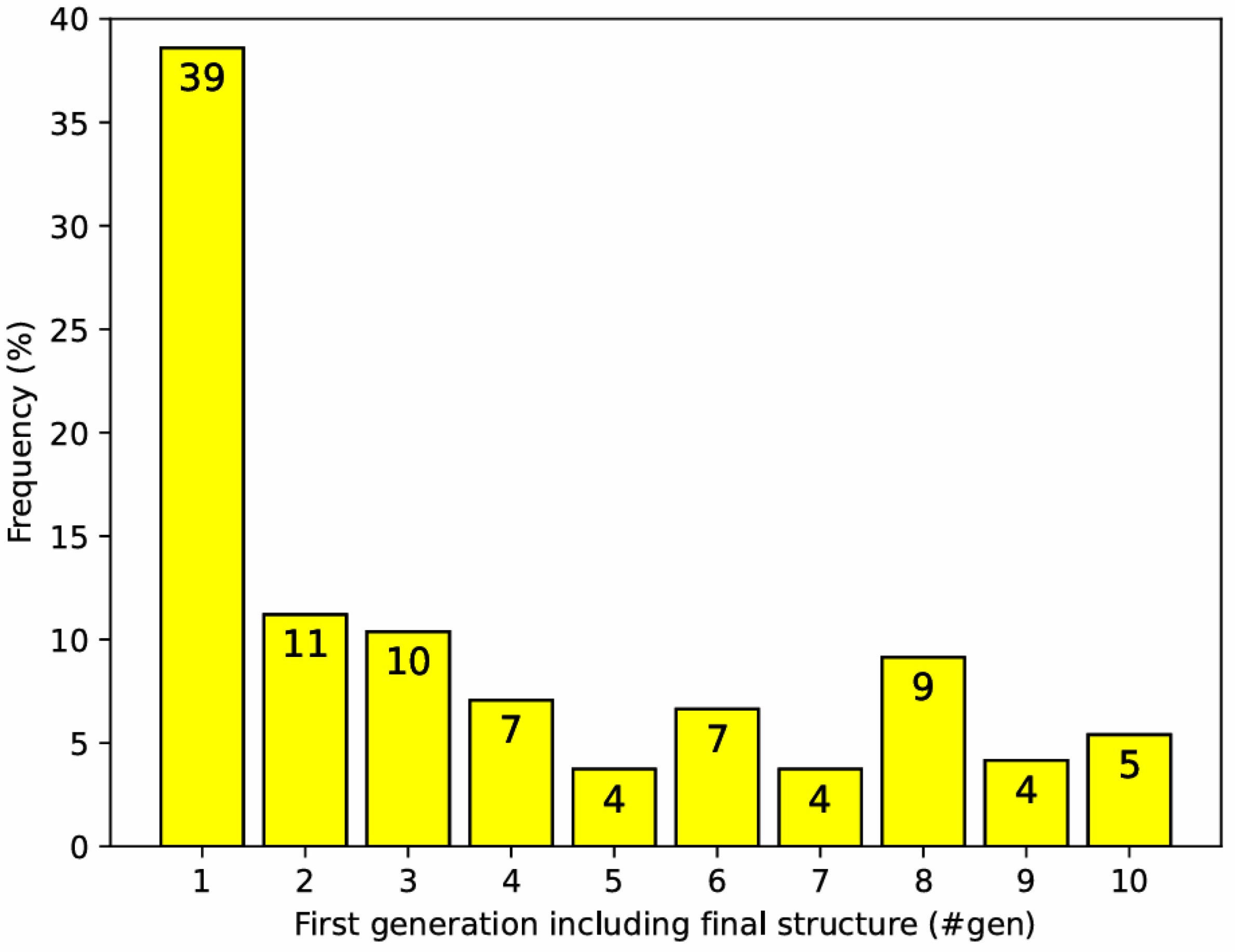
3.3. USPEX Convergence
4. Discussion
5. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GB-FF | Graph-Based Force Field |
| D-GAT | Directed Graph Attention Network |
| USPEX | Universal Structure Predictor: Evolutionary Xtallography |
| CCDC | Cambridge Crystallographic Data Center |
| CSP | Crystal Structure Prediction |
| MP | Molecular Packing |
| GAFF | Generalized Amber Force Field |
References
- Gavezzotti, A. Are Crystal Structures Predictable? Acc. Chem. Res. 1994, 27, 309–314. [Google Scholar] [CrossRef]
- Hunnisett, L.M.; Nyman, J.; Francia, N.; Abraham, N.S.; Adjiman, C.S.; Aitipamula, S.; Alkhidir, T.; Almehairbi, M.; Anelli, A.; Anstine, D.M.; et al. The seventh blind test of crystal structure prediction: Structure generation methods. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2024, 80, 517–547. [Google Scholar] [CrossRef]
- Zhou, D.; Bier, I.; Santra, B.; Jacobson, L.D.; Wu, C.; Garaizar Suarez, A.; Almaguer, B.R.; Yu, H.; Abel, R.; Friesner, R.A.; et al. A robust crystal structure prediction method to support small molecule drug development with large scale validation and blind study. Nat. Commun. 2025, 16, 2210. [Google Scholar] [CrossRef] [PubMed]
- Holden, J.R.; Du, Z.; Ammon, H.L. Prediction of possible crystal structures for C-, H-, N-, O-, and F-containing organic compounds. J. Comput. Chem. 1993, 14, 422–437. [Google Scholar] [CrossRef]
- van Eijck, B.P.; Kroon, J. Upack program package for crystal structure prediction: Force fields and crystal structure generation for small carbohydrate molecules. J. Comput. Chem. 1999, 20, 799–812. [Google Scholar] [CrossRef]
- Beaucamp, S.; Bernand-Mantel, A.; Mathieu, D.; Agafonov, V. Ab initio solid-state heats of formation of molecular salts from ion packing and crystal modelling: Application to ammonium crystals. Mol. Phys. 2004, 102, 253–258. [Google Scholar] [CrossRef]
- Khakimov, D.V.; Pivina, T.S. Salts of ethylenediamine and diethylenetriamines: Modeling of crystal structure and estimation of enthalpies of formation. Russ. Chem. Bull. 2025, 74, 354–360. [Google Scholar] [CrossRef]
- Alberga, D.; Ciofini, I.; Mangiatordi, G.F.; Pedone, A.; Lattanzi, G.; Roncali, J.; Adamo, C. Effects of Substituents on Transport Properties of Molecular Materials for Organic Solar Cells: A Theoretical Investigation. Chem. Mater. 2016, 29, 673–681. [Google Scholar] [CrossRef]
- Bhattacharya, L.; Brown, A.; Sharma, S.; Sahu, S. Computational Design of Crescent Shaped Promising Nonfullerene Acceptors with 1,4-Dihydro-2,3-quinoxalinedione Core and Different Electron-withdrawing Terminal Units for Photovoltaic Applications. J. Phys. Chem. A 2022, 126, 7110–7126. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Zhang, X.; Fan, J.; Song, Y.; Fan, J.; Wang, C.K.; Lin, L. Novel Deep Red Thermally Activated Delayed Fluorescence Molecule with Aggregation-Induced Emission Enhancement: Theoretical Design and Experimental Validation. J. Phys. Chem. Lett. 2022, 13, 4711–4720. [Google Scholar] [CrossRef] [PubMed]
- BIOVIA, Dassault Systèmes. BIOVIA Materials Studio Software; Dassault Systèmes: San Diego, CA, USA, 2022. [Google Scholar]
- Moxnes, J.F.; Hansen, F.K.; Jensen, T.L.; Sele, M.L.; Unneberg, E. A Computational Study of Density of Some High Energy Molecules. Propellants Explos. Pyrotech. 2016, 42, 204–212. [Google Scholar] [CrossRef]
- Li, X.; Wang, C.; Liu, Y.; Yin, S. Energetic molecule specific polarizable force field. FirePhysChem 2021, 1, 179–184. [Google Scholar] [CrossRef]
- Ghule, V.D.; Nirwan, A. Role of forcefield in density prediction for CHNO explosives. Struct. Chem. 2018, 29, 1375–1382. [Google Scholar] [CrossRef]
- Chen, G.; Jaffrelot Inizan, T.; Plé, T.; Lagardère, L.; Piquemal, J.P.; Maday, Y. Advancing Force Fields Parameterization: A Directed Graph Attention Networks Approach. J. Chem. Theory Comput. 2024, 20, 5558–5569. [Google Scholar] [CrossRef] [PubMed]
- Rackers, J.A.; Wang, Z.; Lu, C.; Laury, M.L.; Lagardère, L.; Schnieders, M.J.; Piquemal, J.P.; Ren, P.; Ponder, J.W. Tinker 8: Software Tools for Molecular Design. J. Chem. Theory Comput. 2018, 14, 5273–5289. [Google Scholar] [CrossRef] [PubMed]
- Glass, C.W.; Oganov, A.R.; Hansen, N. USPEX—Evolutionary crystal structure prediction. Comput. Phys. Commun. 2006, 175, 713–720. [Google Scholar] [CrossRef]
- Oganov, A.R.; Glass, C.W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 2006, 124, 244704. [Google Scholar] [CrossRef]
- Oganov, A.R.; Lyakhov, A.O.; Valle, M. How Evolutionary Crystal Structure Prediction Works—and Why. Acc. Chem. Res. 2011, 44, 227–237. [Google Scholar] [CrossRef] [PubMed]
- Lyakhov, A.O.; Oganov, A.R.; Stokes, H.T.; Zhu, Q. New developments in evolutionary structure prediction algorithm USPEX. Comput. Phys. Commun. 2013, 184, 1172–1182. [Google Scholar] [CrossRef]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural message passing for Quantum chemistry. In Proceedings of the 34th International Conference on Machine Learning—Volume 70. JMLR.org, 2017, ICML’17, Sydney, Australia, 6–11 August; 2017; pp. 1263–1272. [Google Scholar]
- Heid, E.; Greenman, K.P.; Chung, Y.; Li, S.C.; Graff, D.E.; Vermeire, F.H.; Wu, H.; Green, W.H.; McGill, C.J. Chemprop: A Machine Learning Package for Chemical Property Prediction. J. Chem. Inf. Model. 2023, 64, 9–17. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Maday, Y. Directed message passing based on attention for prediction of molecular properties. Comput. Mater. Sci. 2023, 229, 112443. [Google Scholar] [CrossRef]
- Harger, M.; Li, D.; Wang, Z.; Dalby, K.; Lagardère, L.; Piquemal, J.; Ponder, J.; Ren, P. Tinker-OpenMM: Absolute and relative alchemical free energies using AMOEBA on GPUs. J. Comput. Chem. 2017, 38, 2047–2055. [Google Scholar] [CrossRef]
- Lagardère, L.; Jolly, L.H.; Lipparini, F.; Aviat, F.; Stamm, B.; Jing, Z.F.; Harger, M.; Torabifard, H.; Cisneros, G.A.; Schnieders, M.J.; et al. Tinker-HP: A massively parallel molecular dynamics package for multiscale simulations of large complex systems with advanced point dipole polarizable force fields. Chem. Sci. 2018, 9, 956–972. [Google Scholar] [CrossRef]
- Adjoua, O.; Lagardère, L.; Jolly, L.H.; Durocher, A.; Very, T.; Dupays, I.; Wang, Z.; Inizan, T.J.; Célerse, F.; Ren, P.; et al. Tinker-HP: Accelerating Molecular Dynamics Simulations of Large Complex Systems with Advanced Point Dipole Polarizable Force Fields Using GPUs and Multi-GPU Systems. J. Chem. Theory Comput. 2021, 17, 2034–2053. [Google Scholar] [CrossRef]
- Bond, A.D. A survey of thermal expansion coefficients for organic molecular crystals in the Cambridge Structural Database. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2021, 77, 357–364. [Google Scholar] [CrossRef]
- van der Lee, A.; Dumitrescu, D.G. Thermal expansion properties of organic crystals: A CSD study. Chem. Sci. 2021, 12, 8537–8547. [Google Scholar] [CrossRef]
- Tom, R.; Rose, T.; Bier, I.; O’Brien, H.; Vázquez-Mayagoitia, A.; Marom, N. Genarris 2.0: A random structure generator for molecular crystals. Comput. Phys. Commun. 2020, 250, 107170. [Google Scholar] [CrossRef]
- Kadan, A.; Ryczko, K.; Wildman, A.; Wang, R.; Roitberg, A.; Yamazaki, T. Accelerated Organic Crystal Structure Prediction with Genetic Algorithms and Machine Learning. J. Chem. Theory Comput. 2023, 19, 9388–9402. [Google Scholar] [CrossRef] [PubMed]
- Chmiela, S.; Vassilev-Galindo, V.; Unke, O.T.; Kabylda, A.; Sauceda, H.E.; Tkatchenko, A.; Müller, K.R. Accurate global machine learning force fields for molecules with hundreds of atoms. Sci. Adv. 2023, 9, eadf0873. [Google Scholar] [CrossRef] [PubMed]
- Bidault, X.; Chaudhuri, S. How Accurate Can Crystal Structure Predictions Be for High-Energy Molecular Crystals? Molecules 2023, 28, 4471. [Google Scholar] [CrossRef] [PubMed]
- Rice, B.M.; Sorescu, D.C. Assessing a Generalized CHNO Intermolecular Potential through ab Initio Crystal Structure Prediction. J. Phys. Chem. B 2004, 108, 17730–17739. [Google Scholar] [CrossRef]
- Sun, H. COMPASS: An ab Initio Force-Field Optimized for Condensed-Phase Applications. Overview with Details on Alkane and Benzene Compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- Mayo, S.L.; Olafson, B.D.; Goddard, W.A. DREIDING: A generic force field for molecular simulations. J. Phys. Chem. 1990, 94, 8897–8909. [Google Scholar] [CrossRef]
- Sun, H.; Mumby, S.J.; Maple, J.R.; Hagler, A.T. An ab Initio CFF93 All-Atom Force Field for Polycarbonates. J. Am. Chem. Soc. 1994, 116, 2978–2987. [Google Scholar] [CrossRef]
- Mathieu, D. Molecular Energies Derived from Deep Learning: Application to the Prediction of Formation Enthalpies Up to High Energy Compounds. Mol. Inform. 2021, 41, 2100064. [Google Scholar] [CrossRef]
- Kim, C.K.; Cho, S.G.; Kim, C.K.; Park, H.; Zhang, H.; Lee, H.W. Prediction of densities for solid energetic molecules with molecular surface electrostatic potentials. J. Comput. Chem. 2008, 29, 1818–1824. [Google Scholar] [CrossRef]
- Politzer, P.; Martinez, J.; Murray, J.S.; Concha, M.C. An electrostatic correction for improved crystal density predictions of energetic ionic compounds. Mol. Phys. 2010, 108, 1391–1396. [Google Scholar] [CrossRef]
- Rice, B.M.; Byrd, E.F.C. Evaluation of electrostatic descriptors for predicting crystalline density. J. Comput. Chem. 2013, 34, 2146–2151. [Google Scholar] [CrossRef]
- Beaucamp, S.; Mathieu, D.; Agafonov, V. Optimal partitioning of molecular properties into additive contributions: The case of crystal volumes. Acta Crystallogr. Sect. B Struct. Sci. 2007, 63, 277–284. [Google Scholar] [CrossRef] [PubMed]
- Wespiser, C.; Mathieu, D. Application of Machine Learning to the Design of Energetic Materials: Preliminary Experience and Comparison with Alternative Techniques. Propellants Explos. Pyrotech. 2023, 48, e202200264. [Google Scholar] [CrossRef]

| Model | MIN | MAX | ARD | ARE |
|---|---|---|---|---|
| PFF | −35.8 | +9.6 | −1.2 | 4.0 |
| DREIDING | −15.3 | +4.1 | −5.1 | 5.4 |
| COMPASS | −13.0 | +30.4 | +5.7 | 6.4 |
| GB-FF | −4.2 | +12.1 | +6.1 | 6.3 |
| GB-FF/USPEX | −8.0 | +29.0 | +5.8 | 6.2 |
| Model | MIN | MAX | ARD | ARE |
|---|---|---|---|---|
| PFF | −38.9 | +4.4 | −5.9 | 6.1 |
| DREIDING | −19.3 | −0.8 | −9.7 | 9.7 |
| COMPASS | −17.2 | +24.2 | +0.7 | 3.3 |
| GB-FF | −8.8 | +6.8 | +1.1 | 2.4 |
| GB-FF/USPEX | −12.4 | +23.0 | +0.8 | 3.4 |
| Compound | CSD | Space | Exp. | COMPASS | GB-FF | GB-FF | |||
|---|---|---|---|---|---|---|---|---|---|
| Code | Group | (P.P.) | (USPEX) | (Relaxed) | |||||
| RDX | CTMTNA02 | Pbca | 1.82 | 1.806 | (−0.8) | 1.854 | (+1.9) | 1.809 | (−0.6) |
| TNT | ZZZMUC01 | P21/c | 1.65 | 1.792 | (+8.6) | 1.712 | (+3.8) | 1.691 | (+2.5) |
| NTO | QOYJOD05 | P21/c | 1.91 | 1.960 | (+2.6) | 1.965 | (+2.9) | 1.911 | (+0.1) |
| DNAM | QEVVIX | Pnma | 1.95 | 1.989 | (+2.0) | 1.983 | (+1.7) | 2.031 | (+4.1) |
| CL-20 | PUBMUU | P21/n | 2.04 | 2.065 | (+1.2) | 2.012 | (−1.3) | 2.034 | (−0.3) |
| DADNE | SEDTUQ03 | P21/n | 1.89 | 2.021 | (+6.9) | 2.023 | (+7.0) | 1.955 | (+3.4) |
| -HMX | OCHTET | Fdd2 | 1.87 | 1.805 | (−3.5) | 1.868 | (−0.1) | 1.871 | (+0.1) |
| -HMX | OCHTET12 | P21/c | 1.96 | 1.873 | (−4.4) | 1.868 | (−4.7) | 1.908 | (−2.6) |
| ARE from raw equilibrium densities (0 K): | 6.7 | 6.4 | 5.9 | ||||||
| ARE from scaled equilibrium densities (298 K): | 3.8 | 2.9 | 1.7 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mathieu, D. Fast Conversion of Molecular Diagrams into Plausible Crystal Structures Using Graph-Based Force Fields. AI Chem. 2025, 1, 2. https://doi.org/10.3390/aichem1010002
Mathieu D. Fast Conversion of Molecular Diagrams into Plausible Crystal Structures Using Graph-Based Force Fields. AI Chemistry. 2025; 1(1):2. https://doi.org/10.3390/aichem1010002
Chicago/Turabian StyleMathieu, Didier. 2025. "Fast Conversion of Molecular Diagrams into Plausible Crystal Structures Using Graph-Based Force Fields" AI Chemistry 1, no. 1: 2. https://doi.org/10.3390/aichem1010002
APA StyleMathieu, D. (2025). Fast Conversion of Molecular Diagrams into Plausible Crystal Structures Using Graph-Based Force Fields. AI Chemistry, 1(1), 2. https://doi.org/10.3390/aichem1010002






