Abstract
Quantum image transmission is a critical enabler for next-generation communication systems, allowing for the reliable exchange of high-quality visual data over error-prone quantum channels. Existing quantum-encoding schemes, however, often suffer from limited efficiency and reduced robustness under noisy conditions. This work introduces a novel multi-qubit phase-shift keying (PSK) encoding framework to enhance both fidelity and reliability in quantum image transmission. In the proposed system, source-encoded images (JPEG/HEIF) are converted into bitstreams, segmented into varying qubit sizes from 1 to 8, and mapped onto multi-qubit states using quantum PSK modulation. By exploiting multi-qubit superposition and phase modulation, the scheme improves spectral efficiency while maintaining resilience to channel noise. The encoded quantum states are transmitted through noisy channels and reconstructed via inverse quantum operations combined with classical post-processing to recover the original images. Experimental results demonstrate substantial performance improvements, evaluated using peak signal-to-noise ratio (PSNR), structural similarity index (SSIM), and universal quality index (UQI). Compared to superposition-only approaches, the proposed method achieves up to 3 dB SNR gain for higher qubit sizes, while single-qubit encoding remains limited due to reduced phase utilization. Moreover, relative to classical communication systems, the proposed multi-qubit PSK scheme consistently outperforms across all tested qubit sizes, highlighting its effectiveness for reliable, efficient, and high-fidelity quantum image transmission.
1. Introduction
The demand for reliable and high-quality image transmission has grown rapidly with the increasing integration of visual data into modern communication networks. Applications such as medical diagnostics, intelligent surveillance, remote sensing, and real-time multimedia streaming require the delivery of image content with minimal distortion, even in the presence of channel impairments. Since images often carry large amounts of data and are highly sensitive to distortion compared to text or numerical information, preserving quality during transmission remains a significant challenge. To address this, classical communication systems have long relied on compression standards such as joint photographic experts group (JPEG) [] and high-efficiency image file format (HEIF) [], adaptive modulation schemes that adjust to channel conditions, and advanced error-correcting codes [] that mitigate the impact of noise. These methods have indeed enabled important gains in efficiency and reliability, allowing classical systems to support a wide range of image-based applications.
As communication networks continue to scale in capacity and complexity, classical systems are increasingly constrained by both practical limitations in robustness and fundamental theoretical limits, raising important questions about their long-term suitability for next-generation communication. Compression inevitably introduces artifacts when operating under strict bandwidth constraints. Adaptive modulation is bounded by Shannon’s capacity [], which defines the maximum achievable throughput in noisy environments. Even state-of-the-art error-correcting codes require significant redundancy, increasing both bandwidth usage and computational cost. Moreover, in dynamic and error-prone environments, even a single bit error can propagate during reconstruction, causing visible degradations such as blurring, blocking artifacts, or the loss of structural details. These issues become even more critical in real-time applications, where transmission delays or image corruption cannot be tolerated. Although incremental improvements in compression, coding, and modulation may extend the capabilities of classical systems, they cannot fundamentally overcome these barriers. This realization has driven researchers to investigate alternative paradigms, with quantum communication emerging as a compelling candidate to achieve the levels of fidelity, efficiency, and robustness required for future image transmission.
Quantum communication [] therefore has gained significant attention as a promising solution to the limitations of classical systems. Unlike traditional methods, where information is represented by binary symbols, quantum communication uses qubits governed by the principles of quantum mechanics. This fundamental shift allows for new modes of transmission that extend beyond the boundaries of classical information theory. For example, superposition [] enables a single qubit to occupy multiple states simultaneously, providing an expanded encoding space beyond binary logic. Entanglement [] creates correlations that can be preserved over long distances, supporting coordinated transmission across distributed systems. Together, these properties open up the possibility of communication schemes with higher capacity and inherent resistance to many forms of channel noise. In addition, phase modulation in the quantum domain introduces another powerful degree of freedom, allowing information to be encoded in both amplitude and phase. By exploiting this dual representation, quantum communication can achieve higher-dimensional encoding and potentially surpass the efficiency, reliability, and robustness of classical methods. These advantages make quantum communication an especially attractive pathway for next-generation image transmission systems, where maintaining both fidelity and resilience under noisy conditions is of critical importance.
In the context of quantum image transmission, single-qubit encoding serves as the most basic encoding scheme, where each pixel value or bitstream segment is directly mapped onto the state of an individual qubit []. While this provides a straightforward and intuitive foundation, its usefulness is limited because each qubit carries only a small amount of information. This results in low spectral efficiency and substantial resource requirements for transmitting large-scale images. Moreover, single-qubit encodings are highly susceptible to channel noise, as even minor disturbances, such as depolarizing or amplitude-damping errors, can significantly degrade image quality. To address these limitations, multi-qubit superposition encoding can be used [], enabling multiple states to be represented simultaneously and allowing for more compact data representations. Although this increases overall transmission capacity and demonstrates the advantages of quantum parallelism, reliance solely on amplitude superposition leaves the encoding process incomplete. In particular, the phase domain, which represents one of the most powerful degrees of freedom in quantum mechanics, remains underutilized, restricting the achievable fidelity and robustness of reconstructed images.
In addition to the incomplete use of quantum state resources, practical quantum channels present further challenges due to the presence of decoherence, depolarizing noise, amplitude damping, and phase damping. These impairments can severely distort transmitted quantum states, leading to a rapid decline in image fidelity. While quantum error-correcting codes (QEC) [] offer theoretical mechanisms to counter such effects, they are computationally expensive and difficult to scale for large image transmissions, making them impractical for real-world deployment []. This has created an urgent need for encoding frameworks that are inherently noise-resilient, capable of maintaining high fidelity even under imperfect channel conditions, and efficient enough to be implemented at scale.
A promising direction toward this goal is the adoption of multi-qubit phase shift keying (PSK) encoding, which combines the advantages of multi-qubit superposition with the expressive capability of phase modulation [,]. Unlike previous approaches that rely solely on amplitude-based superposition [,], the proposed multi-qubit PSK framework leverages both quantum parallelism and phase variation, enabling richer and more precise representations of image data within higher-dimensional Hilbert spaces. This dual encoding strategy can improves encoding efficiency and noise resilience but also ensures scalability as the number of qubits increases. By addressing the inherent limitations of single-qubit [] and superposition-only methods [], the proposed approach establishes a practical and high-fidelity pathway for quantum image transmission in next-generation communication systems. To the best of our knowledge, no prior research has integrated this dual superposition–phase encoding mechanism or applied it to quantum image transmission, marking a distinctly novel contribution of this work.
Therefore, this study examines multi-qubit PSK encoding as a framework for quantum image transmission and evaluates its effectiveness in achieving reliable, high-fidelity communication under noisy channel conditions. The overall process begins with source coding, where classical images are compressed using JPEG or HEIF to reduce redundancy. The compressed bitstream may be optionally protected by polar coding to improve resilience to noise. Next, the data are mapped into quantum states through multi-qubit superposition encoding, after which phase modulation is applied to enable multi-qubit PSK representation. The encoded quantum states are transmitted through a noisy channel, and at the receiver, the inverse operations are carried out. This includes phase demodulation, multi-qubit quantum decoding, channel decoding if applied, and finally source decoding, which reconstructs the transmitted image. The performance of the system is evaluated under noisy channel conditions using widely accepted image quality metrics such as peak signal-to-noise ratio (PSNR), structural similarity index measure (SSIM) [], and universal quality index (UQI) []. Comparative analysis is performed against both superposition-only quantum methods and classical communication systems to demonstrate the advantages of multi-qubit PSK encoding. The results confirm that the proposed approach provides measurable gains in both efficiency and robustness, achieving higher fidelity in reconstructed images across varying qubit dimensions. The key contributions of this study are as follows.
- Proposal of a new advanced quantum-encoding technique based on multi-qubit PSK encoding, integrating superposition and phase encoding to achieve improved scalability and robustness.
- Development of a quantum image transmission system that is designed to be highly noise-resilient while ensuring superior image quality, even under challenging channel conditions.
- Comprehensive evaluation using objective image quality metrics, including PSNR, SSIM, and UQI, accompanied by a comparative analysis with existing quantum and classical communication approaches to confirm the superior fidelity and resilience of the proposed framework.
The remainder of this paper is organized as follows. Section 2 reviews related work on quantum communication and quantum image transmission. Section 3 introduces the theoretical foundations and system model of multi-qubit PSK encoding. Section 4 presents the results and discussion, and Section 5 concludes the paper with key insights and future research directions.
2. Related Works
The development of quantum communication [] is initially motivated by the need for secure information transfer. Early investigations are concentrated on quantum key distribution (QKD), which is offered as a method of achieving theoretically unbreakable cryptographic security by utilizing the fundamental principles of quantum mechanics [,,]. Landmark protocols such as BB84 and E91 are introduced and experimentally validated [,], demonstrating secure key sharing over optical fiber and free-space channels. These contributions lay the foundation for the first practical quantum communication networks, and the role of QKD in secure communications is strongly established. Alongside QKD, advances in quantum teleportation further reinforce the promise of quantum communication, as the transfer of quantum states between distant parties is enabled without requiring the physical transmission of the actual particles [,,]. This milestone illustrates the ability of quantum information to be preserved across long distances, and new insights into entanglement distribution and quantum repeaters are provided. Building on these achievements, the focus of the field is gradually broadened beyond cryptographic primitives [,]. Research is directed toward secure media communication, in which the challenge lies not only in protecting sensitive data but also in ensuring the integrity, fidelity, and robustness of transmitted visual and multimedia content [,,,]. This progression illustrates how quantum communication, initially evolved as a specialized solution for information-theoretic security, is transformed into a versatile framework to support advanced information processing and high-quality data transmission.
Quantum superposition is identified as a key enabler for efficient and high-quality quantum communication []. Superposition allows qubits to exist in linear combinations of basis states, providing an expanded encoding space compared to classical binary systems. This property has been leveraged in single-qubit quantum communication systems for image transmission, employing Hadamard-based encoding combined with classical error correction []. While such approaches successfully demonstrate the feasibility of transmitting image data over a quantum channel, they are limited to single-qubit processing and thus cannot exploit inter-qubit correlations or quantum parallelism. Consequently, although conceptually straightforward, these schemes suffer from low spectral efficiency and high sensitivity to noise in practical implementations. Even small channel disturbances, such as decoherence, depolarizing noise, or amplitude damping, are shown to significantly degrade fidelity, making large-scale image reconstruction unreliable. Similar superposition-based methods are also extended to quantum multiple-input multiple-output (MIMO) architectures and even quantum video transmission [,], confirming the potential of quantum resources to enhance capacity. However, the inherent noise vulnerability of single-qubit encoding and the limited error tolerance constrain their applicability. To overcome these shortcomings, QEC is incorporated into image and video transmission frameworks [,,]. Although QEC has been theoretically proven to be effective in reducing error rates, the associated computational and resource overhead is recognized to be prohibitively high, rendering these techniques impractical for large-scale multimedia systems. This outcome underscores the necessity of encoding strategies that are not only robust to noise but also computationally feasible and scalable.
In response to the shortcomings of single-qubit methods, multi-qubit superposition encoding is investigated []. By distributing information across multiple qubits simultaneously, encoding capacity is improved and greater scalability than single-qubit approaches is demonstrated. The idea of mapping larger data blocks into multi-qubit superposition states also opens pathways for parallel data representation and transmission. While this represents a clear advancement, superposition-only encoding schemes are still considered insufficient []. A key limitation is that reliance is placed solely on amplitude superposition without exploiting phase information, which is one of the most powerful degrees of freedom in quantum mechanics []. Phase encoding is recognized as enabling access to higher-dimensional Hilbert spaces and allowing for more compact and noise-tolerant data representations []. Consequently, the absence of phase utilization leaves multi-qubit superposition encoding vulnerable to channel impairments and prevents it from reaching its full potential in terms of efficiency and robustness.
Parallel to these developments, frequency-domain quantum-encoding schemes are also proposed for image transmission []. By transforming image data into the frequency domain, redundancy in frequency components is leveraged to achieve greater noise resilience []. However, the adoption of frequency domain techniques comes at the cost of substantial implementation complexity. The need for repeated frequency transformations and operations in the quantum domain introduces significant computational overhead, scalability challenges, and concerns regarding practical deployment. As a result, while frequency domain encoding offers advantages in terms of robustness, its complexity restricts its applicability in large-scale or real-time image transmission systems [].
According to prior research, recent advancements in quantum image transmission have revealed fundamental limitations in existing encoding methods. The proposed multi-qubit PSK framework differs fundamentally from existing quantum phase-encoded and superposition-based methods. Unlike phase-based QKD schemes [] (e.g., BB84 variants) that employ randomized phase modulation for secrecy, our approach uses deterministic phase mapping via the phase (S) gate to encode classical image bitstreams into structured quantum states. This transforms phase from a cryptographic variable into a fidelity-optimizing encoding resource. Single-qubit superposition based schemes enable direct bit-to-qubit mapping but offer low spectral efficiency and are highly vulnerable to noise []. Multi-qubit superposition approaches enhance capacity yet typically exploit only amplitude information, leaving the phase domain largely unused, and thus limiting fidelity and robustness. Moreover, conventional QEC techniques, while effective, are computationally expensive and difficult to scale for high-dimensional image data []. Motivated by these challenges, this work introduces a scalable multi-qubit PSK encoding framework that jointly leverages superposition and phase modulation to improve spectral efficiency, fidelity, and noise resilience in quantum image transmission. Therefore, our proposed study presents a novel multi-qubit PSK encoding scheme for high-fidelity image transmission over quantum channels.
In this approach, quantum superposition is integrated with phase encoding in a structured manner [], thereby enabling more efficient utilization of the quantum state space. To the best of current knowledge, this is the first multi-qubit PSK encoding scheme specifically developed for quantum image transmission, marking a significant step forward in advancing quantum communication techniques. By leveraging the joint advantages of superposition and phase modulation, the framework achieves improved noise resilience, higher fidelity, and efficient scalability across different qubit dimensions. These characteristics establish the scheme as a promising foundation for practical quantum communication systems. In particular, its ability to balance robustness, efficiency, and complexity provides strong potential for deployment in next-generation networks where reliable and high-quality image transmission is required under realistic noisy channel conditions.
3. Methodology
The proposed multi-qubit PSK encoding-based quantum communication system is illustrated in Figure 1. The framework is designed to be independent of the input data, meaning that any image format can be processed without restriction. Input images are first source coded using standard formats such as JPEG or HEIF and then converted into binary bitstreams. These bitstreams may be optionally protected using polar channel coding with a code rate of 1/2 to improve resilience against noise. The resulting data are then mapped onto quantum states according to the selected qubit size, ranging from 1 to 8. A Hadamard transformation is applied to generate multi-qubit superposition states, which are subsequently phase encoded with the corresponding phase information to produce multi-qubit PSK states. These encoded states are transmitted through the quantum channel. At the receiver, inverse operations are performed: phase demodulation and inverse Hadamard transformation are applied to recover the quantum states, which are then decoded through quantum measurements. If channel coding is used, polar decoding is applied to correct residual errors, and finally, source decoding reconstructs the transmitted image with high fidelity.
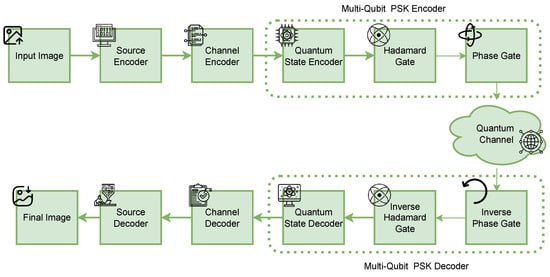
Figure 1.
Block diagram of the proposed multi-qubit PSK encoding-based quantum communication system.
To provide a clearer understanding of the system workflow, the functional blocks illustrated in Figure 1 are described individually in the following subsections.
3.1. Input Image
In the proposed method, any image can be provided as input, regardless of the compression, color format, or resolution. For this study, a subset of 100 images from the Microsoft COCO dataset with a resolution of and low to high spatial information (SI) [] is used as the primary input dataset. For further evaluations, 50 images from the ImageNet dataset with a resolution of and medium SI [], as well as 50 images from a Kaggle 4K dataset with high SI [], are also included. These datasets are selected to ensure a wide range of SI, characterized by the amount of texture, edges, and object details within an image. By incorporating images with low, medium, and high SI, the evaluation covers both simple and highly complex visual content.
3.2. Source Encoder and Decoder
In the proposed system, the input images are compressed using standard source encoding techniques before transmission. JPEG [] and HEIF [] codecs are employed as the source encoders, with compression controlled by varying the quantization parameter (QP) values to ensure equal bandwidth utilization across all encoding qubit sizes. To maintain consistent quantum channel bandwidth across different multi-qubit configurations, higher-qubit systems are compressed more aggressively by assigning lower QP values, while lower-qubit systems use higher QP values. This ensures that all configurations produce qubit streams of approximately equal length, keeping the product of qubit count and per-symbol bitrate roughly constant (). For JPEG compression, the QP values are 100, 94, 88, 79, 72, 60, 50, and 40 for Q1 to Q8, respectively, and for HEIF compression, the QP values are 100, 70, 60, 54, 50, 45, 43, and 41 for Q1 to Q8, respectively. This allocation achieves fair bandwidth distribution while allowing meaningful performance comparisons.
To ensure equal bandwidth utilization in the multi-qubit transmission system, the bitstreams are compressed such that their sizes are balanced across the quantum-encoding modes. This guarantees that no particular source encoding format dominates the channel usage, thereby providing a fair basis for evaluating performance.
At the receiver, the corresponding JPEG and HEIF decoders are applied to reconstruct the images from the received bitstreams. The reconstructed outputs are then analyzed using objective quality metrics to assess the effectiveness of the proposed framework.
3.3. Channel Encoder and Decoder
In the proposed system, polar codes [] are employed as the channel coding method. QEC techniques are not adopted, since their implementation is associated with very high complexity, and the motivation of this research is to avoid such complex QEC methods while still providing a noise-robust encoding strategy.
Polar codes are considered one of the most advanced error correction methods in the classical domain [], as they achieve channel capacity under successive cancelation decoding and demonstrate superior performance compared to many conventional error correction codes, such as low-density parity check (LDPC) codes [], turbo codes [] and Reed-Solomon codes []. In this study, a code rate of 1/2 is selected as it provides a suitable balance between redundancy (for error protection) and throughput efficiency (for bandwidth utilization). This configuration ensures that reliable error correction can be achieved without imposing excessive overhead on the system.
3.4. Multi-Qubit PSK Encoder
In the proposed framework, the multi-qubit PSK encoder is responsible for mapping the channel-encoded bitstreams into multi-qubit PSK modulated states for transmission. The bitstreams are first segmented according to the selected qubit size, with encoding modes ranging from 1 to 8 qubits. The maximum encoding size is limited to 8 qubits in this study, as this dimension is sufficient to match the requirements of pixel-level representation while avoiding excessive system complexity. Nevertheless, the encoding scheme is scalable and can be extended to any qubit size, depending on the requirements of the communication system and the available quantum hardware.
In the proposed framework, the multi-qubit PSK encoder is designed as a sequential process consisting of several distinct stages. The encoder structure is therefore explained under the following sub-sections.
3.4.1. Quantum State Encoder
In the single-qubit scenario, each classical bit from the polar-encoded codeword is mapped to a quantum state () in the computational basis. A classical bit 0 is encoded as , and a classical bit 1 is encoded as , as shown in Equations (1) and (2).
Practically, the process is carried out as follows: all qubits are first initialized in the ground state by default hardware operations. If the input bit is 1, a single-qubit Pauli-X gate is applied to flip the corresponding qubit from to . If the input bit is 0, no operation is applied and the qubit remains in the state. This initialization ensures that each bit is represented as a pure quantum basis state, forming the foundation of the quantum state encoder.
In the case of two qubits, pairs of consecutive classical bits are mapped into one of the four computational basis states of the two-qubit Hilbert space, as expressed in Equation (3).
The corresponding states are represented as four-dimensional column vectors, as shown in Equations (4)–(7). These two-qubit basis states can also be constructed explicitly by taking the tensor (Kronecker) product of the single-qubit states defined in Equations (1) and (2).
This representation can naturally be extended to larger numbers of qubits. For the general case of k qubits, a block of k classical bits is mapped into a single computational basis state of the -dimensional Hilbert space, as defined in Equation (8).
For example, the three-bit sequence is encoded as the three-qubit state shown in Equation (9).
In this way, the classical information is systematically converted into quantum states, with the dimensionality of the Hilbert space increasing exponentially with the number of encoded qubits.
3.4.2. Hadamard Gate
Once the computational basis states are constructed, the corresponding Hadamard transform [] is applied to encode these states into superposition states. For a single qubit, the Hadamard operation is represented by the matrix shown in Equation (10).
When this operator is applied to the single-qubit computational basis states defined in Equations (1) and (2), the resulting superposition states are obtained as in Equation (11).
For higher-dimensional systems, the corresponding Hadamard gates are constructed using the tensor (Kronecker) product of single-qubit Hadamard matrices. For example, the two-qubit Hadamard operator is given by Equation (12).
Applying to the two-qubit basis states produces the corresponding two-qubit superposition states, as shown in Equations (13)–(16).
These results show explicitly that the two-qubit Hadamard transform produces equal-weighted superpositions of all four basis states, with relative phases determined by the input basis state.
In general, for a system of k qubits, the Hadamard operation is defined as in Equation (17), which, when applied to a computational basis state , produces an equal superposition of states with appropriate phase coefficients.
3.4.3. Phase Gate
The phase gate is a unitary operator that introduces a phase shift into a quantum state. For a single qubit, this is given by the well-known S gate, defined as in Equation (18).
When extended to multiple qubits, the phase operation is represented as the tensor product of single-qubit S gates. For two qubits, this yields Equation (21).
Applying the two-qubit phase operator from Equation (21) to the Hadamard superposition states defined in Equations (13)–(16) yields the phase-encoded vectors shown in Equations (22)–(25).
More generally, for k qubits, the multi-qubit phase operator is defined as the tensor product of k single-qubit S gates.
Applying to the Hadamard superposition state produces the multi-qubit phase-encoded state. Each computational basis component acquires a deterministic phase factor , as expressed in Equation (27), where denotes the Hamming weight of the basis index j.
where is the equal-amplitude superposition of k qubits and is the corresponding phase-encoded state. This deterministic phase modulation converts the real-valued superposition into a complex-valued vector in the -dimensional Hilbert space, effectively increasing the number of distinguishable configurations and breaking the superposition-only limitation. Each basis component now carries both amplitude and phase information, which enhances geometric separation between states and improves robustness against noise during transmission.
These phase-encoded states are subsequently transmitted through the noisy quantum channel, where they are subject to decoherence and other quantum noise effects before being decoded at the receiver. This hybrid amplitude–phase encoding forms the basis of the proposed multi-qubit PSK framework, allowing higher information density and improved fidelity in quantum communication.
3.5. Quantum Channel
In order to evaluate the robustness of the proposed multi-qubit PSK transmission scheme, we simulate the propagation of quantum states through a noisy communication channel. The transmitted state is represented by a density operator, and its evolution is modeled as a completely positive trace-preserving map that accounts for several physically relevant error processes. In this framework, five major sources of quantum noise are considered: bit-flip, phase-flip, depolarization, amplitude damping, and phase damping [].
Bit-flip errors arise when a qubit state is inverted, causing a transition between and . This process is characterized by a probability and is described by Equation (28), where X denotes the Pauli-X operator.
An analogous effect occurs in phase-flip noise, where the relative sign of the component is inverted. With probability , this transformation is expressed in Equation (29), where Z is the Pauli-Z operator.
Depolarizing noise represents complete uncertainty in the qubit state. The original state is replaced by the maximally mixed operator with probability , as formulated in Equation (30), where denote the Pauli operators.
Amplitude damping captures energy dissipation effects such as photon loss or spontaneous emission. With parameter , this process is described by Equation (31), where the Kraus operators are defined in Equation (32).
Phase damping, by contrast, destroys quantum coherence without affecting state populations. The corresponding map is given in Equation (33), with the Kraus operators specified in Equation (34).
The combined effect of all error sources is modeled as a convex mixture, as shown in Equation (35).
To connect the error probabilities with physical channel quality, we parameterize them in terms of the signal-to-noise ratio (SNR). The SNR in decibels is defined by Equation (36), where is fixed and is varied.
A total channel error probability is then obtained as an inverse function of the linear SNR, as expressed in Equation (37).
This mapping ensures that higher SNR corresponds to lower overall error probability, providing a reproducible relationship between classical SNR and quantum noise.
The distribution of across the five noise processes is randomized by drawing weights from a uniform distribution, as defined in Equation (38), and scaling them according to Equation (39).
This ensures the normalization condition shown in Equation (40), which guarantees that the overall channel error probability remains equal to .
By explicitly defining the mapping of SNR to total and individual noise probabilities, this model allows for reproducible simulation of quantum channel noise and facilitates evaluation of multi-qubit PSK transmission under varying channel conditions [,].
The inclusion of these five error mechanisms provides a comprehensive abstraction of real-world quantum noise []. In practical communication environments, qubits simultaneously experience state inversion, phase disturbance, depolarization due to imperfect isolation, energy loss arising from spontaneous emission, and loss of coherence through environmental coupling. By combining these processes into the unified channel model of Equation (35), the proposed framework reflects the heterogeneous and stochastic nature of realistic quantum networks []. This enables the performance of the multi-qubit PSK transmission system to be analyzed under conditions that closely approximate practical implementations, ensuring that robustness against noise is evaluated in a meaningful and experimentally relevant manner.
3.6. Multi-Qubit PSK Decoder
Since noise distorts the ideal quantum states, the next step is to identify the closest valid phase encoded state from the phase encoded codebook , where each corresponds to a possible transmitted phase encoded states. The decoder performs this matching using the minimum Euclidean distance criterion, as shown in Equation (41).
where denotes the Euclidean (Hilbert space) norm, denotes the received noisy phase-encoded superposition state after transmission through the quantum channel, and represents the mapped phase-encoded state at the receiver.
The multi-qubit PSK decoder then compensates for the phase modulation introduced during encoding. This is done by applying the conjugate transpose phase operator (inverse phase operator) of Equation (26) to the noisy mapped phase encoded superposition state . The resulting state can be represented as in Equation (42).
Once the nearest superposition state is identified, the inverse Hadamard transform (which is identical to the Hadamard transform itself, since ) is applied to map it back into the computational basis state , as shown in Equation (43).
Finally, a projective measurement () in the computational basis produces the estimated classical bitstring, as shown in Equation (44). This means that the quantum state is measured and the outcome is matched to one of the possible classical values.
As an example, for the two-qubit case (), the inverse phase modulation operator is defined in Equation (45).
After applying the two-qubit inverse phase gate to the mapped noisy two-qubit PSK states, the noisy superposition states can be retrieved. Subsequently, by applying the corresponding Hadamard gate, the original computational basis states can be recovered at the receiver, as shown in the example of Equation (46).
Measurement of then produces the classical bitstring 01. More generally, for a k-qubit system, measurement yields a classical bitstring .
3.7. Final Image Bitstream Recovery and Benchmarking
After the quantum decoding process, the received classical bitstream is first polar decoded (if channel coding is applied) and then source decoded to reconstruct the image. To evaluate the intrinsic performance of the proposed system, an uncoded scenario is also considered, where no channel coding is applied. In addition, a superposition-only system is modeled [] without phase encoding and decoding, while all other configurations remain identical to the multi-qubit PSK system. For fairness, a baseline classical communication system is also considered, employing binary phase-shift keying (BPSK) modulation with equivalent bandwidth, evaluated both with polar coding at a code rate of and without channel coding.
4. Results and Discussion
The performance of the proposed system is evaluated using both objective quality metrics and subjective experiments. Objective evaluation is carried out using PSNR, SSIM, and UQI, which provide quantitative measures of the reconstructed image quality. In addition, subjective experiments are conducted to visually assess the perceptual quality of the reconstructed images. Performance is compared across both uncoded and channel-coded configurations for JPEG and HEIF image formats, with qubit sizes ranging from 1 to 8. Furthermore, the proposed quantum communication system is compared against a classical system with equivalent bandwidth, as well as quantum systems employing only superposition (amplitude-only states without phase encoding), in order to highlight the advantages of the proposed multi-qubit PSK-based approach.
The following subsection presents the performance of the proposed method across different image formats under both uncoded and channel-coded scenarios. In all figures, solid lines with square markers denote the multi-qubit PSK system (Quantum PSK), dashed lines with circle markers denote the superposition-only (SUP) system, and dash-dot lines with diamond markers denote the classical BPSK system. For consistency, the tables also use the labels PSK to represent the multi-qubit PSK system and SUP to represent the superposition-only system. Furthermore, all results represent average values over 1000 independent simulation runs for each image across the entire dataset. The variability across runs is negligible (e.g., dB for PSNR and for SSIM/UQI). Because these fluctuations are minimal, error bars are omitted, ensuring the figures remain clear while still reflecting statistically robust trends.
4.1. Performance Evaluation for JPEG Image Transmission in the Uncoded Scenario
In the JPEG uncoded scenario, the performance differences across encoding schemes are first evident in the PSNR curves, as shown in Figure 2a. As the qubit size increases, the performance of the proposed system improves, with higher PSNR values indicating better reconstruction quality. This demonstrates that the proposed multi-qubit PSK encoding effectively enhances resilience against channel noise as the encoding qubit size increases, even without channel coding. At high SNR, systems with smaller qubit sizes achieve higher peak PSNR values because the total transmission energy is concentrated over fewer states under the bandwidth normalization constraint. However, these systems are less resilient to noise at low SNR due to their limited exploitation of phase information. In contrast, the decline in maximum PSNR for larger qubit sizes results from the trade-off between noise resilience and bandwidth-constrained compression. Increasing the qubit size k expands the Hilbert space, enabling more robust multi-qubit phase encoding and improved resistance to channel noise. Yet, to maintain consistent channel bandwidth across qubit configurations, larger-qubit systems require more aggressive compression, which lowers the per-state energy (, where is the amplitude of the j-th computational basis state in the multi-qubit superposition) and introduces additional distortion, thereby reducing PSNR.
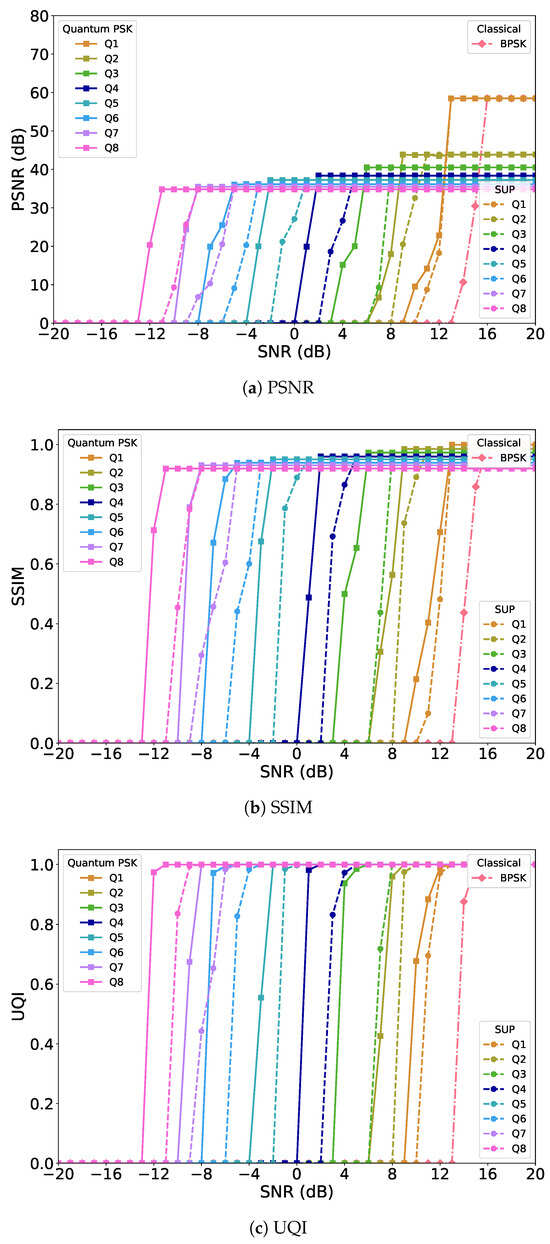
Figure 2.
Performance comparison of JPEG image transmission in the uncoded scenario: (a) PSNR, (b) SSIM, and (c) UQI.
A similar trend is observed in the SSIM results as shown in Figure 2b. Smaller-qubit systems can reach higher maximum SSIM values, approaching nearly perfect structural similarity at high SNR, but degrade rapidly in noisy conditions. Higher-qubit PSK systems, on the other hand, sacrifice some peak SSIM but provide much stronger robustness, maintaining higher structural fidelity in low to mid-SNR regions compared to the small-qubits. The UQI plots further confirm this behavior as shown in Figure 2c. Systems with small qubit sizes achieve the highest peak UQI values at large SNR, but their quality drops sharply at low SNR. Higher-qubit PSK systems demonstrate greater noise resilience, with UQI curves that improve more gradually but remain stable across a wider SNR range.
Taken together, these results highlight a clear trade-off between peak reconstruction quality and noise resilience. Smaller-qubit systems achieve higher maximum quality but are more fragile in noisy environments, whereas higher-qubit PSK systems are more robust but reach lower peak values because the available energy is spread across more phase states under the same bandwidth utilization. Across all metrics, the proposed multi-qubit PSK system consistently outperforms the superposition-only baseline, offering an effective SNR gain of approximately 2–3 dB through the inclusion of phase encoding. In the single-qubit case, the performance closely follows that of the superposition-only system, since a single qubit cannot fully exploit phase information. Nevertheless, even the single-qubit scheme achieves around a 3 dB SNR gain over the classical uncoded BPSK baseline, confirming the intrinsic advantage of quantum encoding. The rationale for comparing the proposed multi-qubit quantum PSK system primarily with classical BPSK is that BPSK already offers the highest noise resilience among classical PSK schemes. Higher-order classical PSK (e.g., QPSK, 8-PSK) exhibits lower robustness and would not provide additional meaningful insight. The focus of this work is on quantum parallelism and multi-qubit PSK encoding, which enable higher fidelity, spectral efficiency, and noise robustness beyond classical limits, consistent with theoretical results on quantum channel capacities exceeding Shannon limits.
It is also important to consider the complexity associated with higher-qubit configurations. As the qubit size increases, the state space grows exponentially, leading to higher computational and implementation complexity in terms of encoding, modulation, and detection. Despite this overhead, the results demonstrate that multi-qubit PSK systems remain highly robust, even under very noisy channel conditions and without the assistance of channel coding. This robustness stems from the richer phase representation available in higher qubit spaces, which enables more effective error tolerance and information recovery. Consequently, while smaller-qubit systems achieve higher peak quality, the higher-qubit multi-qubit PSK configurations are particularly advantageous in scenarios where communication must be sustained over severely degraded channels.
4.2. Performance Evaluation for JPEG Image Transmission in the Channel-Coded Scenario
In the JPEG channel-coded scenario, polar coding with a code rate of 1/2 is applied before transmission. The inclusion of channel coding significantly improves the robustness of all transmission schemes against channel noise as shown in Figure 3. Importantly, the application of channel coding does not alter the maximum attainable values of PSNR, SSIM, or UQI. These peak values are fundamentally constrained by the JPEG compression process itself, and therefore remain unchanged. With channel coding, a distinct coding gain is observed, as the system can achieve the same reconstruction quality at much lower SNRs than in the uncoded scenario. In other words, the curves for PSNR, SSIM, and UQI shift leftward on the SNR axis. On average, all systems benefit from an approximate 3 dB SNR gain compared to their uncoded counterparts.
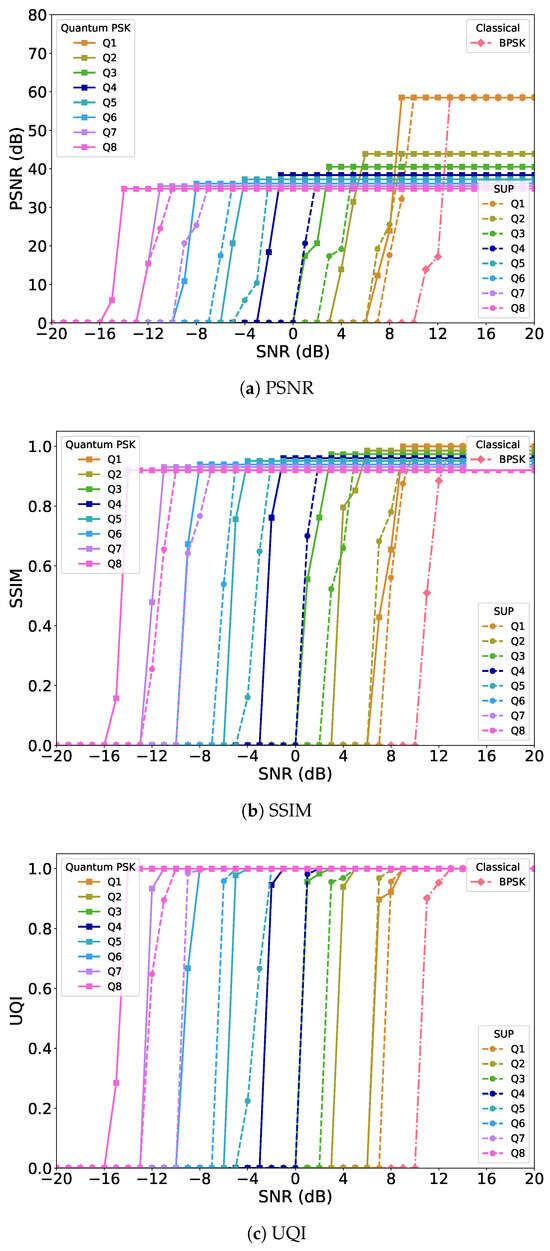
Figure 3.
Performance comparison of JPEG image transmission in the channel-coded scenario: (a) PSNR, (b) SSIM, and (c) UQI.
When examining the impact of qubit size under channel coding, the same behavior as in the uncoded case is observed: as the number of qubits increases, the performance of the system improves due to the enhanced ability to exploit phase information. Higher qubit sizes allow for more finely divided phase spaces, which improves noise resilience. Consequently, multi-qubit PSK systems consistently outperform the superposition-only quantum systems, achieving an additional 2–3 dB channel SNR gain, especially at higher qubit sizes. However, for the single-qubit configuration, the performance gain remains limited, since a single qubit cannot fully utilize the available phase modulation degrees of freedom. While it still provides an advantage compared to classical channel coded BPSK, the margin is smaller compared to the gains observed with multi-qubit systems.
Looking at the results, the PSNR curves as shown in Figure 3a show that multi-qubit PSK systems converge to their saturation values more quickly than both the superposition-only and classical baselines. With channel coding, the SNR required to reach a visually lossless level of quality is substantially lower. In SSIM as shown in Figure 3b, a similar effect is observed: quantum PSK schemes approach values near 1.0, corresponding to nearly perfect structural similarity, at much lower SNR values compared to the uncoded case. The UQI results as shown in Figure 3c reinforce this trend, with channel coding accelerating the convergence towards unity, particularly for higher qubit sizes. This demonstrates that polar coding not only provides additional robustness to noise but also amplifies the advantages already inherent to phase encoding in multi-qubit PSK systems.
Overall, the channel-coded results confirm two important findings. First, channel coding improves the noise tolerance of all schemes by shifting their performance curves leftward by approximately 3 dB, without changing the maximum achievable quality. Second, multi-qubit PSK systems benefit the most from the combination of polar coding and phase encoding, consistently outperforming both the superposition-only systems and the classical BPSK baseline. The performance gain of 2–3 dB for multi-qubit PSK relative to superposition-only systems remains consistent with the uncoded scenario, but now occurs at much lower SNR levels, making the system far more practical in realistic noisy channels.
4.3. Performance Evaluation for HEIF Image Transmission in the Uncoded Scenario
In the HEIF uncoded scenario, no channel coding is applied, so the transmission quality is determined purely by the intrinsic robustness of the encoding method and qubit configurations as shown in Figure 4. The HEIF format itself sets the maximum achievable PSNR, SSIM, and UQI values, and because of its more advanced compression efficiency compared to JPEG, these maximum values are consistently higher across all schemes. This demonstrates that HEIF preserves more information for a given bitrate, enabling better reconstruction quality at high SNR conditions.
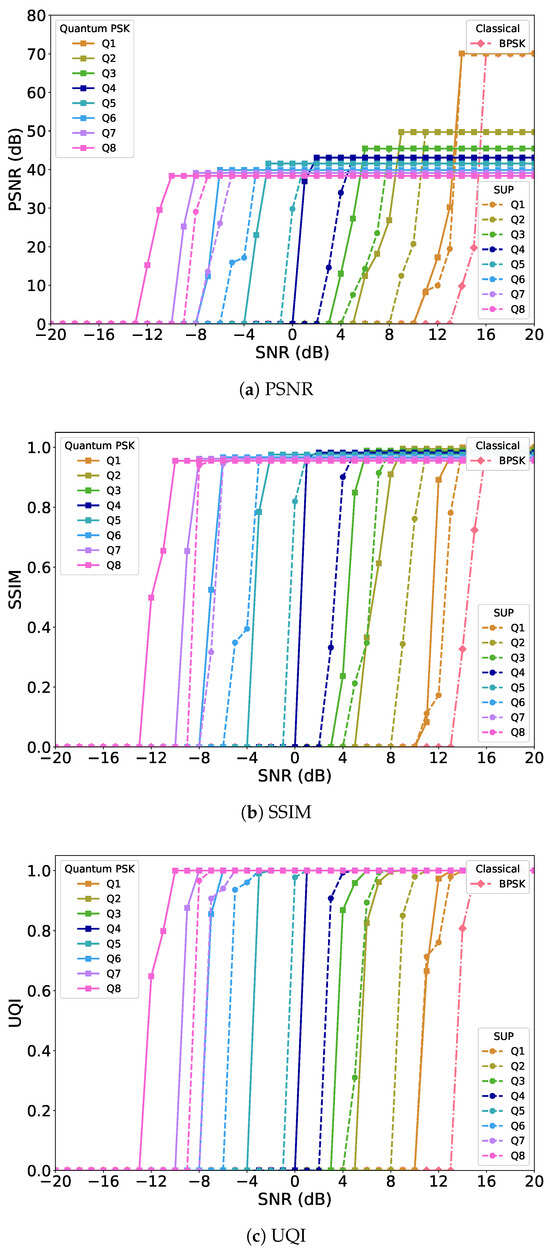
Figure 4.
Performance comparison of HEIF image transmission in the uncoded scenario: (a) PSNR, (b) SSIM, and (c) UQI.
The way each system approaches these limits, however, depends strongly on qubit size. Systems with small qubit sizes, such as single qubits, tend to reach higher peak values at large SNR. However, these small-qubit systems are fragile to noise: their PSNR, SSIM, and UQI values degrade sharply at low SNR because limited phase information restricts noise resilience. As the number of qubits increases, the energy is spread across more states, which reduces the maximum attainable values slightly, but the systems become much more robust to noise. Higher qubit PSK schemes show smoother curves, maintaining stable quality across a broader SNR range, confirming that richer phase encoding enhances tolerance to channel impairments even without channel coding. Compared to the superposition-only baselines, multi-qubit PSK consistently provides about a 2–3 dB channel SNR gain with higher-qubit encoding.
The single-qubit case nearly overlaps with the superposition-only system, similar to the JPEG system, since a single qubit cannot fully exploit phase modulation. Even so, it still achieves around a 3 dB SNR gain relative to the classical uncoded BPSK baseline, confirming the inherent advantage of quantum-based encoding. Overall, the HEIF uncoded results show two key outcomes: first, the maximum achievable quality (PSNR, SSIM, UQI) is higher than in JPEG due to the superior compression efficiency of HEIF; and second, while small-qubit systems maximize peak values, higher-qubit PSK systems provide superior robustness in noisy environments, making them better suited for practical quantum image transmission.
4.4. Performance Evaluation for HEIF Image Transmission in the Channel-Coded Scenario
In the HEIF channel-coded scenario, the inclusion of channel coding significantly improves the overall robustness of the system against channel noise, but it does not change the absolute maximum values of PSNR, SSIM, or UQI. These saturation values are determined entirely by the HEIF compression format, which is more efficient than JPEG and therefore capable of delivering higher peak reconstruction quality. This difference is visible across all three metrics: HEIF consistently reaches higher maxima than JPEG, regardless of the modulation or qubit configuration. What channel coding does is effectively shift the performance curves along the SNR axis. In practical terms, this means that the same levels of PSNR, SSIM, and UQI, which in the uncoded case could only be obtained under high-SNR conditions, can now be achieved at significantly lower SNR values. The effective gain from polar coding is around 3 dB across all schemes, demonstrating that channel coding primarily enhances noise resilience rather than increasing peak quality.
Examining the PSNR results shown in Figure 5a, one clear outcome is that multi-qubit PSK systems converge toward their saturation levels much more quickly when channel coding is present. Without coding, only high SNR values could push the PSNR toward the maximum possible limit, but with coding, near-optimal PSNR can be obtained under moderate SNR. Small-qubit systems still retain the highest peak PSNR values at very high SNR, but their fragility at low SNR remains evident. Higher-qubit PSK systems, in contrast, benefit most from channel coding: although their absolute peak values are slightly lower, they maintain consistently strong PSNR performance across a wider range of channel conditions, demonstrating their resilience.
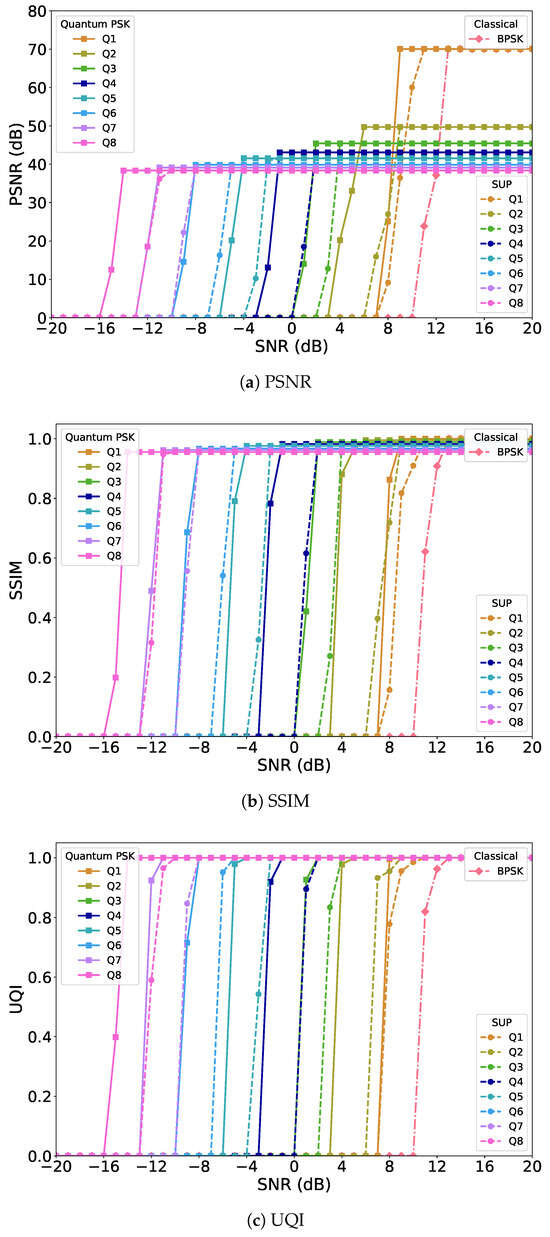
Figure 5.
Performance comparison of HEIF image transmission in the channel coded scenario: (a) PSNR, (b) SSIM, and (c) UQI.
The same trend can be observed in SSIM as shown in Figure 5b. With channel coding, all quantum PSK configurations rapidly climb toward structural similarity values near 1.0, meaning that the transmitted and reconstructed images are nearly identical in structure even under moderate channel noise. The smaller-qubit systems, as before, achieve the highest asymptotic SSIM values, but they show sharp declines when noise increases. The higher-qubit systems achieve slightly lower peaks, but with polar coding they remain stable and deliver consistently higher SSIM at low-to-mid SNR compared to the uncoded case. This stability highlights the strength of combining multi-qubit PSK with polar coding in preserving perceptual image quality.
The UQI curves reinforce the same interpretation as shown in Figure 5c. For uncoded systems, UQI performance climbed slowly and only reached high values at large SNR. With channel coding, UQI rises much more quickly, and higher-qubit PSK systems in particular achieve near-unity UQI across a wide range of SNR conditions. This confirms that the joint effect of phase encoding and error correction yields a robust transmission scheme that is resistant to severe channel degradation.
When comparing systems, the relative order remains unchanged from the uncoded scenario. Multi-qubit PSK outperforms superposition-only systems by an additional 2–3 dB effective SNR gain, demonstrating the continued advantage of explicit phase modulation. The single-qubit PSK configuration remains close to the superposition-only baseline since it cannot fully exploit phase information, but it still shows an advantage of about 3 dB compared to the classical BPSK baseline, even with channel coding applied. This indicates that quantum encoding, even in its simplest form, provides inherent benefits over classical modulation.
Taken together, the HEIF channel-coded results highlight several key points. First, HEIF offers higher maximum reconstruction quality than JPEG, and these maxima are preserved with or without channel coding. Second, channel coding does not alter these limits but instead reduces the SNR threshold required to reach them, providing an average coding gain of around 3 dB. Third, higher-qubit PSK systems combine the advantages of phase encoding and error correction to deliver both strong robustness and high perceptual quality, outperforming both superposition-only systems and the classical baseline. These results confirm that HEIF, when combined with polar coding and multi-qubit PSK encoding, represents the most effective configuration for reliable quantum image transmission in noisy and bandwidth-limited channels.
4.5. Performance of the Proposed System for Different Image Resolutions and Subjective Experiment Results
The SNR gains achieved by both the proposed multi-qubit PSK system and the superposition-only system are presented in Table 1, with each compared against the classical BPSK baseline in the uncoded scenarios. The labels “Q1–Q8” correspond directly to the number of qubits used in the multi-qubit encoding (i.e., Q1 = 1 qubit, Q2 = 2 qubits, …, Q8 = 8 qubits).

Table 1.
Maximum SNR gains (in dB) achieved by each qubit system compared to the classical BPSK configuration.
In addition, the SNR gain is empirically calculated based on a given quality threshold Q (e.g., PSNR), using Equation (47).
where and are the channel SNR values required by the baseline classical system and the proposed quantum system, respectively, to achieve the same quality Q. This definition aligns the quality curves of both systems and provides a fair, reproducible comparison without relying solely on raw BER values.
This comparison highlights the advantages of quantum-based transmission methods over conventional approaches. From the results, it is evident that the proposed multi-qubit PSK system consistently achieves higher SNR gains than the superposition-only configurations. This demonstrates the benefit of combining superposition with phase modulation, as it enables the system to more effectively utilize the available bandwidth while resisting the effects of channel noise. The superposition-only system also provides improvements over the classical baseline, but its performance gain is more limited compared to the full multi-qubit PSK system. This indicates that while superposition contributes to efficiency, the inclusion of PSK modulation is necessary to maximize performance.
Another key observation from Table 1 is that the measured SNR gains remain stable across different image compression formats, SI, and resolutions. This consistency suggests that the proposed approach is robust and largely independent of the specific image format, relying only on the quantum-encoding method. Overall, the results confirm that the multi-qubit PSK system provides superior performance compared to both the classical BPSK baseline and the superposition-only methods, establishing it as a more reliable and scalable solution for quantum communication of images.
To evaluate perceptual quality, a subjective experiment is conducted using the double stimulation method [] with 50 participants aged 18 to 65 years, drawn from academic and technical backgrounds, including individuals with prior experience in image and video processing. Each participant rated the visual quality of received images on a 0–100 scale using the mean opinion score (MOS) methodology: ‘bad’ (0–20), ‘poor’ (21–40), ‘fair’ (41–60), ‘good’ (61–80), and ‘excellent’ (81–100). The average MOS values plotted in Figure 6 represent the mean scores between all participants. The variation among individual ratings is small (standard deviation ), indicating high consistency between the participants. The results show that subjective MOS trends closely follow objective metrics such as PSNR and SSIM, confirming the reliability of the performance evaluation of the proposed system.
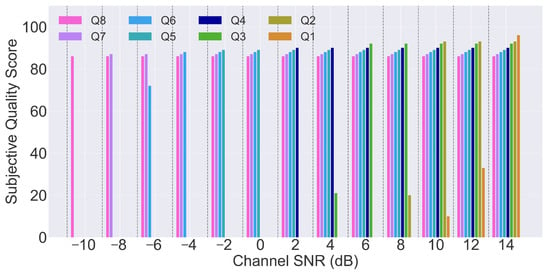
Figure 6.
Subjective Experiment Results for the JPEG Uncoded Scenario.
4.6. Relative Advantage of Multi-Qubit PSK over Superposition-Only Systems
The superior performance of the multi-qubit PSK system compared to the superposition-only baseline can be attributed to the additional degrees of freedom provided by phase modulation. In the superposition-only scheme, Hadamard encoding produces equal-amplitude states whose distinguishability depends solely on the distribution of probability amplitudes across the computational basis. This inherently limits the geometrical separation between signal points in the Hilbert space, making the states highly susceptible to noise perturbations, particularly in low-SNR regimes. By contrast, the multi-qubit PSK system introduces phase rotations across the basis states, thereby mapping the transmitted information onto a richer signal constellation that spans both amplitude and phase domains. This extension of the signal space increases the distinguishability of adjacent symbols through enhanced geometrical separation, improving robustness against noise and fading impairments.
As the number of qubits increases, the available phase states scale with , allowing for finer partitioning of the unit circle and more distinguishable quantum states within the same bandwidth. This scalability enables multi-qubit PSK to exploit the full dimensionality of the Hilbert space, whereas superposition-only states remain constrained to an amplitude-limited subset. While the bit-per-qubit ratio remains 1 for all qubit systems, the advantage of the proposed multi-qubit PSK scheme lies in its ability to encode phase relationships across multiple qubits simultaneously, thereby fully exploiting the -dimensional Hilbert space. By exploiting multi-qubit superposition states, the system can encode more complex phase patterns, improving efficiency, error resilience, and robustness against noise without increasing the number of qubits per bit. In this way, the multi-qubit PSK framework extends the encoding capability of conventional single-qubit, enabling higher-dimensional state vector utilization and more efficient quantum information representation. The practical effect, as seen in the performance curves, is an average channel SNR gain of approximately 2–3 dB for the PSK-based scheme relative to the superposition baseline. At the single-qubit, the performance gap is negligible since phase modulation cannot be fully exploited; however, as qubit size increases, the divergence becomes pronounced, with multi-qubit PSK maintaining higher PSNR, SSIM, and UQI values in noisy channels. This confirms that phase encoding is not merely an incremental extension of superposition, but a fundamental enhancement that leverages the full quantum state space for robust and scalable information transmission.
In addition, the proposed method is applicable to uncompressed formats such as Bitmap (BMP) and Portable Network Graphics (PNG), as well as medical images in Digital Imaging and Communications in Medicine (DICOM) format, by adjusting the qubit encoding size. While higher-qubit encoding requires more bandwidth, preventing direct comparison under equal bandwidth constraints, the framework operates at the bit level and is compatible with any image type, demonstrating broad applicability across compression schemes and formats.
4.7. Complexity Analysis: Multi-Qubit PSK vs. Superposition-Only Systems
The computational and implementation complexity of the multi-qubit PSK system can be assessed relative to the superposition-only baseline. In the superposition-only scheme, state preparation requires only k Hadamard gates to create an equal-amplitude superposition, resulting in a circuit depth of one layer and linear gate scaling. Decoding involves only the inverse Hadamard transform followed by measurement, which is similarly shallow. The overall latency of this scheme is therefore minimal.
The multi-qubit PSK system, however, introduces additional phase gates during encoding and corresponding inverse phase operations during decoding. This increases both circuit depth and gate count, since each computational basis state requires an appropriate phase shift. In a straightforward, unoptimized implementation, the number of phase operations scales as , and classical post-processing must discriminate among phase states rather than only amplitude patterns. This naturally introduces some additional latency compared to the superposition-only baseline.
Despite these increases, the computational and latency overheads remain practically manageable. Phase gates are diagonal unitaries, which are relatively simple to implement with high precision and low error rates on current quantum hardware. Optimized designs can further reduce the number of operations and associated latency. On the classical side, phase-state discrimination is structured and efficiently implementable, keeping post-processing delays reasonable. For moderate qubit counts (e.g., ), which suffice for high-fidelity image transmission in our experiments, the overall latency remains acceptable for practical applications.
Moreover, the additional complexity and latency are justified by substantial performance gains. By exploiting both amplitude and phase across multiple qubits, the multi-qubit PSK system achieves higher fidelity, better noise resilience, and improved spectral efficiency compared to the superposition-only baseline. In real-world quantum image transmission, the slight increase in gate depth and processing time is outweighed by the benefits of more reliable and higher-quality image reconstruction.
In summary, while the multi-qubit PSK system introduces additional gate operations, circuit depth, and modest latency compared to superposition-only schemes, these overheads are fully manageable, scalable, and justified by the resulting improvements in robustness, fidelity, and practical feasibility for high-quality quantum image transmission.
4.8. Scalability and Future Applications
The scalability of the multi-qubit PSK framework is one of its most attractive features. This multi-qubit PSK system can seamlessly extend to higher qubit dimensions by increasing the modulation order . As k grows, the available phase space expands, enabling the construction of higher and more noise-resilient constellations without fundamentally altering the encoding and decoding procedures. This scalability suggests that the scheme can be adapted beyond still image transmission to more demanding tasks such as video streaming, quantum internet protocols, or quantum sensor networks, where robustness under noisy channels is a critical requirement.
From a practical perspective, the reliance on phase rotations as the primary modulation mechanism ensures that scalability does not translate into prohibitive hardware costs. Phase gates are among the most fault-tolerant operations on current quantum devices, and their simplicity makes them well suited for near-term quantum hardware. Combined with classical channel coding, the framework offers a hybrid quantum–classical strategy that is both implementable and extendable. In the long term, the ability of multi-qubit PSK to operate over a wide range of qubit sizes positions it as a candidate for scalable quantum communication infrastructures, where future applications may include integration with distributed quantum computing, cloud-based quantum service, and next-generation multimedia transmission systems.
4.9. Simulation Basis and Roadmap for Future Implementation
The present study has been conducted entirely in a simulation environment. This choice is motivated by two primary factors. First, current quantum hardware remains limited in terms of qubit coherence times, gate fidelity, and error rates, which makes it impractical to implement high-dimensional multi-qubit PSK systems in real devices at this stage. Second, simulation allows for controlled evaluation of performance across a wide range of channel conditions, qubit sizes, and encoding strategies, which would be infeasible to explore experimentally given present-day hardware constraints. By using numerical simulation, we are able to isolate the impact of modulation, channel coding, and source compression schemes without being restricted by device imperfections.
Looking forward, the roadmap for practical implementation involves several key milestones. In the near term, small-scale prototypes can be realized on existing noisy intermediate-scale quantum (NISQ) devices by implementing single and two-qubit PSK encoding circuits and validating the noise-resilience advantages experimentally. As hardware matures, particularly with improvements in gate fidelity and error correction, higher multi-qubit constellations can be tested, enabling the transmission of more complex image or video data. In the longer term, the integration of multi-qubit PSK with quantum error-corrected architectures, quantum repeaters, and hybrid quantum–classical systems will pave the way for full-scale deployment. This roadmap ensures that the current simulation results serve not only as a theoretical validation but also as a stepping stone toward scalable real-world quantum communication systems.
5. Conclusions and Future Works
In this work, a novel framework for quantum image transmission based on multi-qubit PSK encoding is introduced. By combining quantum superposition with phase encoding, higher-dimensional Hilbert spaces are exploited, enabling both scalability and robustness under noisy channels. Consistent improvements in image fidelity are demonstrated through PSNR, SSIM, and UQI. Channel SNR gains of up to 3 dB are achieved over superposition-only quantum methods at higher qubit counts, with the eight-qubit configuration delivering the most significant benefits despite the increased complexity. In contrast, the benefits of PSK encoding in the single-qubit case remain limited due to the restricted phase space. Furthermore, gains of up to 26 dB are obtained with eight-qubit encoding when compared with classical BPSK transmission, confirming the superiority of the proposed approach, regardless of the image compression format. Multi-qubit PSK encoding is shown to outperform superposition-only schemes by leveraging the additional phase dimension, which allows for a more efficient utilization of the quantum state space. As the number of encoded qubits increases, the dimensionality of the Hilbert space expands, resulting in consistent improvements in robustness and fidelity. Notably, these SNR gains are largely independent of image compression, resolution, or source domain, demonstrating that the performance advantages are stable across a wide range of transmission conditions. Overall, the results indicate that multi-qubit PSK provides clear and repeatable improvements over both classical BPSK and superposition-only systems, while maintaining scalability as the encoding size grows.
Despite these encouraging results, several challenges remain that motivate future research. First, while our evaluation is conducted in a simulation, experimental validation on quantum hardware is necessary to assess the practical feasibility of the proposed scheme under real-world conditions, where decoherence and hardware imperfections are inevitable. Deploying multi-qubit PSK on NISQ devices requires careful consideration of decoherence times, gate fidelities, phase precision, and qubit connectivity constraints, all of which can impact achievable fidelity and limit the number of reliably encoded qubits. Second, while this study demonstrates the advantages of phase-domain encoding, further work is needed to integrate multi-qubit PSK with computationally feasible QEC strategies for large-scale image transmission. Third, extending the framework to video transmission and adaptive encoding techniques could broaden its applicability to dynamic multimedia scenarios. Finally, integration with quantum networking protocols and hybrid quantum–classical architectures will be essential for realizing end-to-end systems capable of supporting practical quantum-enhanced image and video communication.
Author Contributions
Conceptualization, U.J.; methodology, U.J.; software, U.J. and T.F.; validation, U.J. and A.F.; formal analysis, A.F.; investigation, A.F.; resources, U.J.; data curation, U.J.; writing—original draft preparation, U.J.; writing—review and editing, T.F.; visualization, U.J.; supervision, A.F.; project administration, A.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original data presented in the study are openly available in the Microsoft COCO dataset at https://cocodataset.org (accessed on 4 May 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| HEIF | High-Efficiency Image Format |
| JPEG | Joint Photographic Experts Group |
| LDPC | Low-Density Parity-Check |
| MIMO | Multi-Input Multi-Output |
| MOS | Mean Opinion Score |
| NISQ | Noisy Intermediate Scale Quantum |
| PSNR | Peak Signal-to-Noise Ratio |
| QEC | Quantum Error Correction |
| QKD | Quantum Key Distribution |
| QP | Quantization Parameters |
| SNR | Signal-to-Noise Ratio |
| SSIM | Structural Similarity Index Measure |
| UQI | Universal Quality Index |
References
- Wallace, G. The JPEG still picture compression standard. IEEE Trans. Consum. Electron. 1992, 38, xviii–xxxiv. [Google Scholar] [CrossRef]
- Hannuksela, M.M.; Lainema, J.; Malamal Vadakital, V.K. The High Efficiency Image File Format Standard [Standards in a Nutshell]. IEEE Signal Process. Mag. 2015, 32, 150–156. [Google Scholar] [CrossRef]
- Li, Y. Analysis and Methodological Advancements in Software-Defined Error Correction Codes. In Proceedings of the 2024 4th International Signal Processing, Communications and Engineering Management Conference (ISPCEM), Montreal, QC, Canada, 28–30 November 2024; pp. 133–138. [Google Scholar] [CrossRef]
- Shannon, C.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Champaign, IL, USA, 1949. [Google Scholar]
- Jayasinghe, U.; Fernando, T.; Ganearachchi, Y.; Samarathunga, P.; Fernando, A. Quantum Communication Based Image Transmission With Transmit and Receive Diversity in MIMO Communication Systems. IEEE Trans. Consum. Electron. 2025, 71, 2500–2507. [Google Scholar] [CrossRef]
- Sridhar, G.T.; P, A.; Tabassum, N. A Review on Quantum Communication and Computing. In Proceedings of the 2023 2nd International Conference on Applied Artificial Intelligence and Computing (ICAAIC), Salem, India, 4–6 May 2023; pp. 1592–1596. [Google Scholar] [CrossRef]
- Zou, N. Quantum Entanglement and Its Application in Quantum Communication. J. Physics Conf. Ser. 2021, 1827, 012120. [Google Scholar] [CrossRef]
- Jayasinghe, U.; Samarathunga, P.; Ganearachchi, Y.; Fernando, T.; Fernando, A. Quantum communications for image transmission over error-prone channels. Electron. Lett. 2024, 60, e13300. [Google Scholar] [CrossRef]
- Jayasinghe, U.; Kushantha, N.; Fernando, T.; Fernando, A. A Robust Multi-Qubit Quantum Communication System for Image Transmission over Error Prone Channels. IEEE Trans. Consum. Electron. 2025, 71, 7551–7558. [Google Scholar] [CrossRef]
- Thakur, V.S.; Kumar, A.; Das, J.; Dev, K.; Magarini, M. Quantum Error Correction Codes in Consumer Technology: Modeling and Analysis. IEEE Trans. Consum. Electron. 2024, 70, 7102–7111. [Google Scholar] [CrossRef]
- Roffe, J. Quantum error correction: An introductory guide. Contemp. Phys. 2019, 60, 226–245. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Turkeshi, X.; Sierant, P. Error-Resilience Phase Transitions in Encoding-Decoding Quantum Circuits. Phys. Rev. Lett. 2024, 132, 140401. [Google Scholar] [CrossRef]
- Jayasinghe, U.; Samarathunga, P.; Ganearachchi, Y.; Fernando, T.; Fernando, A. Adaptive Coding-Based Quantum Communication System for Image Transmission. Electron. Lett. 2025, 61, e70299. [Google Scholar] [CrossRef]
- Horé, A.; Ziou, D. Is there a relationship between peak-signal-to-noise ratio and structural similarity index measure? Iet Image Process. 2013, 7, 12–24. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A. A universal image quality index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Hasan, S.R.; Chowdhury, M.Z.; Sayem, M.; Jang, Y.M. Quantum Communication Systems: Vision, Protocols, Applications, and Challenges. IEEE Access 2023, 11, 15855–15877. [Google Scholar] [CrossRef]
- Peelam, M.S.; Sai, S.; Chamola, V. Explorative Implementation of Quantum Key Distribution Algorithms for Secure Consumer Electronics Networks. IEEE Trans. Consum. Electron. 2024, 70, 5576–5584. [Google Scholar] [CrossRef]
- Brazaola-Vicario, A.; Ruiz, A.; Lage, O.; Jacob, E.; Astorga, J. Quantum key distribution: A survey on current vulnerability trends and potential implementation risks. Opt. Contin. 2024, 3, 1438–1460. [Google Scholar] [CrossRef]
- Yan, X.Y.; Zhou, N.R.; Gong, L.H.; Wang, Y.Q.; Wen, X.J. High-dimensional quantum key distribution based on qudits transmission with quantum Fourier transform. Quantum Inf. Process. 2019, 18, 271. [Google Scholar] [CrossRef]
- Ul Ain, N.; Waqar, M.; Bilal, A.; Kim, A.; Ali, H.; Ullah Tariq, U.; Shahroz Nadeem, M. A Novel Approach Based on Quantum Key Distribution Using BB84 and E91 Protocol for Resilient Encryption and Eavesdropper Detection. IEEE Access 2025, 13, 32819–32833. [Google Scholar] [CrossRef]
- Zulfa, M.F.; Anwar, K. Development of Quantum Key Distribution (QKD) with E91 Protocol for Future Secure Quantum Networks. J. Phys. Conf. Ser. 2025, 2980, 012038. [Google Scholar] [CrossRef]
- Langenfeld, S.; Welte, S.; Hartung, L.; Daiss, S.; Thomas, P.; Morin, O.; Distante, E.; Rempe, G. Quantum Teleportation between Remote Qubit Memories with Only a Single Photon as a Resource. Phys. Rev. Lett. 2021, 126, 130502. [Google Scholar] [CrossRef]
- Fu, Y.; Li, D.; Hua, X.; Jiang, Y.; Zhu, Y.; Zhou, J.; Yang, X.; Tan, Y. A Scheme for Quantum Teleportation and Remote Quantum State Preparation of IoT Multiple Devices. Sensors 2023, 23, 8475. [Google Scholar] [CrossRef] [PubMed]
- Harraz, S.; Cong, S.; Nieto, J.J. Protected Quantum Teleportation Through Noisy Channel by Weak Measurement and Environment-Assisted Measurement. IEEE Commun. Lett. 2022, 26, 528–531. [Google Scholar] [CrossRef]
- Giroti, I.; Malhotra, M. Quantum Cryptography: A Pathway to Secure Communication. In Proceedings of the 2022 6th International Conference on Computation System and Information Technology for Sustainable Solutions (CSITSS), Bangalore, India, 21–23 December 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Cherkaoui Dekkaki, K.; Tasic, I.; Cano, M.D. Exploring Post-Quantum Cryptography: Review and Directions for the Transition Process. Technologies 2024, 12, 241. [Google Scholar] [CrossRef]
- Qu, Z.; Fu, X.; Sun, L.; Muhammad, G. QDICP: A Quantum Blockchain Model for Copyright Protection of Digital Images in Consumer Electronics. IEEE Trans. Consum. Electron. 2024, 71, 5189–5200. [Google Scholar] [CrossRef]
- Mallick, B.; Parida, P.; Nayak, C.; Khalifa, T.; Kumar Panda, M.; Ali, N.; Uttam Patil, G.; Prasad, B. Multi-Channel Multi-Protocol Quantum Key Distribution System for Secure Image Transmission in Healthcare. IEEE Access 2025, 13, 62476–62505. [Google Scholar] [CrossRef]
- Janani, T.; Brindha, M. A secure medical image transmission scheme aided by quantum representation. J. Inf. Secur. Appl. 2021, 59, 102832. [Google Scholar] [CrossRef]
- Hariprasad, Y.; Iyengar, S.; Chaudhary, N.K. Securing the Future: Advanced Encryption for Quantum-Safe Video Transmission. IEEE Trans. Consum. Electron. 2024, 71, 140–153. [Google Scholar] [CrossRef]
- Yasmineh, S. Foundations of Quantum Mechanics. Encyclopedia 2022, 2, 1082–1090. [Google Scholar] [CrossRef]
- Jayasinghe, U.; Samarathunga, P.; Fernando, T.; Fernando, A. Transmit and Receive Diversity in MIMO Quantum Communication for High-Fidelity Video Transmission. Algorithms 2025, 18, 436. [Google Scholar] [CrossRef]
- Jayasinghe, U.; Samarathunga, P.; Fernando, T.; Ganearachchi, Y.; Fernando, A. Image Transmission Over Quantum Communication Systems With Three-Qubit Error Correction. Electron. Lett. 2025, 61, e70205. [Google Scholar] [CrossRef]
- Jayasinghe, U.; Samarathunga, P.; Pollwaththage, N.; Ganearachchi, Y.; Fernando, T.; Fernando, A. Quantum Communication for Video Transmission Over Error-Prone Channels. IEEE Trans. Consum. Electron. 2025, 71, 1148–1155. [Google Scholar] [CrossRef]
- Jayasinghe, U.; Pollwaththage, N.; Ganearachchi, Y.; Samarathunga, P.; Fernando, T.; Fernando, A. Quantum Communication based Image Transmission over Error-Prone Channels with Three-Qubit Stabilizer Code. In Proceedings of the 2025 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 11–14 June 2025; pp. 1–6. [Google Scholar] [CrossRef]
- Ballentine, L.E. Quantum Mechanics: A Modern Development, 2nd ed.; World Scientific Publishing Company: Singapore, 2014; p. 740. [Google Scholar]
- Raychev, N. Formalized Operators with Phase Encoding. J. Quantum Inf. Sci. 2015, 5, 101–108. [Google Scholar] [CrossRef]
- Jayasinghe, U.; Fernando, T.; Fernando, A. High-Fidelity Image Transmission in Quantum Communication with Frequency Domain Multi-Qubit Techniques. Algorithms 2025, 18, 501. [Google Scholar] [CrossRef]
- Deb, S.; Pan, W. Quantum Image Compression: Fundamentals, Algorithms, and Advances. Computers 2024, 13, 185. [Google Scholar] [CrossRef]
- Pathak, N.K.; Chaudhary, S.; Sangeeta; Kanseri, B. Phase encoded quantum key distribution up to 380 km in standard telecom grade fiber enabled by baseline error optimization. Sci. Rep. 2023, 13, 15868. [Google Scholar] [CrossRef] [PubMed]
- Lin, T.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. In Computer Vision—ECCV 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Lecture Notes in Computer Science Springer: Cham, Switzerland, 2014; Volume 8693, pp. 740–755. [Google Scholar] [CrossRef]
- ImageNet. ImageNet: A Large-Scale Hierarchical Image Database. Available online: https://www.image-net.org/ (accessed on 30 May 2025).
- Kaggle Contributor. Images 4K. [Online]. Available online: https://www.kaggle.com/datasets/evgeniumakov/images4k (accessed on 30 May 2025).
- Pathak, P.; Bhatia, R. Performance Analysis of Polar codes for Next Generation 5G Technology. In Proceedings of the 2022 3rd International Conference for Emerging Technology (INCET), Belgaum, India, 27–29 May 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Arikan, E. Systematic Polar Coding. IEEE Commun. Lett. 2011, 15, 860–862. [Google Scholar] [CrossRef]
- Gallager, R. Low-density parity-check codes. Ire Trans. Inf. Theory 1962, 8, 21–28. [Google Scholar] [CrossRef]
- Berrou, C.; Pyndiah, R.; Adde, P.; Douillard, C.; Le Bidan, R. An overview of turbo codes and their applications. In Proceedings of the European Conference on Wireless Technology, Paris, France, 3–4 October 2005; pp. 1–9. [Google Scholar] [CrossRef]
- Berman, A.; Shany, Y.; Tamo, I. Explicit Subcodes of Reed-Solomon Codes That Efficiently Achieve List Decoding Capacity. IEEE Trans. Inf. Theory 2025, 71, 5898–5911. [Google Scholar] [CrossRef]
- Tiwari, S.; Bharti, G.K.; Kumar Chhipa, M. Theoretical Investigation of Single-Qubit Hadamard Gate. In Proceedings of the 2025 IEEE International Conference on Interdisciplinary Approaches in Technology and Management for Social Innovation (IATMSI), Gwalior, India, 6–8 March 2025; Volume 3, pp. 1–5. [Google Scholar] [CrossRef]
- Chakraborty, M.; Mukherjee, A.; Nag, A.; Chandra, S. Hybrid Quantum Noise Model to Compute Gaussian Quantum Channel Capacity. IEEE Access 2024, 12, 14671–14689. [Google Scholar] [CrossRef]
- International Telecommunication Union (ITU). Methodologies for the Subjective Assessment of the Quality of Television Pictures; ITU-R Recommendation BT.500; International Telecommunication Union: Geneva, Switzerland, 2022. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).