Implementation of Advection–Diffusion and Linear Orographic Schemes for Nowcasting Precipitation ^†

Abstract

Accurate precipitation nowcasting is essential for short-term forecasting, but it remains challenging due to the dynamic nature of rainfall mechanisms. This study implements and evaluates two schemes for improving precipitation nowcasting: (1) an advection–diffusion scheme and (2) an advection–diffusion scheme integrated with the linear theory of orographic precipitation. These schemes are implemented into the Local Analysis and Prediction System (LAPS) to produce short-term precipitation forecasts and applied to a case study involving a rainfall event over the Athens metropolitan area in Greece. These schemes are compared against the default LAPS nowcasting module based on a first-order advection scheme (control). The first-order advection scheme, while computationally efficient, lacks the ability to simulate rainfall field evolution due to its exclusion of diffusion processes and orographic effects, leading to inaccurate nowcasts. To address these limitations, the advection–diffusion scheme is introduced to capture the precipitation evolution, and the third scheme integrates the linear theory of orographic precipitation to account for the influence of topography. Preliminary results show improvements in the spatiotemporal distribution of the nowcasted precipitation. These findings suggest that incorporating diffusion and orographic effects can enhance the accuracy of short-term precipitation forecasts, though further evaluation across diverse meteorological events is needed to confirm general applicability.

1. Introduction

Accurate precipitation nowcasting is an important component of short-term weather forecasting, particularly for hydrometeorological risk management and urban flood prevention [1]. Despite its importance, achieving high precision in precipitation nowcasts remains a significant challenge due to the inherently dynamic and complex nature of rainfall generation and evolution [2]. Conventional nowcasting techniques, such as first-order advection schemes, often fail to capture the full spatial and temporal variability of rainfall [3]. These methods, while computationally efficient, tend to neglect key physical processes such as diffusion and orographic influences, resulting in limited forecast accuracy.

To address these limitations, recent studies have proposed incorporating advection–diffusion frameworks that better represent the dispersion and evolution of precipitation systems [4]. Additionally, the influence of complex terrain on rainfall distribution, through orographic lifting and related microphysical processes, has been shown to significantly affect precipitation patterns and intensity [5]. The realism and reliability of short-term precipitation forecasts can be improved by including these physical processes in operational forecasting systems.

This study implements and evaluates two advanced nowcasting schemes within the Local Analysis and Prediction System (LAPS) [6]. The first scheme enhances the traditional approach by incorporating an advection–diffusion framework that accounts for the dispersion of precipitation fields. The impact of terrain on rainfall distribution is addressed by the second scheme that further integrates the linear theory of orographic precipitation. Both schemes are applied to a significant rainfall event over the Athens metropolitan area, Greece, on 29 September 2018 at 08:00 UTC. Their performance is systematically compared against the default LAPS nowcasting module, which relies on a first-order advection scheme.

The primary objective is to determine if the inclusion of diffusion processes and orographic effects can significantly improve the temporal and spatial accuracy of short-term precipitation forecasts. A comprehensive set of standard metrics is used for verification in order to evaluate forecast skill and reliability. Preliminary results demonstrate that the proposed enhancements provide improvements over the control experiment, suggesting that physically informed nowcasting schemes incorporating diffusion and terrain effects can offer more accurate and robust precipitation predictions.

2. Description of the Numerical Schemes

This study evaluates two precipitation nowcasting schemes implemented within LAPS, each with increasing physical complexity. The baseline is the default LAPS nowcasting module, a first-order advection scheme.

2.1. First-Order Advection Scheme

The control scheme is a first-order advection scheme. Its mathematical formulation is given by the following discrete form:

$${\displaystyle \frac{1}{\mathsf{\Delta }t}}\left(R_{i,j}^{t+1}-R_{i,j}^t\right)+{\displaystyle \frac{u}{\mathsf{\Delta }x}}\left(R_{i,j}^t-R_{i-1,j}^t\right)+{\displaystyle \frac{v}{\mathsf{\Delta }y}}\left(R_{i,j}^t-R_{i,j-1}^t\right)=0$$

(1)

This scheme predicts the precipitation at a future time step ($R_{i,j}^{t+1}$) at a specific grid point (i, j) based on the current precipitation ($R_{i,j}^t$) and the horizontal transport, or advection, by the wind. The wind components u and v represent the velocity in the x and y directions, respectively. This formulation operates under the assumption that precipitation is only transported by the wind, without considering any processes that might cause it to spread out or any local mechanisms for its generation or dissipation [7].

2.2. Advection–Diffusion Scheme

The second scheme enhances the baseline by incorporating spatial diffusion alongside horizontal transport. It is based on the following two-dimensional advection–diffusion equation:

$${\displaystyle \frac{\partial R}{\partial t}}=-u{\displaystyle \frac{\partial R}{\partial x}}-v{\displaystyle \frac{\partial R}{\partial y}}+k\left({\displaystyle \frac{{\partial }^{2}R}{\partial x^2}}+{\displaystyle \frac{{\partial }^{2}R}{\partial y^2}}\right)$$

(2)

Here, u and v are the wind velocity components in the x and y-directions, respectively. k is the diffusion coefficient. For this study, k is set to 0.1 [8] to parameterize the spreading effect.

To numerically solve the diffusion term, we apply the Crank–Nicolson scheme with operator splitting, offering improved accuracy [9]. This implicit method preserves second-order accuracy in space.

This scheme represents an intermediate level of complexity, effectively capturing the general transport and diffusive spreading of precipitation fields. However, this scheme does not explicitly account for terrain effects on precipitation.

2.3. Advection–Diffusion Scheme Integrated with Linear Theory of Orographic Precipitation

The third scheme extends the previous advection–diffusion framework by explicitly incorporating the influence of terrain on precipitation through the Linear Theory of Orographic Precipitation [5]. This scheme integrates two distinct components:

2.3.1. Advection–Diffusion

The background precipitation field is calculated using the same advection–diffusion equation and numerical implementation described in Section 2.2. This component provides a precipitation field that is independent of terrain influences.

2.3.2. Linear Theory of Orographic Precipitation

The second component models precipitation enhancement due to terrain-induced airflow dynamics and microphysical processes, based on the Linear Theory of Orographic Precipitation [5]. Key physical elements include the following:

• Depth of the moist layer:

$$H_w=-{\displaystyle \frac{R_v·T^2}{L\gamma }}$$

(3)

where γ is the environmental lapse rate, $R_v$ is the gas constant for vapor, T is the temperature, and L is the latent heat.

• Thermodynamics uplift sensitivity factor:

$$C_W={\displaystyle \frac{{\rho }_{ref}\ast {\Gamma }_m}{\gamma }}$$

(4)

where ${\rho }_{ref}$ is the water vapor saturation density and ${\Gamma }_m$ the moist adiabatic lapse rate.

• Moist static stability (Brunt-Vaisala frequency)

$$N_m^2={\displaystyle \frac{g}{T}}\left(\gamma -{\Gamma }_m\right)$$

(5)

where g is the gravitational acceleration.

• Spectral Representation of Terrain:

The terrain height h(x,y) is transformed into spectral space via a 2D Fourier transform $\widehat{h}\left(k,l\right)$ with horizontal wavenumbers k and l.

• Intrinsic Frequency:

$$\sigma =u·k+v·l$$

(6)

• Transfer function for orographic precipitation:

$$\widehat{P}\left(k,l\right)={\displaystyle \frac{C_{w}i\sigma \widehat{h}\left(k.l\right)}{\left(1-im{H}_w\right)\left(1+i\sigma {\tau }_c\right)\left(1+i\sigma {\tau }_f\right)}},$$

(7)

where m is the vertical wavenumber, through τ_c and τ_f are cloud microphysical delay timescales.

An inverse Fast Fourier Transform is used to convert $\widehat{P}\left(k,l\right)$ back the spatial pattern of orographic precipitation. The orographic precipitation field is combined with the background advected–diffused precipitation to produce the final precipitation nowcast, capturing both large-scale transport and localized terrain-induced enhancements.

2.4. Experimental Setup

In this study, the LAPS domain was configured to cover the Attica region with a fine horizontal grid spacing of 1 km and 41 vertical levels, resulting in a total of 110 × 110 × 41 = 496,100 grid points. The following three sensitivity experiments were conducted:

• Control: First-Order Advection Scheme.
• AD: Advection–Diffusion Scheme.
• ADLOP: Advection–Diffusion Integrated with Linear Theory of Orographic Precipitation

Initial conditions were derived from GFS near-analysis forecasts on 0.25° × 0.25° and X-band dual-polarization (XPOL) radar data. The experiments were conducted on 29 September 2018. LAPS was run at 08:00 UTC, producing analysis fields and precipitation nowcasts for a 1.5 h, up to 09:30 UTC using a time step of 2.5 min.

3. Results and Discussion

The performance of the three nowcasting schemes—the control (first-order advection), advection–diffusion (AD), and advection–diffusion integrated with linear theory of orographic precipitation (ADLOP)—was evaluated by examining the spatial distribution of forecasted precipitation and through statistical verification metrics.

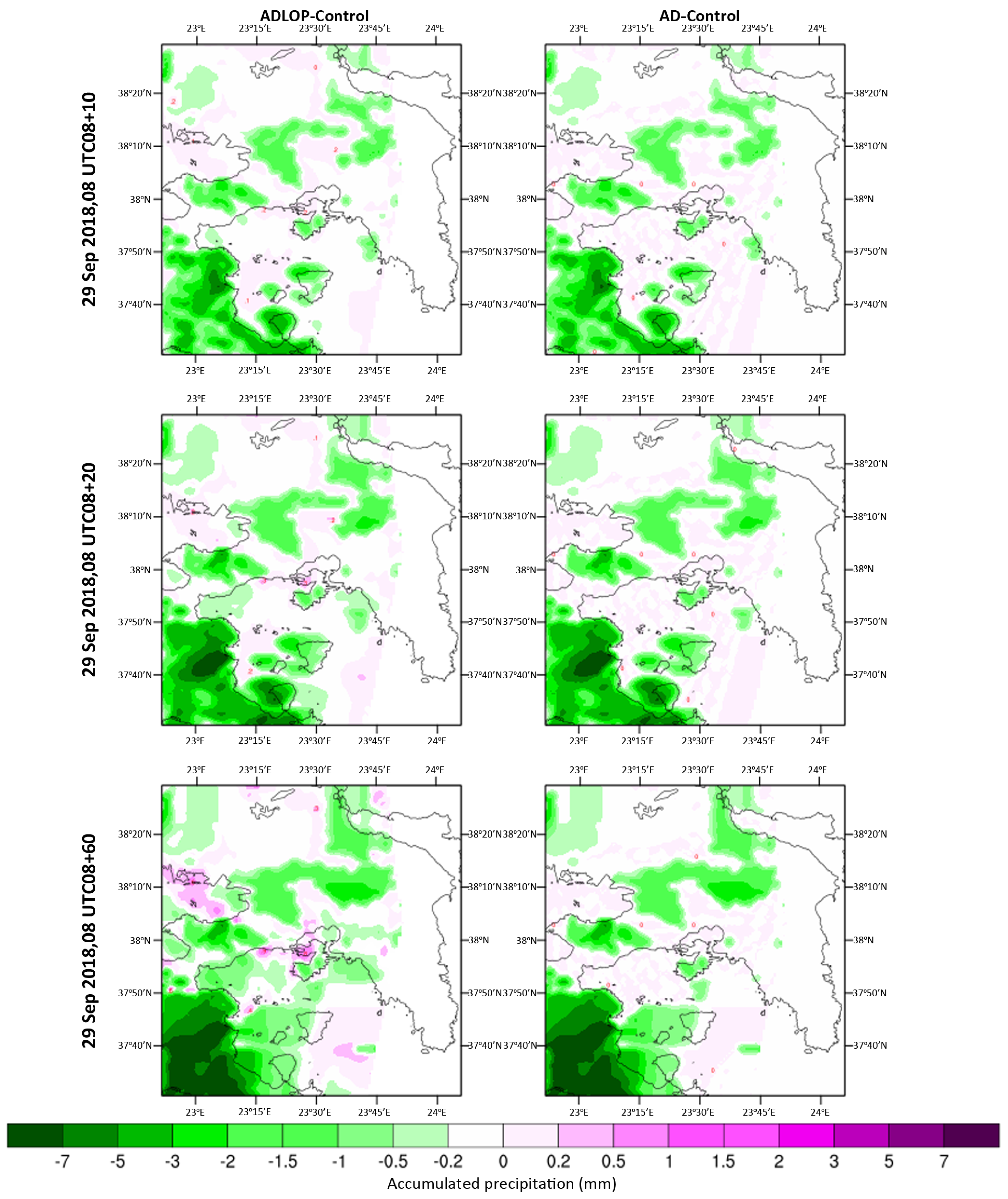
Figure 1 displays panel plots of 10 min differences in accumulated precipitation (in mm) for the LAPS nowcasts on 29 September 2018, at three forecast times: 08:10, 08:20, and 09:00 UTC. The left column displays the difference between the ADLOP scheme and the control scheme (ADLOP-Control), while the right column shows the difference between the AD scheme and the control scheme (AD-Control). In these plots, negative values (green shades) indicate areas where the enhanced schemes predict less precipitation than the control, whereas positive values (magenta shades) signify regions of higher predicted precipitation by the enhanced schemes. The introduction of the diffusion component in the AD scheme reduces the intensity of high-precipitation cores compared to the control scheme. This suggests an improved representation of the spreading of rainfall fields, a process not accounted for by the first-order advection scheme. Furthermore, the incorporation of the linear theory of orographic precipitation (LOP) in the ADLOP scheme further improves the spatial precipitation patterns by explicitly accounting for the influence of topography on rainfall distribution, particularly at longer lead times.

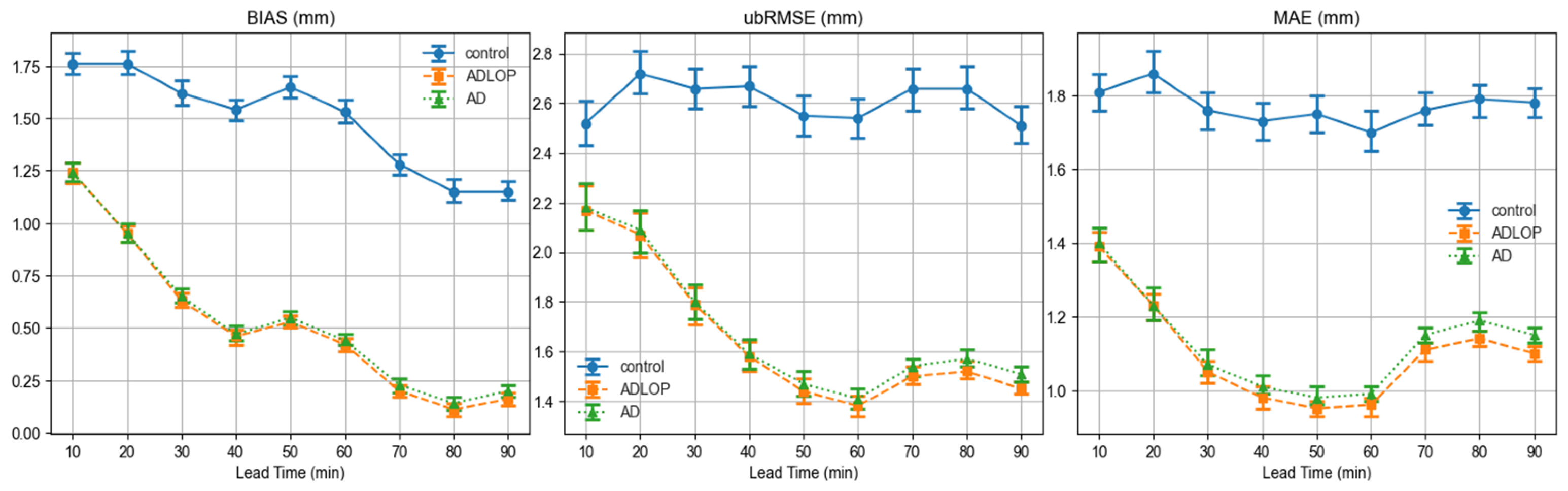
To assess the forecast skill, a comprehensive verification analysis was conducted using standard statistical metrics: BIAS, unbiased Root Mean Square Error (ubRMSE), and Mean Absolute Error (MAE). These metrics were computed for forecast lead times ranging from +10 to +90 min, with 10 min increments, by comparing each nowcasting scheme against the XPOL radar data that are not assimilated in LAPS (Figure 2).

Figure 2 (left column) depicts the BIAS scores. The control consistently overestimates precipitation across all lead times, starting at 1.76 mm at +10 min and decreasing to 1.15 mm at +90 min. The introduction of diffusion in the AD scheme significantly reduces the bias down to 0.2 mm at +90 min. The ADLOP scheme, which combines diffusion with the linear theory of orographic precipitation, produces similarly reduced bias values down to 0.16 mm at +90 min. The incorporation of diffusion, both with and without orographic dynamics, leads to a significantly more balanced nowcasting, with bias values decreasing approximately by over ≈71% relative to the first-order advection scheme at 60 min.

The ubRMSE scores are presented in the middle column of Figure 2. The ADLOP scheme (advection–diffusion integrated with linear theory of orographic precipitation) achieves the lowest ubRMSE scores throughout the forecast horizon, starting at 2.17 mm at +10 min and decreasing to 1.45 mm at +90 min. This performance reflects improved consistency and reduced random and structural errors. The AD scheme also outperforms the control, though it yields slightly higher scores than ADLOP across all lead times.

The MAE scores, shown in the right column of Figure 2, confirm the above findings: the ADLOP scheme produces the smallest errors throughout the forecast period. At +60 min, MAE is reduced from 1.7 mm in the control scheme to 0.96 mm in the ADLOP scheme—representing a ≈44% improvement. The AD scheme achieves a similar reduction at 0.99 mm—approximately a 42% improvement. This demonstrates that both schemes reflect their superior performance in capturing the spatial structure of precipitation fields. It should be noted that these findings are based on preliminary analyses.

4. Conclusions

This study presents preliminary evidence that physically enriched nowcasting schemes can enhance the accuracy of short-term precipitation forecasts compared to a first-order advection scheme, though further evaluation across diverse weather events is necessary to confirm broader applicability. The control scheme (first-order advection), while computationally efficient, exhibits systematic overestimation and lacks the physical complexity required to simulate the temporal and spatial evolution of precipitation fields.

The inclusion of a diffusion component (AD scheme) improves forecast performance by better representing the spatial spreading and smoothing of precipitation patterns. The most substantial improvements are achieved when linear orographic precipitation effects are included (ADLOP), which enhances the ability to capture localized intensification of rainfall due to terrain-induced uplift.

The verification metrics—BIAS, ubRMSE, and MAE—support the superiority of the enhanced approaches, with the ADLOP scheme achieving the lowest values across most time steps. Additionally, visual analysis also suggests that the enhanced schemes produce more physically realistic spatial distributions. These results affirm that incorporating diffusion and linear orographic precipitation mechanisms can lead to more accurate nowcasting systems. Additional experiments and sensitivity tests are in the authors’ near future plans.