Assessment of Moving Average (MA) Method for Rainfall Prediction in Yogyakarta, Indonesia †
Abstract
1. Introduction
2. Materials and Methods
2.1. Time Series Model
2.2. Model Evaluation
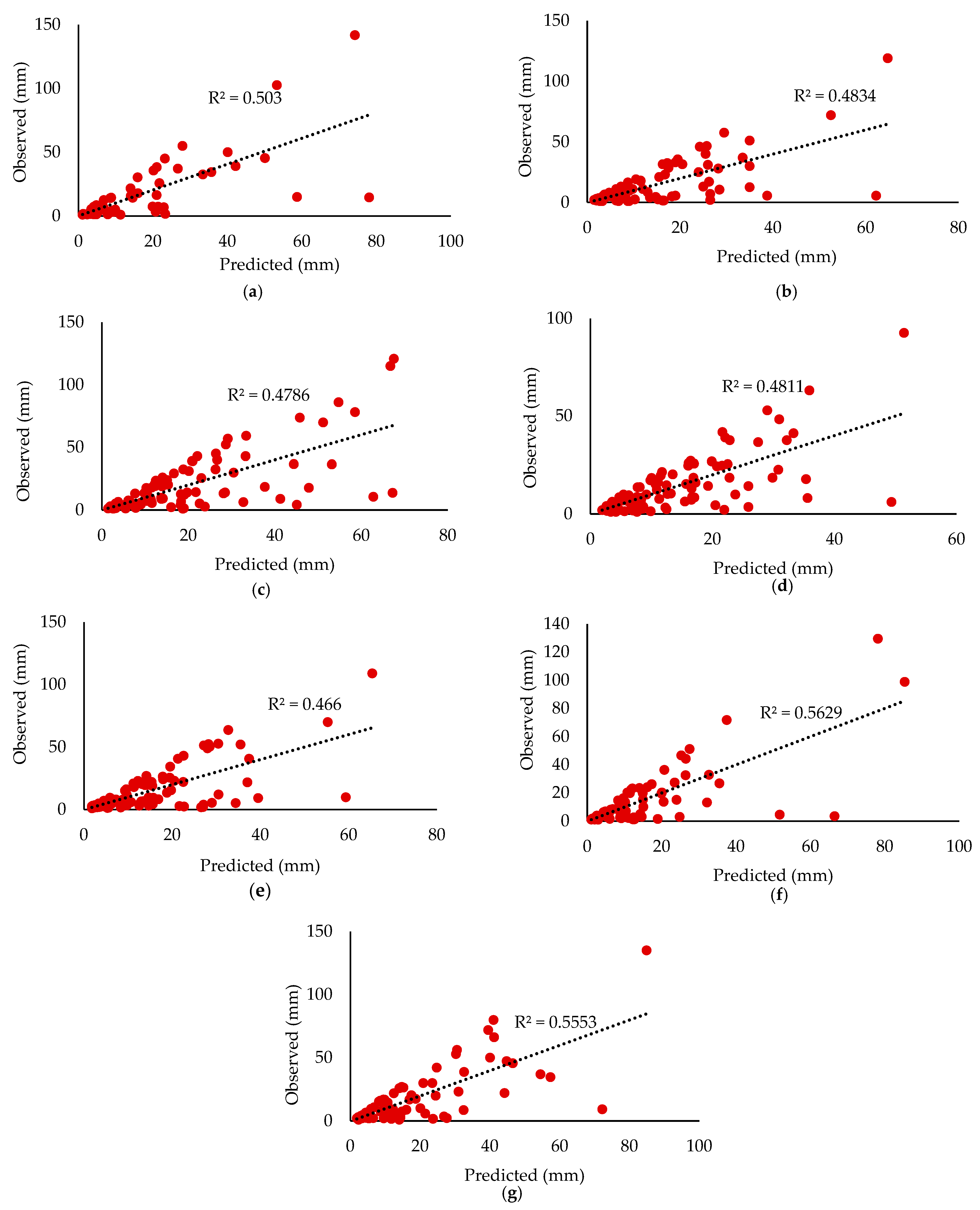
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Koerniawan, M.D. Recreation Park and Thermal Comfort: Site Measurement and Predictive Simulations in Assessment of Open Spaces in Taman Impian Jaya Ancol, Jakarta, Indonesia. In Proceedings of the 5th Yellow Sea Rim International Exchange Meeting on Building Environment and Energy 2010 (YSRIM), Yi Fu Building at Tongji University, Shanghai, China, 27 February–1 March 2010. [Google Scholar]
- As-syakur, A.R.; Tanaka, T.; Osawa, T.; Mahendra, M.S. Indonesian rainfall variability observation using TRMM multi-satellite data. Int. J. Remote Sens. 2013, 34, 7723–7738. [Google Scholar] [CrossRef]
- Saragih, I.J.A.; Rumahorbo, I.; Yudistira, R.; Sucahyono, D. Prediksi Curah Hujan Bulanan Di Deli Serdang Menggunakan Persamaan Regresi Dengan Prediktor Data Suhu Dan Kelembapan Udara. J. Meteorol. Klimatol. Geofis. 2021, 7, 6–14. [Google Scholar]
- Matei, M.; Raischi, M.; Ciobotaru, N.; Laslo, L.; Boboc, M.; Zamfir, A.S.; Deák, G. Flood Protective Measures in Divici–Pojejena Wetland, Caras-Severin County, Romania. J. Environ. Prot. Ecol. 2017, 18, 235–245. [Google Scholar]
- Nurfaida, W.; Ramdhani, H.; Shimozono, T.; Triawati, I.; Sulaiman, M. Rainfall trend and variability over Opak River basin, Yogyakarta, Indonesia. J. Civ. Eng. Forum 2021, 7, 109–120. [Google Scholar] [CrossRef]
- Barman, U.; Choudhury, R.D.; Hussain, A.E.; Dahal, M.J.; Barman, P.; Hazarika, M. Comparative Assessment of AR, MA and ARMA for the Time Series Forecasting of Assam and Meghalaya Rainfall Division. In Proceedings of the 2020 International Conference on Computational Performance Evaluation (ComPE), Shillong, India, 2–4 July 2020; pp. 507–511. [Google Scholar] [CrossRef]
- Saputro, D.R.S.; Mattjik, A.A.; Boer, R.; Wigena, A.H.; Djuraidah, A. Pendugaan Data Tidak Lengkap Curah Hujan Di Kabupaten Indramayu Dengan Kringing & Rata-rata Bergerak (Moving Average) Berdasarkan Data Tahun 1980–2000. In Proceedings of the Seminar Nasional Statistika Universitas Diponegoro 2011, Tembalang Semarang, Indonesia, 21 May 2011. [Google Scholar]
- Nurlifa, A.; Kusumadewi, S. Sistem Peramalan Jumlah Penjualan Menggunakan Metode Moving Average Pada Rumah Jilbab Zaky. INOVTEK Polbeng Seri Inform. 2017, 2, 18. [Google Scholar] [CrossRef][Green Version]
- Solver. Moving Average. 2016. Available online: https://www.solver.com/moving-average (accessed on 9 May 2022).
- Ul-Saufie, A.Z.; Yahya, A.S.; Ramli, N.; Hamid, H. Comparison Between Multiple Linear Regression and Feed forward Back propagation Neural Network Models For Predicting PM10 Concentration Level Based On Gaseous And Meteorological Parameters. Int. J. Adv. Sci. Technol. 2011, 1, 42–49. [Google Scholar]
- Mehdizadeh, S. Using AR, MA, and ARMA Time Series Models to Improve the Performance of MARS and KNN Approaches in Monthly Precipitation Modeling under Limited Climatic Data. Water Resour. Manag. 2020, 34, 263–282. [Google Scholar] [CrossRef]


| No | Stations | Coordinate | |
|---|---|---|---|
| Latitude | Longitude | ||
| 1 | Kedung Keris | 110.5946 | −7.86922 |
| 2 | Panggang | 110.4241 | −8.01411 |
| 3 | Ngawen | 110.7046 | −7.81578 |
| 4 | Playen | 110.5188 | −7.90919 |
| 5 | Tepus | 110.6258 | −8.1055 |
| 6 | Wanagama | 110.5308 | −7.89597 |
| 7 | Gedangan | 110.5809 | −7.80728 |
| Performance Indicators | Equation | Better Predictability if |
|---|---|---|
| Mean Absolute Error (MAE) | MAE = (2) | Closer to 0 |
| Normalised Absolute Error (NAE) | NAE = (3) | Closer to 0 |
| Root Mean Square Error (RMSE) | (4) | Closer to 0 |
| Index of Agreement (IA) | IA = (5) | Closer to 1 |
| Prediction Accuracy (PA) | PA = (6) | Closer to 1 |
| Coefficient of Determination (R2) | R2 = (7) | Closer to 1 |
| Panggang | Gedangan | Kedung Keris | Ngawen | Wanagama | Tepus | Playen | |
|---|---|---|---|---|---|---|---|
| Valid (frequency) | 3650 | 3650 | 3285 | 3650 | 3650 | 2921 | 2190 |
| Missing (frequency) | 0 | 0 | 365 | 0 | 0 | 729 | 1460 |
| Mean (mm) | 5.418 | 5.136 | 5.609 | 4.355 | 5.673 | 4.316 | 5.636 |
| Median (mm) | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Standard Deviation (mm) | 15.012 | 12.596 | 14.376 | 10.797 | 14.319 | 14.094 | 24.936 |
| Minimum (mm) | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Maximum (mm) | 285.20 | 265.50 | 277.60 | 190.70 | 264.20 | 211.80 | 560.00 |
| PI | Panggang | Gedangan | Kedung Keris | Ngawen | Wanagama | Tepus | Playen | Barman et al. [6] | Mehdizadeh [11] |
|---|---|---|---|---|---|---|---|---|---|
| MAE (mm) | 10.475 | 8.772 | 12.211 | 7.115 | 9.702 | 8.350 | 9.595 | 121.97 | 5.01 |
| NAE | 0.552 | 0.587 | 0.580 | 0.498 | 0.603 | 0.546 | 0.527 | - | - |
| RMSE (mm) | 18.278 | 13.748 | 17.420 | 10.721 | 14.023 | 14.291 | 15.135 | 150.41 | 6.58 |
| PA | 0.709 | 0.695 | 0.692 | 0.694 | 0.683 | 0.750 | 0.745 | - | - |
| IA | 0.806 | 0.803 | 0.799 | 0.801 | 0.794 | 0.846 | 0.840 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jamal, N.A.; Mohamed Noor, N.; Jafri, I.A.M.; Wibowo, G.J. Assessment of Moving Average (MA) Method for Rainfall Prediction in Yogyakarta, Indonesia. Environ. Earth Sci. Proc. 2025, 33, 5. https://doi.org/10.3390/eesp2025033005
Jamal NA, Mohamed Noor N, Jafri IAM, Wibowo GJ. Assessment of Moving Average (MA) Method for Rainfall Prediction in Yogyakarta, Indonesia. Environmental and Earth Sciences Proceedings. 2025; 33(1):5. https://doi.org/10.3390/eesp2025033005
Chicago/Turabian StyleJamal, Nur Ain, Norazian Mohamed Noor, Izzati Amani Mohd Jafri, and Gurawan Jati Wibowo. 2025. "Assessment of Moving Average (MA) Method for Rainfall Prediction in Yogyakarta, Indonesia" Environmental and Earth Sciences Proceedings 33, no. 1: 5. https://doi.org/10.3390/eesp2025033005
APA StyleJamal, N. A., Mohamed Noor, N., Jafri, I. A. M., & Wibowo, G. J. (2025). Assessment of Moving Average (MA) Method for Rainfall Prediction in Yogyakarta, Indonesia. Environmental and Earth Sciences Proceedings, 33(1), 5. https://doi.org/10.3390/eesp2025033005







