Comprehensive Review of Metrics and Measurements of Quantum Systems

Abstract

Quantum computing promises to offer significant computational advantages over classical computing, leveraging principles such as superposition and entanglement. This necessitates effective metrics and measurement techniques for evaluating quantum systems, aiding in their development and performance optimization. However, due to fundamental differences in computing paradigms and current immaturity of quantum software abstractions, classical software and hardware metrics may not directly apply to quantum computing, where the distinction between software and hardware can still be somewhat indiscernible compared to classical computing. This paper provides a comprehensive review of existing quantum software and hardware metrics in the scientific literature, highlighting key challenges in the field. Additionally, it investigates the application of Functional Size Measurement (FSM), based on the COSMIC ISO 19761 FSM Method, to measure quantum software. Three FSM approaches are analyzed by applying them to Shor’s and Grover’s algorithms, with measurement results compared to assess their effectiveness. A comparative analysis highlights the strengths and limitations of each approach, emphasizing the need for further refinement. The insights from this study contribute to the advancement of quantum metrics, especially software metrics and measurement, paving the way for the development of a unified and standardized approach to quantum software measurement and assessment.

1. Introduction

Quantum computing promises unprecedented computational advantages and speedups over classical computing, leveraging principles such as superposition and entanglement [1]. These capabilities enable quantum computers to solve certain problems exponentially faster than their classical counterparts. As quantum hardware advances at a rapid pace, it becomes increasingly essential to develop robust, efficient, and reliable quantum software [2]. To achieve this, effective metrics, measurement (unless stated otherwise, Measurements in this paper does not refer to the measurement of a quantum particle, but rather refers to concepts related to measuring the size and attributes of a quantum system) methods and tools to evaluate quantum software. Thus, understanding how to assess quantum software is crucial for the future of quantum computing.

Computer hardware metrics are essential for evaluating system performance, diagnosing issues, and optimizing resource utilization in classical computing environments ranging from personal computers to large-scale data centers. These metrics include CPU usage, memory consumption, disk I/O, network throughput, temperature, power consumption, and GPU load, all of which help ensure system reliability, security, and efficiency [3]. Among these, execution time—the duration a system takes to complete a specific task—is a crucial performance indicator that directly impacts efficiency in software execution, real-time processing, and benchmarking. Execution time is influenced by several factors, including CPU clock speed, core count, cache size, RAM speed, disk type, and instruction set architecture, making it a key metric in high-performance computing and energy-efficient system design [4]. By utilizing profiling tools like Intel VTune, NVIDIA Nsight, or benchmarking software, developers and system administrators can analyze execution time to improve system responsiveness, reduce power consumption, and enhance user experience in applications ranging from gaming to artificial intelligence [5].

Transitioning from classical hardware metrics to quantum systems, Quantum hardware is evaluated today using a range of performance metrics that determine its computational capability and practical limitations. For example, Quantum Volume (QV), introduced by IBM, measures a quantum system’s overall capability by considering factors such as gate fidelity, qubit connectivity, and circuit depth, providing a standardized benchmark for comparing different quantum processors [6]. Circuit Layer Operations Per Second (CLOPS) assesses the speed at which a quantum processor can execute quantum circuits, reflecting its real-time computational efficiency [7]. Another crucial metric, qubit coherence time, represents the duration a qubit retains its quantum state before decoherence, which directly impacts the feasibility of running deep quantum circuits [8]. Gate fidelity quantifies the accuracy of quantum gate operations by comparing their actual performance against ideal theoretical models, ensuring the reliability of quantum computations [9]. Additionally, error rates measure noise levels that introduce inaccuracies in quantum calculations, affecting the stability and precision of quantum algorithms [10]. Collectively, these metrics shape our understanding of quantum processor capabilities and their suitability for various quantum algorithms.

Software metrics provide a mathematical framework for mapping the entities of a software system to numerical values [11]. These metrics allow for the assessment of classical software systems by extracting relevant entities and calculating corresponding metric values. A software metrics tool implements these metric definitions, facilitating automated evaluations.

The term “software metrics” encompasses a wide range of activities related to measurement in software engineering. These activities include generating numbers that characterize properties of software code, developing models that predict software resource requirements and quality, and quantifying aspects of quality control and assurance, such as recording and monitoring defects during development and testing. While software metrics offer many benefits, their most significant contribution lies in providing information to support managerial decision-making during the software development phase [12].

However, applying classical software metrics to quantum systems presents unique challenges due to the distinct nature of quantum computing. It is unclear how well classical methods can be adapted to quantum contexts, or whether entirely new metrics should be developed. The core challenge stems from quantum phenomena like superposition, entanglement, and quantum interference, which introduce complexities absent in classical computing. These fundamental properties introduce complexities that diverge from classical computing paradigms [9,13], necessitating novel approaches to software measurement. Furthermore, the rapidly evolving landscape of quantum hardware, coupled with resource constraints and scalability issues, further complicates the task of assessing quantum software performance [14].

Measurement in software engineering has traditionally served as a vital tool for evaluating performance, complexity, and maintainability, enabling developers to ensure the quality and efficiency of their systems [15,16,17]. These metrics allow for the quantitative assessment of aspects such as code size, maintainability, and system performance, helping developers to predict software behavior and optimize system functionality. However, these classical software metrics often fall short when applied to quantum software due to the fundamental differences in architecture, computation, and execution models [18,19]. As a result, there is an emerging need to establish a dedicated framework for quantum software measurement, which can cater to these distinctive features.

Current research in this field remains in its infancy, with scholars like Sicilia et al. (2022) [18] emphasizing the lack of comprehensive approaches for measuring quantum software artifacts and processes. Without well-defined metrics, developers and researchers are left without the tools to assess the effectiveness of quantum programs, hindering progress in this rapidly evolving domain. Furthermore, Zhao [19] argues for the development of size and structure metrics specifically designed for quantum software, which can enable more precise and structured evaluations across different levels of software abstraction.

Functional Size Measurement (FSM) is a standardized approach used in software engineering to quantify the functional requirements of a system based on the services it provides to its users. FSM evaluates software by assessing its functionality from the user’s perspective, focusing on what the software does rather than how it is implemented. The functional size is typically expressed in function points, a unit that enables developers and project managers to estimate project scope, cost, and size in a technology-independent manner [20]. FSM has been formalized in various international standards, including COSMIC ISO 19761 [21], which is recognized for its applicability across a wide range of software types and domains [22]. By providing a consistent measure, FSM allows for accurate benchmarking, project estimation, and performance evaluation, helping to improve software development practices and outcomes. To date, only three significant studies [23,24,25] have explored the use of functional size measurement techniques tailored to quantum software. All three studies were based on the COSMIC method—ISO 19761 [22], a well-established functional size measurement approach for classical software, and have sought to adapt this classical measurement approach to the unique characteristics of quantum systems.

This paper aims to explore the multifaceted challenges in quantum software measurement as documented in the scientific literature. Throughout this exploration, we investigate current methodologies, metrics, and tools for quantum software measurement, discussing their implications for software assessment. Furthermore, we address the challenges that arise due to the different nature of quantum computers, highlighting opportunities for innovation and enhancement. In addition, we apply three COSMIC-based Functional Size Measurement approaches to different quantum algorithms: Shor’s algorithm [26] for factoring, Grover’s algorithm [27] for search. By comparing the results across these diverse quantum algorithms, we aim to assess the applicability and limitations of each measurement approach.

The paper is structured as follows: Section 2 provides overviews of classical hardware and software metrics and measurements as a comparative and conceptual bridge to quantum systems. Section 3 examines quantum metrics discussed in the scientific literature. Section 4 explores the challenges in developing quantum software metrics. Section 5 focuses on COSMIC-based measurement approaches for quantum software. Finally, Section 6 presents conclusions and future directions.

2. Overview of Classical Computer Metrics

This section does not aim to provide a comprehensive survey of classical computing metrics, measurements, or tools. Instead, it offers an illustrative overview that supports the main focus of the paper: quantum metrics and measurements and their development. The inclusion of classical metrics serves a twofold purpose. First, it assists readers who come from classical computing backgrounds in transitioning their understanding to quantum systems, using familiar benchmarks and evaluation methods. Second, it offers quantum computing practitioners a set of conceptual analogies and historical precedents from the well-established classical domain, helping to envision what future metrics and measurement practices in quantum computing might look like.

2.1. Classical Hardware Metrics

Classical hardware (HW) metrics serve as fundamental indicators for assessing computing system performance, resource efficiency, and reliability. These metrics enable system designers, engineers, and administrators to monitor and optimize both hardware and software interactions, ensuring optimal functionality across various computing environments [3].

Understanding these metrics is valuable in the context of quantum systems, especially since many early quantum algorithms are executed within hybrid classical-quantum workflows. Furthermore, metrics like CLOPS (Circuit Layer Operations Per Second) and QPack draw conceptual parallels with classical notions of throughput, utilization, and execution speed.

• CPU Utilization: Reflects how effectively a processor executes active threads, with implications for energy efficiency and task scheduling [28].
• Memory Usage: Indicates the proportion of RAM consumed by active processes, directly affecting program execution speed and concurrency [4].
• Disk I/O Throughput: Measures the rate of data transfer to/from storage media. High-performance data-driven applications (e.g., simulators for quantum algorithms) rely on efficient disk I/O [29].
• Network Throughput and Latency: Quantify data transfer rates and delays across communication channels—relevant for distributed quantum-classical systems and cloud-based quantum computing [30].
• Power Consumption and Thermal Metrics: Important for sustaining high-performance computing tasks and ensuring thermal stability, which is also a concern in cryogenically cooled quantum devices [31].
• Cache Hit/Miss Rate: Influences instruction execution time and latency. Optimization of cache behavior is central in minimizing memory-bound bottlenecks in simulators and QPU controllers [3].
• Instruction Per Cycle (IPC): Used to estimate the instruction throughput per clock cycle. High IPC correlates with efficient use of processor pipelines and can guide workload scheduling across CPU-GPU-accelerator configurations [4].
• GPU Load (Cross-Vendor): Tracks the utilization of graphics and general-purpose processing units. In addition to NVIDIA Nsight [32], platforms like AMD’s Radeon GPU Profiler [33] and cross-platform tools such as CodeXL [34] offer comprehensive insights for heterogeneous systems.

Measurement Techniques and Tools

To obtain these metrics, developers rely on a suite of profiling and diagnostic tools, including both vendor-specific and open-source options. These tools are relevant not only for performance benchmarking but also for informing the architectural co-design of classical and quantum processing units.

• Intel VTune Profiler: A detailed performance analysis tool for CPU-bound workloads, providing insights into threading, memory access, and vectorization [35].
• NVIDIA Nsight Systems: Focuses on GPU utilization, kernel launch efficiency, and memory transfer bottlenecks [32].
• AMD Radeon GPU Profiler: Provides detailed analysis of shader and compute workloads for AMD GPUs, supporting real-time bottleneck identification [33].
• CodeXL (AMD): A now-deprecated but historically important open-source tool for profiling heterogeneous systems combining CPU and GPU workloads [34].
• Sysprof (Linux): A system-wide Linux profiler that integrates with the GNOME environment, offering low-overhead tracing and per-process breakdowns useful in hybrid performance scenarios [36].
• Perf (Linux): A command-line profiling tool for tracking system calls, context switches, CPU cycles, and cache behavior [5].

These tools, along with the metrics they compute, have directly inspired and shaped the development of emerging quantum performance measures. For example, CLOPS mirrors classical throughput metrics, while thermal and energy usage benchmarks carry over to cryogenic control systems in superconducting qubit platforms. Consequently, an understanding of classical HW profiling remains essential for designing scalable, efficient, and interoperable quantum-classical architectures.

2.2. Classical Software Metrics

In software engineering, for classical computers, metrics and measurements play a crucial role in evaluating the quality [14], complexity [37], and maintainability [38] of software systems. By quantifying various attributes of software artifacts, metrics provide valuable insights into the development process and facilitate informed decision-making. This introduction aims to elucidate the fundamental concepts of major classical software metrics and measurement techniques, laying the groundwork for understanding their significance in software development practices.

At its core, software metrics encompass quantitative measures used to assess different aspects of software products, processes, and resources. These metrics serve as objective indicators of software quality and performance, enabling stakeholders to monitor progress, identify potential risks, and prioritize improvement efforts. By applying systematic measurement techniques [39], software engineers can gain valuable insights into the characteristics and behavior of software systems, ultimately leading to more effective software development and management practices.

The literature review on software metrics encompasses various dimensions, including product metrics, process metrics, and resource metrics. Product metrics focus on evaluating the properties and characteristics of software artifacts, such as code complexity, size, and cohesion [19]. Process metrics, on the other hand, assess the efficiency and effectiveness of software development processes [23,25], providing insights into factors such as productivity, cycle time, and defect density. Resource metrics quantify the resources expended during software development, including time, effort, and cost.

Among the multitude of software metrics available, several key metrics have emerged as foundational components of software measurement. These metrics address critical aspects of software quality and performance, serving as essential tools for software engineers and project managers alike. Some of the major classical software metrics are lines of code (LOC), cyclomatic complexity, coupling and cohesion measures, and defect density [19].

2.3. Functional Size Measurement

Functional size measurement methods focus on quantifying the functional requirements of software systems, providing a standardized way to measure the size of software functionalities [40]. Unlike traditional lines of code-based metrics, functional size measurement methods assess software size based on the functionality delivered to users rather than the implementation details. This approach enables a more accurate and objective assessment of software size and effort estimation [41].

A second-generation functional size measurement method is the COSMIC (Common Software Measurement International Consortium) method–ISO 19761, which focuses on measuring the functional size of software from a user’s perspective. COSMIC measures functional size regarding functional user transactions, representing discrete interactions between the user and the software system. By quantifying these transactions and considering factors such as data movements and processing logic, COSMIC provides a robust measure of software size independent of implementation technologies [41].

Other functional size measurement methods, such as NESMA (Netherlands Software Metrics Association) Function Point Analysis and Mark II, offer alternative approaches to quantifying software size based on functional requirements and user interactions [42].

By understanding the basic concepts of these major classical software metrics and measurement techniques, software professionals can enhance their ability to assess and improve software quality, productivity, and maintainability. Through the systematic application of software metrics, organizations can optimize their software development processes, mitigate risks, and deliver higher-quality software products to meet the evolving needs of stakeholders and users.

Although not comprehensive, the classical software and hardware metrics and measurements of this section are not included as isolated historical references, but as conceptual and structural blueprints from which meaningful quantum metrics and measures can be derived.

3. Related Work on Quantum Metrics and Measurements

Over the past decade, researchers have introduced a variety of approaches to measure the performance of both quantum hardware and software. This section highlights key quantum metrics and benchmarking frameworks found in the literature, alongside performance evaluation strategies that offer crucial insights into the broader landscape of quantum system assessment. The authors of these works propose essential methodologies, standardized guidelines, and curated metric collections that collectively contribute to defining, evaluating, and advancing quantum performance assessment.

These benchmarking protocols span multiple layers of the quantum stack—from individual components to integrated systems—and often incorporate considerations for hardware-agnostic implementation, statistical soundness, and reproducibility. Moreover, in addition to focusing on hardware and systems, several studies extend their contributions to quantum software engineering by addressing challenges in project estimation, management strategies, and predictive modeling. These works introduce tailored tools and frameworks that help practitioners navigate the unique demands of quantum software development, such as metric selection, estimation accuracy, and agile project success.

Together, the studies reviewed in this section underscore the increasing need for robust and scalable evaluation methodologies that can support the fair comparison, efficient planning, and strategic execution of quantum computing initiatives across both hardware and software domains. Nevertheless, most of the metrics and measurements in this Section are specific to analyzing system properties such as size, performance, scalability, and related characteristics. However, there exists, one might argue, a crucial test [43] that could be considered a metric as well. This test, which is device-independent, certifies whether the system is indeed quantum. For instance, if a company claims to offer a Quantum Random Number Generator (QRNG) device, this test would verify whether the device truly harnesses the intrinsic uncertainties of quantum mechanical systems to generate randomness, rather than relying on classical processes.

3.1. Quantum Hardware Metrics

Quantum hardware performance is commonly evaluated using a set of benchmark metrics. Most of the metrics in the scientific literature are in the Noisy Intermediate-Scale Quantum (NISQ) era; these metrics assess the raw capabilities of quantum processors without active error correction. However, for long-term scalability, fault-tolerant quantum computing (FTQC) introduces additional metrics crucial for characterizing systems capable of robust quantum error correction.

Quantum Volume (QV) [6,44] is a measure that focuses on low-level, hardware-related aspects of quantum devices. QV is used to benchmark noisy intermediate-scale quantum devices (NISQ) by taking into account all relevant hardware parameters: performance and design parameters. It also includes the software behind circuit optimizations and is architecture-independent, that is, it can be used on any system that can run quantum circuits. It quantifies the largest square quantum circuit—where the number of qubits in the circuit equals the number of gate layers—that a device can successfully implement with high fidelity. To determine a device’s quantum volume, randomized square circuits of increasing size are generated, where each layer consists of a random permutation of qubit pairs followed by the application of random two-qubit gates. These circuits are compiled according to the hardware constraints and executed repeatedly to evaluate the heavy output probability, which is the likelihood of measuring outcomes that occur more frequently than the median output in the ideal distribution. A circuit size is considered successfully implemented if this probability exceeds ${\displaystyle \frac{2}{3}}$ on average. The quantum volume is then defined as $2^n$ where n is the largest square circuit that meets this criterion. It is intended to be a practical way of measuring progress towards improved gate error rates in near-term quantum computing.

Another hardware benchmark is the Circuit Layer Operations per Second (CLOPS) [7], which is more concerned with the performance of a Quantum Processing Unit (QPU). Wack et al. [7] identified three key attributes for quantum computing performance: quality, scale, and speed. Quality is the size of a quantum circuit that can be faithfully executed and is measured by the mentioned QV metric. Scale is measured by the number of qubits in the system. And for the Speed attribute, measuring CLOPS is introduced. The CLOPS measure is a derived one and is calculated as the ratio of the total number of QV layers executed to the total execution time. In general, the CLOPS benchmark is a speed benchmark that is designed to allow the system to leverage all quantum resources on a device to run a collection of circuits as fast as possible.

Qpack Scores, presented by Donkers et al., 2022 [45], is another benchmark that aims to be application-oriented and cross-platform for quantum computers and simulators. It provides a quantitative insight into how well Noisy Intermediate Scale Quantum (NISQ) systems can perform. In particular, systems that make use of scalable Quantum Approximate Optimization Algorithm (QAOA) and Variational Quantum Eigensolver (VQE) applications. QPack scores comprise different sub-scores. The need for sub-scores arose from the fact that some quantum computers may be fast but inaccurate, while other systems are accurate but have longer execution times, which led to the realization that quantum systems cannot be benchmarked solely on a single factor. Qpack combines the following 4 sub-scores to form the overall sub-score. Runtime, Accuracy, Scalability, and Capacity. Runtime calculates the average execution time of quantum circuits on quantum computers. The Accuracy sub-score measures how close the actual outcome of an execution compares to an ideal quantum computer simulator. Scalability provides insight into how well the quantum computer can handle an increase in circuit sizes. Finally, the Capacity score indicates how usable the qubits in a quantum computer are compared to the actual number of qubits provided. These benchmarks are run on different quantum computers using the cross-platform library LibKet, which allows for the collection of quantum execution data to be used as a performance indicator.

Another study, Ref. [46], attempts to quantify environmentally induced decoherence in quantum systems, which is another important factor affecting the amount of error in quantum measurements. In particular, Fedichkin et al. [46] tackled the problem from a physics and a mathematical point of view, exploiting approaches based on the asymptotic relaxation time scales and fidelity measures of decoherence, ultimately formulating an approach to measure the deviation of the actual density matrix, from the ideal one describing the system without considering environmental interactions.

In “A Functional Architecture for Scalable Quantum Computing” Sete et al. 2016 [47] presented a functional architecture for superconducting quantum computing systems as well as introduced the total quantum factor (TQF) as a performance metric for a quantum processor. To calculate TQF, the average coherence time of all qubits on the chip is divided by the longest gate time in the qubits’ universal set and is then multiplied by the number of qubits. TQF gives rough estimates of the size of the quantum circuit that can be run before the processor’s performance decoheres.

While Quantum Volume (QV), CLOPS, QPack, and related metrics offer vital insights into NISQ systems, a comprehensive evaluation of quantum hardware requires the inclusion of fault-tolerant quantum computing (FTQC) metrics, which are essential for future-ready, scalable architectures. FTQC leverages quantum error correction codes to encode logical qubits using multiple physical qubits, enabling computations that can be arbitrarily long despite hardware imperfections.

As quantum computing advances beyond the Noisy Intermediate-Scale Quantum (NISQ) era, fault tolerance becomes essential to achieving large-scale, reliable computation. In this context, several new metrics have been proposed that assess the hardware readiness of systems under fault-tolerant quantum computing (FTQC) models.

The “logical error rate” is a key metric that quantifies the probability of a logical qubit incurring an error during an operation. Unlike physical qubit errors, logical error rates are suppressed through quantum error correction and can be exponentially reduced by increasing the resources used for encoding. Logical qubits are typically constructed using error-correcting codes such as the surface code, and achieving a sufficiently low logical error rate is a prerequisite for scalable quantum computation [48,49].

Another essential metric is the code distance, which denotes the minimum number of physical qubit errors required to cause a logical error. For example, in a surface code of distance d, up to $\lfloor {\displaystyle \frac{d-1}{2}}\rfloor$ errors can be corrected. Larger code distances result in lower logical error rates but also increase the physical qubit overhead. Code distance plays a crucial role in determining how many physical qubits are needed to achieve target error suppression levels [50,51].

Resource overhead is another central consideration in fault-tolerant systems. It refers to the ratio between physical and logical qubits and includes all ancillary components required for error correction, such as syndrome qubits and magic state factories. Studies have shown that realizing a single logical qubit in practical fault-tolerant architectures often requires thousands of physical qubits, depending on the underlying code and target error rates [52,53].

A further challenge lies in the cost of implementing non-Clifford operations, particularly the T gate. While Clifford gates such as H, S, and CNOT are easier to realize fault-tolerantly, T gates require special procedures such as magic state distillation, which are resource-intensive. As a result, T-count (the total number of T gates) and T-depth (the depth of T gates in a circuit) have become widely adopted performance metrics for estimating the practicality of quantum algorithms in FTQC systems [54,55].

FTQC architectures also rely on maintaining physical error rates below a certain threshold—typically around ${10}^{-3}$—to ensure that error correction codes function effectively. This threshold, known as the fault-tolerance threshold, marks the regime in which increasing code distance leads to exponentially lower logical error rates. Hardware that fails to meet this criterion cannot scale using current fault-tolerant strategies [50,56].

To complement circuit-level metrics, system-level evaluations such as space-time volume are used to assess the scalability of a quantum processor. This metric quantifies the total resources consumed by a quantum computation as the product of the number of physical qubits and the execution time. It is particularly useful for estimating the real-world cost of executing large quantum algorithms in a fault-tolerant regime [48].

Table 1. Summary of Hardware Metrics for NISQ and Fault-Tolerant Quantum Computing.

Metric	NISQ Era (Present)	FTQC Era (Scalable Future)
Quantum Volume (QV)	Measures largest square circuit executable with fidelity $>{\displaystyle \frac{2}{3}}$ [6]	Not meaningful due to assumption of high-noise regimes
CLOPS	Circuit execution rate across qubit layers [7]	Not defined for logical circuits; replaced by space-time metrics
QPack	Combines runtime, accuracy, scalability, and capacity across QAOA/VQE [45]	Application-level metric, limited by lack of error correction
TQF	Coherence-based approximation for circuit size limits [47]	Informative only without error correction
Decoherence Metrics	Environment-induced fidelity loss [46]	Replaced by logical error suppression models
Logical Error Rate (${ϵ}_L$)	Not applicable	Probability of error per logical gate after encoding [48,49]
Code Distance (d)	Not applicable	Minimum number of errors needed to corrupt logical state [50,51]
Physical-to-Logical Qubit Ratio	Not used	Key metric for evaluating encoding overhead [52,53]
T-count/T-depth	Not needed in NISQ circuits	Critical cost metric for non-Clifford operations [54,55]
Threshold Error Rate	Not applicable	Upper bound on physical error for scalable fault tolerance [56]
Space-Time Volume	Not used	Total resources = qubits × time [48]

provides a comparative overview of hardware performance metrics relevant to both present-day Noisy Intermediate-Scale Quantum (NISQ) systems and future fault-tolerant quantum computing (FTQC) architectures. It highlights the shift in evaluation focus from near-term metrics such as Quantum Volume, CLOPS, and QPack, which emphasize raw circuit execution capabilities and hardware-software integration, to long-term, scalability-centric metrics like logical error rate, code distance, and T-count, which account for error correction overhead and fault-tolerant design constraints. This contrast underscores the evolving landscape of quantum benchmarking as systems move from experimental prototypes toward practical, error-resilient computing platforms.

3.2. Quantum Software Metrics

Jianjun Zhao, in “Some Size and Structure Metrics for Quantum Software” [19], proposed some extensions of classical software metrics into quantum software metrics. Zhao first considered some Basic Size metrics. These metrics include Code Size, Design Size, and Specification Size. An example of Code Size metrics includes Lines of Code (LOC), which is the most commonly used metric of source code program length. Secondly, for Design Size metrics, Zhao proposed the usage of quantum architectural description language (qADL) as an extension to classical architectural description language (ADL) to formally specify the architectures of a quantum software system. For the Specification Size metric, Zhao referred to Quantum Unified Modeling Language (Q-UML) as an extension to the general purpose, well-known Unified Modeling Language (UML). Basic Structure metrics were also considered. Examples include McCabe’s Complexity Metric, as well as Henry and Kafura’s information flow Metric.

Finžgar et al. [57] introduced QUARK. The QUARK framework aims to facilitate the development of application-level benchmarks. Written in Python 3.12, it aims to be modular and extensible. The architecture of the framework comprises 5 components. Benchmark Manager, which orchestrates the execution of the benchmark. Application, which defines the workload, validation, and evaluation function. Mapping translates the application data and problem specification into a mathematical formulation that is suitable for a solver. The solver is responsible for finding feasible and high-quality solutions to the proposed problem. And Device, which is the quantum device that the problem would be run on. After executing the benchmarks, QUARK collects the generated data and executes the validation and evaluation functions. In general, it tries to ensure the reproducibility and verifiability of solutions by automating and standardizing benchmarking systems’ critical parts.

In their endeavor to enhance the comprehensibility and accessibility of quantum circuits, J. A. Cruz-Lemus et al. [58] introduce a set of metrics that are categorized into distinct classes. The initial classification concerns circuit size, delineating circuit width as the number of qubits and circuit depth as the maximal count of operations on a qubit. Subsequently, the concept of circuit density is introduced, quantified by the number of gates applied at a specific step to each qubit, with metrics encompassing maximum density and average density. Further classifications pertain to the number of gates within the circuit, commencing with single-qubit gates. Within this domain, metrics are proposed to enumerate the quantity of Pauli X, Y, and Z gates individually, alongside their collective count, the quantity of Hadamard gates, the proportion of qubits initially subject to said gates, the count of other gates, and the aggregate count of single-qubit gates. Moving forward, the authors introduce metrics to calculate the average, maximal quantity, and ratio of CNOT and TOFFOLI gates applied to qubits, in addition to their collective counts, as of multi-qubit gates. Aggregate metrics are composed of the total count of gates, the total count of controlled gates, and the ratio of single gates to total gates. Furthermore, oracles and controlled oracles are addressed, wherein their counts, averages, and maximal depths are identified, along with the ratio of qubits influenced by them. Lastly, measurements are addressed, highlighting the quantity and proportion of qubits measured, alongside the percentage of ancilla qubits utilized. The authors emphasize the need for validating this set of metrics to ascertain their comprehensiveness. Notably, the authors refrain from providing explicit elucidation on how these metrics may enhance the understandability of quantum circuits.

Martiel et al. [59] introduce the Atos Q-score, a benchmark designed to evaluate the performance of quantum processing units (QPUs) in solving combinatorial optimization problems. The Q-score is application-centric, hardware-agnostic, and scalable, providing a measure of a processor’s effectiveness in solving the MaxCut problem using a quantum approximate optimization algorithm (QAOA). The objective of the MaxCut problem is to identify a subset S of the vertex set of a graph in a way that maximizes the count of edges connecting S with its complement. The authors assess the Q-score, which involves running the QAOA for a MaxCut instance and evaluating its performance in both noisy and noise-free systems. They later mention that the Q-score can be used to assess the effectiveness of the software stack. Additionally, the authors discuss the scalability of the Q-score and its potential applications for tracking QPU performance as the number of qubits and problem sizes increase. Furthermore, they introduce an open-source Python package for computing the Q-score, offering a useful resource for researchers and developers to measure the Q-score of any QPUs integrated with the library.

Ghoniem et al. [60] aimed at measuring the performance of a quantum processor based on the number of quantum gates required for various quantum algorithms. Experimental evaluations were conducted on nine IBM back-end Quantum Computers, employing four different algorithms: a 5-Qubit entangled circuit algorithm, a 5-Qubit implementation of Grover’s quantum search algorithm, a 5-Qubit implementation of Simon’s quantum algorithm, and the 7-Qubit implementation of Steane’s error correction quantum algorithm. Additionally, quantitative data on the number of quantum gates after the transpilation process using the default and maximum optimization settings were collected. This facilitated the analysis of how the availability and compatibility of different gate sets impact the total number of quantum gates needed for executing the various quantum algorithms. The default optimization level led to fewer gates in all algorithms except Simon’s. Four of the nine backends exhibited a decrease in the number of gates when using the maximum level compared to the default optimization level.

QUANTIFY [61] is an open-source framework for the quantitative analysis of quantum circuits based on Google’s own Cirq framework. QUANTIFY includes as part of its key features analysis and optimization methods, semi-automatic quantum circuit rewriting, and others. The architecture of QUANTIFY is designed in a classical workflow manner consisting of four-step types: (1) circuit synthesis, (2) gate-level transpilation (e.g., translation from one gate set into another), (3) circuit optimization, and (4) analysis and verification. It also provides several metrics to verify the circuit under study, such as the number of Clifford+T (T-count), Hadamard, and CNOT gates, as well as the depth of the circuit and the Clifford+T gates (T-depth).

In the rapidly evolving field of quantum software, it is paramount to ensure the presence of quality assurance measures, especially if quantum computers are to be used on large-scale real-world applications in the following years. This is what Díaz Muñoz A. et al. [62] set out to do by accommodating a series of classical quality metrics to the quantum realm, in addition to introducing novel measurements geared specifically towards hybrid (quantum/classical) systems maintainability. The paper expands upon the work performed by J. A. Cruz-Lemus et al. [58] to develop a set of quantum software-specific metrics in 2 main areas. First, they introduce numerous metrics for gate counts that were not mentioned in the original work, such as counts for S, T, RX, RY, RZ, CP, and Fredkin gates, among others. Second, they explore the Number of initialization and restart operations via the following metrics: Number and Percentage of qubits with any reset (to 0 state) or initialize (to arbitrary state) operations.

SupermarQ [63] attempts to methodically adapt benchmarking methodology from classical computing to the quantum one. While the work is primarily focused on quantum benchmark design, the authors do come up with 6 metrics termed feature vectors to evaluate quantum computer performance on said benchmarks. Program communication, which ranges from zero for sparse connections to nearly one for dense connections, aims to measure the amount of communication required between qubits. Meanwhile, Critical-Depth, representing the circuit’s minimal time, focuses on two-qubit interactions, with larger numbers indicating greater serialization. The significance of entanglement in a given circuit, known as the Entanglement Ratio, is also captured by measuring the proportion of 2 qubit interactions. Parallelism quantifies the amount of parallel operations that a certain algorithm maintains without being majorly affected by correlated noise events (cross-talk). Applications with high parallelism pack many operations into a limited circuit depth; as a result, their parallelism characteristic is close to 1. Qubit activity is captured throughout execution by Liveness, which shows the frequency of active vs idle qubits. Lastly, Measurement emphasizes reset operations and mid-circuit measurement, relating their frequency to the overall depth of the circuit.

3.3. Benchmarking Frameworks and Performance Evaluation Strategies

Acuaviva et al. [64] present a set of general guidelines intended to assist practitioners in designing fair and effective quantum benchmarks, thereby supporting the development of quantum processors in a well-founded and consistent manner. Their methodology adapts key principles from classical benchmarking to address the distinct characteristics, limitations, and opportunities inherent to quantum computing. The authors analyze the fundamental components of classical benchmarks and their corresponding metrics, identifying the quality attributes required for a benchmark to be considered robust. They evaluate existing quantum metrics and benchmarks from the literature to determine their alignment with these attributes. To promote clarity and consistency in the field, they introduce precise definitions of commonly used terms in quantum benchmarking. Additionally, they propose a structured benchmarking framework highlighting critical factors to consider in benchmark design, aiming to advance the standardization of quantum performance evaluation. Recognizing inconsistencies in current terminology and conceptual frameworks, the authors advocate for the adoption of a standardized vocabulary to foster clearer communication within the community and enable more accurate assessments of quantum system performance. They also propose the establishment of Standard Performance Evaluation for Quantum Computers (SPEQC), a nonprofit organization dedicated to defining standardized criteria for benchmarking quantum devices, to eliminate subjectivity, improve reliability, and support meaningful progress in the field. Through this proposed framework and continued community collaboration, the authors aim to steer the development of quantum performance evaluation in a rigorous and forward-looking direction, while remaining cautious of potential distortions, as cautioned by Goodhart’s Law.

The authors in [65] present a comprehensive set of benchmarking protocols that span the entire quantum computing stack—from individual components to full systems—including their integration with high-performance computing (HPC) and cloud infrastructures, as well as the evaluation of application-level performance. While some of these benchmarks are already established and adopted within the community, others remain less mature. However, it is rare for these benchmarks to be accompanied by standardized implementations, evaluation software, or example datasets that could facilitate practices such as continuous integration and deployment. Developing hardware-agnostic, statistically rigorous, and computationally efficient evaluation routines remains a substantial challenge, in addition to the ongoing efforts to define benchmarking protocols in an open and standardized manner. The authors emphasize that benchmarking efforts should not be developed in isolation. Instead, they must be closely aligned with broader quantum computing initiatives across the full stack—from hardware and software to HPC and cloud platforms. Rather than pursuing a single centralized initiative, the authors advocate for multiple focused activities targeting specific domains such as quantum components, quantum error correction (QEC), HPC, cloud integration, and application benchmarking. This approach allows for the necessary depth and scope to produce standards that may gain international recognition. The integration of these benchmarks into formal standardization processes, the authors argue, should be overseen by organizations equipped to work within established international frameworks such as ISO and CEN-CENELEC. This requires appointing national-level representatives and coordinating efforts at the EU level to ensure the integrity and reliability of the proposed benchmarks, ultimately paving the way for their global adoption.

The authors in [66] discuss quantum characterization, verification, and validation (QCVV), highlighting its crucial role in enabling scientists and engineers to analyze, understand, and improve the performance of quantum information-processing devices. In their tutorial, they review the foundational principles of QCVV and present a broad range of tools and protocols employed by quantum researchers. The core models and concepts—including quantum states, measurements, and processes—are clearly defined and explained, with emphasis on how these elements are used to probe and assess target systems or operations. The authors survey protocols that span from basic qubit characterization techniques to more sophisticated benchmarking methodologies. Throughout the work, they provide illustrative examples, detailed protocol descriptions, and critical evaluations of each method, discussing their respective advantages, limitations, and scalability for future large-scale quantum computing systems. This tutorial serves both as an introductory guide for newcomers and a comprehensive reference for experienced practitioners in the field of quantum benchmarking and device characterization.

Lall et al. [67] present a curated collection of quantum performance metrics designed to enable objective, comprehensive benchmarking of emerging quantum processors. Their work aims to support standardized performance comparisons by defining not only the metrics themselves but also the methodologies for their evaluation. These metrics span various aspects of quantum device performance—including speed, quality, and stability—and address multiple levels of benchmarking, from component-level to application-level. Each metric is consistently documented with definitions, evaluation methodologies, assumptions, limitations, and references, and is supported by open-source software implementations. This software suite facilitates practical evaluation on emulators or hardware, ensuring clarity, transparency, and reproducibility by avoiding hidden optimizations and clearly exposing all parameters used. The authors also provide an introductory overview of quantum computing concepts and hardware platforms to ensure accessibility for non-experts. Emphasizing the dynamic and rapidly evolving nature of the field, they frame their metric collection and accompanying tools as a living resource that will be updated with new developments and insights over time. They note the varying maturity levels of existing metrics, highlighting that while some, such as randomized benchmarking fidelities, are well-established, others—particularly those aimed at full application benchmarking—still suffer from significant variability and lack of standardization. A key challenge identified by the authors is the inconsistency in how even well-known metrics are implemented, often leading to difficulties in making reliable, quantitative comparisons across platforms. This fragmentation poses risks for accurately gauging progress toward quantum advantage. To address this, the authors stress the importance of reducing the number of benchmarking approaches to a minimal, representative set agreed upon by hardware vendors, algorithm developers, and end users. They advocate for internationally coordinated standardization efforts and propose a set of work items to guide such initiatives. Through their contribution, the authors aim to accelerate the development of standardized benchmarks, thereby facilitating fair comparisons and more meaningful progress in the quantum computing landscape.

3.4. Quantum Software Project Estimation, Management Strategies

Shameem et al. [68] address a notable gap in the quantum software engineering domain by identifying and validating 13 key metrics essential for the development of commercially viable, high-quality quantum software products. These metrics are organized into four distinct categories—management, process, programming, and complexity—marking one of the first systematic categorizations specifically designed for quantum software. To evaluate the relative significance of each metric, the authors apply the fuzzy Analytic Hierarchy Process (fuzzy-AHP), offering practitioners a prioritized framework to improve estimation accuracy and project management effectiveness. Their findings highlight the importance of early consideration of factors such as access to quantum hardware, the presence of quantum software estimation data repositories, ongoing knowledge exchange, and the impact of technological volatility. By introducing a taxonomical framework tailored to the unique characteristics of quantum software development, the study provides a foundational tool for structuring project estimation and management practices in this emerging field. The authors suggest that future work could expand upon their findings by exploring additional relevant metrics that influence the quantum software development lifecycle. Furthermore, they propose that their current results could inform the creation of a readiness model for quantum software estimation, helping practitioners determine optimal strategies for planning and executing quantum development projects.

In [69], the authors examine the emerging discipline of Quantum Software Engineering, which combines foundational principles from classical software engineering with the novel paradigms of quantum computing. This integration is essential for guiding developers and system architects in the design of innovative quantum applications and advancing the broader quantum computing landscape. The central objective of the study was to identify key challenges and their underlying causes in agile-based quantum software development and to propose a predictive model—referred to as the Agile-Quantum Software Project Success Prediction Model (AQSSPM)—to estimate project outcomes. To construct this model, the authors conducted a survey among quantum software practitioners to gather empirical data on project experiences and challenges. They then applied a combination of genetic algorithms (GA) with machine learning methods—namely Naive Bayes Classifiers (NBC) and Logistic Regression (LR)—to predict the probability of success in agile-quantum projects. The integration of GA with NBC resulted in a significant improvement in success prediction accuracy, increasing from 53.17% to 99.68% while reducing associated costs from 0.463% to 0.403%. Similarly, the combination of GA with LR raised the prediction accuracy from 55.52% to 98.99% and lowered costs from 0.496% to 0.409%. The authors also identified several critical factors influencing the success of agile quantum software projects, including the necessity of domain-specific expertise, effective cross-disciplinary collaboration, resource availability, responsiveness to rapid technological changes, and growing commercial interest in quantum solutions. These insights are expected to serve as valuable inputs for both researchers and practitioners, offering a strategic foundation for improving success rates in quantum software development. As part of their future work, the authors plan to test AQSSPM across diverse quantum projects to assess its generalizability and resilience. They also aim to enhance the model by integrating additional predictive algorithms to improve performance and accuracy. Furthermore, the authors propose conducting longitudinal studies to evaluate the long-term efficacy of the model in dynamic quantum development environments. Finally, they intend to develop a comprehensive set of practitioner-oriented guidelines, complete with best practices and case-based examples, to facilitate real-world application of the proposed model.

4. Challenges Facing the Development of Quantum Software Metrics

This section delves into the key challenges facing the development of quantum software metrics, exploring the unique obstacles posed by quantum systems and some of the limitations of the existing approaches outlined above.

To begin our discussion, we first consider hardware-oriented metrics, their merits, their limitations, and thus the need for software-oriented metrics as well. Hardware-oriented metrics like QV [6,44] and CLOPS [7] account for critical factors such as circuit depth, error rates, and execution speed, which are essential for understanding the capabilities of quantum devices. For example, Quantum Volume (QV) evaluates the largest random square circuit a device can reliably execute, incorporating both the number of qubits and the effective error rate. This provides a holistic measure of a device’s ability to handle complex computations while accounting for noise and errors. Similarly, CLOPS measures the speed of quantum circuit execution, reflecting how efficiently a Quantum Processing Unit (QPU) can process quantum operations. This is particularly useful for applications requiring rapid iterations, such as variational quantum algorithms. QPack Scores [45] goes a step further by combining runtime, accuracy, scalability, and capacity into a single benchmark, offering a more nuanced evaluation of a quantum system’s performance across different dimensions.

These metrics also draw analogies to classical computing benchmarks, such as FLOPS (Floating Point Operations Per Second) and LINPACK, which measure the performance of classical processors and supercomputers. By providing standardized ways to compare quantum devices, QV and CLOPS help bridge the gap between classical and quantum computing, offering familiar frameworks for performance evaluation. Additionally, metrics like QV explicitly consider the interplay between circuit depth and error rates, which are critical for assessing the feasibility of running quantum algorithms on noisy intermediate-scale quantum (NISQ) devices. For instance, QV incorporates the effective error rate and the achievable circuit depth, providing a measure of how well a device can maintain coherence and accuracy as circuit complexity increases. Equation (1) [6,44] defines how the quantum volume metric quantifies the space-time volume occupied by a model circuit with random two-qubit gates that can be reliably executed on a given device; where n is the number of qubits required to run a given algorithm, $n^{\prime }$ the number of active qubits, ${ϵ}_{\mathrm{eff}}$ the effective error rate, which specifies how well a device can implement arbitrary pairwise interactions between qubits, and the achievable circuit depth d is given to be $\simeq {\displaystyle \frac{1}{n{ϵ}_{\mathrm{eff}}}}$.

$$V_Q=\underset{n^{\prime }\le n}{max}min\left[n^{\prime },{\left({\displaystyle \frac{1}{n^{\prime }{ϵ}_{\mathrm{eff}}\left(n^{\prime }\right)}}\right)}^2\right]$$

(1)

One major challenge facing these approaches is the probabilistic nature of quantum systems. Quantum computers produce probabilistic results due to the inherent uncertainty in quantum mechanics. This poses a problem for metrics like QV and QPack Scores, which rely on comparing outcomes to ideal simulations. The lack of repeatability in quantum results means that benchmarks may yield inconsistent results across multiple runs, complicating the evaluation process. Additionally, hardware-oriented metrics are often tailored to specific device architectures and gate sets, making them less applicable to other platforms. For example, QV assumes a specific circuit structure (random square circuits) that may not reflect the requirements of real-world applications, while CLOPS focuses on execution speed but does not account for the quality of results, which can vary significantly depending on the algorithm and hardware noise.

More importantly, however, is the lack of software considerations of these approaches. Hardware-oriented metrics like QV, CLOPS, and QPack Scores fail to address the unique challenges of quantum software development. For instance, Quantum Volume (QV) measures the largest random square circuit a device can reliably execute, but does not provide any insights into the efficiency or quality of the algorithms running on the device. A high QV score does not guarantee that a quantum algorithm will perform well or produce accurate results, as it does not account for the specific requirements of the algorithm or the effectiveness of error mitigation techniques.

Similarly, CLOPS measures the speed of quantum circuit execution but does not evaluate the quality of the results or the efficiency of the underlying algorithms. A device with high CLOPS might execute circuits quickly but produce inaccurate results due to high error rates or poor error mitigation. This lack of consideration for software quality limits the usefulness of CLOPS in assessing the overall performance of quantum systems.

QPack Scores attempt to address some of these limitations by combining runtime, accuracy, scalability, and capacity into a single benchmark. However, they still focus primarily on hardware performance and do not provide a comprehensive evaluation of quantum software. For example, QPack Scores do not account for the usability of quantum programming frameworks, the maintainability of quantum code, or the effectiveness of error mitigation techniques. These aspects are critical for the development of practical quantum applications but are overlooked by hardware-oriented metrics.

To fully realize the potential of quantum computing, it is essential to develop software metrics that address the unique challenges of quantum software development. These metrics should evaluate the efficiency, robustness, and maintainability of quantum algorithms, as well as the usability of quantum programming frameworks and the effectiveness of error mitigation techniques.

Since classical software metrics have been extensively researched and refined over decades, it is perhaps worth considering whether such measures could be extended to the quantum case. Indeed, it is possible to have already existing software metrics and simply modify them to account for some quantum attributes, such as the number of qubits, reads, and writes from quantum registers, in addition to classical registers, and so on.

Such an approach has been considered, evidenced by Jianjun Zhao [19], who suggested many notable extensions of classical software metrics, as discussed in the literature review above. The LOC measure for the quantum code shows how he attempted a coherent extension. Zhao divided the result into several aspects, accounting for the different aspects of a quantum computer. Those aspects are the number of LOC, the number of LOC related to quantum gate operations, the number of LOC related to quantum measurements, the total number of qubits used, and the total number of unique quantum gates used.

Nevertheless, it must be acknowledged that programming on a quantum computer, albeit having some similarities to classical computing, is significantly different. One of the primary challenges in extending classical metrics to quantum software lies in the unique architecture and resource constraints of quantum systems. Quantum algorithms are executed on quantum circuits composed of qubits and quantum gates, with performance heavily influenced by factors such as qubit coherence times, gate fidelity, and error rates. Metrics like lines of code, which are designed to evaluate classical code structure, fail to capture the intricacies of quantum circuits, such as gate depth, entanglement patterns, or the trade-offs between circuit width and depth.

The approach of counting specific gates in quantum circuits, as seen in the works of J. A. Cruz-Lemus et al. [58], QUANTIFY [61], and Díaz Muñoz A. et al. [62], represents a significant step toward developing quantum-specific software metrics. By focusing on gate counts—such as the number of single-qubit gates (e.g., Pauli X, Y, Z, Hadamard), multi-qubit gates (e.g., CNOT, TOFFOLI), and specialized gates (e.g., Clifford+T, S, T, RX, RY, RZ)—these metrics aim to provide a quantitative basis for evaluating the complexity, efficiency, and resource usage of quantum circuits. However, while this approach offers a more quantum-specific perspective compared to classical metrics, it is not without its limitations and challenges.

Counting gates, while useful, does not fully capture the complexity or performance of a quantum circuit. Quantum circuits are influenced by factors such as qubit connectivity, gate fidelity, error rates, and the depth of the circuit (i.e., the number of sequential operations). A circuit with a low gate count but poor qubit connectivity might require extensive SWAP operations to execute, increasing its effective depth and runtime. Similarly, a circuit with a high number of low-fidelity gates might perform worse than a circuit with fewer but higher-fidelity gates. Gate-counting metrics alone fail to account for these nuances, potentially leading to misleading assessments of circuit efficiency or quality.

Furthermore, Quantum hardware platforms often support different native gate sets, which are the fundamental operations that a particular quantum device can execute natively and efficiently. For example, IBM’s quantum processors typically use a gate set consisting of single-qubit gates (e.g., X, Y, Z, S, T, Hadamard) and the CNOT gate [70], while trapped-ion systems like those from IonQ may support native gates such as Mølmer-Sørensen gates for multi-qubit interactions [71]. Similarly, photonic quantum computers may rely on continuous-variable operations rather than discrete gate sets [72]. This diversity in hardware architectures means that a circuit optimized for one device may require significant transpilation—translation into a different gate set—to run on another device. As a result, gate counts can vary dramatically depending on the underlying hardware, making metrics like T-count or CNOT counts inconsistent and difficult to compare across platforms. For instance, a quantum circuit with a low T-count on one device might transpile into a circuit with a high number of native gates on another device, rendering the original metric meaningless in the new context.

This lack of universality resulting from the abundance of quantum hardware architectures is perhaps the most apparent challenge facing the development of quantum software metrics. In fact, the problem extends even further with various architectures being better at certain algorithms than others. In a study conducted by Linke et al. [73], they compare the performance of an Ion-Trap quantum computer with a superconducting quantum computer on some small quantum circuits. It was discovered that the ion-trap computer’s increased connectivity allowed it to have a higher relative success rate on the Toffoli circuit (which had more two-qubit gates) than the Margolis circuit, where both computers performed similarly. The authors concluded that the performance of an algorithm is intrinsically linked to the underlying hardware architecture; hence, any set of metrics aimed at measuring software performance would need to account for this.

Subsequently, it could be said that, unlike classical computing, where hardware and software metrics are often treated as separate domains, quantum computing remains deeply intertwined with its hardware due to the field’s infancy and the unique challenges posed by quantum mechanics. The direct link between hardware and software in quantum systems means that any meaningful software metrics must account for the underlying hardware architecture, including qubit connectivity, gate fidelity, and error rates. This interdependence complicates the development of universal quantum software metrics, as performance can vary significantly across different devices and algorithms. As a result, quantum software metrics must be designed to bridge the gap between hardware capabilities and software requirements, ensuring they remain relevant across diverse platforms and applications.

Although the works referenced in Section 3.3 do not directly propose intrinsic metrics, but rather focus on benchmarking frameworks and performance evaluation strategies, they provide invaluable insights into the broader landscape of quantum device assessment. The authors in these studies present essential methodologies, guidelines, and collections of metrics that collectively serve to define, standardize, and enhance the process of quantum performance evaluation. These benchmarking protocols address various layers of quantum computing, from individual components to full systems, including integration with high-performance computing (HPC) and cloud infrastructures, as well as application-level performance. Their emphasis on the development of consistent, transparent, and reproducible benchmarking practices contributes to the ongoing effort to build universally accepted evaluation standards across quantum platforms. In this sense, while the authors’ focus is on frameworks for performance benchmarking, their work remains highly relevant and provides foundational references for researchers aiming to develop or adopt robust evaluation strategies for quantum computers.

In addition, the works referenced in Section 3.4 focus primarily on project estimation, management strategies, and predictive modeling; they offer invaluable insights into the broader field of quantum software engineering. By addressing the unique challenges associated with quantum software development—such as metric definition, estimation accuracy, and agile project success—these studies contribute foundational tools and frameworks that support the structured and scalable growth of the discipline. Together, they highlight the growing need for tailored methodologies that can guide effective planning, execution, and evaluation of quantum software projects in an increasingly complex technological landscape.

One promising approach to addressing these challenges is the adaptation of functional size measurement methods, such as the COSMIC ISO 19761 standard [22], which is widely used in classical software engineering to measure the functional size of software systems. The COSMIC method focuses on quantifying the functionality delivered to users, making it potentially adaptable to quantum software by accounting for quantum-specific operations such as qubit manipulations, gate applications, and measurements. By extending this method to include quantum functionalities, it may be possible to develop a standardized framework for measuring the size and functionality of quantum algorithms in a hardware-agnostic manner.

Despite the early stage of quantum computing development, compared to classical computing, functional size measurement (FSM) remains valuable, particularly in identifying system-level requirements such as non-functional requirements (NFRs) and guiding the integration of error correction schemes. In classical software engineering, FSM techniques like COSMIC have been used not only to estimate development effort but also to systematically analyze architectural complexity and compliance with system constraints. This parallels emerging needs in quantum software, where even though control and interfaces are classical, the algorithmic behavior and required quantum resources (e.g., qubit registers, entanglement depth, measurement granularity) are intrinsically linked to functional behavior. Moreover, FSM provides a structured way to express what the system does, independent of how it is implemented, making it especially useful in quantum environments where hardware is still evolving. Historically, the COSMIC method has demonstrated flexibility across domains, and its adaptability to quantum contexts aligns with this tradition. The presence of a dedicated task force within the COSMIC community on quantum software sizing [74] further underscores the growing consensus that early metric development is not only appropriate but essential to support scalable, verifiable quantum systems in the near future.

The following section showcases three different approaches developed on the COSMIC method for quantum software, highlighting its potential as a foundation for quantum software metrics.

5. Quantum Software Measurement Approaches Based on COSMIC ISO 19761

5.1. Overview of COSMIC ISO 19761

The COSMIC (Common Software Measurement International Consortium) ISO 19761 standard [22] is a widely adopted functional size measurement (FSM) method used for classical software. It was developed to provide a consistent and universal approach to measuring the functional size of software based on its functional user requirements (FURs). COSMIC is primarily focused on quantifying the data movements between the software and its users or external systems, making it a flexible and scalable model applicable to various types of software applications, including business applications, real-time systems, and now emerging domains like quantum software.

5.1.1. Key Principles of COSMIC ISO 19761

The COSMIC method measures software size by analyzing functional processes, which are triggered by user inputs and lead to responses. A functional process consists of sub-processes known as data movements. These data movements are categorized into four main types:

• Entry (E): Represents data entering the system from an external user or another system.
• Exit (X): Involves data exiting the system, typically in response to an entry or internal process.
• Read (R): Refers to the system accessing or retrieving data from a persistent storage.
• Write (W): Indicates the storage or writing of data into persistent storage.

Each data movement reflects how the system interacts with its environment and is fundamental to defining the functional size of the software. The functional size is expressed in COSMIC Function Points (CFP), a unit that reflects the amount of functionality provided by the software based on its data movements. By abstracting the functional size, COSMIC enables comparison across different software projects and systems, independent of programming language or technology.

5.1.2. Benefits of COSMIC ISO 19761

• Technology-Independent: COSMIC is designed to be neutral. It can be applied to a wide variety of software domains, including traditional business systems, real-time systems, and more complex areas such as telecommunications, control systems, and embedded software. This adaptability holds promise for quantum systems, where standardized measurement approaches are still emerging.
• Scalability: COSMIC is adaptable to both small and large systems, and it has been applied in diverse industries such as banking [75], telecommunications [76], and aerospace.
• Accuracy and Precision: By focusing on functional user requirements and the actual interactions between the system and its users, COSMIC offers precise and repeatable measurements. This level of accuracy is crucial for project estimation, cost analysis, and performance benchmarking.

5.1.3. COSMIC in the Context of Quantum Software

Recent studies have adapted COSMIC for use in quantum systems by reinterpreting the traditional data movements (Entry, Exit, Read, Write) in the context of quantum processes [23,24,25]. For example, in quantum algorithms, the entry could correspond to initializing quantum states, while the exit could represent the collapse of quantum states into classical bits during measurement. As quantum computing progresses, frameworks like COSMIC offer a foundational approach to measuring software size in this new domain, enabling comparisons between classical and quantum systems. However, challenges remain in fully adapting COSMIC to account for the intricacies of quantum operations and algorithms, such as entanglement and non-local data movement.

5.2. The Three Quantum COSMIC Measurement Approaches

To date, only three significant studies [23,24,25] have investigated the adaptation of functional size measurement specifically for quantum software, based on the COSMIC method—ISO 19761 [21]. We present a comparison of these three approaches in terms of the inputs used for measurement, functional processes, data movement types, and their respective units. All three approaches define the size of the circuit as the number of COSMIC Functional Points (CFP) of the identified functional processes. However, each of the three measurement approaches offers a slightly different technique as to what is considered in the circuit as a functional process.

5.2.1. Approach 1 [23]: Gates’ Occurrences

This approach treats each gate as a functional process, counting multiple occurrences of the same gate type as separate processes. It measures the COSMIC functional size in CFP by identifying data movements in Qiskit corresponding to operations by quantum gates and qubit measurements.

• Identify each circuit as a system.
• Identify each gate as a functional process and count gates.
• Assign one Entry and Exit data movement per gate.
• Identify measurement commands as Data Writes.
• Identify reads from classical bits as Data Reads.
• Assign 1 CFP for each Entry, Exit, Read, and Write.
• Aggregate CFPs for each functional process to calculate its size.
• Aggregate all CFPs to determine the system’s functional size.

In Step 1, analyze each circuit separately, then aggregate CFPs across circuits. Steps 2–3 count gates and assign 2 CFPs per gate for Entry and Exit movements. Step 4 assigns 1 CFP per measurement (treated as a Write), and Step 5 adds 1 CFP per data Read (reading the result of the measurement). Finally, Step 8 aggregates all CFPs to calculate the software’s total functional size.

5.2.2. Approach 2 [24]: Gates’ Types

This approach is differentiated from the first one in that it identifies types rather than occurrences. It accounts for each type of gate as a functional process, with functional process input and functional process output. This approach clearly distinguishes between ancillary qubits and input vectors, with the latter being groups of qubits defined by the size of the problem instance. Additionally, tensored operators acting on these input vectors are operators performing the same function, and those contributing to a shared task are grouped into their respective functional processes.

Directives for Identifying the Functional Processes

• An operator acts on qubits, and common action leads to an operator type. For instance, if a circuit contains an X gate acting on qubit $q_0$ and also contains an X gate acting on qubit $q_1$, identify one X gate functional process type. Similarly, for a $CX$ gate with qubit $q_0$ controlling $q_1$ and a $CX$ gate with qubit $q_1$ controlling $q_0$.
• Identify an Input functional process that conveys the input state(s).
• A vector (string of bits) and a separate value are considered different types.
• Identify one functional process for all operators with a common action in the circuit.
• Identify one functional process for n-tensored operator variants, identifying another functional process for each different n.
• Identify one functional process type for each operator type defined by a human user (these operators are often indicated by $U_f$ in the literature).

It is important to note several remarks for this approach, which would help better understand how to properly apply it.

For inputs, a vector (a string of bits) and a separate value are considered different types and each is considered a functional process (a different layer), with 1 Entry and 1 Write for each, resulting in 2 CFP per entry unless COSMIC measurement begins after state preparation of the qubits is finished. For example, if one input is a string of bits and another is a separate value, a separate Entry and Write are counted for each, totaling 4 CFP. Each gate, even if repeated, is a Functional Process considered as a layer with 1 Entry, x Reads, and x Writes, based on the number of wires entering and exiting; CNOT and swap gates involve 1 Read and 1 Write, as they likely read from one wire and operate on another. Measurement, if present, is a layer involving an Entry, Read, and Write on the classical register. For each Entry, Exit, Read, or Write, 1 CFP is counted.

5.2.3. Approach 3 [25]: Q-COSMIC

This approach is more abstract than the previous two approaches. It extends COSMIC to Q-COSMIC by adhering to the principles of Quantum-Unified Modelling Language (Q-UML), which is an attempt to generalize UML for quantum software projects to abstract implementation details. The authors argue that since COSMIC is a measurement technique applied to software design documents—most notably UML diagrams—it is natural to showcase Q-COSMIC through Q-UML diagrams.

The three phases of a Q-COSMIC analysis:

• Strategy

• Determine the purpose of the COSMIC measurement.
• Define the functional users and identify each as a functional process.
• Specify the scope of the Functional User Requirements (FURs) to be measured.

After that, a context diagram is generated.

• Mapping

• Map the FURs onto a COSMIC Generic Software Model.
• Identify the data movements needed for specific software functionality.

• Measurement

• Count and aggregate the data movements for each use case, with each movement representing functionality that contributes to the size of the software project/system.

In the following subsections, we will introduce the Quantum Algorithm classes to which we will compare and contrast the three COSMIC approaches we discussed above.

5.3. Quantum Algorithm Classes

We focused on two key classes of quantum algorithms as defined by Nielsen & Chuang (2010) [9]: Quantum Fourier Transform (QFT) and Quantum Search, based on their prominence in quantum computing. While these are significant, they represent relatively simple quantum algorithms; however, they were primarily chosen because they are widely known and provide foundational insights into quantum computing.

The following algorithms represent each class:

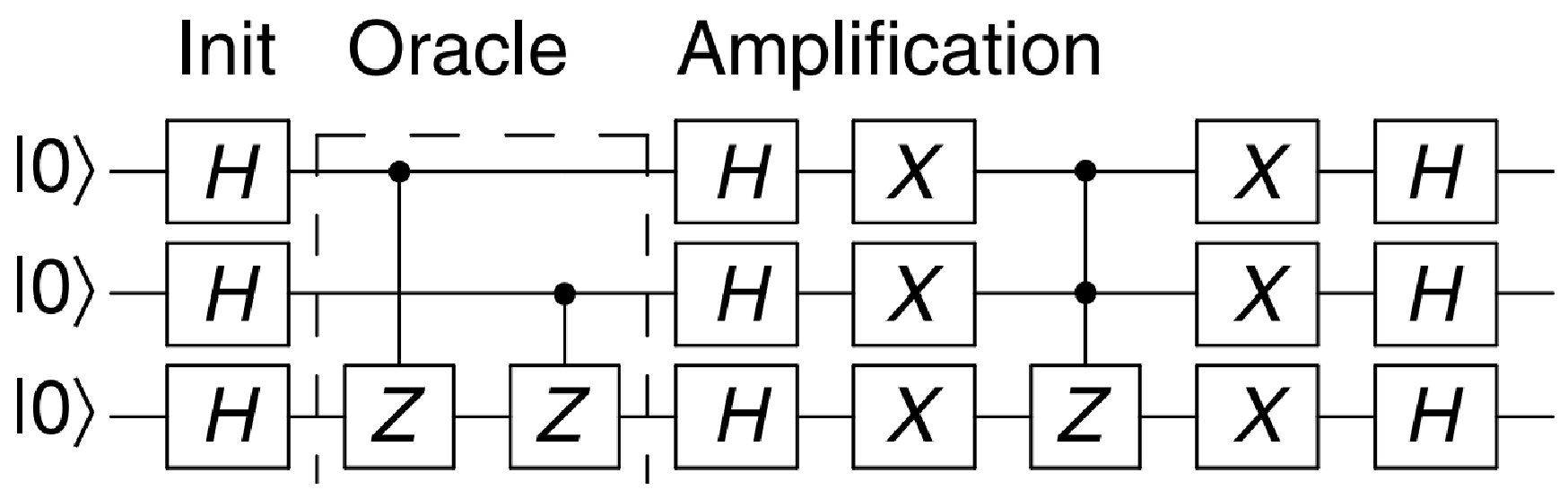
• Grover’s Algorithm for the Quantum Search class, due to its efficiency in searching unstructured databases. Figure 1 shows the circuit implementing Grover’s algorithm.
• Shor’s Algorithm for the QFT class, since it is one of the most famous applications. Shor’s algorithm uses the QFT to find patterns that help in factoring large numbers, solving a problem that classical computers find hard. This makes it a potential threat to modern encryption methods, which rely on the difficulty of factoring large numbers to secure data. Figure 2 is a simplified circuit implementing Shor’s algorithm to find the prime factors of 21.

5.4. Measurement Comparison

In this section, we investigate the measurement results of applying the different approaches when measuring the size of quantum software implementing Shor’s algorithm and Grover’s algorithm.

Table 2. A Summary of the Findings of the 3 approaches (Approach 3 according to [25]).

Approach	Data Movement Type	Grover’s	Shor’s
1	Entry	18	20
	Exit	18	20
	Write	3	3
	Read	3	3
	Total	42 CFPs	46 CFPs
2	Entry	5	9
	Write	5	9
	Read	4	7
	Total	14 CFPs	25 CFPs
3 UC1	Entry	NA	2
	Exit	NA	2
	QEntry	NA	1
	QExit	NA	1
	Total	NA	6 CFPs
3 UC2	Total	NA	4 CFPs

compares and summarizes the results of three approaches.

• Approach 1 [23]: Gates’ Occurrences

We applied this approach to the quantum circuit in Figure 1, which implements Grover’s algorithm. The circuit consists of:

• A total of 18 quantum gates, where 1 functional process is identified for each gate, with 1 entry and 1 exit for each process.
• A total of 3 measurement operations, where we identified 1 write operation and 1 read operation for each (the measurement operation is omitted from the circuit for brevity).

We applied this approach to the quantum circuit in Figure 2, which implements Shor’s algorithm to factor the number 21. The circuit consists of:

• A total of 20 quantum gates, where 1 functional process is identified for each gate, with 1 entry and 1 exit for each process.
• A total of 3 measurement operations, where we identified 1 write and 1 read for each.

• Approach 2 [24]

First, we applied this approach to Grover’s algorithm to the circuit in Figure 1.

• Input Functional Processes

  –

  Identify a functional process for the input vector. Count 1 Entry and 1 Write

• Operation Functional Processes

  –

  Identify 3 functional processes for the Hadamard, Controlled Z, and X gates acting on the input vector. Count 3 Entry, 3 Read, and 3 Write.

• Measurement Functional Processes

  –

  Identify a functional process for measuring the input vector. Count 1 Entry, 1 Read, and 1 Write.

Next, we apply the same approach to Shor’s algorithm in Figure 2 as follows:

• Input Functional Processes

  –

  Identify a functional process for the input vector consisting of qubits (c0, c1, c2). Count 1 Entry and 1 Write.

  –

  Identify a functional process for the input vector consisting of qubits (q0, q1). Count 1 Entry and 1 Write.

• Operation Functional Processes

  –

  Identify 3 functional processes for the Hadamard, $S^{†}$, and $T^{†}$ gates acting on the input vector consisting of qubits (c0, c1, c2). Count 3 Entry, 3 Read, and 3 Write.

  –

  Identify 2 functional processes for the CNOT and X gates acting on the input vector consisting of qubits (q0, q1). Count 2 Entry, 2 Read, and 2 Write.

• Measurement Functional Processes

  –

  Identify a functional process for measuring the input vector consisting of qubits (c0, c1, c2). Count 1 Entry, 1 Read, and 1 Write.

  –

  Identify a functional process for measuring the input vector of qubits (q0, q1). Count 1 Entry, 1 Read, and 1 Write.

• Approach 3 [25]: Q-COSMIC

The Q-COSMIC analysis of the factoring software using Shor’s algorithm involves two use cases: UC1 (quantum) and UC2 (classical). UC1 has six total data movements: two Exits (2X), two Entries (2E), one Quantum Exit (1QX), and one Quantum Entry (1QE), resulting in 6 QCFP (Q-COSMIC Functional Points). UC2, a classical system, has 4 CFPv5. The total functional size is 10 points, with 60 % (6 CFP) from the classical layer and 40 % (4 QCFP) from the quantum layer.

5.5. Discussion

The three approaches to adapting the COSMIC method for quantum software—Approach 1 (Gates’ Occurrences), Approach 2 (Gates’ Types), and Approach 3 (Q-COSMIC)—offer distinct perspectives on measuring the functional size of quantum circuits. Each approach has its strengths and limitations, and their application to quantum algorithms like Grover’s and Shor’s reveals important insights into the challenges of quantifying quantum software size.

Approach 1: Gates’ Occurrences treats each gate occurrence as a separate functional process, assigning Cosmic Functional Points (CFPs) based on data movements such as Entry, Exit, Read, and Write. For example, in Grover’s algorithm, 18 gates result in 18 functional processes, each contributing 2 CFPs (Entry and Exit), while measurements add additional CFPs for Reads and Writes. This method is straightforward and granular, capturing every operation in the circuit. Its strength lies in its granularity, providing a detailed breakdown of every gate and measurement operation, which is useful for fine-grained analysis. However, this approach struggles with scalability, as the CFP count can become excessively high for large circuits with many gates. Additionally, it does not account for gate types or hardware-specific optimizations, potentially leading to inflated metrics for circuits with repeated gates.

Approach 2: Gates’ Types groups gates by type rather than occurrences, treating each gate type as a functional process. For example, all Hadamard gates in a circuit are counted as a single functional process. This reduces redundancy and focuses on the diversity of operations rather than their frequency. The strength of this approach is its efficiency, as it reduces the CFP count by grouping similar gates, making it more scalable for larger circuits. It also emphasizes the functional intent of the circuit, aligning more closely with the purpose of the operations. However, it may lose detail by overlooking the impact of repeated operations, which could be significant in some algorithms. Additionally, identifying and grouping gate types requires a deeper understanding of the circuit’s structure, which may not always be straightforward.

Approach 3: Q-COSMIC is the most abstract of the three, extending COSMIC to quantum software through Quantum-Unified Modelling Language (Q-UML). It focuses on functional processes at a higher level, such as input preparation, quantum operations, and measurements, rather than individual gates. For example, in Shor’s algorithm, it distinguishes between quantum and classical layers, assigning CFPs based on data movements between these layers. The strength of this approach lies in its abstraction, providing a high-level view of the software’s functionality, making it suitable for design and architectural analysis. It is also hardware-agnostic, as it focuses on functional processes rather than specific gates, making it adaptable across platforms. However, it may lack granularity, as it does not capture the intricacies of gate-level operations, which are critical for performance optimization. Additionally, its reliance on Q-UML and higher-level abstractions may make it less accessible for developers focused on implementation details.

From the comparison, several key insights emerge. First, there is a trade-off between granularity and scalability. Approach 1 offers high granularity but struggles with scalability for large circuits, while Approach 2 strikes a balance by grouping gate types, reducing redundancy while maintaining functional relevance. Approach 3 sacrifices granularity for scalability and abstraction, making it more suitable for high-level design. Second, hardware dependence varies across the approaches. Approach 1 and Approach 2 are more sensitive to hardware-specific gate sets and optimizations, as they rely on gate-level details. In contrast, Approach 3, being more abstract, is less affected by hardware variations, making it more universal but less precise for size evaluation. Third, the approaches differ in their focus on functionality versus operational details. Approach 1 and Approach 2 focus on operational details (gates and measurements), which are critical for performance tuning, while Approach 3 emphasizes functional processes, aligning more closely with software engineering principles and design considerations.

Finally, the applicability to quantum algorithms varies across the approaches. For algorithms like Grover’s and Shor’s, Approach 1 and Approach 2 provide detailed insights into gate-level size, which is useful for optimization. Approach 3, while less detailed, offers a broader perspective on the algorithm’s functional requirements, which is valuable for system design and integration. Together, these approaches demonstrate the need for a multi-layered framework that combines granular gate-level metrics with higher-level functional analysis, ensuring comprehensive evaluation of quantum software across different stages of development and deployment. This layered approach would address the unique challenges of quantum software while leveraging the strengths of each method.

6. Conclusions

This paper explored the challenges of developing quantum software metrics and evaluated three distinct adaptations of the COSMIC ISO 19761 method for measuring quantum software functional size. Given the inherent complexities of quantum computing, including hardware dependencies, probabilistic execution, and unique programming paradigms, establishing reliable software metrics is crucial for assessing quantum algorithm efficiency and scalability. Our analysis highlighted the shortcomings of hardware-oriented metrics, such as Quantum Volume (QV) and CLOPS, and examined how COSMIC-based approaches can offer a structured way to measure quantum software size.

6.1. Main Contributions

This work makes several key contributions to the field of quantum metrics, especially software metrics:

Identifying the Gaps in Hardware-Oriented Metrics: We outlined the limitations of existing hardware-driven metrics (e.g., QV, CLOPS, QPack Scores) and demonstrated their inadequacy in capturing quantum software characteristics such as maintainability, algorithmic efficiency, and functional size.

Extending Classical Software Metrics and measurements to Quantum Computing: We examined the feasibility of adapting classical software engineering metrics, particularly the COSMIC ISO 19761 method, to quantum software. We discussed the challenges in extending traditional metrics and highlighted the necessity of integrating quantum-specific attributes such as qubit usage, gate types, and measurement operations.

Comparing Three COSMIC-Based Approaches for Quantum Software Measurement:

Approach 1: Gates’ Occurrences—Provides a fine-grained analysis by treating each gate as a separate functional process but suffers from scalability issues.

Approach 2: Gates’ Types—Groups gates by type, reducing redundancy while maintaining relevance, offering a balance between detail and efficiency.

Approach 3: Q-COSMIC—Abstracts functional processes using Q-UML, making it hardware-agnostic and suitable for high-level software analysis but less precise for gate-level optimization.

Demonstrating Applicability to Real Quantum Algorithms: We applied these approaches to well-known quantum algorithms (Grover’s and Shor’s) to illustrate their effectiveness, revealing trade-offs between granularity, scalability, and hardware dependence.

These contributions lay the foundation for a structured, scalable, and functionally relevant measurement framework for quantum software, bridging the gap between classical and quantum software engineering.

6.2. Limitations and Future Work

This work primarily concentrates on benchmarking quantum hardware within the NISQ era, emphasizing near-term metrics and measurements. As such, it does not explore the full spectrum of practical challenges associated with running large-scale fault-tolerant quantum algorithms on current hardware prototypes.

While this study provides a significant step toward quantum software metrics, several challenges remain:

Hardware Dependence and Standardization Challenges: Gate-level metrics are highly sensitive to the underlying quantum hardware. As quantum computing platforms evolve, it will be necessary to develop metrics that remain meaningful across different architectures. This could involve establishing a standardized quantum software benchmarking framework.

Integration with Quantum Software Development Tools: To ensure practical adoption, quantum software metrics should be integrated into existing quantum programming environments (e.g., Qiskit, Cirq, PennyLane). Future work could focus on developing automated tools that compute COSMIC-based quantum metrics directly from quantum circuit representations.

Expanding Functional Size Metrics for Hybrid Quantum-Classical Systems: Many quantum algorithms rely on classical pre- and post-processing. Extending COSMIC-based approaches to hybrid quantum-classical workflows will be essential for measuring the full computational size of quantum applications.

Empirical Validation through Real-World Case Studies: The proposed measurement approaches should be tested on a broader range of quantum applications beyond Grover’s and Shor’s algorithms, including optimization problems, quantum machine learning, and error-corrected quantum systems.

The field remains in its early stages. There is a clear need for continued research to develop more precise and comprehensive measurement techniques that can support the evolving landscape of quantum software engineering. A standardized, scalable, and hardware-aware measurement framework would not only enhance the evaluation of quantum software performance but also facilitate benchmarking, optimization, and interoperability across different quantum platforms. As quantum computing moves closer to practical applications, establishing such a framework will be essential for ensuring the reliability, efficiency, and scalability of quantum software solutions in the future. Hence, future work will aim to expand this study by incorporating a deeper performance analysis of quantum systems under fault-tolerant execution models. This includes assessing resource overheads of error correction, quantifying logical gate performance, and proposing standardized metrics tailored to long-term scalability in fault-tolerant quantum computing environments.