Thermodynamics Analysis of Cryogenic Supercritical Hydrogen Storage System Based on Multi-Stage Joule–Brayton Cycle
Abstract
1. Introduction
| Hydrogen Storage Process | Storage Density (kg/m3) | SEC (kWh/kg) | Exergy Efficiency (%) | |
|---|---|---|---|---|
| LH2 | Existing plants [25] | 70.85 | 11–15 | - |
| Tang Lu [26] | 70.85 | - | 38.52/40.17 | |
| Cao Xuewen [28] | 70.85 | 9.802 | 41.4 | |
| Yujing Bi [30] | 70.85 | 9.703 | 39.1 | |
| Sun [32] | 70.85 | 5.664 | 52.77 | |
| CcH2 | Zekai Song [40] | 63.36 | 5.432 | 43.88 |
| Jingxuan Xu [41] | 72.53 | 5.87 | 49.74 | |
| Haocheng Wang [43] | 71.59 | 6.42 | - | |
2. System Description
3. Process Construction Basis
3.1. Assumptions and Initial Parameters
- The influence of fluid kinetic energy and gravitational potential energy on fluid is ignored;
- The process is stable and will not be disturbed by external disturbance;
- The ambient temperature is 30 °C;
- There is no pressure drop in water coolers and heat exchangers;
- In total, 90% of the mechanical work produced by the expansion machines is recovered by the compressors;
- The flow temperature at the exit of all water coolers is the same as the ambient temperature;
- The fluid pipeline between all equipment is insulated from the outside world;
- The parameters of the feed gas are 30 °C, 102 kPa, 2 kgH2/s;
- The minimum temperature difference for heat exchange in the multi-flow heat exchanger is 3 °C.
3.2. Specific Energy Consumption
3.3. Coefficient of Performance
3.4. Exergy Efficiency
4. Process Simulation and Optimization
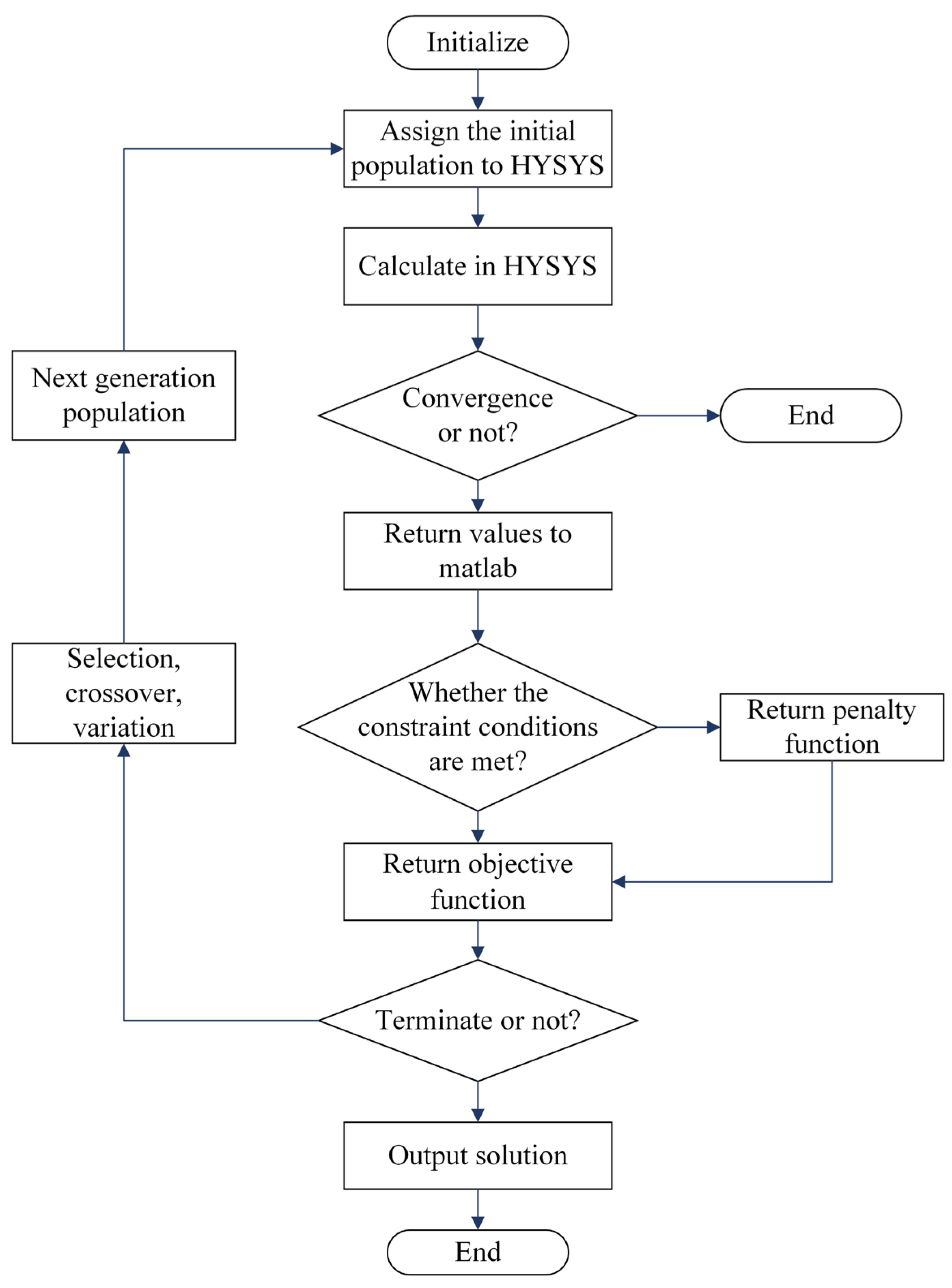
4.1. Optimization Method
4.2. Objective Function
4.3. Optimization Variable
4.4. Constraints and Penalty Function
5. Results and Analysis
5.1. Results
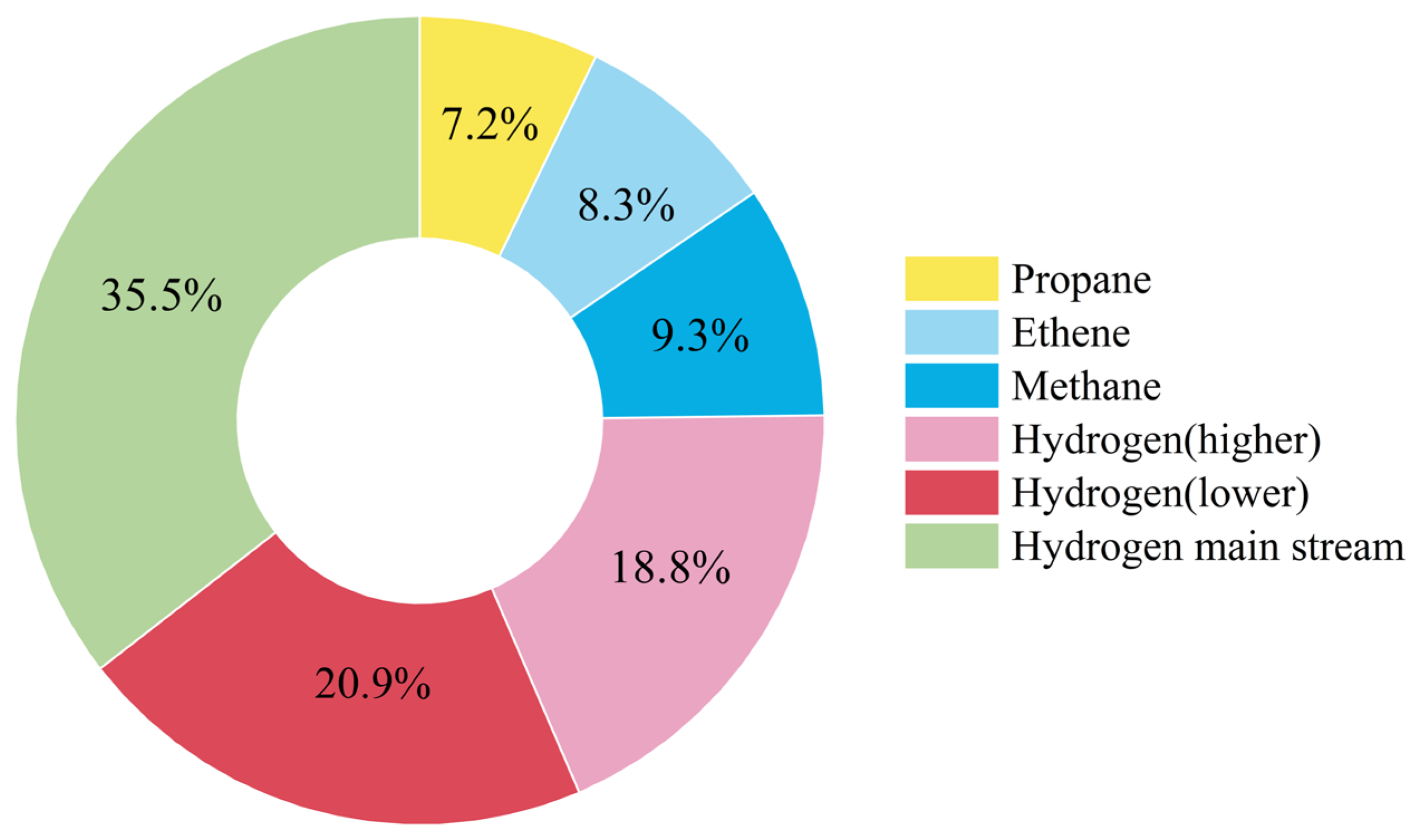
5.2. Energy Consumption Analysis
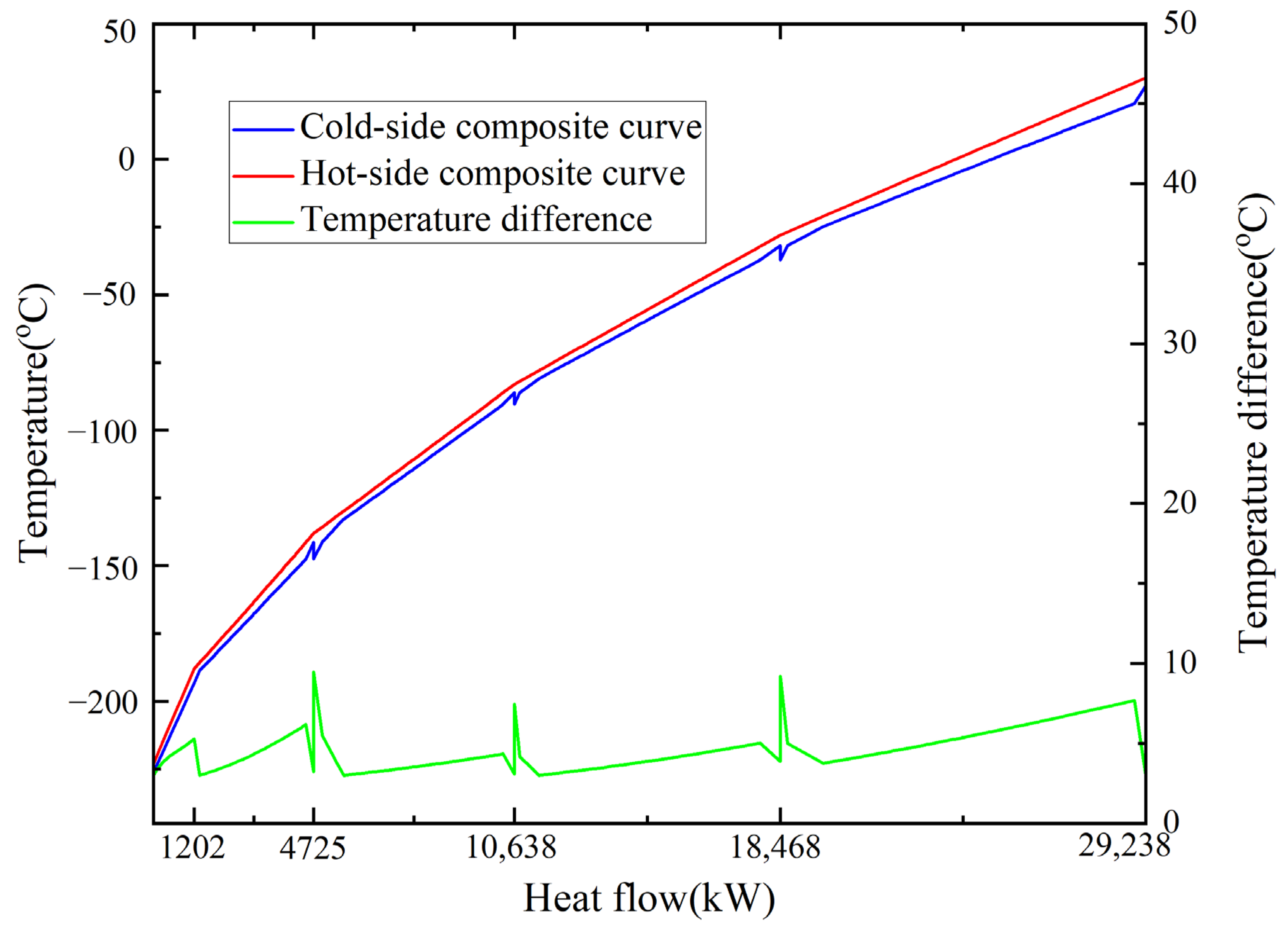
5.3. Heat Transfer Analysis
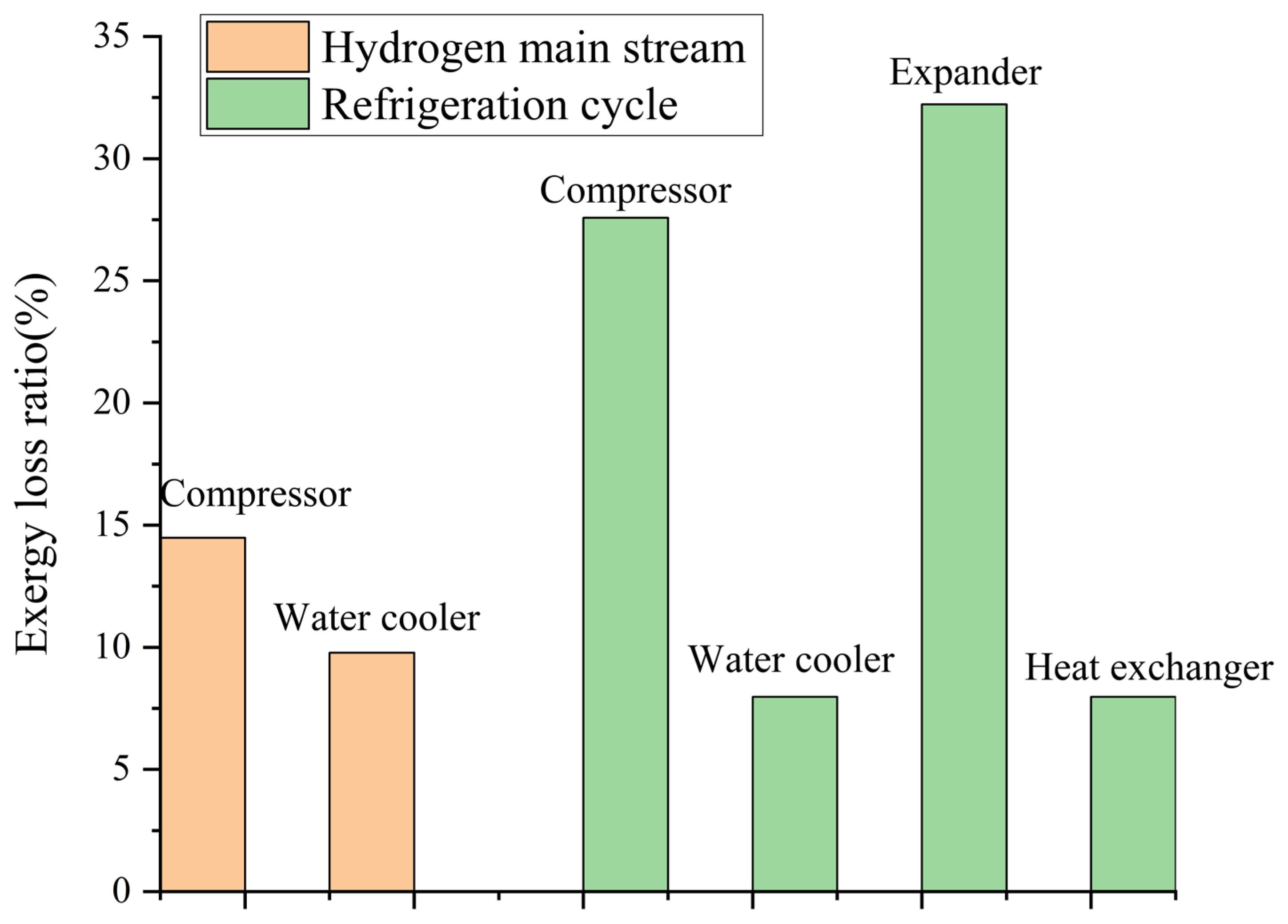
5.4. Exergy Analysis
6. Conclusions
- 1.
- The expansion machines are used to recover the mechanical work, which effectively reduce the energy consumption of cooling hydrogen. With an SEC as low as 5.71 kWh/kgH2, the system can provide a reference for medium and large supercritical hydrogen storage systems.
- 2.
- The cascade arrangement of the J-B cycle improves the performance of the multi-flow heat exchanger because of the small heat transfer temperature difference between the gaseous refrigerant and the hydrogen main stream.
- 3.
- Exergy efficiency of the system is 56.2%. Exergy loss from the compressors and expanders is the most significant. The multi-flow heat exchangers have the minimum exergy loss.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | Abbreviations | ||
| e | exergy | CcH2 | cryogenic compressed hydrogen |
| h | enthalpy | COP | coefficient of performance |
| m | mass flow | DCMR | dual cascade mixed refrigerant |
| p | pressure | DOE | Department of Energy |
| s | entropy | DPMR | dual parallel mixed refrigerant |
| T | temperature | EXE | exergy efficiency |
| W | power | GA | genetic algorithm |
| IPCC | Intergovernmental Panel on Climate Change | ||
| Subscripts | LH2 | liquid hydrogen | |
| COM/C | compressor | LMTD | logarithmic mean temperature difference |
| COOL | water cooler | LNG | liquefied natural gas |
| EXP/E | expander | MR | mixed refrigerant |
| HX | heat exchanger | MRJT | mixed refrigerant Joule–Thomson |
| H2 | hydrogen | MTD | minimum temperature difference |
| in | inlet flow | RBC | reverse Brayton cycle |
| out | outlet flow | SEC | specific energy consumption |
References
- U.S. Energy Information Administration. International Energy Outlook 2023; U.S. Department of Energy: Washington, DC, USA, 2023.
- Chapman, A.; Itaoka, K.; Farabi-Asl, H.; Fujii, Y.; Nakahara, M. Societal penetration of hydrogen into the future energy system: Impacts of policy, technology and carbon targets. Int. J. Hydrogen Energy 2020, 45, 3883–3898. [Google Scholar] [CrossRef]
- Midilli, A.; Dincer, I. Hydrogen as a renewable and sustainable solution in reducing global fossil fuel consumption. Int. J. Hydrogen Energy 2008, 33, 4209–4222. [Google Scholar] [CrossRef]
- Andrews, J.; Shabani, B. Re-envisioning the role of hydrogen in a sustainable energy economy. Int. J. Hydrogen Energy 2012, 37, 1184–1203. [Google Scholar] [CrossRef]
- Turner, J.A. Sustainable Hydrogen Production. Science 2004, 305, 972–974. [Google Scholar] [CrossRef]
- Berry, G.D.; Aceves, S.M. The case for hydrogen in a carbon constrained world. J. Energy Resour. Technol. 2005, 127, 89–94. [Google Scholar] [CrossRef]
- Song, J.; Zhu, Y.; Liang, D.; Cheng, Q.; Yao, D.; Bao, W. Hydrogen energy system for renewable energy consumption. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2021; Volume 233, p. 01083. [Google Scholar]
- Züttel, A. Hydrogen storage methods. Naturwissenschaften 2004, 91, 157–172. [Google Scholar] [CrossRef]
- Bondarenko, V.L.; Ilyinskaya, D.N.; Kazakova, A.A.; Kozlovtsev, P.S.; Lavrov, N.A.; Razenko, E.A. Hydrogen Storage. Chem. Pet. Eng. 2022, 57, 1026–1032. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, X.; Xu, P.; Liu, P.; Zhao, Y.; Yang, J. Development of high pressure gaseous hydrogen storage technologies. Int. J. Hydrogen Energy 2012, 37, 1048–1057. [Google Scholar] [CrossRef]
- Aziz, M. Liquid Hydrogen: A Review on Liquefaction, Storage, Transportation, and Safety. Energies 2021, 14, 5917. [Google Scholar] [CrossRef]
- Barthélémy, H. Hydrogen storage—Industrial prospectives. Int. J. Hydrogen Energy 2012, 37, 17364–17372. [Google Scholar] [CrossRef]
- Sakintuna, F.; Lamari-Darkrim, M. Hirscher, Metal hydride materials for solid hydrogen storage: A review. Int. J. Hydrogen Energy 2007, 32, 1121–1140. [Google Scholar] [CrossRef]
- Principi, G.; Agresti, F.; Maddalena, A.; Russo, S.L. The problem of solid state hydrogen storage. Energy 2009, 34, 2087–2091. [Google Scholar] [CrossRef]
- Aceves, S.M.; Berry, G.D.; Rambach, G.D. Insulated pressure vessels for hydrogen storage on vehicles. Int. J. Hydrogen Energy 1998, 23, 583–591. [Google Scholar] [CrossRef]
- Züttel, A. Materials for hydrogen storage. Mater. Today 2003, 6, 24–33. [Google Scholar] [CrossRef]
- Stetson, N.T.; Bowman, R.C., Jr.; Olson, G.L. Overview of Hydrogen Storage, Transportation, Handling, and Distribution. In Handbook of Hydrogen Energy; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Larsen, A.H.; Simon, F.E.; Swenson, C.A. The Rate of Evaporation of Liquid Hydrogen Due to the Ortho-Para Hydrogen Conversion. Rev. Sci. Instrum. 1948, 19, 266–269. [Google Scholar] [CrossRef]
- Zhuzhgov, A.V.; Krivoruchko, O.P.; Isupova, L.A.; Mart’yanov, O.N.; Parmon, V.N. Low-Temperature Conversion of ortho-Hydrogen into Liquid para-Hydrogen: Process and Catalysts. Review. Catal. Ind. 2018, 10, 9–19. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, Y.; Dong, X.; Yang, J.; Guo, H.; Gong, M. Thermodynamic analysis of low-temperature and high-pressure (cryo-compressed) hydrogen storage processes cooled by mixed-refrigerants. Int. J. Hydrogen Energy 2022, 47, 28932–28944. [Google Scholar] [CrossRef]
- Dewar, J. Liquid Hydrogen. Science 1900, 11, 641–651. [Google Scholar] [CrossRef]
- Krasae-in, S.; Stang, J.H.; Neksa, P. Development of large-scale hydrogen liquefaction processes from 1898 to 2009. Int. J. Hydrogen Energy 2010, 35, 4524–4533. [Google Scholar] [CrossRef]
- Nandi, T.K.; Sarangi, S. Performance and optimization of hydrogen liquefaction cycles. Int. J. Hydrogen Energy. 1993, 18, 131–139. [Google Scholar] [CrossRef]
- McIntosh, G.E. Hydrogen liquefiers since 1950. In AIP Conference Proceedings; Waynert, J., Barclay, J., Breon, S., Daly, E., Demko, J., Dipirro, M., Hull, J., Kelley, P., Kittel, P., Klebaner, A., et al., Eds.; American Institute of Physics: Melville, NY, USA, 2004; Volume 710, pp. 9–15. [Google Scholar]
- Raab, M.; Simon, M.; Ralph-Uwe, D. Comparative techno-economic assessment of a large-scale hydrogen transport via liquid transport media. Int. J. Hydrogen Energy 2021, 46, 11956–11968. [Google Scholar] [CrossRef]
- Tang, L. Hydrogen Liquefaction Process Design and System Simulation Based on Liquid Nitrogen Precooling. Master’s Thesis, Zhejiang University, Hangzhou, China, 2011. [Google Scholar]
- Quack, H. Conceptual design of a high efficiency large capacity hydrogen liquefier. In AIP Conference Proceedings; AIP: Madison, WI, USA, 2002; pp. 255–263. [Google Scholar]
- Cao, X. Design and analysis of a new type of dual-pressure Linde-Hampson hydrogen liquefaction process. Chem. Ind. Eng. Prog. 2021, 40, 6663–6669. [Google Scholar]
- Xu, J.; Lu, Y.; Song, Z.; Chen, X.; Lin, W. Optimal design and analysis of a liquid hydrogen and LNG coproduction system with multistage multicycle cascade refrigeration system. Int. J. Hydrogen Energy 2024, 49, 1432–1449. [Google Scholar] [CrossRef]
- Bi, Y.; Ju, Y. Conceptual design and optimization of a novel hydrogen liquefaction process based on helium expansion cycle integrating with mixed refrigerant pre-cooling. Int. J. Hydrogen Energy 2022, 47, 16949–16963. [Google Scholar] [CrossRef]
- Ansarinasab, H.; Mehrpooya, M.; Mohammadi, A. Advanced exergy and exergoeconomic analyses of a hydrogen liquefaction plant equipped with mixed refrigerant system. J. Clean. Prod. 2017, 144, 248–259. [Google Scholar] [CrossRef]
- Sun, H.; Xu, J.; Wang, C.; Geng, J.; Rong, G.; Gao, X. Optimization and analysis of a cascaded dual mixed refrigerant hydrogen liquefaction process considering the influence of pre-cooling stages. Int. J. Hydrogen Energy 2023, 48, 31653–31670. [Google Scholar] [CrossRef]
- Aasadnia, M.; Mehrpooya, M. Conceptual design and analysis of a novel process for hydrogen liquefaction assisted by absorption precooling system. J. Clean. Prod. 2018, 205, 565–588. [Google Scholar] [CrossRef]
- Yilmaz, C.; Kaska, O. Performance analysis and optimization of a hydrogen liquefaction system assisted by geothermal absorption precooling refrigeration cycle. Int. J. Hydrogen Energy 2018, 43, 20203–20213. [Google Scholar] [CrossRef]
- Moreno-Blanco, J.; Petitpas, G.; Espinosa-Loza, F.; Elizalde-Blancas, F.; Martinez-Frias, J.; Aceves, S.M. The storage performance of automotive cryo-compressed hydrogen vessels. Int. J. Hydrogen Energy 2019, 44, 16841–16851. [Google Scholar] [CrossRef]
- Moreno-Blanco, J.; Petitpas, G.; Espinosa-Loza, F.; Elizalde-Blancas, F.; Martinez-Frias, J.; Aceves, S.M. The fill density of automotive cryo-compressed hydrogen vessels. Int. J. Hydrogen Energy 2019, 44, 1010–1020. [Google Scholar] [CrossRef]
- Moreno-Blanco, J.; Camacho, G.; Valladares, F.; Aceves, S.M. The cold high-pressure approach to hydrogen delivery. Int. J. Hydrogen Energy 2020, 45, 27369–27380. [Google Scholar] [CrossRef]
- Fu, H.; Lv, C.; Meng, J.; He, M.; Wu, J.; Gong, L. Strength and fatigue study of on-board type III cryo-compressed hydrogen storage cylinder. Int. J. Hydrogen Energy 2024, 57, 1081–1088. [Google Scholar] [CrossRef]
- U.S. Department of Energy. On-Board Hydrogen Storage Systems—Projected Performance and Cost Parameters; U.S. Department of Energy: Washington, DC, USA, 2010.
- Song, Z.; Xu, J.; Chen, X. Design and optimization of a high-density cryogenic supercritical hydrogen storage system based on helium expansion cycle. Int. J. Hydrogen Energy 2024, 49, 1401–1418. [Google Scholar] [CrossRef]
- Xu, J.; Song, Z.; Chen, X.; Yang, Q. Design and optimization of high-density cryogenic supercritical hydrogen storage systems integrating with dual mixed refrigerant cycles. Energy 2024, 290, 130124. [Google Scholar] [CrossRef]
- Xu, J.; Huang, F.; Chen, X.; Yang, Q.; Zhang, H. Design and optimization of cryogenic supercritical hydrogen storage system coupled with mixed refrigerant and gas expansion cycle. Appl. Therm. Eng. 2024, 243, 122606. [Google Scholar] [CrossRef]
- Lu, Y.; Chen, X.; Xu, J.; Tian, Y.; Zhang, H. Techno-economic analysis of an advanced polygeneration liquid air energy storage system coupled with LNG cold energy, solar energy, and hydrate based desalination. Energy Convers. Manag. 2023, 297, 117726. [Google Scholar] [CrossRef]
- Aspen Technology, Inc. Aspen HYSYS, V12; AspenTech: Bedford, MA, USA, 2020.
- Incer-Valverde, J.; Mörsdorf, J.; Morosuk, T.; Tsatsaronis, G. Power-to-liquid hydrogen: Exergy-based evaluation of a large-scale system. Int. J. Hydrogen Energy 2023, 48, 11612–11627. [Google Scholar] [CrossRef]
- Xu, J.; Lin, W. Research on systems for producing liquid hydrogen and LNG from hydrogen-methane mixtures with hydrogen expansion refrigeration. Int. J. Hydrogen Energy 2021, 46, 29243–29260. [Google Scholar] [CrossRef]
- Yin, L.; Ju, Y. Process optimization and analysis of a novel hydrogen liquefaction cycle. Int. J. Refrig. 2020, 110, 219–230. [Google Scholar] [CrossRef]


| Equipment | Equation of Exergy Loss |
|---|---|
| Compressor | |
| Cooler | |
| Expander | |
| Heat exchanger |
| Parameters | Value |
|---|---|
| Maximum number of generation | 500 |
| Population size | 233 |
| Crossover fraction | 0.8 |
| Migration fraction | 0.05 |
| Stopping criteria (stall generations) | 50 |
| Parameters | Property | Units | Lower Limit | Upper Limit |
|---|---|---|---|---|
| MP | Molar flow | kmol/h | 800 | 2800 |
| PP1 | Pressure | kPa | 100 | 200 |
| PP3 | Pressure | kPa | 200 | 450 |
| PP5 | Pressure | kPa | 450 | 900 |
| ME | Molar flow | kmol/h | 2200 | 4000 |
| PE1 | Pressure | kPa | 100 | 200 |
| PE4 | Pressure | kPa | 200 | 450 |
| PE6 | Pressure | kPa | 450 | 900 |
| MM | Molar flow | kmol/h | 2500 | 4500 |
| PM1 | Pressure | kPa | 100 | 200 |
| PM5 | Pressure | kPa | 200 | 450 |
| PM7 | Pressure | kPa | 450 | 900 |
| MHH | Molar flow | kmol/h | 3500 | 5500 |
| PHH1 | Pressure | kPa | 100 | 200 |
| PHH6 | Pressure | kPa | 200 | 450 |
| PHH8 | Pressure | kPa | 450 | 900 |
| MLH | Molar flow | kmol/h | 3000 | 5000 |
| PLH1 | Pressure | kPa | 100 | 200 |
| PLH7 | Pressure | kPa | 200 | 450 |
| PLH9 | Pressure | kPa | 450 | 900 |
| PLH11 | Pressure | kPa | 900 | 1700 |
| TLH3 | Temperature | °C | −151 | −141 |
| TLH4 | Temperature | °C | −96 | −86 |
| TLH5 | Temperature | °C | −41 | −31 |
| TLH6 | Temperature | °C | 17 | 27 |
| Stream | Temperature /°C | Pressure /kPa | Molar Flow /(kmol/h) | Exergy/(kJ/kg) |
|---|---|---|---|---|
| P1 | −24.85 | 136.35 | 2451 | 23.8 |
| P2 | 27.00 | 136.35 | 2451 | 16.4 |
| P3 | 61.60 | 321.21 | 2451 | 66.6 |
| P4 | 30.00 | 321.21 | 2451 | 62.9 |
| P5 | 68.46 | 797.99 | 2451 | 114.8 |
| P6 | 30.00 | 797.99 | 2451 | 109.3 |
| E1 | −80.93 | 186.81 | 3465 | 88.8 |
| E2 | −37.22 | 186.81 | 3465 | 64.7 |
| E3 | 20.55 | 186.81 | 3465 | 53.6 |
| E4 | 69.08 | 380.29 | 3465 | 120.2 |
| E5 | 30.00 | 380.29 | 3465 | 115.3 |
| E6 | 67.46 | 652.29 | 3465 | 166.0 |
| E7 | 30.00 | 652.29 | 3465 | 161.4 |
| E8 | −28.00 | 652.29 | 3465 | 169.7 |
| M1 | −132.86 | 125.18 | 3731 | 173.3 |
| M2 | −90.44 | 125.18 | 3731 | 97.4 |
| M3 | −31.87 | 125.18 | 3731 | 46.1 |
| M4 | 20.55 | 125.18 | 3731 | 32.7 |
| M5 | 86.43 | 272.22 | 3731 | 165.3 |
| M6 | 30.00 | 272.22 | 3731 | 152.2 |
| M7 | 84.28 | 512.20 | 3731 | 261.3 |
| M8 | 30.00 | 512.20 | 3731 | 249.1 |
| M9 | −28.00 | 512.20 | 3731 | 260.8 |
| M10 | −83.00 | 512.20 | 3731 | 305.7 |
| HH1 | −188.71 | 106.83 | 5059 | 2334.5 |
| HH2 | −147.48 | 106.83 | 5059 | 1255.4 |
| HH3 | −86.09 | 106.83 | 5059 | 456.3 |
| HH4 | −31.87 | 106.83 | 5059 | 152.6 |
| HH5 | 20.55 | 106.83 | 5059 | 65.5 |
| HH6 | 141.64 | 299.63 | 5059 | 1592.3 |
| HH7 | 30.00 | 299.63 | 5059 | 1334.6 |
| HH8 | 139.48 | 751.17 | 5059 | 2715.9 |
| HH9 | 30.00 | 751.17 | 5059 | 2466.7 |
| HH10 | −28.00 | 751.17 | 5059 | 2541.6 |
| HH11 | −83.00 | 751.17 | 5059 | 2833.6 |
| HH12 | −138.00 | 751.17 | 5059 | 3492.2 |
| LH1 | −226.15 | 141.52 | 4654 | 4608.3 |
| LH2 | −193.27 | 141.52 | 4654 | 2849.3 |
| LH3 | −141.22 | 141.52 | 4654 | 1486.9 |
| LH4 | −86.09 | 141.52 | 4654 | 802.3 |
| LH5 | −31.87 | 141.52 | 4654 | 498.6 |
| LH6 | 20.55 | 141.52 | 4654 | 411.4 |
| LH7 | 120.42 | 338.06 | 4654 | 1661.7 |
| LH8 | 30.00 | 338.06 | 4654 | 1483.2 |
| LH9 | 115.43 | 706.11 | 4654 | 2552.2 |
| LH10 | 30.00 | 706.11 | 4654 | 2390.4 |
| LH11 | 124.60 | 1582.22 | 4654 | 3579.8 |
| LH12 | 30.00 | 1582.22 | 4654 | 3386.3 |
| LH13 | −28.00 | 1582.22 | 4654 | 3461.5 |
| LH14 | −83.00 | 1582.22 | 4654 | 3754.9 |
| LH15 | −138.00 | 1582.22 | 4654 | 4419.3 |
| LH16 | −188.00 | 1582.22 | 4654 | 5690.0 |
| Parameters | Value |
|---|---|
| Compressor power consumption (kW) | 48,913.8 |
| Power recovered by the expander (kW) | 8665.4 |
| The flow rate of mainstream hydrogen (kg/h) | 7200 |
| SEC (kWh/kg) | 5.71 |
| EXE (%) | 56.2 |
| Equipment | Before Optimization | Optimize |
|---|---|---|
| COM-1 | 2.85 | 2.36 |
| COM-2 | 2.82 | 2.48 |
| COM-3 | 2.24 | 2.04 |
| COM-4 | 2.16 | 1.72 |
| COM-5 | 2.46 | 2.17 |
| COM-6 | 2.44 | 1.88 |
| COM-7 | 2.85 | 2.80 |
| COM-8 | 3.05 | 2.51 |
| COM-9 | 2.62 | 2.39 |
| COM-10 | 2.64 | 2.09 |
| COM-11 | 2.70 | 2.24 |
| Refrigerant of Cycle | COP |
|---|---|
| Propane | 1.770 |
| Ethene | 1.657 |
| Methane | 1.805 |
| Hydrogen (higher temperature) | 1.140 |
| Hydrogen (lower temperature) | 0.994 |
| Before Optimization | Optimized | ||||
|---|---|---|---|---|---|
| MITD/°C | LMTD/°C | MITD/°C | LMTD/°C | UA/(kW/°C) | |
| HX-1 | 5.00 | 6.41 | 3.00 | 5.27 | 2044 |
| HX-2 | 5.00 | 6.85 | 3.00 | 3.88 | 2017 |
| HX-3 | 5.00 | 5.69 | 3.00 | 3.72 | 1590 |
| HX-4 | 4.72 | 4.94 | 3.00 | 4.22 | 836 |
| HX-5 | 5.02 | 6.64 | 3.00 | 4.21 | 285 |
| Equipment | Exergy Loss/kW | Exergy Damage Rate/% |
|---|---|---|
| COM-1 | 234.32 | 1.72 |
| COM-2 | 236.69 | 1.74 |
| COM-3 | 273.51 | 2.01 |
| COM-4 | 208.77 | 1.53 |
| COM-5 | 318.03 | 2.34 |
| COM-6 | 262.75 | 1.93 |
| COM-7 | 536.07 | 3.94 |
| COM-8 | 486.67 | 3.58 |
| COM-9 | 426.98 | 3.14 |
| COM-10 | 369.37 | 2.71 |
| COM-11 | 400.91 | 2.95 |
| COM-12 | 322.67 | 2.37 |
| COM-13 | 325.04 | 2.39 |
| COM-14 | 326.13 | 2.40 |
| COM-15 | 327.25 | 2.40 |
| COM-16 | 331.23 | 2.43 |
| COM-17 | 339.46 | 2.49 |
| EXP-1 | 455.44 | 3.35 |
| EXP-2 | 477.25 | 3.51 |
| EXP-3 | 613.11 | 4.50 |
| EXP-4 | 1301.84 | 9.56 |
| EXP-5 | 1538.26 | 11.30 |
| COOL-1 | 3.75 | 0.03 |
| COOL-2 | 5.49 | 0.04 |
| COOL-3 | 4.90 | 0.04 |
| COOL-4 | 4.61 | 0.03 |
| COOL-5 | 13.06 | 0.10 |
| COOL-6 | 12.24 | 0.09 |
| COOL-7 | 257.68 | 1.89 |
| COOL-8 | 249.25 | 1.83 |
| COOL-9 | 178.54 | 1.31 |
| COOL-10 | 161.77 | 1.19 |
| COOL-11 | 193.49 | 1.42 |
| COOL-12 | 216.34 | 1.59 |
| COOL-13 | 219.76 | 1.61 |
| COOL-14 | 220.97 | 1.62 |
| COOL-15 | 221.52 | 1.63 |
| COOL-16 | 224.33 | 1.65 |
| COOL-17 | 227.53 | 1.67 |
| HX-1 | 209.49 | 1.54 |
| HX-2 | 192.95 | 1.42 |
| HX-3 | 255.72 | 1.88 |
| HX-4 | 331.76 | 2.44 |
| HX-5 | 95.25 | 0.70 |
| Overall exergy loss | 13,612.11 | 100.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, R.; Yue, T.; Xu, J.; Wu, W.; Chen, X.; Dou, B. Thermodynamics Analysis of Cryogenic Supercritical Hydrogen Storage System Based on Multi-Stage Joule–Brayton Cycle. Cryo 2025, 1, 6. https://doi.org/10.3390/cryo1020006
Wan R, Yue T, Xu J, Wu W, Chen X, Dou B. Thermodynamics Analysis of Cryogenic Supercritical Hydrogen Storage System Based on Multi-Stage Joule–Brayton Cycle. Cryo. 2025; 1(2):6. https://doi.org/10.3390/cryo1020006
Chicago/Turabian StyleWan, Ruiqi, Tenglong Yue, Jingxuan Xu, Wenjie Wu, Xi Chen, and Binlin Dou. 2025. "Thermodynamics Analysis of Cryogenic Supercritical Hydrogen Storage System Based on Multi-Stage Joule–Brayton Cycle" Cryo 1, no. 2: 6. https://doi.org/10.3390/cryo1020006
APA StyleWan, R., Yue, T., Xu, J., Wu, W., Chen, X., & Dou, B. (2025). Thermodynamics Analysis of Cryogenic Supercritical Hydrogen Storage System Based on Multi-Stage Joule–Brayton Cycle. Cryo, 1(2), 6. https://doi.org/10.3390/cryo1020006






