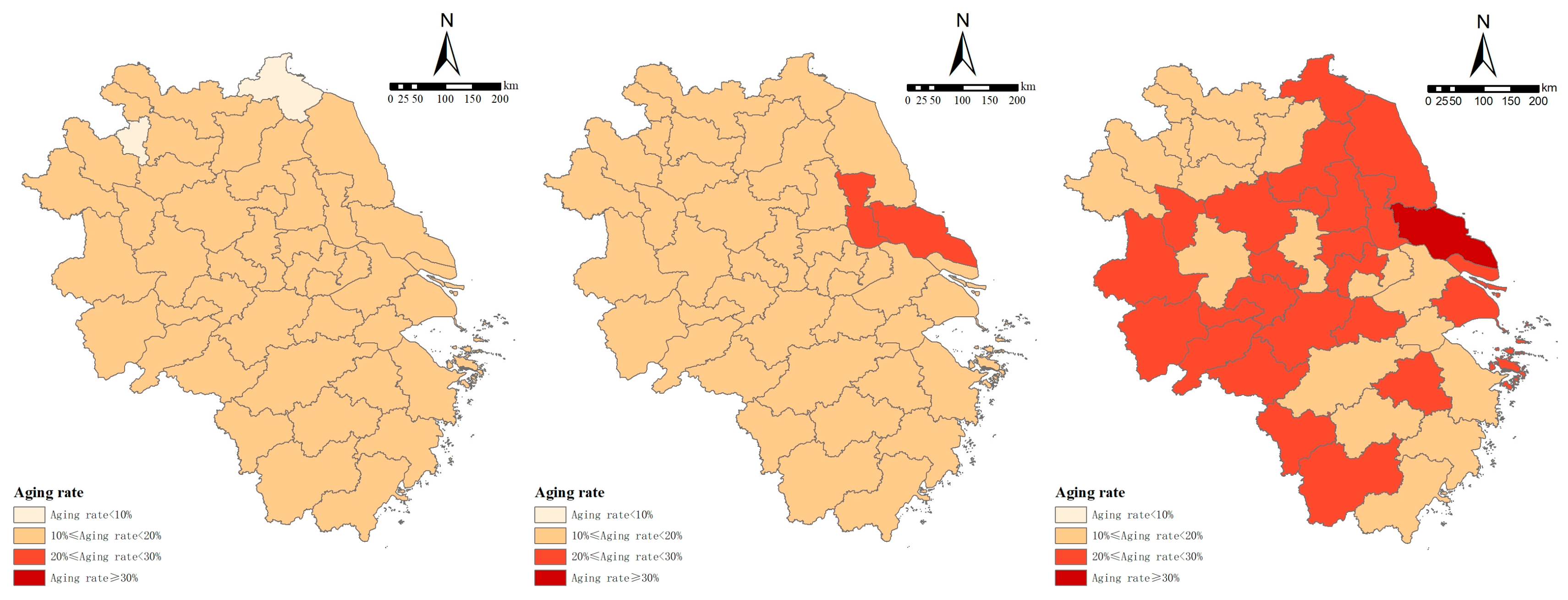
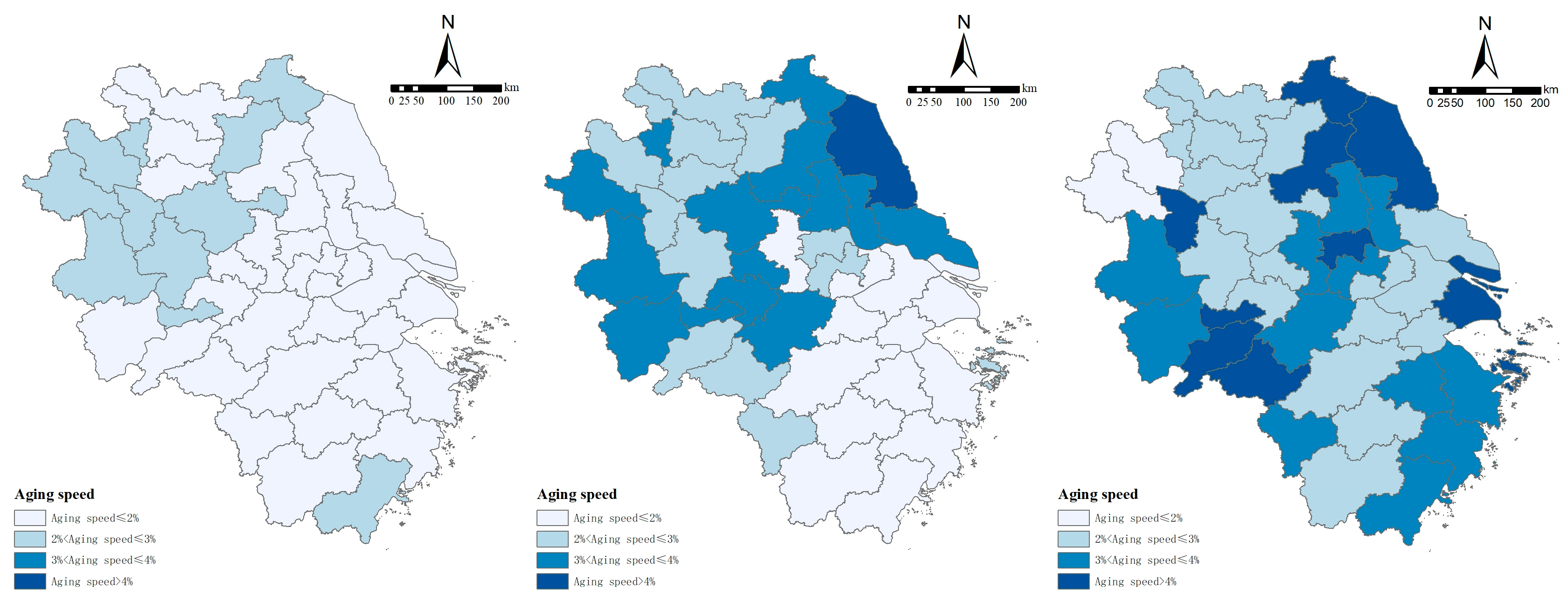
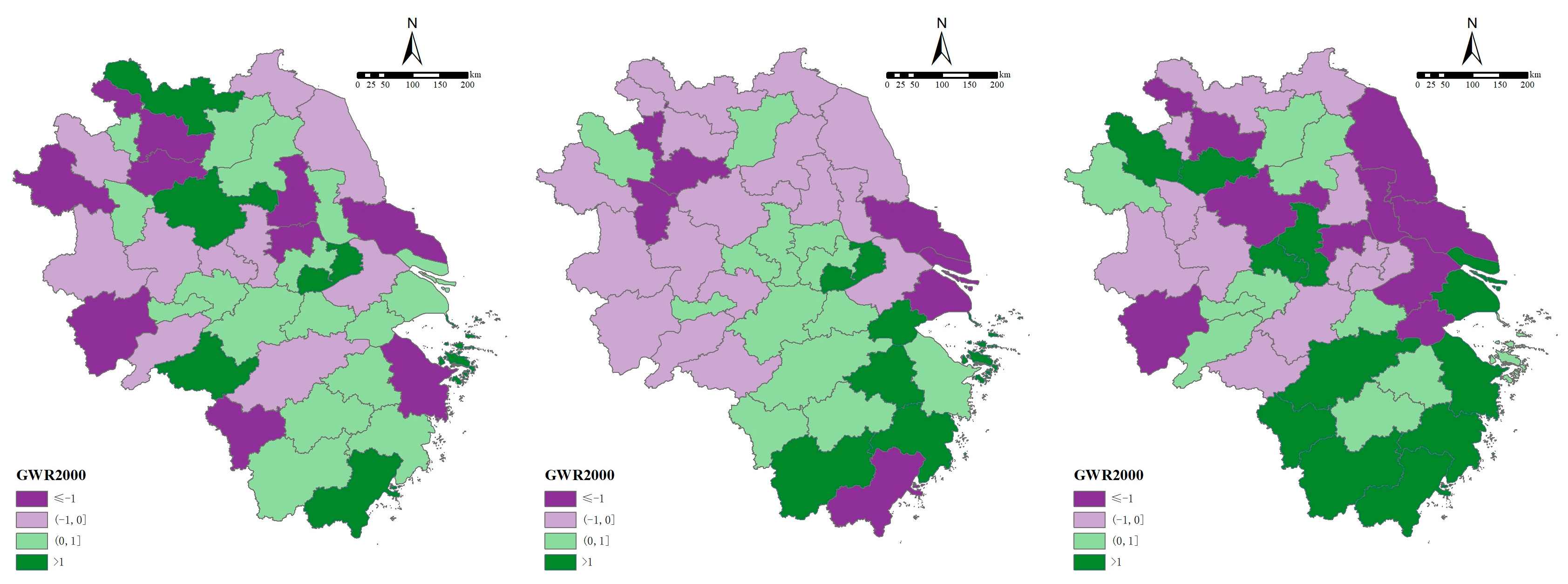
5.1. Single Indicator
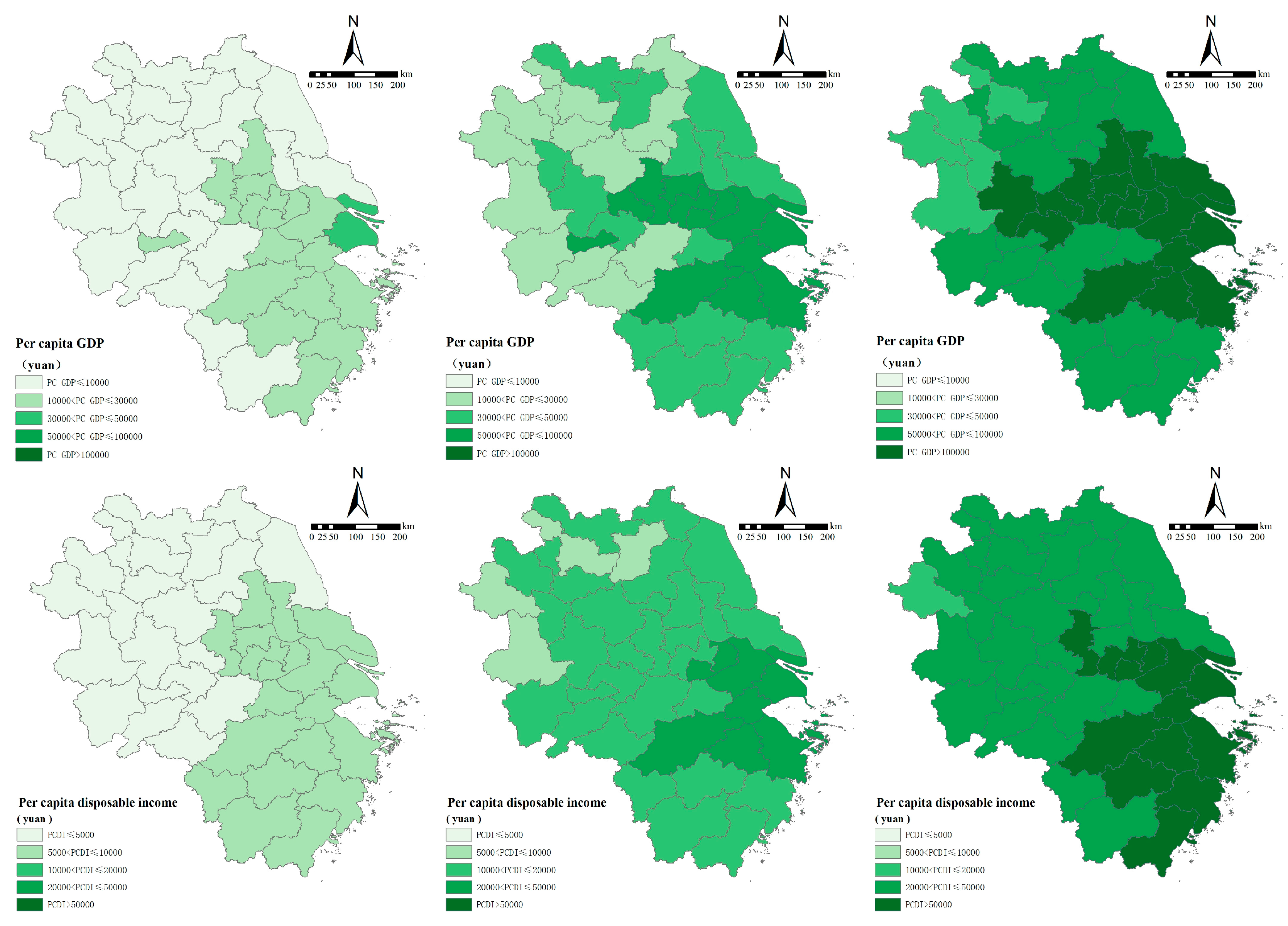
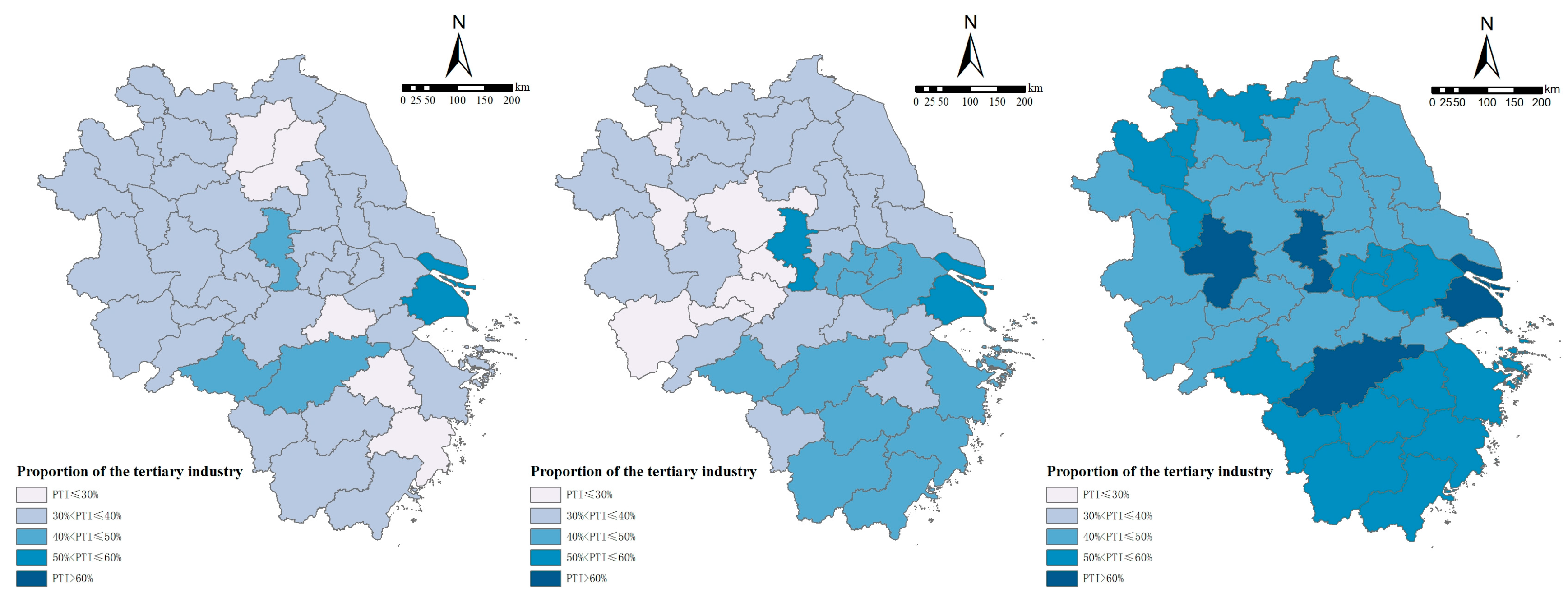
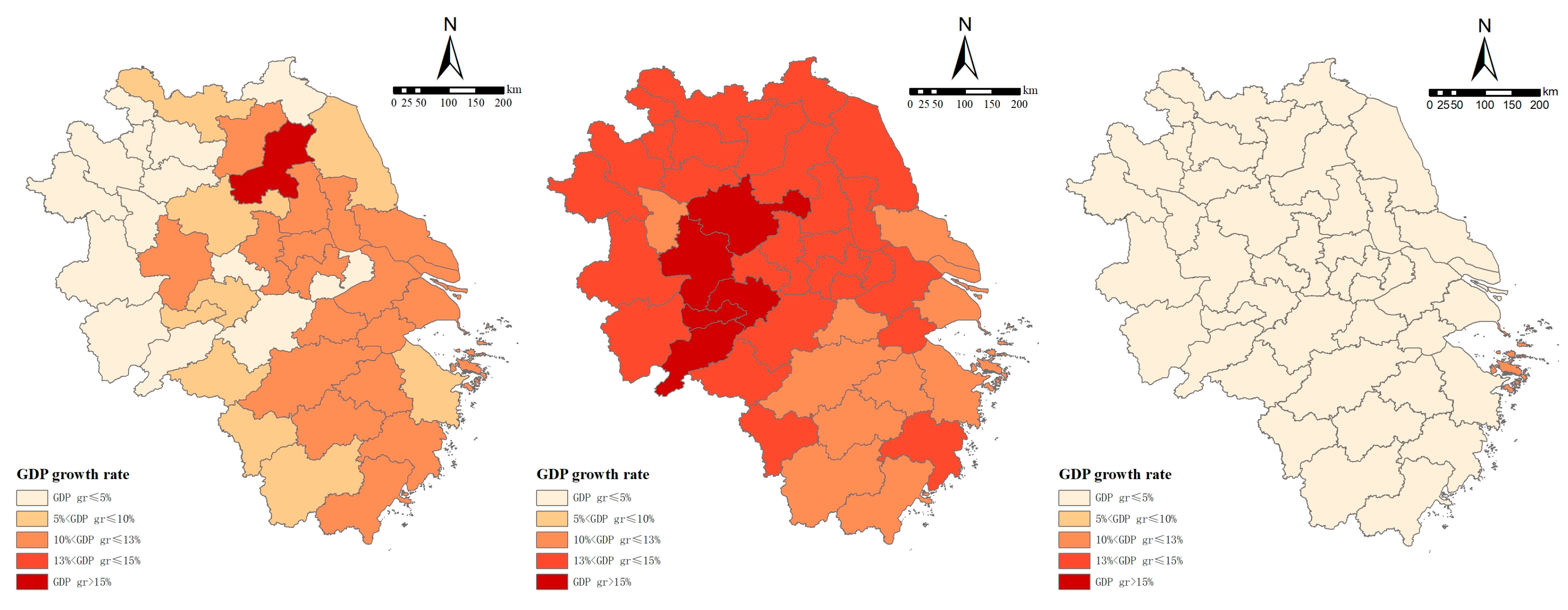
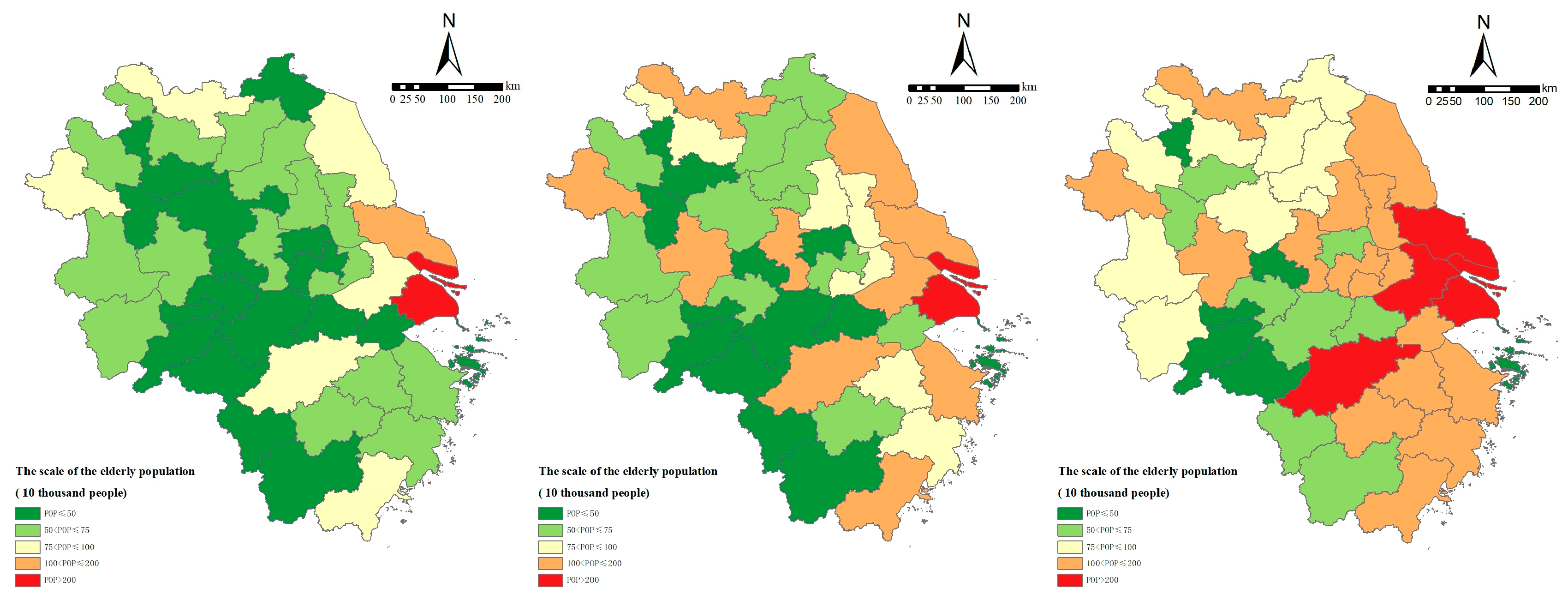
To explore the mechanism through which population aging affects different dimensions of economic growth, this section uses three-phase data on population aging and economic growth from 2000 to 2020. The indicators of aging scale, structure, and speed are incorporated into a two-way fixed-effects panel regression model to investigate the impact mechanisms of the aging scale, structure, and speed on the GDP, per capita GDP, residents’ disposable income, and GDP growth rate. For the aging scale, two indicators are selected: the size of the elderly population and elderly population density; for the aging structure, four indicators are used: the aging rate, elderly dependency ratio, longevity coefficient, and proportion of younger elderly; and for the speed of aging, the change rate of the aging rate is employed. The benchmark regression results are shown in
Table 4.
In terms of the mechanism of the impact of population aging on the GDP, both the size and density of the elderly population passed the 1% significance test, with coefficients of 0.970 and 0.319, respectively, which indicates a significant positive effect on the total GDP. This effect may benefit from the economic effects of elderly population agglomeration in core cities: the concentration of elderly populations in cities such as Shanghai and Nanjing has spurred the development of specialized consumer markets for elderly care services and healthcare, boosting economic output. The longevity coefficient passed the 1% significance level with a coefficient of 0.614, which suggests that the longevity coefficient has a significant positive effect on the total GDP. This reflects that, as the population of those aged 80 and above grows, their demand for high-end elderly care services such as medical nursing, rehabilitation, and aging-friendly home renovations has increased significantly, thereby generating a “silver economy”.
It is worth noting that the impacts of the aging rate and elderly dependency ratio were not significant. As a relative indicator, the aging rate is heavily influenced by regional economic disparities: high aging rates coexist with strong economies in core cities, while low aging rates in marginal cities correspond to low economic bases, which dilutes the overall correlation. The non-significant negative effect of the elderly dependency ratio may be due to the gradual improvement of the social security system in the Yangtze River Delta, which has alleviated some family care burdens and weakened the direct impact of traditional dependency pressures on the total economic output. In addition, the speed of aging was significant at the 10% level with a coefficient of −0.700, which indicates that excessive aging can inhibit economic aggregate growth in the short term due to a shrinking labor supply and surging social security expenditures.
Regarding the mechanism of impact of population aging on the per capita GDP, the size of the elderly population passed the 1% significance level with a coefficient of −1.737. As they are non-working-age individuals, the expansion of the elderly population directly increases the denominator (total population), while the silver economy they bring is less than the economic output of working-age populations, which leads to a decrease in the per capita GDP. The elderly population density passed the 1% significance level with a coefficient of 1.766, which indicates a significant positive effect on the per capita GDP. This suggests that, in core areas with high urbanization levels, the agglomeration effect of high-quality public services and industrial resources can effectively enhance the per capita output. The aging rate passed the 1% significance level with a coefficient of 8.337. This result may seem contradictory to traditional theory, but actually reflects the special development path of the Yangtze River Delta’s core areas: cities such as Shanghai and Suzhou have successfully offset the impact of declining labor quantities through technological progress and industrial upgrading. The elderly dependency ratio passed the 1% significance level with a coefficient of −3.492, which indicates that the traditional elderly care model of relying on children still has a negative impact on per capita wealth accumulation. The longevity coefficient, the proportion of younger elderly, and the speed of aging were all significantly negative, which suggests that increased elderly care costs brought by more long-lived seniors inhibit the per capita GDP.
Concerning the mechanism of impact of population aging on urban and rural residents’ disposable income, the elderly population density passed the 5% significance level with a coefficient of 0.599, which is consistent with the logic that “high density corresponds to high economic levels”—cities with concentrated elderly populations often have more complete income distribution systems and social security institutions. The aging rate passed the 1% significance level with a coefficient of 6.761, which is also related to the higher pension and property income of elderly groups in core areas. The elderly dependency ratio passed the 1% significance level with a coefficient of −5.379, indicating that, in marginal areas with insufficient social security coverage, increased family care burdens squeeze the actual purchasing power of disposable income. The proportion of younger elderly passed the 1% significance level with a coefficient of −0.664, suggesting that the rise in the proportion of younger elderly has not released the expected “silver workforce” dividend but instead has had a negative impact on resident income due to low employment participation and social security pressures.
In terms of the mechanism of impact of population aging on the GDP growth rate, the elderly population density passed the 10% significance level with a coefficient of −0.841, and the aging rate passed the 1% significance level with a coefficient of −7.454, both indicating that mature economies with high aging levels tend to experience slower growth due to rising labor costs and a diminishing marginal efficiency of capital. The elderly dependency ratio passed the 1% significance level with a coefficient of 5.436, and the proportion of younger elderly passed the 10% significance level with a coefficient of 0.724, revealing that rising elderly dependency ratios drive technological innovation and younger elderly supplement labor gaps through employment participation or intergenerational care, indirectly supporting economic growth rates.
For control variables, fixed-asset investment and the number of patent authorizations were significantly positive for the GDP, per capita GDP, and residents’ disposable income, reflecting the driving role of physical capital accumulation and technological progress on economic scale and quality. Their significant negative effects on the GDP growth rate align with the law of diminishing marginal returns to investment. The number of social employees was significantly positive only for residents’ disposable income, as expanded employment directly increases the household wage income, demonstrating the direct pull of labor quantity on current income. The average education years was significantly positive only for the total GDP, as education enhances human capital to promote technological innovation and production efficiency, with its long-term cumulative effects more significantly impacting total economic growth. The Gini coefficient was significantly negative for the GDP, per capita GDP, residents’ disposable income, and GDP growth rate (at least passing the 5% significance test), indicating that income inequality inhibits economic performance by suppressing consumer demand and social stability.
5.2. Composite Indicators
The previous analysis of the mechanism of impact of population aging on economic growth levels was based on a single indicator for both the dependent and independent variables. However, in the actual economic operation and process of population aging, there are complex interrelations among various factors. In this case, explaining this impact with a single indicator may not be accurate enough. Therefore, this study, based on the indicator system constructed in
Table 1 and
Table 2, uses the entropy method to determine weights and performs a comprehensive measurement of population aging and economic growth levels. The composite score of the economic growth level is taken as the dependent variable, while the composite score of the population aging level is taken as the independent variable, and the model is analyzed. The regression results are shown in
Table 5.
Table 5 reports the regression results of the impact of population aging on economic growth in the Yangtze River Delta cities under different model specifications. Models (1) and (2) are mixed OLS regressions, corresponding to situations with and without control variables, respectively. Models (3) and (4) are fixed-city and -year two-way fixed-effects models. The results show that, regardless of whether control variables are included, the impact of the aging level on economic growth is significant at the 1% significance level, which indicates that the baseline regression model has strong robustness. Further comparison of the models’ fit shows that the R
2 of model (4) reaches 0.973, which is higher than the 0.891 of the mixed OLS, and the F-statistic is 473.4, which is significantly higher than the 167.9 of the mixed OLS model. This indicates that the two-way fixed-effects model has the best explanatory power among all models. Therefore, the regression results of model (4) are used as the core basis for analysis in this section.
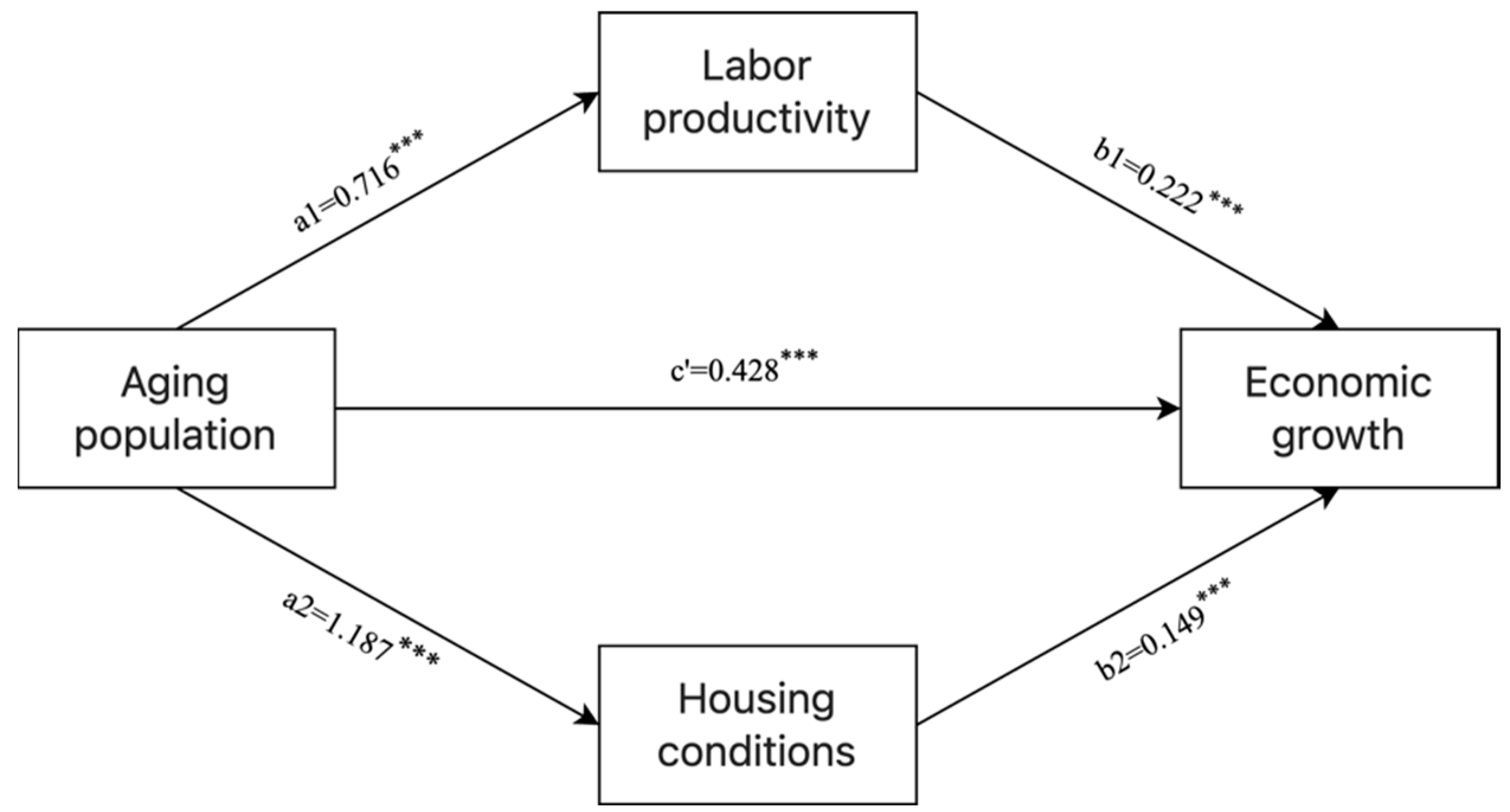
In terms of core explanatory variables, after isolating these confounding factors, the net effect of population aging on economic growth is clearly presented: the regression coefficient for the level of population aging in the Yangtze River Delta city region is 0.428, and it is significant at the 1% level. This indicates that, for every 1-unit increase in the aging level, the comprehensive economic growth score rises significantly by 0.428 units. This result breaks the traditional belief that “aging inevitably hampers economic growth” and shows that, in the Yangtze River Delta region, population aging has a significant positive impact on economic growth through mechanisms such as improvements in labor quality, human capital accumulation, and industrial upgrading.
The traditional view of the negative impact of aging is largely based on the national average, focusing on linear mechanisms like the shrinking labor supply and rising social security expenditures. However, these assumptions often rely on the premise that the economy is in a stage of slow technological progress, has a simple industrial structure, and has insufficient human capital accumulation. In contrast, the Yangtze River Delta, as one of China’s most economically dynamic and innovative regions, exhibits a more complex transformation in the interaction between aging and economic growth.
From a mechanism perspective, population aging in the Yangtze River Delta transforms into a positive driver of economic growth through multiple channels. First, the aging process forces the industrial structure to upgrade toward technology- and knowledge-intensive industries. Faced with rising labor costs, enterprises in the Yangtze River Delta accelerate automation and intelligent transformation, driving the manufacturing industry from “labor-driven” to “technology-driven.” This transformation not only mitigates the negative effects of a shrinking workforce but also creates new growth space through improvements in total factor productivity. Second, the relatively high level of human capital accumulation in the region allows the elderly population to continue participating in the production process. In core cities like Shanghai, Suzhou, and Hangzhou, the elderly have higher education levels and longer life expectancies. Through flexible retirement systems, reemployment mechanisms, and volunteer services, their wealth of professional experience and industry insights becomes a productive resource, forming a silver-haired human capital dividend. Third, the “silver economy” driven by aging has become a new growth pole. The elderly population’s demand for healthcare, rehabilitation care, age-friendly products, and smart elderly services has led to rapid expansion in related industries, forming a complete industry chain from product research and development to service supply. This not only boosts consumption but also nurtures new economic growth points. Fourth, the well-developed social security system and regional collaboration mechanisms in the Yangtze River Delta have alleviated the negative impact of aging. Through institutional innovations such as cross-region settlement of medical insurance and coordinated pension resource allocation, the three provinces and one city have reduced the public service pressure brought by aging, making their economic growth less constrained by traditional pension burdens.
The regression results of control variables also contain rich economic implications. The coefficient of social fixed-asset investment is 0.092, significant at the 1% level, indicating that, as a traditional driver of economic growth, fixed-asset investment still has a sustained positive driving effect on the economy of the Yangtze River Delta. Through expanding the production scale and improving infrastructure, it provides a solid foundation for economic growth. The coefficient of the Gini coefficient is −0.111 and is negatively significant at the 5% level, suggesting that reducing income inequality has a positive effect on economic growth. This aligns with the economic logic that “expansion of the middle-income group promotes the upgrading of the consumer market.” A more balanced income distribution can effectively boost aggregate social demand and drive economic growth. The coefficient of patent grants is 0.166 and is positively significant at the 5% level, reflecting the important role of innovation outcomes in driving economic growth in the Yangtze River Delta. Technological innovation has become the core driving force for high-quality economic development. The regression result for the number of employed persons varies between models. In the two-way fixed-effects model, the coefficient is positive but not significant, while, in the mixed OLS regression, the coefficient is negative and significant at the 1% level. This contradiction may arise from the control of city-specific heterogeneity in the fixed-effects model. After removing time-invariant city characteristics, the expansion of the labor force size may weaken its impact on economic growth. Additionally, due to factors like rising labor costs and higher skill requirements in the Yangtze River Delta, the mixed OLS model may show a negative relationship between labor quantity and economic growth. The coefficient of education level is 0.122 and is positively significant at the 1% level, fully reflecting the strong promoting effect of human capital accumulation on economic growth. Higher education levels not only directly improve labor productivity but also enhance innovation ability, promote technological absorption, and optimize the employment structure, providing sustainable endogenous power for economic growth in the Yangtze River Delta.
Overall, the regression results of model (4) not only verify the special promoting effect of population aging on economic growth in the Yangtze River Delta but also reveal the complex mechanisms of impact of multi-dimensional factors such as investment, income distribution, innovation, labor structure, and human capital on regional economic development.
5.3. Endogeneity Treatment
In the previous benchmark regression, the positive effect of population aging in the Yangtze River Delta on economic growth has been verified. However, there may be endogeneity issues. Specifically, one is reverse causality: economic growth may increase the level of population aging through improvements in medical conditions, extended life expectancy, etc.; the second is omitted variables: although city and year fixed-effects were controlled for and control variables were added in the previous regression, economic growth may still be influenced by other unobserved factors. To address this, this section introduces the number of healthcare professionals in health institutions as an instrumental variable to mitigate the endogeneity problem of the model (
Table 6). The rationale for this choice is as follows: the allocation of health resources is significantly related to population aging, and a sufficient number of medical professionals can improve health levels and extend life expectancy, directly increasing the aging level and thus meeting the “relevance” requirement for instrumental variables; the number of healthcare professionals is more determined by regional medical planning, historical healthcare resource distribution, and other exogenous policy factors, and does not have reverse causality with the current level of economic growth, meeting the “exogeneity” requirement for instrumental variables. Model (1) presents the two-way fixed-effect regression result with the number of healthcare professionals as the instrumental variable. The result shows that the Kleibergen–Paap rk LM statistic passes the 10% significance test, indicating no identification problem; the Kleibergen–Paap rk Wald F statistic value exceeds the 10% critical value, suggesting no weak instrument problem. After addressing endogeneity, the coefficient of the effect of population aging on economic growth rises to 0.917 and is significant at the 1% level. This result is significantly higher than the coefficient from the benchmark regression, suggesting that the benchmark model may have underestimated the effect due to endogeneity. The instrumental variable approach, by severing the reverse causality chain and controlling for omitted variables, more accurately captures the true promoting effect of population aging on economic growth. As the number of medical professionals increases and regional aging intensifies, the accumulation of human capital and the effective supply of labor improve, further positively driving economic growth.
To further verify the robustness of the endogeneity treatment, this study adopts a method from Gu Hongming [
22] and selects the proportion of the population aged 65 and above as an instrumental variable in model (2). This indicator is highly correlated with the endogenous explanatory variable, “aging level,” and, as a lagging population structure indicator, it is less affected by reverse economic growth impacts, satisfying the relevance and exogeneity requirements for an instrumental variable. The model passes both the identification test and the weak instrument test. The effect of population aging on economic growth is significant at the 5% level, with a coefficient of 0.236. Although this coefficient is lower than the estimate when the number of healthcare professionals is used as the instrumental variable, the sign remains consistent and statistically significant, indicating that the positive effect of population aging on economic growth is stable across different instrument choices. This result reflects the reliability of the endogeneity treatment and suggests that the mechanism through which population aging affects economic growth may vary depending on the perspective of the selected instrumental variable. However, the core conclusion remains unchanged, which further reinforces the robustness of the finding that population aging in the Yangtze River Delta has a positive effect on economic growth.
5.5. Heterogeneity Analysis
5.5.1. Threshold Effect Analysis
To further explore the nonlinear relationship between population aging and economic growth in the Yangtze River Delta, this section tests the existence of threshold effects and determines the number of thresholds.
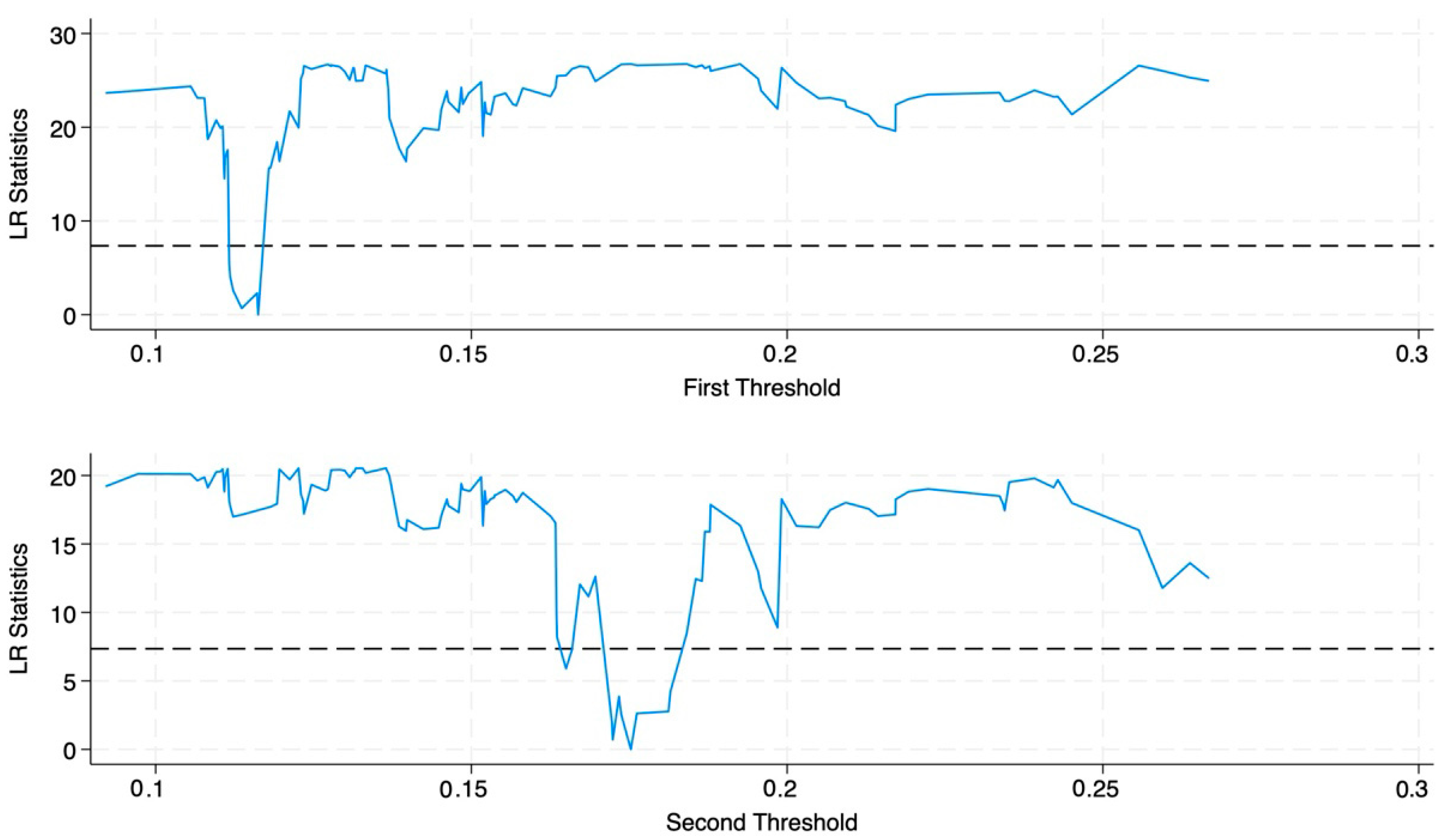
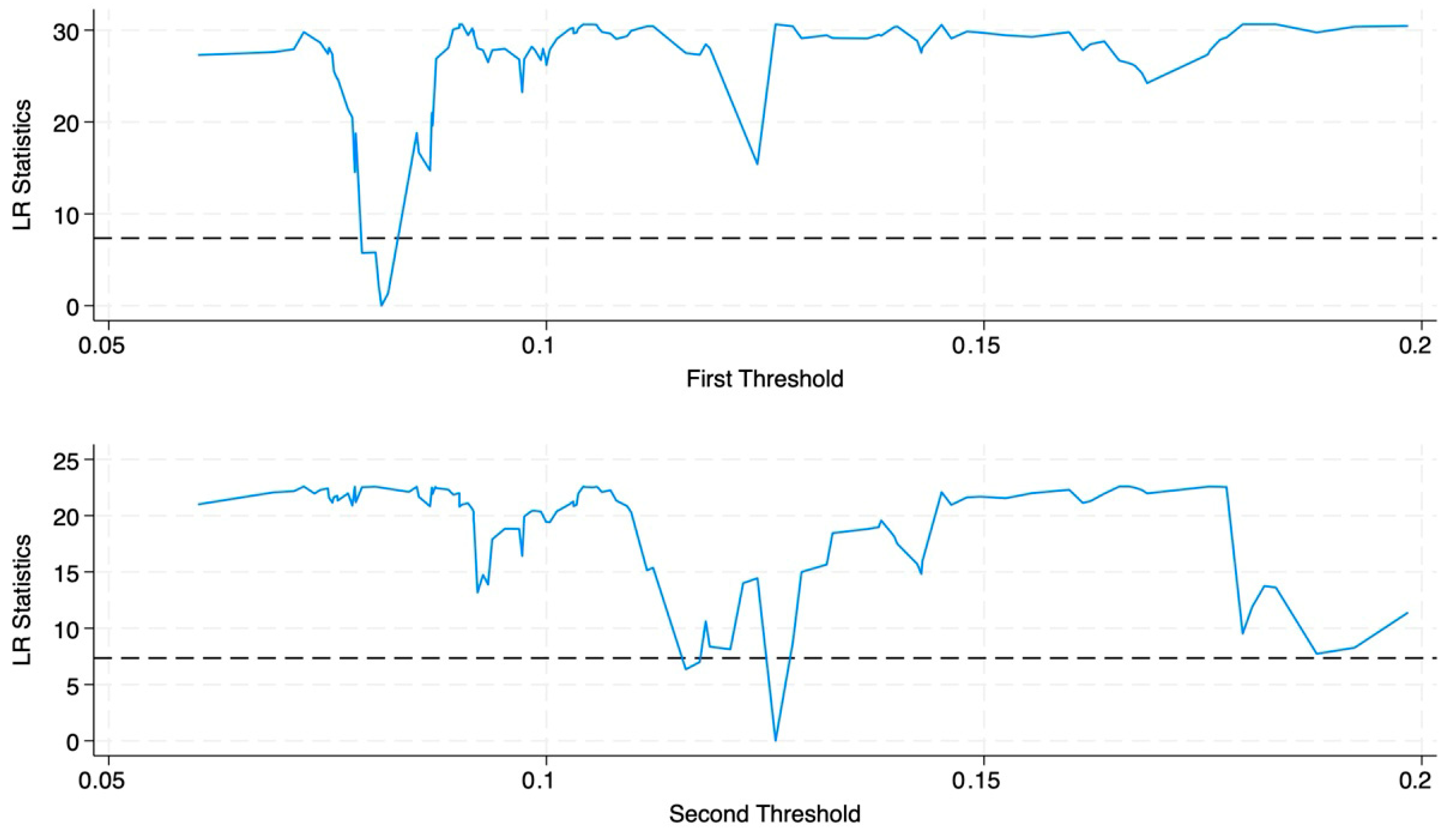
Table 8 presents the tests and threshold values using the proportion of the population aged 60 and above and the proportion aged 65 and above as threshold variables. The results show that the single thresholds of both variables passed the significance test at the 1% level, and the dual thresholds passed the 5% significance test. However, the F-statistic for the triple threshold did not pass the significance test, indicating that the model has dual thresholds. Regarding the threshold values, the first threshold for the population aged 60 and above, as a proportion of the total population, is 11.63% and the second threshold is 17.53%. For the population aged 65 and above, the first threshold is 8.12% and the second threshold is 12.62%. Combining the LR test statistics in
Figure 8 and
Figure 9, it is found that the LR values corresponding to the threshold estimates are significantly smaller than the critical value of 7.35, so it can be concluded that the threshold estimates are real and valid.
After confirming the significant nonlinear relationship between population aging and economic growth through strict threshold effect tests, the threshold value of the proportion of the population aged 60 and above was incorporated into the baseline regression model to further analyze the economic impact mechanisms at different stages of aging (
Table 9).
This study shows that, when the proportion of the population aged 60 and above is below 11.63%, the aging process significantly promotes economic growth, with a coefficient of 0.442 at the 1% confidence level. During this stage, the elderly population dividend released in the early stages of aging plays a role, as the demand for industries such as healthcare and eldercare services surges with the expanding elderly population, stimulating the consumption market and increasing participation in social production due to the wealth of experience of the elderly, and thereby injecting vitality into economic growth. When the proportion is between 11.63% and 17.53%, the positive effect of aging on economic growth weakens, with the coefficient decreasing to 0.180 at the 10% significance level. In this phase, the negative effects of aging begin to emerge, with issues such as reduced labor supply and increased social security burdens gradually becoming prominent and counteracting some of the positive driving effects, which leads to a decline in the aging elasticity of economic growth. However, when the proportion exceeds 17.53%, the coefficient rises to 0.282 and passes the 1% significance test. This may be due to the deepening of aging forcing policy adjustments and technological innovations. The government increases support for the eldercare industry and companies accelerate their intelligent transformation to fill the labor gap, which stimulates new sources of economic growth and strengthens the role of aging in promoting economic growth. The robustness test using the proportion of the population aged 65 and above as a threshold variable yields results that are consistent with the above conclusions, further confirming the strong stability and reliability of the nonlinear mechanism of impact of population aging on economic growth.
5.5.2. Sub-Sample Analysis
Considering the significant differences in the aging process and economic development stages among the four provinces and cities in the Yangtze River Delta, this section conducts a sub-sample regression analysis on Anhui, Jiangsu, and Zhejiang (Shanghai is not included due to insufficient sample size) in order to reveal the regional heterogeneity of the impact of population aging on economic growth.
The regression results in
Table 10 show that the effect of population aging on economic growth in Anhui province does not pass the significance test. This may be closely related to the current economic development characteristics of the province: As a relatively underdeveloped province in the Yangtze River Delta, Anhui has long faced pressure of labor outflow, with a large number of working-age laborers migrating to economic hubs like Jiangsu, Zhejiang, and Shanghai. This has led to more “passive aging” in the region, where the aging population has a counteracting effect on economic growth, resulting in no significant impact.
In contrast, the regression results for Jiangsu show a significant positive effect of population aging on the economic growth at the 5% significance level, with a coefficient of 0.513. This is closely linked to the province’s high economic development level and optimized industrial structure. As a manufacturing powerhouse in the Yangtze River Delta, Jiangsu has faced labor cost increases earlier. The aging population has accelerated the transition of the labor market to a “quality-oriented” one, forcing enterprises to increase their investments in human capital and technological innovation. This has driven industry to upgrade toward high-end manufacturing and modern services. At the same time, Jiangsu’s comprehensive social security system and health services have effectively improved the health participation capacity of the elderly workforce, thus significantly promoting economic growth through human capital accumulation and industrial structure optimization.
The regression results for Zhejiang show a significant positive effect of population aging on economic growth at the 10% significance level, with a coefficient of 0.369. As a major province for private and digital economies, Zhejiang has a notable feature of clustered development of small- and medium-sized enterprises, high innovation vitality, and efficient technology transformation. Population aging has driven enterprises to accelerate their automation and intelligent upgrades to address the marginal decline in the labor force. Meanwhile, Zhejiang’s per capita disposable income has long been among the highest in the country, and the consumption structure upgrade under aging has opened new space for economic growth. This has allowed the positive effects of aging to be manifested under the dual support of innovation-driven growth and consumption upgrading.
The differences in the regression results across the three provinces reflect that the mechanism by which aging impacts economic growth diverges with changes in regional development levels, industrial structures, and labor market characteristics. They also provide empirical evidence that supports differentiated responses to population aging within the Yangtze River Delta: underdeveloped areas need to prioritize solving the dual constraints of labor outflow and lagging industrial transformation, while more developed areas can leverage their advantages in human capital and technological innovation to turn aging into a structural driving force for high-quality economic development.