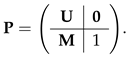Zero-Inflated Distributions of Lifetime Reproductive Output
Abstract
1. Introduction
2. Notation
3. Zero-Inflated Distributions
- The moments are also mixtures. Thus,where is the ith moment of the distribution , and similarly for , .
- All of the moments (except for that of order zero) of are zero.
- The moments of , the distribution conditional on survival to maturation, are
4. Calculating the Zero-Inflated Distribution
- 1.
- We begin by generating the moments of LRO using the Markov chain with rewards (MCWR) method. You can generate as many as desired; here, we will consider the first moment (the mean), the second moment (which provides the variance), and the third moment (which provides the skewness) of the distribution . These moments of LRO are provided as vectors , , and , the calculation of which is given in Appendix A.1. The moments for ‘lifetime’ reproduction; i.e., starting from the first age class, are
- 2.
- Next, obtain the probability of failing to mature using the absorbing Markov chain created from . The transition matrixThe matrix is written in column-to-row orientation and contains transition probabilities from living states to absorbing states. We create two absorbing states: the first corresponds to death before maturity, the second to maturity before death [22,23]. Define as the set of age classes for which fertility is greater than 0. An individual that reaches the set is absorbed in the ‘maturity before death’ absorbing state.The resulting mortality matrix isCreate a new transition matrix , which is equal to except that the that columns corresponding to are zero:Calculate the fundamental matrix corresponding to ,The matrix giving probabilities of absorption isRow 1 of gives the probabilities of death before maturity starting from each possible stage. Thus, starting from birth,The calculation is easily implemented in a few lines of Matlab code.
- 3.
- Calculate the moments and statistics of the conditional distribution g from the moments of h and the probability of death before maturation, as in Equation (4),
- 4.
- Choose a distribution for g that can be parameterized by its moments. Here, we consider the Poisson distribution with parameter and the negative binomial with shape and scale parameterswhere denotes the variance.
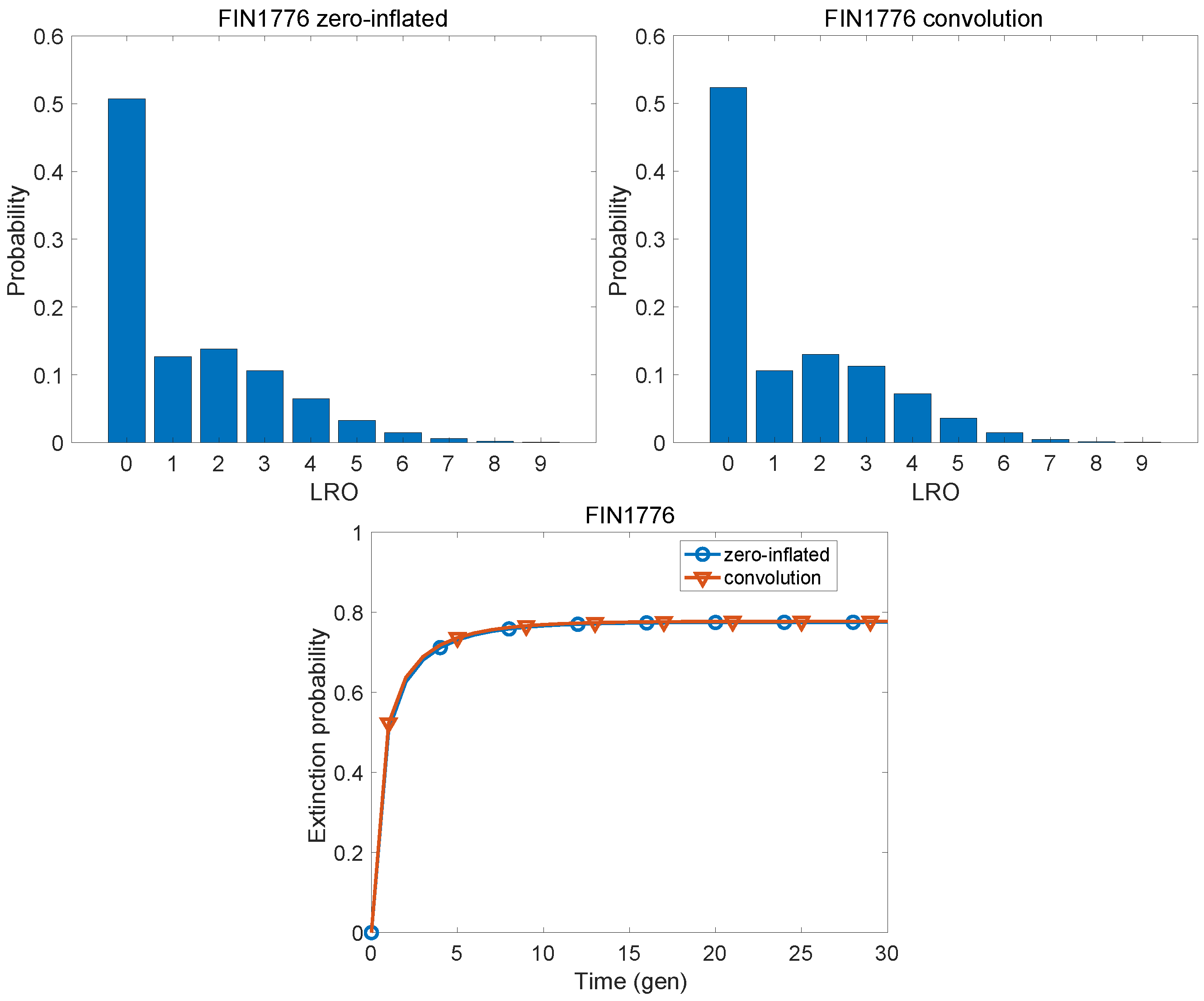
5. The Convolution Method as a Standard of Comparison
An Example
6. Extinction
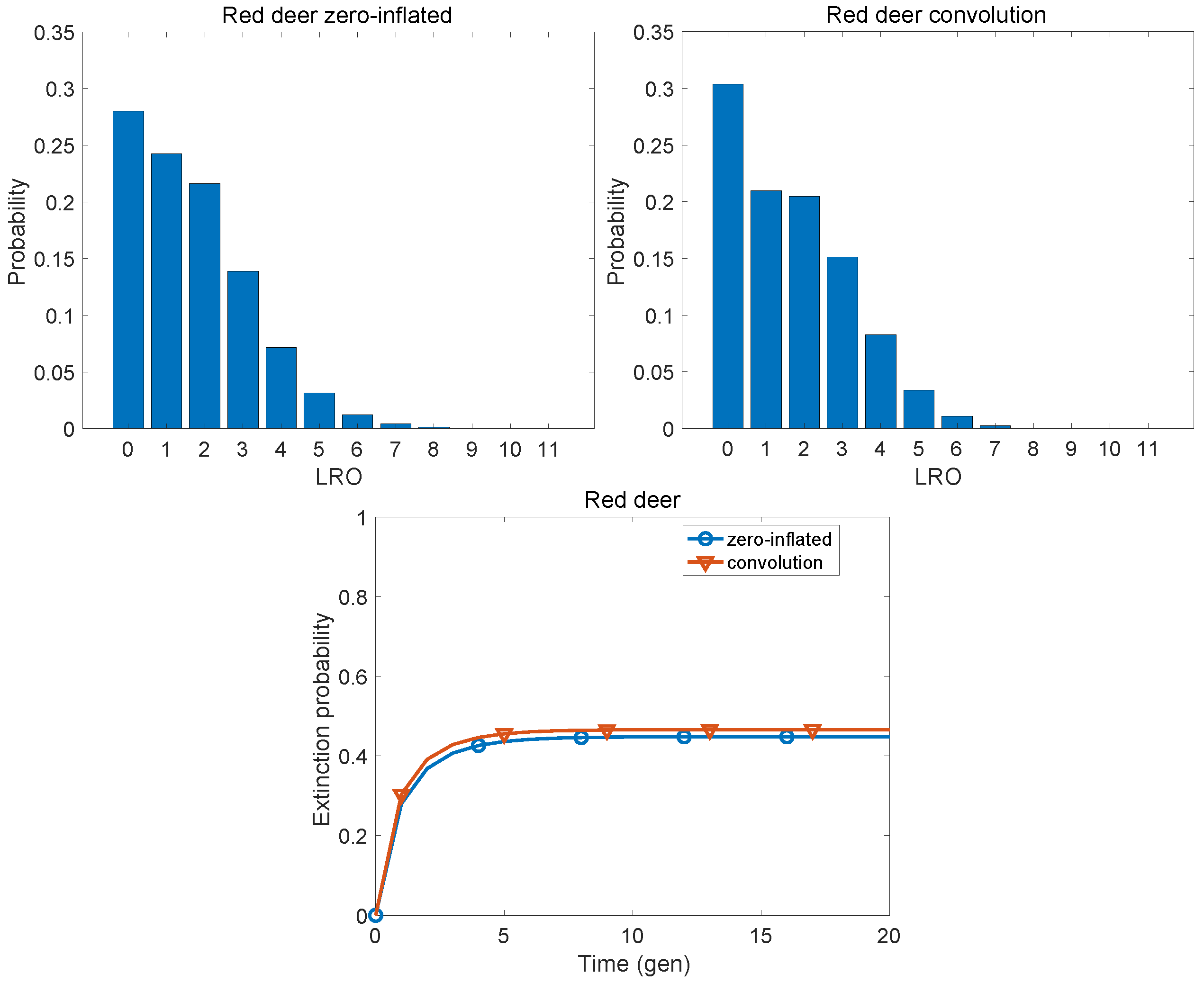
7. Case Studies: A Gallery of Zero-Inflated Distributions
7.1. Demographic Transitions
7.2. Extremes of Fertility and Mortality
7.3. Non-Human Populations
8. Discussion
8.1. Stochasticity, Not Heterogeneity
8.2. Some Open Problems
- Doubly-inflated distributions. Failure to survive to maturity is not the only reason that an individual may have an inherently zero reproductive output. Other causes (e.g., infertility due to medical causes, failure to marry, joining certain religious orders) would make the distribution of LRO doubly inflated. In such a case, the conditional distribution would also be zero-inflated. Methods given in Böhning et al. [19] and Beckett et al. [18] may enable this second level of zero-inflation (and perhaps more) to be estimated.
- How to evaluate the fit of ? Some of the moments of will be used to estimate the parameters of the chosen distribution (Poisson or negative binomial here). The moments that are not used for estimation can provide some insight into the goodness of fit, but it is hard to know how to evaluate the comparisons, and the concept of statistical ‘significance’ does not apply. The Kullback–Liebler divergence between the zero-inflated and the convolution distribution quantifies the difference, but it is an open problem of how to evaluate this quantity (i.e., how big a difference is big?).
- One motivation for the zero-inflated distribution model is the possibility of calculating the sensitivity of and to changes in the demographic parameters. The sensitivities of all the moments of LRO, calculated from the MCWR, are known [8]. So are those of the Markov chain from which is calculated [42,43]. It should be possible to apply these results to calculate the sensitivity of , , and to life history changes.
- Choosing a parametric distribution for is a challenge. The Poisson and negative binomial distributions are easy choices, inspired by the patterns shown in the first convolution-based analyses [11]. The negative binomial distribution is flexible in shape and reduces to, as special cases, the geometric or the Poisson distribution. There are several stochastic birth-death processes that lead to negative binomial distributions of population size [44,45,46]. Arguing purely by analogy, these might be relevant to the accumulation of offspring by an individual after reaching the set of reproductive stages.
- The zero-inflated calculations are unlikely to work when is not a well-behaved function. For example, the age-specific fertility of the polychaete Streblospio benedicti in laboratory culture is strongly bimodal (for unknown reasons, see [47]). This carries over to a bimodal distribution of LRO. The convolution method captures this nicely, but neither the zero-inflated Poisson nor the zero-inflated negative binomial does so (unpublished results). It is unknown how often such multimodal age-specific fertility schedules occur; dealing with them is an open problem.
- An interesting research problem is the application of the zero-inflated model to empirical measurements of lifetime reproduction (e.g., the kittiwake case of Figure 1), even without the availability of the age-specific mortality and fertility schedules needed for the MCWR or convolution calculations. There exist maximum likelihood estimates for the zero-inflated Poisson and zero-inflated negative binomial distributions, which may be useful [48,49].
8.3. Do We Need This?
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LRO | lifetime reproductive output |
| LRS | lifetime reproductive success |
| TFR | total fertility rate |
| life expectancy at birth | |
| KLD | Kullback–Leibler divergence |
| ZIP | zero-inflated Poisson distribution |
| ZINB | zero-inflated negative binomial distribution |
Appendix A
Appendix A.1. MCWR Calculation of the Moments of LRO
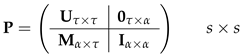
References
- Keilman, N.; Tymicki, K.; Skirbekk, V. Measures for human reproduction should be linked to both men and women. Int. J. Popul. Res. 2014, 1–10. [Google Scholar] [CrossRef]
- Clutton-Brock, T.H. Reproductive Success: Studies of Individual Variation in Contrasting Breeding Systems; University of Chicago Press: Chicago, IL, USA, 1988. [Google Scholar]
- Crow, J.F. Some possibilities for measuring selection intensities in man. Hum. Biol. 1958, 30, 1–13. [Google Scholar]
- Snyder, R.E.; Ellner, S.P. Pluck or luck: Does trait variation or chance drive variation in lifetime reproductive success? Am. Nat. 2018, 191, E90–E107. [Google Scholar] [CrossRef] [PubMed]
- Steiner, U.K.; Tuljapurkar, S. Neutral theory for life histories and individual variability in fitness components. Proc. Natl. Acad. Sci. USA 2012, 109, 4684–4689. [Google Scholar] [CrossRef] [PubMed]
- van Daalen, S.F.; Caswell, H. Demographic sources of variation in fitness. In Human Evolutionary Demography; Burger, O., Lee, R., Sear, R., Eds.; Open Book Publishers: Cambridge, UK, 2024; pp. 345–360. [Google Scholar]
- Caswell, H. Beyond R0: Demographic models for variability of lifetime reproductive output. PLoS ONE 2011, 6, e20809. [Google Scholar] [CrossRef] [PubMed]
- van Daalen, S.F.; Caswell, H. Lifetime reproductive output: Individual stochasticity, variance, and sensitivity analysis. Theor. Ecol. 2017, 10, 355–374. [Google Scholar] [CrossRef]
- van Daalen, S.F.; Caswell, H. Variance as a life history outcome: Sensitivity analysis of the contributions of stochasticity and heterogeneity. Ecol. Model. 2020, 147, 198856. [Google Scholar] [CrossRef]
- Tuljapurkar, S.; Zuo, W. Mutations and the distribution of lifetime reproductive success. J. Indian Inst. Sci. 2022, 102, 1269–1275. [Google Scholar] [CrossRef]
- Tuljapurkar, S.; Zuo, W.; Coulson, T.; Horvitz, C.; Gaillard, J.-M. Skewed distributions of lifetime reproductive success: Beyond mean and variance. Ecol. Lett. 2020, 23, 748–756. [Google Scholar] [CrossRef]
- Tuljapurkar, S.; Zuo, W.; Coulson, T.; Horvitz, C.; Gaillard, J.-M. Distributions of LRS in varying environments. Ecol. Lett. 2021, 24, 1328–1340. [Google Scholar] [CrossRef]
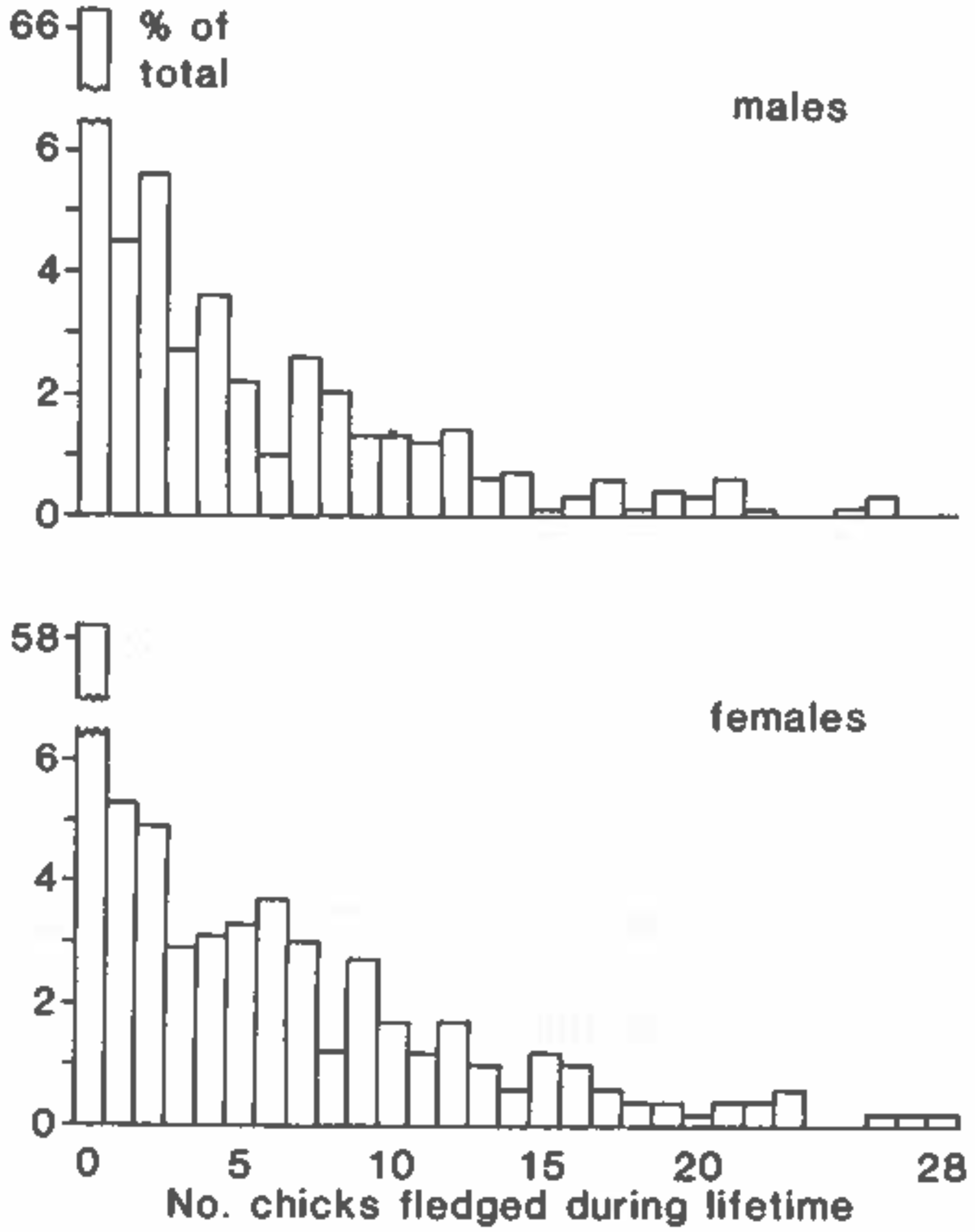
- Steiner, U.K.; Tuljapurkar, S.; Orzack, S.H. Dynamic heterogeneity and life history variability in the kittiwake. J. Anim. Ecol. 2010, 79, 436–444. [Google Scholar] [CrossRef]
- van Daalen, S.; Caswell, H. Lifetime reproduction and the second demographic transition: Stochasticity and individual variation. Demogr. Res. 2015, 33, 561–588. [Google Scholar] [CrossRef]
- van Daalen, S.F.; Hernández, C.M.; Caswell, H.; Neubert, M.G.; Gribble, K.E. The contribution of maternal age heterogeneity to variance in lifetime reproductive output. Am. Nat. 2022, 199, 603–616. [Google Scholar] [CrossRef] [PubMed]
- Thomas, C.S.; Coulson, J.C. Reproductive success of kittiwake gulls, Rissa tridactlya. In Reproductive Success; Clutton-Brock, T.H., Ed.; University of Chicago Press: Chicago, IL, USA, 1985; Chapter 16; pp. 251–262. [Google Scholar]
- Adarabioyo, M.; Ipinyomi, R. Comparing zero-inflated Poisson, zero-inflated negative binomial and zero-inflated geometric in count data with excess zero. Asian J. Probab. Stat. 2019, 4, 1–10. [Google Scholar] [CrossRef]
- Beckett, S.; Jee, J.; Ncube, T.; Pompilus, S.; Washington, Q.; Singh, A.; Pal, N. Zero-inflated Poisson (ZIP) distribution: Parameter estimation and applications to model data from natural calamities. Involv. J. Math. 2014, 7, 751–767. [Google Scholar] [CrossRef]
- Böhning, D.; Dietz, E.; Schlattmann, P. Zero-inflated count models and their applications in public health and social science. In Applications of Latent Trait and Latent Class Models in the Social Sciences; Rost, J.E., Langeheine, R., Eds.; Waxmann Verlag: Munster, Germany, 1997; Chapter 32; pp. 333–344. [Google Scholar]
- Haslett, J.; Parnell, A.; Sweeney, J. A general framework for modelling zero inflation. arXiv 2018, arXiv:1805.00555. [Google Scholar] [CrossRef]
- Amico, M.; Van Keilegom, I. Cure models in survival analysis. Annu. Rev. Stat. Its Appl. 2018, 5, 311–342. [Google Scholar] [CrossRef]
- Caswell, H. Matrix Population Models: Construction, Analysis, and Interpretation, 2nd ed.; Sinauer Associates: Sunderland, MA, USA, 2001. [Google Scholar]
- Caswell, H. Applications of Markov chains in demography. In MAM2006: Markov Anniversary Meeting; Boson Books: Raleigh, NC, USA, 2006; pp. 319–334. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley and Sons: New York, NY, USA, 1999. [Google Scholar]
- Turpeinen, O. Fertility and mortality in Finland since 1750. Popul. Stud. 1979, 33, 101–114. [Google Scholar] [CrossRef]
- Harris, T.E. The Theory of Branching Processes; Springer: Berlin/Heidelberg, Germany, 1963. [Google Scholar]
- HMD. Human Mortality Database. Technical Report, University of California, Berkeley (USA), and Max Planck Institute for Demographic Research (Germany). 2022. Available online: www.mortality.org (accessed on 29 May 2025).
- Human Fertility Database. Max Planck Institute for Demographic Research (Germany) and the Vienna Institute of Demography (Austria). 2019. Available online: www.humanfertility.org (accessed on 29 May 2025).
- Eaton, J.W.; Mayer, A.J. The social biology of very high fertility among the Hutterites: The demography of a unique population. Hum. Biol. 1953, 25, 206–264. [Google Scholar]
- Gurven, M.; Kaplan, H. 2007. Longevity among hunter-gatherers: A cross-cultural examination. Popul. Dev. Rev. 2007, 33, 321–365. [Google Scholar] [CrossRef]
- Hill, K.; Hurtado, A.M. Aché Life History: The Ecology and Demography of a Foraging People; Aldine de Gruyter: New York, NY, USA, 1996. [Google Scholar]
- Blurton-Jones, N. Demography and Evolutionary Ecology of Hadza Hunter-Gatherers; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- John, A.M. The Plantation Slaves of Trinidad, 1783–1816: A Mathematical and Demographic Enquiry; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Brodie, J.F. A Review of American Bison (Bos Bison) Demography and Population Dynamics; American Bison Society Working Paper 2; Wildlife Conservation Society: New York, NY, USA, 2008. [Google Scholar]
- Benton, T.G.; Grant, A.; Clutton-Brock, T.H. Does environmental stochasticity matter? Analysis of red deer life-histories on Rum. Evol. Ecol. 1995, 9, 559–574. [Google Scholar] [CrossRef]
- Caswell, H. Stage, age and individual stochasticity in demography. Oikos 2009, 118, 1763–1782. [Google Scholar] [CrossRef]
- Caswell, H. The contributions of stochasticity and social inequality to lifespan variability. Demogr. Res. 2023, 49, 309–354. [Google Scholar] [CrossRef]
- Hartemink, N.; Missov, T.I.; Caswell, H. Stochasticity, heterogeneity, and variance in longevity in human populations. Theor. Popul. Biol. 2017, 114, 107–117. [Google Scholar] [CrossRef]
- Tuljapurkar, S.; Edwards, R.D. Variance in death and its implications for modeling and forecasting mortality. Demogr. Res. 2011, 24, 497–526. [Google Scholar] [CrossRef]
- Vaupel, J.W. Inherited frailty and longevity. Demography 1988, 25, 277–287. [Google Scholar] [CrossRef]
- Waples, R.S.; Reed, T.E. Null models for the opportunity for selection. Am. Nat. 2023, 201, 779–793. [Google Scholar] [CrossRef]
- Caswell, H. Sensitivity analysis of discrete Markov chains via matrix calculus. Linear Algebra Its Appl. 2013, 438, 1727–1745. [Google Scholar] [CrossRef]
- Caswell, H. Sensitivity Analysis: Matrix Methods for Demography and Ecology. In Demographic Research Monographs; Springer Nature: Cham, Switzerland, 2019. [Google Scholar]
- Johnson, N.L.; Kotz, S.; Kemp, A.W. Univariate Discrete Distributions, 2nd ed.; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Kendall, D.G. On some modes of population growth leading to R.A. Fisher’s logarithmic series distribution. Biometrika 1948, 35, 6–15. [Google Scholar] [CrossRef]
- Kendall, D.G. 1949. Stochastic processes and population growth. J. R. Stat. Soc. Ser. B (Methodol.) 1949, 11, 230–282. [Google Scholar] [CrossRef]
- Levin, L.A.; Caswell, H.; DePatra, K.D.; Creed, E.L. Demographic consequences of larval development mode: Planktotrophy vs. lecithotrophy in Streblospio benedicti. Ecology 1987, 68, 1877–1886. [Google Scholar] [CrossRef]
- Cohen, A.C. An extension of a truncated Poisson distribution. Biometrics 1960, 16, 446–450. [Google Scholar] [CrossRef]
- Cohen, A.C. A note on certain discrete mixed distributions. Biometrics 1966, 22, 566–572. [Google Scholar] [CrossRef] [PubMed]
- Snyder, R.E.; Ellner, S.P. We happy few: Using structured population models to identify the decisive events in the lives of exceptional individuals. Am. Nat. 2016, 188, E28–E45. [Google Scholar] [CrossRef] [PubMed]
- Caswell, H.; Zarulli, V. Matrix methods in health demography: A new approach to the stochastic analysis of healthy longevity and DALYs. Popul. Health Metrics 2018, 16, 8. [Google Scholar] [CrossRef]
- Howard, R.A. Dynamic Programming and Markov Processes; Wiley: New York, NY, USA, 1960. [Google Scholar]
- Caswell, H.; van Daalen, S.F. Healthy longevity from incidence-based models: More kinds of health than stars in the sky. Demogr. Res. 2021, 45, 397–452. [Google Scholar] [CrossRef]
- Dudel, C.; Myrskylä, M. Estimating the number and length of episodes in disability using a Markov chain approach. Popul. Health Metrics 2020, 18, 1–9. [Google Scholar] [CrossRef]
- Owoeye, S.M.; Oseni, B.M.; Gayawan, E. Estimating lifetime malnourished period and its statistics based on the concept of Markov chain with reward. Heliyon 2020, 6, e04073. [Google Scholar] [CrossRef]
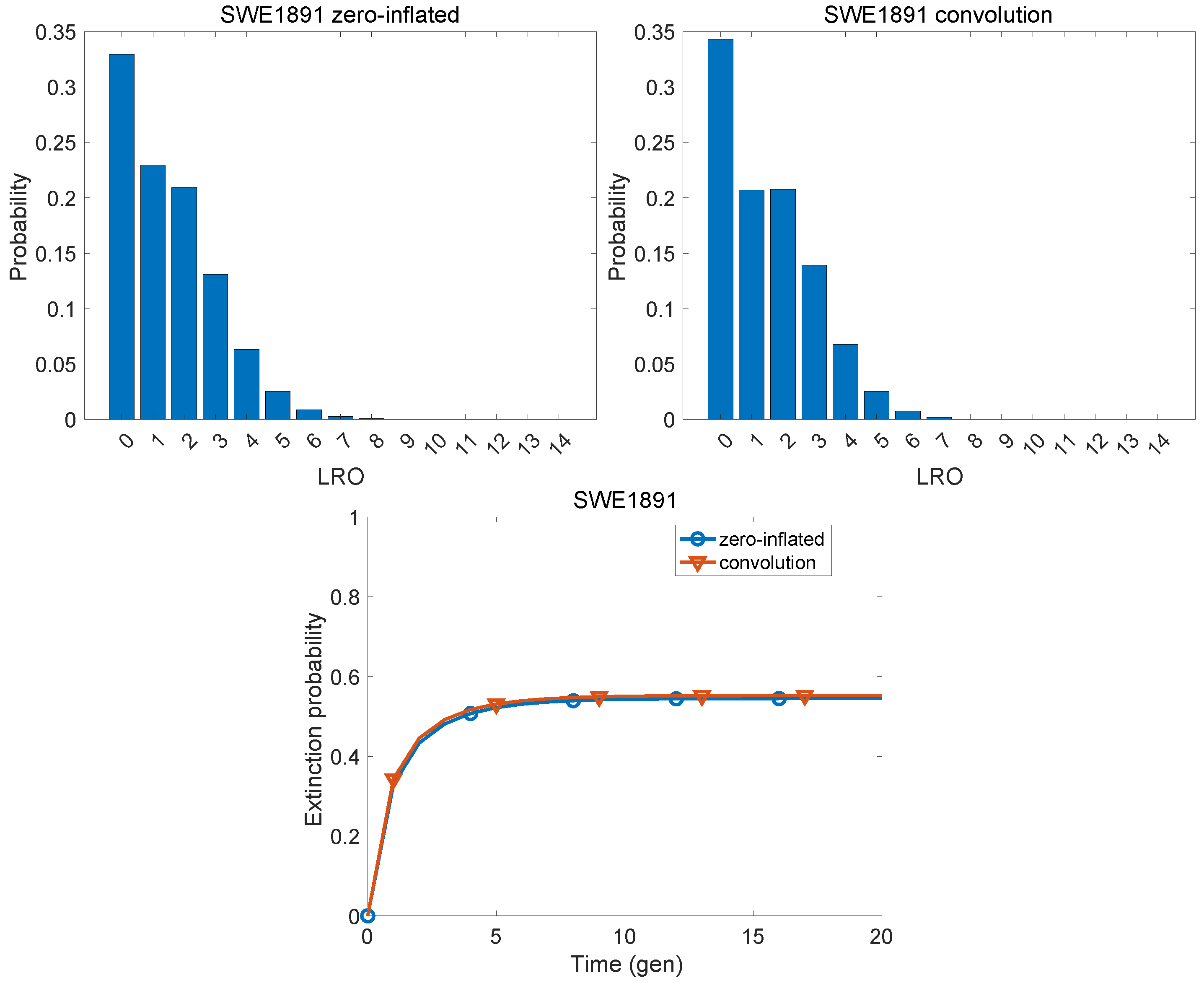
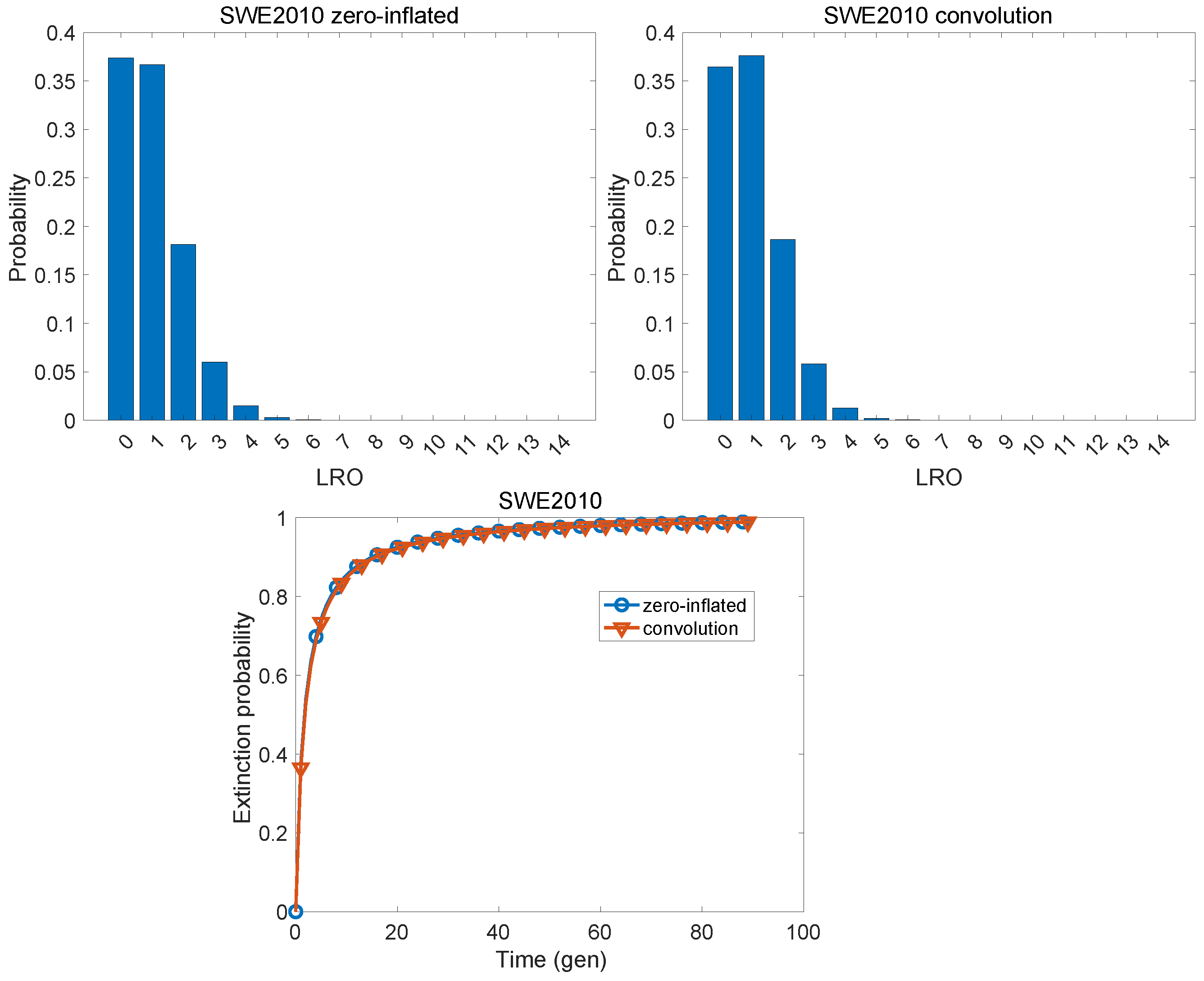
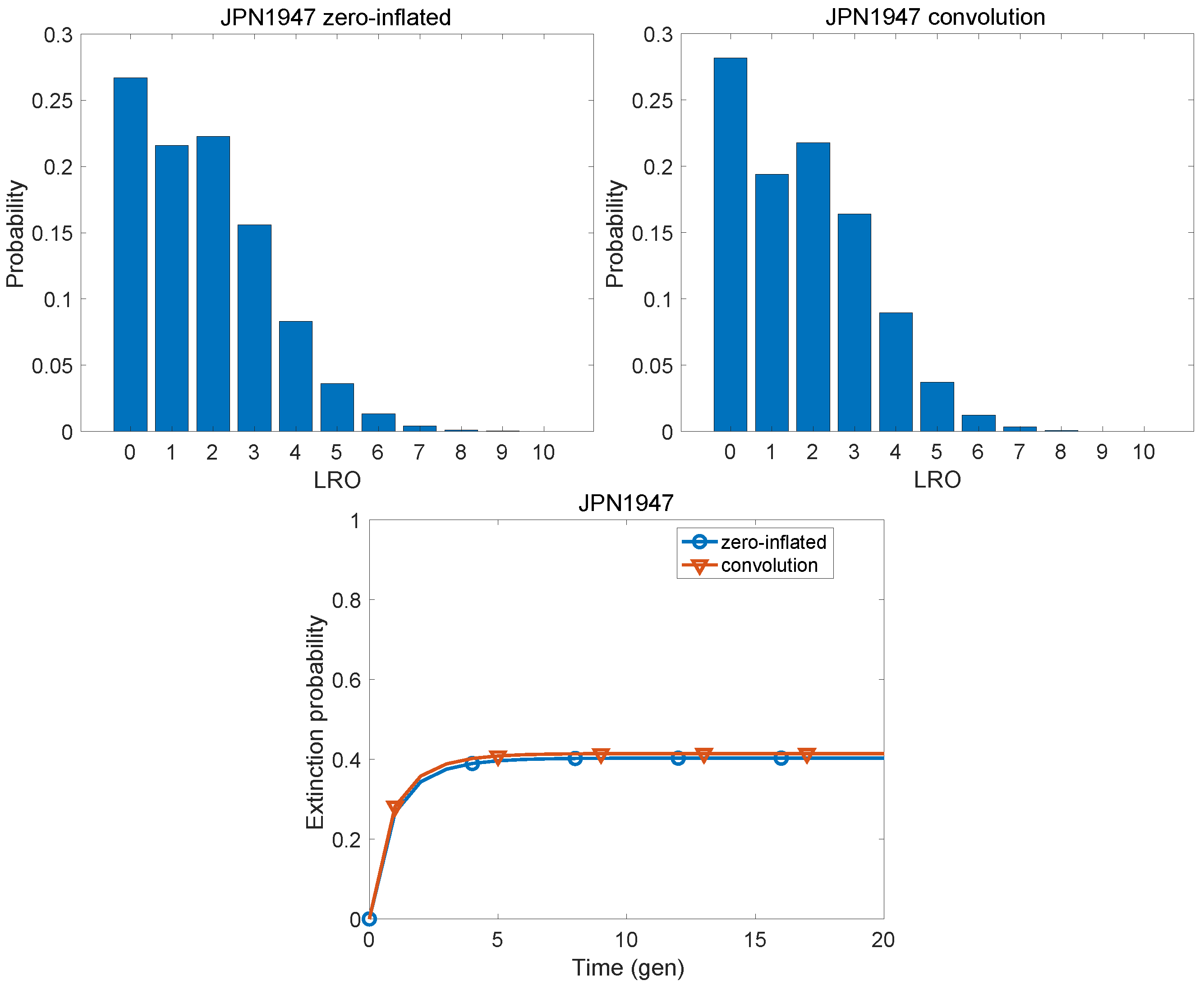

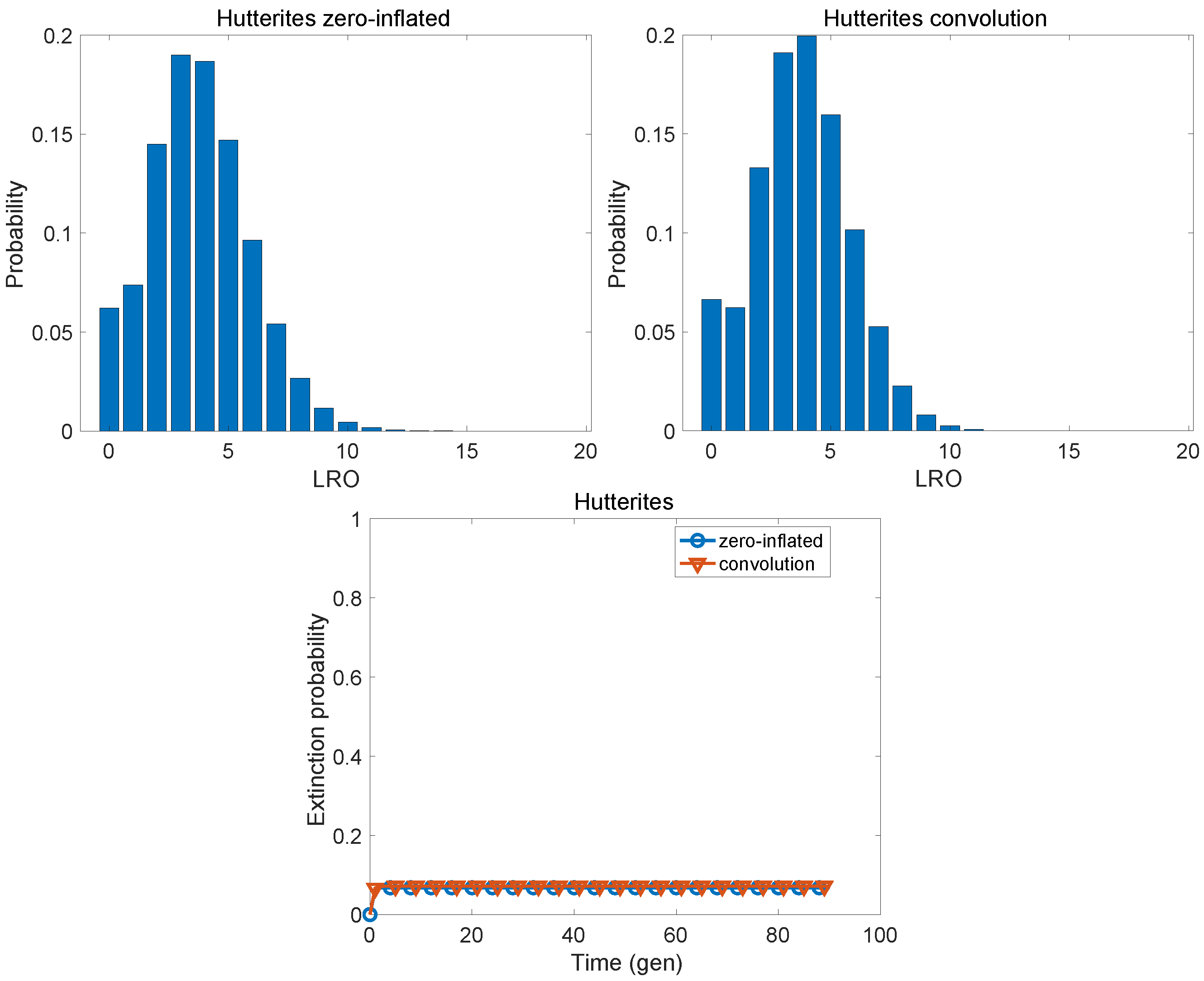
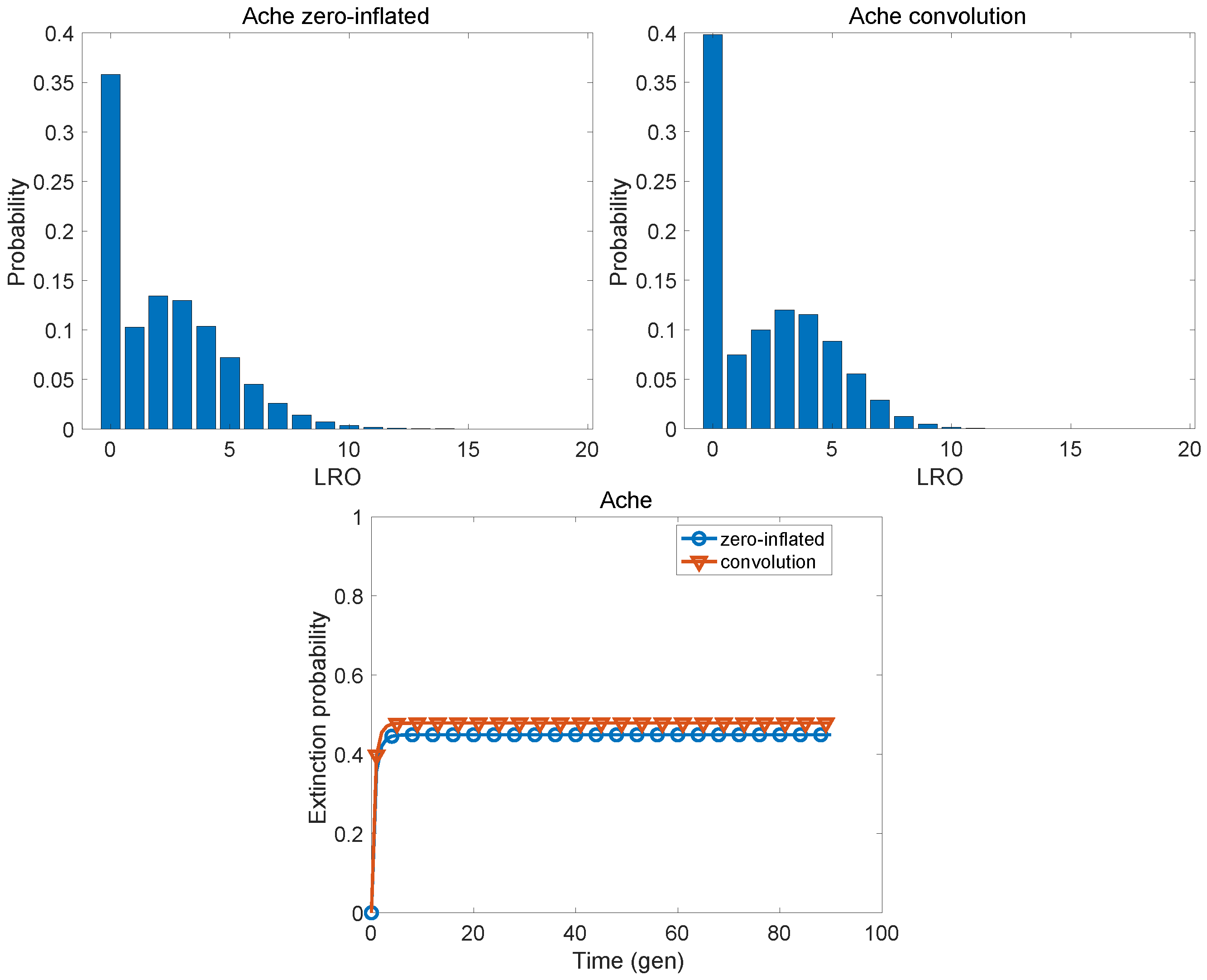
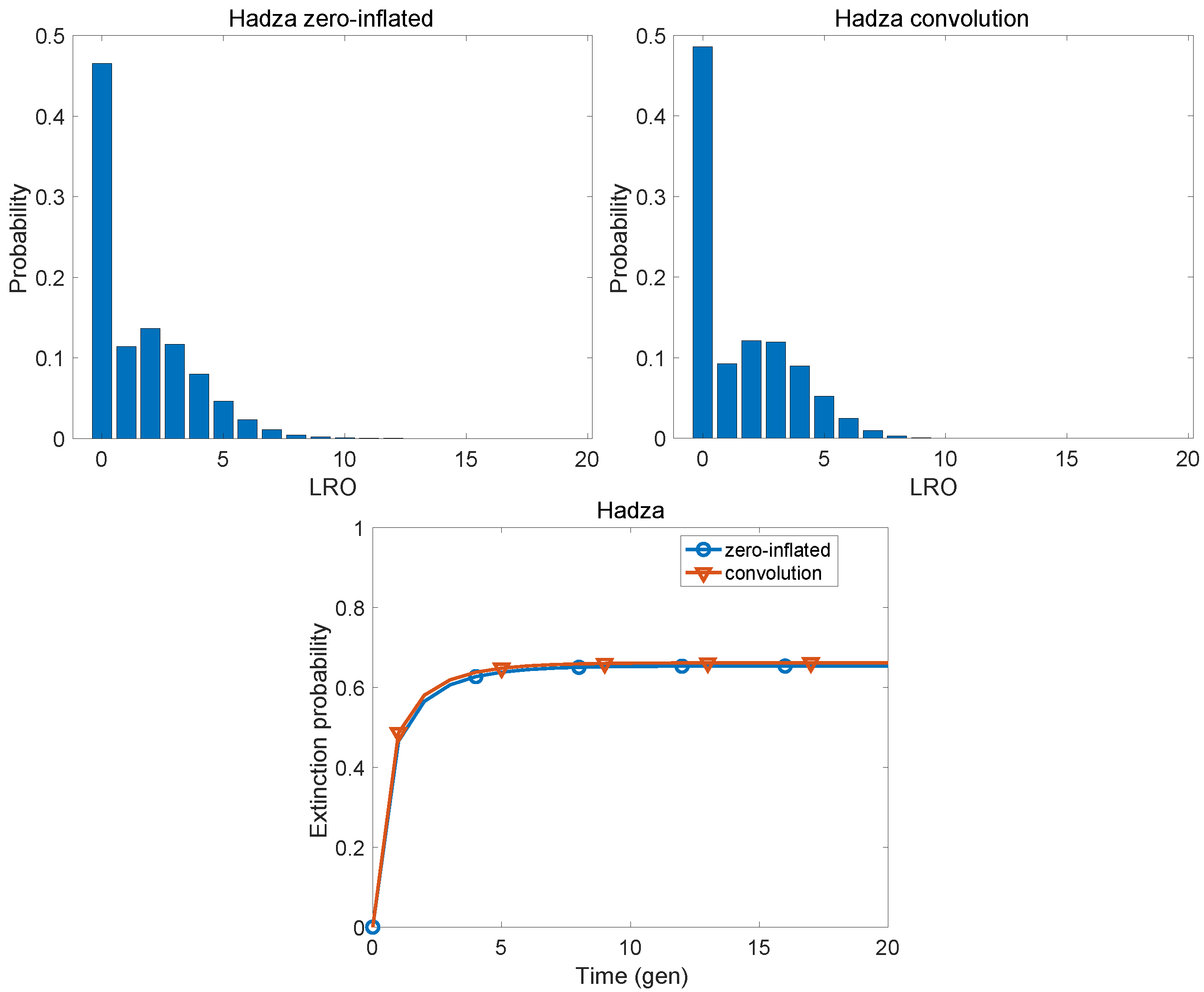
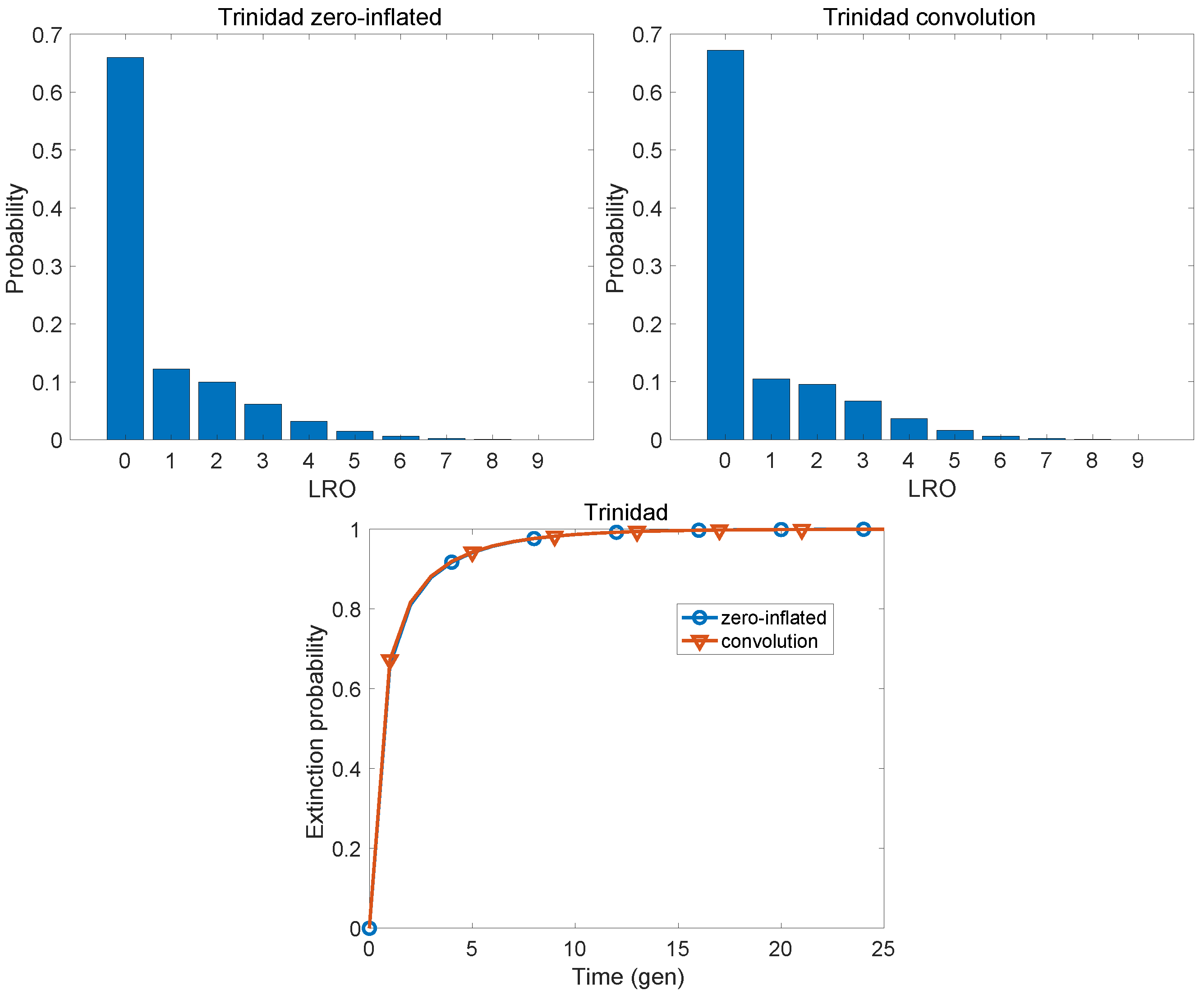
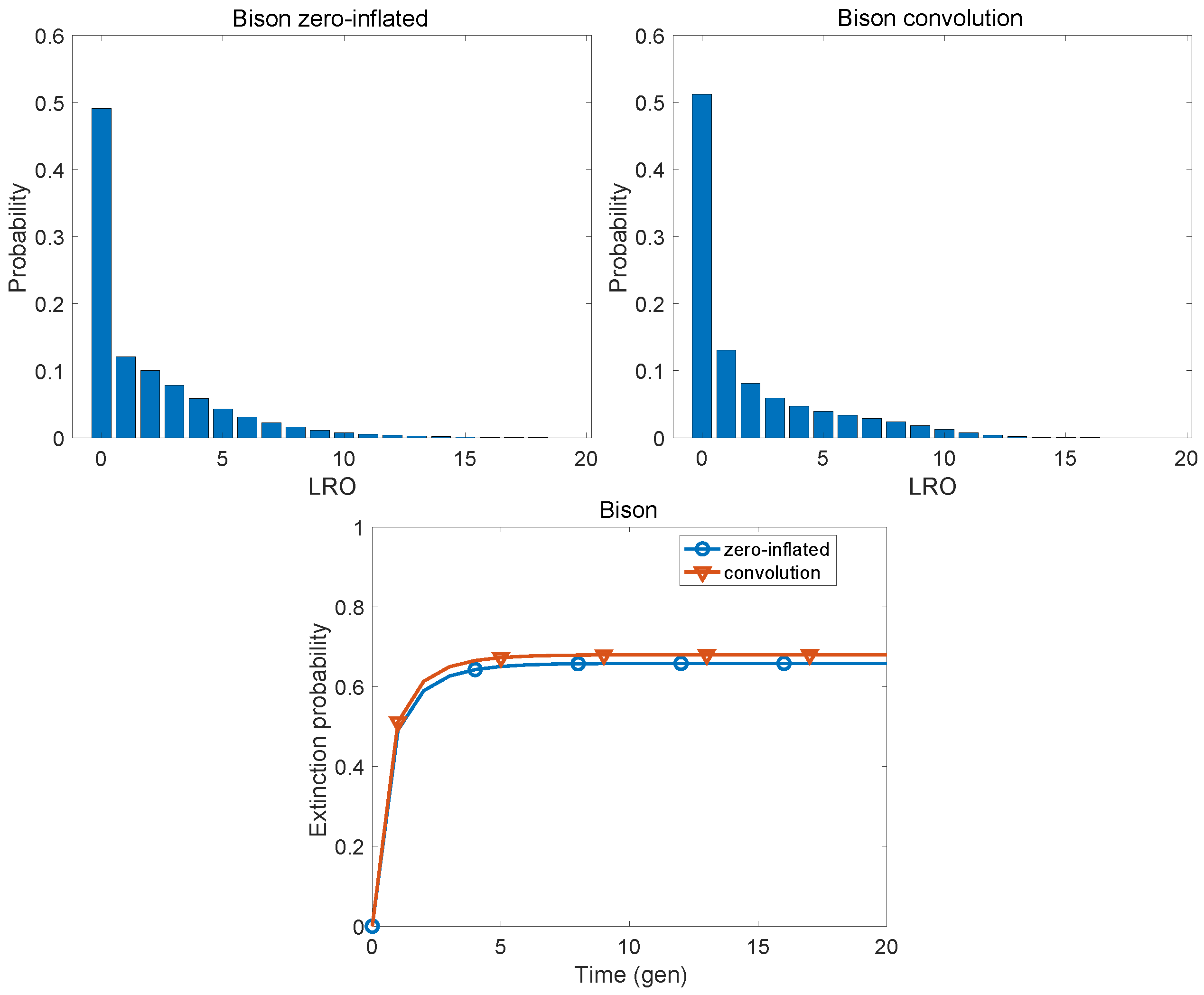
| Population | KLD | |
|---|---|---|
| Finland, 1776 | 0.0052 | 0.4450 |
| Sweden, 1891 | 0.0032 | 0.1992 |
| Sweden, 2010 | 0.0034 | |
| Japan, 1947 | 0.0036 | 0.1603 |
| Japan, 2019 | 0.0029 | |
| Hutterites | 0.0071 | 0.0433 |
| Ache | 0.0265 | 0.3214 |
| Hadza | 0.0082 | 0.4146 |
| Trinidad plantation slaves | 0.0036 | 0.5730 |
| American bison | 0.0241 | 0.3693 |
| Red deer | 0.0091 | 0.1323 |
| Zero-Inflated | Conditional | |||||
|---|---|---|---|---|---|---|
| Population | Mean | Var | Skew | Mean | Var | Skew |
| Finland, 1776 | 1.303 | 2.852 | 1.161 | 2.351 | 2.682 | 0.521 |
| Sweden, 1891 | 1.499 | 2.148 | 0.819 | 1.871 | 1.985 | 0.638 |
| Sweden, 2010 | 0.986 | 0.940 | 0.930 | 0.990 | 0.940 | 0.926 |
| Japan, 1947 | 1.767 | 2.432 | 0.671 | 2.110 | 2.187 | 0.566 |
| Japan, 2019 | 0.667 | 0.645 | 1.160 | 0.669 | 0.655 | 1.156 |
| Hutterites | 3.763 | 4.027 | 0.174 | 3.933 | 3.540 | 0.311 |
| Ache | 2.238 | 5.427 | 0.712 | 3.263 | 4.569 | 0.321 |
| Hadza | 1.566 | 3.607 | 1.015 | 2.674 | 3.197 | 0.455 |
| Trinidad plantation slaves | 0.773 | 1.801 | 1.860 | 1.811 | 2.339 | 0.769 |
| American bison | 1.900 | 7.882 | 1.628 | 3.102 | 9.147 | 1.057 |
| Red deer | 1.660 | 2.354 | 0.740 | 1.913 | 2.229 | 0.622 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caswell, H. Zero-Inflated Distributions of Lifetime Reproductive Output. Populations 2025, 1, 19. https://doi.org/10.3390/populations1030019
Caswell H. Zero-Inflated Distributions of Lifetime Reproductive Output. Populations. 2025; 1(3):19. https://doi.org/10.3390/populations1030019
Chicago/Turabian StyleCaswell, Hal. 2025. "Zero-Inflated Distributions of Lifetime Reproductive Output" Populations 1, no. 3: 19. https://doi.org/10.3390/populations1030019
APA StyleCaswell, H. (2025). Zero-Inflated Distributions of Lifetime Reproductive Output. Populations, 1(3), 19. https://doi.org/10.3390/populations1030019