The Sum of the Solid Angles of an n-Simplex

Abstract

It was known in antiquity that the sum of the three angles of a triangle equals $\pi$. Surprisingly, it was not until 1952 that the corresponding question for a tetrahedron was addressed. In that year, J.W. Gaddum proved that the sum of the four solid angles in a tetrahedron lies within the interval of $[0,2\pi ]$ and those lower and upper bounds are the best possible. In 2020, H. Katsuura showed that $2\pi$ was unachievable. In this paper, we generalize these results to show that for a non-degenerate n-simplex in ${\mathbb{R}}^n$ with $n\ge 3$, the solid angles at the vertices add up to a positive number that is less than one-half the $(n-1)$-dimensional area of the unit sphere in ${\mathbb{R}}^n$. We also show that there are examples for which the sum can be made arbitrarily close to the extreme values of 0 and one-half the $(n-1)$-dimensional area of the unit sphere in ${\mathbb{R}}^n$.

1.  Introduction

This article concerns solid angles measured in a Euclidean space of a dimension of at least three. For $n\ge 3$, the $(n-1)$-dimensional solid angle subtended by $S\subset {\mathbb{R}}^n$ as measured at a point $p\in {\mathbb{R}}^n$ is defined as follows: Radially project the set onto an $(n-1)$-dimensional sphere centered at p and measure the $(n-1)$-dimensional area of that projection, then normalize the result by dividing by the $(n-1)$st power of the radius of the sphere (this general definition can also be applied in case $n=2$, and it gives the value one expects (in radians), but it sounds and feels awkward to say “solid angle” when dealing with an angle in the plane). The unit of measurement for a solid angle in 3-space is the steradian (symbol “sr”)—a derived unit in the International System of Units. There does not seem to be a standard unit of measurement for solid angles where $n\ge 4$, although hypersteradian is sometimes used. The range of possible values for the measure of solid angles in ${\mathbb{R}}^n$ is from 0 up to the $(n-1)$-dimensional area of the unit sphere in ${\mathbb{R}}^n$.

It was known in antiquity that the sum of the three angles of a triangle equals $\pi$, but it was not until 1952 that the corresponding question for a tetrahedron was addressed. In that year, J.W. Gaddum [1] proved that the sum of the four solid angles in a tetrahedron lies within the interval of $[0,2\pi ]$ and those lower and upper bounds are the best possible. In 2020, H. Katsuura [2] showed that $2\pi$ was unachievable.

An n-simplex, $\Delta$, equals the set of all convex combinations of its $n+1$ vertices, $p_0,p_1,\dots ,p_n$. The simplex is said to be degenerate if all the vertices, and hence all of $\Delta$, lie in an $(n-1)$-dimensional hyperplane; otherwise the simplex is non-degenerate.

The purpose of this article is to show that, for a non-degenerate n-simplex in ${\mathbb{R}}^n$, $n\ge 3$, if we measure the solid angle of the simplex at each of its $n+1$ vertices and then add those $n+1$ values, that sum will always be strictly less than one-half the area of the unit $(n-1)$-sphere. Indeed, we will show that that sum can come arbitrarily close to zero. Finally, to address the other end of the range of possibilities, we will show that the sum can come arbitrarily close to one-half the area of the unit $(n-1)$-sphere.

Notation 1.

We will have occasion to use both $k=n-1$ and $k=n$ in the following notation.

1. 

The origin in ${\mathbb{R}}^k$ will be denoted by $\mathbf{0}$ and the standard unit basis vectors will be denoted by ${\mathbf{e}}_1,{\mathbf{e}}_2,\dots ,{\mathbf{e}}_k$.

2. 

We will measure the $(k-1)$-dimensional area of sets in ${\mathbb{R}}^k$ using the $(k-1)$-dimensional Hausdorff measure denoted as ${\mathcal{H}}^{k-1}$.

3. 

We will use ${\mathbb{S}}^{k-1}(p,r)$ to denote the $(k-1)$-dimensional sphere of radius r centered at $p\in {\mathbb{R}}^k$.

4. 

We let $A_{k-1}$ denote the $(k-1)$-dimensional area of the unit sphere in ${\mathbb{R}}^k$, i.e., $A_{k-1}={\mathcal{H}}^{k-1}\left[{\mathbb{S}}^{k-1}(\mathbf{0},1)\right]$ . It is known (Section 3.2.13 of [3] gives a derivation) that

$$A_{k-1}={\displaystyle \frac{2{\pi }^{k/2}}{\Gamma (k/2)}}=\left\{\begin{array}{ccc}{\displaystyle \frac{2{\pi }^m}{(m-1)!}}& \mathrm{if}& n=2m,\hfill \\ {\displaystyle \frac{2^{2m+1}{\pi }^{m}m!}{\left(2m\right)!}}& \mathrm{if}& n=2m+1.\hfill \end{array}\right.$$

5. 

For $S\subset {\mathbb{R}}^k$ and $p\in {\mathbb{R}}^k$, we will write

$$S-p=\{x-p:x\in S\}\mathrm{and}-S=\{-x:x\in S\}.$$

Remark 1.

For those studying geometric analysis, the Hausdorff measure is a standard choice for a lower-dimensional measure in Euclidean space (though it is not the only possible choice). One can find its definition in §2.1 of [4]. The essential fact that we need is that if$S\subset {\mathbb{R}}^k$ is a set for which there is a classical value for its $(k-1)$-dimensional area, then ${\mathcal{H}}^{k-1}\left[S\right]$ equals that value.

It will be convenient to always translate to the origin the point at which we wish to measure a solid angle. With that completed, the radial projection of the set on a sphere about the origin coincides with the intersection of the sphere and the cone generated by the set. We will also further simplify by making the chosen sphere the unit sphere.

Definition 1.

Suppose that $S\subset {\mathbb{R}}^n$.

1. 

Following [5] , S is called a cone if it is closed under positive scalar multiplication, that is, $\lambda x\in S$ whenever $x\in S$ and $\lambda >0$.

2. 

We define the cone generated by S, denoted as $\mathrm{cone}\left[S\right]$, by setting

$$\mathrm{cone}\left[S\right]=\{\lambda x:x\in S,\lambda >0\}.$$

Because we will be dealing with sets that contain the origin, we note the following fact: $\mathbf{0}\in S$ if and only if $\mathrm{cone}\left[S\right]=\{\lambda x:x\in S,\lambda \ge 0\}$.

3. 

If S is a Borel set, then the solid angle subtended by S as measured at; $\mathbf{0}$ will be denoted as ${\mathcal{S}}_{\mathbf{0}}\left(S\right)$. (The right-hand side of (1) begs the question of measurability. This is where it is convenient to note that because ${\mathcal{H}}^{n-1}$ is a Borel regular measure, ${\mathcal{S}}_{\mathbf{0}}\left(S\right)$ is well-defined for any Borel set $S\subset {\mathbb{R}}^n$. See §1.7 of [4]).

$${\mathcal{S}}_{\mathbf{0}}\left(S\right)={\mathcal{H}}^{n-1}\left[{\mathbb{S}}^{n-1}(\mathbf{0},1)\cap \mathrm{cone}\left[S\right]\right].$$

(1)

Recall that an n-simplex, $\Delta$, equals the set of all convex combinations of its $n+1$ vertices, $p_0,p_1,\dots ,p_n$. That is,

$$\Delta =\left\{{\sum }_{\ell =0}^n{\lambda }_{\ell }{p}_{\ell }:{\sum }_{\ell =0}^n{\lambda }_{\ell }=1,\mathrm{where}0\le {\lambda }_{\ell }\mathrm{for}0\le \ell \le n\right\}.$$

It is a routine exercise to prove the following lemma.

Lemma 1.

Let $p_0,p_1,\dots ,p_n$  be the vertices of the simplex Δ, and let $0\le i\le n$ be an integer. Then, Δ is non-degenerate if and only if the n vectors

$$p_0-p_i,p_1-p_i,\dots ,p_{i-1}-p_i,p_{i+1}-p_i,\dots ,p_n-p_i$$

are linearly independent.

To form the sum of the solid angles at the vertices of $\mathrm{\Delta }$, we will translate each vertex in turn to the origin and measure the solid angle subtended by the translated simplex as measured at the origin. The formal statement of our main result is the following.

Theorem 1.

Let $p_0,p_1,\dots ,p_n$ be the vertices of a non-degenerate n-simplex Δ, and let ${\mathcal{S}}_{\mathbf{0}}(\Delta -p_i)$ be the solid angle of Δ measured at $p_i$.

1. 

It holds that ${\displaystyle 0<\sum _{i=0}^n{\mathcal{S}}_{\mathbf{0}}(\Delta -p_i)<\frac{A_{n-1}}{2}.}$

2. 

For any $ϵ>0$, there exists a non-degenerate n-simplex $\Delta \subset {\mathbb{R}}^n$ such that

$$0<\sum _{i=0}^n{\mathcal{S}}_{\mathbf{0}}(\Delta -p_i)<ϵ.$$

3. 

For any $ϵ>0$, there exists a non-degenerate n-simplex $\Delta \subset {\mathbb{R}}^n$ such that

$${\displaystyle \frac{A_{n-1}}{2}}-ϵ<\sum _{i=0}^n{\mathcal{S}}_{\mathbf{0}}(\Delta -p_i)<{\displaystyle \frac{A_{n-1}}{2}}.$$

2. Theorem 1 Part 1

Let $\Delta \subset {\mathbb{R}}^n$ be a non-degenerate n-simplex with vertices $p_0,p_1,\dots ,p_n$. In this section, it will be convenient to assume that $p_0=\mathbf{0}$. This leads to no loss of generality.

When the vertex $p_i$ is translated to the origin, we obtain the congruent n-simplex $\Delta -p_i$ and we have

$$\begin{array}{cc}\hfill \mathrm{cone}[\Delta -p_i]& =\left\{{\sum }_{\ell =0}^n{\lambda }_{\ell }(p_{\ell }-p_i):0\le {\lambda }_{\ell }\mathrm{for}0\le \ell \le n\right\}.\hfill \end{array}$$

(2)

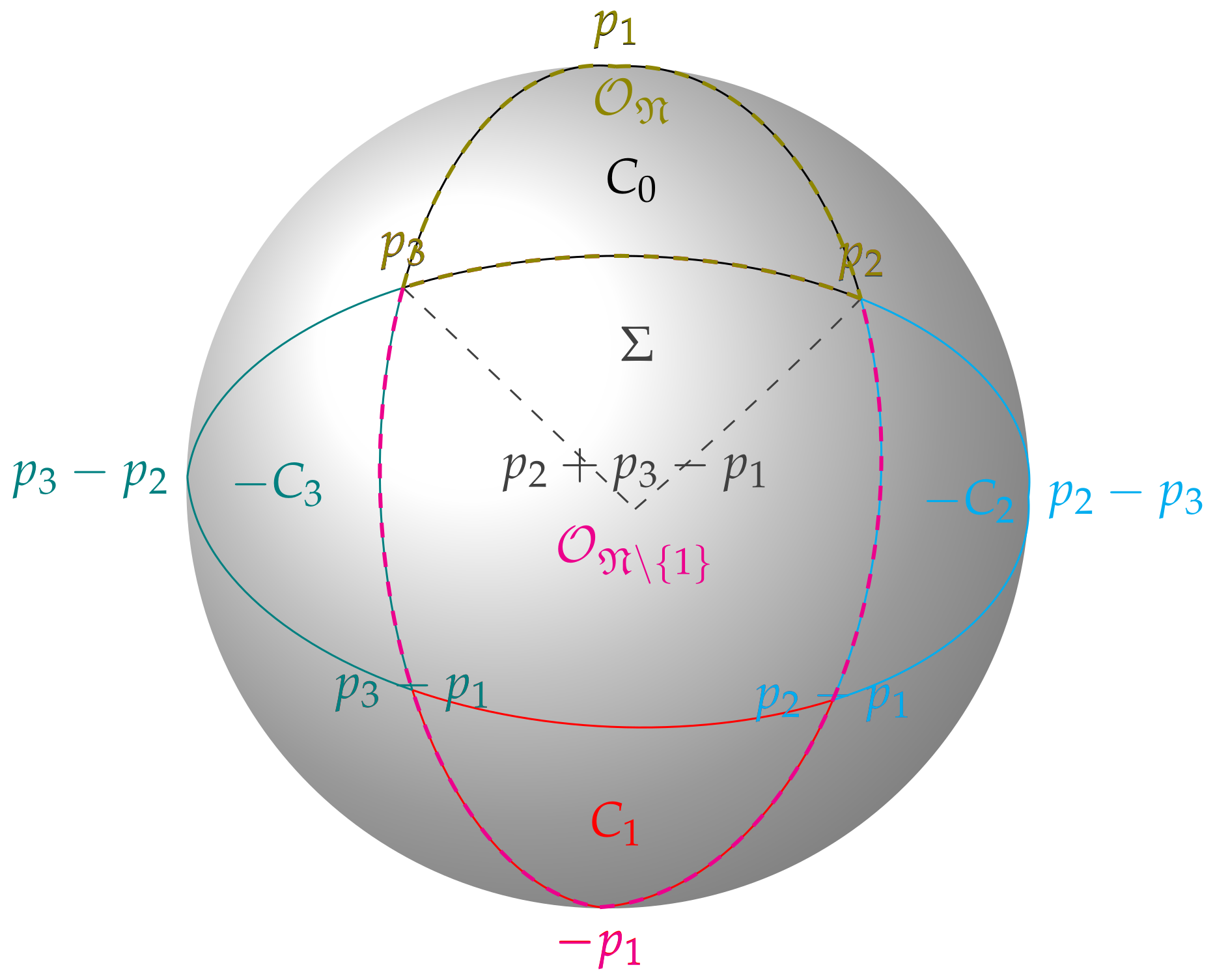
Note that the term ${\lambda }_i(p_i-p_i)=\mathbf{0}$ is included in the summation (2). The interior of the cone generated by $\Delta -p_i$ will be denoted by $C_i$ (see Figure 1). $C_i$ is given by

$$C_i=\left\{{\sum }_{\ell =0}^n{\lambda }_{\ell }(p_{\ell }-p_i):0<{\lambda }_{\ell }\mathrm{for}0\le \ell \le n\right\}.$$

(3)

Because the boundary of the cone generated by $\Delta -p_i$ is contained in the union of n hyperplanes, we have

$${\mathcal{H}}^{n-1}\left[{\mathbb{S}}^{n-1}(\mathbf{0},1)\cap \mathrm{cone}[\mathrm{\Delta }-p_i]\right]={\mathcal{H}}^{n-1}\left[{\mathbb{S}}^{n-1}(\mathbf{0},1)\cap C_i\right].$$

We conclude that

$${\mathcal{S}}_{\mathbf{0}}(\mathrm{\Delta }-p_i)={\mathcal{S}}_{\mathbf{0}}\left(C_i\right).$$

(4)

Lemma 2.

There exist linearly independent vectors $w_1,w_2,\dots ,w_n$ such that

$$p_i·w_j={\delta }_{ij},\mathrm{for}i,j\in \{1,2\dots ,n\},\mathrm{where}{\delta }_{ij}=\left\{\begin{array}{c}1\mathit{if}i=j,\hfill \\ 0\mathit{if}i\ne j.\hfill \end{array}\right.$$

(5)

Proof. 

Because $\mathrm{\Delta }$ is non-degenerate and because of our assumption that $p_0=\mathbf{0}$, we know from Lemma 1 that the set $\left\{p_i\right\}$ is linearly independent. Let P be the matrix, the ith column of which is $p_i$. Letting $w_j$ be the jth column of the transpose of $P^{-1}$, we see that (5) holds. The linear independence of $w_1,w_2,\dots ,w_n$ then follows from (5). □

Notation 2.

Set $\mathfrak{N}=\{1,2,\dots ,n\}$. Let the vectors $w_1,w_2,\dots ,w_n$ be as in Lemma 2. For $\sigma \subset \mathfrak{N}$, let ${\mathcal{O}}_{\sigma }$ be the set of $x\in {\mathbb{R}}^n$ such that

$$\left\{\begin{array}{cc}\hfill x·w_j>0& \mathrm{if}j\in \sigma ,\hfill \\ \hfill x·w_j<0& \mathrm{if}j\notin \sigma .\hfill \end{array}\right.$$

(6)

If x satisfies the conditions in (6) and $\lambda >0$, then $\lambda x$ also satisfies the conditions in (6). Therefore, ${\mathcal{O}}_{\sigma }$ is a cone. For a fixed j, the condition $x·w_j>0$ defines a half-space. Likewise, the condition $x·w_j<0$ defines a half-space. Thus, ${\mathcal{O}}_{\sigma }$ is the intersection of n half-spaces.

Lemma 3. 

1. 

Let $\sigma ,{\sigma }^{\prime }$ be subsets of $\mathfrak{N}$. If $\sigma \ne {\sigma }^{\prime }$, then ${\mathcal{O}}_{\sigma }$ and ${\mathcal{O}}_{{\sigma }^{\prime }}$ are disjoint open sets.

2. 

For each $\sigma \subset \mathfrak{N}$, ${\mathcal{S}}_{\mathbf{0}}\left({\mathcal{O}}_{\sigma }\right)>0$ holds.

3. 

The complement of the union of the sets ${\mathcal{O}}_{\sigma }$ is the union of n linear subspaces each of dimension $n-1$.

4. 

It holds that ${\displaystyle \sum _{\sigma \subset \mathfrak{N}}{\mathcal{S}}_{\mathbf{0}}\left({\mathcal{O}}_{\sigma }\right)=A_{n-1}}$.

Proof. 

• Part 1 in Lemma 3. It is immediate that each ${\mathcal{O}}_{\sigma }$ is an open set. Assume that $\sigma \ne {\sigma }^{\prime }$. Arguing by contradiction, we suppose that $x\in {\mathcal{O}}_{\sigma }\cap {\mathcal{O}}_{{\sigma }^{\prime }}$. Since $\sigma \ne {\sigma }^{\prime }$, there is either a j with $j\in \sigma$ and $j\notin {\sigma }^{\prime }$ or a j with $j\notin \sigma$ and $j\in {\sigma }^{\prime }$. In the first case, we have $x·w_j>0$ because $x\in {\mathcal{O}}_{\sigma }$ and $0>x·w_j$ because $x\notin {\mathcal{O}}_{\sigma }^{\prime }$, a contradiction. The second case is handled similarly.
• Part 2 in Lemma 3. For $\sigma \subset \mathfrak{N}$, ${\mathcal{O}}_{\sigma }$ is a cone, so ${\mathcal{S}}_{\mathbf{0}}\left({\mathcal{O}}_{\sigma }\right)={\mathcal{H}}^{n-1}[{\mathbb{S}}^{n-1}(\mathbf{0},1)\cap {\mathcal{O}}_{\sigma }]$ holds. Since ${\mathcal{O}}_{\sigma }$ is open, to show that ${\mathcal{H}}^{n-1}[{\mathbb{S}}^{n-1}(\mathbf{0},1)\cap {\mathcal{O}}_{\sigma }]>0$, we need only show that ${\mathbb{S}}^{n-1}(\mathbf{0},1)\cap {\mathcal{O}}_{\sigma }\ne \varnothing$. To see this, set $x={\sum }_{i\in \sigma }{p}_i-{\sum }_{j\notin \sigma }{p}_j$. By (5), we have $x\in {\mathcal{O}}_{\sigma }$. Since ${\mathcal{O}}_{\sigma }$ is a cone, we have $x/\left|x\right|\in {\mathbb{S}}^{n-1}(\mathbf{0},1)\cap {\mathcal{O}}_{\sigma }$.
• Part 3 in Lemma 3. From (6), we see that the complement of the union of the ${\mathcal{O}}_{\sigma }$ equals

  $$Z=\bigcup _{j=1}^n\{x\in {\mathbb{R}}^n:x·w_j=0\},$$

  (7)

  which is the union of n linear subspaces of dimension $n-1$.
• Part 4 in Lemma 3. The set Z exhibited in (7) is a cone, because $x·w_j=0$ holds if and only if $\left(\lambda x\right)·w_j=0$, when $\lambda >0$. Observe that the intersection of a linear subspace of dimension $n-1$ with ${\mathbb{S}}^{n-1}(\mathbf{0},1)$ is an $(n-2)$-dimensional sphere of radius 1 centered at the origin, and thus that intersection has ${\mathcal{H}}^{n-1}$-measure 0. So by Part 3, we have ${\mathcal{H}}^{n-1}[{\mathbb{S}}^{n-1}(\mathbf{0},1)\cap Z]=0$. Finally, using Part 1, we have

  $$\begin{array}{cc}\hfill {\mathcal{H}}^{n-1}\left[{\mathbb{S}}^{n-1}(\mathbf{0},1)\right]& ={\mathcal{H}}^{n-1}[{\mathbb{S}}^{n-1}(\mathbf{0},1)\cap Z]+{\mathcal{H}}^{n-1}\left[{\mathbb{S}}^{n-1}(\mathbf{0},1)\cap \left({\cup }_{\sigma \subset \mathfrak{N}}{\mathcal{O}}_{\sigma }\right)\right]\hfill \\ \hfill & =\sum _{\sigma \subset \mathfrak{N}}{\mathcal{H}}^{n-1}[{\mathbb{S}}^{n-1}(\mathbf{0},1)\cap {\mathcal{O}}_{\sigma }]=\sum _{\sigma \subset \mathfrak{N}}{\mathcal{S}}_{\mathbf{0}}\left({\mathcal{O}}_{\sigma }\right).\hfill \end{array}$$
•  □

Lemma 4.

The following hold:

1. 

$C_0={\mathcal{O}}_{\mathfrak{N}}$ and $-C_0={\mathcal{O}}_{\varnothing }$.

2. 

For $i=1,2,\dots ,n$, ${\displaystyle C_i\subset {\mathcal{O}}_{\mathfrak{N}\setminus \left\{i\right\}}\mathrm{and}-C_i\subset {\mathcal{O}}_{\left\{i\right\}}.}$

3. 

If $n\ge 3$, then 

$$\left\{C_0,C_1,\dots ,C_n\right\}\cup \left\{-C_0,-C_1,\dots ,-C_n\right\}$$

is a family of $2(n+1)$ distinct pairwise disjoint sets.

Proof. 

• Part 1 in Lemma 4. Let $x\in C_0$. Then by (3),

  $$x=\sum _{\ell =0}^n{\lambda }_{\ell }(p_{\ell }-p_0)=\sum _{\ell =1}^n{\lambda }_{\ell }{p}_{\ell }$$

  for some ${\lambda }_{\ell }$, with ${\lambda }_{\ell }>0$ for $l=1,\dots ,n.$
  For j with $1\le j\le n$, we have $x·w_j={\lambda }_j>0$. Thus we have $x\in {\mathcal{O}}_{\mathfrak{N}}$ and $-x\in {\mathcal{O}}_{\varnothing }$. Since $x\in C_0$ was arbitrary, we have $C_0\subset {\mathcal{O}}_{\mathfrak{N}}$ and $-C_0\subset {\mathcal{O}}_{\varnothing }$.
  We see the converse as follows: Since the vectors $p_1,p_2,\dots ,p_n$ are linearly independent, any $y\in {\mathbb{R}}^n$ can be written $y={\sum }_{\ell =1}^n{\lambda }_{\ell }{p}_{\ell }$. If y is in ${\mathcal{O}}_{\mathfrak{N}}$, then for each j, ${\lambda }_j=y·w_j>0$ holds. Thus for $y\in {\mathcal{O}}_{\mathfrak{N}}$, we have

  $$y=\sum _{\ell =1}^n{\lambda }_{\ell }{p}_{\ell }=\sum _{\ell =1}^n{\lambda }_{\ell }(p_{\ell }-p_0)$$

  with all the ${\lambda }_{\ell }$ being positive. We conclude that $y\in C_0$. Arguing similarly, we see that ${\mathcal{O}}_{\varnothing }\subset -C_0$.
• Part 2 in Lemma 4. Let $x\in C_i$. Then by (3),

  $$x=\sum _{\ell =0}^n{\lambda }_{\ell }(p_{\ell }-p_i)=\sum _{\ell =1}^n{\lambda }_{\ell }{p}_{\ell }$$

  for some ${\lambda }_{\ell }$, with ${\lambda }_{\ell }>0$, for $l=1,\dots ,n.$
  For any integer j with $1\le j\le n$ and $j\ne i$, we have

  $$x·w_j=\sum _{\ell =0}^n{\lambda }_{\ell }(p_{\ell }·w_j-p_i·w_j)={\lambda }_j>0.$$
  We also have

  $$\begin{array}{cc}\hfill x·w_i& =\sum _{\ell =0}^n{\lambda }_{\ell }(p_{\ell }·w_i-p_i·w_i)=\sum _{\ell =0}^n{\lambda }_{\ell }{p}_{\ell }·w_i-\sum _{\ell =0}^n{\lambda }_{\ell }{p}_i·w_i\hfill \\ \hfill & =\sum _{\ell =0}^n{\lambda }_{\ell }{\delta }_{\ell i}-\sum _{\ell =0}^n{\lambda }_{\ell }{\delta }_{ii}={\lambda }_i-\sum _{\ell =0}^n{\lambda }_{\ell }=-\sum _{\ell =0}^{i-1}{\lambda }_{\ell }-\sum _{\ell =i+1}^n{\lambda }_{\ell }<0.\hfill \end{array}$$
  Thus we have $x\in {\mathcal{O}}_{\mathfrak{N}\setminus \left\{i\right\}}$ and $-x\in {\mathcal{O}}_{\left\{i\right\}}$.
• Part 3 in Lemma 4. Through Part 1 and Part 2, we know that

  $$\left.\begin{array}{cc}{C}_0\subset {\mathcal{O}}_{\mathfrak{N}},\hfill & -C_0\subset {\mathcal{O}}_{\varnothing }\hfill \\ C_i\subset {\mathcal{O}}_{\mathfrak{N}\setminus \left\{i\right\}},\hfill & -C_i\subset {\mathcal{O}}_{\left\{i\right\}},\hfill & \hfill \mathrm{for}i=1,2,\dots ,n.\end{array}\right\}$$

  (8)
  So it suffices to show that (8) exhibits $2(n+1)$ pairwise disjoint sets. Through Lemma 3, the sets in (8) will be disjointed provided that the following subsets of $\mathfrak{N}$ are distinct:

  $$\left.\begin{array}{cc}\mathfrak{N},\hfill & \varnothing \hfill \\ \mathfrak{N}\setminus \left\{i\right\},\hfill & \left\{i\right\},\hfill & \hfill \mathrm{for}i=1,2,\dots ,n.\end{array}\right\}$$

  (9)
  Because $n\ge 3$, the set $\mathfrak{N}\setminus \left\{i\right\}$ has more elements than the singleton set $\left\{j\right\}$, so (9) does represent $2(n+1)$ distinct sets.
•  □

We can now prove Part 1 of our main result when $n\ge 4$. The case $n=3$ will require more work.

Proof of Theorem 1 Part 1 when n = 4 .

 

By (4) and the fact that ${\mathcal{S}}_{\mathbf{0}}\left(C_i\right)={\mathcal{S}}_{\mathbf{0}}(-C_i)$, we have

$$2\sum _{i=0}^n{\mathcal{S}}_{\mathbf{0}}(\mathrm{\Delta }-p_i)=\sum _{i=0}^n{\mathcal{S}}_{\mathbf{0}}\left(C_i\right)+\sum _{i=0}^n{\mathcal{S}}_{\mathbf{0}}(-C_i).$$

Each of the $2(n+1)$ cones in ${\{C_i,-C_i\}}_{i=0}^n$ is contained in a distinct open cone ${\mathcal{O}}_{\sigma }$, $\sigma \subset \mathfrak{N}$. Since $n\ge 4$ implies $2(n+1)<2^n$, there are more cones ${\mathcal{O}}_{\sigma }$ than there are $C_i$’s and $-C_i$’s, so there must be some solid angle not accounted for by the $C_i$’s and $-C_i$’s.

Through Lemma 3, Part 2, we have ${\mathcal{S}}_{\mathbf{0}}\left({\mathcal{O}}_{\sigma }\right)>0$, for each $\sigma \subset \mathfrak{N}$. Through Lemma 4, Part 1, we have ${\mathcal{O}}_{\mathfrak{N}}=C_0$ and ${\mathcal{O}}_{\varnothing }=-C_0$. Thus we know ${\mathcal{S}}_{\mathbf{0}}\left(C_0\right)>0$, and we have

$$\begin{array}{cc}\hfill 0& <2\sum _{i=0}^n{\mathcal{S}}_{\mathbf{0}}\left(C_i\right)=\sum _{i=0}^n{\mathcal{S}}_{\mathbf{0}}\left(C_i\right)+\sum _{i=0}^n{\mathcal{S}}_{\mathbf{0}}(-C_i)\hfill \\ \hfill & \le {\mathcal{S}}_{\mathbf{0}}\left({\mathcal{O}}_{\mathfrak{N}}\right)+{\mathcal{S}}_{\mathbf{0}}\left({\mathcal{O}}_{\varnothing }\right)+\sum _{i=1}^n{\mathcal{S}}_{\mathbf{0}}\left({\mathcal{O}}_{\mathfrak{N}\setminus \left\{i\right\}}\right)+\sum _{i=1}^n{\mathcal{S}}_{\mathbf{0}}\left({\mathcal{O}}_{\left\{i\right\}}\right)\hfill \\ \hfill & <\sum _{\sigma \subset \mathfrak{N}}{\mathcal{S}}_{\mathbf{0}}\left({\mathcal{O}}_{\sigma }\right)=A_{n-1}.\hfill \end{array}$$

(10)

 □

When $n=3$, there are four $C_i$’s and four $-C_i$’s. Since there are eight cones ${\mathcal{O}}_{\sigma }$, $\sigma \subset \mathfrak{N}$, we have no left-over ${\mathcal{O}}_{\sigma }$ to create the strict inequality that we obtained in (10). Instead, we will need to use the fact that there is yet another non-empty open cone $\mathrm{\Sigma }$, disjointed from $C_1$ and also contained in ${\mathcal{O}}_{\mathfrak{N}\setminus \left\{1\right\}}$. That cone is what we exhibit in Lemma 5 (see Figure 1).

Lemma 5.

Suppose that $n=3$ and let Σ denote the open cone generated by the n-simplex with vertices $p_0=\mathbf{0}$, $p_2$, $p_3$, and $-p_1+p_2+p_3$. Then the following hold:

1. 

$\varnothing \ne \mathrm{\Sigma }\subset {\mathcal{O}}_{\mathfrak{N}\setminus \left\{1\right\}}$,

2. 

$\mathrm{\Sigma }\cap C_1=\varnothing$.

Proof. 

• Part 1 in Lemma 5. Let $x\in \mathrm{\Sigma }$. Then x can be written as

  $$\begin{array}{ccc}\hfill x& =& {\lambda }_1\left(-p_1+p_2+p_3\right)+{\lambda }_2{p}_2+{\lambda }_3{p}_3\hfill \\ \hfill & =& -{\lambda }_1{p}_1+({\lambda }_1+{\lambda }_2)p_2+({\lambda }_1+{\lambda }_3)p_3,\hfill \end{array}$$

  (11)

  for some positive numbers ${\lambda }_1$, ${\lambda }_2$, and ${\lambda }_3$. Hence, $\mathrm{\Sigma }$ is non-empty. We then see that $x·w_1=-{\lambda }_1<0$, $x·w_2={\lambda }_1+{\lambda }_2>0$, and $x·w_3={\lambda }_1+{\lambda }_3>0$, so we have $x\in {\mathcal{O}}_{\mathfrak{N}\setminus \left\{1\right\}}$.
• Part 2 in Lemma 5. By (3), any point $y\in (\mathrm{\Delta }-p_1)$, as defined in Notation 1, Part 5, can be written in the form

  $$\begin{array}{ccc}\hfill y& =& {\mu }_1\left(-p_1\right)+{\mu }_2(p_2-p_1)+{\mu }_3(p_3-p_1)\hfill \\ \hfill & =& -({\mu }_1+{\mu }_2+{\mu }_3)p_1+{\mu }_2{p}_2+{\mu }_3{p}_3,\hfill \end{array}$$

  (12)

  for some choice of positive numbers ${\mu }_{\ell }$. If $x=y\in \mathrm{\Sigma }\cap C_1$, then comparing (11) and (12), we see that

  $${\lambda }_1={\mu }_1+{\mu }_2+{\mu }_3,{\lambda }_1+{\lambda }_2={\mu }_2,{\lambda }_1+{\lambda }_3={\mu }_3.$$

  So we have

  $${\lambda }_1={\mu }_1+({\lambda }_1+{\lambda }_2)+({\lambda }_1+{\lambda }_3),$$

  and thus

  $${\mu }_1=-({\lambda }_1+{\lambda }_2+{\lambda }_3),$$

  contradicting the fact that all the $\lambda$’s and $\mu$’s are positive. □

Proof of Theorem 1 Part 1 when n = 3 .

 

Arguing similarly to the proof of Theorem 1 part 1 when $n\ge 4$, we use Lemmas 3–5 to obtain

$$\begin{array}{cc}\hfill 0& <\sum _{i=0}^3{\mathcal{S}}_{\mathbf{0}}\left(C_i\right)+\sum _{i=0}^3{\mathcal{S}}_{\mathbf{0}}(-C_i)\hfill \\ \hfill & <{\mathcal{S}}_{\mathbf{0}}\left(C_0\right)+\left({\mathcal{S}}_{\mathbf{0}}\left(C_1\right)+\mathcal{S}\left(\mathrm{\Sigma }\right)\right)+{\mathcal{S}}_{\mathbf{0}}\left(C_2\right)+{\mathcal{S}}_{\mathbf{0}}\left(C_3\right)+\sum _{i=0}^3{\mathcal{S}}_{\mathbf{0}}(-C_i)\le \sum _{\sigma \subset \mathfrak{N}}{\mathcal{S}}_{\mathbf{0}}\left({\mathcal{O}}_{\sigma }\right)=A_2.\hfill \end{array}$$

 □

3. Theorem 1 Part 2

In order to make all the solid angles of an n-simplex small, we will split the vertices into two tightly clustered groups in widely separated orthogonal planes.

In this section, it will no longer be convenient to assume that the origin is one of the vertices. Also, in order to avoid confusion, we will not use the index 0 on any of the vertices. When $n=3$, the orthogonal planes are actually orthogonal lines.

Figure 2 illustrates such an arrangement when $n=3$.

In the figure, one line is the horizontal line passing through p and the other line is the vertical line through q. The points p and q are chosen so that the distance between the lines is $\rho =|p-q|$. Two points, $p_1$ and $p_2$, are chosen on the line through p. Similarly, two points, $q_1$ and $q_2$, are chosen on the line through q. We let d be an upper bound for $|p_2-p_1|$ and $|q_2-q_1|$.

It would be laborious to make an exact computation of the solid angles in the simplices we will construct. Instead we will show that the cone generated at any vertex lies in the part of ${\mathbb{S}}^{n-1}(\mathbf{0},1)$ contained between a plane through the origin and another parallel plane (The part of ${\mathbb{S}}^2(0,1)$ between two parallel planes is called a zone of two bases). The next lemma will provide an estimate, (13), for the area of that region.

Lemma 6.

Suppose that $n\ge 3$. For $h\ge 0$, it holds that

$${\mathcal{H}}^{n-1}\left[{\mathbb{S}}^{n-1}(\mathbf{0},1)\cap \{z:0\le z·{\mathbf{e}}_n\le h\}\right]\le A_{n-2}h.$$

(13)

Proof. 

If we write $z=(x,y)$, where $z\in {\mathbb{R}}^n$, $x\in {\mathbb{R}}^{n-1}$, and $y\in \mathbb{R}$, what we need to prove is that

$${\mathcal{H}}^{n-1}\left\{(x,y)\in {\mathbb{R}}^{n-1}\times \mathbb{R}:\sqrt{1-h^2}\le \left|x\right|\le 1,y=\sqrt{1-x^2}\right\}\le A_{n-2}h.$$

(14)

Let $f:{\mathbb{R}}^{n-1}\cap \{x:|x|\le 1\}\to \mathbb{R}$ be given by $f\left(x\right)=\sqrt{1-{\left|x\right|}^2}$. Then the quantity on the left-hand side of (14) is given by the integral

$${\int }_S\sqrt{1+{\left|Df\right|}^2}d{\mathcal{L}}^{n-1}={\int }_S{\displaystyle \frac{1}{\sqrt{1-{\left|x\right|}^2}}}d{\mathcal{L}}^{n-1},$$

(15)

where $S=\{x\in {\mathbb{R}}^{n-1}:\sqrt{1-h^2}<|x|<1\}$ and ${\mathcal{L}}^{n-1}$ is that Lebesgue measure on ${\mathbb{R}}^{n-1}$. Because the integrand in (15) is constant for constant values of $|x|$, we can use what is essentially the “method of cylindrical shells” from first-year calculus. We see that

$$\begin{array}{ccc}\hfill {\int }_S{\displaystyle \frac{1}{\sqrt{1-{\left|x\right|}^2}}}d{\mathcal{L}}^{n-1}& =& A_{n-2}{\int }_{\sqrt{1-h^2}}^1{r}^{n-2}{(1-r^2)}^{-1/2}dr\hfill \\ & \le & A_{n-2}{\int }_{\sqrt{1-h^2}}^{1}r{(1-r^2)}^{-1/2}dr=A_{n-2}h.\hfill \end{array}$$

 □

As indicated in the opening paragraph of this section, our plan for constructing a simplex with a small total solid angle involves separating the vertices into two groups.

We follow that plan in the notation below. The key parameter in estimating the solid angle is the ratio $d/\rho$, so to simplify the example, we will vary only $\rho$. We also simplify by letting the smaller group have two vertices.

Notation 3.

Suppose that $n\ge 3$. Set $\ell =n-1$.

1. 

Set $p_1=-\frac{1}{2}\rho {\mathbf{e}}_1$ and $p_2={\mathbf{e}}_2-\frac{1}{2}\rho {\mathbf{e}}_1$.

2. 

Set $q_1=\frac{1}{2}\rho {\mathbf{e}}_1$ and $q_j={\mathbf{e}}_{j+1}+\frac{1}{2}\rho {\mathbf{e}}_1$, for $j=2,3\dots ,n-1$.

Proof of Theorem 1 Part 2.

 

Let $ϵ>0$ be given. With the notation above, if we choose a positive $\rho$ so that $\rho >(n+1)A_{n-2}/ϵ$, then we will show below that the sum of the solid angles of $\mathrm{\Delta }$ measured at its vertices is less than $ϵ$.

We estimate the solid angle of $\mathrm{\Delta }$ measured at $q_{n-1}$, the other cases are similar, but simpler, and yield the same estimate.

A generic point of the open cone generated by $\mathrm{\Delta }-q_{n-1}$ is

$$\begin{array}{ccc}\hfill x& =& {\lambda }_1(p_1-q_{n-1})+{\lambda }_2(p_2-q_{n-1})++\sum _{j=1}^{n-2}{\mu }_j(q_j-p_1)\hfill \\ & =& {\lambda }_1(-\rho {\mathbf{e}}_1-{\mathbf{e}}_n)+{\lambda }_2(-\rho {\mathbf{e}}_1+{\mathbf{e}}_2-{\mathbf{e}}_n)-{\mu }_1{\mathbf{e}}_n\hfill \\ & & +\sum _{j=2}^{n-2}{\mu }_j(-\rho {\mathbf{e}}_1+{\mathbf{e}}_{j+1}-{\mathbf{e}}_n)\hfill \\ & =& -\left({\lambda }_1+{\lambda }_2+\sum _{j=2}^{n-2}{\mu }_j\right)\rho {\mathbf{e}}_1+{\lambda }_2{\mathbf{e}}_2-\sum _{j=2}^{n-2}{\mu }_j{\mathbf{e}}_{j+1}\hfill \\ & & -\left({\lambda }_1+{\lambda }_2+\sum _{j=2}^{n-2}{\mu }_j\right){\mathbf{e}}_n,\hfill \end{array}$$

where the ${\lambda }_i$ and ${\mu }_j$ are all positive. Observe then that

$$x·{\mathbf{e}}_n=-\left({\lambda }_1+{\lambda }_2+\sum _{j=2}^{n-2}{\mu }_j\right)\mathrm{and}\left|x\right|\ge \left({\lambda }_1+{\lambda }_2+\sum _{j=2}^{n-2}{\mu }_j\right)\rho .$$

Thus we have

$${\mathbb{S}}^{n-1}(\mathbf{0},1)\cap \mathrm{cone}[\mathrm{\Delta }-q_{n-1}]\subset {\mathbb{S}}^{n-1}(\mathbf{0},1)\cap \{z:0\ge z·{\mathbf{e}}_n\ge -1/\rho \}.$$

Since reflection through an $(n-1)$-dimensional plane preserves area, Lemma 6 gives us the estimate

$${\mathcal{S}}_{\mathbf{0}}(\mathrm{\Delta }-q_{n-1})\le A_{n-2}/\rho <{\displaystyle \frac{ϵ}{n+1}},$$

and the result follows. □

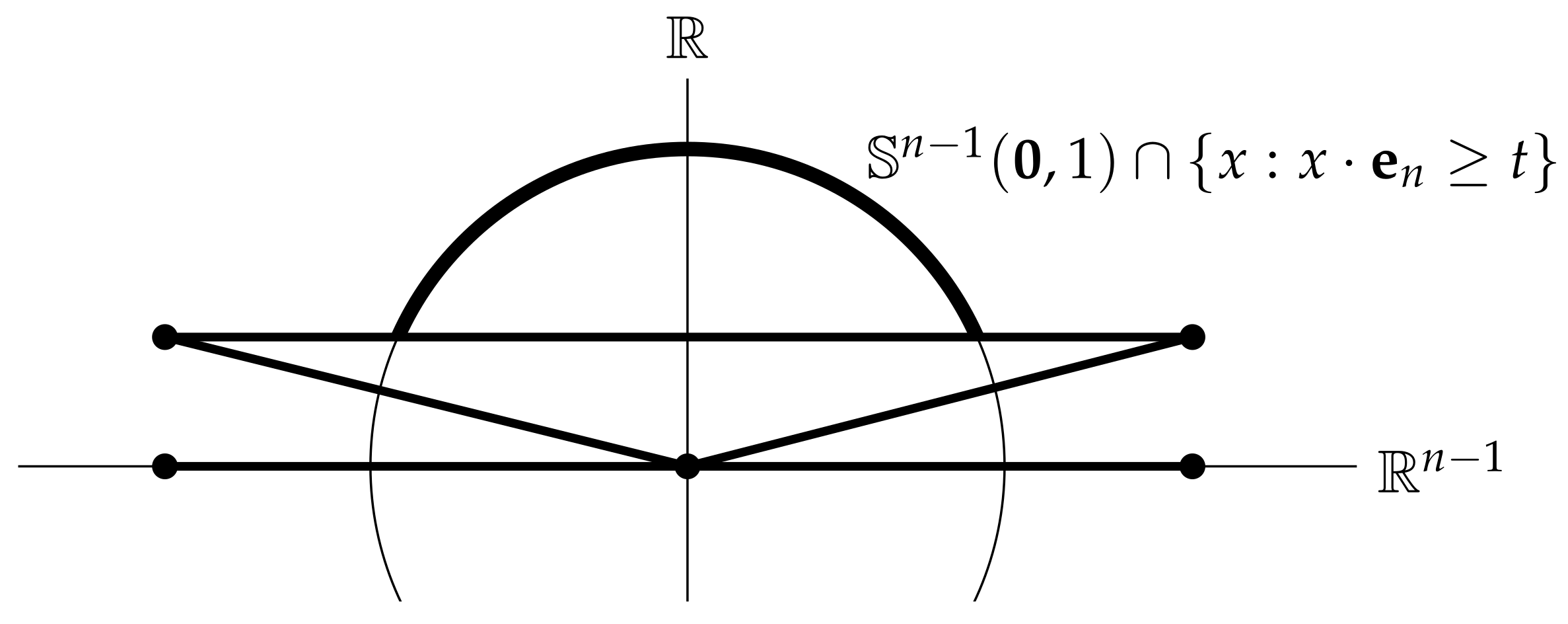
4. Theorem 1 Part 3

We identify ${\mathbb{R}}^n$ with ${\mathbb{R}}^{n-1}\times \mathbb{R}$. Start with an $(n-1)$-simplex, D, in ${\mathbb{R}}^{n-1}$ that contains the unit sphere in ${\mathbb{R}}^{n-1}$. Appending $\mathbf{0}$ to the set of vertices of D would create a degenerate n-simplex—something we have been avoiding. So first we lift the vertices of D slightly in the direction of ${\mathbf{e}}_n$, then we append $\mathbf{0}$. Since D contains the unit ball in ${\mathbb{R}}^{n-1}$, the lifted simplex will have almost an entire hemisphere above it and the angle subtended at $\mathbf{0}$ by the lifted simplex can be made as close to $A_{n-1}/2$ as we wish (see Figure 3). The remainder of this section seeks to make the preceding intuition precise.

Proof of Theorem 1 Part 3.

 

First, we need to construct an $(n-1)$-simplex $\mathrm{\Delta }\subset {\mathbb{R}}^{n-1}\times \left\{0\right\}$ containing ${\mathbb{S}}^{n-2}(\mathbf{0},1)\times \left\{0\right\}$. To that end, consider the $(n-1)$-simplex ${\mathrm{\Delta }}^{\prime }$ in ${\mathbb{R}}^{n-1}\times \left\{0\right\}$ $w_i=\sqrt{n-1}(1+\sqrt{n-1}){\mathbf{e}}_i$, $i=1,2,\dots ,n-1$, for its first $n-1$ vertices and with the origin, $\mathbf{0}$, for its nth vertex. It is a routine exercise to check that the distance from $p={\sum }_{\ell =1}^{n-1}{\mathbf{e}}_{\ell }$ to each of the faces of ${\mathrm{\Delta }}^{\prime }$ equals 1. Thus ${\mathbb{S}}^{n-2}(p,1)\times \left\{0\right\}\subset {\mathrm{\Delta }}^{\prime }$.

We then translate by $-p$, to define the simplex $\mathrm{\Delta }\subset {\mathbb{R}}^{n-1}\times \left\{0\right\}$ with $v_i=\sqrt{n-1}(1+\sqrt{n-1}){\mathbf{e}}_i-{\sum }_{\ell =1}^{n-1}{\mathbf{e}}_{\ell }$, $i=1,2,\dots ,n-1$, for its first $n-1$ vertices and with $v_n=-p=-{\sum }_{\ell =1}^{n-1}{\mathbf{e}}_{\ell }$ for its nth vertex. We see that $\mathrm{\Delta }$ contains ${\mathbb{S}}^{n-2}(\mathbf{0},1)\times \left\{0\right\}$.

Let $ϵ>0$ be given. Choose a positive t with $t<ϵ/A_{n-2}$. Let $\mathrm{\Delta }\left(t\right)$ be the n-simplex with vertices $p_0=\mathbf{0}$ and

$$p_i=v_i+t{\mathbf{e}}_n,i=1,2,\dots ,n.$$

The cone generated by $\mathrm{\Delta }\left(t\right)$ contains

$${\mathbb{S}}^{n-1}(\mathbf{0},1)\cap \{x:x·{\mathbf{e}}_n\ge t\},$$

so

$${\mathcal{S}}_{\mathbf{0}}\left(\mathrm{\Delta }\left(t\right)\right)\ge {\displaystyle \frac{A_{n-1}}{2}}-{\mathcal{H}}^{n-1}\left[{\mathbb{S}}^{n-1}(\mathbf{0},1)\cap \{x:x·{\mathbf{e}}_n<t\}\right]$$

holds. Using the estimate

$${\mathcal{H}}^{n-1}\left[{\mathbb{S}}^{n-1}(\mathbf{0},1)\cap \{x:x·{\mathbf{e}}_n<t\}\right]\le A_{n-2}t$$

from Lemma 6, we see that

$$\sum _{i=0}^n{\mathcal{S}}_{\mathbf{0}}[\mathrm{\Delta }\left(t\right)-p_i]\ge {\mathcal{S}}_{\mathbf{0}}\left(\mathrm{\Delta }\left(t\right)\right)\ge {\displaystyle \frac{A_{n-1}}{2}}-A_{n-2}t>{\displaystyle \frac{A_{n-1}}{2}}-ϵ,$$

as required. □