A Discrete Schwarzian Derivative via Circle Packing
Abstract
1. Introduction
2. Background
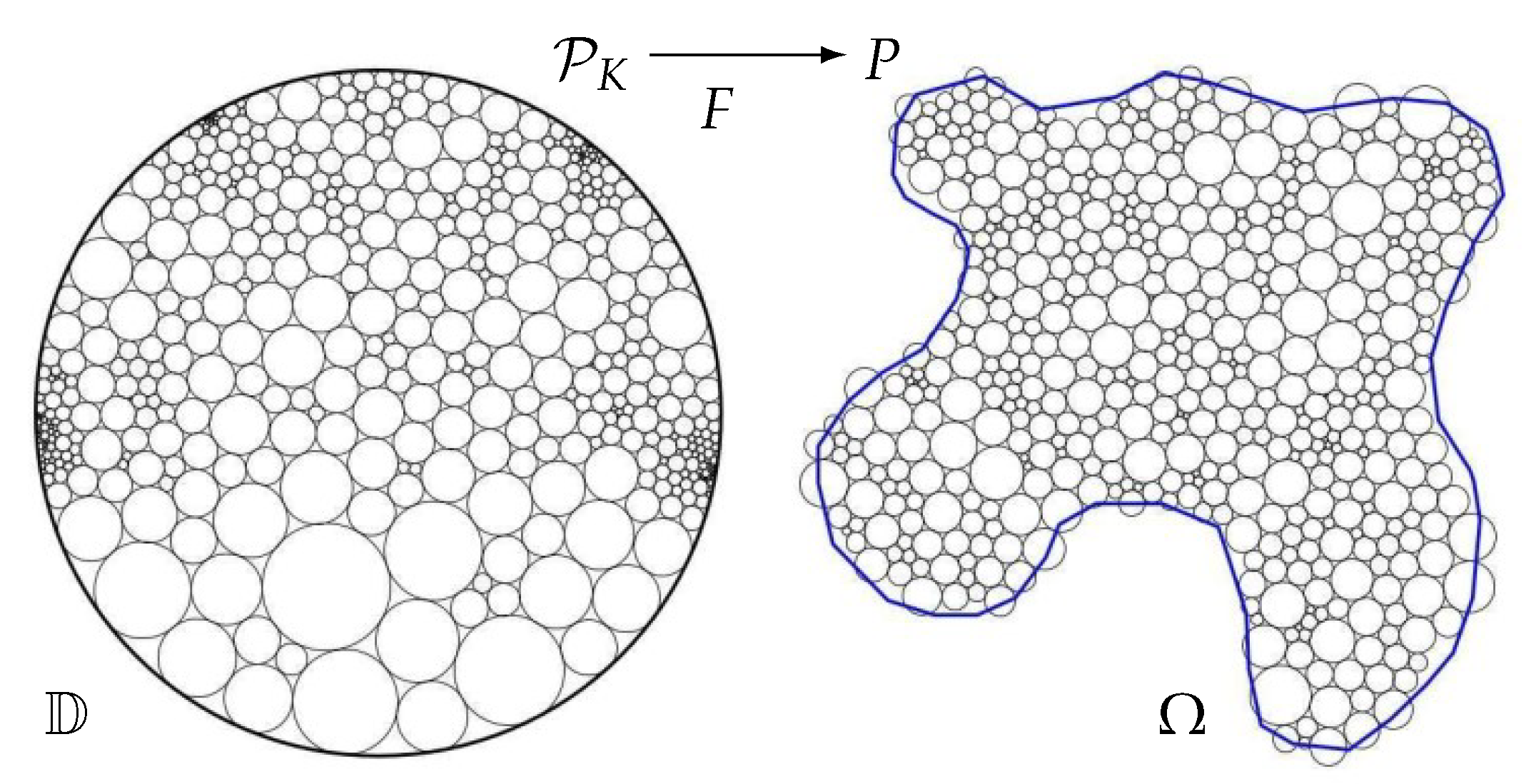
2.1. On Circle Packing
2.2. On Discrete Analytic Functions
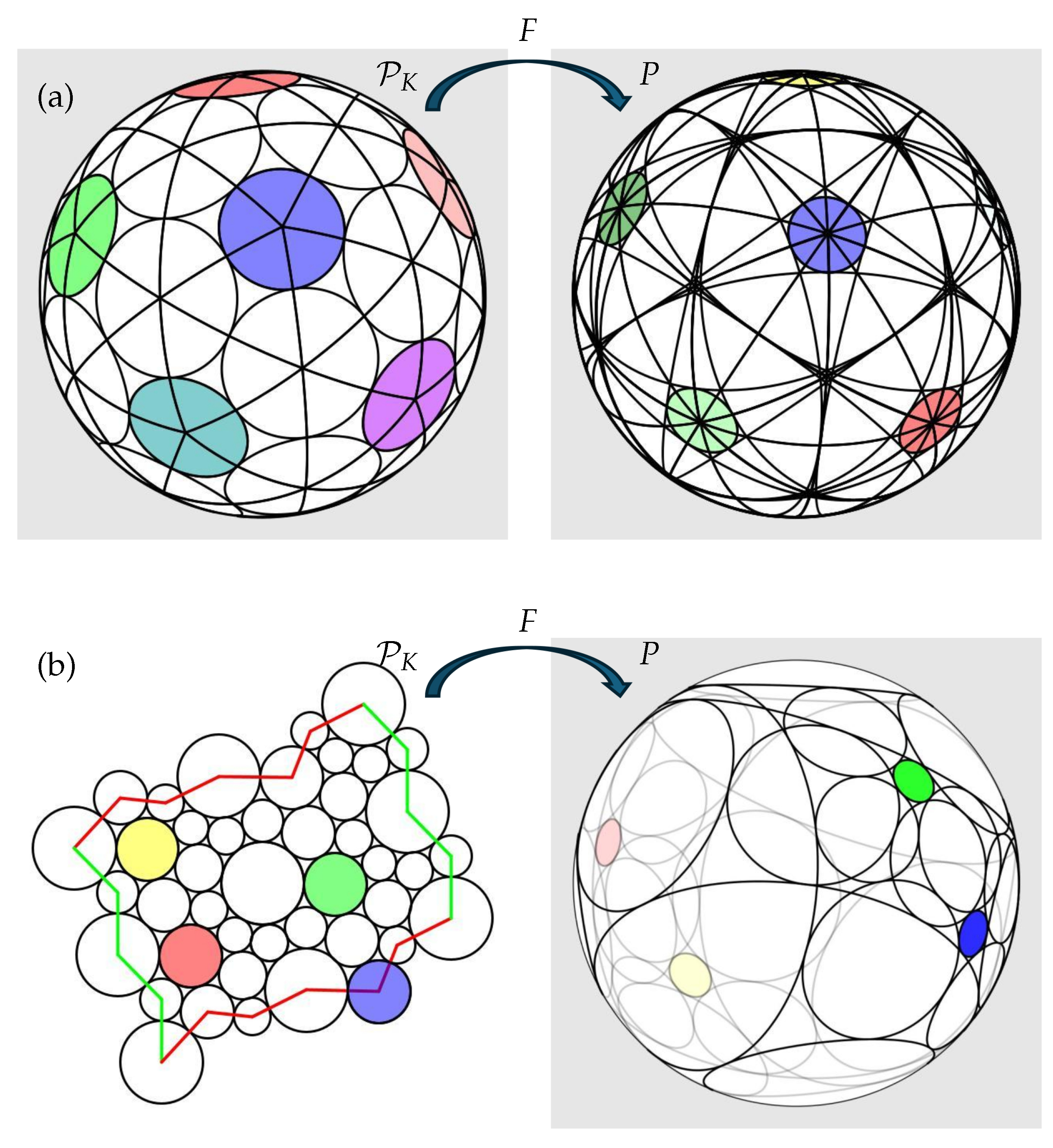
2.3. On Möbius Transformations
3. Classical, Discrete, and Intrinsic
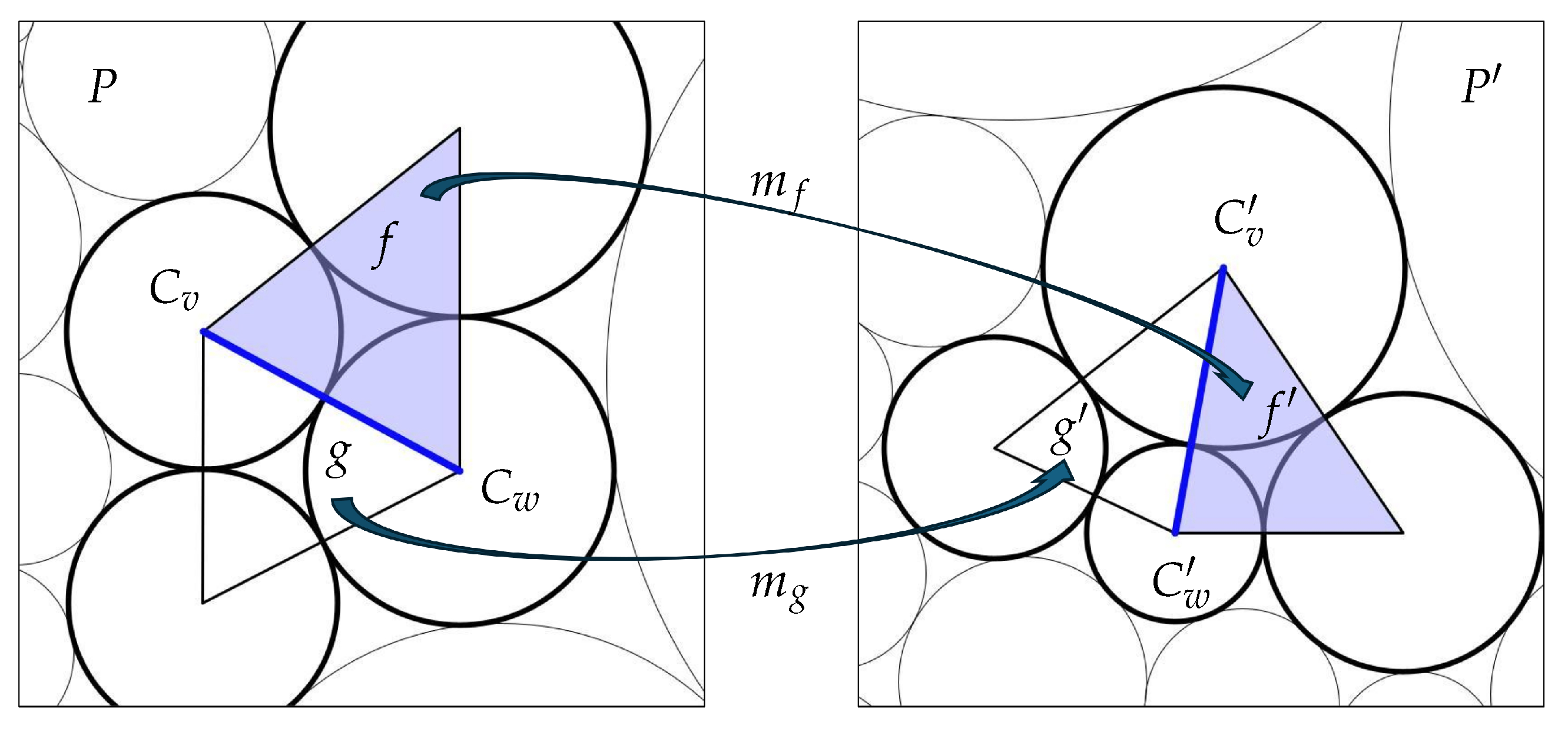
3.1. Patches
- Suppose that denotes the edge e but with the opposite orientation. Then, , implying .
- if and only if is the identity.
- If F itself were Möbius, then and for every interior edge e. Conversely, if for every interior edge e, then a simple face-to-face continuation argument would show that F itself is Möbius, with for every face f.
- Suppose we follow F by a Möbius transformation m, say . The new face Möbius maps for are and . Since and , note thatThe operator M is therefore Möbius invariant. In particular, this implies that the discrete Schwarzian derivative of a discrete analytic function F displays Möbius invariance like that of the Schwarzian derivative of a classical analytic function .
- Pre-composition with a Möbius transformation is a different matter. Computations in Appendix A.3 show that the discrete chain rule under pre-composition diverges slightly from the classical rule of (3); see (A10).
- It is very likely that, if a sequence of discrete analytic functions converges on compacta to a classical analytic function , then the sequence also converges on compacta to . Results of Z–X. He and Oded Schramm in [13] can be used to confirm this for packings with hexagonal combinatorics, but it remains open for more general circle packings.
3.2. Intrinsic Schwarzians
4. Packing Layouts
The Difficulty
- Criteria: Given a label R of putative radii, one can directly compute the set of associated angle sums at the vertices of K. R is a packing label if and only if is an integer multiple of for every interior v.
- Monotonicities: There are simple monotonicities in the effects that adjustments in radius labels have on associated angle sums. In particular, a packing label is the zero set of a convex functional, guaranteeing the existence and uniqueness (and computability) of solutions.
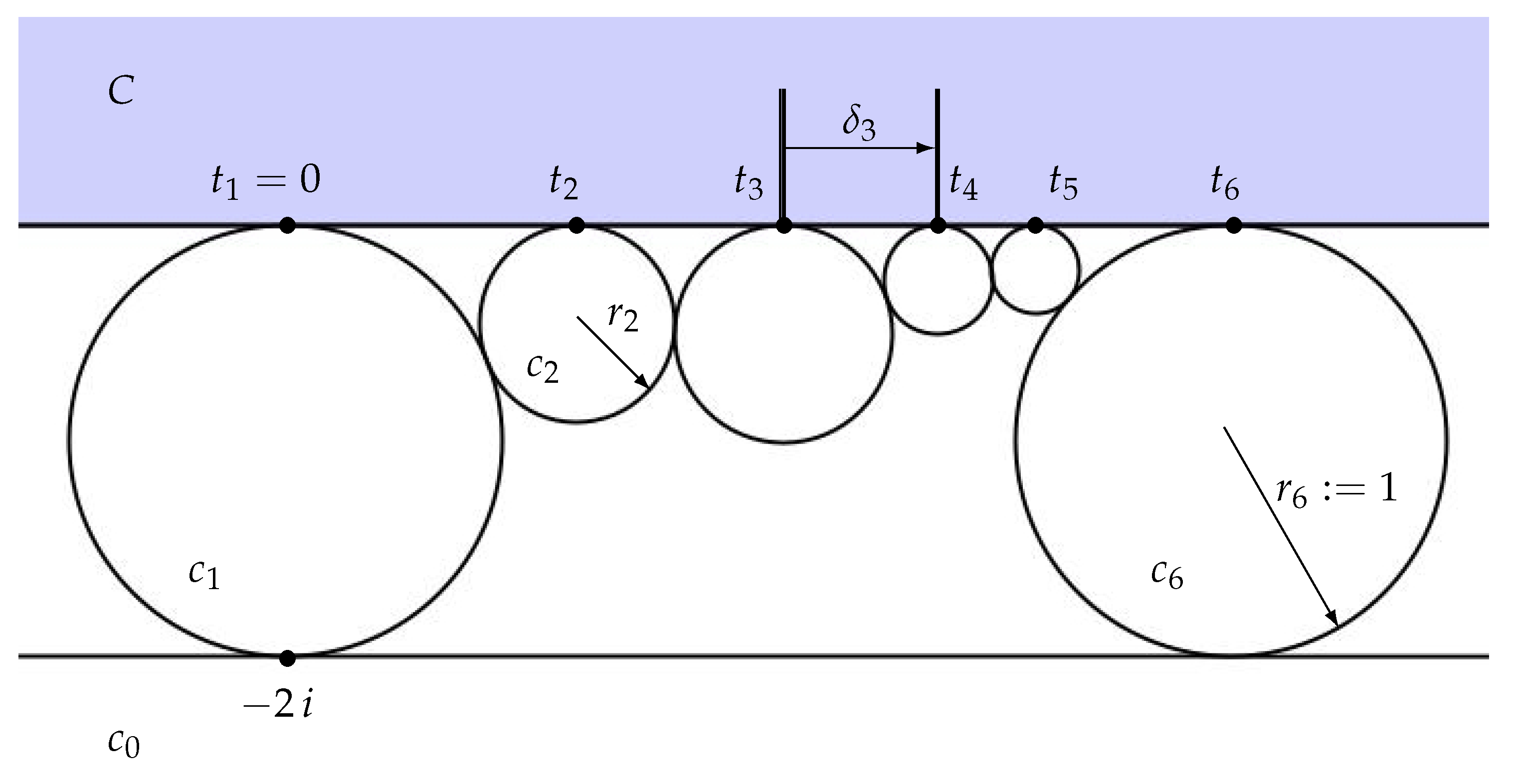
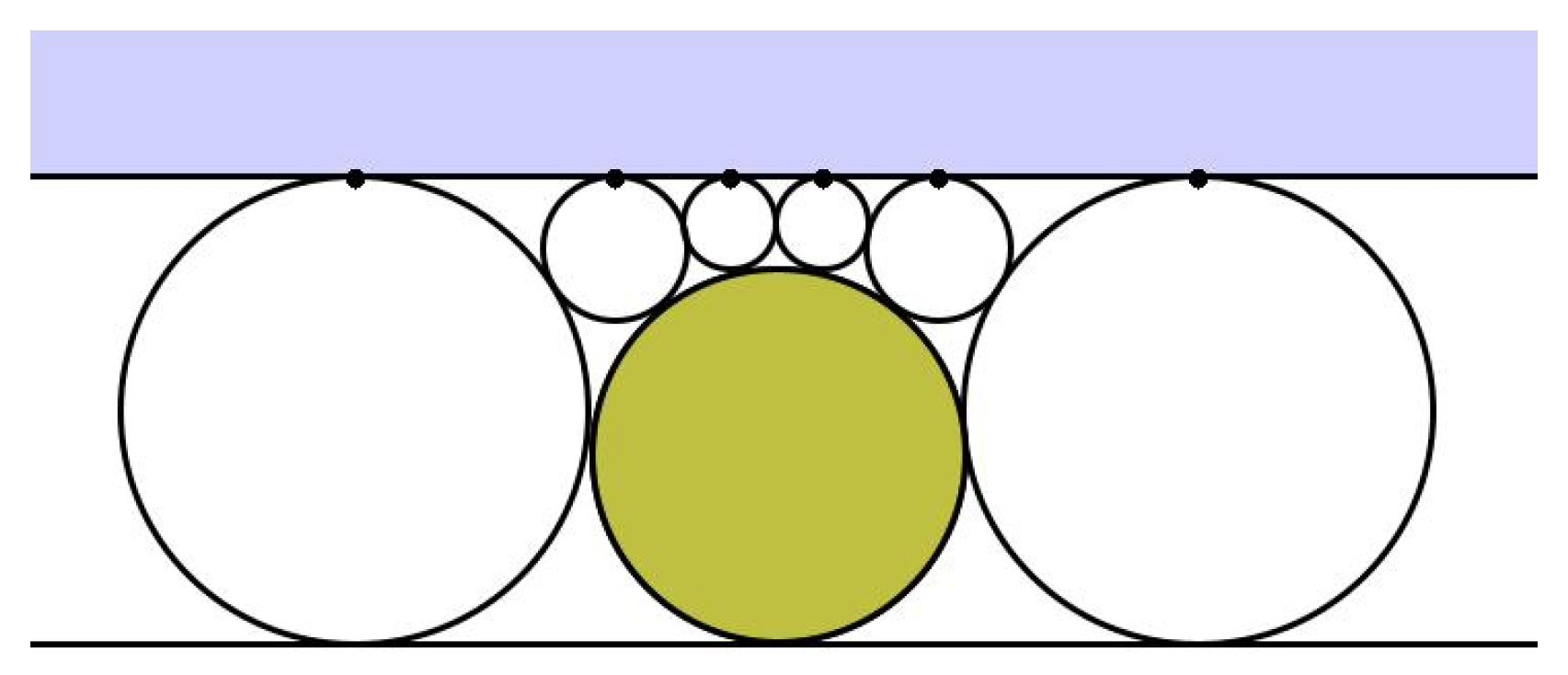
5. Flowers
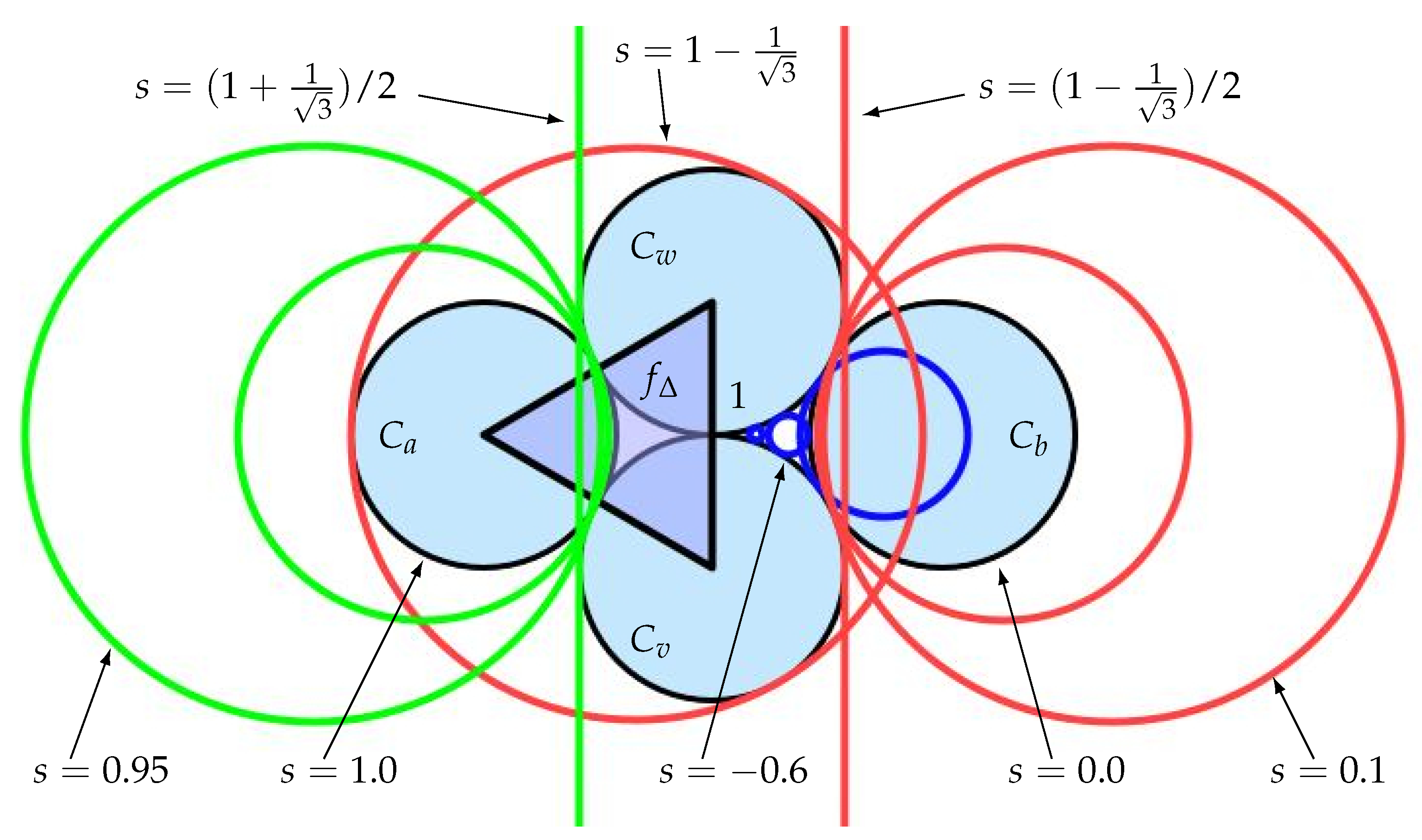
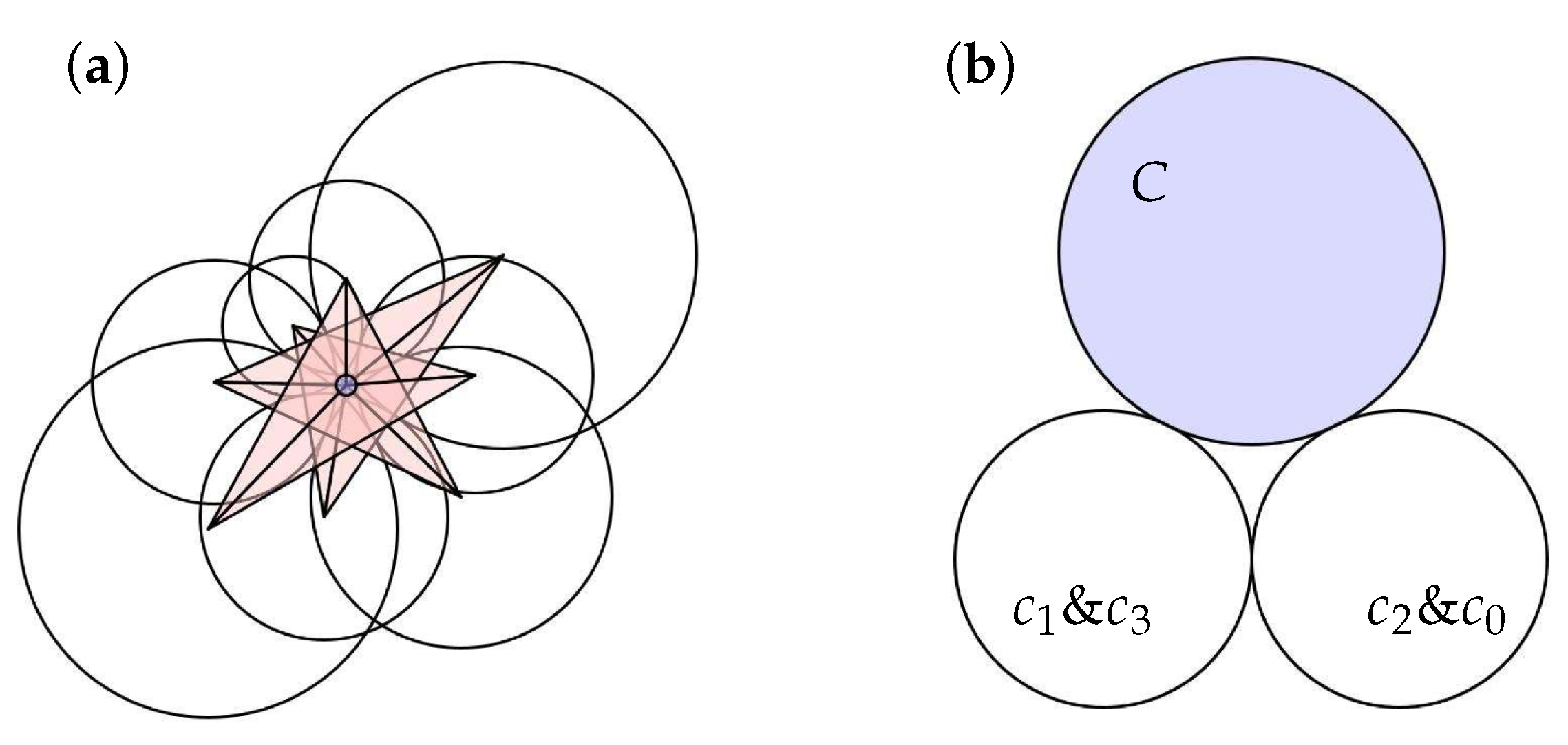
5.1. Notation and Preliminaries
- (a)
- The flower may fail to close; that is, may fail to be tangent to .
- (b)
- The patch may fail to have schwarzian .
- (c)
- The patch may fail to have schwarzian .
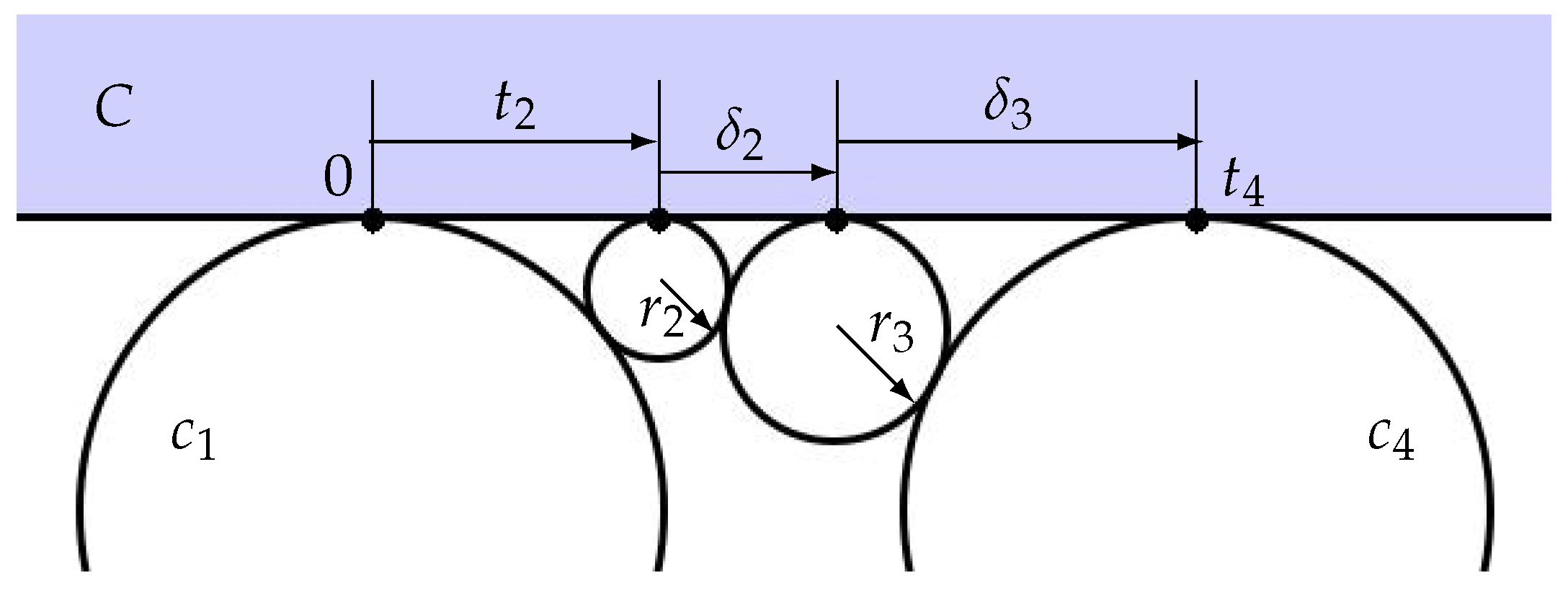
5.2. Flower Layouts
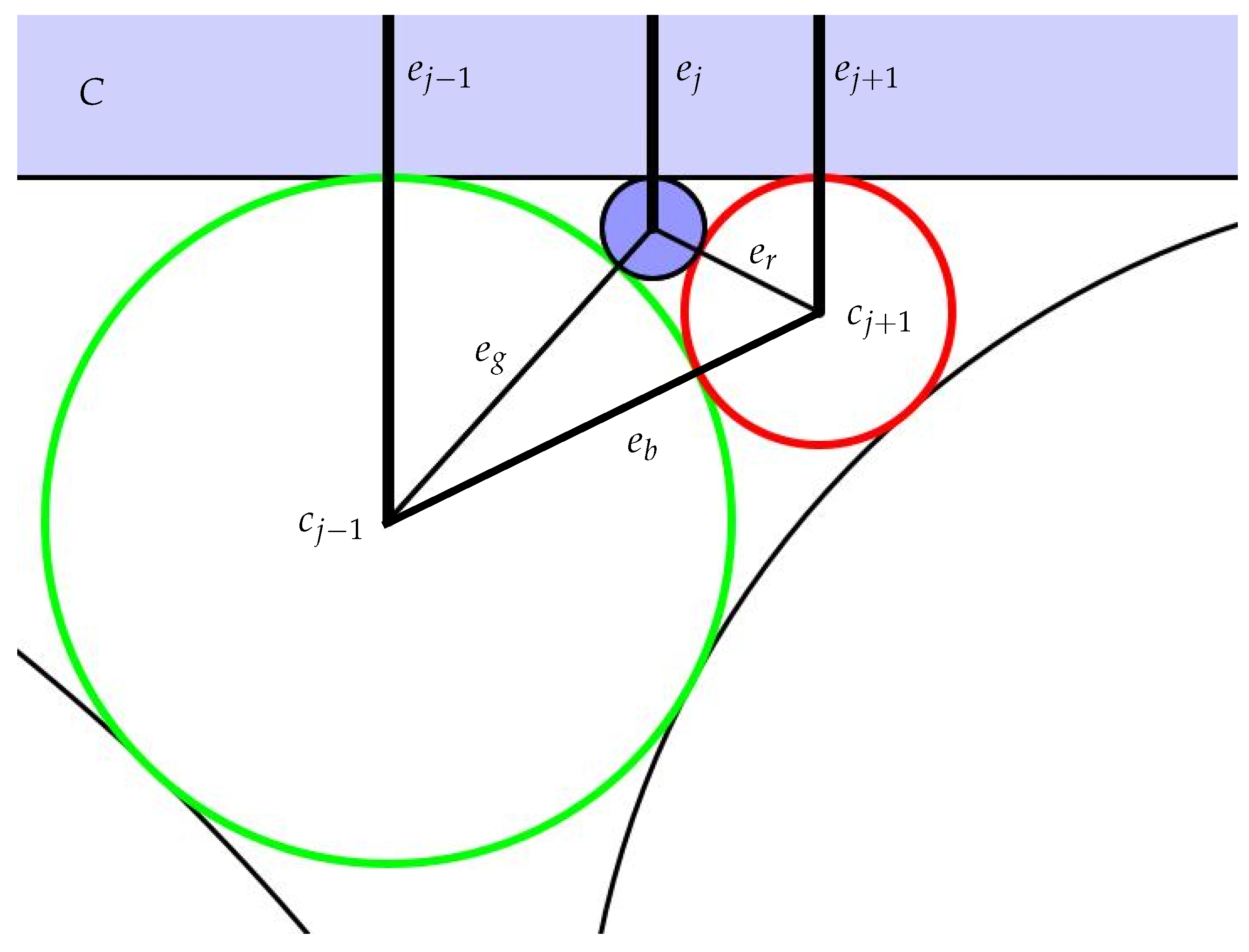
- (1)
- We start with the half planes C and and the circle in their normalized positions.
- (2)
- With in place and given the schwarzian for its edge, the formulas of (A2) in Appendix A.1 yield the tangency point and radius of .
- (3)
- With and in place and given , we are in the “generic” Situation 3 of Appendix A.1, but in the special case where . In particular, we can place by using (A3) to compute radius and displacement , leading to tangency point .
- (4)
- Hereafter, we remain in the generic Situation 3, so we can place the remaining petals by inductively applying (A3) to compute radii and the displacements to determine the tangency points .
- (a)
- If , fails to be tangent to —and the flower does not close up.
- (b)
- If after the final application of (A3) would mean that is not the schwarzian for patch .
- (c)
- If then (A1) tells us that is not the schwarzian for patch .
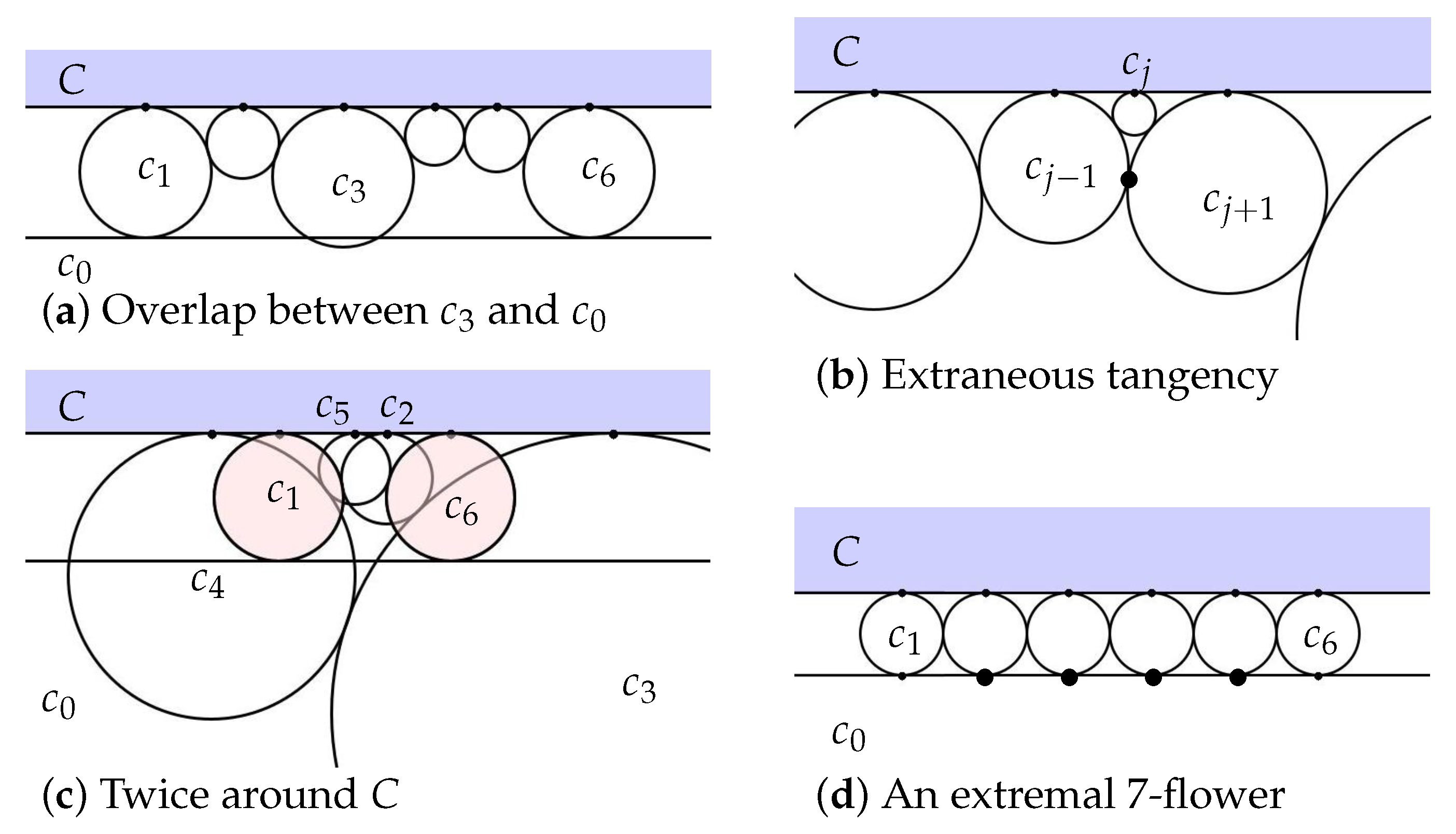
5.3. Important Observations
5.4. Un-Branched Flowers
5.4.1. 3-Flowers
5.4.2. 4-Flowers
- Apply (A2) to compute the tangency point and radius of :
- Apply (A4) with and to compute
5.4.3. Five-Flowers
- Applying (A3) with , , and :
- Using radii from above and the mandated :
- Setting and in (A4) implies
5.4.4. 6-Flowers
- Applying (A3) with and as computed earlier gives
- Applying (A4) with and gives
5.4.5. The General Case
- (i)
- The functions and are particularly valuable in light of Lemma 1. (Remember, these labels are cyclic mod.) In a packing label , any one of its entries may be written as , where is the sequence of entries preceding (or the reverse of the entries following ).
- (ii)
- Additional relationships pertaining to the normalized flower may be extracted from the formulas of Appendix A.1. Here are some examples:
- (iii)
- A careful look at the formulas for a normalized flower will show that the radii , reciprocal roots , and tangency points of the petals are all rational functions of the u-parameters (likewise for the s-parameters). Moreover, these rational functions have their coefficients in the number field .
- (iv)
- The rational functions and polynomials also have coefficients in . Note that, for each n, is a pole of . On a practical note, unlike expressions such as (10), the functions and are independent of the flower normalization.
- (v)
- The functions have intriguing self-referential behavior under cyclic shifts and reversals, and this would seem to make them quite special. For example, these expressions show how the can be nested; here, denotes the sequence .The explicit expressions would be quite messy, but would express the labels of (14) directly as functions of the parameters .
5.5. Univalent Flowers
5.6. Branched Flowers
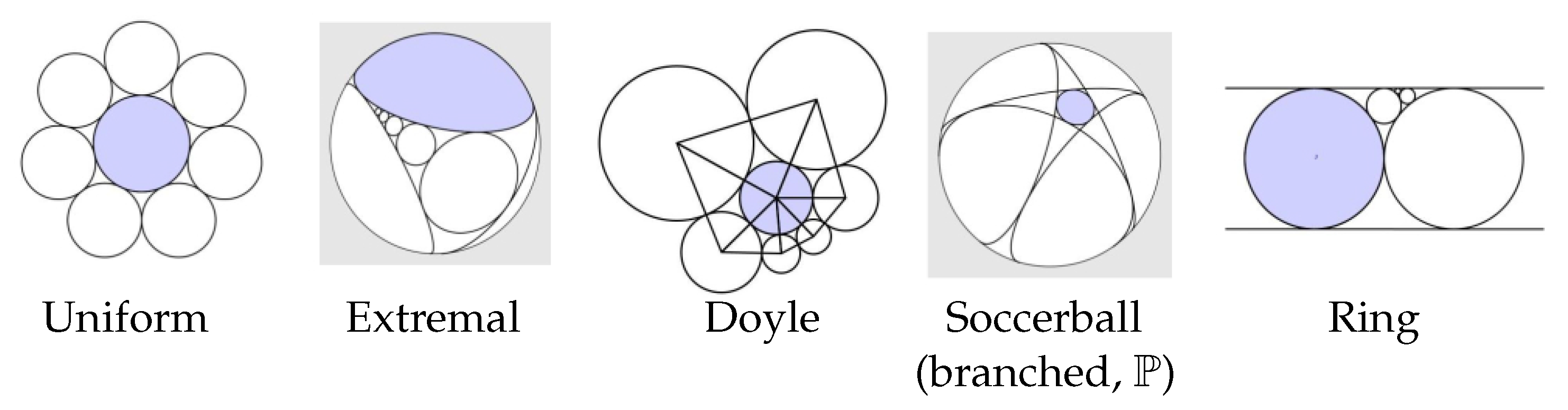
6. Special Classes of Flowers
6.1. Uniform Flowers
6.2. Extremal Flowers
6.3. Soccerball Flowers
6.4. Doyle Flowers
6.5. Ring Lemma Flowers
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Layout Computations


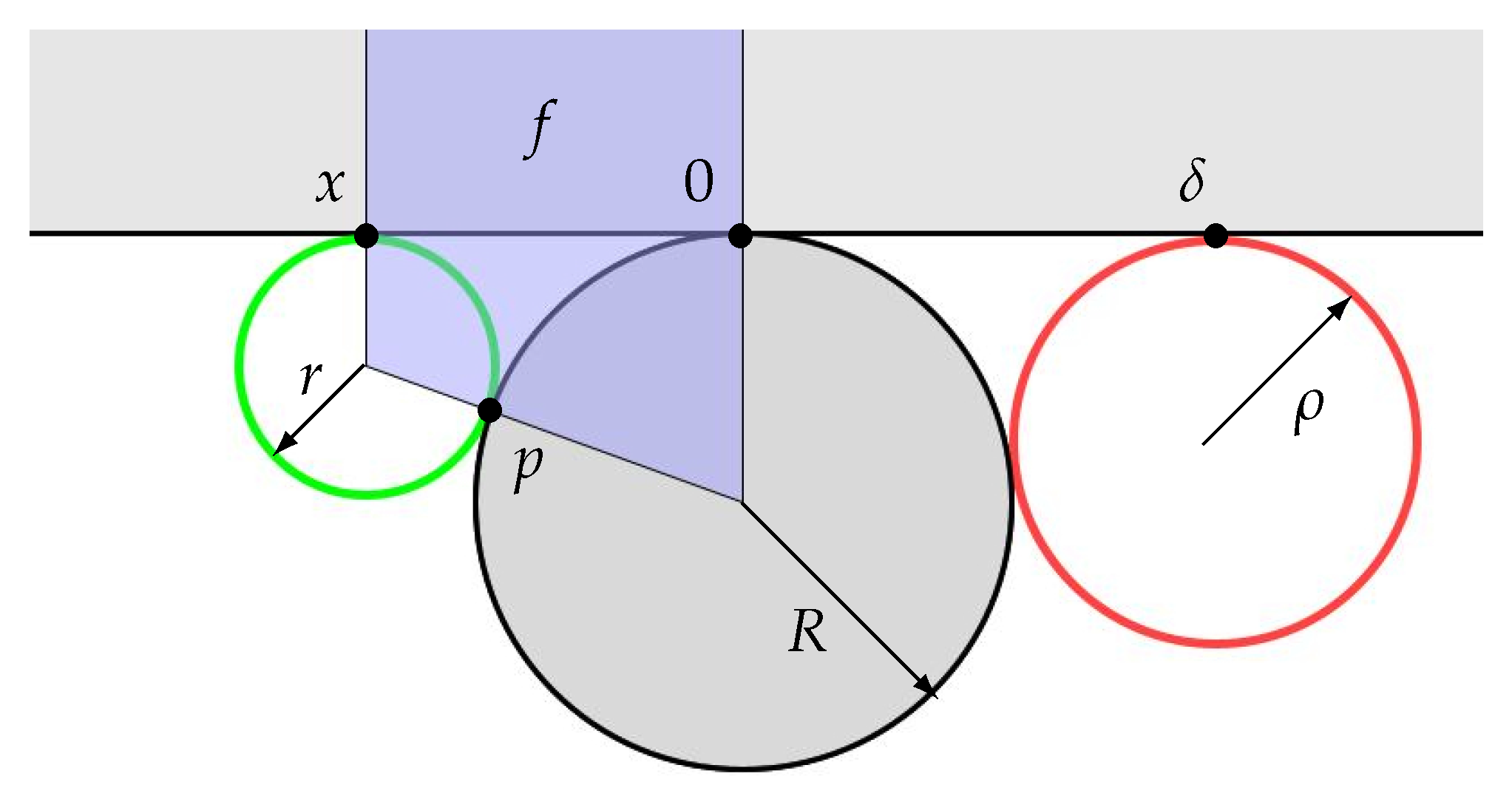
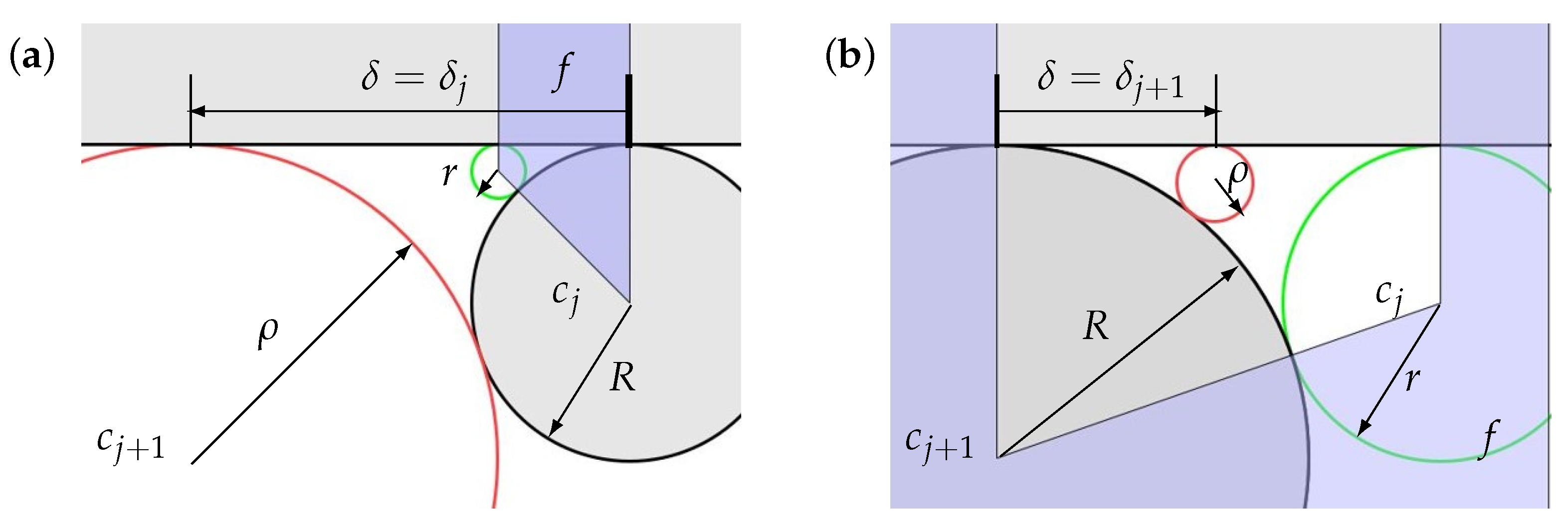
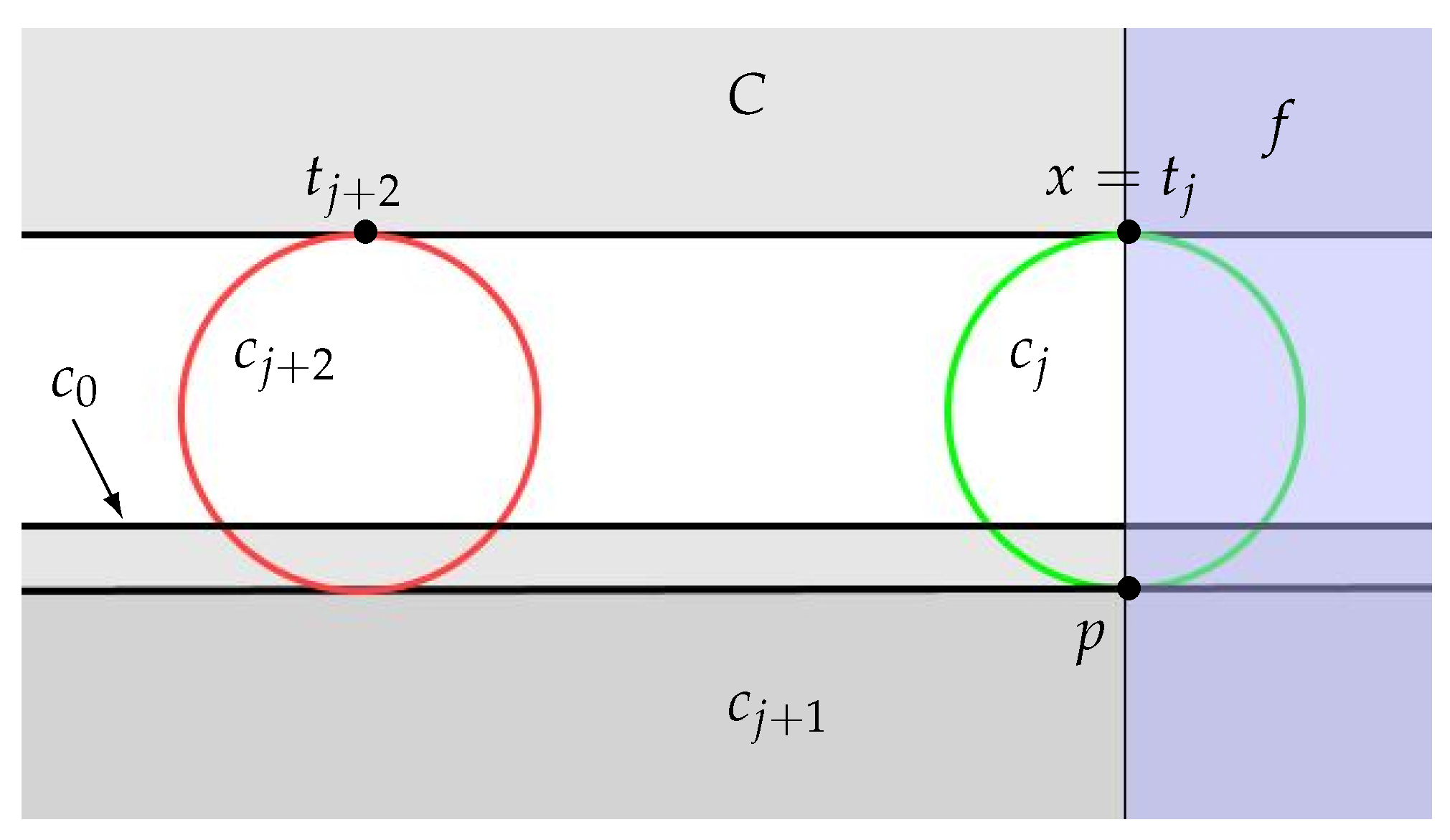
Appendix A.2. Uniform Petals
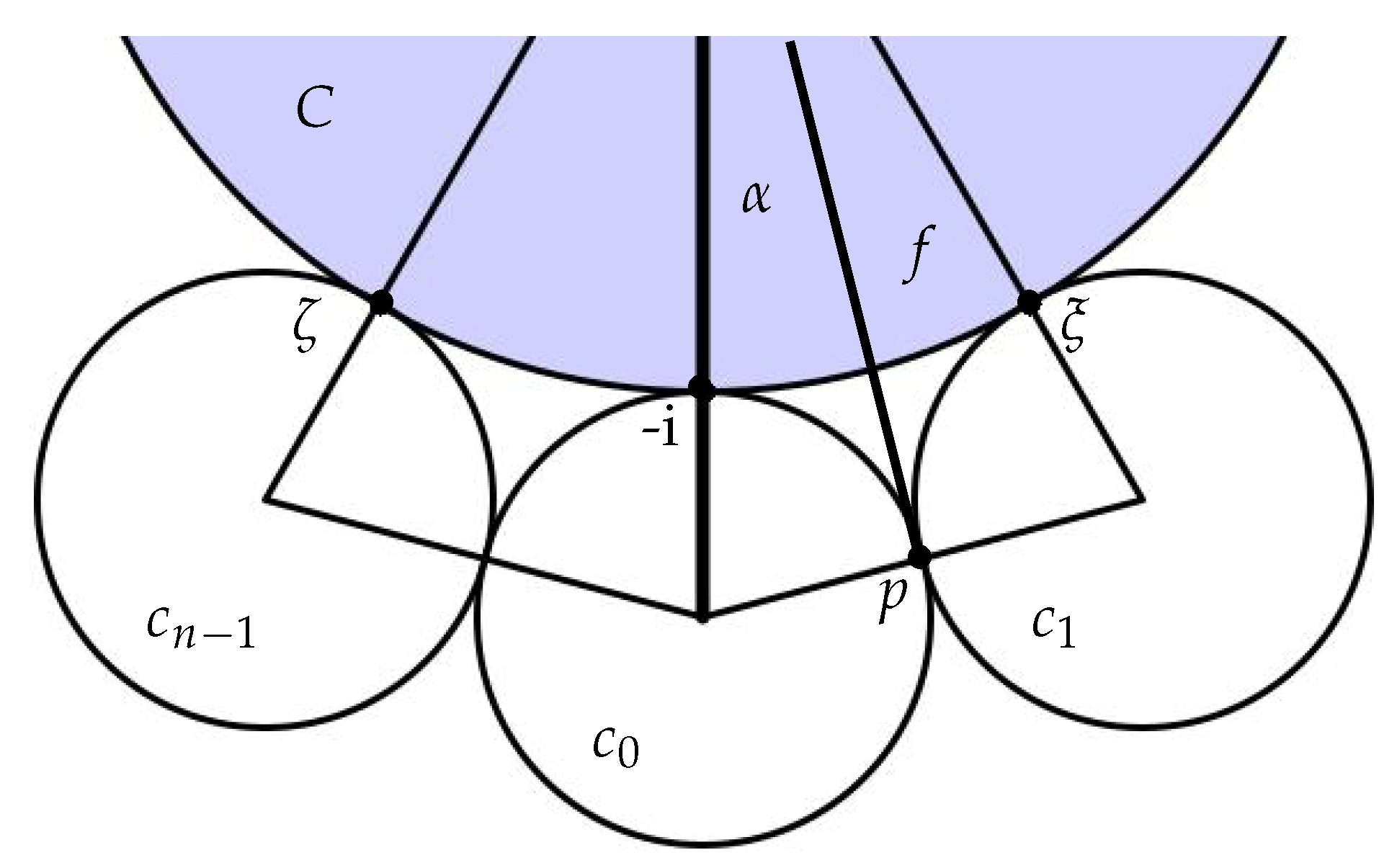
Appendix A.3. Special Computations
References
- Thurston, W. The finite Riemann mapping theorem. Invited talk, “An International Symposium at Purdue University in celebration of de Branges’ proof of the Bieberbach conjecture”, Purdue University, March 1985 (unpublished).
- Sass, C.; Stephenson, K.; Williams, G.B. Circle packings on conformal and affine tori. In Computational Algebraic and Analytic Geometry, Contemporary Mathematics; American Mathematical Society: Providence, RI, USA, 2012; Volume 572, pp. 211–220. [Google Scholar]
- Kojima, S.; Mizushima, S.; Tan, S.P. Circle packings on surfaces with projective structures. J. Differ. Geom. 2003, 63, 349–397. [Google Scholar] [CrossRef]
- Stephenson, K. Introduction to Circle Packing: The Theory of Discrete Analytic Functions; Cambridge University Press: New York, NY, USA, 2005; ISBN 0-521-82356-0. QA640.7.S74. [Google Scholar]
- Rodin, B.; Sullivan, D. The convergence of circle packings to the Riemann mapping. J. Differ. Geom. 1987, 26, 349–360. [Google Scholar] [CrossRef]
- Bowers, P.L.; Stephenson, K. Conformal Tilings I: Foundations, Theory, and Practice. Conform. Geom. Dyn. 2017, 21, 1–63. [Google Scholar] [CrossRef]
- Hurdal, M.K.; Stephenson, K. Cortical cartography using the discrete conformal approach of circle packings. NeuroImage 2004, 23 (Suppl. S1), S119–S128. [Google Scholar] [CrossRef] [PubMed]
- Hagh, V.F.; Corwin, E.I.; Stephenson, K.; Thorpe, M.F. A broader view on jamming: From spring networks to circle packing. Soft Matter 2019, 15, 3076–3084. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Dreifus, G.; Beard, B.; Glick, A.; Messing, A.; Hassen, A.A.; Lindahl, J.; Smith, T.; Failla, J.; Post, B.; et al. Graded infill structure of wind turbine blade core accounting for internal stress in big area additive manufacturing. In Proceedings of the CAMX—Composites and Advanced Materials Expo, Dallas, TX, USA, 15–18 October 2018. [Google Scholar]
- Stephenson, K. CirclePack Software 1992–2024. Available online: https://github/kensmath/CirclePack (accessed on 9 September 2025).
- Orick, G.L. Computational Circle Packing: Geometry and Discrete Analytic Function Theory. Ph.D. Thesis, University of Tennessee, Knoxville, TN, USA, 2010. directed by Kenneth Stephenson. [Google Scholar]
- Schramm, O. Circle patterns with the combinatorics of the square grid. Duke Math. J. 1997, 86, 347–389. [Google Scholar] [CrossRef]
- He, Z.X.; Schramm, O. The C∞-convergence of hexagonal disk packings to the Riemann map. Acta Math. 1998, 180, 219–245. [Google Scholar] [CrossRef]
- Lam, Y.Y. CMC-1 surfaces via osculating Möbius transformations between circle patterns. Trans. Amer. Math. Soc. 2024, 377, 3657–3690. [Google Scholar] [CrossRef]
- Bauer, D.; Stephenson, K.; Wegert, E. Circle packings as differentiable manifolds. Contrib. Algebra Geom. 2012, 53, 399–420. [Google Scholar] [CrossRef]
- Collins, C.R.; Stephenson, K. A circle packing algorithm. Comput. Geom. Theory Appl. 2003, 25, 233–256. [Google Scholar] [CrossRef]
- Beardon, A.F.; Dubejko, T.; Stephenson, K. Spiral hexagonal circle packings in the plane. Geom. Dedicata 1994, 49, 39–70. [Google Scholar] [CrossRef]
- Hansen, L.J. On the Rodin and Sullivan ring lemma. Complex Var. Theory Appl. 1988, 10, 23–30. [Google Scholar] [CrossRef]
- Aharonov, D. The sharp constant in the ring lemma. Complex Var. Theory Appl. 1997, 33, 27–31. [Google Scholar] [CrossRef]
- Aharonov, D.; Stephenson, K. Geometric sequences of discs in the Apollonian packing. Algebra I Anal. Dedic. Goluzin 1997, 9, 104–140. [Google Scholar]
- Soddy, F. The Kiss Precise. Nature 1936, 137, 1021, poem. [Google Scholar] [CrossRef]
- Collins, C.R.; Driscoll, T.A.; Stephenson, K. Curvature flow in conformal mapping. Comput. Methods Funct. Theory 2003, 3, 325–347. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stephenson, K. A Discrete Schwarzian Derivative via Circle Packing. Geometry 2025, 2, 16. https://doi.org/10.3390/geometry2040016
Stephenson K. A Discrete Schwarzian Derivative via Circle Packing. Geometry. 2025; 2(4):16. https://doi.org/10.3390/geometry2040016
Chicago/Turabian StyleStephenson, Kenneth. 2025. "A Discrete Schwarzian Derivative via Circle Packing" Geometry 2, no. 4: 16. https://doi.org/10.3390/geometry2040016
APA StyleStephenson, K. (2025). A Discrete Schwarzian Derivative via Circle Packing. Geometry, 2(4), 16. https://doi.org/10.3390/geometry2040016





