Energy, Exergy, Economic, and Environmental (4E) Performance Analysis and Multi-Objective Optimization of a Compressed CO₂ Energy Storage System Integrated with ORC

Abstract

Current CO₂-based energy storage systems still face several unsolved technical challenges, including strong thermal destruction between the multi-stage compression and expansion processes, significant exergy destruction in heat exchange units, limited utilization of low-grade heat, and the lack of an integrated comprehensive performance framework capable of simultaneously evaluating thermodynamic, economic, and environmental performance. Although previous studies have explored various compressed CO₂ energy storage (CCES) configurations and CCES–Organic Rankine Cycle (ORC) couplings, most works treat the two subsystems separately, neglect interactions between the heat exchange loops, or overlook the combined effects of exergy losses, cost trade-offs, and CO₂-emission reduction. These gaps hinder the identification of optimal operating conditions and limit the system-level understanding needed for practical application. To address these challenges, this study proposes an innovative system that integrates a multi-stage CCES system with ORC. The system introduces ethylene glycol as a dual thermal carrier, coupling waste-heat recovery in the CCES with low-temperature energy utilization in the ORC, while liquefied natural gas (LNG) provides cold energy to improve cycle efficiency. A comprehensive 4E (energy, exergy, economic, and environmental) assessment framework is developed, incorporating thermodynamic modeling, exergy destruction analysis, CEPCI-based cost estimation, and environmental metrics including primary energy saved (PES) and CO₂ emission reduction. Sensitivity analyses on the high-pressure tank (HPT) pressure, heat exchanger pinch temperature difference, and pre-expansion pressure of propane (P₃₀) reveal strong nonlinear effects on system performance. A multi-objective optimization combining NSGA-II and TOPSIS identifies the optimal operating condition, achieving 69.6% system exergy efficiency, a 2.07-year payback period, and 1087.3 kWh of primary energy savings. The ORC subsystem attains 49.02% thermal and 62.27% exergy efficiency, demonstrating synergistic effect between the CCES and ORC. The results highlight the proposed CCES–ORC system as a technically and economically feasible approach for high-efficiency, low-carbon energy storage and conversion.

1. Introduction

With the continuous development of the global economy and the growth of the population, the demand for energy has shown a rising trend [1]. The rapid expansion of renewable energy has introduced severe intermittency and grid-stability challenges, emphasizing the urgent need for efficient and low-carbon energy storage technologies [2,3]. Among existing options—electrochemical, mechanical, and thermal—mechanical–thermal storage using CO₂ offers unique potential owing to its favorable thermophysical properties, such as a low critical point (31.1 °C, 7.38 MPa) and high compressibility [4,5,6]. These characteristics enable high energy density and efficient heat recovery compared to conventional compressed air energy storage (CAES) systems, while utilizing CO₂ as an abundant industrial by-product contributes to emission reduction [7,8]. Consequently, CO₂-based energy storage systems are regarded as a promising approach for improving the utilization of renewable energy [9,10].

The energy storage system based on CO₂ has significant advantages, in recent years, scholars have performed a lot of research on CO₂ energy storage systems and achieved certain results. Zhang et al. [11] proposed a CCES system based on Brayton cycle using hot water as the thermal storage medium; the round-trip efficiency is 60% and exergy efficiency is 52.64%, with energy density at 2.6 kWh/m³ under the typical transcritical operation condition. Under supercritical condition, round-trip efficiency can reach 71.41% and exergy efficiency can achieve 71.38%, showing a promising prospect of CCES system. Li et al. [12] compared the performance between CCES and the CAES in aquifers by numerical methods. Results indicate that, compared with CAES, CCES has lower reservoir pressure, less cracking risk, occupies only 11.8% of the space of CAES, and has higher energy efficiency, proving the superiority of CCES performance. Liu et al. [13] analyzed the thermodynamic and economic performance of a novel CCES system. The results of multi-objective optimization suggest that the optimal exergy efficiency of the system is 61.39% with a USD 0.25/kWh unit product cost. Huang et al. [14] evaluated the dynamic performance of the CCES system, comparing the thermodynamic performance between dynamic and steady-state operating condition. Round-trip efficiency varies between 16.7% and 56.7% under different operation modes, which emphasizes the importance of dynamic performance in system design and operation. Liu et al. [15] developed and compared the thermodynamic and economic performance of four different CCES solutions by parametric analysis. The optimal performance system is found and the comprehensive performance of the optimal system is given under certain operating conditions, where round-trip efficiency and energy density achieve 71.54% and 40.61 kWh/m³, separately. The present value is USD 3.03 million and the levelized cost of electricity (LCOE) is USD 0.1109/kWh.

Extensive research has explored CCES concepts with varying configurations and storage conditions. However, practical application still faces challenges in thermal management and overall system optimization, prompting efforts to integrate multi-stage compression/expansion, heat-recovery schemes, and auxiliary thermodynamic cycles such as ORC [16,17]. In recent years, scholars have performed a lot of research on CO₂ energy storage systems and its integration with ORC. Zhang et al. [18] proposed a transcritical CCES system integrated with ORC; conventional and advanced exergy is carried out and two different operating conditions are studied on the integrated system. In real condition, exergy efficiency of system is 34.26% and 43.48% under unavoidable conditions. This analysis provides the direction for system optimization from the perspective of exergy analysis, but the economic and environmental performance needs to be studied. Liu et al. [19] developed a CCES system integrated with ORC and solar energy, evaluating the thermodynamic and economic performance under different operating conditions. Multi-objective optimization was applied based on the sensitivity analysis. The result shows that under the optimal operating condition, highest energy storage efficiency achieved 81.1% and the levelized cost of storage is USD 0.318/kWh, respectively. Xu et al. [20] developed a novel liquid carbon dioxide energy storage system (LCES) based on the ORC and compared its performance with the liquid air energy storage system (LAES). The results of energy and exergy analysis indicate that the round-trip efficiency and exergy efficiency of LCES are significantly higher than LAES, reaching 45.35% and 67.2%, respectively. The isentropic efficiency and the inlet temperature of the turbine have significant effects on the output power and energy generated per unit volume of both systems. Li et al. [21] developed a mathematical model for an LNG cold energy recovery system based on a two-stage ORC integrated with LCES. The influence of key parameters on thermodynamic performance and economic performance was analyzed. The conclusion indicates that the maximum energy storage density can reach 4.05 kWh/m³, the maximum daily power generation profit is USD 12,624, and compared with the traditional LNG Rankine cycle system, the total annual profit of this system has increased by USD 320,000.

Zhang et al. [22] proposed a CCES integrated with ORC, evaluated the system performance from the exergy and exergoeconomic perspective, and analyzed the critical parameters’ influence on integrated system. The net power output, system exergy efficiency, and total product unit cost were 27.736 MW, 66.64%, and USD 20.34/GJ, respectively. Multi-objective optimization was also applied on the research and the result indicates that, at the optimum operating point, exergy efficiency of system is 72.6%, the total cost rate of exergy destruction is USD 452.35/h and total product unit cost is USD 18.49/GJ.

Prior CCES–ORC studies have improved thermal performance, but few have evaluated full 4E performance, particularly the interactions between exergy destruction, economic, and environmental indicators such as CO₂ avoidance. These gaps hinder a holistic understanding of design trade-offs between efficiency, cost, and sustainability.

This study bridges these gaps by proposing a multi-stage CCES–ORC integrated system that uses ethylene glycol as a bidirectional heat-transfer medium and LNG cold energy for enhanced thermal coupling. Propane is selected as the working fluid for the ORC due to its low boiling point and high latent heat. A unified 4E assessment framework is established to quantify system-level performance, followed by multi-objective optimization (NSGA-II + TOPSIS) to determine optimal design parameters. Notably, the CO₂ used in this system is assumed to be supplied by an advanced post-combustion carbon capture system [23]. The novelty of this work lies in (i) introducing ethylene glycol for dual heat-carrier integration, (ii) developing an integrated 4E evaluation model, and (iii) providing quantitative optimization insights that balance thermodynamic, economic, and environmental performance. The results offer design guidelines for next-generation renewable-integrated energy storage systems.

2. System Description

Figure 1 shows the schematic diagram of the proposed integrated system. The integrated system includes two parts: compressed CO₂ energy storage system and ORC. CCES system consists of compressors (C₁, C₂, and C₃), turbines (T₁, T₂ and T₃), heat exchangers (HEX₁ to HEX₆), a cold reservoir (CR), a hot reservoir (HR), and a high-pressure tank (HPT). ORC consists of heat exchangers (HEX₇ and HEX₈), turbines (T₄ and T₅), pump2 (P₂) and an LNG storage tank. The numbered labels in the figure (1–35) denote the thermodynamic state points of the working fluids (CO₂, ethylene glycol, propane, and LNG) at different stages of compression, heat transfer, expansion, and the organic Rankine cycle. The abbreviations and full names of each component are listed in

Table 1. Abbreviations of each component in the integrated system.

ABS	Absorber	DES	Desorber
C	Compressor	T	Turbine
HEX	Heat exchanger	HPT	High-pressure tank
CR	Cold reservoir	HR	Hot reservoir
P	Pump

.

In the CO₂ capture system, CO₂ in the flue gas is absorbed by the mixed amine solution in the absorber (ABS) and is then desorbed in the desorber (DES) by the cold energy of the LNG, after being captured by the absorption system. During the charge process of CCES system, CO₂ is compressed by the three-stage compressors, C₁, C₂, and C₃ (state 1–7), to continuously increase the pressure to the supercritical state, and then stored in HPT, ready for the power generation in discharge process. To maintain efficiency and safety, each compression stage is cooled by cold ethylene glycol in heat exchangers, HEX₁, HEX₂, and HEX₃ (state 15–20), during which the heat absorbed will be stored in HR and reused in the discharge process and ORC.

During the discharge process of CCES system, high-pressure CO₂ supplied by HPT absorbs the heat in heat exchangers HEX₄, HEX₅, and HEX₆ (state 21–26) of hot ethylene glycol supplied by HR. Then turbines (T₁, T₂ and T₃) use the multi-stage expansion of CO₂ at high pressure to recover energy, which is converted into electricity by electrical generators (state 8–14). Finally, in the discharge process, cold ethylene glycol is mixed and ready for use in ORC.

In ORC, the propane is first heated by mixed ethylene glycol from the CCES system in HEX₇, then expands in T₄; ethylene glycol cooled by propane returns to CR and is ready for the next cycle in the CCES system (state 27–31). LNG supplied by the LNG storage tank absorbs the heat of propane in HEX₈ and expands through T₅; then, the propane cooled down by LNG is pumped in P₂ (state 32–35). The power generated by T₄ and T₅ can be used in multi-stage compression during the charge process of the CCES system to reduce the need for external power generation.

To sum up, the proposed integrated system combines the CCES system with an ORC subsystem; CO₂ is first compressed to the supercritical state and generates power in CCES system, during which the heat generated is absorbed by cold ethylene glycol and released in the discharge process and ORC. The whole process utilizes heat exchange and staged energy conversion processes to optimize energy storage and generation, ensuring a continuous and efficient power supply while minimizing energy wastage.

3. Thermodynamic Modeling

To facilitate system performance analysis and simplify the thermodynamic model, our assumptions are listed as follows:

(1) The system operates under a stable state [24].

(2) Heat loss and cold energy loss in the whole process are neglected [25].

(3) The variation in potential energy and kinetic energy in the whole process are neglected [26].

(4) Friction loss and pressure loss of each component are neglected [27].

3.1. System Thermodynamic Modeling Based on the First Law of Thermodynamics

In the charge process of CCES system, CO₂ is compressed to a supercritical state by three-stage compressors. Total power consumed by compressors (C₁, C₂, and C₃) in the charge process and pump (P₂) in ORC can be calculated as follows [28]:

$${\dot{W}}_C={\dot{m}}_{in}\left(h_{out}-h_{in}\right)={\displaystyle \frac{{\dot{m}}_{in}\left(h_{out,s}-h_{in}\right)}{{\eta }_C}},$$

(1)

$${\dot{W}}_P={\dot{m}}_{in}\left(h_{out}-h_{in}\right)={\displaystyle \frac{{\dot{m}}_{in}\left(h_{out,s}-in\right)}{{\eta }_P}},$$

(2)

where ${\dot{W}}_C$ and ${\dot{W}}_P$ stand for the power consumed by compressors and pump. $\dot{m}$ denotes the mass flow rate of working fluid into compressors and pump. The subscripts $in$ and $out$ means the inlet and outlet of the compressors and pump. $h$ denotes the specific enthalpy. ${\eta }_C$ and ${\eta }_P$ represent isentropic efficiency of compressors and pump, separately. The subscript $s$ means the isentropic process of compressors and pump.

Isentropic efficiency of the compressors ${\eta }_C$ and pump ${\eta }_P$ can be defined as follows [29]:

$${\eta }_C={\displaystyle \frac{h_{out,s}-h_{in}}{h_{out}-h_{in}}},$$

(3)

$${\eta }_P={\displaystyle \frac{h_{out,s}-h_{in}}{h_{out}-in}},$$

(4)

Output power of turbines (T₁, T₂, T₃, T₄ and T₅) in the whole integrated system can be calculated as follows [30]:

$${\dot{W}}_T={\dot{m}}_{in}\left(h_{in}-h_{out}\right)={\eta }_T{\dot{m}}_{in}\left(h_{in}-h_{out,s}\right),$$

(5)

where $W_T$ denotes the output power of turbines and subscript $T$ stands for turbine. ${\eta }_T$ represents the isentropic efficiency of turbines.

Isentropic efficiency of the turbine ${\eta }_T$ can be defined as

$${\eta }_T={\displaystyle \frac{h_{in}-h_{out}}{h_{in}-h_{out,s}}},$$

(6)

According to the law of thermodynamics, heat transfer through heat exchangers in the system can be calculated using energy balance equation and $ϵ$-$NTU$ method.

For counter-flow [31]:

$$ϵ={\displaystyle \frac{1-\exp \left[-NTU\left(1-C_R\right)\right]}{1-C_R\exp \left[-NTU\left(1-C_R\right)\right]}},$$

(7)

$$NTU={\displaystyle \frac{UA}{C_{min}}},$$

(8)

$$C_R={\displaystyle \frac{C_{min}}{C_{max}}},$$

(9)

where $ϵ$ is effectiveness of heat exchanger. $NTU$ is the number of transfer unit. $C_R$ refers to capacity ratio. $U$ is the overall heat transfer coefficient. $A$ is the heat exchange area. $C_{min}$ and $C_{max}$ are the minimum heat capacity flux and maximum heat capacity flux, respectively.

For each heat exchanger, heat transfer can be calculated as follows [32]:

$${\dot{Q}}_{HEX}={\dot{m}}_{hot}\left(h_{hot,in}-h_{hot,out}\right)={\dot{m}}_{cold}\left(h_{cold,out}-h_{cold,in}\right),$$

(10)

where ${\dot{Q}}_{HEX}$ represents the heat energy transferred in heat exchanger. The subscripts $hot$ and $cold$ denote the hot and cold fluids of the heat exchanger.

3.2. System Modeling Based on the Second Law of Thermodynamics

To further analyze the inefficient parts of energy conversion and the irreversible losses of the system, based on the second law of thermodynamics, exergy analysis is introduced here [33]:

$${\dot{E}}_j={\dot{m}}_j\left[\left(h_j-h_0\right)-T_0\left(s_j-s_0\right)\right],$$

(11)

where ${\dot{E}}_j$ represents the exergy flow rate of $j$-th material stream. $T$ denotes temperature. $s$ denotes the specific entropy. Subscript $0$ stands for the environment state.

According to the exergy balance, the exergy destruction rate ${\dot{E}}_{D,k}$ of the $k$-th component can be calculated as follows:

$${\dot{E}}_{D,k}={\dot{E}}_{F,k}-{\dot{E}}_{P,k},$$

(12)

where ${\dot{E}}_{F,k}$ and ${\dot{E}}_{P,k}$ represent the fuel exergy rate and product exergy rate of the $k$-th component, respectively. The fuel exergy and product exergy equations of each component in the system are listed in

Table 2. Exergy balance equations for each component of the integrated system.

Components	Exergy Balance Equation
	${\dot{\mathit{E}}}_{\mathit{D},\mathit{k}}={\dot{\mathit{E}}}_{\mathit{F},\mathit{k}}-{\dot{\mathit{E}}}_{\mathit{P},\mathit{k}}$
C1	${\dot{E}}_{D,C1}=W_{C1}-\left({\dot{E}}_2-{\dot{E}}_1\right)$
C2	${\dot{E}}_{D,C2}=W_{C2}-\left({\dot{E}}_4-{\dot{E}}_3\right)$
C3	${\dot{E}}_{D,C3}=W_{C3}-\left({\dot{E}}_6-{\dot{E}}_5\right)$
T1	${\dot{E}}_{D,T1}=\left({\dot{E}}_9-{\dot{E}}_{10}\right)-W_{T1}$
T2	${\dot{E}}_{D,T2}=\left({\dot{E}}_{11}-{\dot{E}}_{12}\right)-W_{T2}$
T3	${\dot{E}}_{D,T3}=\left({\dot{E}}_{13}-{\dot{E}}_{14}\right)-W_{T3}$
T4	${\dot{E}}_{D,T4}=\left({\dot{E}}_{30}-{\dot{E}}_{31}\right)-W_{T4}$
T5	${\dot{E}}_{D,T5}=\left({\dot{E}}_{34}-{\dot{E}}_{35}\right)-W_{T5}$
HEX1	${\dot{E}}_{D,\mathrm{HEX}1}=\left({\dot{E}}_2-{\dot{E}}_3\right)-\left({\dot{E}}_{16}-{\dot{E}}_{15}\right)$
HEX2	${\dot{E}}_{D,\mathrm{HEX}2}=\left({\dot{E}}_4-{\dot{E}}_5\right)-\left({\dot{E}}_{18}-{\dot{E}}_{17}\right)$
HEX3	${\dot{E}}_{D,\mathrm{HEX}3}=\left({\dot{E}}_6-{\dot{E}}_7\right)-\left({\dot{E}}_{20}-{\dot{E}}_{19}\right)$
HEX4	${\dot{E}}_{D,\mathrm{HEX}4}=\left({\dot{E}}_{21}-{\dot{E}}_{22}\right)-\left({\dot{E}}_9-{\dot{E}}_8\right)$
HEX5	${\dot{E}}_{D,\mathrm{HEX}5}=\left({\dot{E}}_{23}-{\dot{E}}_{24}\right)-\left({\dot{E}}_{11}-{\dot{E}}_{10}\right)$
HEX6	${\dot{E}}_{D,\mathrm{HEX}6}=\left({\dot{E}}_{25}-{\dot{E}}_{26}\right)-\left({\dot{E}}_{13}-{\dot{E}}_{12}\right)$
HEX7	${\dot{E}}_{D,\mathrm{HEX}7}=\left({\dot{E}}_{27}-{\dot{E}}_{28}\right)-\left({\dot{E}}_{30}-{\dot{E}}_{29}\right)$
HEX8	${\dot{E}}_{D,\mathrm{HEX}8}=\left({\dot{E}}_{31}-{\dot{E}}_{32}\right)-\left({\dot{E}}_{34}-{\dot{E}}_{33}\right)$
P2	${\dot{E}}_{D,P2}=W_{P2}-\left({\dot{E}}_{29}-{\dot{E}}_{32}\right)$

.

3.3. System Economic Analysis Modeling

The economic performance of the integrated system is an essential factor for system implementation in engineering. The total cost ($C_{total}$) of this integrated system typically consists of the cost of equipment purchase ($C_{EP}$), cost of installation ($C_I$), cost of operation and maintenance ($C_{OM}$), and cost of electricity purchase ($C_E$), as expressed in Equations (32)–(37) [34,35]:

$$C_{total}=C_{EP}+C_{OM}+C_I+C_E,$$

(13)

$$C_{EP}={\sum }_{k=1}^n{C}_k,$$

(14)

$$C_k=C_{original}{\displaystyle \frac{CEPC{I}_{2024}}{CEPC{I}_{original}}},$$

(15)

$$C_{OM}=0.06·C_{EP},$$

(16)

$$C_I=0.9·C_{EP},$$

(17)

$$C_E=C_e·{\dot{W}}_{input}·\tau =C_e·({\dot{W}}_{C1}+{\dot{W}}_{C2}+{\dot{W}}_{C3}+{\dot{W}}_{P2})·\tau ,$$

(18)

where $C_k$ presents the cost of each component purchase; the details are shown in

Table 3. Cost calculation for each component.

Components	Cost Function	CEPCI (Year)
Compressor [36]	$C_{com}=\left({\displaystyle \frac{71.1·\dot{m}}{0.93-{\eta }_C}}\right)·PR·lnPR$	381.7 (1996)
Turbine [36]	$C_{tur}=\left({\displaystyle \frac{479.34·\dot{m}}{0.93-{\eta }_T}}\right)·lnPR·\left(1+e^{\left(0.036·T_{in}-54.4\right)}\right)$	381.7 (1996)
Heat exchanger [37]	$C_{HEX}=\mathrm{\lambda }·\left(UA\right)=\mathrm{\lambda }·\left({\displaystyle \frac{Q_{HEX}}{LMTD}}\right)$	444.2 (2004)
Pump [36]	$C_{pump}=1120·{{\dot{W}}_P}^{0.8}$	444.2 (2004)

. $C_{original}$ represents the original cost estimate of the reference year. $CEPC{I}_{2024}$ and $CEPC{I}_{original}$ denote the CEPCI for the year of 2024 and CEPCI of the reference year, respectively. $C_e$ is the electricity purchase price. $\tau$ represents the annual operation time of integrated system.

3.4. System Environmental Analysis Modeling

To assess the environmental impact of integrated systems, the primary energy saved ($PES$) and the avoided CO₂ emissions ($\Omega$) are introduced as the environmental evaluation metrics here [37]. The PES evaluates the amount of primary energy saved by the ORC system based on the quoted energy efficiency of the power plant (${\eta }_q=52\%$), which is expressed as the following equation (38):

$$PES={\displaystyle \frac{1}{{\eta }_q}}\left({\dot{W}}_{net}+{\displaystyle \frac{Q_{ORC}}{EE{R}_{ORC}}}\right),$$

(19)

$${\dot{W}}_{net}=\left({\dot{W}}_{T4}+{\dot{W}}_{T5}\right)-{\dot{W}}_{P2},$$

(20)

where ${\dot{W}}_{net}$ stands for the net power output of the ORC and $EE{R}_{ORC}$ denotes the cooling reference energy efficiency ratio (5.2) [38].

$\Omega$ is selected to assess the integrated system contribution to avoid CO₂ emissions, which can be calculated as

$$\Omega =EF\left({\dot{W}}_{net}+{\displaystyle \frac{Q_{ORC}}{EE{R}_{ORC}}}\right)+{\dot{M}}_{CCS},$$

(21)

where $EF$ represents the emission factor (0.308 kg CO₂/kWh). ${\dot{M}}_{CCS}$ represents the carbon capture amount by CO₂ capture system.

3.5. System Performance Evaluation Criteria

The evaluation criteria contribute to evaluate the integrated system performance more accurately; several indexes are introduced in this section.

To estimate the efficiency of energy that can be stored and then recovered in the CCES system, ${\eta }_{Conversion}$ is defined to measure the effectiveness of the energy storage process:

$${\eta }_{Conversion}={\displaystyle \frac{{\dot{W}}_{Recovered}}{{\dot{W}}_{Expended}}}={\displaystyle \frac{{\dot{W}}_{T1}+{\dot{W}}_{T2}+{\dot{W}}_{T3}}{{\dot{W}}_{C1}+{\dot{W}}_{C2}+{\dot{W}}_{C3}}},$$

(22)

where ${\dot{W}}_{Recovered}$ and ${\dot{W}}_{Expended}$ represent the energy recovered in the discharge process and energy expended in the charge process, respectively.

To evaluate the total energy conversion efficiency of the integrated system, ${\eta }_{Thermal}$ can be defined as

$${\eta }_{Thermal}={\displaystyle \frac{{\dot{W}}_{Output}}{{\dot{W}}_{Input}}}={\displaystyle \frac{{\dot{W}}_{T1}+{\dot{W}}_{T2}+{\dot{W}}_{T3}+{\dot{W}}_{T4}+{\dot{W}}_{T5}}{{\dot{W}}_{C1}+{\dot{W}}_{C2}+{\dot{W}}_{C3}}},$$

(23)

where ${\dot{W}}_{Output}$ and ${\dot{W}}_{Input}$ denote the output energy and input energy of the integrated system, respectively.

To measure the efficiency of input energy converted into useful outputs and the losses due to irreversibility of integrated system, the exergy efficiency ${\eta }_{ex,system}$ of the integrated system is defined as

$${\eta }_{ex,system}={\displaystyle \frac{E_{Output}}{E_{Input}}},$$

(24)

where $E_{Output}$ and $E_{Input}$ mean all forms of energy introduced into the system and the energy forms of the system output, respectively.

The total cycle efficiency ${\eta }_{ORC}$ of ORC system can be calculated as follows [39]:

$${\eta }_{ORC}={\displaystyle \frac{{\dot{W}}_{net}}{{\dot{Q}}_{hot}}},$$

(25)

${\dot{Q}}_{hot}$ stands for the heat transferred from the hot source entering the ORC system.

The exergy efficiency ${\eta }_{ex,ORC}$ of ORC system is defined as follows [40]:

$${\eta }_{ex, ORC}={\displaystyle \frac{{\dot{W}}_{net}}{{\dot{E}}_{in}}},$$

(26)

where ${\dot{E}}_{in}$ denotes the exergy of hot source and LNG before entering the ORC system.

The cold exergy recovery efficiency ${\eta }_{LNG}$ of the ORC system is given as follows [41]:

$${\eta }_{LNG}={\displaystyle \frac{{\dot{W}}_{net}}{{\dot{E}}_{in,L} -{\dot{ E}}_{out,L}}},$$

(27)

where ${\dot{E}}_{in,L}$ and ${\dot{E}}_{out,L}$ are the input and output exergy of the LNG, respectively.

To evaluate the economic performance of integrated system, levelized cost of electricity (LCOE) is introduced as the evaluation criteria, which is defined as the economic cost per unit of electricity generated [42]:

$$LCOE={\displaystyle \frac{\left(C_{EP}+C_I+C_{OM}\right)·CRF+C_E}{{\dot{W}}_{Output}·\tau }},$$

(28)

CRF denotes the capital recovery factor, which can be calculated as follows [43]:

$$CRF={\displaystyle \frac{i{\left(1+i\right)}^n}{{\left(1+i\right)}^n-1}},$$

(29)

where $i$ represents the interest rate (12%) and $n$ represents the service time of the integrated system (25 years) [44,45].

The payback period (PBP) of integrated system is defined as follows [46]:

$$PBP={\displaystyle \frac{C_{total}}{{\dot{W}}_{Output}·\tau }},$$

(30)

3.6. Model Validation

According to the above calculation model, the system model established on the Matlab 2023 platform and the physical properties required of working fluids are obtained from Refprop 10.0. To ensure the accuracy of the subsequent work of the system, it is necessary to verify the critical parameters and components.

Since it is difficult to find an experimental system in the existing literature similar to the simulation model established in this paper, the accuracy of components is individually validated here. Result shown in

Table 4. Validation of CCES system.

Term	This Work	Ref [47]	Relative Error (%)
C1 power (kW)	74.18	73.77	−0.56%
C2 power (kW)	68.79	68.14	−0.95%
C3 power (kW)	50.88	51.23	0.69%
T1 power (kW)	49.57	49.18	−0.79%
T2 power (kW)	52.81	52.21	−1.15%
T3 power (kW)	55.98	55.67	−0.55%
Exergy Destruction by all Compressors (kW)	20.26	20.96	3.31%

and

Table 5. Validation of ORC system.

Term	This Work	Ref [48]	Relative Error
ORC cycle efficiency	21.05%	20.97%	−0.38%
ORC net power (kW)	1508.2	1495.15	−0.87%
turbine power (kW)	1586.18	1573.63	−0.80%
pump power (kW)	77.98	78.48	0.63%

, comparing current parameters in the system and data in the literature, [47,48], the maximum relative error is 3.31%, which demonstrates the reliability of the current system model and can be used for further research.

4. Discussion

4.1. System Basic Working Condition

The performance of the integrated system under the basic operating condition is present in this section. Initial input parameters for the basic design are shown in

Table 6. Input parameters of the integrated system under basic operating condition.

Parameter	Value
Ambient temperature, $T_0$ (K)	273.15
Ambient pressure, $P_0$ (kPa)	101.3
$\mathrm{Inlet}\mathrm{temperature}\mathrm{of}\mathrm{C}1,T_1$ (K) [49]	298.15
Inlet pressure of C1, $P_1$ (kPa) [49]	101.3
The final pressure of CO2 store in HPT (kPa)	9200
Mass flow of CO2 captured (kg/h) [23]	4.16
Isentropic efficiency of compressors ${\eta }_C$ (%) [50]	85
Isentropic efficiency of turbines ${\eta }_T$(%) [50]	85
Isentropic efficiency of pump ${\eta }_P$ (%) [50]	85
Pinch temperature difference in heat exchangers, $\Delta T_{min}$ [51]	5
Initial pressure of propane, P30 (kPa) [18]	500
Initial temperature of propane, $T_{30}$ (K) [18]	121.85
Initial temperature of LNG, $T_{33}$ (K) [18]	111.8
Initial pressure of LNG, $P_{33}$ (kPa) [18]	1500
Temperature of ethylene glycol from CR (K)	278.15
Pressure of ethylene glycol from CR (kPa)	101.3
Cost coefficient of heat exchangers, $\mathrm{\lambda }$ [37]	2143
Charging and discharging time (h) [8]	8 h
Annual cycle times [8]	365

. The thermodynamic properties of each point in the integrated system under basic operating condition are summarized in

Table 7. Thermodynamic properties of each state point of the integrated system.

Stream	Working Fluid	P (kPa)	T (K)	$\dot{\mathit{m}}$ (kg/h)	h (kJ/kg)	$\mathbf{s}(\mathbf{kJ}/\mathbf{kg}\mathit{·}$K)
1	CO2	101	298.15	4.16	439.87	2.48
2	CO2	454.44	428.47	4.16	525.84	2.52
3	CO2	454.44	288.15	4.16	493.77	2.42
4	CO2	2044.71	417.27	4.16	604.57	2.46
5	CO2	2044.71	288.15	4.16	475.54	2.09
6	CO2	9200	422.31	4.16	574.92	2.12
7	CO2	9200	288.15	4.16	231.05	1.09
8	CO2	9200	288.15	4.16	231.05	1.09
9	CO2	9200	365.97	4.16	478.36	1.87
10	CO2	2044.71	259.82	4.16	157.08	0.84
11	CO2	2044.71	365.98	4.16	540.31	2.29
12	CO2	454.44	274.44	4.16	473.61	2.34
13	CO2	454.44	365.97	4.16	551.17	2.60
14	CO2	101	278.00	4.16	479.51	2.64
15	Ethylene Glycol	101	278.15	1.39	−530.10	−1.4293
16	Ethylene Glycol	101	422.86	1.39	−430.20	−1.0948
17	Ethylene Glycol	101	278.15	1.56	−530.10	−1.4293
18	Ethylene Glycol	101	408.82	1.56	−187.20	−0.4261
19	Ethylene Glycol	101	278.15	7.67	−530.10	−1.4293
20	Ethylene Glycol	101	352.91	7.67	−343.38	−0.8365
21	Ethylene Glycol	101	370.97	5.94	−331.20	−0.8022
22	Ethylene Glycol	101	298.15	5.94	−482.82	−1.2652
23	Ethylene Glycol	101	370.97	1.79	−331.20	−0.8022
24	Ethylene Glycol	101	269.82	1.79	−561.59	−1.5454
25	Ethylene Glycol	101	370.97	2.89	−331.20	−0.8022
26	Ethylene Glycol	101	326.27	2.89	−504.17	−1.3379
27	Ethylene Glycol	101	301.49	10.63	−500.63	−1.3257
28	Ethylene Glycol	101	278.15	10.63	−530.10	−1.4293
29	Propane	500	121.85	0.79	−125.74	−0.71
30	Propane	500	296.47	0.79	595.83	2.44
31	Propane	100	247.33	0.79	533.89	2.49
32	Propane	100	121	0.79	−127.87	−0.73
33	LNG	1500	111.8	0.71	2.50	−0.00725
34	LNG	1500	238.27	0.71	739.85	4.65
35	LNG	600	194.91	0.71	661.93	4.723335

. The results of the evaluation metrics of the integrated system under basic operating condition are shown in

Table 8. 4E properties of the integrated system under basic operating condition.

Form	Parameter	Value
Energy	${\eta }_{Conversion}$ (%)	74.03
	${\eta }_{Thermal}$ (%)	90.66
	${\eta }_{ORC}$ (%)	19.82
	${\eta }_{LNG}$ (%)	27.91
Exergy	${\eta }_{ex,ORC}$ (%)	17.70
	${\eta }_{ex,system}$ (%)	62.41
Economic	LCOE (USD/kWh)	0.73
	PBP (year)	2.51
Environmental	PES (kWh)	627.09
	$\Omega$ (kg/h)	100.43

. It should be noted that the constant outlet temperature of EG from HEX₇ is implemented in practice by the appropriate sizing of the heat exchanger and feedback control of the working-fluid flow rates, so that only small temperature fluctuations occur around the design value.

The details of exergy analysis for each component are displayed in

Table 9. Exergy analysis for each component in the integrated system.

Component	${\dot{\mathit{E}}}_{\mathit{F}}$ (kW)	${\dot{\mathit{E}}}_{\mathit{P}}$ (kW)	${\dot{\mathit{E}}}_{\mathit{D}}$ (kW)	${\mathit{\eta }}_{\mathit{e}\mathit{x}}$ (%)
C1	487.15	439.55	47.60	90.23%
C2	461.23	415.01	46.22	89.98%
C3	413.72	372.99	40.72	90.16%
T1	278.24	234.19	44.05	84.17%
T2	352.49	298.59	53.90	84.71%
T3	366.35	310.85	55.51	84.85%
T4	62.03	51.78	10.25	83.47%
T5	72.50	57.93	14.57	79.90%
P2	0.54	0.36	0.18	66.16%
HEX1	442.85	435.14	7.70	98.26%
HEX2	733.97	725.94	8.03	98.91%
HEX3	991.67	925.38	66.29	93.32%
HEX4	953.89	911.19	42.70	95.52%
HEX5	683.99	669.89	14.10	97.94%
HEX6	424.14	398.96	25.18	94.06%
HEX7	207.60	64.20	143.39	30.93%
HEX8	656.73	446.37	210.36	67.97%

and comparison of exergy efficiency, exergy destruction, and the contribution of each component for exergy destruction under basic operating condition are presented Figure 2. As shown in Figure 2a, the three components with the highest exergy efficiency are HEX₂ (98.91%), HEX₁ (98.26%), and HEX₅ (97.94%). HEX₇ has the lowest exergy efficiency (30.93%), followed by P₂ (66.16%) and HEX₈ (67.97%). HEX₇ and HEX₈ show the highest values of exergy destruction, aligning with their significant percentages in Figure 2b. As shown in Figure 2b, the largest segment (25.32%) suggests that the most significant source of exergy destruction is HEX₈, which also has the largest exergy destruction in the system (210.36 kW). Several other notable contributions include 17.26% (HEX₇), 7.98% (HEX₃), and 6.68% (T₃). The smallest contribution (0.02%) by P₂ indicates a nearly negligible amount of exergy destruction.

To sum up, the result of exergy analysis shows that heat exchangers in the ORC system (HEX₇ and HEX₈) are the major components where exergy destruction happens. These energy losses can be reduced by enhancing heat-transfer efficiency through larger or micro-channel surfaces and better temperature-profile matching via two-stage preheating/condensation or a split-stream design, enabling more efficient heat exchange between the cold and hot fluids.

Figure 3 illustrates the distribution of components for total capital cost under the basic operating condition of the integrated system. Total capital cost of the integrated system amounts to USD 430,279.97. The system cost is analyzed from two major parts: CCES constitutes 92.4% of the total investment, and the ORC accounts for the remaining 7.6%. Turbines dominate the cost within the CCES system, representing 62.6% of its capital investment and compressors account for 37%. Heat exchangers have negligible cost contribution, only 0.3%. In the ORC system, turbines take up 87.2% which also dominates the cost of subsystem. Pumps contribute 9.7% and heat exchangers in the ORC subsystem show a relatively higher proportion than in the CCES system, reaching 3.1%. This result suggests that the turbine is the most cost-intensive across both subsystems, followed by the compressor. Consequently, efforts in cost reduction should prioritize improving the performance of turbines to reduce required capacities and cost–performance trade-off optimization should be considered.

4.2. Sensitivity Analysis of Integrated System

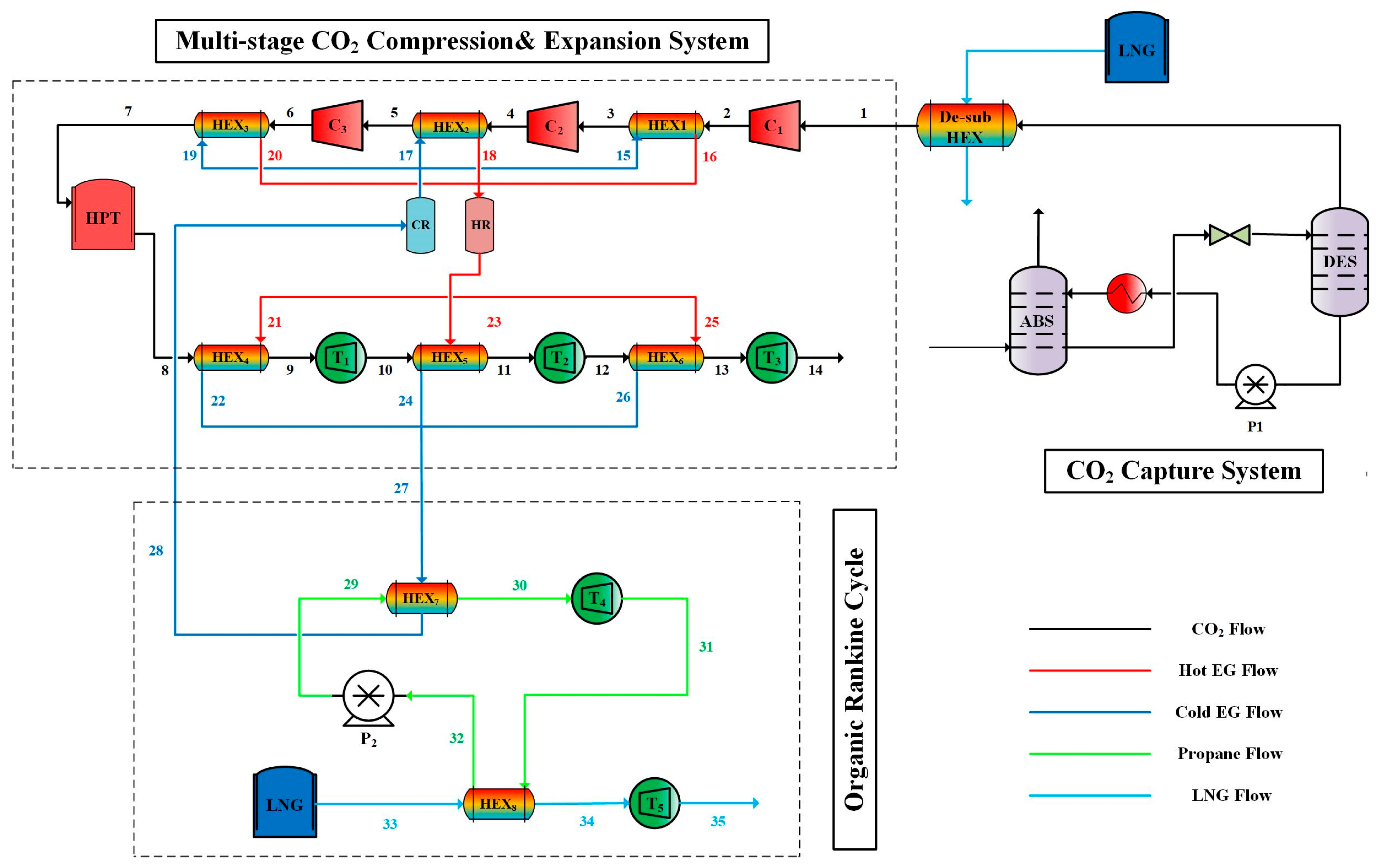
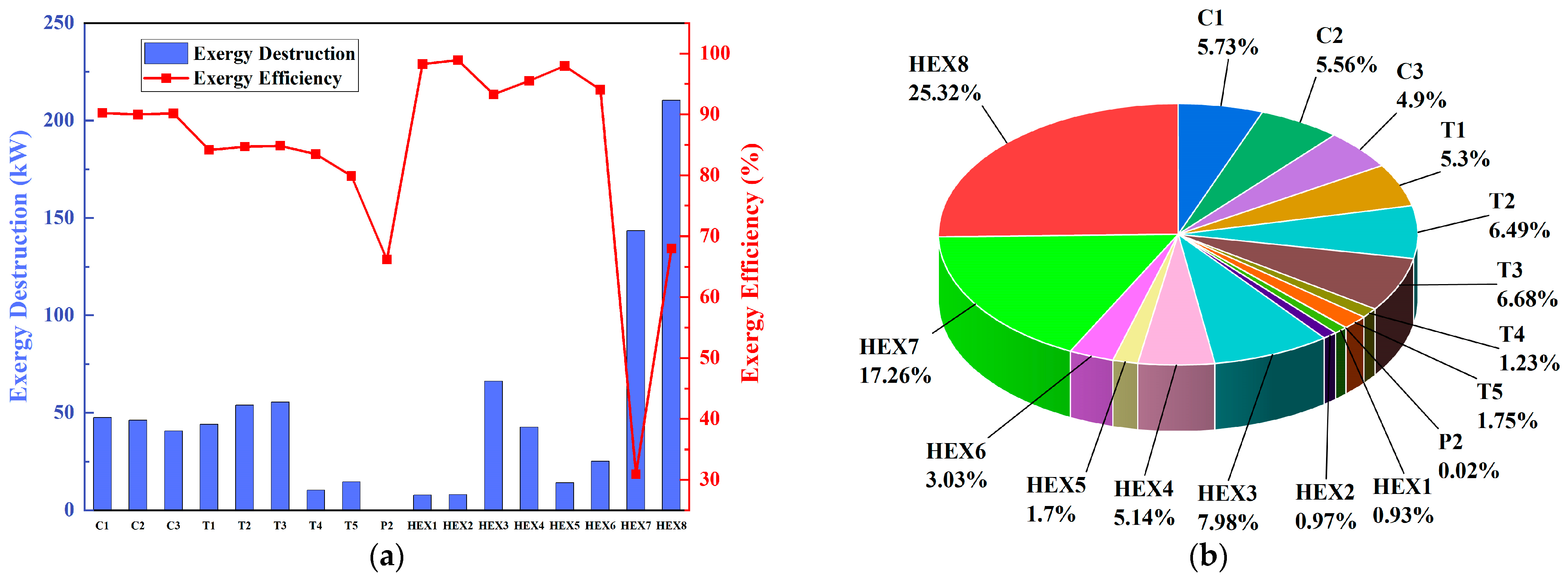
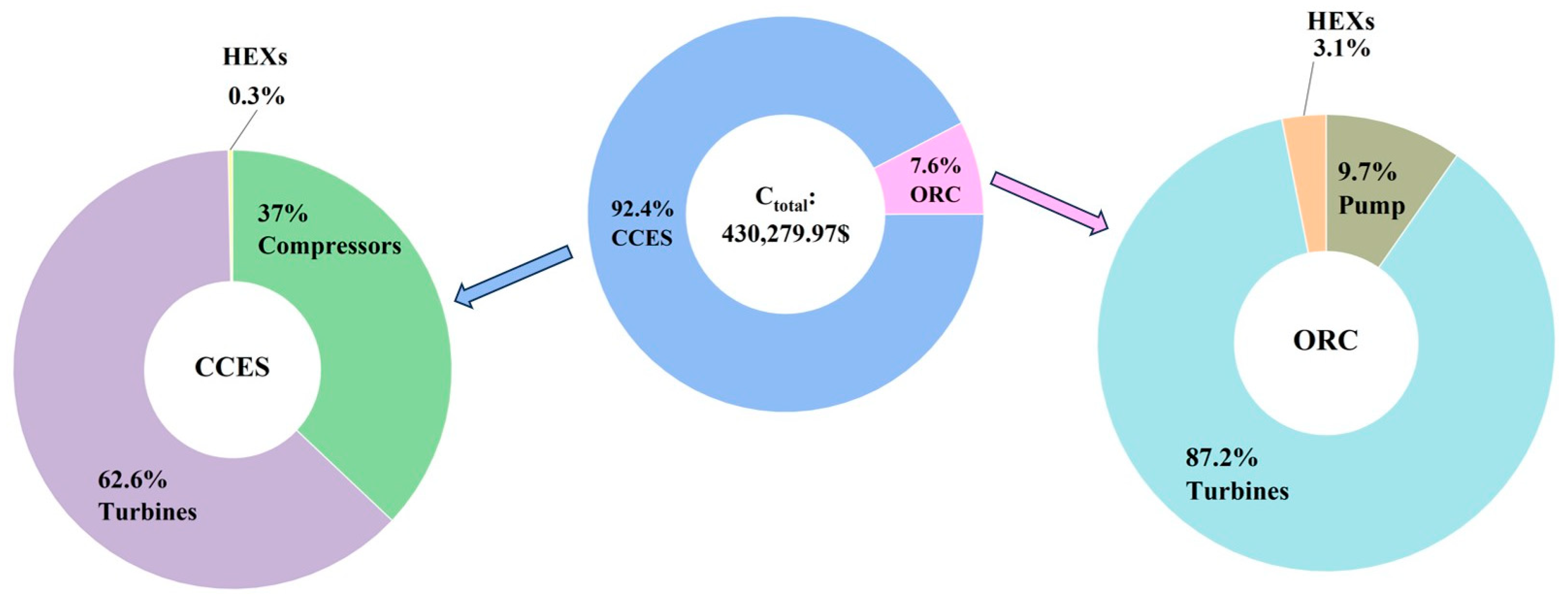
Considering the impact of different critical parameters on the integrated system’s performance, three parameters are selected for sensitivity analysis in this section: pressure of HPT and pinch temperature difference in HEXs and P₃₀ (the pre-expansion pressure of propane in the ORC). The pressure of HPT determines the pressure ratio of compressors and the stored energy level of CO₂, thereby affecting both the charging and discharging efficiencies. Pinch temperature difference in HEXs influences the heat-recovery ability and thermal match between fluids, which are essential for high system efficiency. P₃₀ strongly affects the expansion ratio, net power output, and exergy efficiency of the ORC subsystem. Since these three parameters directly determine the energy conversion, heat-utilization, and power generation performance of the integrated system, they are selected as the primary critical parameters for the sensitivity analysis.

4.2.1. The Effects of Pressure of HPT

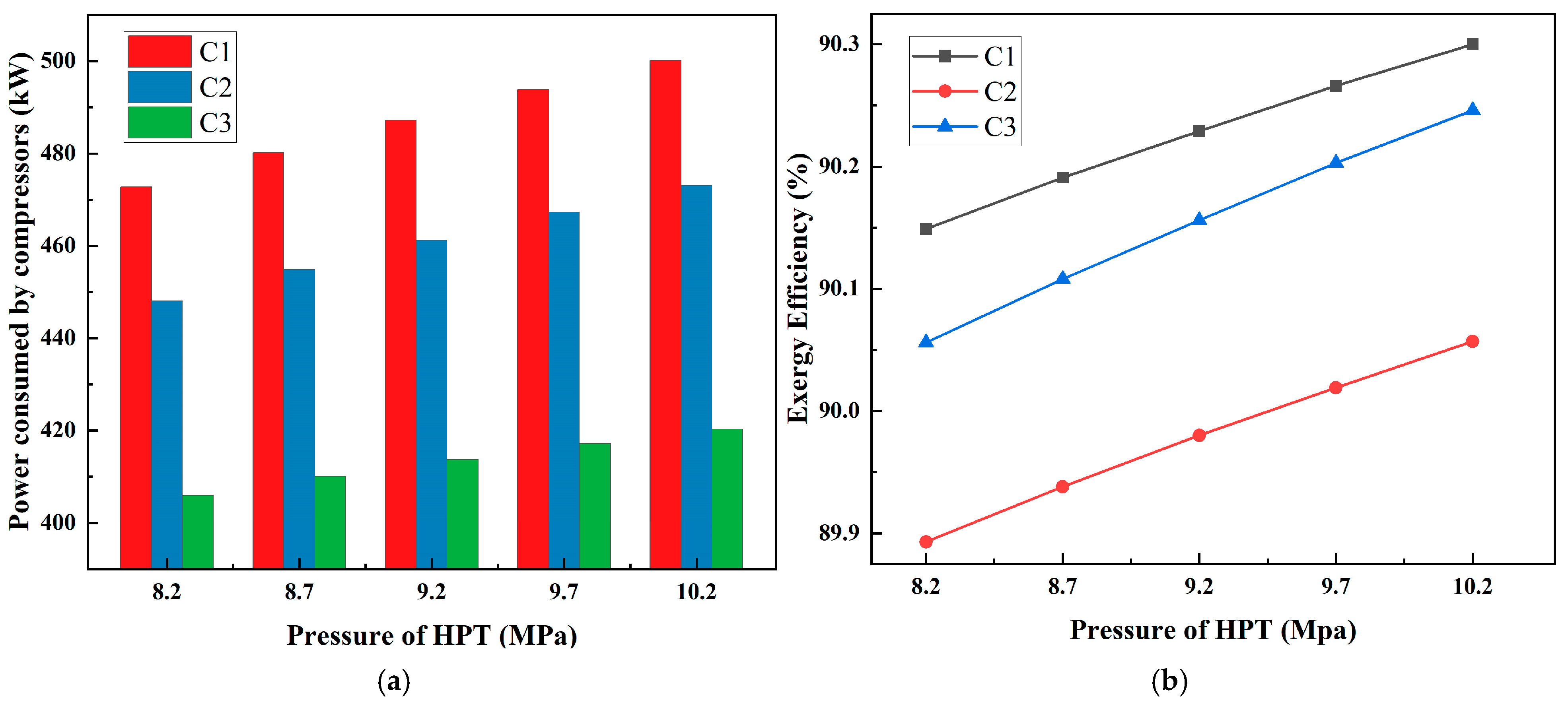
In this section, the pressure of HPT is selected to vary from 8.2 MPa to 10.2 MPa in the charge process of CCES system, as this range represents a practical operating interval that ensures stable CO₂ storage while maintaining safe compressor and tank conditions.

Figure 4 illustrates how the power consumption and exergy efficiency of three compressors (C₁, C₂, and C₃) vary under increasing pressure of HPT in the charge process of the CCES system. As shown in Figure 4a, all three compressors show an increasing trend in power consumption as the pressure of the HPT rises from 8.2 MPa to 10.2 MPa. C₁ consistently shows the highest power consumption among all compressors and increase from 472.74 kW to 500.15 kW, C₂ displays moderate power consumption, in the middle range between C₁ and C₃ and increase from 448.06 kW to 473.07 kW. C₃ shows the lowest power consumption across all pressures and increase from 405.91 kW to 420.24 kW. This trend of increased power consumption is due to the compression line of the CCES, the pressure ratio of the three compressors keep increasing which requires more power consumption. Figure 4b expresses the relationship between exergy efficiency and the pressure of HPT. Exergy efficiency of each compressor measures the effectiveness with which the compressor converts input energy into useful work. All compressors show an increase in exergy efficiency with increasing pressure of HPT. C₁ has the highest exergy efficiency among all compressors and shows a consistent increase from 90.14% to 90.30%. C₃ also shows an increase but lower than C₁, rising from 90.05% to 90.24%. C₂ displays the lowest exergy efficiency but also has a small increase from 89.89% to 90.05%. This suggests that as the pressure of HPT increases, although the energy demand is higher, the compressors operate more effectively in terms of converting input energy into useful output.

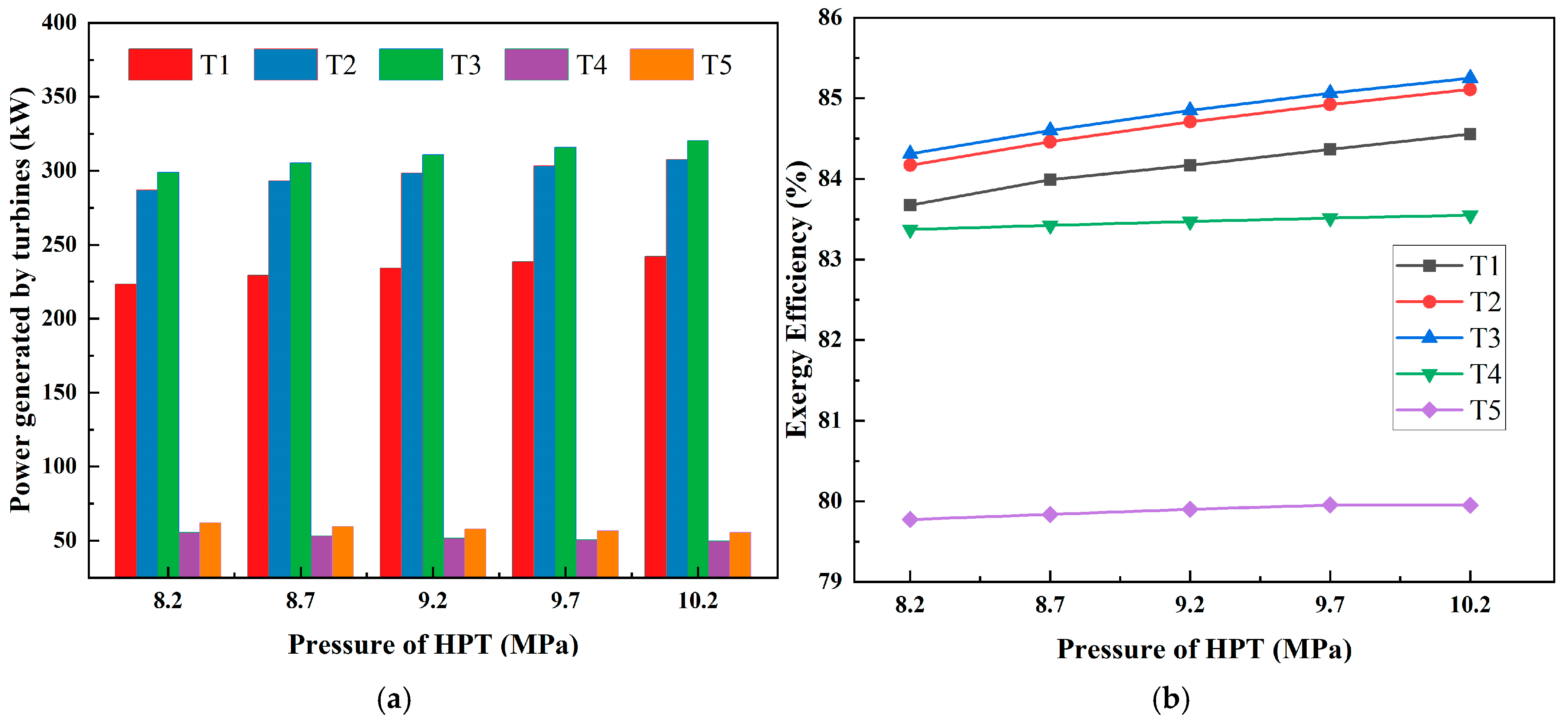
Figure 5 describes the power generation and exergy efficiency of five turbines (T₁ to T₅) under various pressures of HPT. As shown in Figure 5a, T₁, T₂, and T₃ produce higher power compared to T₄ and T₅, with T₂ and T₃ producing the most. T₄ and T₅ produce significantly less power, especially noticeable at higher pressures since T₄ decreases from 55.42 kW to 49.69 kW and T₅ also decreases 62.03 kW to 55.50 kW, whereas T₁ increases from 223.31 kW to 242.11 kW, T₂ increases from 286.94 kW to 307.62 kW, and T₃ increases from 298.86 kW to 320.33 kW when the pressure of HPT rises. The upward trend in the power output of T₁, T₂, and T₃ can be explained by how, as the pressure of HPT increases, the heat absorbed by ethylene glycol during the compression process in CCES also increases, which in turn leads to an increase in the thermal energy that can be utilized by the turbines during the expansion process. The decrease in the power output of T₄ and T₅ is due to the outlet temperature of the hot fluid EG from HEX₇ in the ORC remaining unchanged (the temperature returned to CCES), which results in a decrease in the mass flow rate of propane in the ORC. The trend of each turbine of exergy efficiency under the increasing pressure of HPT is shown in Figure 5b. T₁, T₂, and T₃ display a steady increase in exergy efficiency as the pressure of HPT rises, in which T₁ increases from 83.67% to 84.45%, T₂ increases from 84.17% to 85.11%, and T₃ increases from 84.31% to 85.25%, suggesting that these turbines are effectively converting available energy into useful work at higher pressure of HPT. T₄ and T₅ also shows an increase, but at a slower rate than T₁, T₂, and T₃, in which T₄ rises from 83.37% to 83.54% and T₅ rises from 79.77% to 79.95%, indicating less sensitivity to the pressure of HPT changes.

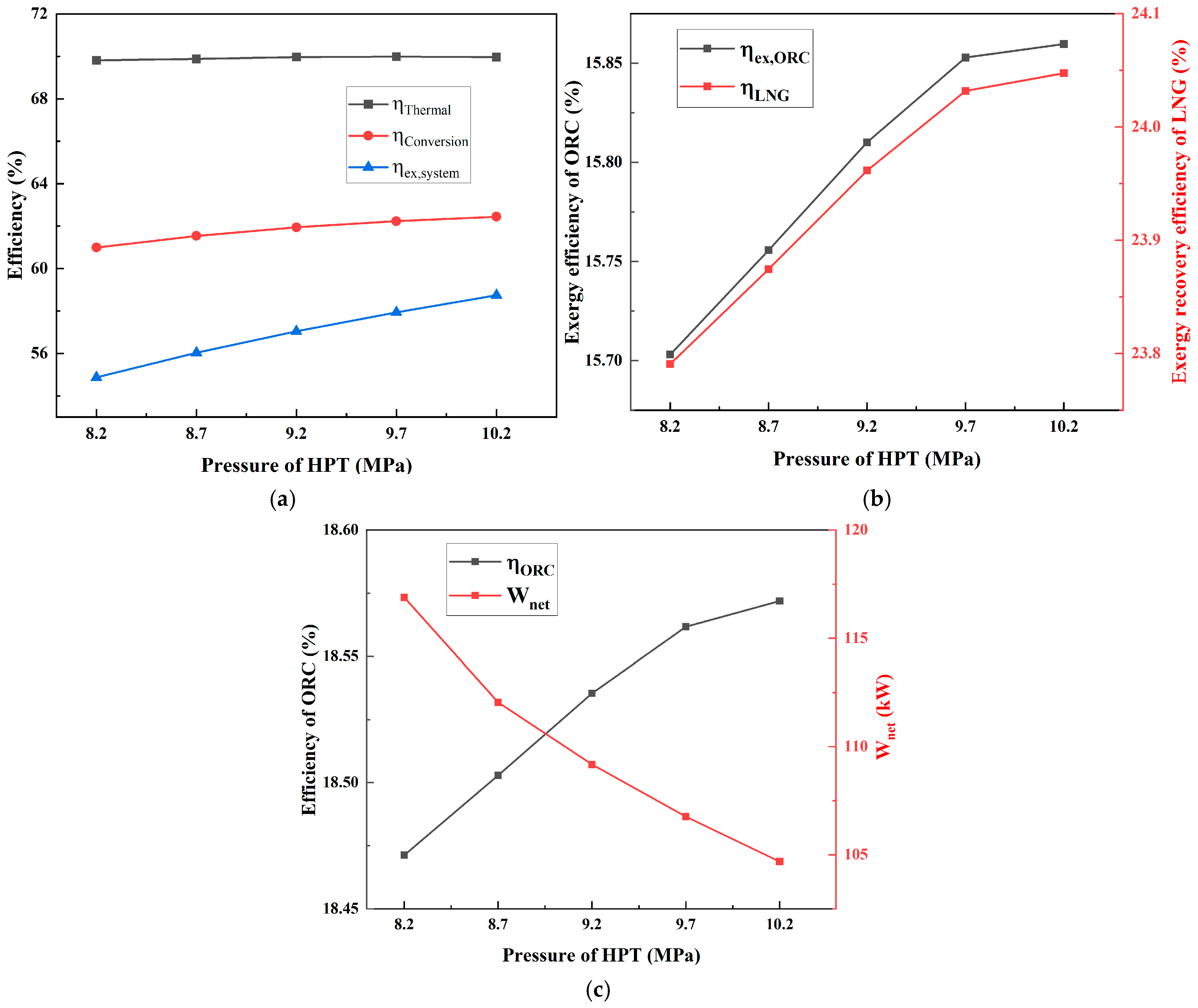
Figure 6 illustrates various efficiency metrics for the integrated system. Figure 6a describes the relationship between the pressure of HPT and three different efficiency metrics (${\eta }_{Thermal}$, ${\eta }_{Conversion}$ and ${\eta }_{ex,system}$). With the increase in pressure of HPT from 8.2 MPa to 10.2 Mpa, ${\eta }_{Thermal}$ is nearly constant, with very little variation of around 69.81% to 69.96%. ${\eta }_{Conversion}$ shows a steady increase from 60.98% to 62.44%, indicating improvements in the energy conversion process in the CCES system as the pressure of HPT increases. ${\eta }_{ex,system}$ also increases from 54.87% to 58.73%, which implies that the integrated system is becoming more effective at using the available energy to do work.

As shown in Figure 6b, with the increase in pressure of HPT from 8.2 MPa to 10.2 Mpa, ${\eta }_{ORC}$ gradually increases from 18.47% to 18.57%. This result indicates that the ORC system becomes more efficient in its energy conversion process under higher pressure of HPT. However, $W_{net}$ shows a clear downward trend from 116.88 kW to 104.68 kW as the pressure of HPT increases, showing that while the system may be operating more efficiently, the output power available from the ORC system is less.

As shown in Figure 6c, ${\eta }_{ex, ORC}$ and ${\eta }_{LNG}$ raise simultaneously as the pressure of HPT rises. ${\eta }_{ex, ORC}$ increases from 15.70% to 15.86%, suggesting that ORC components are better utilizing the available thermal energy as the pressure of HPT increases. The increase of ${\eta }_{LNG}$ (from 23.79% to 24.04%) indicates that the use of LNG in ORC for cooling is becoming more efficient under higher pressure of HPT.

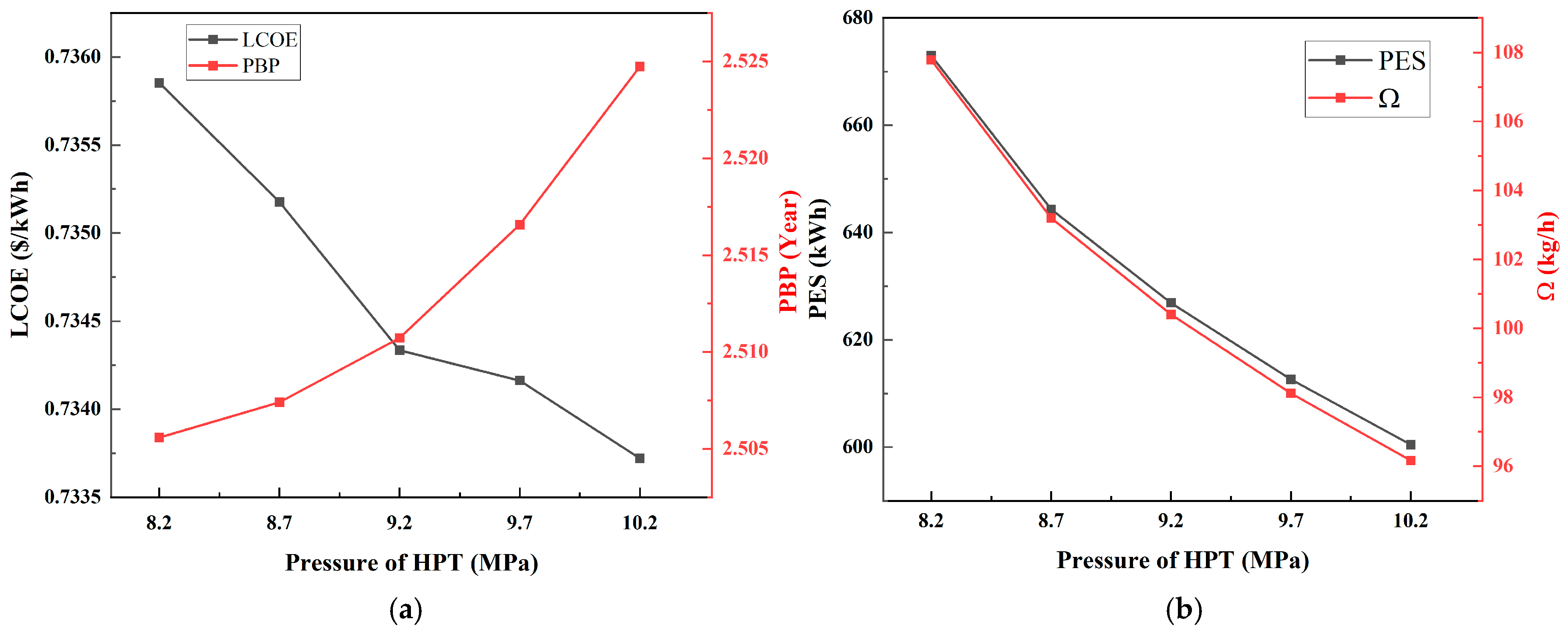
Figure 7a shows that integrated system economic performance varies under different pressure of HPT. LCOE decreases significantly from USD 0.7358/kWh to USD 0.7337/kWh as the pressure increases from 8.2 to 10.2 MPa, reaching a minimum value around 10.2 MPa, suggesting that higher pressure of HPT leads to less cost-effective electricity generation. PBP shows an increasing trend from 2.5 Years to 2.52 Years as the pressure rises, suggesting that the time to recover investments extends as pressure of HPT increases.

As shown in Figure 7b, with the increase in pressure of HPT from 8.2 MPa to 10.2 Mpa, PES decreases consistently from 672.97 kWh to 600.46 kWh. This trend implies that the higher pressure of HPT makes the integrated system less efficient in terms of energy conservation and output per energy input. $\Omega$ decreases simultaneously from 107.78 kg/h to 96.17 kg/h since $W_{net}$ decreased. In general, the decreasing trends in both PES and $\Omega$ at higher pressure of HPT indicate a decreasing trend in terms of environmental sustainability and efficiency.

In conclusion, increasing the pressure of HPT enhances thermodynamic performance (${\eta }_{Conversion}$, ${\eta }_{ex,system}$ and ${\eta }_{ORC}$) and slightly improves economic indicators (lower LCOE), but at the cost of reduced environmental benefits (lower PES and $\Omega$) and slightly longer PBP. Therefore, the pressure of HPT represents a critical trade-off parameter in system design and optimization, and its optimal range must be carefully selected depending on the priority of performance metrics.

4.2.2. The Effects of Pinch Temperature Difference

In this section, to investigate the impact of different pinch temperature difference in HEXs on the system performance, four temperature values (3 K, 5 K, 7 K and 9 K) are selected as variables. In addition, the small pinch temperature differences represent idealized designs and may require additional constraints on the heat exchanger area and pressure drop in a detailed engineering-scale study.

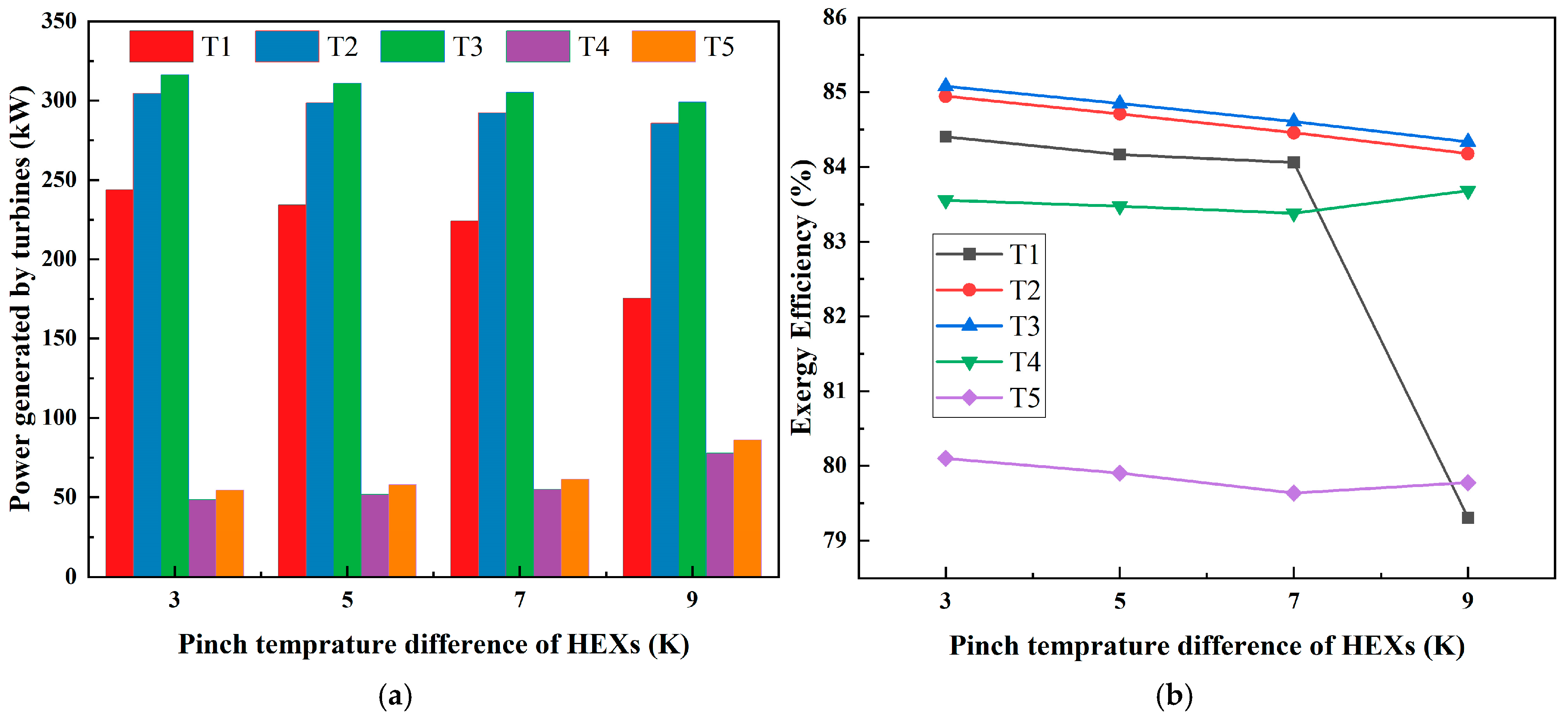
Figure 8 illustrates the power generation and exergy efficiency of five turbines (T₁ to T₅) under various pinch temperature differences in HEXs. As shown in Figure 8a, turbines in the charge process (T₁, T₂, and T₃) show a decreasing trend of power generation with rising pinch temperature difference from 3 K to 9 K. T₁ reduces from 243.7 kW to 175.47 kW and drops dramatically when pinch temperature difference increases to 9 K, which is similar to the exergy efficiency in Figure 8b. T₂ and T₃ have similar power generation; T₂ decreases from 304.54 kW to 285.67 kW and T₃ decreases from 316.31 kW to 299.07 kW. In contrast to the turbines of the charge process, T₄ and T₅ rise simultaneously as the pinch temperature difference rises. T₄ increases from 48.57 kW to 77.85 kW and T₅ increases from 54.46 kW to 86.06 kW. The decrease in the power output of T₁-T₃ is due to the increasing HEXs’ pinch temperature difference, which leads to a reduction in the heat transfer, and the amount of heat available for the turbines to utilize also decreases. The increase in HEXs’ pinch temperature difference leads to an increase in the propane mass flow in the ORC. As a result, the power output of T₄ and T₅ show an upward trend.

As shown in Figure 8b, with the increase in pinch temperature difference from 3 K to 9 K, the exergy efficiency of T₁, T₂, and T₃ all decrease; while T₃ has the highest exergy efficiency and decreases from 85.07% to 84.33%, T₂ has a similar decreasing trend with T₃, from 84.94% to 84.17%. T₁ shows a noticeable decrease as pinch temperature difference increases, particularly dropping at 9 K, from 84.40% to 79.30%. The exergy efficiency of T₄ and T₅ are lower than turbines in the charge process, especially that of T₅, showing the lowest exergy efficiency among all turbines from 80.1% to 79.77%, and lowest exergy efficiency is reached when pinch temperature difference is 7 K. T₄ shows a simultaneous trend with T5 of exergy efficiency from 83.55% to 83.68%, which also reaches the lowest exergy efficiency when pinch temperature difference is 7 K.

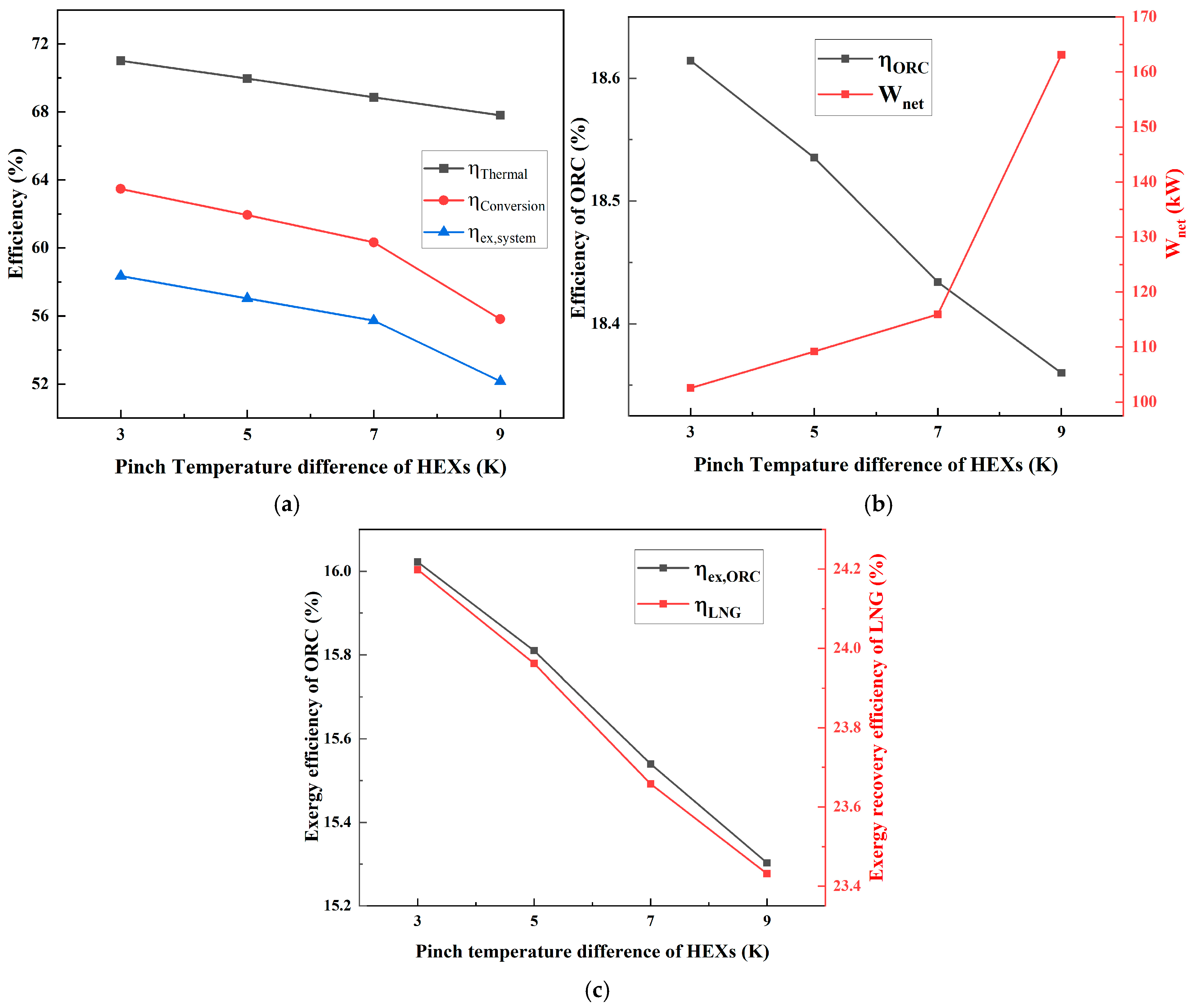
Figure 9 illustrates different efficiency metrics of the integrated system under different pinch temperature differences in HEXs. As shown in Figure 9a, ${\eta }_{Thermal}$ remains relatively stable as the pinch temperature difference increases from 3 K to 9 K, only slightly decreasing from 71.01% to 67.80%. This stability suggests that ${\eta }_{Thermal}$ is less sensitive to variations in pinch temperature difference. ${\eta }_{Conversion}$ decreases significantly from 63.47% to 55.81% as the pinch temperature difference increases, suggesting that higher pinch temperature difference negatively affects the energy conversion process, due to the reduced thermal driving force. ${\eta }_{ex,system}$ also shows a notable decrease from 58.34% to 52.15% with higher pinch temperature difference. This indicates increasing inefficiencies and energy losses in the system as the pinch temperature difference in HEXs increases. A larger pinch temperature difference causes less heat transfer, which results in less energy recovery and conversion and ability of the integrated system to utilize available energy and exergy also declines as energy losses rise with less heat transfer.

As shown in Figure 9b, ${\eta }_{ORC}$ decreases from 18.61% to 18.36% with increasing pinch temperature difference, suggesting that the ORC becomes thermodynamically less efficient, as less heat exchange leads to less effective energy conversion. Contrary to the trend of ${\eta }_{ORC}$, $W_{net}$ initially increases with increasing pinch temperature difference but then sharply rises at the highest pinch temperature difference from 102.53 kW to 163.12 kW.

As shown in Figure 9c, ${\eta }_{ex, ORC}$ and ${\eta }_{LNG}$ show a simultaneously downward trend under different pinch temperature of HEXs’ rises. ${\eta }_{ex, ORC}$ decreases steadily from 16.02% to 15.3% as pinch temperature rise which indicates that lower pinch temperature is more favorable for energy conversion process. ${\eta }_{LNG}$ consistently decreases from 24.19% to 23.43% with higher pinch temperature difference. This further confirms that energy efficiency in such thermal process is compromised at higher pinch temperature due to low effective heat transfer.

Therefore, the performance improvement achieved by reducing the pinch temperature difference in HEXs can be regarded as the expected upper limit value of the performance enhancement that can be systematically achieved in the design of HEX7 and HEX8 by adopting advanced heat transfer technologies.

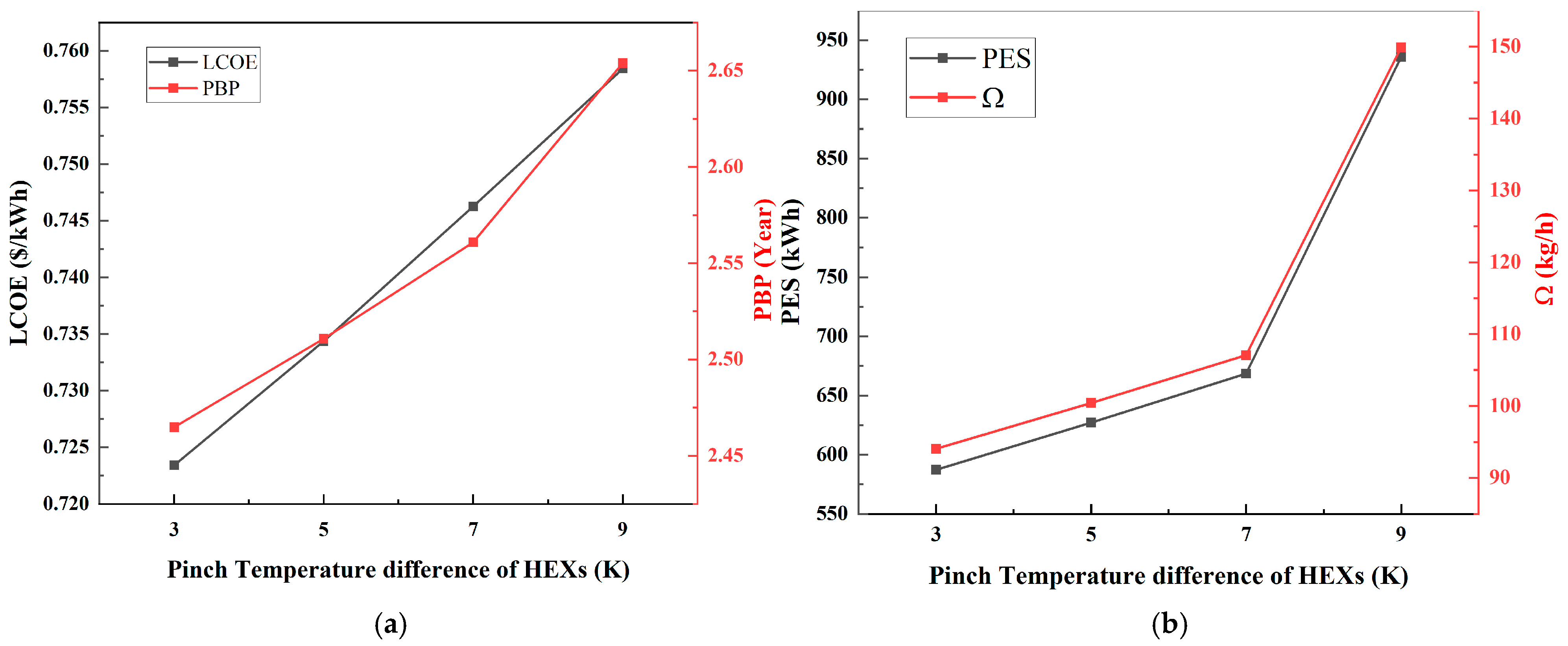
Figure 10 illustrates how pinch temperature difference in HEXs affects the economic and environmental performance of the integrated system. As shown in Figure 10a, LCOE shows a clear upward trend as the pinch temperature difference increases from 3 K to 9 K. The rising LCOE from USD 0.723/kWh to USD 0.758/kWh indicates that larger pinch temperature difference reduces heat transfer effectiveness, leading to lower system efficiency and thus higher electricity generation cost. PBP also increases from about 2.45 years to 2.65 years as the pinch temperature rises. This suggests that system investment is recovered more slowly when thermal transfer is poorer.

Figure 10b describes the environmental performance of the integrated system. There is a notable jump in PES as the pinch temperature difference increases, rising sharply from around 587.22 kWh to 935.92 kWh. This increase suggests that the energy saving of the integrated system becomes better at higher pinch temperature difference. This trend is consistent with $W_{net}$. Another environmental metric of Ω similarly shows a steep increase from about 94.04 kg/h to 149.89 kg/h. This reflects that despite lower thermal efficiency, the system could be effectively offsetting more CO₂ at higher pinch temperature difference.

In conclusion, these results show a complex interaction between economic cost, environmental impact, and system efficiency as influenced by the pinch temperature difference in HEXs. Higher pinch temperature difference, while negative to cost-effectiveness and basic thermal performance, enhances other aspects like energy savings and avoided CO₂ emissions. These insights could be critical for making decisions about operating parameters and optimization of the integrated system.

4.2.3. The Effects of P₃₀

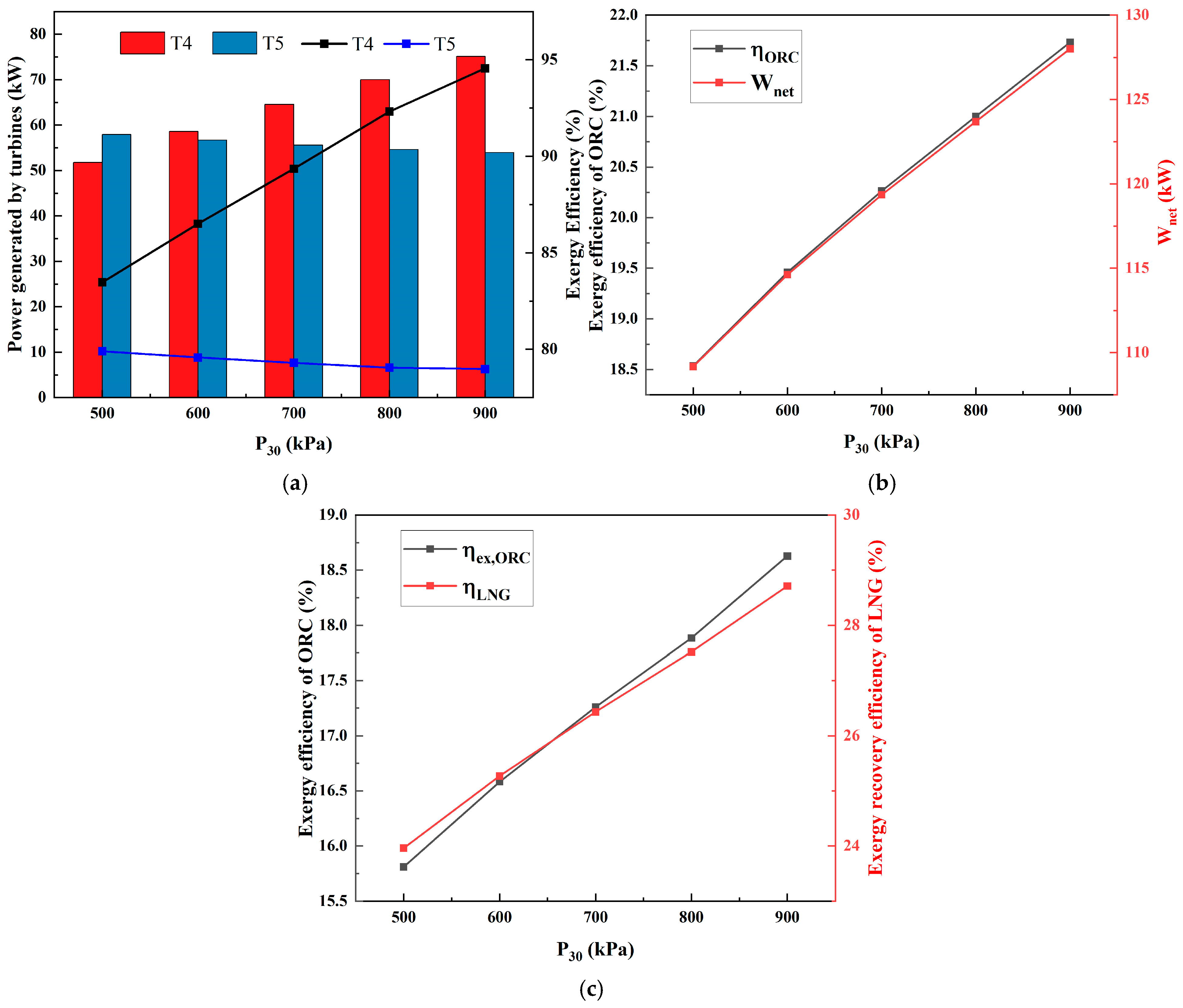
Figure 11 illustrates the influence of P₃₀ (the pre-expansion pressure of propane in the ORC) on the performance of turbines and ORC system efficiency. As shown in Figure 11a, with P₃₀ rising from 300 kPa to 900 kPa, the power output of T₄ increases significantly from 51.78 kW to 75.10 kW; exergy efficiency of T₄ also increases steadily from 83.47% to 94.55%. This result indicates that T₄ performs better at higher propane initial pressure. On the contrary, the power output of T₅ decreases from 57.93 kW to 53.96 kW; the exergy of T₅ also shows a slight downward trend from 79.90% to 78.98%, suggesting that T₅ is negatively affected by higher P₃₀. The decrease in the output power of T₅ is due to the drop in the outlet temperature of T₄ (the propane inlet temperature of HEX₈), which leads to a reduction in heat exchange, further causing the outlet temperature and mass flow rate of LNG at HEX₈ to decrease, resulting in a reduction in the available heat for T₅.

As shown in Figure 11b, both ${\eta }_{ORC}$ and $W_{net}$ increase linearly and significantly with P₃₀ rising; ${\eta }_{ORC}$ increases from 18.53% to 21.73% and $W_{net}$ increases from 109.17 kW to 127.99 kW. Increasing P₃₀ increases the expansion ratio and specific work output in ORC, improving both efficiency and net power. This confirms that higher pre-expansion pressure of propane is favorable for the performance of the ORC system.

As shown in Figure 11c, ${\eta }_{ex, ORC}$ and ${\eta }_{LNG}$ both show a positive correlation with P₃₀. ${\eta }_{ex, ORC}$ increases from 15.81% to 18.62% and ${\eta }_{LNG}$ increases from 23.96% to 28.71%. This is because the higher propane pressure increases the expansion work potential in the ORC system, reducing irreversibility and improving exergy utilization.

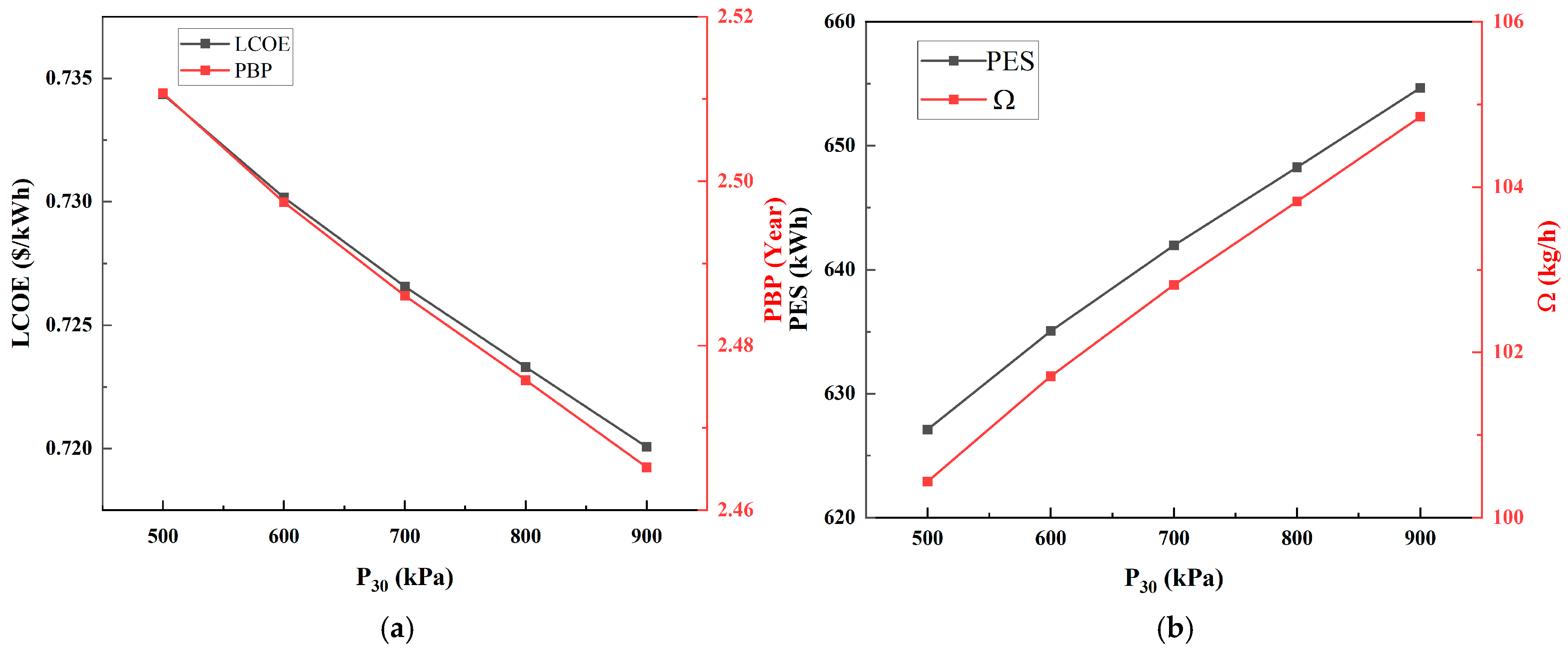
Figure 12 shows how the varying P₃₀ affects the economic and environmental performance of the integrated system. As shown in Figure 12a, as P₃₀ increase from 500 kPa to 900 kPa, LCOE and PBP have a downward trend simultaneously. LCOE reduces from USD 0.734/kWh to USD 0.720/kWh and PBP reduces from 2.51 years to 2.46 years. This indicates economic improvement at higher propane pressure, due to an improved expansion ratio and reduced irreversibility. The ORC system becomes more efficient, leading to lower LCOE and PBP.

The environmental performance of integrated system under varying P₃₀ is shown in Figure 12b. PES and Ω both show an upward trend as P₃₀ increases. PES rises from 627.09 kWh to 654.66 kWh and Ω increases from 100.43 kg/h to ~104.85 kg/h. This is because higher P₃₀ improves energy conversion effectiveness, leading to greater substitution of fossil fuel-based power. As a result, more CO₂ emissions are avoided and PES is enhanced.

In general, increasing P₃₀ significantly enhances the overall performance of the integrated system. As P₃₀ rises, both thermal and exergy efficiencies improve, $W_{net}$ increases, and the system becomes more economically attractive with a lower LCOE and shorter PBP. Additionally, environmental benefits are improved, as shown by higher PES and Ω. Therefore, treating P₃₀ as a key optimization parameter is an effective strategy to achieve high efficiency, economic viability, and environmental sustainability in system design and operation.

4.3. Multi-Objective Optimization

According to the sensitivity analysis results above, it is clear that the system’s key performance indicators have a significant impact on the design variables, and there are often conflicts among the indicators, such as the increase of ${\eta }_{ex,system}$ usually accompanied by the decrease in PES and the increase in PBP; increasing PES improves environmental friendliness at the expense of system efficiency and higher cost investment. To design the best overall performance and explore the optimal trade-off relationship between different performance metrics of the integrated system, ${\eta }_{ex,system}$, PBP, and PES are selected as the objective functions for the multi-objective optimization. Based on the results of sensitivity analysis, the decision parameters selected are the pressure of HPT (8.2–10.2 MPA), pinch temperature difference in HEXs (3–9 K), and P₃₀ (500–900 kPa). The non-dominated sorting generic algorithm-II (NSGA-II) algorithm is used in this research. The basic specifications of the algorithm are set as 100 population size, 200 generations, a mutation factor of 0.05, and a crossover factor of 0.8, respectively [34].

The final optimal point needs to be determined from the obtained Pareto curve. In this research, the TOPSIS method is selected because it provides an objective and efficient way to select the optimal solution based on its closeness to the ideal point:

$$d_i^{+}=\sqrt{{\sum }_{j=1}^n{\left(v_{ij}-v_j^{+}\right)}^2},$$

(31)

$$d_i^{-}=\sqrt{{\sum }_{j=1}^n{\left(v_{ij}-v_j^{-}\right)}^2}$$

(32)

where $v_{ij}$ denotes the matrix of all solutions on Pareto boundary. $v_j^{+}$ and $v_j^{-}$ are the best and worst value of all metrics (depends on the direction of optimization), respectively. $d_i^{+}$ and $d_i^{-}$ are the distance between the decision point and the positive/negative ideal solution, respectively.

Closeness Coefficient can be calculated as

$$C_l={\displaystyle \frac{d_i^{-}}{d_i^{+}+d_i^{-}}},$$

(33)

Figure 13 shows the result of multi-objective optimization of the integrated system. The green points represent the Pareto-optimal solutions, where improving one objective would compromise at least one other objective. The proposed integrated system achieves an optimal ${\eta }_{ex,system}$ from 69.6% to 70.3%, PBP from 2.07 to 2.11 years, and PES from 920 to 1080 kWh. As ${\eta }_{ex,system}$ increases, PBP generally rises, but PES may fluctuate, indicating nonlinear relationships among those objectives. The red star marks the best compromise solution determined by TOPSIS and has the ${\eta }_{ex,system}$ of 69.58%, PBP of 2.07 years, and PES of 1087.3 kWh. The operation parameters and the objective functions of the best compromise solution are shown in

Table 10. Operating parameters and objective functions under the optimal point.

Term	Parameter	Value
Operating parameters	Pressure of HPT (MPa)	8.53
	Pinch temperature difference in HEXs (K)	7.1
	P30 (kPa)	885.39
Objective functions	${\eta }_{ex,system}$ (%)	69.58
	PBP (year)	2.07
	PES (kWh)	1087.3

and the system performance evaluation metrics under the optimal point are shown in

Table 11. System performance evaluation metrics under the optimal point.

Term	Parameter	Value
Energy	${\eta }_{Conversion}$ (%)	58.22
	${\eta }_{Thermal}$ (%)	84.37
	${\eta }_{ORC}$ (%)	49.02
	${\eta }_{LNG}$ (%)	99.03
Exergy	${\eta }_{ex,ORC}$ (%)	62.27
	${\eta }_{ex,system}$ (%)	69.58
Economic	LCOE (USD/kWh)	0.72
	PBP (year)	2.07
Environmental	PES (kWh)	1087.3
	$\Omega$ (kg/h)	174.13

. Compared with the initial base condition, the ORC system performance has been greatly improved under the optimal solution in which ${\eta }_{ORC}$ increases from 19.82% to 49.02%, ${\eta }_{ex, ORC}$ increases from 17.70% to 62.27%, and ${\eta }_{LNG}$ increases from 27.91% to 62.27%.

5. Conclusions

In this paper, an integrated system combining the multi-stage CCES and ORC is proposed. The thermodynamic model of the integrated system is established and verified. 4E analysis is selected to evaluate the performance of the integrated system, and the influence of key parameters such as the pressure of HPT, pinch temperature difference in HEXs, and P₃₀ on the system is studied. Based on the result of the sensitivity analysis, the optimal operating conditions of the system are selected by multi-objective optimization. The results show that the integrated system has good economic feasibility and environmental performance, effectively utilizes multi-grade thermal energy, and enhances the overall energy efficiency through staged conversion and recovery processes. The main conclusions are as follows:

(1) Under the basic operating condition, ${\eta }_{Thermal}$ and ${\eta }_{ex,system}$ of the integrated system are 90.66% and 62.41%, respectively. LCOE and PBP are USD 0.73/kWh and 2.51 years and PES and $\Omega$ are 627.09 kWh and 100.43 kg/h, respectively. Exergy analysis suggests that HEX₇ and HEX₈ in the ORC system are the dominant sources of irreversibility, highlighting them as priorities for future thermal management improvements.

(2) Sensitivity analysis reveals clear performance trends.

(a)

Higher pressure of HPT improves CCES conversion efficiency but reduces ORC output and lowers environmental benefits. This establishes a thermodynamic–environmental trade-off.

(b)

Higher pinch temperature difference in HEXs weaken heat-transfer capability, decreasing both energy and exergy efficiency of the full system. However, stronger temperature gradients may increase ORC output.

(c)

In contrast, raising the P₃₀ markedly enhances ORC power generation, exergy efficiency, and environmental performance, making it the most influential parameter for improving subsystem performance.

Overall, across all parameter ranges, the integrated system maintains stable efficiency and demonstrates clear physical couplings between CCES compression heat, ORC power generation, and exergy losses.

(3) Based on multi-objective optimization and the TOPSIS decision method, ${\eta }_{ex,system}$, PBP and PES are taken as the objective functions to evaluate the system from multiple perspectives. The optimum operating conditions are determined as the pressure of HPT = 8.53 MPa, pinch temperature difference in HEXs = 7.1 K, and P₃₀ = 885.39 kPa. The optimal solution achieves 69.58% system exergy efficiency, a short PBP of 2.07 years, and 1087.3 kWh of primary energy savings with 174.13 kg/h of CO₂ emissions avoided. The optimized configuration has shortened the investment payback period and significantly reduced energy consumption. This indicates that the proposed system is economically viable and beneficial to the environment.

In conclusion, the sensitivity analysis and the comprehensive 4E framework and NSGA-II + TOPSIS optimization method of this system provide a comprehensive approach for evaluating and improving the hybrid energy storage system. From a scientific perspective, this research clarifies the thermodynamic coupling mechanism between the CCES and ORC subsystems and identifies the key sources of energy loss, providing insights for system-level efficiency improvement. From an engineering perspective, the proposed design demonstrates a feasible path towards efficient and low-carbon energy storage and offers practical guidelines for heat exchange integration, pressure management, and economic sustainability optimization in future renewable energy applications. Although the proposed integrated system shows promising 4E performance, several aspects need further investigation to enhance its applicability and stability in real-world scenarios:

(1) Dynamic Modeling and Control: The current study is based on steady-state analysis. Future work should focus on the dynamic behavior of the integrated system under varying load conditions and transient disturbances. Developing advanced control strategies will be essential to ensure system stability and optimal performance in practical applications.

(2) Experimental Validation: While the current model has been verified by existing studies, experimental validation using pilot-scale or laboratory-scale prototypes is necessary to confirm system feasibility and identify potential deviations from theoretical models.

(3) System Integration with Renewable Energy Sources: Future research can explore the integration of this system with intermittent renewable energy sources such as solar PV or wind power. Matching the charging/discharging cycle of CCES with renewable variability can improve energy dispatch flexibility and reduce reliance on fossil-fuel backup systems.