Comparative Analysis of Optimal Control and Reinforcement Learning Methods for Energy Storage Management Under Uncertainty

Abstract

The challenge of optimally controlling energy storage systems under uncertainty conditions, whether due to uncertain storage device dynamics or load signal variability, is well established. Recent research works tackle this problem using two primary approaches: optimal control methods, such as stochastic dynamic programming, and data-driven techniques. This work’s objective is to quantify the inherent trade-offs between these methodologies and identify their respective strengths and weaknesses across different scenarios. We evaluate the degradation of performance, measured by increased operational costs, when a reinforcement learning policy is adopted instead of an optimal control policy, such as dynamic programming, Pontryagin’s minimum principle, or the Shortest-Path method. Our study examines three increasingly intricate use cases: ideal storage units, storage units with losses, and lossy storage units integrated with transmission line losses. For each scenario, we compare the performance of a representative optimal control technique against a reinforcement learning approach, seeking to establish broader comparative insights.

1. Introduction

Optimal control of energy storage systems is vital in modern power systems [1]. In addition to classical optimization methods, such as linear programming, dynamic programming, quadratic programming, and Pontryagin’s minimum principle, we see, in recent years, a noticeable growth in machine learning methods, and specifically in reinforcement learning (RL) methods, for managing storage devices. The strength of such methods lies in the fact that they can produce a highly accurate and efficient classification, despite the high dimensions of the feature space.

The literature exploring this problem is vast. For example, [2] describes a dynamic programming approach to maximize the value of energy storage systems in grid applications under uncertain energy prices. Similarly, [3] addresses microgrid management using a stochastic programming model to minimize expected energy costs, demonstrating scalability and cost savings with a customized stochastic dual dynamic programming algorithm. Recent research has also explored reinforcement learning for storage control. For instance, [4] introduces a deep reinforcement learning framework for optimizing battery storage, incorporating a lithium-ion battery degradation model and a noisy network architecture for effective action space exploration. In [5], Double Deep Q-Learning is used to optimize community battery storage in microgrids. Work [6] proposes an effective real-time scheduling model for multiple battery energy storage systems (MBES) that balances short-term operational goals with long-term lifespan benefits. To optimize this model under uncertain conditions, the paper introduces a novel piece-wise linear function-based continuous approximate dynamic programming (PLFC-ADP) algorithm. The proposed algorithm effectively manages the computational complexity of MBES scheduling while achieving a near-optimal solution. Further, paper [7] focuses on optimizing energy management for microgrids connected to a main grid, which is challenging due to the fluctuating nature of renewable energy and market prices. The study models these uncertainties using probabilistic and stochastic methods and evaluates the effectiveness of the stochastic dual dynamic programming (SDDP) algorithm. The results demonstrate that the SDDP algorithm provides robust strategies that closely match the optimal solutions found through dynamic programming and Monte Carlo simulations, leading to improvements in performance and cost reduction. Comparative studies, such as [8], evaluate reinforcement learning against traditional dynamic programming for energy management in hybrid electric vehicles, showing RL’s ability to achieve global optimality in infinite-horizon control problems. Another study, [9], compares various reinforcement learning architectures, including policy iteration and value iteration, for storage control problems using a benchmarked analytical solution.

As can be seen from the above literature review, reinforcement learning methods are increasingly used for solving energy storage optimal control problems. Paper [10] focuses on energy storage management under fluctuating market prices and production from renewable sources. The authors employ two deep reinforcement learning algorithms, DDPG and PPO, to address the electricity arbitrage problem, and the proposed solution is compared to an model-predictive control method. Work [11] also concerns with electricity arbitrage, where the cost of electricity varies based on the time of day, reflecting supply–demand conditions. This paper proposes an energy management optimization strategy that minimizes the users costs by controlling battery charging/discharging, based on pricing and battery state, which is modeled as a Markov decision process, and solved using a Soft Actor–Critic algorithm. The proposed method is compared to the PPO algorithm, and to stochastic programming methods. From a slightly different perspective, study [12] proposes an energy management strategy for islanded microgrids. It uses probabilistic modeling to handle the uncertainty in renewable energy generation, loads, and market conditions, and employs a deep reinforcement learning agent, specifically, a Soft Actor–Critic agent, that makes use of the wavelet transform to extract essential features from fluctuating renewable energy sources. The proposed strategy addresses renewable energy uncertainties and power fluctuations by controlling active power and frequency, with a focus on minimizing computational burden and time. Simulation results demonstrate the improvements in computational efficiency compared to a DDPG method. Work [13] presents a novel strategy for optimizing home energy management (HEM) systems, which traditionally focus on active power and cost savings while neglecting reactive power. The research formulates the problem as a Markov decision process and proposes a deep reinforcement learning (DRL) approach to handle uncertainties in user behavior and environmental factors. By strategically controlling flexible loads and energy storage, the proposed methodology not only achieves a 31.5% reduction in electricity bills but also significantly improves the power factor from 0.44 to 0.9. Moreover, paper [14] introduces a hybrid framework for predicting a battery’s end-of-life (EOL) and quantifying its uncertainty by combining Gaussian process regression (GPR) and the Kalman filter. The methodology transforms the degradation curve forecasting into a prediction of virtual degradation rates and acceleration, which is then executed using an iterative GPR strategy. The effectiveness of the approach is validated on a lithium-ion battery dataset, demonstrating that it provides more accurate EOL predictions with a narrower range of uncertainty compared to a particle filter framework.

Contribution: However, despite the rise of AI-driven control techniques for energy storage systems, their performance compared to traditional optimal-control methods such as stochastic dynamic programming or Pontryagin’s minimum principle remains unclear. In this light, our aim in this paper is to quantify the trade-offs between these approaches, specifically evaluating the operational cost incurred by reinforcement learning policies, when operating under uncertainty conditions, thus extending recent studies such as [15,16,17]. Using three progressively complex energy storage scenarios, ideal storage, lossy storage, and lossy storage with transmission line losses, we analyze the performance and characterize the advantages and disadvantages of each approach.

2. Fundamental Challenges in the Solution of Energy Storage Optimal-Control Problems, and the Need for Reinforcement-Learning

All energy storage optimal-control problems share one common trait, which is that they are computationally demanding. Essentially, this is because such problems require deciding on an optimal function, usually power or energy, for which values should be found for each and every point in time. As a result, the number of decision variables is large, and the computational power required to find an optimal solution is substantial. Another challenge is that the resulting optimization problems are often not convex, either since the objective function is not convex, or since the decision variables are not defined over a convex set.

While such optimal control problems are in essence quite complex, traditional methods can still solve them efficiently, and with acceptable runtimes, under several simplifying assumptions, most notably, that the stochastic signals involved in the process, for example the load signals, are known in advance. Several examples of such methods are the Shortest-Path (SP) method [15], Pontryagin’s minimum principle [16], dynamic programming (DP) [17], and model-predictive control (MPC) [18]. All these methods require considerable prior knowledge of the system dynamics and input signals. For instance, classic application of the Pontryagin’s minimum principle or dynamic programming requires full knowledge of the physical model, including the dynamics of the storage device and the load signal. Such requirements are often not realistic, either since exact knowledge of the physical model is not available, or since the input signals cannot be predicted accurately. There exist, of course, stochastic versions of the same algorithms, such as stochastic dynamic-programming or model-predictive control. Nevertheless, these methods also require, at the very least, a detailed statistical model, which is often not available.

Due to these challenges, we are witnessing today an emerging trend of using machine learning methods, specifically reinforcement learning methods, for solving energy storage optimal control problems [19]. The major advantage of this approach, in comparison to the existing traditional solution methods, is that full knowledge of the system model and input signals, or their statistics, is often not required, since the reinforcement learning algorithm is designed to “learn” these directly from the data samples and improves its performance based on the knowledge acquired from exploration. The reinforcement learning algorithms themselves vary greatly: Some of them require a detailed physical model and relatively accurate statistical knowledge, while some of them do not and learn only based on actual data. Thus, one may say that reinforcement learning algorithms are distributed over a spectrum, which includes “model-based” methods at one extreme and “model-free” methods at the other extreme. Nevertheless, nearly all reinforcement learning methods will require less prior knowledge in comparison to traditional methods. This idea is illustrated in Figure 1.

In light of this emerging trend, it is important to quantify what is lost in terms of performance when the physical model is not exactly known, or the statistical description of the input signals is incomplete. While, in this paper, we do not provide a full theoretical answer to this question, we continue to explore it based on a number of typical case studies.

3. Methodology and Results of the Case Studies

We have structured the following case studies as a deliberate progression, arranged in order of ascending complexity. The initial case establishes a foundational scenario, and each subsequent study introduces additional layers or variables, building directly on the previous ones. This tiered approach means that with each new level of complexity, the amount of inherent uncertainty to be managed also increases systematically. Therefore, the following case studies are presented with an integrated structure that combines methodology and results. This format was intentionally chosen to clearly associate the specific procedures used in each case with the findings they produced. Therefore, each case study begins with a description of the methodology, followed directly by an analysis of the resulting data.

3.1. Ideal Storage Devices with Convex Cost Functions

To initiate our comparative analysis, we first address the classical problem of managing an ideal grid-connected energy storage device. This scenario, extensively explored in prior literature using traditional optimal control methods, for instance, in [15,17], serves as a crucial baseline. In this study, we develop a systematic approach to tackle this problem using reinforcement learning methods. These RL techniques operate with incomplete information regarding the system’s model dynamics. A key objective here is to meticulously demonstrate and quantify the effects of this missing knowledge on the operational results, especially when contrasted with traditional optimal control methods that presume and operate with complete, deterministic knowledge of both the system model and all relevant signals, such as load and generation profiles. This initial, simplified case is fundamental for understanding the performance degradation that might occur when relying on data-driven approaches under ideal conditions where optimal control is expected to excel.

In this context, we consider a system comprising a grid-connected storage device and a photovoltaic (PV) panel, as illustrated in Figure 2. This configuration involves the storage device being charged from both the main electrical grid and the local PV generation system. Subsequently, the stored energy, along with direct generation, is used to supply an aggregated electrical load, which is characterized by its active power consumption. The active power demand of this load, denoted as $P_a\left(t\right):{\mathbb{R}}_{\ge 0}\to \mathbb{R}$, is modeled as a continuous positive function over a finite and known time interval $[0,T]$. Complementing this, the renewable energy generated by the PV system is represented by $P_{pv}\left(t\right):{\mathbb{R}}_{\ge 0}\to \mathbb{R}$, a piece-wise continuous and semi-positive function reflecting the available solar power. The net power consumption of the load is then defined as $P_L\left(t\right)=P_a\left(t\right)-P_{pv}\left(t\right)$. The charging or discharging power of the storage unit, $P_s\left(t\right)$, is determined by the balance between the power drawn from the grid, $P_g\left(t\right):{\mathbb{R}}_{\ge 0}\to \mathbb{R}$, and the net load demand, such that $P_s\left(t\right)=P_g\left(t\right)-P_L\left(t\right)$. Correspondingly, $E_g\left(t\right)$, $E_L\left(t\right)$, and $E_s\left(t\right)$ represent the cumulative generated energy from the grid, the cumulative energy consumed by the load, and the energy stored in the battery, respectively. These energy quantities are derived by integrating their respective power functions over time, formally, $E\left(t\right)={\int }_0^{T}P\left(\tau \right)\mathrm{d}\tau$. For this foundational scenario, complexities such as internal storage losses or transmission line losses are intentionally omitted to establish an unambiguous performance benchmark for an ideal system.

The power drawn from or supplied to the grid, $P_g\left(t\right)$, is the primary controllable variable in this system. Its usage is characterized by a fuel consumption function, $f\left(P_g\left(t\right)\right)\in {\mathbb{R}}_{\ge 0}$, which quantifies the cost, for example, fuel consumed or monetary cost, associated with generating power $P_g\left(t\right)$ at any time $t\in [0,T]$. This cost function can also be interpreted more broadly to represent other objectives, such as minimizing carbon emissions or other environmental impacts linked to power generation. A critical assumption, following the original work [15] in the paper, is that this function $f\left(P_g\left(t\right)\right)$ is twice differentiable and strictly convex, meaning its second derivative $f^{\prime \prime }\left(P_g\left(t\right)\right)>0$. This convexity is significant as it generally ensures that any local minimum found is also the global minimum, simplifying the optimization process. The overall objective is to minimize the total cost of fuel consumption over the entire period, $F:={\int }_0^{T}f\left(P_g\left(t\right)\right)\mathrm{d}t$. This leads to the formulation of the following optimization problem:

$$\begin{array}{cccc}\hfill \underset{\left\{P_g(·)\right\}}{\mathrm{minimize}}& \hfill & & {\int }_0^{T}f\left(P_g\left(t\right)\right)\mathrm{d}t,\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \hfill & \hfill E_g\left(t\right)& ={\int }_0^T{P}_g\left(\tau \right)\mathrm{d}\tau ,\hfill \\ \hfill & \hfill & \hfill E_L\left(t\right)& \le E_g\left(t\right)\le E_L\left(t\right)+E_{max},\hfill \\ \hfill & \hfill & \hfill \mathrm{for}0& \le t\le T,E_g\left(0\right)=E_L\left(0\right),\hfill \\ \hfill & \hfill & \hfill E_g\left(T\right)& =E_L\left(T\right).\hfill \end{array}$$

(1)

These constraints ensure energy balance, respect the storage capacity limits ($E_{max}$), and define the operational cycle of the storage.

An optimal solution to this problem, under the assumption of complete knowledge, can be efficiently found using the Shortest-Path method, as introduced in the work [15] in the paper. This method posits that the optimal trajectory of generated energy, $E_g\left(t\right)$, corresponds to a minimal-cost path. This path is constrained to lie between the cumulative energy demand $E_L\left(t\right)$ and the maximum possible stored energy level $E_L\left(t\right)+E_{max}$. The identification of this path is achieved by applying Dijkstra’s algorithm to a specially constructed graph that represents the feasible energy states and transitions over time. To construct this graph, the continuous time horizon $[0,T]$ is discretized into N uniform intervals of duration $\mathsf{\Delta }t$, such that $t_k=k\mathsf{\Delta }t$ for $k=0,\dots ,N$. At each discrete time step $t_k$, the permissible energy levels $E_g\left(t_k\right)$ are bounded by $E_L\left(t_k\right)\le E_g\left(t_k\right)\le E_L\left(t_k\right)+E_{max}$. The search graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$ is then defined where each vertex $v_k^j\in \mathcal{V}$ signifies a discretized energy level $E_g^{\left(j\right)}\left(t_k\right)$ at time $t_k$, and each edge $e_k^{j\to \ell }\in \mathcal{E}$ represents a feasible transition from an energy state $E_g^{\left(j\right)}\left(t_k\right)$ at time $t_k$ to another state $E_g^{(\ell )}\left(t_{k+1}\right)$ at the subsequent time step $t_{k+1}$. These transitions are governed by feasible charging/discharging rates, $\mathsf{\Delta }{E}_k^{j\to \ell }=E_g^{(\ell )}\left(t_{k+1}\right)-E_g^{\left(j\right)}\left(t_k\right)$, which must be within the range $[0,E_{max}]$ (assuming $E_{max}$ can also represent maximum charge/discharge capability within a $\mathsf{\Delta }t$ interval). The power drawn from the generator for such a transition is $P_{g,k+1}^{(\ell )}=(E_g^{(\ell )}\left(t_{k+1}\right)-E_L\left(t_{k+1}\right))/\mathsf{\Delta }t$. The weight assigned to each edge, $w_k^{j\to \ell }$, is determined by the cost function $w_k^{j\to \ell }=f\left(P_{g,k+1}^{(\ell )}\right)$, leveraging the strict convexity of $f(·)$. Due to the continuous nature of $E_g$, a uniform discretization with resolution $\delta E$ is applied in the energy space, yielding a finite set of allowable energy levels at each time step. This results in a layered graph structure, where layers correspond to time steps $t_k$, and nodes within each layer represent feasible energy states at that step. Dijkstra’s algorithm then systematically explores paths starting from the initial node $v_0^{\left(0\right)}=E_g\left(t_0\right)=E_L\left(t_0\right)$, expanding paths of incrementally increasing cumulative cost until it reaches a terminal node at $t_N=T$ that satisfies the end condition $E_g\left(t_N\right)=E_L\left(t_N\right)$. The path identified with the overall minimum cumulative cost dictates the optimal energy dispatch trajectory for the storage system. This method’s efficacy is fundamentally tied to the availability of complete prior knowledge of system dynamics and load signals.

In contrast, the reinforcement learning formulation approaches the problem by replacing the assumption of a deterministic and fully known load function with a generative or learned model of the environment. The environment is conceptualized as an MDP, characterized by a continuous state space $\mathcal{S}$ and a continuous action space $\mathcal{A}$. At each discrete time step k, the state of the system $s_k$ is defined by a tuple $s_k=(E_{s,k},H_k,P_{L,k})$, where $E_{s,k}$ is the state of charge of the battery, $H_k$ indicates the current hour of the day, providing temporal context, and $P_{L,k}$ is the net load demand at that time $t_k$. The action $a_k\in \mathcal{A}$, taken by the RL agent, determines the amount of energy $\mathsf{\Delta }{E}_k$ to be charged into or discharged from the battery, constrained by $a_k=\mathsf{\Delta }{E}_k$, with $\mathsf{\Delta }{E}_k\in [0,E_{max}]$ for charging, with similar bounds for discharging, representing the energy transfer limit, and also by the battery’s maximum capacity, $E_{s,k}+\mathsf{\Delta }{E}_k\le E_{max}$. Following an action $a_k$, the system transitions deterministically, in this ideal, lossless model, to a new state $s_{k+1}$, and the agent receives a scalar reward $r_k$. This reward is defined by the negative of the generation cost, $r_k=-f\left(P_{g,k}\right)$, where $P_{g,k}=(E_{s,k+1}-E_L\left(t_{k+1}\right))/\mathsf{\Delta }t$. This interaction process unfolds over the specified time horizon until a terminal time $t_N$ is reached, yielding a complete trajectory of states, actions, and rewards, and, thus, a cumulative reward or cost. The core objective for the RL agent is to learn an optimal policy $\pi :\mathcal{S}\to \mathcal{A}$ that minimizes the expected cumulative operational cost over time. This learning occurs through trial and error or experience, without explicit programming of the optimal strategy, making it suitable for model-free approaches where the agent directly optimizes its policy based on environmental interactions.

To empirically evaluate and compare these methodologies, the optimal control policy derived from the Shortest-Path method was implemented in MATLAB R2024a, while three distinct model-free RL algorithms—Soft Actor–Critic (SAC), Proximal Policy Optimization (PPO), and Twin Delayed DDPG (TD3)—were implemented in Python 3.9 using the Stable-Baselines library, version 2.7.1a3. The corresponding code files are accessible via a public git repository [20]. The operational task is to determine a policy that specifies the generation actions, consequently inducing charging or discharging of the storage unit, over a 24 h interval, setting $T=24$ h for this study. The selection of these model-free RL approaches was driven by their widespread use in various control applications, particularly for energy storage, owing to their general applicability and relative ease of adaptation to new or poorly defined domains where system dynamics are not explicitly modeled.

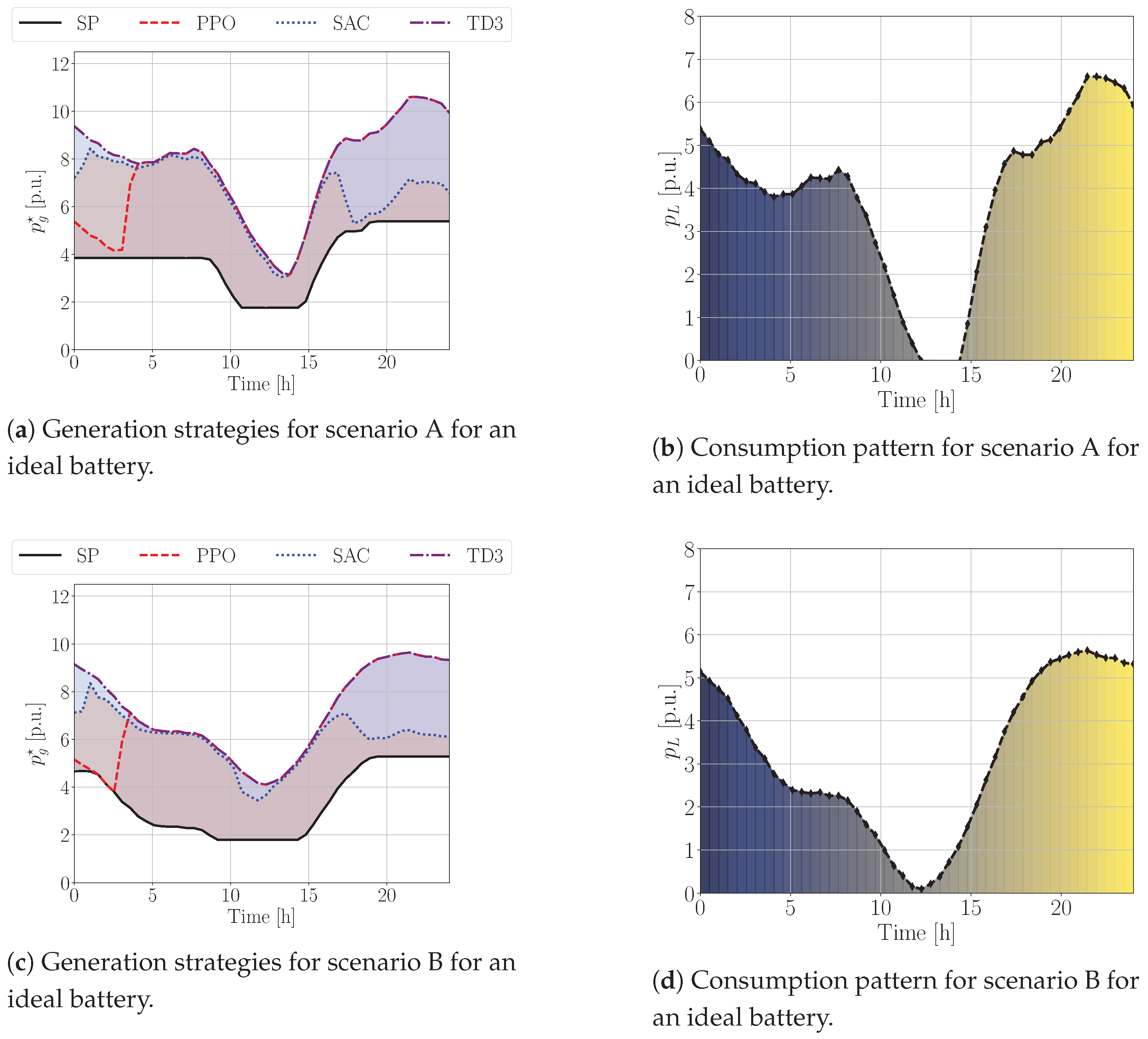
Results: The results from this first scenario, presented in Figure 3, are interesting, and back up the initial assumptions. None of the examined RL methods succeeded in learning an effective operational policy when benchmarked against the optimal path determined by the classical Shortest-Path algorithm. An intriguing secondary observation was the similarity in the policies learned by both the PPO and TD3 methods. This is noteworthy because PPO employs a stochastic policy search, whereas TD3 relies on a deterministic policy. This convergence to similar policies, despite algorithmic differences, offers several insights into the underlying structure of this specific control problem.

Firstly, if two different days exhibit similar patterns of energy demand and PV production, and if their initial storage conditions are close, they are likely to result in similar operational policies. This consistency can be attributed to the fact that the value function, which the RL agent seeks to optimize, is Cauchy bounded, implying that small changes in input conditions lead to correspondingly small changes in output values or actions. Secondly, the inherent dynamics governing the interactions among the system’s components, the storage device, PV generation, grid power, and load demand are assumed to be time invariant in this idealized model. This means that the fundamental relationships and operational characteristics of the system do not change over the simulation period, providing a stable learning environment. Thirdly, the reward function, derived from the strictly convex generation cost function $f\left(P_g\left(t\right)\right)$, is itself convex. A convex reward landscape is bereft of local minima, which means that different optimization algorithms, even if they explore the solution space differently, are more likely to be guided towards the same global optimum or a similar region of high performance. Finally, the reward function may exhibit symmetries concerning certain actions or states, thereby guiding different algorithms towards similar policies. For instance, consider two distinct scenarios: one (state $s_0$) where high PV production fully meets the current demand, but high future demand is predicted, prompting a decision to charge the storage with $\mathsf{\Delta }{P}_s=1$ [p.u.]. Another scenario (state $s_1$) might involve low PV production and an empty storage unit, necessitating the purchase of 1 [p.u.] from the grid merely to satisfy the current demand. Despite these being entirely different operational situations, they could potentially yield the same immediate reward (cost). If such reward equivalences are common, RL algorithms might develop policies that are relatively insensitive to the nuanced differences between these states, causing disparate algorithms like PPO and TD3 to converge towards similar, possibly generalized, strategies. This insensitivity, if it leads to overlooking critical state distinctions, could also contribute to the observed suboptimal performance of the RL agents compared to the fully informed optimal control solution. The daily costs over a 100-day test set, shown in Figure 4 and

Table 1. Mean and variance of the daily cost of power generation for each algorithm over a 100 day test period.

Algorithm	Mean	Var
SP	711.85	70,854.35
PPO	2428.24	27,1321.64
SAC	1935.02	15,4239.84
TD3	2787.36	34,2948.40

, further quantify this performance gap, with RL methods incurring substantially higher mean costs. Specifically, the PPO algorithm resulted in $2428.24$ USD/p.u., the SAC algorithm resulted in $1935.02$ USD/p.u., and the TD3 resulted in $2787.36$ USD/p.u., in comparison to the optimal control approach, using the SP algorithm, that resulted in $711.85$ USD/p.u. Moreover, the model-free RL approaches exhibited greater variance compared to the SP method. The cost deviations depicted in Figure 5 highlight the tighter concentration of costs around the mean for SP, which is mostly within $\pm 300$ USD/p.u., in comparison to a wider spread for the RL algorithms, as evident by examining the PPO and TD3 results, which exceed $\pm 1000$ USD/p.u.

3.2. Grid Connected Lossy Storage Devices

To continue the comparative analysis and delve into more realistic operational conditions, we now introduce a model with more intricate dynamics by incorporating a lossy storage device, as detailed in work [16]. This progression from an ideal to a lossy model inherently increases the complexity and the amount of uncertainty that both traditional optimal control and reinforcement learning algorithms must handle. The presence of energy losses during charging, discharging, and even self-decay introduces a new layer of challenge in optimizing the storage operation for minimal cost.

To formally incorporate these battery losses, we define an efficiency function $\eta :\mathbb{R}\to [0,1]$ as a piece-wise continuous function. This function characterizes the efficiency of the storage device and depends on the power flowing into or out of it, $P_s\left(t\right)$, and it is defined as

$$\eta \left(P_s\left(t\right)\right)=\left\{\begin{array}{cc}{\eta }_{\mathrm{ch},t}\left(P_s\left(t\right)\right){\eta }_{\mathrm{decay}},\hfill & \mathrm{if}{P}_s\left(t\right)>0\left(\mathrm{charging}\right),\hfill \\ {\eta }_{\mathrm{dis},t}^{-1}\left(P_s\left(t\right)\right){\eta }_{\mathrm{decay}},\hfill & \mathrm{if}{P}_s\left(t\right)<0\left(\mathrm{discharging}\right).\hfill \end{array}\right.$$

(2)

Here, ${\eta }_{\mathrm{ch},t}\left(P_s\left(t\right)\right)$ represents the charging efficiency, ${\eta }_{\mathrm{dis},t}\left(P_s\left(t\right)\right)$ is the discharging efficiency, and ${\eta }_{\mathrm{decay}}$ accounts for inherent energy decay or self-discharge over time. Furthermore, we assess a generalized non-affine dynamic model for the battery’s state of charge, $E_s\left(t\right)$, which is defined by the following differential equation:

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{E}_s\left(t\right)=\eta \left(P_s\left(t\right)\right)P_s\left(t\right).$$

(3)

This dynamic model directly links the rate of change of stored energy to the power flow and the state-dependent efficiency. This formulation leads to the following optimization problem:

$$\begin{array}{cccc}\hfill \underset{\left\{P_s(·)\right\}}{\mathrm{minimize}}& \hfill & & {\int }_0^T\left(f\left(P_s\left(t\right)\right)+c\left(E_s\left(t\right)\right)\right)\mathrm{d}t,\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \hfill & & {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{E}_s\left(t\right)=\eta \left(P_s\left(t\right)\right)P_s\left(t\right),\hfill \\ \hfill & \hfill & & E_s\left(0\right)=0,\hfill \\ \hfill & \hfill & & E_s\left(T\right)=0,\hfill \end{array}$$

(4)

where $f\left(P_s\left(t\right)\right)$ is the primary cost function, accounting for generation cost, as the power flowing bidirectionally from the battery $P_s\left(t\right)$ influences $P_g\left(t\right)$). The function $c:\mathbb{R}\to [0,\infty )$ introduces a penalty for violating storage capacity constraints. This penalty function is defined as

$$c\left(x\right):=\left\{\begin{array}{cc}{\displaystyle \frac{\mathcal{Q}}{2E_{max}}}{(x-E_{max})}^2,\hfill & \mathrm{for}x>E_{max}\left(\mathrm{overcharged}\right),\hfill \\ 0,\hfill & \mathrm{for}0\le x\le E_{max}(\mathrm{within}\mathrm{limits}),\hfill \\ {\displaystyle \frac{\mathcal{Q}}{2E_{max}}}{x}^2,\hfill & \mathrm{for}x<0\left(\mathrm{over}\text{-}\mathrm{discharged}\right),\hfill \end{array}\right.$$

(5)

with $\mathcal{Q}>0$ being a large penalty coefficient. By setting $\mathcal{Q}$ to a sufficiently large value, we implicitly enforce that the stored energy $E_s\left(t\right)$ remains within the operational bounds $[0,E_{max}]$, as deviations would incur extremely high costs. Solving for the optimal energy storage trajectory $E_s\left(t\right)$ and the corresponding power flow $P_s\left(t\right)$ allows for the determination of the grid power $P_g\left(t\right)$ and generated energy $E_g\left(t\right)$ through the system’s power balance equations. For this scenario, Pontryagin’s minimum principle is employed as the classical optimal control method to find an analytical solution.

Consequently, the explicit analytical solution derived using PMP is described by the dynamics of the optimal state ${\widehat{E}}_s\left(t\right)$ and an associated Lagrange multiplier, the costate variable, $\widehat{\lambda }\left(t\right)$. The optimal rate of change of stored energy is ${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{\widehat{E}}_s\left(t\right)=\eta \left({\widehat{P}}_s\left(t\right)\right){\widehat{P}}_s\left(t\right)$, with boundary conditions ${\widehat{E}}_s\left(0\right)={\widehat{E}}_s\left(T\right)=0$. The costate variable evolves according to ${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\widehat{\lambda }\left(t\right)=c^{\prime }\left({\widehat{E}}_s\left(t\right)\right)$, where $c^{\prime }\left({\widehat{E}}_s\left(t\right)\right)$ is the derivative of the penalty function. The optimal storage power ${\widehat{P}}_s\left(t\right)$ is then determined based on $\widehat{\lambda }\left(t\right)$, the net load $P_L\left(t\right)$, and the charging or discharging efficiencies, referred to as ${\eta }_{ch}$ and ${\eta }_{dis}$ in this context:

$${\widehat{P}}_s\left(t\right)=\left\{\begin{array}{cc}{\eta }_{\mathrm{ch}}\widehat{\lambda }\left(t\right)-P_L\left(t\right),\hfill & \mathrm{for}{P}_L\left(t\right)<{\eta }_{\mathrm{ch}}\widehat{\lambda }\left(t\right),\hfill \\ {\eta }_{\mathrm{dis}}^{-1}\widehat{\lambda }\left(t\right)-P_L\left(t\right),\hfill & \mathrm{for}{P}_L\left(t\right)>{\eta }_{\mathrm{dis}}^{-1}\widehat{\lambda }\left(t\right),\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(6)

This solution provides the benchmark optimal control policy under the assumption of known loss characteristics.

The RL formulation for this lossy storage case closely mirrors that of the ideal storage scenario, with the crucial difference lying in the definition of the MDP’s state transition function. To accurately reflect the system’s behavior, the transition function must now explicitly account for the energy losses inherent in the storage device. When the agent takes an action $a_k=\mathsf{\Delta }{E}_k$, representing the energy intended to be charged or discharged before losses, the resulting next state $s_{k+1}^{\prime }$, which is the new state of charge $E_{s,k+1}$, is calculated as $E_{s,k+1}=(E_{s,k}+\mathsf{\Delta }{E}_k){\eta }_{\mathrm{effective},k}$. This occurs under the assumption that the transition respects the battery’s physical capacity limits, formally, $0\le E_{s,k+1}\le E_{max}$. The term ${\eta }_{\mathrm{effective},k}$ represents the effective efficiency for that specific transition. If $\mathsf{\Delta }{E}_k\ne 0$, meaning active charging or discharging occurs, ${\eta }_{\mathrm{effective},k}$ incorporates both the relevant charge or discharge efficiency, denoted by ${\eta }_{\mathrm{ch}}$ or ${\eta }_{\mathrm{dis}}$, respectively, and the self-decay component ${\eta }_{\mathrm{decay}}$. If $\mathsf{\Delta }{E}_k=0$, meaning no active charging or discharging, then ${\eta }_{\mathrm{effective},k}$ simply reflects the self-decay ${\eta }_{\mathrm{decay}}$ over the time step $\mathsf{\Delta }t$. This modification ensures that the RL agent learns to operate the storage device while being subjected to realistic energy loss dynamics.

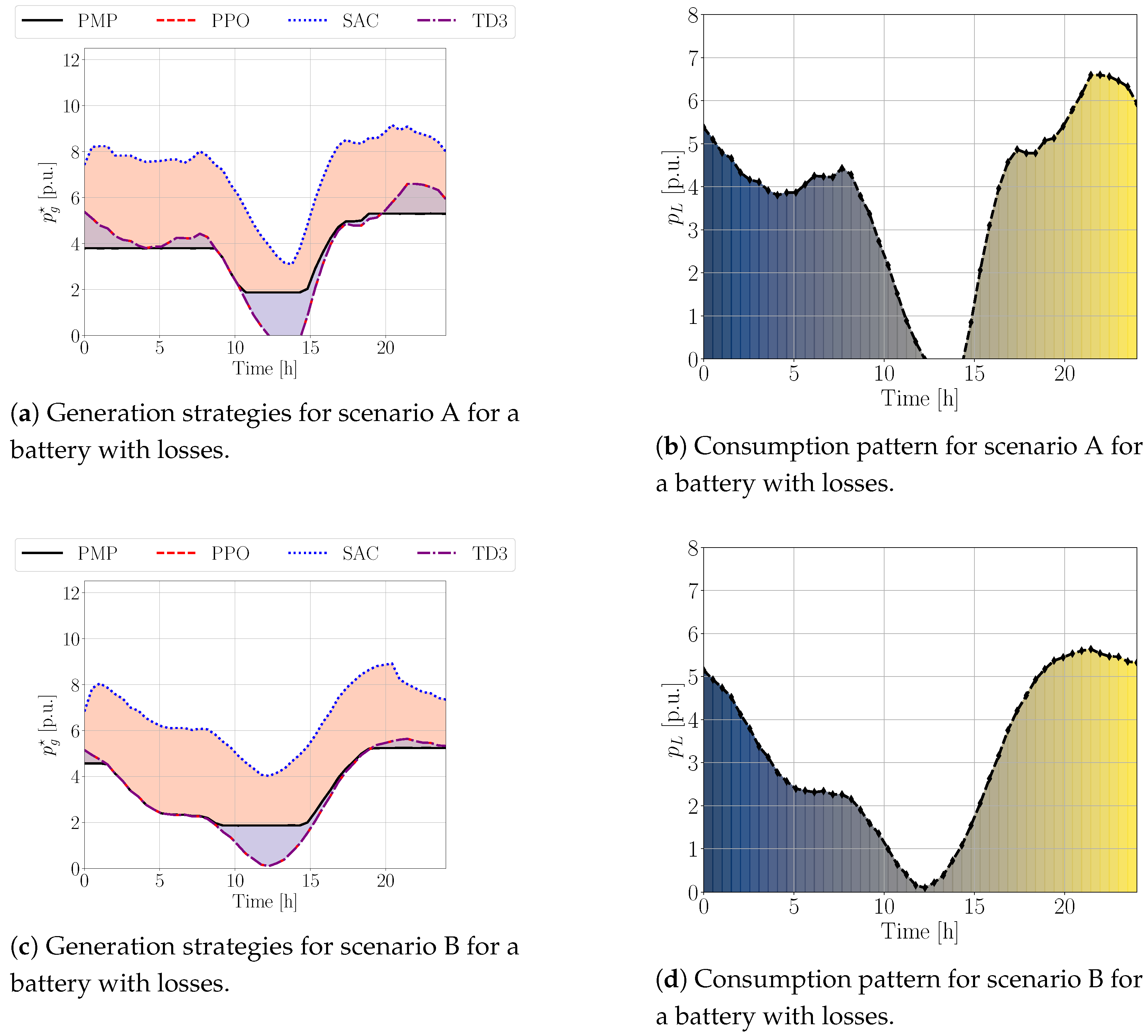
Results: The experimental results for this scenario, presented in Figure 6, reveal a notable shift in comparative performance. While the classical PMP algorithm still achieved the lowest operational costs, the performance gap between the optimal control algorithm and some of the RL methods narrowed considerably. Specifically, the policies learned by PPO and TD3 were again observed to be quite similar, and their mean daily operational costs were significantly closer to the PMP benchmark than in the ideal storage case. As shown in

Table 2. Mean and variance of the daily cost of power generation for each algorithm over a 100-day test period.

Algorithm	Mean	Var
PMP	705.82	69,024.48
PPO	748.17	88,234.85
SAC	2280.81	20,7902.61
TD3	748.17	88,234.85

of the original paper, the PMP method achieved a mean daily cost of $705.82$ USD/p.u. Remarkably, both PPO and TD3 achieved mean costs of $748.17$ USD/p.u., which is only approximately $6\%$ higher than the PMP optimal. This suggests that when the uncertainty, in the form of power loss, is primarily confined to the internal dynamics of the storage device, these RL algorithms can learn the storage behavior quite effectively and achieve a substantial improvement in their relative cost performance, even without explicit prior knowledge of the loss model. The SAC algorithm, however, did not perform as well, with a mean cost of $2280.81$ USD/p.u., indicating its potential struggles with this specific problem configuration or hyperparameter tuning.

An interesting observation from Table 2 is that the mean and variance of the classical PMP algorithm’s costs were lower than those of the SP algorithm in the ideal case, with $705.82$ [USD/p.u.] in comparison to $711.85$ [USD/p.u.] achieved by the SP algorithm. This might suggest that PMP, which is well suited for continuous-time optimal control problems, handles the continuous dynamics of the lossy storage model more adeptly than the Dijkstra-based SP method would if applied to a discretized version of this more complex problem. Furthermore, the mean costs for PPO and TD3 also decreased compared to their performance in the ideal case, with $748.17$ USD/p.u. in comparison to $2428.24$ USD/p.u. for PPO and $2787.36$ USD/p.u. for TD3. This may be atributed to the improvement to their inherent ability to navigate and learn within large and complex state spaces, allowing them to capture some of the nuances of the lossy environment more effectively than they did in the simpler ideal environment where their learning seemed less focused. However, it is also crucial to note that the introduction of model complexity in the form of losses led to an increase in the variance of the daily costs for all RL algorithms. Figure 7, which presents the daily costs, and Figure 8, which presents the deviations of the costs, visually confirm these trends, showing PPO and TD3 tracking much closer to the PMP optimal than in the first scenario, while SAC remains significantly higher. The cost deviations for PMP remained tightly centered, mostly within $\pm 200$ USD/p.u., whereas SAC exhibited the largest spread, indicating higher variability.

3.3. Storage Devices Within a Transmission Grid with Losses

In this section, we advance our comparative analysis by eliminating an additional simplifying assumption. We now introduce and analyze a model that incorporates power losses occurring over the transmission lines situated between the power generation source and the consumer block, which includes the energy storage system. This represents the most complex scenario in our study, aiming to capture a more comprehensive set of uncertainties that real-world systems face. The system under consideration can be conceptualized as consisting of a primary power source, modeled as a synchronous generator, and a non-linear aggregated load, similarly to the illustration in Figure 2. This non-linear load block comprises the photovoltaic generation unit, the energy storage device with a defined capacity $E_{max}$, and the end-consumer load that consumes active power $P_L\left(t\right):{\mathbb{R}}_{\ge 0}\to \mathbb{R}$. A key modeling assumption here is that the components encapsulated within this non-linear load block (PV, storage, and consumer load) are located in close physical proximity to each other, rendering the energy transmission between these internal components effectively lossless. However, the transmission from the main synchronous generator to this aggregated load block is subject to losses.

To perform this analysis, we adopt a distributed circuit model perspective, specifically considering a short-length transmission line. The power generated at the source, $P_g\left(t\right)$, and the power received at the aggregated load and storage blocks are related through a loss model. It is denoted by $P_{\mathrm{received}}\left(t\right)=P\left(t\right)+P_L\left(t\right)$, with $P\left(t\right)$ being the power flowing bidirectionally from storage and $P_L\left(t\right)$ being the consumer load demand. The power generated by the source, $P_g\left(t\right)$, must be greater than $P_{\mathrm{received}}\left(t\right)$ to compensate for these losses. We approximate the generated power required as

$$P_g\left(t\right)\approx (P\left(t\right)+P_L\left(t\right))+\alpha {(P\left(t\right)+P_L\left(t\right))}^2.$$

(7)

Here,$P\left(t\right)$ is the power flowing into or from the storage device. The term $\alpha {(P\left(t\right)+P_L\left(t\right))}^2$ represents the quadratic transmission losses, where $\alpha ={\displaystyle \frac{R}{|V_g{|}^2}}$ is a constant determined by the transmission line resistance R and the square of the magnitude of the line voltage $V_g$. Such a quadratic relationship for transmission losses is a well-established approximation in power systems literature, as discussed, for example, by [23]. This formulation leads to the following optimization problem:

$$\begin{array}{cccc}\hfill & \mathrm{minimize}\hfill & \hfill & \underset{0}{\overset{T}{\int }}f\left(P\left(t\right)+P_L\left(t\right)+\alpha {(P\left(t\right)+P_L\left(t\right))}^2\right)\mathrm{d}t,\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill & \hfill & {\displaystyle \frac{\mathrm{d}{E}_s\left(t\right)}{\mathrm{d}t}}=\eta \left(E_s\left(t\right)\right)·P\left(t\right),\hfill \\ \hfill & \hfill & & 0\le E_s\left(t\right)\le E_{max},\hfill \\ \hfill & \hfill & & E_s\left(0\right)=0,E_s\left(T\right)=0.\hfill \end{array}$$

(8)

The function $f(·)$ is the cost of generation at the source, now applied to the total power $P_g\left(t\right)$ that includes losses. The term $\eta \left(E_s\left(t\right)\right)$ represents the efficiency of the storage device itself, as in the previous lossy storage scenario, potentially including charge, discharge and decay effects. For this complex problem, dynamic programming (DP) is chosen as the classical optimal control method.

To apply DP, the problem is discretized. We define a time resolution $\mathsf{\Delta }t=T/N$, with discrete time steps $t_i=i\mathsf{\Delta }t$ for $i=0,\dots ,N$. Accordingly, the energy stored at time $t_i$ is $E_{s,i}=E_s\left(i\mathsf{\Delta }t\right)$, and the power values are approximated as constant over each interval: $P_i=P\left(i\mathsf{\Delta }t\right)$, $P_{L,i}=P_L\left(i\mathsf{\Delta }t\right)$, and $P_{g,i}=P_g\left(i\mathsf{\Delta }t\right)$. The discrete version of the optimization problem is given by

$$\begin{array}{cccc}\hfill & \underset{\left\{P_i\right\}}{\mathrm{minimize}}\hfill & \hfill & \mathsf{\Delta }t\sum _{i=1}^{N}f(P_i+P_{L,i}+\alpha {(P_i+P_{L,i})}^2),\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill & \hfill & {\displaystyle \frac{E_{s,i}-E_{s,i-1}}{\mathsf{\Delta }t}}=\eta \left(E_{s,i}\right)P_i,\mathrm{for}i=1,\dots ,N,\hfill \\ \hfill & \hfill & & 0\le E_{s,i}\le E_{max},\mathrm{for}i=1,\dots ,N,\hfill \\ \hfill & \hfill & & E_{s,0}=0,E_{s,N}=0.\hfill \end{array}$$

(9)

Here, $\eta \left(E_{s,i}\right)$ represents the aggregated energy loss efficiency of the storage device for the i-th interval.

For the reinforcement learning solution in this scenario, the model must now account for transmission line losses in addition to the storage’s internal losses. Consequently, the state transition function is further modified. When an action $a_k=\mathsf{\Delta }{E}_k$ is taken from a state $s_k$ with storage energy $E_{s,k}$, the resulting next state $s_{k+1}^{\prime }$ with storage energy $E_{s,k+1}$ is determined by a two-stage loss application. First, the energy $\mathsf{\Delta }{E}_k$ is subject to transmission line losses, represented by an efficiency factor ${\eta }_{\mathrm{tr}}$. The energy effectively reaching or leaving the storage block is then $\mathsf{\Delta }{E}_k{\eta }_{\mathrm{tr}}$. This amount is then subject to the storage’s internal charge or discharge and decay efficiencies, collectively denoted by ${\eta }_{\mathrm{storage},k}$, similarly to $\eta$ in the previous case study. Thus, the new state of charge might be approximated as $E_{s,k+1}\approx (E_{s,k}+\mathsf{\Delta }{E}_k{\eta }_{\mathrm{tr}}){\eta }_{\mathrm{storage},k}$. This compounded loss model should make the environment significantly more challenging for the RL agent to learn and control optimally.

Results: The experimental results for this third scenario, presented in Figure 9, demonstrate a further degradation in the performance of the RL algorithms when compared to the DP optimal solution. As detailed in

Table 3. Mean and variance of the daily cost of power generation for each algorithm over a 100-day test period.

Algorithm	Mean	Var
DP	773.10	89,220.93
PPO	1165.14	14,6485.45
SAC	1293.96	10,9379.59
TD3	2779.89	34,2000.82

, the DP method achieved a mean daily cost of $773.10$ USD/p.u.. In contrast, the PPO algorithm resulted in a mean cost of $1165.14$ USD/p.u., a $51\%$ increase over DP. SAC incurred $1293.96$ USD/p.u., resulting in a $67\%$ increase, and TD3 performed notably worse with a mean cost of $2779.89$ USD/p.u., showing a $260\%$ increase, more than 3.5 times higher than the DP algorithm. These results underscore the difficulty RL methods face when dealing with external, system-level uncertainties like transmission line losses, which are not directly part of the storage device’s internal dynamics that the agent might more easily learn through interaction. The mean and variance of the classical DP algorithm also increased in this scenario compared to PMP in the lossy-storage-only case, where the mean value increased to $773.10$ in comparison to $705.82$ when applying PMP, and the value of the variance increased to $89,220.93$ in comparison to $69,024.48$ when applying PMP. This reflects the added difficulty posed by the transmission losses even for the optimal control approach. However, for all RL algorithms, there was a general trend of performance improvement relative to their own baseline in the ideal case, but a degradation compared to the lossy-storage case for PPO and SAC, while TD3 remained poor. This suggests that while RL can handle some forms of uncertainty, the nature and location of that uncertainty, whether it is internal, and is captured by the model, or external to the modeled MDP, significantly impacts its effectiveness.

A particularly interesting observation in this scenario was that the PPO and TD3 algorithms no longer produced similar policies, unlike in the previous two cases. The policy generated by the PPO algorithm, which employs a stochastic policy search, was observed to be smoother and more effective than that of the TD3 algorithm, which relies on a deterministic policy. This divergence and the superior performance of PPO further emphasize the potential benefits of using stochastic policies when navigating environments with highly unpredictable or complex dynamics, such as those introduced by combined storage and transmission losses. The deterministic policy of TD3 appeared more vulnerable to these compounded uncertainties, leading to significantly higher operational costs. 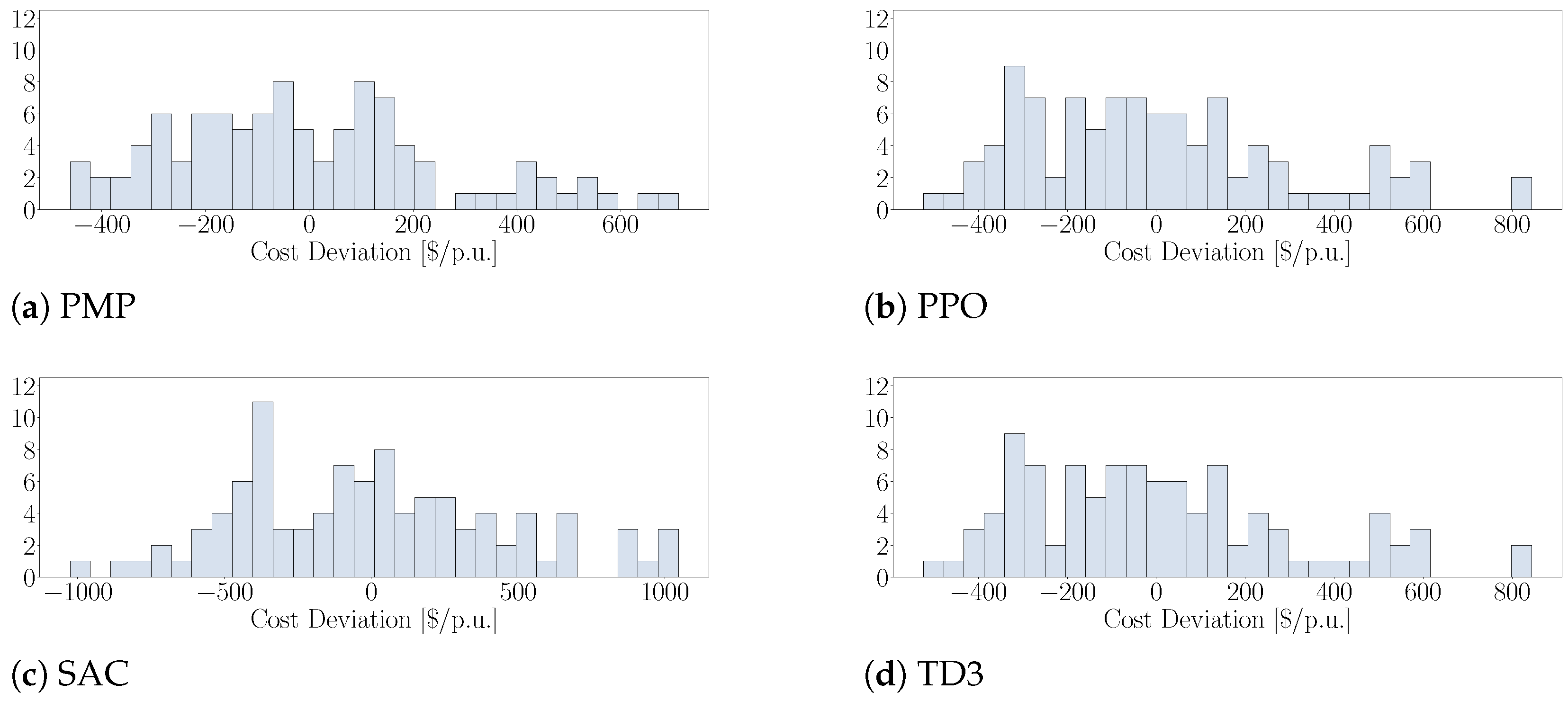The daily cost comparisons in Figure 10 and the cost deviation histograms in Figure 11 of the original paper visually corroborate these findings, showing PPO and SAC performing relatively better than TD3 but all RL methods trailing the DP benchmark by a wider margin than in the previous scenario. The cost deviations for PPO and SAC remained largely within $\pm 600$ USD/p.u. of their mean, while TD3 exhibited a very wide spread, up to $\pm 1500$ USD/p.u., confirming that its deterministic policy struggled significantly with the unpredictable dynamics of this scenario.

Figure 10 presents for each algorithm the daily cost of energy production over a test set of 100 days. The mean and variance for each algorithm are presented in Table 3.

The results in the table show few trends. (a) The mean and variance of the classical algorithm has increased. This is caused by the additional uncertainty of the dynamic model. (b) For all RL algorithms, we see improvement in the performance, which highlights their effectiveness when operating in highly uncertain environments, with stochastic transitions. (c) The PPO algorithm indeed achieves better results than TD3, which further emphasizes the effectiveness of using stochastic policies for such unpredictable model dynamics. The deviation from the mean of the daily costs of each algorithm over these 100 test days is depicted in Figure 11.

4. Discussion

The optimal control of energy storage systems in uncertain environments poses a significant challenge. Data-driven approaches, especially reinforcement learning, offer a solution by learning input signal statistics and system dynamics directly from data, eliminating the need for prior knowledge. However, this comes at a greater computational cost than traditional optimal control methods, such as stochastic dynamic programming. To understand these trade-offs, this work directly compares these two approaches. Our focus is on quantifying the performance loss incurred when the storage unit’s dynamics are uncertain and learned through a data-driven method. Thus, this analysis expands upon earlier works like [16,17], which assume complete and accurate knowledge of the energy storage device’s dynamics and full control capabilities.

Our results show several interesting trends that may help answer both questions raised in Section 2. First and foremost, we observe that if perfect knowledge of the physical model exists, one can achieve results far superior to those achieved by statistical learning. However, when comparing the results in Section 3.1 and Section 3.2, for ideal and lossy storage devices, respectively, it may be observed that the overall cost difference for the RL solution and the optimal control algorithm solution diminishes. For the ideal storage case, as indicated by Figure 3 and Table 1, the RL algorithms demonstrated significantly higher operational costs than those achieved by the optimal SP solution, with mean daily costs of $2428.24$, $1935.02$, and $2787.36$ for PPO, SAC, and TD3, respectively, compared to $711.85$ for SP—a 172% to 291% increase. In the lossy storage scenario, as may be seen from Figure 6 and Table 2, while the classical PMP solution achieved a lower mean cost of $705.82$, both PPO and TD3 achieved similar mean costs of $748.17$, corresponding to a modest increase of approximately 6%. This suggests that when uncertainty that stems from the power loss is confined to the storage devices, RL algorithms can learn the storage behavior effectively, and achieve improvement in the overall cost, although they do not possess prior knowledge about this type of loss.

Nevertheless, when the uncertainty, in the form of power loss, originates from the transmission lines, as in Section 3.3, RL performance degrades, as evidenced by the increased mean and variance. Under transmission losses, as may be viewed in Figure 9 and Table 3, RL performance degraded again, with PPO, SAC, and TD3 incurring mean daily costs of $1165.14$, $1293.96$, and $2779.89$, respectively, compared to $773.10$ for DP—indicating an increase of 51% to 260%.

This highlights the difficulty RL faces when dealing with external, system-level uncertainties that are not directly part of its training process. These findings suggest that the type of uncertainty plays an important role in determining the effectiveness of RL-based control. Generally speaking, reinforcement learning methods perform better with internal energy storage dynamics than with external, system-level uncertainties because they are designed to learn from interactions within a defined environment, such as the state of charge of a battery. The internal dynamics of the storage device, like losses from charging and discharging, are directly observable through the agent’s actions and the resulting state changes, allowing the agent to learn and adapt to them effectively, even without explicit prior knowledge. In this scenario, the uncertainty is part of the system’s core dynamics, which the RL agent is trained to handle. Conversely, external uncertainties, such as losses from a transmission grid, are often difficult to capture within the defined state–action–reward framework of the RL model. The agent’s actions may not directly influence or perceive these external factors in a way that allows for effective learning, leading to a degradation in performance.

Crucially, the dominant paradigm for RL is the Markov decision process, a mathematical framework for modeling sequential decision-making in stochastic environments. The foundational assumption of this framework is the Markov property, which posits that the current state $s_k$ encapsulates all information from the history of the process that is relevant for predicting the future. In other words, the probability of transitioning to the next state $s_{k+1}$ depends only on the current state $s_k$ and the chosen action $a_k$, not on the sequence of states and actions that preceded it. The agent’s ability to learn an effective control strategy is, therefore, fundamentally constrained by the information content of the state tuple. Any system dynamics, disturbances, or sources of uncertainty that are not captured by or directly correlated with these three variables are, from the agent’s perspective, unobservable. They manifest as unpredictable noise in the state transitions or reward signals, confounding the learning process. This intrinsic limitation of the agent’s worldview is the primary determinant of its performance across the different scenarios. Thus, these external factors are not captured in the agent’s state representation, effectively breaking the core Markov property and rendering the environment partially observable. This misalignment between the problem structure and the RL agent’s worldview is the fundamental root of the observed performance dichotomy.

The second scenario presented in the paper, which introduces a lossy storage device, provides a compelling case study in how RL can effectively manage certain types of uncertainty. In this scenario, the ideal, lossless battery model is replaced with a more realistic one. Despite this added complexity, the performance of the RL agents, particularly PPO and TD3, improves dramatically relative to the optimal control benchmark. This counterintuitive result, that adding uncertainty improved relative performance, can be explained by examining the nature of that uncertainty through the lens of the MDP. The battery losses, while complex and non-linear, are internal to the system being controlled. They are a direct, physical consequence of the agent’s actions on the state of the system. When the agent takes an action $a_k$, for example, commanding a certain power flow $\mathsf{\Delta }{E}_k$, the resulting change in the state variable $E_{s,k+1}$ is directly affected by the efficiency $\eta$. This effect is consistently observable through the state–action–reward loop. Although the agent does not have an explicit mathematical model of the function $\eta \left(P_s\left(t\right)\right)$, its model-free learning algorithm is designed precisely for such situations. Through trial and error, the agent can implicitly learn the mapping from its actions to their consequences, effectively building an internal model of the battery’s lossy behavior. In this context, the uncertainty is a stable, learnable feature of the environment’s transition dynamics. The problem, while more challenging, remains a well-posed MDP. The agent’s state representation contains the necessary information to learn the effects of its actions. The success of the RL agents in this scenario is, therefore, not an anomaly, but a confirmation of their core strength: discovering effective control policies in systems with unknown or complex dynamics without requiring an explicit, a priori model.

The third and most complex scenario, which adds transmission line losses to the lossy storage model, causes a significant degradation in RL performance. The empirical results show the performance gap, between traditional optimal control approaches to model-free approaches, widening once again. The root cause of this failure lies in the fact that the transmission loss is an external uncertainty from the perspective of the agent’s defined MDP. This creates a critical violation of the Markov property. The reward, or cost, received by the agent is no longer a function of just its current state and action. The same action from the exact same state can result in vastly different costs depending on the instantaneous value of the external load $P_L\left(t\right)$, which is not fully captured in the state representation. This transforms the problem into a partially observable Markov decision process (POMDP), where the agent must act based on incomplete information about the true state of the system. Standard model-free RL algorithms, such as those used in the paper, namely, PPO, SAC, and TD3, are not inherently designed to solve POMDPs. They operate under the assumption that the state is fully observable. When this assumption is violated, the agent cannot reliably attribute outcomes to its actions. It becomes unable to distinguish between stochasticity in the environment and the deterministic effects of unobserved state variables. This leads to a confused and inefficient learning process, resulting in a suboptimal policy that cannot effectively plan for the consequences of its actions, hence the observed performance collapse.

In all examined cases, optimal control methods outperformed RL, likely due to the presence of epistemic uncertainty, which RL struggles to handle effectively. This may have implications for robustness analysis of RL methods in energy storage applications. These findings also reveal one key limitation of reinforcement learning methods, which is that model-free methods must be retrained for each new scenario. This prevents direct transfer of the trained agent, for instance, from one household to another. Consequently, incorporating model-based elements, or at least embedding system dynamics into the training process, becomes crucial. This enables the agent to generalize more effectively, and to apply the learned knowledge across varying problems, even with differing underlying statistical patterns.

In this paper, the entire framework is built around the unique characteristics of battery energy storage systems. The optimization problems are explicitly defined by the physical constraints of an energy storage unit, the analysis progressively introduces complexities that are characteristic of real-world BESSs, and the resulting plots exhibit the optimal generation under the operation of BESSs as ancillary services. However, the insights of the comparative analysis, between optimal control and reinforcement learning methods, presented in this work, can be extended to several other applications beyond the management of a BESS. This type of research may aid in quantifying the trade-offs between performance, computational requirements, and the amount of prior knowledge each methodology demands in different contexts. Naturally, the choice of the technology for the energy storage device is crucial for the whole comparative analysis, since it is based on the specific dynamics of a BESS, and the immediate question that arises is whether this will repeat itself when simulating different types of energy storage technologies, or whether these findings were limited, for some reason, to the specific chosen MDP formulation.

5. Conclusions

In this work, we compare traditional optimal control methods with data-driven reinforcement learning approaches for managing energy storage systems under uncertainty. The results reveal a key trend: While methods based on perfect physical models are always superior, the performance gap between them and reinforcement learning narrows as specific uncertainties are added. In an ideal, lossless scenario, the RL algorithms performed very poorly, incurring significantly higher operational costs than the optimal control solution. However, when internal uncertainties like battery power loss were introduced, the RL methods’ performance improved dramatically, achieving costs only slightly higher than the optimal benchmark. This suggests that RL is effective at learning and managing uncertainties that are confined to the device it is controlling, and are observable for the agent, even without explicit prior knowledge.

Beyond BESS management, future research may consider challenges that are present in systems such as electric vehicles (EVs), microgrid management, and home energy management systems. They can benefit from the key insight of this paper, stating that reinforcement learning methods are better at handling a system’s internal uncertainties than external, system-level ones. This suggests that a model-free RL approach would be most effective when the primary challenges are internal to the system, such as managing EV battery degradation or optimizing a microgrid’s internal components and losses. However, the paper demonstrates that RL performance degrades significantly when faced with external uncertainties that are not part of the training environment. This approach allows RL agents to generalize more effectively, leading to more robust and superior performance when compared to methods that only consider internal system dynamics. Moreover, the analysis can be extended to supply chain logistics, where RL could optimize tactical decisions by learning the complex, emergent dynamics of a firm’s internal operations. For supply chains, internal uncertainty involves variability within a company’s own control, such as production line yield, machine downtime, and warehouse processing times. External uncertainty consists of major, unmodeled disruptions to the broader network.