A Network Psychometric Analysis of Math Anxiety Factors in Italian Psychology Students
Abstract
1. Introduction
- Evaluation MA, which refers to anxiety related to the assessment of one’s mathematical abilities, often in formal academic settings (such as taking a math exam or answering questions in class).
- Everyday/Social MA, triggered in daily situations where math is required, often with social implications (e.g., calculating change, splitting bills, or remembering phone numbers).
- Passive Observation MA, experienced when passively observing math-related activities without direct involvement (e.g., watching someone solve a problem or listening to a math lecture).
2. Materials and Methods
2.1. Participants
2.2. Materials
MAS-IT Scale
2.3. Data Analysis
2.3.1. Confirmatory Factor Analysis
2.3.2. Exploratory Graph Analysis
- Correlation Matrix Estimation. This step employs the cor_auto method to estimate correlations based on data type, allowing for the evaluation of correlations between all pairs of variables.
- Graphical Least Absolute Shrinkage and Selection Operator (GLASSO). The GLASSO algorithm is applied to the correlation matrix to estimate a sparse partial correlation network, retaining stronger connections while penalizing weaker ones. This approach effectively identifies the strongest connections between items, yielding a clear and interpretable network structure.
- Community Detection and Factor Estimation. This step groups items into clusters (i.e., factors) based on their network connections. These clusters represent latent constructs, where items within the same cluster exhibiting strong associations (Golino & Epskamp, 2017).
2.3.3. Correlation Between EGA and MAS-UK Factors
3. Results
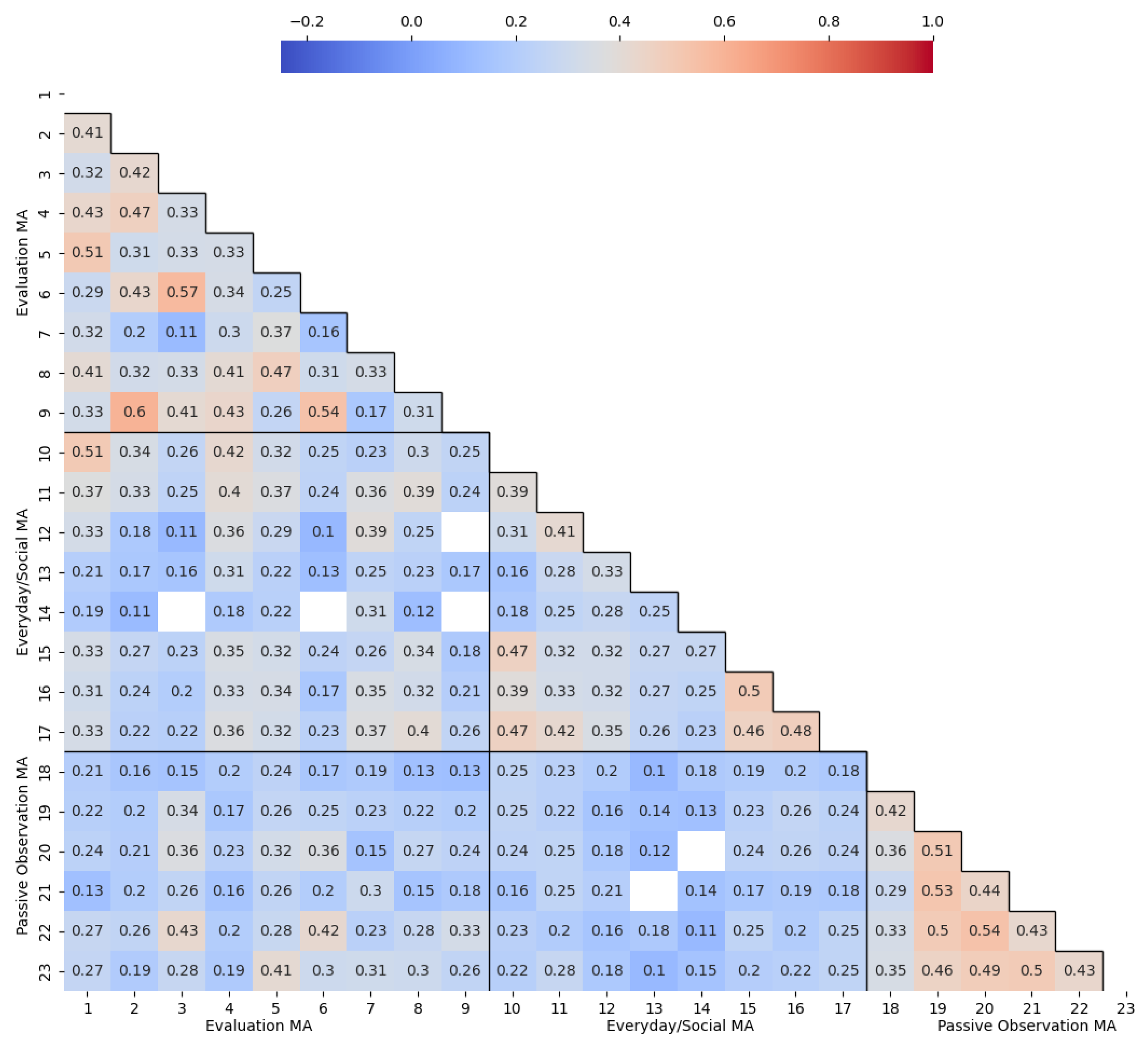
3.1. Correlational Analysis
3.2. Confirmatory Factor Analysis with the UK 3-Factor Model
3.3. Exploratory Graph Analysis
3.3.1. Network Estimation
3.3.2. Network Factors and Interpretation
3.3.3. Network Factors and Correlational Analysis
3.3.4. Redundancy Between Items
3.3.5. Unique Variable Analysis
- Items 2 and 9 (wTO = 0.249): both concerning math abilities evaluation in front of a class.
- Items 3 and 6 (wTO = 0.220): both involving a math test.
- Items 4 and 13 (wTO = 0.217): item 4 concerns a math operation in front of a class, while item 13 concerns the memorization of a phone number.
- Items 6 and 9 (wTO = 0.206): both regarding math evaluation in the class environment.
3.3.6. Interpretation of Redundant Items
3.3.7. Item Stability Analysis
3.3.8. Interpretation of Item Stability Analysis with Bootstrapping
3.3.9. Total Entropy Fit Index and Item Stability
3.4. Confirmatory Analysis of the 4-Factor Structure of MAS-IT
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Factor | Item | MAS-UK Item | MAS-IT Item |
|---|---|---|---|
| Evaluation MA | 1 | Having someone watch you multiply 12 × 23 on paper | Avere qualcuno che mi guarda moltiplicare 12 × 23 su carta |
| 2 | Being asked to write an answer on the board at the front of a maths class | Se mi viene chiesto di scrivere una risposta alla lavagna all’inizio di una lezione di matematica | |
| 3 | Taking a maths exam | Sostenere un esame di matematica | |
| 4 | Being asked to calculate £9.36 divided by four in front of several people | Se mi viene chiesto davanti a molte altre persone di calcolare EUR 9.36 diviso per 4 | |
| 5 | Calculating a series of multiplication problems on paper | Calcolare una serie di moltiplicazioni su carta | |
| 6 | Being given a surprise maths test in a class | Dover affrontare un test di matematica a sorpresa in una classe | |
| 7 | Being asked to memorize a multiplication table | Dover memorizzare una tabellina | |
| 8 | Being asked to calculate three fifths as a percentage | Se mi viene chiesto di calcolare i 3/5 di una percentuale | |
| 9 | Being asked a maths question by a teacher in front of a class | Se mi viene chiesta una domanda di matematica da un/una insegnante di fronte alla classe | |
| Evaluation MA Everyday/Social MA | 10 | Adding up a pile of change | Calcolare la somma degli spiccioli di un resto |
| 11 | Being asked to add up the number of people in a room | Se mi viene chiesto di sommare il numero di persone in una stanza | |
| 12 | Calculating how many days until a person’s birthday | Calcolare quanti giorni mancano al compleanno di una persona | |
| 13 | Being given a telephone number and having to remember it | Ricevere un numero di telefono e doverlo ricordare | |
| 14 | Working out how much time you have left before you set off to work or place of study | Calcolare quanto tempo mi rimane prima di partire per il lavoro o il luogo di studio | |
| 15 | Working out how much change a cashier should have given you in a shop after buying several items | Calcolare quanto resto dovrebbe avermi dato un cassiere in un negozio dopo aver acquistato diversi articoli | |
| 16 | Deciding how much each person should give you after you buy an object that you are all sharing the cost of | Decidere quanto ogni persona dovrebbe darmi dopo aver acquistato un oggetto di cui condividete il costo | |
| 17 | Working out how much your shopping bill comes to | Calcolare quanto sia il conto di uno scontrino | |
| Passive observation MA | 18 | Reading the word “algebra” | Leggere la parola “algebra” |
| 19 | Listening to someone talk about maths | Ascoltare qualcuno che parla di matematica | |
| 20 | Reading a maths textbook | Leggere un testo di matematica | |
| 21 | Watching someone work out an algebra problem | Guardare qualcuno risolvere un problema di algebra | |
| 22 | Sitting in a maths class | Frequentare una lezione di matematica | |
| 23 | Watching a teacher/lecturer write equations on the board | Guardare un/una insegnante scrivere equazioni alla lavagna |
| Item | Mean | St.Dev. | Median | Skewness | Kurtosis | SE |
|---|---|---|---|---|---|---|
| 1 | 2.28 | 1.24 | 2.00 | 0.61 | −0.76 | 0.07 |
| 2 | 3.30 | 1.16 | 3.00 | −0.14 | −0.91 | 0.06 |
| 3 | 3.54 | 1.02 | 4.00 | −0.30 | −0.54 | 0.06 |
| 4 | 3.00 | 1.28 | 3.00 | −0.01 | −1.09 | 0.07 |
| 5 | 1.57 | 0.84 | 1.00 | 1.57 | 2.28 | 0.05 |
| 6 | 3.77 | 1.10 | 4.00 | −0.58 | −0.50 | 0.06 |
| 7 | 1.45 | 0.85 | 1.00 | 2.15 | 4.39 | 0.05 |
| 8 | 2.25 | 1.16 | 2.00 | 0.64 | −0.53 | 0.06 |
| 9 | 3.61 | 1.16 | 4.00 | −0.43 | −0.69 | 0.06 |
| 10 | 2.14 | 1.14 | 2.00 | 0.79 | −0.26 | 0.06 |
| 11 | 1.72 | 0.92 | 1.00 | 1.06 | 0.13 | 0.05 |
| 12 | 1.56 | 0.88 | 1.00 | 1.48 | 1.41 | 0.05 |
| 13 | 2.22 | 1.11 | 2.00 | 0.74 | −0.12 | 0.06 |
| 14 | 1.65 | 0.92 | 1.00 | 1.53 | 1.98 | 0.05 |
| 15 | 1.75 | 0.95 | 1.00 | 1.23 | 0.95 | 0.05 |
| 16 | 1.69 | 0.97 | 1.00 | 1.38 | 1.25 | 0.05 |
| 17 | 1.58 | 0.85 | 1.00 | 1.58 | 2.28 | 0.05 |
| 18 | 1.29 | 0.64 | 1.00 | 2.41 | 6.12 | 0.04 |
| 19 | 1.45 | 0.75 | 1.00 | 1.90 | 3.91 | 0.04 |
| 20 | 1.73 | 0.93 | 1.00 | 1.25 | 1.04 | 0.05 |
| 21 | 1.37 | 0.73 | 1.00 | 2.19 | 4.88 | 0.04 |
| 22 | 1.71 | 0.88 | 1.00 | 1.18 | 0.86 | 0.05 |
| 23 | 1.50 | 0.78 | 1.00 | 1.70 | 2.89 | 0.04 |
| Factor | Items | Content | Stability Scores |
|---|---|---|---|
| Factor I | 1, 4, 5, 7, 8, 11, 12, 13, 14 | Evaluation of math skills in everyday and social situations | Moderate to high stability scores (0.65 ≤ S ≤ 0.93) |
| Factor II | 2, 3, 6, 9 | Math evaluation in academic settings with peers or exams | Very high stability scores (0.89 ≤ S ≤ 0.96) |
| Factor III | 10, 15, 16, 17 | Daily math for calculating change and managing cash | Lowest stability scores (S = 0.38) |
| Factor IV | 18, 19, 20, 21, 22, 23 | Correspondence to Passive Observation MAS-UK factor | Almost perfect stability score (0.98 ≤ S ≤ 1) |
| Item | Factor I | Factor II | Factor III | Factor IV |
|---|---|---|---|---|
| 1 | 0.594 | – | – | – |
| 2 | – | 0.842 | – | – |
| 3 | – | 0.801 | – | – |
| 4 | 0.738 | – | – | – |
| 5 | 0.683 | – | – | – |
| 6 | – | 0.858 | – | – |
| 7 | 0.650 | – | – | – |
| 8 | 0.539 | – | – | – |
| 9 | – | 0.850 | – | – |
| 10 | – | – | 0.739 | – |
| 11 | 0.539 | – | – | – |
| 12 | 0.515 | – | – | – |
| 13 | 0.717 | – | – | – |
| 14 | 0.650 | – | – | – |
| 15 | – | – | 0.736 | – |
| 16 | – | – | 0.737 | – |
| 17 | – | – | 0.747 | – |
| 18 | – | – | – | 0.759 |
| 19 | – | – | – | 0.743 |
| 20 | – | – | – | 0.720 |
| 21 | – | – | – | 0.774 |
| 22 | – | – | – | 0.694 |
| 23 | – | – | – | 0.720 |
References
- American Psychiatric Association. (2013). Diagnostic and statistical manual of mental disorders: Dsm-5. American Psychiatric Association. [Google Scholar]
- Ashcraft, M. H. (2002). Math anxiety: Personal, educational, and cognitive consequences. Current Directions in Psychological Science, 11(5), 181–185. [Google Scholar] [CrossRef]
- Ashcraft, M. H., & Krause, J. A. (2007). Working memory, math performance, and math anxiety. Psychonomic Bulletin and Review, 14, 243–248. [Google Scholar] [CrossRef] [PubMed]
- Blazer, C. (2011). Strategies for reducing math anxiety. ERICC BlazerResearch Services, Miami-Dade County Public Schools. [Google Scholar]
- Brown, T. A. (2015). Confirmatory factor analysis for applied research. Guilford Publications. [Google Scholar]
- Capraro, M. M., Capraro, R. M., & Henson, R. K. (2001). Measurement error of scores on the mathematics anxiety rating scale across studies. Educational and Psychological Measurement, 61, 373–386. [Google Scholar] [CrossRef]
- Caviola, S., Primi, C., Chiesi, F., & Mammarella, I. C. (2017). Psychometric properties of the Abbreviated Math Anxiety Scale (AMAS) in Italian primary school children. Learning and Individual Differences, 55, 174–182. [Google Scholar] [CrossRef]
- Christensen, A. P., Garrido, L. E., & Golino, H. (2023). Unique variable analysis: A network psychometrics method to detect local dependence. Multivariate Behavioral Research, 58(6), 1165–1182. [Google Scholar] [CrossRef] [PubMed]
- Christensen, A. P., & Golino, H. (2021). Estimating the stability of psychological dimensions via bootstrap exploratory graph analysis: A Monte Carlo simulation and tutorial. Psych, 3(3), 479–500. [Google Scholar] [CrossRef]
- Cipora, K., Santos, F. H., Kucian, K., & Dowker, A. (2022). Mathematics anxiety—Where are we and where shall we go? Annals of the New York Academy of Sciences, 1513(1), 10–20. [Google Scholar] [CrossRef]
- Cuder, A., Pellizzoni, S., Di Marco, M., Blason, C., Doz, E., Giofrè, D., & Passolunghi, M. C. (2024). The impact of math anxiety and self-efficacy in middle school STEM choices: A 3-year longitudinal study. British Journal of Educational Psychology, 94, 1091–1108. [Google Scholar] [CrossRef]
- Devine, A., Hill, F., Carey, E., & Szucs, D. (2018). Cognitive and emotional math problems largely dissociate: Prevalence of developmental dyscalculia and mathematics anxiety. Journal of Educational Psychology, 110(3), 431. [Google Scholar] [CrossRef]
- Golino, H. F., & Epskamp, S. (2017). Exploratory graph analysis: A new approach for estimating the number of dimensions in psychological research. PLoS ONE, 12, e0174035. [Google Scholar] [CrossRef]
- Guerrera, C. S., Platania, G. A., Boccaccio, F. M., Sarti, P., Varrasi, S., Colliva, C., Grasso, M., De Vivo, S., Cavallaro, D., Tascedda, F., Pirrone, C., Drago, F., Di Nuovo, S., Blom, J. M. C., Caraci, F., & Castellano, S. (2023). The dynamic interaction between symptoms and pharmacological treatment in patients with major depressive disorder: The role of network intervention analysis. BMC Psychiatry, 23(1), 885. [Google Scholar] [CrossRef] [PubMed]
- Hopko, D. R. (2003). Confirmatory factor analysis of the math anxiety rating scale–revised. Educational and Psychological Measurement, 63(2), 336–351. [Google Scholar] [CrossRef]
- Hopko, D. R., Mahadevan, R., Bare, R. L., & Hunt, M. K. (2003). The Abbreviated Math Anxiety Scale (AMAS): Construction, validity, and reliability. Assessment, 10, 178–182. [Google Scholar] [CrossRef] [PubMed]
- Hu, L., & Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling: A Multidisciplinary Journal, 6(1), 1–55. [Google Scholar] [CrossRef]
- Hunt, T. E., Clark-Carter, D., & Sheffield, D. (2011). The development and part validation of a U.K. scale for mathematics anxiety. Journal of Psychoeducational Assessment, 29, 455–466. [Google Scholar] [CrossRef]
- LeFevre, J., DeStefano, D., Coleman, B., & Shanahan, T. (2005). Mathematical cognition and working memory (pp. 361–377). Psychology Press. [Google Scholar]
- Lovibond, P. F., & Lovibond, S. H. (1995). The structure of negative emotional states: Comparison of the Depression Anxiety Stress Scales (DASS) with the beck depression and anxiety inventories. Behaviour Research and Therapy, 33, 335–343. [Google Scholar] [CrossRef]
- Luttenberger, S., Wimmer, S., & Paechter, M. (2018). Spotlight on math anxiety. Psychology Research and Behavior Management, 11, 311–322. [Google Scholar] [CrossRef]
- Maloney, E. A., & Beilock, S. L. (2012). Math anxiety: Who has it, why it develops, and how to guard against it. Trends in Cognitive Sciences, 16(8), 404–406. [Google Scholar] [CrossRef]
- Messer, W. S., Griggs, R. A., & Jackson, S. L. (1999). A national survey of undergraduate psychology degree options and major requirements. Teaching of Psychology, 26, 164–171. [Google Scholar] [CrossRef]
- Onwuegbuzie, A. J., & Wilson, V. A. (2003). Statistics anxiety: Nature, etiology, antecedents, effects, and treatments—A comprehensive review of the literature. Teaching in Higher Education, 8, 195–209. [Google Scholar] [CrossRef]
- Paechter, M., Macher, D., Martskvishvili, K., Wimmer, S., & Papousek, I. (2017). Mathematics Anxiety and statistics anxiety. Shared but also unshared components and antagonistic contributions to performance in statistics. Frontiers in Physiology, 8, 257559. [Google Scholar] [CrossRef] [PubMed]
- Papousek, I., Ruggeri, K., MacHer, D., Paechter, M., Heene, M., Weiss, E. M., Schulter, G., & Freudenthaler, H. H. (2012). Psychometric evaluation and experimental validation of the statistics anxiety rating scale. Journal of Personality Assessment, 94, 82–91. [Google Scholar] [CrossRef] [PubMed]
- Paundra, J., Hamidah, H., Anggita, K. M., Setiawati, R., & Sitepu, A. N. R. S. (2023, July 25–26). The effect of millennial and gen-Z generation disruption on decreasing buying and selling transactions using cash. The 6th International Conference on Vocational Education Applied Science and Technology (ICVEAST 2023) (pp. 548–559), Surakarta, Indonesia. [Google Scholar]
- Piccirilli, M., Lanfaloni, G. A., Buratta, L., Ciotti, B., Lepri, A., Azzarelli, C., Ilicini, S., D’Alessandro, P., & Elisei, S. (2023). Assessment of math anxiety as a potential tool to identify students at risk of poor acquisition of new math skills: Longitudinal study of grade 9 Italian students. Frontiers in Psychology, 14, 1185677. [Google Scholar] [CrossRef]
- Primi, C., Busdraghi, C., Tomasetto, C., Morsanyi, K., & Chiesi, F. (2014). Measuring math anxiety in Italian college and high school students: Validity, reliability and gender invariance of the Abbreviated Math Anxiety Scale (AMAS). Learning and Individual Differences, 34, 51–56. [Google Scholar] [CrossRef]
- Primi, C., Donati, M. A., Izzo, V. A., Guardabassi, V., O’Connor, P. A., Tomasetto, C., & Morsanyi, K. (2020). The Early Elementary School Abbreviated Math Anxiety Scale (the EES-AMAS): A new adapted version of the AMAS to measure math anxiety in young children. Frontiers in Psychology, 11, 1014. [Google Scholar] [CrossRef] [PubMed]
- Richardson, F. C., & Suinn, R. M. (1972). The mathematics anxiety rating scale: Psychometric data. Journal of Counseling Psychology, 19, 551–554. [Google Scholar] [CrossRef]
- Rosseel, Y. (2012). lavaan: An R package for structural equation modeling. Journal of Statistical Software, 48, 1–36. [Google Scholar] [CrossRef]
- Russell-Lasalandra, L. L., Christensen, A. P., & Golino, H. (2024). Generative psychometrics via AI-GENIE: Automatic item generation and validation via network-integrated evaluation. Available online: https://osf.io/preprints/psyarxiv/fgbj4_v1 (accessed on 6 April 2012). [CrossRef]
- Sarti, P., Varrasi, S., Guerrera, C. S., Platania, G. A., Furneri, G., Torre, V., Boccaccio, F. M., Rivi, V., Tascedda, S., Pirrone, C., Santagati, M., Blom, J. M. C., Castellano, S., & Caraci, F. (2025). Exploring apathy components and their relationship in cognitive decline: Insights from a network cross-sectional study. BMC Psychology, 13(1), 129. [Google Scholar] [CrossRef]
- Siew, C. S. Q., McCartney, M. J., & Vitevitch, M. S. (2019). Using network science to understand statistics anxiety among college students. Scholarship of Teaching and Learning in Psychology, 5, 75–89. [Google Scholar] [CrossRef]
- Stanghellini, F., Perinelli, E., Lombardi, L., & Stella, M. (2024). Introducing semantic loadings in factor analysis: Bridging network psychometrics and cognitive networks for understanding depression, anxiety and stress. Advances.in/Psychology, 2, 1–27. [Google Scholar] [CrossRef]
- Stella, M. (2020). Forma mentis networks reconstruct how Italian high schoolers and international STEM experts perceive teachers, students, scientists, and school. Education Sciences, 10(1), 17. [Google Scholar] [CrossRef]
- Stella, M. (2022). Network psychometrics and cognitive network science open new ways for understanding math anxiety as a complex system. Journal of Complex Networks, 10(3), cnac012. [Google Scholar] [CrossRef]
- Stella, M., & Zaytseva, A. (2020). Forma mentis networks map how nursing and engineering students enhance their mindsets about innovation and health during professional growth. PeerJ Computer Science, 6, e255. [Google Scholar] [CrossRef] [PubMed]
- Wilson, V. A. (1999, November 8–10). Mathematics anxiety in secondary school students. Annual Meeting of the Mid-South Educational Research Association, Biloxi, MS, USA. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Franchino, E.; Ciringione, L.; Canal, L.; Epifania, O.M.; Lombardi, L.; Lattanzi, G.; Stella, M. A Network Psychometric Analysis of Math Anxiety Factors in Italian Psychology Students. Psychol. Int. 2025, 7, 48. https://doi.org/10.3390/psycholint7020048
Franchino E, Ciringione L, Canal L, Epifania OM, Lombardi L, Lattanzi G, Stella M. A Network Psychometric Analysis of Math Anxiety Factors in Italian Psychology Students. Psychology International. 2025; 7(2):48. https://doi.org/10.3390/psycholint7020048
Chicago/Turabian StyleFranchino, Emma, Luciana Ciringione, Luisa Canal, Ottavia Marina Epifania, Luigi Lombardi, Gianluca Lattanzi, and Massimo Stella. 2025. "A Network Psychometric Analysis of Math Anxiety Factors in Italian Psychology Students" Psychology International 7, no. 2: 48. https://doi.org/10.3390/psycholint7020048
APA StyleFranchino, E., Ciringione, L., Canal, L., Epifania, O. M., Lombardi, L., Lattanzi, G., & Stella, M. (2025). A Network Psychometric Analysis of Math Anxiety Factors in Italian Psychology Students. Psychology International, 7(2), 48. https://doi.org/10.3390/psycholint7020048










