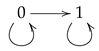1. Preliminaries on Convergence Spaces
Let X be a set. Then, denotes its powerset, denotes the set of (set-theoretic) filters on X, denotes the set of ultrafilters on X, and denotes the set of principal filters on X. Given , let and . For a filter on X, denotes the set of finer ultrafilters; we also write for .
Convergence spaces form a useful generalization of topological spaces. Namely, a
convergence on a set
X is a relation between points of
X and (set-theoretic) filters on
X, denoted by
if
(and
x is interpreted as a limit point for
in
), satisfying
for every
and
for all pairs of filters
and
on
X. The pair
is then called a
convergence space.
A map
between two convergence spaces
and
is
continuous (in symbols
) if
whenever
, where
is the image filter. Let
denote the category of convergence spaces and continuous maps. If
are two convergences on
X, we say that
is
finer than or that
is
coarser than (in symbols
) if the identity map
, that is, if
for every filter
on
X. The set of convergences on a given set is a complete lattice for this order. Moreover,
is a topological category (see [
1] for details), that is, it has all initial (and final) structures. Indeed, if
, there is the coarsest convergence
on
X making
f continuous (to
), namely
if
, and it is initial. If
for
, the supremum
provides an initial lift for the source. As a result,
has products and subspaces. In particular, if
is a convergence space and
, the
induced convergence or
subspace convergence on
A is the initial convergence
for the inclusion map
, that is,
if
.
If a convergence additionally satisfies
for every
, we say that
has finite depth (many authors include the condition (
3) in the axioms of a convergence space; here, we follow [
2]).
A convergence satisfying the stronger condition that
for every
is called a
pretopology, and
is a
pretopological space.
A subset
A of a convergence space
is
ξ-open if
and
-
closed if it is closed for limits, that is,
Let
denote the set of open subsets of
and let
. Similarly, let
denote the set of closed subsets of
. It turns out that
is a topology on
X. Moreover, a topology
on a set
X determines a convergence
on
X by
where
denotes the neighborhood filter of
x for
. In turn,
completely determines
because
, so that we do not distinguish between
and
and identify topologies with special convergences. Moreover, a convergence
on
X determines the topology
on
X, which turns out to be the finest among the topologies on
X that are coarser than
. We call it the
topological modification of and denote it as
. The map T turns out to be a concrete reflector. Hence, the category
of topological spaces and continuous maps is a concretely reflective subcategory of
. Let
denote the closure operator in
.
Just like in the topological case, we will say that a convergence space is if every singleton is closed, and Hausdorff if the limit sets have at most one element.
Consider the
principal adherence operator given by
In general,
but not conversely. In contrast to
, the principal adherence is in general non-idempotent because
need not be closed.
In view of (
4), a convergence
is a pretopology if and only if the
vicinity filter converges to
x for every
, equivalently, if it is determined by its principal adherence via
. The full subcategory
of
formed by pretopological spaces and continuous maps is concretely reflective, with the reflector
given on objects by
On the other hand, the reflector T is given by
so that
; that is, every topology is a pretopology. In fact, a pretopology is a topology if and only if the principal adherence operator is idempotent, in which case
.
We refer the reader to [
2,
3] for a systematic study of convergence spaces and their applications to topological problems. Convergence spaces turn out to form a very convenient setting not only to study purely topological problems but also for Functional Analysis, as shown convincingly in [
4,
5,
6]. The variant category of uniform convergence spaces has its own advantages in this context, as argued in [
7]. An initial promising exploration of the potential of convergence space theory in algebraic topology [
8] and complex geometry [
9] was proposed by Armando Machado in the late 1960s and 1970s, but this has not been explored much further until recently, e.g., [
10,
11,
12]. Despite this extensive body of work developing the theory of convergence spaces as an extension of classical topology, the central topological concept of connectedness has received very limited attention in the context of convergences spaces, in part because it appears at first glance to be completely reduced to the topological notion, as we shall now see.
2. Connectedness
By definition, a convergence space is connected if its only subsets that are both closed and open (clopen) are ∅ and X, equivalently if every continuous map (where carries the discrete topology) is constant.
As a result, it is plain that
is connected if and only if its topological modification
is connected so that the theory of connectedness for convergence spaces is mostly equivalent to the classical one for topological spaces. However, some care is needed for subspaces, as well as for products. We say that a subset
A of a convergence space
is
connected if it is as a subspace, that is, if
is connected. For the reason already outlined, this is equivalent to
being connected, but the subtlety lies in the fact that while
the reverse inequality does not need to hold, e.g., Example V.4.35 in [
2].
Note also that if
and
are convergences on
X with
, then every
-connected subset of
X is also
-connected. In particular, every
-connected subset is also
-connected, but the converse is not true, e.g., Example XII.1.30 in [
2].
Remark 1. Similarly, T does not commute with products, so some care is needed in extending results on the connectedness of products from topological to convergence spaces, but the fact that a product space is connected if and only if each factor is connected remains valid for convergence spaces. Indeed, though Theorem XII.1.31 in [2] is formulated for topological spaces, its proof can easily be adapted to extend the result to arbitrary convergence spaces. See, e.g., Theorem 6.2.3 in [13] for a complete proof. Proposition 1. A subset A of a convergence space is ξ-connected if and only if it is -connected.
Proof. Since
, every
-connected subset is also
-connected. Conversely, if
A is
-connected, that is,
is connected, then so is
because
by Corollary XIV.3.9 in [
2]. If
A is connected for
, it is
-connected, equivalently,
-connected, that is,
-connected. □
In other words, in studying connected subsets of a convergence space, we can restrict ourselves to pretopologies.
The extension to convergence spaces of the topological fact that if is connected and , then B is also connected is:
Proposition 2 ([
2] Prop. XII.1.25)
. If A is a ξ-connected subset of a convergence space and , then B is also ξ-connected. The book [
2] is, however, silent on whether this result would extend if
is replaced by
, even if
is not topological. The first observation is that
Proposition 3. If S is a ξ-connected subset of a convergence space , then is connected.
Proof. If
S is
-connected, it is also
-connected, and thus, so is
by the usual topological result. By Proposition V.4.36 in [
2] or by Lemma 2 below, for
, we have
. Hence,
is
-connected, equivalently,
-connected. □
Hence, if
A is connected and
we can conclude that
B is connected when
B is closed (because
) or when
, but is it always true? We show that the answer is “no” in the general case, and explore when it is “yes”.
We will use the fact that the classical result whereby the union of a family of connected subspaces with a non-empty intersection is again connected extends from topological to convergence spaces:
Proposition 4 ([
2] Corollary XX.1.22)
. If is a collection of connected subspaces of a convergence space , and , then is also a connected subspace. We can refine Proposition 3. To this end, recall that we can define iterations of the adherence of a set by transfinite induction by
and if
has been defined for all
, then
Of course,
for every ordinal
, and there is equality for sufficiently large
. The smallest ordinal
such that
for every subset
A of
is called the
topological defect of . Hence, pretopologies of topological defect 1 are topologies.
Proposition 5. If A is a connected subspace of a convergence space , then is connected for every ordinal α.
Proof. This is clear for , so assume that We proceed with transfinite induction. The case of is clear because A is connected. Suppose that is connected for all . In view of Proposition 4, is connected, and thus, is connected by Proposition 2. □
In view of Proposition 1, we have:
Proposition 6. If is a convergence space with topological defect 1, equivalently, , then ξ-connected subsets and -connected subsets coincide.
To illustrate this proposition, recall from [
14] that a topological space
is
of accessibility, or is an
accessibility space if for each
and every
with
there is a closed subset
F of
X with
and
.
Following [
15], we say that a pretopology
is
topologically maximal within the class of pretopologies if
It is proved in [
15,
16] that a topology is of accessibility if and only if it is topologically maximal within the class of pretopologies. Hence, if
is a convergence for which
is an accessibility space, then
by maximality, so that Proposition 6 applies to the effect that
-connected and
-connected subsets coincide.
To give examples of accessibility spaces, recall that a topological space
X is
Fréchet–Urysohn if whenever
for
and
, there is a sequence
on
A converging to
x. Fréchet–Urysohn spaces in which sequences have unique limits are of accessibility, e.g., [
14]. Hence,
Corollary 1. If is a convergence space for which is a Hausdorff Fréchet–Urysohn topology, then ξ-connected and -connected subsets coincide.
In this paper, we explore when -connected and -connected subsets do or do not coincide.
3. Convergences on Finite Sets and Directed Graphs
Note that finitely deep convergences and pretopologies coincide on finite sets. Moreover, they are entirely determined by the convergence of principal ultrafilters. Denoting with an arrow
if
, a pretopology on a finite set induces a directed graph (digraph) on
X, with a loop at each point, because of (
1).
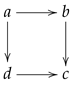
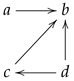
In this paper, we will use graphs to represent certain examples of convergences on finite sets. We will omit the loops at each point in order not to overburden pictures, because they are implicit. Thus, for example, the usual Sierpinski topological space would be denoted by
and not
Note also that the basic example
corresponds to the pretopology
given by
,
and
and is not topological: an open set
O around
c must also contain
b because
; hence,
. By the same token, it must also contain
a, so that
. In particular,
but
. In fact,
is given by the graph
and more generally, if
is a pretopology on a finite set, the digraph for
is the transitive closure of the digraph for
.
In a directed graph, we say a finite sequence of vertices is a path from a to b if , , and for every , that is, in the convergence space interpretation, for every . We say that a path from a to b is in A if for all . In a (non-directed) graph, we may say “a path between a and b” instead. A graph is connected if there is a path between any two vertices. Recall that a directed graph is weakly connected if its underlying (non-directed) graph is connected, and connected if there is a directed path between every pair of vertices.
Proposition 7. A finite convergence space is connected if and only if its underlying digraph is weakly connected.
Proof. Suppose the underlying digraph is not weakly connected, that is, there are a and b with no path from a to b in the underlying (non-directed) graph. Then, the graph-connected component of a is closed and open in the convergence and does not contain b, so that the convergence is not connected. Suppose conversely that the convergence is not connected, so that there are two non-empty disjoint clopen subsets. Pick a and b in these two disjoint sets. There is no path between a and b in the underlying undirected graph, and thus, the underlying digraph is not weakly connected. □
Note that this means that connectedness only depends on the underlying non-directed graph. Hence, a finite convergence space
is connected if and only if its
reciprocal modification , given by
which has the same underlying (non-directed) graph, is connected.
4. Reciprocal Modification and Connectedness
The observation made on finite spaces that connectedness only depends on the reciprocal modification can be extended to general spaces. First, let us extend the definition of
r, as a finite convergence of finite depth only needs to be defined on principal ultrafilters, but
needs to be defined for general filters on an infinite
X. Given a convergence
on
X, its
reciprocal modification is defined by
Proposition 8. The reciprocal modification r is a concrete reflector, which commutes with subspaces and for every convergence space , ξ-clopen and -clopen subsets of X coincide.
Proof. The modification
r is order-preserving (
), contractive (
), and idempotent (
); hence, it is a projector in the sense of [
2]. Moreover, if
and
, then
if
is not a principal ultrafilter. If it is, say
, then
or
. Hence,
or
, so that
. Hence,
r is also a functor, and thus a reflector. In particular, if
, then
, and we only need to verify the reverse inequality. Suppose
, where
. If
is not principal, then
. Otherwise,
, where
and
or
, so that
.
As , , so that every -clopen subset is also -clopen. Let U be a non-empty -clopen subset of X. To see that U is -open, let . If , , and thus, because U is -open. Otherwise, and there is , that is, either and , or and , that is, . Hence, U is -open. To see that U is -closed, let and . If , . Otherwise, for some and either or and because U is -open, so that . Hence, U is -closed. □
Corollary 2. A subset A of a convergence space is ξ-connected if and only if it is -connected.
Proof. As , A is -connected whenever it is -connected. Conversely, assume that A is not -connected, that is, there is a non-empty proper -clopen subset C of A. In view of Proposition 8, C is also -clopen and ; hence, A is not -connected. □
Consider the dual Alexandroff pretopologies
and
associated with a convergence
on
X and defined by
and
respectively. Note that
if and only if
, and thus, a subset of
X is
-open if and only if it is
-closed. Of course, if
is
, then both
and
are discrete.
Proposition 9. If is a convergence space and , thenand more generally,for every ordinal α. In particular, Proof. As , , and if , then there is , so that . Hence, .
Conversely, if , there is a filter with and . If , . Otherwise, there is with and , so that either or and .
Assume that
for every
. Then,
□
5. Enclosing Sets
Let us say that a subset S of a convergence space encloses a connected subspace A if B is connected whenever .
Proposition 2 states that the adherence of a connected set encloses that set. In view of Corollary 2 and Proposition 9, so does its -adherence, which is the union of its -adherence and its -adherence. It turns out to be the largest possible enclosing set.
Lemma 1. Let A be a non-empty connected subset of a convergence space . Then, encloses A if and only if is connected whenever .
Proof. ⟹ is obvious, using the enclosing property with .
⟸: Let . Consider the family of connected subsets of X. As for every , we conclude from Proposition 4 that is also connected. □
As a result of Lemma 1, given a non-empty connected set
A, the
enclosure of A defined by
is the largest (for inclusion) subset of
X that encloses
A, so that
Theorem 1. If A is a non-empty connected subset of a convergence space , then Proof. By Proposition 2 and Corollary 2, .
Suppose and . Then is not connected. Indeed, A is closed in and is also open for . Hence, . □
Remark 2. As a principal adherence operator, is additive (commutes with finite unions), but it may fail to be idempotent. This is easily seen in the case, where . For instance, we can pick a standard non-topological Hausdorff pretopology like the Féron-cross pretopology of Example V.6.1 in [2]. This pretopology on is given by the vicinity filters , where . In that example, the set is connected; , and is closed.
Corollary 3. If is a convergence space and A is a non-empty connected subset, then . In particular, encloses A if and only if .
Let us say that a convergence space has the sandwich property if encloses A for every connected subset A of X. Note that for a convergence space the functorial condition that is equivalent to the fact that for all subsets A of X, so that, in view of Corollary 3, every convergence satisfying this condition also has the sandwich property, but this condition is not necessary for the sandwich property.
Example 1 (A
convergence with the sandwich property for which
).
The usual bisequence pretopology (see, e.g., Example V.4.6 in [2]) is non-topological, and hence satisfies , and it is (in fact, Hausdorff). Its only non-empty connected subsets are the singletons, which are closed, so that it has the sandwich property. Let us describe this example more explicitly for future use: on , consider the pretopology ξ in which each is isolated, that is, , and for every , and . On the other hand, is necessary in Corollary 3:
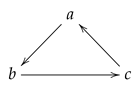
Example 2 (A convergence space with the sandwich property and a connected subset with non-closed adherence)
. Let us consider a triangular directed graph, interpreted as a pretopology. Namely, consider with the pretopology determined by , and .It can easily be seen that every subset is connected (observe that is the antidiscrete topology!); hence, this space has the sandwich property. However, while .
6. T-Subspaces
Let us call a subset
A of a convergence space
a T-
subspace if
. In view of (
5), this is equivalent to
that is, every
-closed set is
-closed. In other words,
A is a T-subspace if and only if
for every subset
B of
A.
In view of the discussion following Proposition 6, the following is clear.
Proposition 10. If is a convergence space and is a T-subspace, then A is ξ-connected if and only if it is -connected.
Here are two prototypic examples of a subset that fails to be a T-subspace:
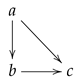
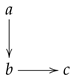
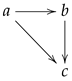
Example 3 (A non-T-subspace (finite example))
. Let with the "line" pretopology given by , and , that is, , , and .Consider the subset . Its subset is -closed but , as the only ξ-open set containing c is X, so that is not -closed. Hence, A is not a T-subspace.
Example 4 (a non-T-subspace (infinite Hausdorff example)). Consider the standard bisequence pretopology of Example 1 and its subset . Note that its subset is -closed but not -closed for , so that A is not a T-subspace.
These two basic examples illustrate the following clear fact.
Proposition 11. If is a convergence space, and , then is not a T-subspace.
Proof. Indeed, if , then S is -closed but not -closed as . □
Corollary 4. If is a convergence space, the following are equivalent:
- (1)
;
- (2)
ξ has topological defect 1;
- (3)
Every subset of X is a T-subspace.
Proof. By definition,
, and we have seen that
implies
because
by Corollary XIV.3.9 in [
2]. Finally,
by Proposition 11 as
for every
if all subsets are T-subspaces. □
Singletons are always T-subspaces because there is only one convergence on a singleton.
Remark 3. Note that a union of two T-subspaces may fail to be a T-subspace. For instance, the two singletons and in Example 3 are T-subspaces but is not. Similarly, the complement of a T-subspace may fail to be a T-subspace. For instance, The singleton in Example 3 is a T-subspace, but its complement is not. Moreover, the intersection of two T-subspaces may fail to be a T-subspace, as the example below illustrates.
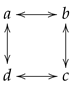
Example 5 (The intersection of two T-subspaces may fail to be a T-subspace)
. Consider the pretopology on given by , , and :The subsets and are T-subspaces as is given byand similarly for B; however, is not a T-subspace as is the discrete topology, while is an homeomorphic copy of the Sierpinski topology Lemma 2. A subset of a convergence space that is either closed or open is a T-subspace.
Proof. Let
, where
is a convergence space. To show that
A is a T-subspace, we show (
9).
Suppose A is closed and is -closed, and let with and . As A is closed, ; hence, , and thus, . Therefore, C is a -closed subset of A.
Suppose A is open and is -open, that is, if and , then . Now, if and , then and because A is open; hence, , and U is -open. □
Remark 4. Note that we can modify the pretopology of Example 5 to ensure that the sets A and B are still T-subspaces with a non-T intersection, but that they are neither open nor closed (nor singletons), by taking the reciprocal modification: Hence, there are non-singleton T-subspaces that are neither closed nor open, even when .
In the finite case, T-subspaces find a somewhat more concrete characterization than (
10).
Proposition 12. Let be a finite convergence space. Then is a T-subspace if and only if for every , if there is a path from a to b, there is also a path from a to b in A.
Proof. Suppose A is not a T-subspace, that is, . In other words, there is that is -closed but not -closed, so that there is with . In other words, there is a path from b to a. Because B is -closed, there is no such path in A. Conversely, suppose that A is a T-subspace and that there is a path from a to b where . Hence, and , so that . Therefore, there is a path from a to b in A. □
7. Sandwiched Sets
In a convergence space without the sandwich property, it makes sense to study the connectedness of sandwiched subsets, where
B is referred to as
sandwiched if there is a connected subspace
A with
. We may then say that
B is
sandwiched by A. Note that if
B is sandwiched by
A, then
is connected by Proposition 3. Moreover, since
A is
-connected, it is also
-connected; hence, every set between
A and its closure, in particular
B, is
-connected by the standard topological result. In other words, every sandwiched set is
-connected but may fail to be
-connected (as there are spaces without the sandwich property). Since a convergence space is connected if and only if its topological modification is connected, a
-connected T-subspace of a convergence space
is also
-connected. In fact, we have
Though -connected subsets and -connected subsets coincide, there are -sandwiched sets that are not -sandwiched and -connected sets that are not -connected, as we shall see in Example 6 below, so that the one-directional vertical arrows cannot be reversed.
On the other hand, all three notions in the first row coincide among T-subspaces (and in the second row for T-subspaces for ), but no horizontal arrow can be reversed in general. Indeed, we have seen that there are sandwiched sets that are not -connected. Moreover, we may have a -connected set that is not sandwiched.
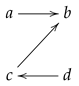
Example 6 (A
-connected set that is not sandwiched)
. Consider the pretopology on given by , , , and :Then is -connected, as is given bybut it is not sandwiched, as the only ξ-connected subsets of A are and , which is ξ-closed. Note also that is the antidiscrete topology, so every subset is -connected and every non-empty subset is -sandwiched because the -closure of a singleton is X. However, is not -connected, and A is not ξ-sandwiched.
We can summarize by the following proposition.
Proposition 13. Let be a convergence space.
- (1)
Every ξ-connected set is sandwiched.
- (2)
Every sandwiched set is -connected.
- (3)
A -connected (in particular, sandwiched) T-subspace is ξ-connected.
- (4)
There are sandwiched sets that are not ξ-connected and -connected subsets that are not sandwiched.
- (5)
If for some ordinal α and ξ-connected set A, then B is ξ-connected.
In particular, every iterated adherence of a connected set is a connected sandwiched set.
8. Conclusions
Though the concept of connectedness has been somewhat ignored in the context of convergence spaces because it appears at first glance to be equivalent to the classical topological notion, it turns out that new interesting phenomena appear when connectedness of subspaces is considered. Interestingly, they can be illustrated even with finite convergence spaces, that is, on graphs.
Key new results include
The fact that connectedness of a subset is equivalent for a convergence or for its reciprocal modification (Corollary 2), and the description of the adherence and closure in this modification (Proposition 9);
The fact that the adherence in the reciprocal modification is the largest enclosing set of a connected subset of a convergence space (Theorem 1);
The introduction of the notion of T-subspace (
Section 6), useful in the context of connectedness but also more broadly, and that there are non-singleton T-subspaces that are neither closed nor open;
The illustration that -connected, -sandwiched, and -connected are truly different notions and how they relate (Proposition 13).