Bornological Approach Nearness

Abstract

We introduce the notion of bornological approach nearness as a unified extension of various classical nearness structures. By redefining completeness within this framework, we establish a generalized version of the Niemytzki–Tychonoff theorem. Our results not only extend known compactness criteria in nearness spaces but also offer a new perspective that incorporates boundedness and bornological methods in the theory of approach spaces.

1. Introduction

The bornological approach to nearness provides a high-level framework that enables the analysis of nearness-like concepts from the perspective of boundedness rather than traditional open sets. This shift in viewpoint has proven especially useful in the study of non-normable structures and generalizations of topological and uniform spaces. Over the years, several classical frameworks have been introduced in this context, including metric spaces, proximity spaces, contiguity spaces, uniform spaces, merotopic spaces, pseudonearness spaces, b-uniform spaces, supertopological spaces, approach spaces, and approach nearness spaces. Each of these models offers a different perspective on the concept of “closeness” or “nearness” in mathematical structures. In particular, near sets in the sense of Peters [1] provide a formal basis for observation, comparison, and classification of perceptual granules in information science. The importance of the near set theory from a perceptual standpoint was highlighted in [1], motivated by applications in image analysis and inspired by the way humans perceive the nearness of physical objects. In essence, the central concern of near set theory is to discover relations between multiple samples based on the degree of similarity or closeness of their feature descriptions. A bornological nearness space, which quantifies nearness among collections of bounded sets, presents a potentially more robust framework for such investigations. This makes the bornological viewpoint particularly attractive in the context of perceptual data analysis, where boundedness plays a fundamental role. Another important direction in the generalization of nearness concepts is the study of generalized approach spaces, particularly those valued in a quantale [2]. In this setting, the notion of potential isomorphisms becomes relevant. It has been shown that the category of generalized approach spaces and injective maps can be encoded using higher-order structures. An alternative approach involves the use of order structures, which are always relative. Two structures are said to be potentially isomorphic if they become isomorphic in some larger model of set theory. This notion is important because sometimes non-isomorphic structures only appear different due to their particular representations, not due to any intrinsic structural difference. A comprehensive study of quantale-valued generalizations of approach spaces can be found in [3]. Closer to classical topological concerns is the concept of supported approach spaces [4]. These spaces are defined as pairs $(X,\delta )$, where X is a set and $\delta :X\times Z^X⟶[0,\infty ]$ is a distance function satisfying specific axioms. Approach spaces [5] serve as a simultaneous generalization of quasi-metric spaces and topological spaces. The category of topological spaces with continuous maps and the category of quasi-metric spaces with non-expansive maps can be both embedded into the category of approach spaces. Each approach space has a quasi-metric and a topological coreflection, but different approach spaces may share the same coreflections. When the coreflections uniquely determine the approach space, it is referred to as supported. Many examples of supported approach spaces appear in the compact case, where contraction mappings play a key role [4]. Furthermore, the notion of completeness in nearness spaces has been explored via various generalizations of Cauchy sequences. For instance, Herrlich [6] used clusters for completing nearness spaces; Carlson [7] employed near-ultrafilters; Herrlich and Bentley [8] introduced bunches for the completion of merotopical spaces (a generalization of nearness spaces); and Leseberg and Vaziry [9] developed the concept of b-completeness in pseudonear spaces via neartapes. In classical analysis, a metric space is compact if and only if it is complete and totally bounded. Carlson extended this result, along with the Niemytzki–Tychonoff theorem, to the setting of nearness spaces using ultrafilter completeness [10]. These generalizations laid the groundwork for further development in approach nearness spaces. In the present study, we aim to build upon these foundations by introducing a new and convenient notion of completeness and by presenting an extended version of the Niemytzki–Tychonoff theorem within the framework of bornological approach nearness spaces.

2. Preliminary Material (PM)

Definition 1. 

A bornology on a set X is a non-empty subset ${\mathcal{B}}^X\subset \underline{P}X$ which possesses the following properties:

(b1) 

$B_1\subset B\in {\mathcal{B}}^X$ implies $B_1\in {\mathcal{B}}^X$;

(b2) 

$B_1,B_2\in {\mathcal{B}}^X$ implying $B_1\cup B_2\in {\mathcal{B}}^X$;

(b3) 

$x\in X$ implies $\left\{x\right\}\in {\mathcal{B}}^X$.

Then, the pair $(X,{\mathcal{B}}^X)$ is called a bornological space [11].

Definition 2. 

An approach bornology (in short apb) on a set X consists of a pair $({\mathcal{B}}^X,\delta )$, where ${\mathcal{B}}^X$ is a bornology on X and $\delta :{\mathcal{B}}^X⟶[0,\infty ]$ is a distance function satisfying the following properties:

(apb1) 

$B\in {\mathcal{B}}^X$ implies $c{l}_{\delta }\left(B\right)\in {\mathcal{B}}^X$, where $c{l}_{\delta }\left(B\right):=\{x\in X:\delta (x,B)=0\}$;

(apb2) 

$x\in X$ and $B\in {\mathcal{B}}^X$ implying $\delta (x,B)\le \delta (x,c{l}_{\delta }\left(B\right))$;

(apb3) 

$x\in X$ implies $\delta (x,\varnothing )=\infty$;

(apb4) 

$x\in X$ implies $\delta (x,\{x\left\}\right)=0$;

(apb5) 

$x\in X$ and $B_1,B_2\in {\mathcal{B}}^X$ implying $\delta (x,B_1\cup B_2)=min\{\delta (x,B_1),\delta (x,B_2)\}$.

• For an approach bornology $({\mathcal{B}}^X,\delta )$, the triple $(X,{\mathcal{B}}^X,\delta )$ is said to be an approach bornological space (in short apb-space), and we denote by APB the corresponding class of apb-spaces.
• For apb-spaces $(X,{\mathcal{B}}^X,{\delta }_X)$ and $(Y,{\mathcal{B}}^Y,{\delta }_Y)$, a function $f:X⟶Y$ is said to be a bb-contraction (in short bbc-map), provided that f is bounded and satisfies the following conditions: $B\in {\mathcal{B}}^Y$ implies $f^{-1}\left[B\right]\in {\mathcal{B}}^X$, and for any $x\in X$ and $B\in {\mathcal{B}}^X$, the inequality ${\delta }_Y(f\left(x\right),f\left[B\right])\le {\delta }_X(x,B)$ holds. By APB², we denote the category whose object class is APB and whose morphisms are the bbc-maps. In this context, we note that bornologies, approach distances, as well as generalized Kuratowski closure operators have a corresponding counterpart in APB [12].

Definition 3. 

An approach distance is a function $\delta :X\times \underline{P}X⟶[0,\infty ]$ such that for any $A,B\subset X$ and $x\in X$, the following conditions are satisfied:

(D1) 

$\delta (x,\{x\left\}\right)=0$;

(D2) 

$\delta (x,\varnothing )=\infty$;

(D3) 

$\delta (x,A\cup B)=min\left\{\delta \right(x,A),\delta (x,B\left)\right\}$;

(D4) 

$\delta (x,A)\le \delta (x,B)+sup\left\{\delta \right(b,A):b\in B\}$.

The pair $(X,\delta )$ is called an approach space [5].

Definition 4. 

A function $v:{\underline{P}}^{2}X⟶[0,\infty ]$ is called an approach nearness on X if for any $\mathcal{A},\mathcal{B}\in {\underline{P}}^{2}X$, the following conditions are satisfied:

(AN1) 

$\mathcal{A}\ll \mathcal{B}$ implies $v\left(\mathcal{A}\right)\le v\left(\mathcal{B}\right)$;

(AN2) 

$\cap \mathcal{A}\ne \varnothing$ implies $v\left(\mathcal{A}\right)=0$;

(AN3) 

$\varnothing \in \mathcal{A}$ implies $v\left(\mathcal{A}\right)=\infty$;

(AN4) 

$v(\mathcal{A}\vee \mathcal{B})\ge min\left\{v\right(\mathcal{A}),v(\mathcal{B}\left)\right\}$;

(AN5) 

$v\left(\{c{l}_v\left(A\right):A\in \mathcal{A}\}\right)\ge v\left(\mathcal{A}\right)$, where $c{l}_v\left(A\right):=\{x\in X:v(\left\{x\right\},A\})=0$.

• The pair $(X,v)$ is called an approach nearness space [10].
• For any approach nearness spaces $(X,v)$, $(Y,w)$, a map $f:X⟶Y$ is called a contraction if $w\left(f\mathcal{A}\right)\le v\left(\mathcal{A}\right)$ for all $\mathcal{A}\in {\underline{P}}^{2}X$. ANEAR denotes the category of approach nearness spaces and contractions.

Definition 5. 

A pair $({\mathcal{B}}^X,h)$, consisting of a bornology ${\mathcal{B}}^X$ and a hull-operator $h:{\mathcal{B}}^X⟶\underline{P}X$, is called a b-topology on X, and the triple $(X,{\mathcal{B}}^X,h)$ is a b-topological space provided that h satisfies the following conditions:

(h1) 

$h(\varnothing )=\varnothing$;

(h2) 

$B\in {\mathcal{B}}^X$ implies $h\left(B\right)\in {\mathcal{B}}^X$;

(h3) 

$B_1\subset B\in {\mathcal{B}}^X$ implies $h\left(B_1\right)\subset h\left(B\right)$;

(h4) 

$x\in X$ implies $x\in h\left(\right\{x\left\}\right)$;

(h5) 

$B_1,B_2\in {\mathcal{B}}^X$ implying $h(B_1\cup B_2)\subset h\left(B_1\right)\cup h\left(B_2\right)$;

(h6) 

$B\in {\mathcal{B}}^X$, implies $h\left(h\right(B\left)\right)\subset h\left(B\right)$ [9].

For b-topological spaces $(X,{\mathcal{B}}^X,h_X)$ and $(Y,{\mathcal{B}}^Y,h_Y)$, a function $f:X⟶Y$ is called a bi-bounded continuous map (in short bic-map) provided that it is bi-bounded and fulfills the following condition (c), i.e.,

(c) 

$B\in {\mathcal{B}}^X$ implies $f\left[h_X\left(B\right)\right]\subset h_Y\left(f\left[B\right]\right)$.

By b-TOP, we denote the category whose objects are the b-topological spaces and whose morphisms are the bic-maps.

Definition 6. 

A pair $({\mathcal{B}}^X,N)$, consisting of a bornology ${\mathcal{B}}^X$ and a nearoperator $N:{\mathcal{B}}^X⟶\underline{P}{\underline{P}}^{2}X$ with ${\mathcal{B}}^X\notin N\left(B\right)\ne \varnothing$ for any $B\in {\mathcal{B}}^X$, is called pseudonearness, and the triple $(X,{\mathcal{B}}^X,N)$ is called the pseudonearness space (in short psn-space) provided that the following axioms are valid:

(psn1) 

$B\in {\mathcal{B}}^X$ and ${\mathcal{S}}_1\ll \mathcal{S}\in N\left(B\right)$ implying ${\mathcal{S}}_1\in N\left(B\right)$;

(psn2) 

$B\in {\mathcal{B}}^X\setminus \{\varnothing \}$ and $\mathcal{S}\in N\left(B\right)$ implying $\left\{B\right\}\cup \mathcal{S}\in \cap \{N\left(F\right):F\in (\mathcal{S}\cap {\mathcal{B}}^X)\cup \left\{B\right\}\}$;

(psn3) 

$B\in {\mathcal{B}}^X$ and ${\mathcal{B}}^X\cap \mathcal{S}\in N\left(B\right)$, $\mathcal{S}\subset \underline{P}X$ implying $\mathcal{S}\in N\left(B\right)$;

(psn4) 

$B\in {\mathcal{B}}^X$ and ${\mathcal{S}}_1,{\mathcal{S}}_2\notin N\left(B\right)$ implying ${\mathcal{S}}_1\vee {\mathcal{S}}_2\notin N\left(B\right)$, where ${\mathcal{S}}_1\vee {\mathcal{S}}_2:=\{F_1\cup F_2:F_1\in {\mathcal{S}}_1,F_2\in {\mathcal{S}}_2\}$;

(psn5) 

$\mathcal{S}\in N(\varnothing )$ implies $\mathcal{S}=\varnothing$;

(psn6) 

$x\in X$ implies $\left\{\right\{x\left\}\right\}\in N\left(\right\{x\left\}\right)$;

(psn7) 

$B\in {\mathcal{B}}^X$ implies $c{l}_N\left(B\right)\in {\mathcal{B}}^X$, where $c{l}_N\left(B\right):=\{x\in X:\left\{B\right\}\in N\left(\left\{x\right\}\right)\}$;

(psn8) 

$B\in {\mathcal{B}}^X$ and $\mathcal{S}\notin N\left(B\right)$ implying $\{c{l}_N\left(F\right):F\in \mathcal{S}\}\notin N\left(B\right)$ [9].

For psn-spaces $(X,{\mathcal{B}}^X,N)$ and $(Y,{\mathcal{B}}^Y,M)$, a function $f:X⟶Y$ is called a binear-map (in short bin-map) provided that it satisfies the following conditions:

(b) 

$f:{\mathcal{B}}^X⟶{\mathcal{B}}^Y$ is bounded;

(i) 

$D\in {\mathcal{B}}^Y$ implies $f^{-1}\left[D\right]\in {\mathcal{B}}^X$;

(n) 

$B\in {\mathcal{B}}^X\setminus \{\varnothing \}$ and $\mathcal{S}\in N\left(B\right)$ imply $f\mathcal{S}\in M\left(f\right[B\left]\right)$.

By PSN, we denote the category of psn-spaces and bin-maps.

3. Bornological Approach Nearness

The striking similarities in the concepts of approach nearness, b-topology, bornology, approach bornology, and pseudonearness [PM], respectively, lead us now to consider the following useful explanations:

Definition 7. 

For a set X, let ${\mathcal{B}}^X$ be a bornology. A pair $({\mathcal{B}}^X,v)$, where $v:\underline{P}{\mathcal{B}}^X⟶[0,\infty ]$ denotes a function, is said to be a bornological approach nearness (in short b-apnearness), provided that the following conditions are satisfied:

(b-apn1) 

$B\in {\mathcal{B}}^X$ implies $c{l}_v\left(B\right)\in {\mathcal{B}}^X$, where $c{l}_v\left(B\right):=\{x\in X:v\left(\{\left\{x\right\},B\}\right)=0)\}$;

(b-apn2) 

${\mathcal{A}}_1$, $\mathcal{A}\in \underline{P}{\mathcal{B}}^X$ and ${\mathcal{A}}_1\ll \mathcal{A}$, implying that $v\left({\mathcal{A}}_1\right)\le v\left(\mathcal{A}\right)$, where ${\mathcal{A}}_1\ll {\mathcal{A}}_2\iff \forall A_1\in {\mathcal{A}}_1\exists A\in \mathcal{A},A_1\supset A$;

(b-apn3) 

$v\left({\mathcal{B}}^X\right)=\infty$;

(b-apn4) 

$x\in X$ implies $v\left(\right\{\left\{x\right\}\left\}\right)=0$;

(b-apn5) 

${\mathcal{A}}_1$, ${\mathcal{A}}_2\in \underline{P}{\mathcal{B}}^X$, implying $v({\mathcal{A}}_1\vee {\mathcal{A}}_2)\ge min\{v\left({\mathcal{A}}_1\right),v\left({\mathcal{A}}_2\right)\}$, where ${\mathcal{A}}_1\vee {\mathcal{A}}_2:=\{A_1\cup A_2:A_1\in {\mathcal{A}}_1,A_2\in {\mathcal{A}}_2\}$;

(b-apn6) 

$\mathcal{A}\in \underline{P}{\mathcal{B}}^X$ implies $v\left(\mathcal{A}\right)\le v\left(\{c{l}_v\left(A\right):A\in \mathcal{A}\}\right)$.

The triple $(X,{\mathcal{B}}^X,v)$ is called a bornological approach nearness space (in short b-apnear space). For b-apnear spaces $(X,{\mathcal{B}}^X,v),(Y,{\mathcal{B}}^Y,w)$, a function $f:X⟶Y$ is called b-apnear contraction (in short bac-map) provided that it is

(bac1) 

bounded by satisfying $\{f\left[B\right]:B\in {\mathcal{B}}^X\}=:f\mathcal{A}\subset {\mathcal{B}}^Y$;

(bac2) 

rebounded by satisfying $D\in {\mathcal{B}}^Y$, which implies that $f^{-1}\left[D\right]\in {\mathcal{B}}^X$;

(bac3) 

$\mathcal{A}\in \underline{P}{\mathcal{B}}^X$ implies $w\left(f\mathcal{A}\right)\le v\left(\mathcal{A}\right)$.

By b-ANEAR, we denote the category, whose objects are the b-apnear spaces and whose morphisms are the bac-maps.

Remark 1. 

Additionally, we note that any b-apnear space $(X,{\mathcal{B}}^X,v)$ with $X\in {\mathcal{B}}^X$ constitutes an approach nearness space $(X,v)$ [10], and every approach nearness space $(X,v)$ is of such a kind. Thus, a b-apnear space $(X,{\mathcal{B}}^X,v)$ is called saturated, provided that $X\in {\mathcal{B}}^X$ is valid, and we denote by SATb-ANEAR the full subcategory of b-ANEAR whose objects are saturated. Hence, SATb-ANEAR and ANEAR are essentially the same constructs.

Remark 2. 

Further, it is interesting to note that for any b-apnear space $(X,{\mathcal{B}}^X,v)$, $c{l}_v:{\mathcal{B}}^X⟶\underline{P}X$ constitutes a b-topological operator, and the pair $({\mathcal{B}}^X,c{l}_v)$ is called the underlying b-topology of $(X,{\mathcal{B}}^X,v)$ [PM].

• In the saturated case, $c{l}_v$ forms a Kuratowski closure operator. In fact, $c{l}_v(\varnothing )=\varnothing$, otherwise $v\left(\right\{\left\{x\right\},\varnothing \left\}\right)=0$ for some $x\in X$, and $v\left({\mathcal{B}}^X\right)=\infty$ contradicts because of ${\mathcal{B}}^X\ll \{\left\{x\right\},\varnothing \}$, implying that $\infty =v\left({\mathcal{B}}^X\right)\le v\left(\{\left\{x\right\},\varnothing \}\right)=0$. $B\in {\mathcal{B}}^X$ implies $c{l}_v\left(B\right)\in {\mathcal{B}}^X$ by (b-apn1). $B_1\subset B\in {\mathcal{B}}^X$ and $x\in c{l}_v\left(B_1\right)$, implying $v(\left\{x\right\},B_1\})=0$, and $\{\left\{x\right\},B\}\ll \{\left\{x\right\},B_1\}$, implying $v\left(\right\{x\},B\})=0$. Thus, $x\in c{l}_v\left(B\right)$. $B\in {\mathcal{B}}^X$ implies $B\subset c{l}_v\left(B\right)$, since $x\in B$ implies $\left\{\right\{x\},B\}\ll \left\{\right\{x\left\}\right\}$; hence, $v\left(\right\{\left\{x\right\},B\left\}\right)\le v\left(\right\{\left\{x\right\}\}=0$, and the claim follows.
• $B_1,B_2\in B^X$ and $x\in c{l}_v(B_1\cup B_2)$, implying $v\left(\{\left\{x\right\},B_1\cup B_2\}\right)=0$. But $\{\left\{x\right\}\cup B_1\}\vee \{\left\{x\right\}\cup B_2\}\ll \{\left\{x\right\},B_1\cup B_2\}$ implies $v(\{\left\{x\right\}\cup B_1\}\vee \{\left\{x\right\}\cup B_2\})\le v(\left\{x\right\},B_1\cup B_2\})$.
• Thus, $min\{v(\{\left\{x\right\}\cup B_1\},v(\left\{x\right\}\cup B_2\})=0$, implying $v\left(\{\left\{x\right\}\cup B_1\}\right)=0$, or $v\left(\{\left\{x\right\}\cup B_2\}\right)=0$; hence, $x\in c{l}_v\left(B_1\right)$ or $x\in c{l}_v\left(B_2\right)$, implying $x\in c{l}_v\left(B_1\right)\cup c{l}_v\left(B_2\right)$.
• To this end, let $B\in {\mathcal{B}}^X$ and $x\in c{l}_v\left(c{l}_v\left(B\right)\right)$. $v\left(\{\left\{x\right\},c{l}_v\left(B\right)\}\right)=0$ implies $v(c{l}_v\left(\left\{x\right\}\right),c{l}_v\left(B\right)\}=0$; hence, $v\left(\right\{\left\{x\right\},B\left\}\right)=0$ is valid, which shows that $x\in c{l}_v\left(B\right)$. Evidently, $c{l}_v$ is symmetric.
• Conversely, any b-topology $({\mathcal{B}}^X,t)$ determines a b-apnearness $({\mathcal{B}}^X,w_t)$ by setting for $\mathcal{A}\in \underline{P}{\mathcal{B}}^X{w}_t\left(\mathcal{A}\right)=0$ if and only if $\cap \left\{t\right(A):A\in \mathcal{A}\}\ne \varnothing$; otherwise, $w_t\left(\mathcal{A}\right):=\infty$. Then, given a bivalent indicating that $v\left(\mathcal{A}\right)\in \{0,\infty \}$, b-apnear space $(X,{\mathcal{B}}^X,v)$ is said to be topological, provided that for $\mathcal{A}\in \underline{P}{\mathcal{B}}^X$, $v\left(\mathcal{A}\right)=0$ iff $\cap \{c{l}_v\left(A\right):A\in \mathcal{A}\}\ne \varnothing$. By denoting TOPb-ANEAR as the full subcategory of b-ANEAR, whose objects are topological, then TOPb-ANEAR and sb-TOP (the category of symmetric b-topological spaces and bic-maps) [PM] are isomorphic.

Example 1. 

Now, we give a further important example.

• For a pseudonearness $({\mathcal{B}}^X,M)$, we consider the function $w_M:\underline{P}{\mathcal{B}}^X⟶[0,\infty ]$ by setting for $\mathcal{A}\in \underline{P}{\mathcal{B}}^X$, $w_M\left(\mathcal{A}\right):=0$ if and only if $\mathcal{A}\in \cap \left\{M\right(A):A\in \mathcal{A}\}$, meaning that the bounded sets of $\mathcal{A}$ are near; otherwise, $w_M\left(\mathcal{A}\right):=\infty$. Then, $(X,{\mathcal{B}}^X,w_M)$ constitutes a bivalent b-apnear space.

Proof. 

For (b-apn1), let $B\in {\mathcal{B}}^X$; our goal is $c{l}_{w_M}\left(B\right)\in {\mathcal{B}}^X$.

• So, let $x\in c{l}_{w_M}\left(B\right)$; hence, $w_M\left(\{\left\{x\right\},B\}\right)=0$, implying $\left\{\right\{x\},B\}\in M\left(\right\{x\left\}\right)\cap M\left(B\right)$. And $\left\{\right\{x\},B\}\in M\left(\right\{x\left\}\right)$ implies $\left\{B\right\}\in M\left(\right\{x\left\}\right)$. Thus, $x\in c{l}_M\left(B\right)$. But $c{l}_M\left(B\right)\in {\mathcal{B}}^X$ implies $c{l}_{w_M}\left(B\right)\in {\mathcal{B}}^X$, which has to be shown.
• For (b-apn2), let for ${\mathcal{A}}_1$, $\mathcal{A}\in \underline{P}{\mathcal{B}}^X$, ${\mathcal{A}}_1\ll \mathcal{A}$; our goal is $w_M\left({\mathcal{A}}_1\right)\le w_M\left(\mathcal{A}\right)$. So, let $w_M\left(\mathcal{A}\right)=0$, then $\mathcal{A}\in \cap \left\{M\right(A):A\in \mathcal{A}\}$. For $A_1\in \mathcal{A}$, we can find $A\in \mathcal{A}$ with $A\subset {\mathcal{A}}_1$; thus, $M\left(A\right)\subset M\left(A_1\right)$, which implies $\mathcal{A}\in M\left(A_1\right)$, and ${\mathcal{A}}_1\in M\left(A_1\right)$ follows by the hypothesis, which shows the claim.
• For (b-apn3), for $\mathcal{A}\in \underline{P}{\mathcal{B}}^X$, let $\varnothing \in \mathcal{A}$. Suppose that $w_M\left(\mathcal{A}\right)=0$, hence $\mathcal{A}\in M(\varnothing )$, implying $\mathcal{A}=\varnothing$, which is contradictory. Thus, $w_M\left(\mathcal{A}\right)=\infty$.
• For (b-apn4), for $\mathcal{A}\in \underline{P}{\mathcal{B}}^X$ and $\cap \mathcal{A}\ne \varnothing$, choose $x\in X\forall A\in \mathcal{A}$, $x\in A$. Thus, for $A\in \mathcal{A}$, $\left\{\right\{x\left\}\right\}\in M\left(\right\{x\left\}\right)\subset M\left(A\right)$ follows such that $\mathcal{A}\ll \left\{\right\{x\left\}\right\}$. Consequently, $\mathcal{A}\in \cap \left\{M\right(A):A\in \mathcal{A}\}$ implies $w_M\left(\mathcal{A}\right)=0$.
• For (b-apn5), for ${\mathcal{A}}_1,{\mathcal{A}}_2\in \underline{P}{\mathcal{B}}^X$ let $w_M({\mathcal{A}}_1\vee {\mathcal{A}}_2)=\infty$ (without restriction ${\mathcal{A}}_1\ne \varnothing \ne {\mathcal{A}}_2$). Then, we can find $A\in {\mathcal{A}}_1\vee {\mathcal{A}}_2$ with ${\mathcal{A}}_1\vee {\mathcal{A}}_2\notin M\left(A\right)$, where $A=A_1\cup A_2$, for some $A_1\in {\mathcal{A}}_1$ and some $A_2\in {\mathcal{A}}_2$. But ${\mathcal{A}}_1\vee {\mathcal{A}}_2\notin M(A_1\cup A_2)$ implies ${\mathcal{A}}_1\vee {\mathcal{A}}_2\notin M\left(A_1\right)\cup M\left(A_2\right)$, and consequently, ${\mathcal{A}}_1\vee {\mathcal{A}}_2\notin M\left(A_1\right)$ and ${\mathcal{A}}_1\vee {\mathcal{A}}_2\notin M\left(A_2\right)$ follow, which imply ${\mathcal{A}}_1\notin M\left(A_1\right)$ and ${\mathcal{A}}_2\notin M\left(A_2\right)$. Thus, $w_M\left({\mathcal{A}}_1\right)=\infty =w_M\left({\mathcal{A}}_2\right)$ leads to $min\{w_M\left({\mathcal{A}}_1\right),w_M\left({\mathcal{A}}_2\right)\}=\infty$.
• Conversely, let $min\{w_M\left({\mathcal{A}}_1\right),w_M\left({\mathcal{A}}_2\right)\}=\infty$. Then, $w_M\left({\mathcal{A}}_1\right)=\infty =w_M\left({\mathcal{A}}_2\right)$ follows. Hence, there exist $A_1\in {\mathcal{A}}_1$, ${\mathcal{A}}_1\notin M\left(A_1\right)$ and $A_2\in {\mathcal{A}}_2$, ${\mathcal{A}}_2\notin M\left(A_2\right)$ as well. Consequently, $A_1\cup A_2\notin {\mathcal{A}}_1\vee {\mathcal{A}}_2$ is obtained. Otherwise, ${\mathcal{A}}_1\vee {\mathcal{A}}_2\in M(A_1\cup A_2)$ implies ${\mathcal{A}}_1\vee {\mathcal{A}}_2\in M\left(A_1\right)$ or ${\mathcal{A}}_1\vee {\mathcal{A}}_2\in M\left(A_2\right)$. In the first case, ${\mathcal{A}}_1\in M\left(A_1\right)$ or ${\mathcal{A}}_2\in M\left(A_1\right)$. But ${\mathcal{A}}_2\in M\left(A_1\right)$ implies $\left\{A_1\right\}\cup {\mathcal{A}}_2\in M\left(A_2\right)$ by the symmetry of M, and thus, ${\mathcal{A}}_2\in M\left(A_2\right)$ is obtained, which is contradictory. The second case can then be handled analogously. Altogether, $w_M({\mathcal{A}}_1\vee {\mathcal{A}}_2)=\infty$ follows. Now, let $w_M({\mathcal{A}}_1\vee {\mathcal{A}}_2)=0$, and suppose that $w_M\left({\mathcal{A}}_1\right)\ne 0\ne w_M\left({\mathcal{A}}_2\right)$. By the bivalence of M, $w_M\left({\mathcal{A}}_1\right)=\infty =w_M\left({\mathcal{A}}_2\right)$ leads to $min\{w_M\left({\mathcal{A}}_1\right),w_M\left({\mathcal{A}}_2\right)\}=\infty$, which is contradictory, and the claim is obtained.
• For (b-apn6), let $\mathcal{A}\in \underline{P}{\mathcal{B}}^X$; our goal is $w_M\left(\mathcal{A}\right)\le w_M\left(\{c{l}_{w_M}\left(A\right):A\in \mathcal{A}\}\right)$. For $w_M\left(\{c{l}_{w_M}\left(A\right):A\in \mathcal{A}\}\right)=0$, we have to show that $\mathcal{A}\in \cap \left\{M\right(A):A\in \mathcal{A}\}$ is valid. So, let $A^{\prime }\in \mathcal{A}$, and then, since $c{l}_{w_M}\left(A^{\prime }\right)\in \{c{l}_{w_M}\left(A\right):A\in \mathcal{A}\}$, $\{c{l}_{w_M}\left(A\right):A\in \mathcal{A}\}\in M\left(c{l}_{W_M}\left(A^{\prime }\right)\right)$ by the hypothesis. Further, we have $\{c{l}_M\left(A\right),A\in \mathcal{A}\}<<\{c{l}_{w_M}\left(A\right):A\in \mathcal{A}\}$ and $M\left(c{l}_{w_M}\left(A^{\prime }\right)\right)\subset M\left(c{l}_M\left(A^{\prime }\right)\right)$, which imply that $\{c{l}_M\left(A\right):A\in \mathcal{A}\}\in M\left(c{l}_M\left(A^{\prime }\right)\right)$ and $\mathcal{A}\in M\left(A^{\prime }\right)$ follow, thus showing the claim.
• Conversely, let $({\mathcal{B}}^X,v)$ be a bivalent b-apnearness; then $({\mathcal{B}}^X,N_v)$ constitutes a pseudonearness, where $N_v(\varnothing ):=\{\varnothing \}$ and for $B\in {\mathcal{B}}^X\setminus \{\varnothing \}$, $N_v\left(B\right):=\{\mathcal{S}\in {\underline{P}}^{2}X:v(\left\{B\right\}\cup (\mathcal{S}\cap {\mathcal{B}}^X))=0\}$, such that the following equations hold:

  (i)

  $w_{N_v}=v$;

  (ii)

  $N_{w_M}=M$.

• For the first equation, we note that $N_v:{\mathcal{B}}^X⟶\underline{P}\left(\underline{P}\left(\underline{P}X\right)\right)$ is near the operator [PM].
• For (psn1), ${\mathcal{S}}_1\ll \mathcal{S}\in N_v\left(B\right)$ and, without restriction, $B\in {\mathcal{B}}^X\setminus \{\varnothing \}$. Then, $v(\left\{B\right\}\cup (\mathcal{S}\cap {\mathcal{B}}^X))=0$ and $v(\left\{B\right\}\cup ({\mathcal{S}}_1\cap {\mathcal{B}}^X))\le v(\left\{B\right\}\cup (\mathcal{S}\cap {\mathcal{B}}^X))$, implying ${\mathcal{S}}_1\in N_v\left(B\right)$.
• For (psn2), now, for $B\in {\mathcal{B}}^X\setminus \{\varnothing \}$, let $\mathcal{S}\in N_v\left(B\right)$. Our goal is $\left\{B\right\}\cup \mathcal{S}\in N_v\left(B\right)$ and $\left\{B\right\}\cup \mathcal{S}\in \cap \{N_v\left(F\right):F\in \mathcal{S}\cap {\mathcal{B}}^X\}$. By the hypothesis, $v(\left\{B\right\}\cup (\mathcal{S}\cap {\mathcal{B}}^X))=0$ implies $v(\left\{B\right\}\cup (\left\{B\right\}\cup \mathcal{S})\cap {\mathcal{B}}^X))=v(\left\{B\right\}\cup (\left\{B\right\}\cup (\mathcal{S}\cap {\mathcal{B}}^X)))=v(\left\{B\right\}\cup (\mathcal{S}\cap {\mathcal{B}}^X))=0$.
• Thus, $\left\{B\right\}\cup \mathcal{S}\in N_v\left(B\right)$. In the following, let $F\in \mathcal{S}\cap {\mathcal{B}}^X$; our goal is $\left\{B\right\}\cup \mathcal{S}\in N_v\left(F\right)$, which means that $v(\left\{F\right\}\cup ((\left\{B\right\}\cup \mathcal{S})\cap {\mathcal{B}}^X)))=0$. But $v(\left\{B\right\}\cup (\mathcal{S}\cap {\mathcal{B}}^X))=v(\left\{F\right\}\cup (\left\{B\right\}\cup (\mathcal{S}\cap {\mathcal{B}}^X)))=v(\left\{F\right\}\cup \left((\{B\cup \mathcal{S})\cap {\mathcal{B}}^X)\right))$, and the claim follows.
• For (psn3), let for $\mathcal{S}\in {\underline{P}}^{2}X$, $\mathcal{S}\cap {\mathcal{B}}^X\in N_v\left(B\right)$. Then, $v(\left\{B\right\}\cup ((\mathcal{S}\cap {\mathcal{B}}^X)\cap {\mathcal{B}}^X))=0$, implying $v(\left\{B\right\}\cup (\mathcal{S}\cap {\mathcal{B}}^X)=0$, and $\mathcal{S}\in N_v\left(B\right)$ is obtained.
• For (psn4), ${\mathcal{S}}_1$, ${\mathcal{S}}_2\in {\underline{P}}^{2}X$ and ${\mathcal{S}}_1\vee {\mathcal{S}}_2\in N_v\left(B\right)$, $B\in {\mathcal{B}}^Y$ imply $v(\left\{B\right\}\cup ({\mathcal{S}}_1\vee {\mathcal{S}}_2))=0$. But $(\left\{B\right\}\cup {\mathcal{S}}_1)\vee (\left\{\mathcal{B}\right\}\cup {\mathcal{S}}_2)<<\left\{B\right\}\cup ({\mathcal{S}}_1\vee {\mathcal{S}}_2)$, implying $v(\left\{B\right\}\cup {\mathcal{S}}_1)\vee \left\{B\right\}\cup {\mathcal{S}}_2)\le v(\left\{B\right\}\cup ({\mathcal{S}}_1\vee {\mathcal{S}}_2))$ and $v(\left\{B\right\}\cup {\mathcal{S}}_1)\vee \left\{B\right\}\cup {\mathcal{S}}_2)\ge min\{v(\left\{B\right\}\cup {\mathcal{S}}_1),v(\left\{B\right\}\cup {\mathcal{S}}_2)\}$. Thus, $v(\left\{B\right\}\cup {\mathcal{S}}_1))=0$ or $v(\left\{B\right\}\cup {\mathcal{S}}_2))=0$, implying ${\mathcal{S}}_1\in N_v\left(B\right)$ or ${\mathcal{S}}_2\in N_v\left(B\right)$.
• For (psn5), the definition is evident.
• For (psn6), since $v\left(\right\{\left\{x\right\}\}=0$, $\left\{\left\{x\right\}\right\}\in N_v\left(\left\{x\right\}\right)$ is valid.
• For (psn7), $B\in {\mathcal{B}}^X$ and $x\in c{l}_{N_v}\left(B\right)$ implies $\left\{B\right\}\in N_v\left(\left\{x\right\}\right)$; hence, $0=v\left(\right\{\left\{x\right\}\}\cup \{B\left\}\right)=v\left(\right\{\left\{x\right\},B\left\}\right)$, implying $x\in c{l}_v\left(B\right)$, and thus, $c{l}_{N_v}\left(B\right)\in {\mathcal{B}}^X$.
• For (psn8), for $\mathcal{S}\in {\underline{P}}^{2}X$ and, without restriction, $B\in {\mathcal{B}}^X\setminus \{\varnothing \}$, let $\{c{l}_{N_v}\left(F\right):F\in \mathcal{S}\}\in N_v\left(B\right)$. Then, $0=v(\left\{B\right\}\cup \{c{l}_{N_v}\left(F\right):F\in \mathcal{S}\}\cap {\mathcal{B}}^X)=v(\left\{B\right\}\cup \{c{l}_{N_v}\left(F\right):F\in \mathcal{S}\cap {\mathcal{B}}^X\})$. But $\left\{c{l}_v\left(B\right)\right\}\cup \{c{l}_v\left(F\right):F\in \mathcal{S}\cap {\mathcal{B}}^X\}\ll \left\{B\right\}\cup \{c{l}_{N_v}\left(F\right):F\in \mathcal{S}\cap {\mathcal{B}}^X\}$, implying $v(\left\{c{l}_v\left(B\right)\right\}\cup \{c{l}_v\left(F\right):F\in \mathcal{S}\cap {\mathcal{B}}^X\})\le v(\left\{B\right\}\cup \{c{l}_{N_v}\left(F\right):F\in \mathcal{S}\cap {\mathcal{B}}^X\})$. Thus, $v(\left\{c{l}_v\left(B\right)\right\}\cup \{c{l}_v\left(F\right):F\in \mathcal{S}\cap {\mathcal{B}}^X\})=0$ with $v(\left\{B\right\}\cup (\mathcal{S}\cap {\mathcal{B}}^X))\ll v(\left\{c{l}_v\left(B\right)\right\}\cup \{c{l}_v\left(F\right):F\in \mathcal{S}\cap {\mathcal{B}}^X\})$, implying $\mathcal{S}\in N_v\left(B\right)$.
• For (i), let for $\mathcal{A}\in \underline{P}{\mathcal{B}}^X$, $v\left(\mathcal{A}\right)=0$; and supposing that $w_{N_v}\left(\mathcal{A}\right)=\infty$, then $\mathcal{A}\notin N_v\left(A\right)$ for some $A\in \mathcal{A}$. $A=\varnothing$ implies $v\left(\mathcal{A}\right)=\infty$, which is contradictory. In the other case, $v\left(\right\{A\}\cup \mathcal{A})=\infty$ is also contradictory. If $v\left(\mathcal{A}\right)=\infty$, then our goal is $w_{N_v}\left(\mathcal{A}\right)=\infty$. By the hypothesis, $\mathcal{A}\ne \varnothing$, because, if not, $\cap \mathcal{A}\ne \varnothing$ implies $v\left(\mathcal{A}\right)=0$, which is contradictory. Choose $A\in \mathcal{A}$; then $A=\varnothing$ implies $\mathcal{A}\notin N_v\left(A\right)$, and hence $w_{N_v}\left(\mathcal{A}\right)=\infty$ follows. In the second case, $A\ne \varnothing$, and if supposing $\mathcal{A}\in N_v\left(A\right)$, $v\left(\right\{A\}\cup \mathcal{A})=0$ follows, which is contradictory, and the claim follows. Note also that the bivalence is of great importance in the former proof.
• For (ii), let, without restriction, $B\in {\mathcal{B}}^X\setminus \{\varnothing \}$. $\mathcal{S}\in N_{w_M}\left(B\right)$ implies $w_M(\left\{B\right\}\cup (\mathcal{S}\cap {\mathcal{B}}^X))=0$. Hence, $\left\{B\right\}\cup (\mathcal{S}\cap {\mathcal{B}}^X)\in M\left(B\right)$, implying $\mathcal{S}\cap {\mathcal{B}}^X\in M\left(B\right)$, and $\mathcal{S}\in M\left(B\right)$ is obtained. Conversely, $\mathcal{S}\in M\left(B\right)$ implies $\left\{B\right\}\cup \mathcal{S}\in \cap \{M\left(F\right):F\in \left\{B\right\}\cup (\mathcal{S}\cap {\mathcal{B}}^X)\}$. Our goal is $w_M(\left\{B\right\}\cup (\mathcal{S}\cap {\mathcal{B}}^X))=0$. For $F\in \left\{B\right\}\cup (\mathcal{S}\cap {\mathcal{B}}^X)$, we have $\left\{B\right\}\cup (\mathcal{S}\cap {\mathcal{B}}^X)\in M\left(F\right)$; hence, $w_M(\left\{B\right\}\cup (\mathcal{S}\cap {\mathcal{B}}^X))=0$, implying $\mathcal{S}\in N_{w_N}\left(B\right)$. To conclude, let for psn-spaces $(X,{\mathcal{B}}^X,M_X)$, $(Y,{\mathcal{B}}^Y,M_Y)$, $f:X⟶Y$ be a function. Then the following statements are equivalent:

  (i)

  $f:(X,{\mathcal{B}}^X,M_X)⟶(Y,{\mathcal{B}}^Y,M_Y)$ is bin-map;

  (ii)

  $f:(X,{\mathcal{B}}^X,w_{M_X})⟶(Y,{\mathcal{B}}^Y,w_{M_Y})$ is bac-map.

• For $\left(i\right)\Rightarrow \left(ii\right)$, let $\mathcal{A}\in \underline{P}{\mathcal{B}}^X$, such that $w_{M_X}\left(\mathcal{A}\right)=0$; our goal is $f\mathcal{A}\in \cap \{M_Y\left(F\right):F\in f\mathcal{A}\}$. $F\in f\mathcal{A}$ implies $F=f\left[A\right]$ for some $A\in \mathcal{A}$; hence, by the hypothesis, $\mathcal{A}\in M_X\left(A\right)$, implying that $f\mathcal{A}\in M_Y\left(f\left[A\right]\right)=M_Y\left(F\right)$, and the claim is obtained.
• For $\left(ii\right)\Rightarrow \left(i\right)$, $\mathcal{S}\in M_X\left(B\right)$ and $B\in {\mathcal{B}}^X\setminus \{\varnothing \}$ imply $\left\{B\right\}\cup \mathcal{S}\in \cap \{M_X\left(F\right):F\in \left\{B\right\}\cup (\mathcal{S}\cap {\mathcal{B}}^X)\}$. Hence, $w_{M_X}(\left\{B\right\}\cup (\mathcal{S}\cap {\mathcal{B}}^X))=0$, implying that $w_{M_Y}(f(\left\{B\right\}\cup (\mathcal{S}\cap {\mathcal{B}}^X))=0$, which means $f(\left\{B\right\}\cup (\mathcal{S}\cap {\mathcal{B}}^X))\in M_Y\left(f\left[B\right]\right)$. Thus, $f(\mathcal{S}\cap {\mathcal{B}}^X)\in M_Y\left(f\left[B\right]\right)$ with $f(\mathcal{S}\cap {\mathcal{B}}^Y)\ll f\mathcal{S}\cap {\mathcal{B}}^X$. Note that f is especially rebounded; hence, $f\mathcal{S}\in M_Y\left(f\left[B\right]\right)$ follows. By denoting 2b-ANEAR as the full subcategory of b-ANEAR, whose objects are the bivalent b-apnear spaces, then the categories 2b-ANEAR and PSN are isomorphic. Hence, PSN can be considered as a fully embedded subcategory of b-ANEAR. □

Example 2. 

For a bornology ${\mathcal{B}}^X$ [PM], we set for $\mathcal{A}\in \underline{P}{\mathcal{B}}^X$, $v_b\left(\mathcal{A}\right):=0$ if and only if $\cap \{F:F\in \mathcal{A}\cup {\mathcal{B}}^X\}\ne \varnothing$; otherwise, $v_b\left(\mathcal{A}\right):=\infty$. Then $v_b$ is a function from $\underline{P}{\mathcal{B}}^X$ into $[0,\infty ]$, which is bivalent such that $({\mathcal{B}}^X,v_b)$ constitutes a b-apnearness. In this context, we call a bivalent b-apnearness $({\mathcal{B}}^X,w)$ sected, provided that for $\mathcal{A}\in \underline{P}{\mathcal{B}}^X$, $w\left(\mathcal{A}\right)=0$ if and only if $x\in \cap \mathcal{A}$ for some $x\in \cap {\mathcal{B}}^X$. Evidently, $({\mathcal{B}}^X,v_b)$ is sected. Now, it is evident that the class of bornological spaces and that of sected b-apnear spaces are of the same cardinality! If one considers bi-bounded maps (in short, bib-maps) between bornological spaces, and denoting by SECb-ANEAR the full subcategory of b-ANEAR (whose objects are sected) and by BORN² the subcategory of BORN (whose morphisms are the bib-maps), then the categories SECb-ANEAR and BORN² are isomorphic.

Before giving an additional important example, we note the following proposition.

Proposition 1. 

Any b-apnear-space $(X,{\mathcal{B}}^X,w)$ has an underlying approach bornology $({\mathcal{B}}^X,d_w)$ [PM], where $({\mathcal{B}}^X,d_w)$ is defined by setting for $x\in X$ and $B\in {\mathcal{B}}^X$, $d_w(x,B):=w\left(\{\left\{x\right\},B\}\right)$.

Proof. 

For (apb1), for $B\in {\mathcal{B}}^X$, let $x\in c{l}_{d_w}\left(B\right)$, then $d_w(x,B)=0$ implies $w\left(\right\{\left\{x\right\},B\left\}\right)=0$; hence, $x\in c{l}_w\left(B\right)$ shows $c{l}_{d_w}\left(B\right)\in {\mathcal{B}}^X$.

• For (apb2), let $x\in X$ and $B\in {\mathcal{B}}^X$; our goal is $d_w(x,B)\le d_w(x,c{l}_{d_w}\left(B\right))$.
• $d_w(x,B)=w\left(\{\left\{x\right\},B\}\right)\le w(\left\{c{l}_w(\left\{x\right\},c{l}_w\left(B\right)\}\right)\le w\left(\{\left\{x\right\},c{l}_{d_w}\left(B\right)\}\right)=d_w(x,c{l}_{d_w}\left(B\right)$.
• For (apb3), $x\in X$ implies $d_w(x,\varnothing )=w\left(\{\left\{x\right\},\varnothing \}\right)\ge w\left({\mathcal{B}}^X\right)=\infty$.
• For (apb4), $x\in X$ implies $w\left(\right\{\left\{x\right\}\left\}\right)=0$, and $d_w(x,\left\{x\right\})=w(\left\{x\right\},\left\{x\right\})$ shows the claim.
• For (apb5), $x\in X$ and $B_1$, $B_2\in {\mathcal{B}}^X$, implying that $d_w(x,B_1\cup B_2)=w\left(\{\left\{x\right\},B_1\cup B_2\}\right)\ge w\left((\left\{x\right\}\cup B_1\}\right)\vee (\left\{x\right\}\cup B_2\}\left)\right)\ge min\{w\left(\{\left\{x\right\}\cup B_1\}\right),w\left(\{\left\{x\right\}\cup B_2\}\right)\}=min\{d_w(x,B_1),d_w(x,B_2)\}=:m$.
• Conversely, we have $\{\left\{x\right\},B_1\cup B_2\}\ll \{\left\{x\right\},B_1\},\{\left\{x\right\},B_2\}$. Consequently, $w\left(\{\left\{x\right\},B_1\cup B_2\}\right)\le w(\left\{x\right\},B_1\}),w(\left\{x\right\},B_2\})$ follow, implying that $d_w(x,B_1\cup B_2)=w\left(\{\left\{x\right\},B_1\cup B_2\}\right)\le min\left\{w(\left\{x\right\},B_1\}\right),w(\left\{x\right\},B_2\}\left)\right\}=min\{d_w(x,B_1),d_w(x,B_2)\}=m$.
• Notably, we point out that $({\mathcal{B}}^X,d_w)$ is particularly symordered. □

Definition 8. 

An apb $({\mathcal{B}}^X,\delta )$ is said to be symordered by satisfying the following conditions:

(so1) 

$({\mathcal{B}}^X,d)$ is symmetric, i.e., $x,z\in X$, implying $\delta (x,\{z\left\}\right)=\delta (z,\{x\left\}\right)$;

(so2) 

$({\mathcal{B}}^X,\delta )$ is ordered, i.e., $B_1\subset B\in {\mathcal{B}}^X$ and $x\in X$, implying $\delta (x,B)\le \delta (x,B_1)$.

By SO-APB², we denote the full subcategory of APB², whose objects are symordered [PM].

Example 3. 

(i) 

For every bornological space $(X,{\mathcal{B}}^X)$, $({\mathcal{B}}^X,{\delta }_b)$ is symordered, where for $x\in X$, $B\in {\mathcal{B}}^X$, ${\delta }_b(x,B):=0$ iff $x\in B$; otherwise, ${\delta }_b(x,B):=\infty$;

(ii) 

For any pseudonearness $({\mathcal{B}}^X,N)$, $({\mathcal{B}}^X,{\delta }_N)$ is symordered, where ${\delta }_N(x,z):=0$ iff $\left\{\right\{x\left\}\right\}\in N\left(B\right)$; otherwise, ${\delta }_N(x,z):=\infty$;

(iii) 

For any b-approach nearness $({\mathcal{B}}^X,w)$, $({\mathcal{B}}^X,d_w)$ is symordered;

(iv) 

For any metric space $(X,d)$, $(\underline{P}X,{\delta }_d)$ is symordered;

(v) 

For any symmetric approach space $(X,\delta )$ [PM], $(\underline{P}X,\delta )$ is symordered.

Now, we return to our proposed example.

Example 4. 

For a symordered apb $({\mathcal{B}}^X,\delta )$, we set for $\mathcal{A}\in \underline{P}{\mathcal{B}}^X$: $v_{\delta }\left(\mathcal{A}\right):=sup\{inf\{\delta (x,A):A\in \mathcal{A}\}:x\in X\}$. Then the pair $({\mathcal{B}}^X,v_{\delta })$ constitutes a b-approach nearness on X.

Proof. 

For (b-apn1), for $B\in {\mathcal{B}}^X$, let $x\in c{l}_{v_{\delta }}\left(B\right)$. Then $v_{\delta }\left(\{\left\{x\right\},B\}\right)=0$ implies $sup\{inf\{\delta (z,A):A\in \left\{\right\{x\},B\}\}:z\in X\}=0$. In particular, $z=x$, implying $0=inf\left\{\delta \right(x,\left\{x\right\}),\delta (x,B\left)\right\}=\delta (x,B)$, and $x\in c{l}_{\delta }\left(B\right)$ follows.

• For (b-apn2), let ${\mathcal{A}}_1$, $\mathcal{A}\in \underline{P}{\mathcal{B}}^X$ with ${\mathcal{A}}_1\ll \mathcal{A}$; our goal is $v_{\delta }\left({\mathcal{A}}_1\right)\le v_{\delta }\left(\mathcal{A}\right)$. For $A_1\in {\mathcal{A}}_1$, we can find $A\in \mathcal{A}$ such that $A\subset A_1$, which, for $x\in X$, implies $\delta (x,A_1)\le \delta (x,A)$. Hence, $i_1^x:=inf\{\delta (x,A_1):A_1\in {\mathcal{A}}_1\}$ is a lower bound of $\left\{\delta \right(x,A):A\in \mathcal{A}\}$. Thus, $i_1^x\le i^x:=inf\{\delta (x,A):A\in \mathcal{A}\}$. But $sup\{i^z:z\in X\}$ is an upper bound of $\{i_1^z:z\in X\}$; hence, $v_{\delta }\left({\mathcal{A}}_1\right)=sup\{i_1^z:z\in X\}\le sup\{i^z:z\in X\}=v_{\delta }\left(\mathcal{A}\right)$.
• For (b-apn3), $v_{\delta }\left({\mathcal{B}}^X\right):=sup\{inf\{\delta (x,B):B\in {\mathcal{B}}^X\}:x\in X\}=:s$. Since $\varnothing \in {\mathcal{B}}^X$, $inf\{\delta (x,B):B\in {\mathcal{B}}^X\}=\infty$ for any $x\in X$. Hence, $\infty =s=v_{\delta }\left({\mathcal{B}}^X\right)$ is obtained.
• For (b-apn4), $x\in X$ implies $v_{\delta }\left(\left\{\left\{x\right\}\right\}\right)=sup\{inf\{\delta (z,B):B\in \left\{\left\{x\right\}\right\}:z\in X\}=:s$. Since $\delta (x,\{x\left\}\right)=0$, $inf\left\{\delta \right(z,B):B\in \{\left\{x\right\}\left\}\right\}=0$ follows for any $z\in X$, which implies $s=0$, and the claim is obtained.
• For (b-apn5), let ${\mathcal{A}}_1$, ${\mathcal{A}}_2\in \underline{P}{\mathcal{B}}^X$; our goal is $v_{\delta }({\mathcal{A}}_1\vee {\mathcal{A}}_2)\ge min\{v_{\delta }\left({\mathcal{A}}_1\right),v_{\delta }\left({\mathcal{A}}_2\right)\}$.
• $v_{\delta }\left({\mathcal{A}}_1\right):=s_1:=sup\{i_1:=inf\{\delta (x,A_1):A_1\in {\mathcal{A}}_1\}:x\in X\}$ and $v_{\delta }\left({\mathcal{A}}_2\right):=s_2:=sup\{i_2:=inf\{\delta (x,A_2):A_2\in {\mathcal{A}}_2\}:x\in X\}$ and $v_{\delta }({\mathcal{A}}_1\vee {\mathcal{A}}_2):=s_3:=sup\{i_3:=inf\{\delta (x,A_1\cup A_2):A_1\in {\mathcal{A}}_1,A_2\in {\mathcal{A}}_2\}:x\in X\}$. Now, for $x\in X$ and $A_1\in {\mathcal{A}}_1$, $A_2\in {\mathcal{A}}_2$, we have $\delta (x,A_1)=\delta (x,A_1\cup A_2)$ or $\delta (x,A_2)=\delta (x,A_1\cup A_2)$. In the first case, $i_1=i_3$ implies $s_1=s_3$, and in the second case, $i_2=i_3$ implies $s_2=s_3$; hence, $s_3\ge min\{s_1,s_2\}$ follows, which shows the claim.
• For (b-apn6), let $\mathcal{A}\in \underline{P}{\mathcal{B}}^X$; we have to show that $v_{\delta }\left(\mathcal{A}\right)\le v_{\delta }\left(\{c{l}_{v_{\delta }}\left(A\right):A\in \mathcal{A}\}\right)$. For $x\in X$ and $A\in \mathcal{A}$, we have $\delta (x,A)\le \delta (x,c{l}_{\delta }\left(A\right))$, which implies $inf\{\delta (x,A):A\in \mathcal{A}\}\le inf\{\delta (x,c{l}_{\delta }\left(A\right)\}:A\in \mathcal{A}\}$. Thus, $inf\{\delta (x,A):A\in \mathcal{A}\}\le sup\{\delta (x,c{l}_{\delta }\left(A\right):A\in \mathcal{A}\}:x\in X\}$ implies $v_{\delta }\left(\mathcal{A}\right)=sup\{inf\{\delta (x,A):A\in \mathcal{A}\}\le sup\{\delta (x,c{l}_{\delta }\left(A\right)\}:A\in \mathcal{A}\}:x\in X\}\le v_{\delta }\left(\{c{l}_{v_{\delta }}\left(A\right):A\in \mathcal{A}\}\right)$, and the claim is obtained as a result. □

Corollary 1. 

For any symordered apb $({\mathcal{B}}^X,\delta )$, $d_{v_{\delta }}\ge \delta$ holds.

Proof. 

For $x\in X$, let $B\in {\mathcal{B}}^X$; then $d_{v_{\delta }}(x,B)=v_{\delta }\left(\{\left\{x\right\},B\}\right)=sup\{inf\{\delta (z,A):A\in \left\{\left\{x\right\}B\right\}\}:z\in X\}=:s$. But $inf\left\{\delta \right(x,\left\{x\right\},\delta (x,B)\}=\delta (x,B)\in \{inf\left\{\delta \right(z,A):A\in \{\left\{x\right\},B\left\}\right\}:z\in X\left\}\right\}$, implying $\delta (x,B)\le s=d_{v_{\delta }}(x,B)$. □

Definition 9. 

An apb $({\mathcal{B}}^X,\delta )$ is said to be b-near surrounded provided that $d_w\ge \delta$ for some b-apn $({\mathcal{B}}^X,w)$.

Remark 3. 

Now, we can state that any symordered apb is b-near surrounded. In particular, this also holds for any symmetric approach space $(X,\delta )$, even when compared with 2.8. Note that this must not hold for any approach space!

• Completeness is a well-known property in topology and is important for several significant results. So, par example, the Niemytzki–Tychonoff theorem [13] for completely regular spaces states that the necessary and sufficient condition for a space being compact is that every compatible uniform structure is complete. To generalize this theorem for a more convenient context of b-approach nearness spaces, we define completeness of b-apnear spaces in a new manner, which differs from that given in [10], but it coincides in serious cases, such as metric, uniform, or proximity spaces, respectively (see also the Section 1).

Definition 10. 

For a b-apnear space $(X,{\mathcal{B}}^X,v)$, $\mathcal{F}\in \underline{P}{\mathcal{B}}^X$ is said to be a filter (in ${\mathcal{B}}^X$) provided it satisfies the following conditions:

(bF1) 

$\varnothing \notin \mathcal{F}\ne \varnothing$;

(bF2) 

$F_1\in \mathcal{F}$ and $F_1\subset F\in {\mathcal{B}}^X$, implying $F\in \mathcal{F}$;

(bF3) 

$F_1$, $F_2\in \mathcal{F}$, implying $F_1\cap F_2\in \mathcal{F}$.

$F\left({\mathcal{B}}^X\right):=\{\mathcal{F}\in \underline{P}{\mathcal{B}}^X:\mathcal{F}$ is a filter in ${\mathcal{B}}^X\}$; this denotes the set of all filters in ${\mathcal{B}}^X$.

Definition 11. 

$\mathcal{P}\in F\left({\mathcal{B}}^X\right)$ is called a primefilter if and only if $\mathcal{P}$ is a maximal element in the set $F\left({\mathcal{B}}^X\right)$, ordered by the inclusion. Note that for any $x\in X$, $x_b:=\{F\in {\mathcal{B}}^X:x\in F\}$ constitutes an primefilter in ${\mathcal{B}}^X$.

Definition 12. 

A b-apnearness $({\mathcal{B}}^X,v)$ is said to be primecomplete provided that for any primefilter $\mathcal{P}$ in ${\mathcal{B}}^X$ with $v\left(P\right)=0$, the intersection $\cap \{c{l}_v\left(F\right),F\in \mathcal{P}\}$ is not empty. In this case, we discuss about primecomplete b-apnearness, and the space $(X,{\mathcal{B}}^X,v)$ is called a primecomplete b-apnear space. In this context, we note that any topological b-apnear space is primecomplete. The next two descriptions generalize the ordinary traditional notions in classically considered spaces like topologies, uniformities, proximities, metrics, and apnearnesses.

Definition 13. 

For a b-apnearness space $(X,{\mathcal{B}}^X,v)$, the underlying b-topology $({\mathcal{B}}^X,c{l}_v)$ is said to be compact provided that $\forall \mathcal{S}\in \underline{P}{\mathcal{B}}^X$ with $\cap \{c{l}_v\left(F\right):F\in \mathcal{S}\}=\varnothing$, where $\exists {\mathcal{S}}_0\subset \mathcal{S}$ is finite such that $\cap \{c{l}_v\left(A\right):A\in {\mathcal{S}}_0\}=\varnothing$.

Definition 14. 

A b-apnearness $({\mathcal{B}}^X,v)$ and the corresponding space $(X,{\mathcal{B}}^X,v)$ are called precompact provided that $\mathcal{A}\in \underline{P}{\mathcal{B}}^X$, and $\mathcal{E}\subset \mathcal{A}$ is finite with $\cap \{F:F\in \mathcal{E}\}\ne \varnothing$, implying $v\left(\mathcal{A}\right)=0$.

Remark 4. 

In this context, we note that $({\mathcal{B}}^X,v)$ is precompact if and only if it satisfies the condition that for any filter $\mathcal{F}\in F\left({\mathcal{B}}^X\right)$, $v\left(\mathcal{F}\right)=0$.

Theorem 1. 

Let $(X,{\mathcal{B}}^X,v)$ be a b-apnear space. Then the underlying b-topology of $({\mathcal{B}}^X,v)$ is compact if and only if $(X,{\mathcal{B}}^X,v)$ is precompact and primecomplete.

Proof. 

Let $({\mathcal{B}}^X,v)$ be compact and $\mathcal{P}$ be a primefilter with $v\left(\mathcal{P}\right)=0$. Then $\{c{l}_v\left(F\right):F\in \mathcal{P}\}=:c{l}_v\mathcal{P}$ is a set of v-closed sets such that any finite subset $\mathcal{S}\subset c{l}_v\mathcal{P}$ satisfies $\cap \{F:F\in \mathcal{P}\}\ne \varnothing$. Thus, by the hypothesis, $\cap \{c{l}_v\left(F\right):F\in \mathcal{P}\}\ne \varnothing$, implying that $({\mathcal{B}}^X,v)$ is primecomplete. On the other hand, to prove that $(X,{\mathcal{B}}^X,v)$ is precompact, let $\mathcal{F}\in F\left({\mathcal{B}}^X\right)$. Then for any subset ${\mathcal{S}}_0\subset \mathcal{F}$, we have $\cap \{c{l}_v\left(F\right):F\in {\mathcal{S}}_0\}\ne \varnothing$; hence, $\cap c{l}_v\left(\mathcal{F}\right)\ne \varnothing$ follows by the hypothesis. Thus, $\{c{l}_v\left(F\right):F\in \mathcal{F}\}\ll \left\{\left\{x\right\}\right\}$ for some $x\in X$, and consequently $v\left(\mathcal{F}\right)\le v\left(\{c{l}_v\left(F\right):F\in \mathcal{F}\}\right)\le v\left(\left\{\left\{x\right\}\right\}\right)=0$, implying that $v\left(\mathcal{F}\right)=0$. By 2.18, $({\mathcal{B}}^X,v)$ is precompact.

• Conversely, let $(X,{\mathcal{B}}^X,v)$ be primecomplete and precompact. For a collection $\mathcal{S}\in \underline{P}{\mathcal{B}}^X$ of v-closed subsets of X such that for all finite subsets ${\mathcal{S}}_0\subset \mathcal{S}$ with $\cap \{F:F\in {\mathcal{S}}_0\}\ne \varnothing$, we obtain $v\left(\mathcal{S}\right)=0$ by the hypothesis. Hence, $\mathcal{S}\subset \mathcal{P}$ for some primefilter $\mathcal{P}\in F\left({\mathcal{B}}^X\right)$ implies $v\left(\mathcal{P}\right)=0$, and $\cap \{c{l}_v\left(F\right):F\in \mathcal{P}\}\ne \varnothing$ follows by the hypothesis. Thus, $\cap \{c{l}_v\left(B\right):B\in \mathcal{S}\}\ne \varnothing$ shows the claim.
• In approaching the announced theorem, a b-apnearness $({\mathcal{B}}^X,v)$ on a b-topological space $({\mathcal{B}}^X,t)$ is said to be t-compatible if and only if $c{l}_v=t$. □

Lemma 1. 

Let a symmetric b-topology $({\mathcal{B}}^X,t)$ be given; then, $({\mathcal{B}}^X,v_c)$ is a compatible precompact b-apnearness on X, where for $\mathcal{A}\in \underline{P}{\mathcal{B}}^X$, $v_c\left(\mathcal{A}\right):=0$ iff $\cap \left\{t\right(F):F\in \mathcal{E}\}\ne \varnothing$, and $\forall \mathcal{E}\subset \mathcal{A}$ is finite; otherwise, $v_c\left(\mathcal{A}\right):=\infty$.

Proof. 

Evidently, $({\mathcal{B}}^X,v_c)$ is a b-apnearness. Now, for $x\in c{l}_{v_c}\left(B\right)$, $v_c\left(\{\left\{x\right\},B\}\right)=0$, implying $t\left(\right\{x\left\}\right)\cap t\left(B\right)\ne \varnothing$, and we can choose $z\in X$ with $z\in t\left(\right\{x\left\}\right)\cap t\left(B\right)$. By the symmetry, we obtain $x\in t\left(z\right)\subset t\left(t\right(B\left)\right)\subset t\left(B\right)$, since $({\mathcal{B}}^X,t)$ is topological.

• Conversely, let $x\in t\left(B\right)$; then by the definition, $v_c\left(\{\left\{x\right\},B\}\right)=0$ implies $x\in c{l}_{v_c}\left(B\right)$, which shows the claim. Finally, let $\mathcal{A}\in \underline{P}{\mathcal{B}}^X,\mathcal{E}\subset \mathcal{A}$ be finite with $\cap \{F:F\in \mathcal{E}\}\ne \varnothing$. Then $x\in c{l}_{v_c}\left(F\right)$ follows for some $x\in X$. By using the compatibility condition, $v_c\left(\mathcal{A}\right)=0$ is obtained by the definition. Now, we are able to formulate the generalization of the Niemytzki–Tychonoff theorem for b-apnear spaces. □

Theorem 2. 

A symmetric b-topological space is compact if and only if every compatible b-apnearness is primecomplete.

Proof. 

Let $({\mathcal{B}}^X,t)$ be a symmetric b-topological space and every compatible b-apnearness be primecomplete. Then, $({\mathcal{B}}^X,v_c)$ is primecomplete as it is t-compatible and, in addition, precompact. By applying the former theorem, $({\mathcal{B}}^X,t)$ is compact. For the converse, use the former theorem as well, and see also the explanations in the Section 1. □

Short Summary 1. 

The present paper provides an extended insight of nearness-like concepts [14], which have always been fruitful in studying topological problems. So, it was possible to integrate the fundamental basics of approach nearness, bornology, b-topology, and pseudonearness as well. Using prime completeness, the generalization of various theorems is carried out in b-approach nearness spaces. As an example, a uniform space is compact if and only if it is complete and totally bounded. Carlson [7] generalized this theorem and the Niemytzki–Tychonoff theorem for a nearness space [2]. And, by the assistance of prime completeness, we have establish these theorems in the framework of b-approach nearness spaces.

Application 1. 

It may surely be of interest to consider the problem of topological extensions of b-apnearness. For example, is it possible to densely embed any bornotopological approach nearness space into a prime complete one, such that in special cases, classical completions are obtained as a result? Moreover, in this context, do we obtain a natural correspondence between strict bornotopological extensions [9] and corresponding bornological b-apnearness spaces? Closely related to the canonical construction which embeds each pseudonear space into a b-complete pseudonear space, we introduce the notion of a so-called bornotopological extension. It turns out that this concept is convenient for studying strict topological extensions. A main result is that we obtain a natural correspondence between equivalence classes of strict bornotopological extensions and preceding pseudonear spaces, which is both onto and one-to-one.

Figure 1 shows the diagram of some important categories.

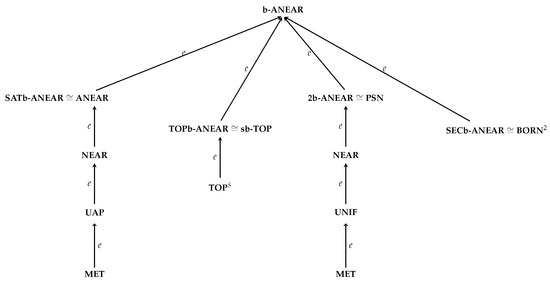
Figure 1. Diagram of some important categories. Legend: e = embedding; ≅: isomorphism. Acronyms: b-NEAR = Category of bornological approach nearness spaces and bac-maps. ANEAR = Category of approach nearness spaces and contractions. NEAR = Category of nearness spaces and n-maps. sb-TOP = Category of symmetric b-topological space and continuous maps. PSN = Category of pseudonear spaces and psn-maps. BORN² = Category of bornological spaces and bib-maps. UAP = Category of uniform approach nearness spaces and contractions. MET = Category of metric spaces and non-expensive maps. TOP² = Category of symmetric topological spaces and continuous maps. UNIF = Category of uniform spaces and uniform contraction maps. SATb-ANEAR = Full subcategory of b-ANEAR, whose objects are saturated. TOPb-ANEAR = Full subcategory of b-ANEAR, whose objects are topological. 2b-ANEAR = Full subcategory of b-ANEAR, whose objects are bivalent. SECb-ANEAR = Full subcategory of b-ANEAR, whose objects are sected.