Novel Statistical Analysis Schemes for Frequency-Modulated Thermal Wave Imaging for Inspection of Ship Hull Materials
Abstract
1. Introduction
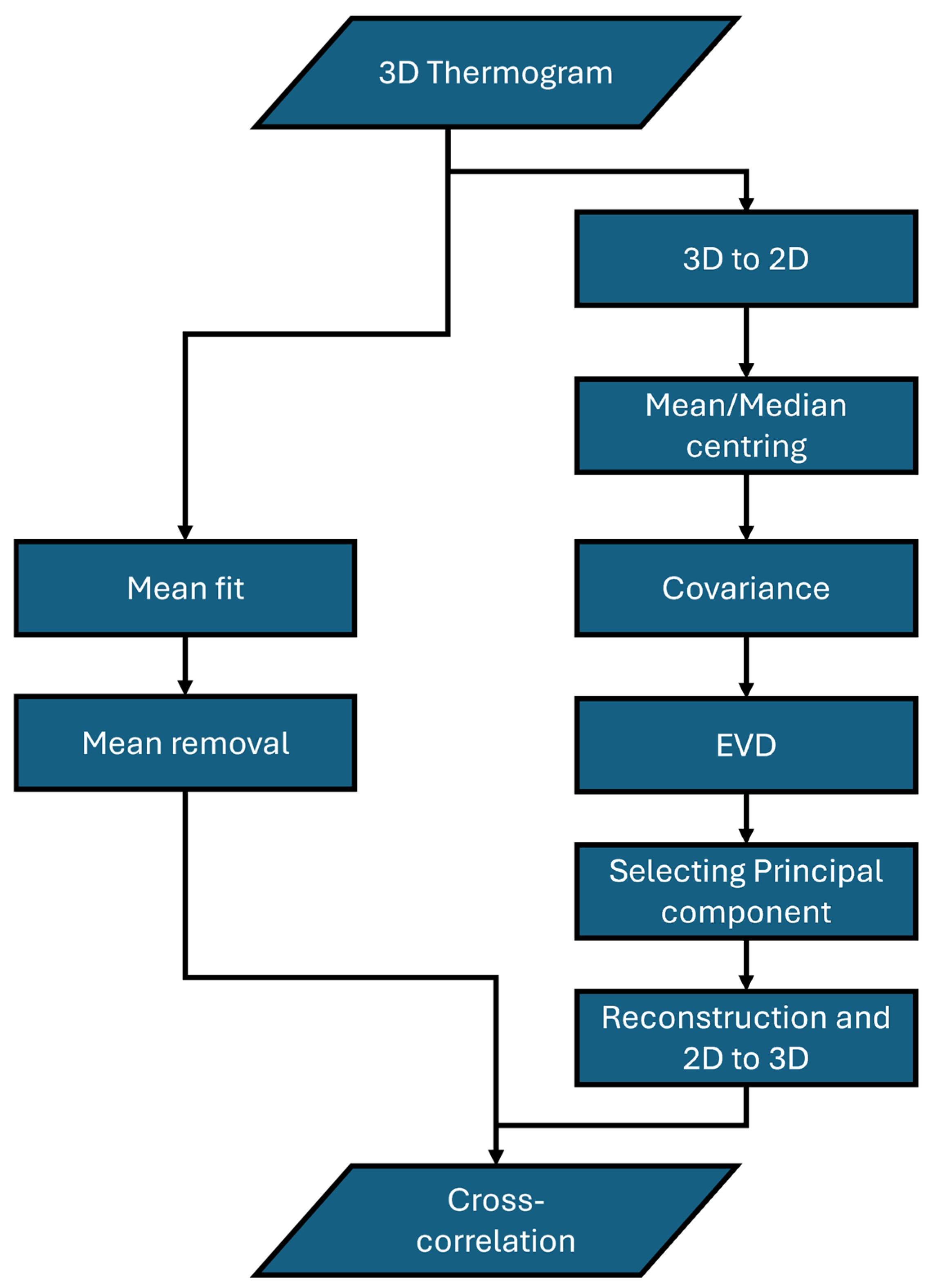
2. Theory
3. Experimentation and Test Sample
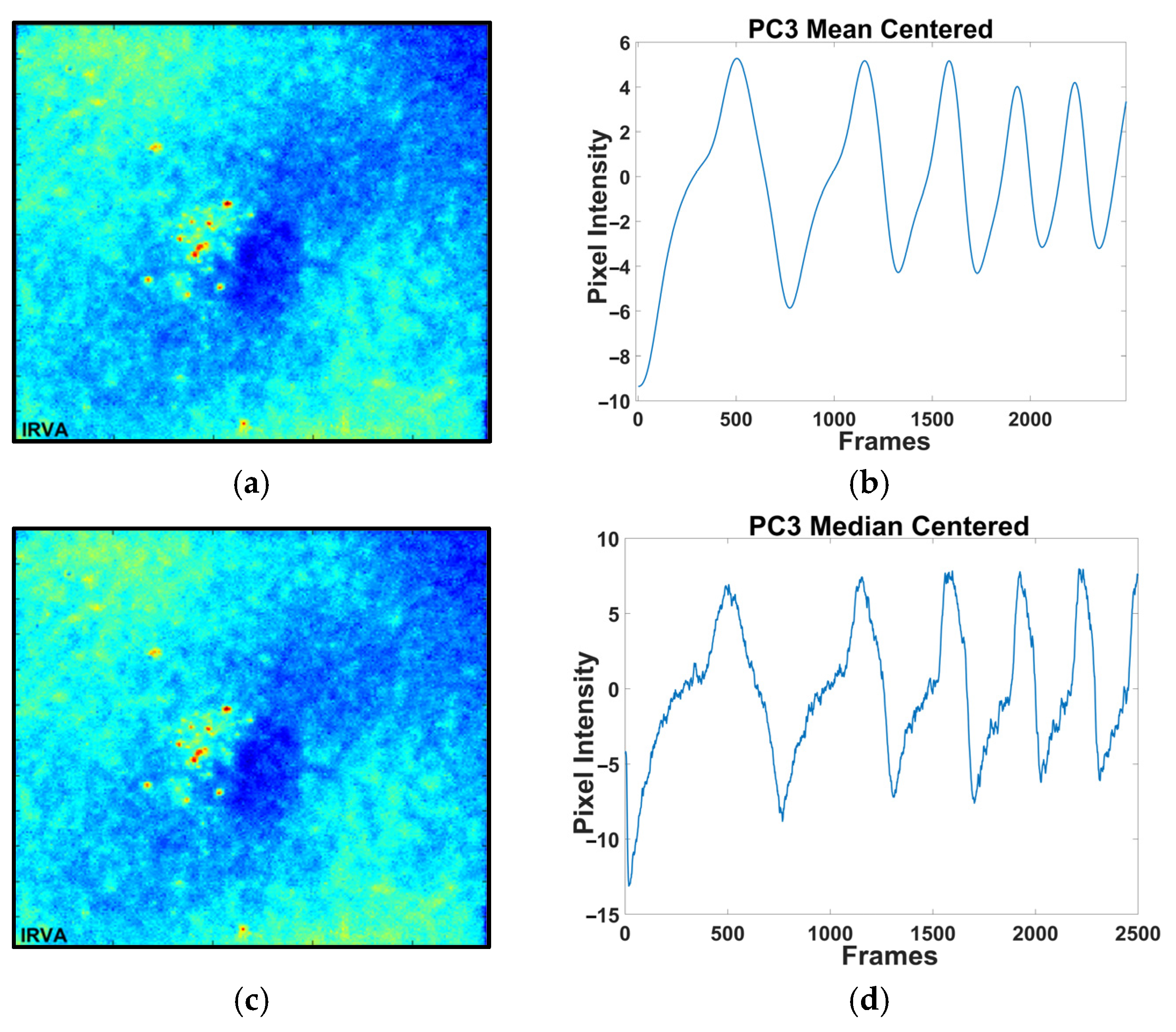
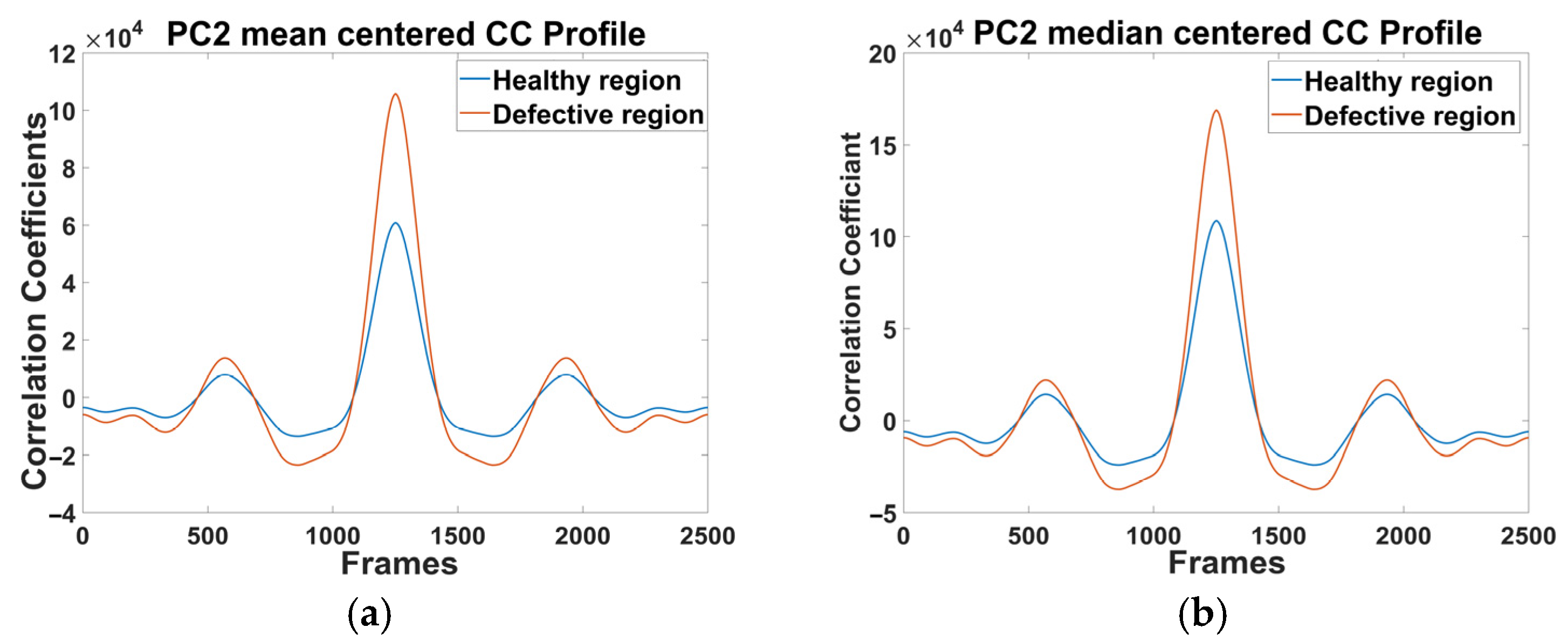
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Maldague, X. Theory and Practice of Infrared Technology for Nondestructive Testing; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Maldague, X.P.V. Introduction to NDT by active infrared thermography. Mater. Eval. 2002, 60, 1060–1073. [Google Scholar]
- Yang, R.; He, Y. Optically and non-optically excited thermography for composites: A review. Infrared Phys. Technol. 2016, 75, 26–50. [Google Scholar] [CrossRef]
- Jena, C.; Sarbhai, N.; Mulaveesala, R.; Tuli, S. Pulsed Thermography Simulation: 1D, 2D and 3D Electro-Thermal Model Based Evaluation. Available online: https://www.ndt.net/?id=4376 (accessed on 10 October 2024).
- Montanini, R. Quantitative determination of subsurface defects in a reference specimen made of Plexiglas by means of lock-in and pulse phase infrared thermography. Infrared Phys. Technol. 2010, 53, 363–371. [Google Scholar] [CrossRef]
- Chernykh, S.E.; Kostin, V.N.; Komolikov, Y.I. Thermal Testing of Corundum Ceramic Plates. Russ. J. Nondestruct. Test. 2023, 59, 977–984. [Google Scholar] [CrossRef]
- Maldague, X.; Marinetti, S. Pulse phase infrared thermography. J. Appl. Phys. 1996, 79, 2694–2698. [Google Scholar] [CrossRef]
- Mulaveesala, R.; Dua, G.; Arora, V.; Siddiqui, J.A.; Muniyappa, A. Pulse compression favourable aperiodic infrared imaging approach for non-destructive testing and evaluation of bio-materials. In Thermosense: Thermal Infrared Applications XXXIX; SPIE: Bellingham, WA, USA, 2017; p. 102140G. [Google Scholar] [CrossRef]
- Tuli, S.; Chatterjee, K. Frequency modulated thermal wave imaging. AIP Conf. Proc. 2012, 1430, 523–526. [Google Scholar] [CrossRef]
- Krapez, J.-C.; Pacou, D.; Gardette, G. Lock-in thermography and fatigue limit of metals. In Proceedings of the 2000 International Conference on Quantitative InfraRed Thermography, QIRT Council, 2000, Reims, France, 18–21 July 2000. [Google Scholar] [CrossRef]
- Chung, Y.; Shrestha, R.; Lee, S.; Kim, W. Thermographic Inspection of Internal Defects in Steel Structures: Analysis of Signal Processing Techniques in Pulsed Thermography. Sensors 2020, 20, 6015. [Google Scholar] [CrossRef]
- Silipigni, G.; Burrascano, P.; Hutchins, D.A.; Laureti, S.; Petrucci, R.; Senni, L.; Torre, L.; Ricci, M. Optimization of the pulse-compression technique applied to the infrared thermography nondestructive evaluation. NDT E Int. 2017, 87, 100–110. [Google Scholar] [CrossRef]
- Vavilov, V.P.; Chulkov, A.O.; Shiryaev, V.V.; Kuimova, M.V.; Zhang, H. Noise suppression in pulsed IR thermographic NDT: Efficiency of data processing algorithms. NDT E Int. 2024, 148, 103240. [Google Scholar] [CrossRef]
- Mulaveesala, R.; Arora, V.; Dua, G.; Rani, A.; Kher, V.; Sharma, A.; Kaur, K. Pulse compression favorable thermal wave imaging methods for testing and evaluation of carbon fibre reinforced polymer. SPIE-Intl. Soc. Opt. Eng. 2020, 11409, 114090S. [Google Scholar] [CrossRef]
- Sharma, A.; Mulaveesala, R.; Arora, V. Novel Analytical Approach for Estimation of Thermal Diffusivity and Effusivity for Detection of Osteoporosis. IEEE Sens. J. 2020, 20, 6046–6054. [Google Scholar] [CrossRef]
- Mulaveesala, R.; Ghali, V.S.; Arora, V. Applications of non-stationary thermal wave imaging methods for characterisation of fibre-reinforced plastic materials. Electron. Lett. 2013, 49, 118–119. [Google Scholar] [CrossRef]
- Mulaveesala, R.; Vaddi, J.S.; Singh, P. Pulse compression approach to infrared nondestructive characterization. Rev. Sci. Instrum. 2008, 79, 9. [Google Scholar] [CrossRef]
- Tabatabaei, N.; Mandelis, A.; Amaechi, B.T. Thermophotonic radar imaging: An emissivity-normalized modality with advantages over phase lock-in thermography. Appl. Phys. Lett. 2011, 98, 163706. [Google Scholar] [CrossRef]
- Tabatabaei, N. Matched-Filter Thermography. Appl. Sci. 2018, 8, 581. [Google Scholar] [CrossRef]
- Ricci, M.; Zito, R.; Laureti, S. Pseudo-noise pulse-compression thermography: A powerful tool for time-domain thermography analysis. NDT E Int. 2024, 148, 103218. [Google Scholar] [CrossRef]
- Gong, J.; Liu, J.; Qin, L.; Wang, Y. Investigation of carbon fiber reinforced polymer (CFRP) sheet with subsurface defects inspection using thermal-wave radar imaging (TWRI) based on the multi-transform technique. NDT E Int. 2014, 62, 130–136. [Google Scholar] [CrossRef]
- Dua, G.; Arora, V.; Mulaveesala, R. Defect Detection Capabilities of Pulse Compression Based Infrared Non-Destructive Testing and Evaluation. IEEE Sens. J. 2021, 21, 7940–7947. [Google Scholar] [CrossRef]
- Rajic, N. Principal component thermography for flaw contrast enhancement and flaw depth characterisation in composite structures. Compos. Struct. 2002, 58, 521–528. [Google Scholar] [CrossRef]
- Yousefi, B.; Sfarra, S.; Sarasini, F.; Castanedo, C.I.; Maldague, X.P.V. Low-rank sparse principal component thermography (sparse-PCT): Comparative assessment on detection of subsurface defects. Infrared Phys. Technol. 2019, 98, 278–284. [Google Scholar] [CrossRef]
- Marinetti, S.; Grinzato, E.; Bison, P.; Bozzi, E.; Chimenti, M.; Pieri, G.; Salvetti, O. Statistical analysis of IR thermographic sequences by PCA. Infrared Phys. Technol. 2004, 46, 85–91. [Google Scholar] [CrossRef]
- Das, P.; Arora, V.; Mulaveesala, R. Novel Insights on Spatio-Temporal Analysis for Frequency Modulated Thermal Wave Imaging Using Principal Component Analysis on Glass Fibre Reinforced Polymer Material. J. Nondestruct. Eval. 2024, 43, 34. [Google Scholar] [CrossRef]
- Ibarra-Castanedo, C.; González, D.; Klein, M.; Pilla, M.; Vallerand, S.; Maldague, X. Infrared image processing and data analysis. Infrared Phys. Technol. 2004, 46, 75–83. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Fleuret, J.; Klein, M.; Théroux, L.-D.; Georges, M.; Ibarra-Castanedo, C.; Maldague, X. Robust Principal Component Thermography for Defect Detection in Composites. Sensors 2021, 21, 2682. [Google Scholar] [CrossRef]
- Milovanović, B.; Gaši, M.; Gumbarević, S. Principal Component Thermography for Defect Detection in Concrete. Sensors 2020, 20, 3891. [Google Scholar] [CrossRef] [PubMed]
- Ghali, V.S.; Mulaveesala, R. Frequency modulated thermal wave imaging techniques for non-destructive testing. Insight Non-Destruct. Test. Cond. Monit. 2010, 52, 475–480. [Google Scholar] [CrossRef]
- Kaur, K.; Mulaveesala, R. An efficient data processing approach for frequency modulated thermal wave imaging for inspection of steel material. Infrared Phys. Technol. 2019, 103, 103083. [Google Scholar] [CrossRef]








| Post-Processing Technique | SNR in dB |
|---|---|
| CC | 34.304 |
| PC1 MEAN | 26.512 |
| PC1 MEDIAN | 26.512 |
| PC2 MEAN | 27.724 |
| PC2 MEDIAN | 27.724 |
| PC2 MEAN CC | 33.676 |
| PC2 MEDIAN CC | 33.676 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, I.; Arora, V.; Babu, P.; Mulaveesala, R. Novel Statistical Analysis Schemes for Frequency-Modulated Thermal Wave Imaging for Inspection of Ship Hull Materials. NDT 2024, 2, 445-455. https://doi.org/10.3390/ndt2040027
Singh I, Arora V, Babu P, Mulaveesala R. Novel Statistical Analysis Schemes for Frequency-Modulated Thermal Wave Imaging for Inspection of Ship Hull Materials. NDT. 2024; 2(4):445-455. https://doi.org/10.3390/ndt2040027
Chicago/Turabian StyleSingh, Ishant, Vanita Arora, Prabhu Babu, and Ravibabu Mulaveesala. 2024. "Novel Statistical Analysis Schemes for Frequency-Modulated Thermal Wave Imaging for Inspection of Ship Hull Materials" NDT 2, no. 4: 445-455. https://doi.org/10.3390/ndt2040027
APA StyleSingh, I., Arora, V., Babu, P., & Mulaveesala, R. (2024). Novel Statistical Analysis Schemes for Frequency-Modulated Thermal Wave Imaging for Inspection of Ship Hull Materials. NDT, 2(4), 445-455. https://doi.org/10.3390/ndt2040027






