Development of Non-Destructive Dynamic Characterization Technique for MMCs: Predictions of Mechanical Properties for Al@Al₂O₃ Composites

Abstract

In the past several decades, many destructive and non-destructive testing techniques have been developed to evaluate the characteristics of metal matrix composites (MMCs). This research aims to calculate the mechanical properties of the Al@Al${}_2$O${}_3$ composites by varying alumina nanoparticles (Al${}_2$O${}_3$ NPs) content using a non-invasive, position sensing detector (PSD) unit-based optical method. The composite was prepared by a powder metallurgy technique, and its characterization was conducted using SEM and XRD to understand its surface morphology and microstructure. The natural frequency and Young’s modulus of the composite were estimated experimentally. Young’s modulus was calculated using this natural frequency. The proposed study shows that Young’s modulus of the composite increases with an increase in Al${}_2$O${}_3$ NPs content in the composition, irrespective of the testing method. Along with this, natural frequency also increases with the increase in the Al${}_2$O${}_3$ NPs content. Evaluated properties were compared with the numerical modeling using COMSOL Multiphysics. The experimental and numerical results are equivalent and within the margin of error. This study illustrates the development of an experimental approach for evaluating the mechanical properties of a composite material. This experimental approach can be used whenever sample dimension and space are constrained to evaluate the mechanical behavior of nanomaterials and nanocomposites.

1. Introduction

Aluminum, a silvery-white metal, has a face-centered-cubic (FCC) crystal structure at room temperature. It is widely used in various applications such as busbars, cooking pans, electric wires, airplane parts, cables, refrigerators, heat exchangers, window frames, beer kegs, etc., because it has excellent corrosion resistance, high thermal conductivity, low specific density, excellent formability, good castability, and high ductility [1,2]. However, aluminum’s lower hardness and mechanical strength limit its use in advanced engineering applications. The mechanical properties of aluminum can be enhanced by alloying with silicon, magnesium, copper, manganese, and zinc [3]. Alloying increases the mechanical properties of aluminum because of second-phase hardening and solid solution hardening due to the restriction of dislocation movement. However, no alloying element shows entirely solid solubility with aluminum.

In recent times, metal matrix composites (MMCs) have attracted the attention of researchers across the globe as they possess strength, low coefficient of thermal expansion, better creep and fatigue resistance, high thermal and electrical conductivity, superior wear and corrosion resistance, low weight, higher elastic modulus, and high service temperature [4]. In the 1980s, there was rapid progress in the development and application of aluminum composites [5,6]. Aluminum composites are widely employed in automation, automobile, aircraft, defense, and aerospace industries because of their improved properties such as high wear resistance, lightweight, low thermal coefficient of expansion, high thermal conductivity, and excellent mechanical strength [7,8]. Aluminum matrix composites have been reinforced with several types of ceramic particles such as B${}_4$C [9], TiC [10], Al${}_2$O${}_3$ [11], SiO${}_2$ [12], BN [13], and SiC [14]. The ceramic particles were added to the aluminum matrix to improve the hardness, thermal conductivity, strength, and wear resistance [15]. However, Al${}_2$O${}_3$-reinforced metal matrix composites are recognized as an advanced group of composites owing to their superior mechanical, anti-corrosion, and wear performance [16]. Synthesis of MMCs has been carried out by various techniques such as physical vapor deposition, molten metal technology, chemical vapor deposition, powder metallurgy, thermal spraying, plasma spraying, electrodeposition, and electroless deposition [17,18]. Among these techniques, powder metallurgy has attracted much attention due to its low production time, simplicity, near-net shape capability, high flexibility, and low cost [19].

Several destructive testing (DT) and non-destructive testing (NDT) methods have been developed in the past few decades to determine the performance of composite materials. The DT methods involve fatigue testing, impact testing, creep testing, hardness testing, shear testing, and torsion testing. In DT methods, tests are performed up to the failure of the composite material to determine its behavior under various loading conditions.However, tested samples cannot be reused after DT. Hence, NDT methods are preferred to save cost, effort, and time compared to DT methods. Numerous NDT methods such as thermography, shearography, radiography, ultrasonic, image processing, and optical methods have gained extensive attention to evaluate the integrity, condition, and properties of composite materials without damaging their effectiveness [20].NDT techniques are essential for evaluating the integrity and quality of materials and structures without causing damage. Nowadays, optical based position sensing detectors (PSD) have emerged as valuable tools in NDT applications due to their non-contact nature, high accuracy, and real-time position and displacement measurement capabilities [21].These detectors primarily focus on position and displacement measurements that indirectly provide insights into certain material characteristics such as natural frequency, stiffness and Youngs modulus etc. Various methods, including axial extensometers, strain gauges, digital image correlation measurement, universal testing, and ultrasound testing, have also been explored to determine the mechanical behavior of materials under different mechanical loading conditions [21,22,23]. In the ultrasound testing method, the elastic properties of materials can be estimated by measuring the attenuation of amplitude or sound velocity [24]. The magnetic-based NDT method measures the hysteresis loops and employs the Barkhausen effect to estimate the mechanical characteristics of magnetic materials [25]. All these techniques have certain drawbacks. Most of the techniques have common criteria and restrictions for assessing the mechanical characteristics of the material, such as the standard shape and size of the sample.

The present work aims to determine the mechanical properties of Al@Al${}_2$O${}_3$ composites using a position-sensing detector (PSD) unit-based optical method. Al@Al${}_2$O${}_3$ composites were fabricated using the powder metallurgy method and the effect of various vol.% of Al${}_2$O${}_3$ on the mechanical properties of Al@Al${}_2$O${}_3$ composite was examined. A scanning electron microscope (SEM) and an X-ray diffractometer (XRD) were used to examine the surface morphology and microstructure of the mechanically milled Al@Al${}_2$O${}_3$ composite powder, respectively. The natural frequencies and corresponding mode shapes of sintered Al@Al${}_2$O${}_3$ composites were experimentally estimated. Al@Al${}_2$O${}_3$ composite was mechanically fixed and excited with a microactuator. The response was recorded by a PSD unit-based optical method. The elastic modulus of the Al@Al${}_2$O${}_3$ composite was estimated using the help of recorded natural frequencies, compression test, and finite element analysis. The obtained results showed that the numerically predicted values are within 11% of the experimentally recorded values.

2. Materials

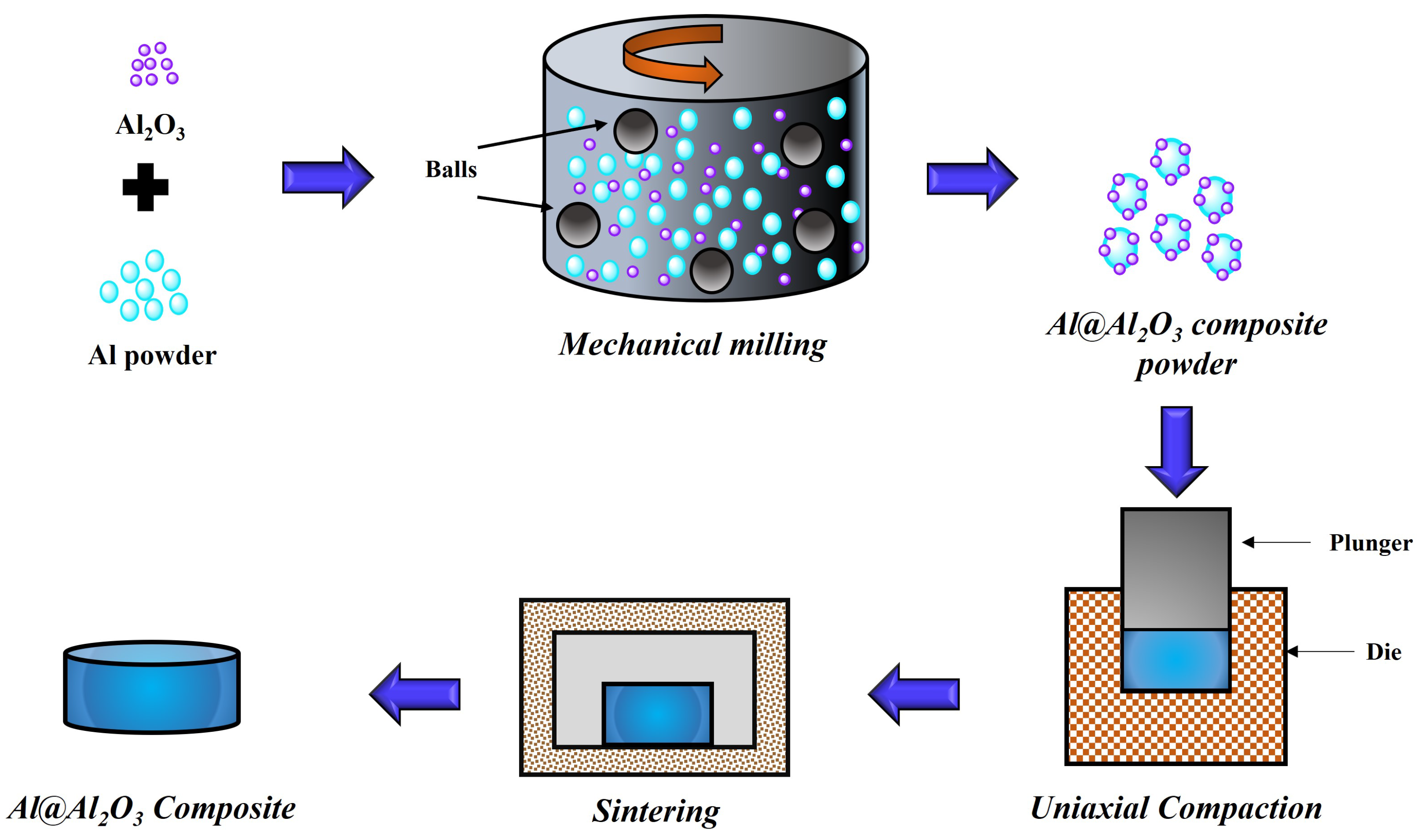
2.1. Experimentation

In this work, both the Al powder (purity: 99%, average particle size: 30–50 $\mathsf{\mu }$m) and Al${}_2$O${}_3$ nanoparticles (purity: 99.9%, average particle size: 50 nm) were procured from Sigma-Aldrich. To study the effects of Al${}_2$O${}_3$ nanoparticles reinforcement, the content of Al${}_2$O${}_3$ nanoparticles was varied as 0, 5, 10, and 15 vol.%. A schematic diagram for the fabrication of Al@Al${}_2$O${}_3$ composite is shown in Figure 1. Initially, Al powder and Al${}_2$O${}_3$ nanoparticles were milled in a high-purity Ar atmosphere for 4 h at a rotational speed of 300 rpm. The stainless-steel balls were used to achieve even dispersion of Al${}_2$O${}_3$ nanoparticles within the Al matrix. Then, the composite powder was compacted in cylindrical high-speed steel die (9 mm diameter pellets) using a universal system (600 MPa). After this, prepared compacts were sintered at 580 °C for 2 h under an Ar atmosphere. After sintering, the composite samples were cooled to room temperature with the furnace. The thickness and diameter of the sintered cylindrical disc shape Al@Al${}_2$O${}_3$ composite were 5.5 mm and 9 mm, respectively.

2.2. Characterization

The surface morphology and distribution of elements of the Al@Al${}_2$O${}_3$ composite powder were examined by using a scanning electron microscope (SEM, FEI-Apreo-S) attached with an energy dispersive X-ray (EDS) facility. X-ray diffraction (XRD, RIGAKU) analysis of the Al@Al${}_2$O${}_3$ composite powder was performed by using CuK$\alpha$ radiation. The compression tests of sintered Al@Al${}_2$O${}_3$ composites were carried out using a BISS UNO 100 universal testing machine with a 0.1 mm/min strain rate at room temperature.

3. Methods

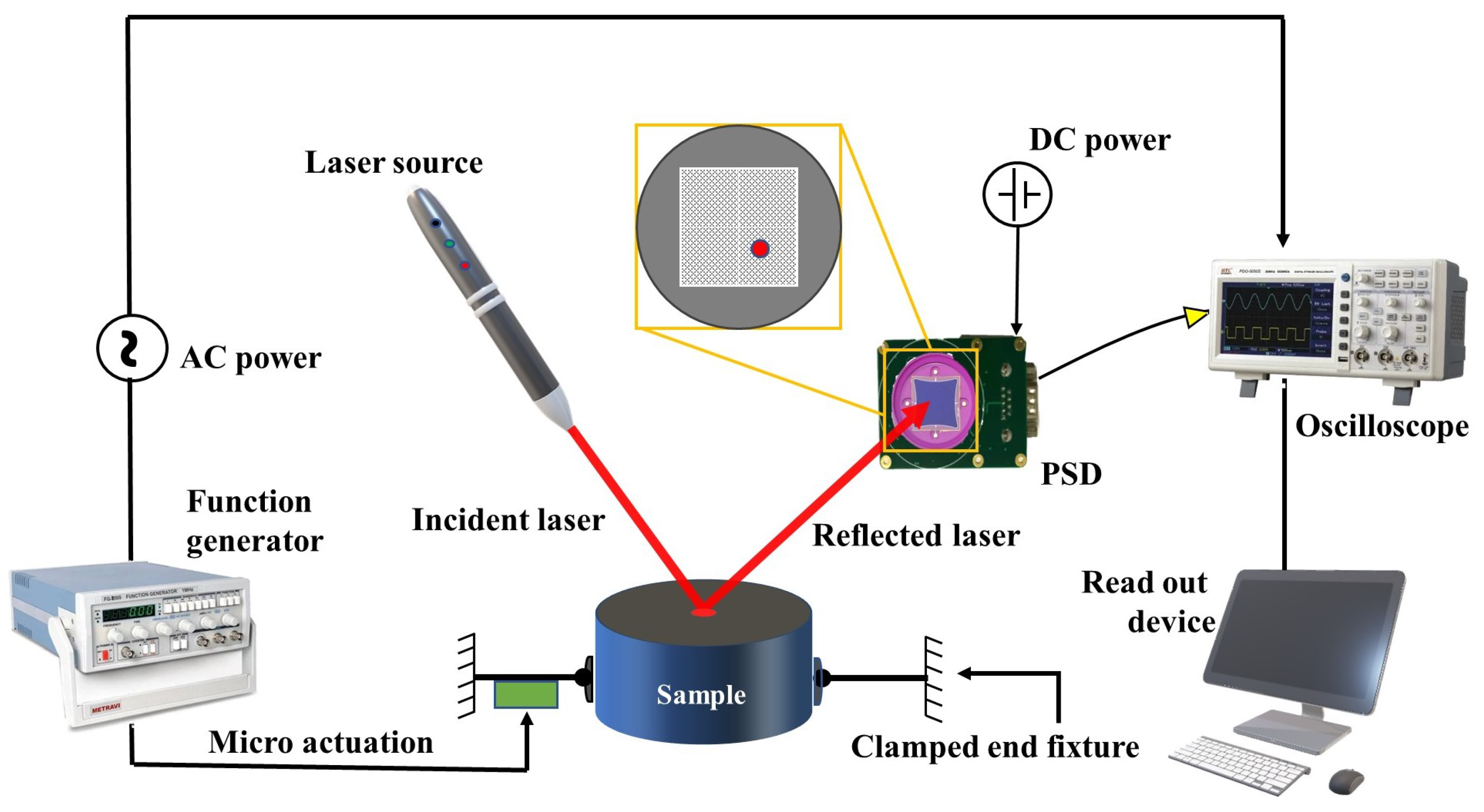
3.1. Non-Invasive PSD-Based Experimental Setup

Figure 2 provides a detailed description of the experimental setup. An external 240 V, 50 Hz AC voltage source drives a laser source with 23 mW of power and a wavelength of 650 nm. A circular fixture was used to hold the Al@Al${}_2$O${}_3$ composites sample. The center of the sample is marked. Activation of the sample is achieved through a microactuator, and the response is measured at a predetermined location using a Position-Sensitive Device (PSD) positioned at the center of the sample. The PSD detects the laser beam (measurement beam) that is directed onto the sample surface, reflecting towards the PSD. This beam captures information about the vibrations of the structure. The displacement of the sample’s center is traced by monitoring the laser position using the PSD [Hamamatsu S5990-1], while the associated displacement amplitude is measured through an AC operating circuit [Hamamatsu C4674-01]. A spectrum analyzer is used to read the output of the circuit. Two channels are used to quantify the displacement amplitude in the X and Y axes. FFT is employed to convert the time domain data into frequency responses, providing insight into the sample’s vibrations at the designated measurement points. Sequential measurements are taken on both the sample and the base to capture their respective responses at the specified measurement position [21].

3.2. Response Measurement

The Al@Al${}_2$O${}_3$ composite sample is securely positioned in a clamped end beam configuration, ensuring uniform cross-section along the specimen. A micro-actuator is employed to induce structural vibrations in the sample, and the resulting transient response is measured using a PSD. To eliminate any base-related modes, the transfer function is determined from the ratio of the sample’s response to the base response. The natural frequency of the sample is identified by the presence of peaks in the frequency response.

3.3. Evaluation of Young’s Modulus

The frequency response of the sample was analyzed to assess its mechanical properties in a clamped end configuration, under the assumption of minimal damping in the system. The elastic modulus was estimated by evaluating the measured natural frequencies. The natural frequency for a clamped end boundary condition for a circular disc is given by [26]

$$E=\frac{f^2{\left(2\pi a^2\right)}^2\left(12\gamma (1-{\upsilon }^2)\right)}{{\lambda }^4{h}^3},$$

(1)

where E is the Young’s Modulus of the sample, f is the natural frequency, a is the diameter of the sample, $\gamma$ is the specific density, $\nu$ is the poison ratio while h is the thickness of the sample and $\lambda$ is the frequency parameter.

3.4. Numerical Modeling

A simplified model of an Al@Al${}_2$O${}_3$ composites unit cell with periodic boundary conditions is analyzed to obtain the homogenized property of the composite. The unit cell is indeed a representative volume element (RVE) that repeats itself to build the complete structure of the composite. The composite unit cell is assumed to be made of Al${}_2$O${}_3$ NPs embedded in aluminum matrix. In the current model, the unit cell is made of Al${}_2$O${}_3$ NPs placed at the center of an aluminum matrix. Three samples are prepared by varying the volume fraction of the Al${}_2$O${}_3$ NPs at 5%, 10% and 15%. The homogenized elastic properties of the composite material are computed based on the individual properties of the Al${}_2$O${}_3$ NPs and Al matrix. A comparison is made against values obtained from the Rule of Mixture (ROM). Further, the Al@Al${}_2$O${}_3$ composite is modeled as a unit cell in COMSOL Multiphysics (COMSOL Multiphysics^® v. 6.1., Stockholm, Sweden). Material properties of modeled geometry have been selected from the previous literature and assigned to the individual components of the composite model [27]. The listed geometrical parameters of the composite for homogenization are shown in

Table 1. Geometrical parameters of the unit cell numerical modeling.

Parameters	Sample
	Al-5%Al${}_2$O${}_3$	Al-10%Al${}_2$O${}_3$	Al-15%Al${}_2$O${}_3$
Radius of Al${}_2$O${}_3$ NP, R (nm)	25	25	25
Volume of Al${}_2$O${}_3$ NP, Vn (nm${}^3$)	65,416.67	65,416.67	65,416.67
Volume ratio, (Vn/[Vn+Vm])	0.05	0.1	0.15
Volume of Al matrix, Vm (nm${}^3$)	621,458.3	588,750	55,6041.7
Side length of unit cell, a (nm)	85.33699	83.81279	82.23104

.

Figure 3 illustrates the techniques employed in the numerical analysis to determine the homogenized property of the composite sample, utilizing a micro–macro decoupling approach. The nonlinear two-scale analysis is carried through the periodic structures (unit cells) and the functional macroscopic constitutive equation [28,29]. Homogenization theory is utilized to solve the two-scale boundary value problems (BVPs) derived from the framework [28,30]. Material parameters for the assumed constitutive model are obtained through several numerical material tests (NMTs) conducted on the unit cell model. Equation (2) shows the governing equation used to model BVPs with external material points for NMTs with arbitrary patterns of macro-scale loading [26],

$$F={\nabla }_{Y\Phi }(X;Y)={\nabla }_{YW}(X;Y)+1=H\left(X\right)+{\nabla }_{YU}(X;Y)+1,$$

(2)

where X represents the macroscopic material point in the macro scale reference configuration and is a dependent variable in the micro-scale kinematics. Here, U denotes the periodic displacement field for Y that corresponds to a change caused by heterogeneity at the micro-scale, 1 is the second-order identity tensor, H is the displacement gradient that is independent of Y, and ${\nabla }_{Y\Phi }$ is the gradient operator for the micro-scale Y. Homogenization is performed on a computational multiscale analysis system (CMAS) by considering the unidirectional Al${}_2$O${}_3$ NPs in an aluminum matrix. The following steps are followed for the homogenization using the constituting materials on a unit cell level and then implemented to the macro-scale leveled Al@Al${}_2$O${}_3$ composites [31,32].

3.4.1. Create a Unit Cell Model

The unit cell model was created in COMSOL. As illustrated in Figure 3, the material properties of the individual constituents were assigned, followed by meshing of the unit cell model.

3.4.2. Homogenization Analysis

After meshing and boundary conditions, a numerical material test was performed, and further, equivalent properties such as modulus of elasticity, density, and poison ratio were calculated. Here, the following brief steps for the NMT analysis are as follows.

• A macroscopic constitutive material model has been made after integrating the Equation (2).
• Conducting NMTs on a unit cell model using Finite Element mesh

  −

  Provide the macroscopic displacement gradient H followed by the relative displacement vector $q^{\left[J\right]}$ of the external points,

  $$q^{\left[J\right]}=H·L^{\left[J\right]}$$

  (3)

  −

  The BVP equations are illustrated as per the following equations.

  $$\left.\begin{array}{c}\nabla y·P=0\\ F=\nabla y·\omega \end{array}\right\}in{y}_0$$

  (4)

  $$P=\tau \left(F\right),$$

  (5)

  $$\left.\begin{array}{c}{\omega }^{\left[J\right]}-{\omega }^{[-J]}=\tilde{H}·L^{\left[J\right]}\\ {\tilde{T}}^{\left[J\right]}=\frac{1}{\partial {y_0}^{\left[J\right]}}{\int }_{\partial {y_0}^{\left[J\right]}}^{.}P.E^{\left[J\right]}ds\end{array}\right\}on\partial {y_0}^{\left[J\right]}$$

  (6)

  On imposing,

  $${\omega }^{\left[J\right]}-{\omega }^{[-J]}=q^{\left[J\right]},$$

  (7)

  where T is a tractive force vector, F is force vector, and P is a nominal stress vector.

  −

  Obtain 1st-Piola–Kirchhoff (PK) or nominal stress $P_{iJ}$ at each incremental step n for all loading patterns $\alpha$ by directly solving the extended micro-scale BVP with the response force vector,

  $$P_{iJ}=\frac{R_i\left[J\right]}{\left|\partial {Y_0}^{\left[J\right]}\right|},$$

  (8)

  where R and $\partial Y_0^{\left[J\right]}$ denote the reaction force and area, respectively.

• Identifying macroscopic parameters for materials

  −

  Calculate the macro-scale 2nd PK stress using NMT data.

  $$S^{[n,\alpha ]}=\left({\left(F^{[n,\alpha ]}\right)}^{-1}{P}^{[n,\alpha ]}\right),$$

  (9)

  and the right-CG deformation tensors C[n,$\alpha$] and store all sets of data over $n_{step}^{\left[\alpha \right]}$

  −

  Create a function with the material parameters p

  −

  Identify the macroscopic material parameters p by solving the obtained algebraic Equation (8), where G and b are the coefficient matrix.

  $$Gp=b.$$

  (10)

  −

  Macroscopic FE-analysis

  Solve the macro-scale BVP using the assumed constitutive model with identified material parameters

3.4.3. Numerical Procedure for Macro Model

The Al@Al${}_2$O${}_3$ composites sample is modeled as a circular disc and assigned homogenized material properties, as shown in

Table 2. Geometrical and homogenized properties used for numerical analysis.

Parameters	Sample
	Al-5%Al${}_2$O${}_3$	Al-10%Al${}_2$O${}_3$	Al-15%Al${}_2$O${}_3$
Young’s Modulus (GPa)	131.97	151.68	170.76
Poison Ratio	0.3416	0.332	0.3288
Density (g/cm${}^3$)	2.76	2.83	2.89
Radius (mm)	12.5	12.5	12.5
Thickness (mm)	10	10	10

in the COMSOL Multiphysics. After the material assignment, the multiphysics domain is selected for the eigen frequency and frequency analysis of the composite material. To restrict the motion of the edge of samples, zero displacement boundary conditions is used along the circumference of the sample. The modal analysis technique is employed to determine the natural frequencies and corresponding mode shapes of the system.

4. Results

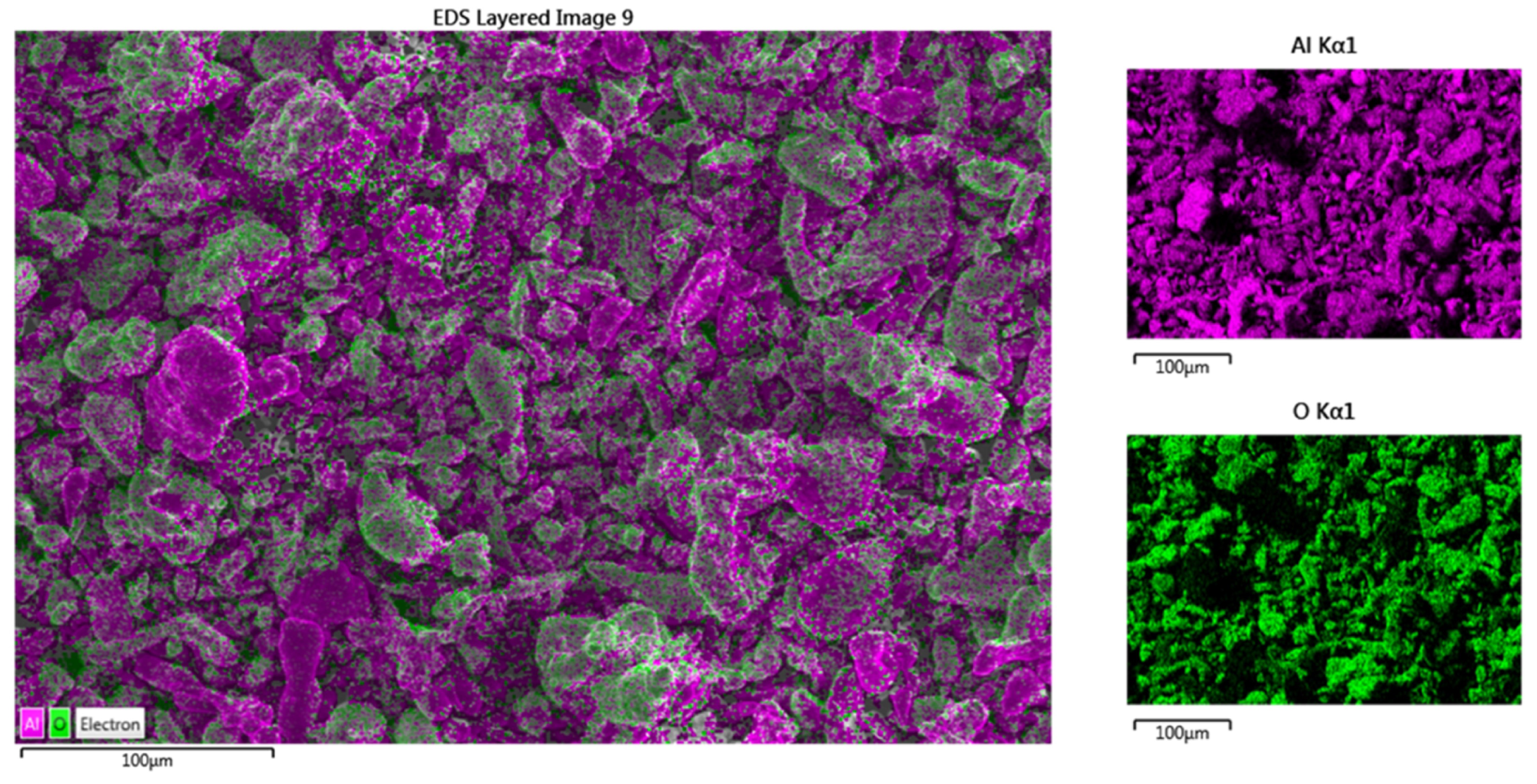
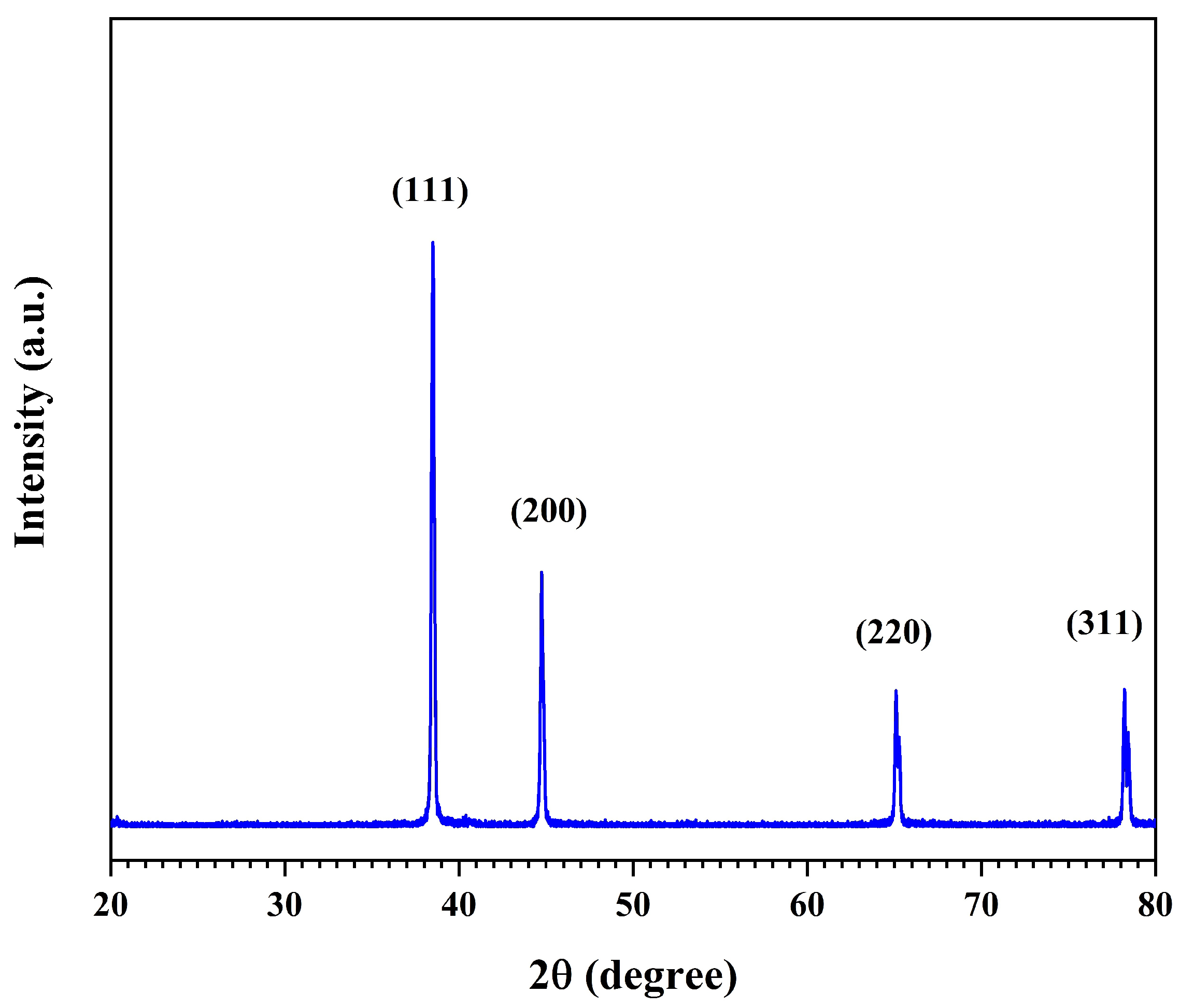
4.1. SEM, EDS and XRD Analysis of Al@Al${}_2$O${}_3$ Composite Powder

Figure 4 shows the SEM micrograph of Al@Al${}_2$O${}_3$ composite powder ball milled at 300 rpm. As shown in Figure 4a,b, the average powder diameter is decreased due to the cracking of Al powder into smaller particles during the ball milling process. In the present work, the average diameter of Al powders reduced from about 50 $\mathsf{\mu }$m to about 20 $\mathsf{\mu }$m, which leads to enhanced Al${}_2$O${}_3$ distribution. The EDS mapping of Al@Al${}_2$O${}_3$ composite powder is illustrated in Figure 5. The EDS mapping of Al@Al${}_2$O${}_3$ composite powder also shows that Al${}_2$O${}_3$ nanoparticles are strongly reinforced into the aluminum matrix. The XRD spectrum of Al@Al${}_2$O${}_3$ composite powder is depicted in Figure 6. The XRD pattern of Al@Al${}_2$O${}_3$ composite powder also indicates that Al${}_2$O${}_3$ nanoparticles are successfully reinforced into the aluminum matrix. However, the intensity of Al${}_2$O${}_3$ peak is low in the XRD spectrum because of the low content of Al${}_2$O${}_3$ nanoparticles.

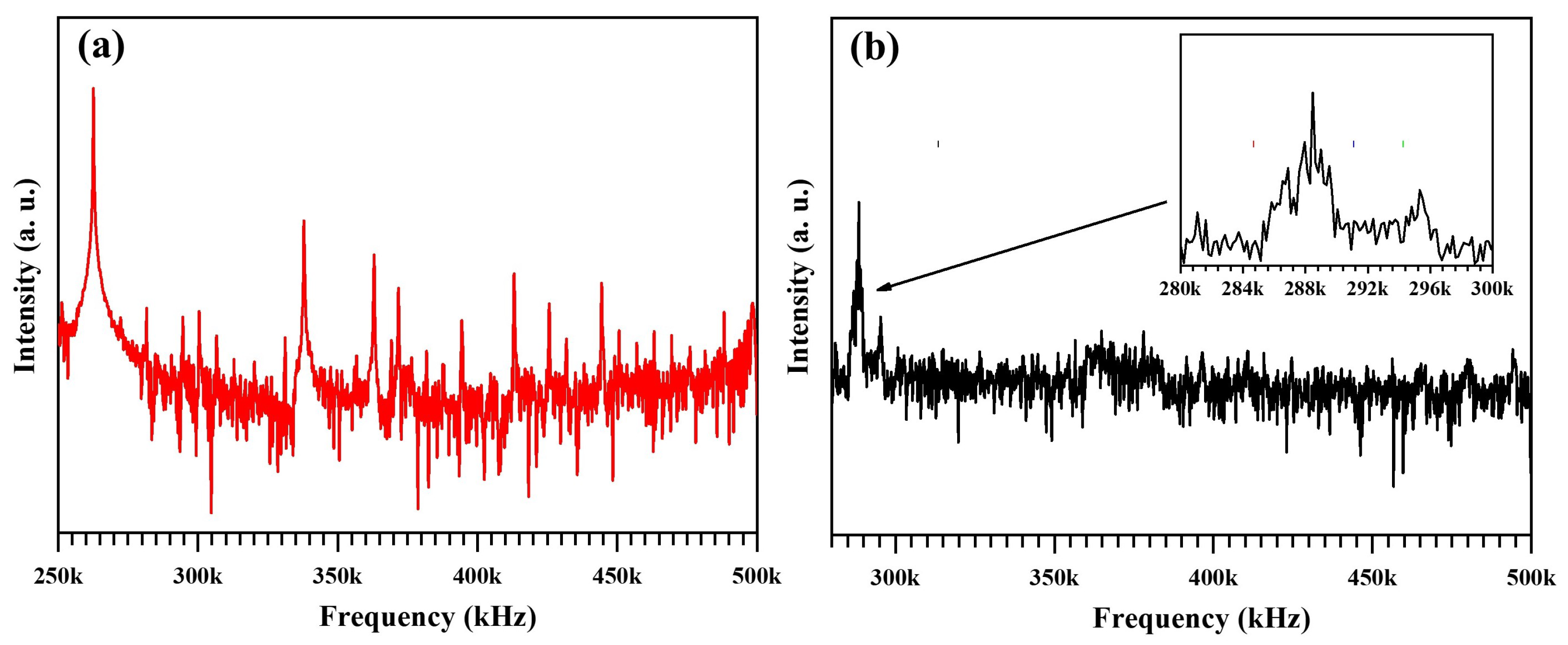
4.2. Experimental Studies

Measurements were taken at the center of the sample. The transient response of the Al@Al${}_2$O${}_3$ composites sample is acquired by exciting the sample with the impulse signal of 10 V (peak to peak) amplitude at 1 MHz frequency. Acquired time domain data were used to convert in frequency domain using Fast Fourier Transform (FFT). Further, the frequency domain data from the spectrum analyzer are processed in MATLAB. The peak in the frequency spectrum represents the natural frequency of the Al@Al${}_2$O${}_3$ composites samples.

Figure 7 shows the frequency response for the structure and the base. Figure 8 shows the transfer function for different samples with prominent peaks. The observed peaks correspond to the prominent natural frequencies, obtained by eliminating the effects of base excitation and other noise factors acting on the base. The transfer function indicates a natural frequency of 262 kHz for pure aluminum, while the composite with a 15 vol.% Al${}_2$O${}_3$ exhibits a natural frequency of 463 kHz. From Figure 8, we can observe that the natural frequency for the composite sample increases with the increase in the Al${}_2$O${}_3$ NPs content in the composite material.

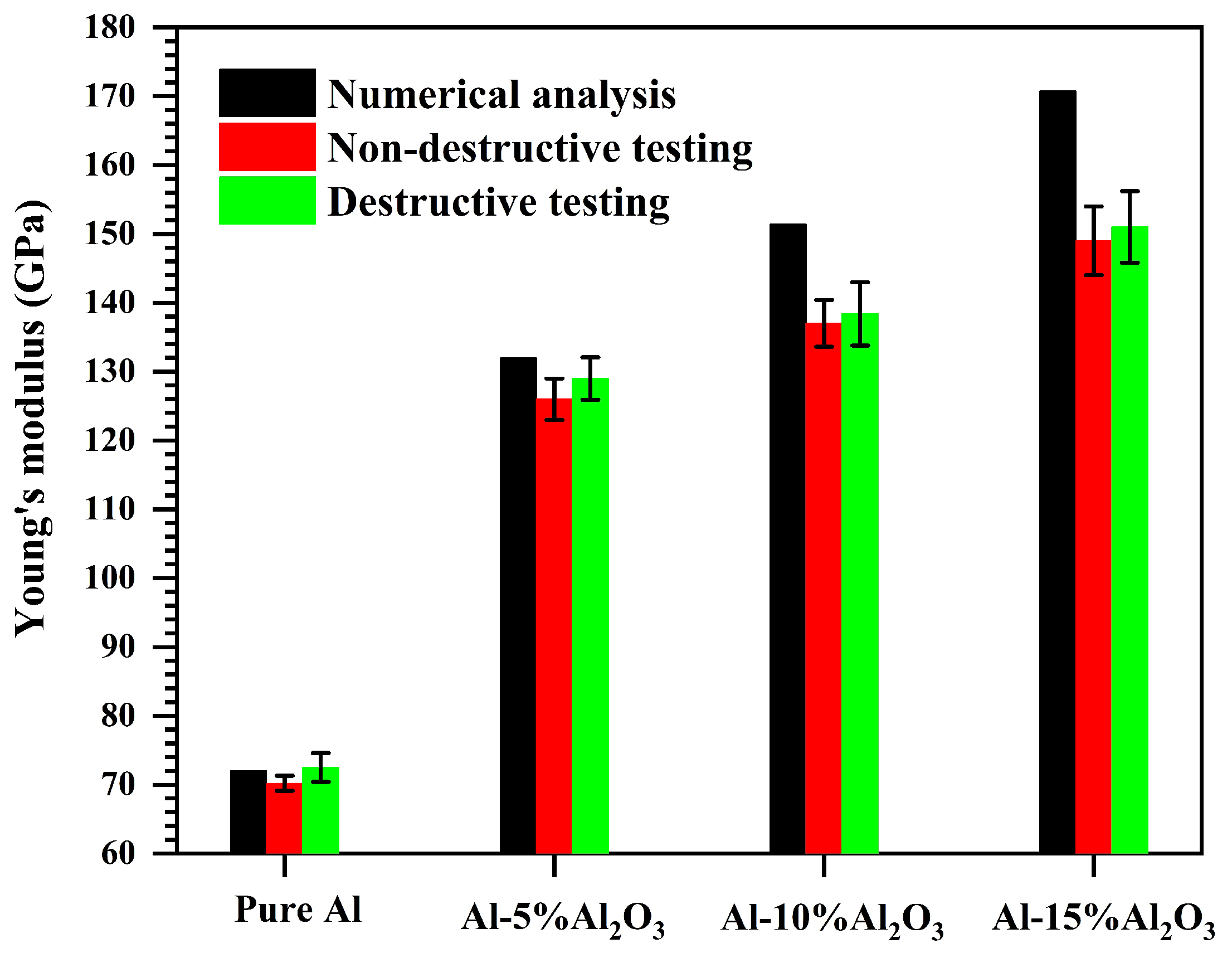
4.3. Comparison of Young’s Modulus for Validation

A comparative study is required to validate the results shown by the proposed non-destructive testing device. In the course of this, Young’s modulus has been used as material property for the comparison of results obtained from different techniques. Here, numerical study and compression (destructive) testing were used along with the proposed non-destructive method to estimate Young’s Modulus. Figure 9 shows the variation in Young’s modulus for different testing techniques with different Al${}_2$O${}_3$ NP content in composite samples. From the numerical analysis, it is observed that there is a increase in Young’s modulus values with an increase in Al${}_2$O${}_3$ NP content in the composite material, as expected due to linear composition dependency of material property, as shown in Equation (1).

The numerical value is the maximum possible strength of the material as it is predicted for the pure metal matrix without defects and best uniform reinforcement of nanofillers. Numerically, pure Al and the composite with 5%, 10%, and 15% volume of Al${}_2$O${}_3$ NPs give Young’s modulus values of 72 GPa, 132 GPa, 151.3 GPa, and 170.7 GPa, respectively. The non-destructive and destructive testing estimated a similar trend as the numerical predictions. It is observed that, the non-destructive analysis estimated a lower range of Young’s modulus values for all composite samples than numerical and destructive compression testing results.

However, the proposed device gives systematic errors of 3.1%, 2.4%, 1% and 1.3% for pure Al and composite with 5%, 10%, and 15% volume of Al${}_2$O${}_3$ NPs with Young’s modulus values of 70.2 GPa, 126 GPa, 137 GPa, and 149 GPa, compared to 72.5, 129.2, 138.4, and 151.1, as estimated from the compression test. The results of the destructive test are the realistic material properties for the composites and show that the increasing strength trend down after Al${}_2$O${}_3$ NP reinforcement, as impurities and defects across the Al matrix increases. The minor systematic error through the device occurred due to environmental interferences associated with the PSD sensor. The comparative study results give confidence and accuracy of estimations of Young’s modulus through the proposed non-destructive method.

4.4. Numerical Studies

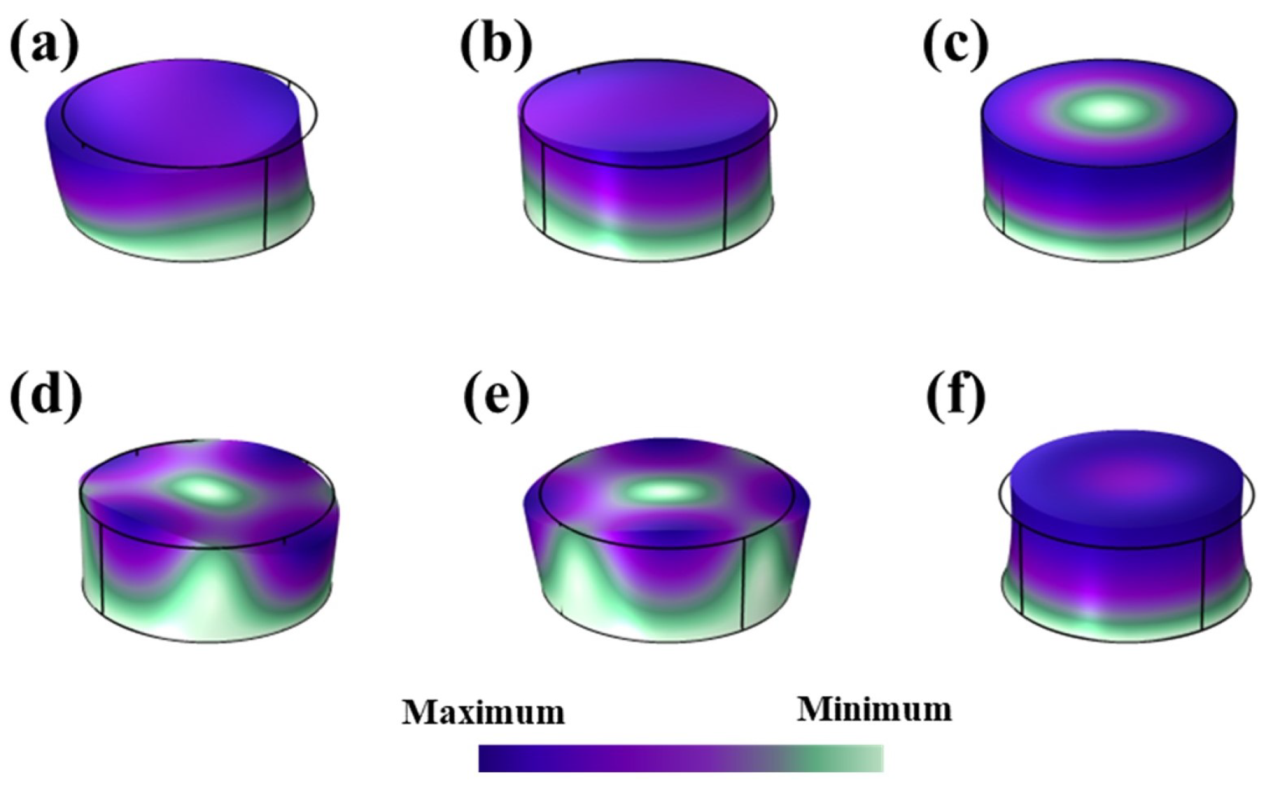
4.4.1. Modal Analysis

Modal analysis is a method to formulate the dynamics characteristic of a sample by calculating its natural frequency and mode shapes. The test was conducted on different compositions of aluminum, and the following results were obtained. Figure 10 represents the mode shape and its corresponding resonant frequency for the pure aluminum sample.

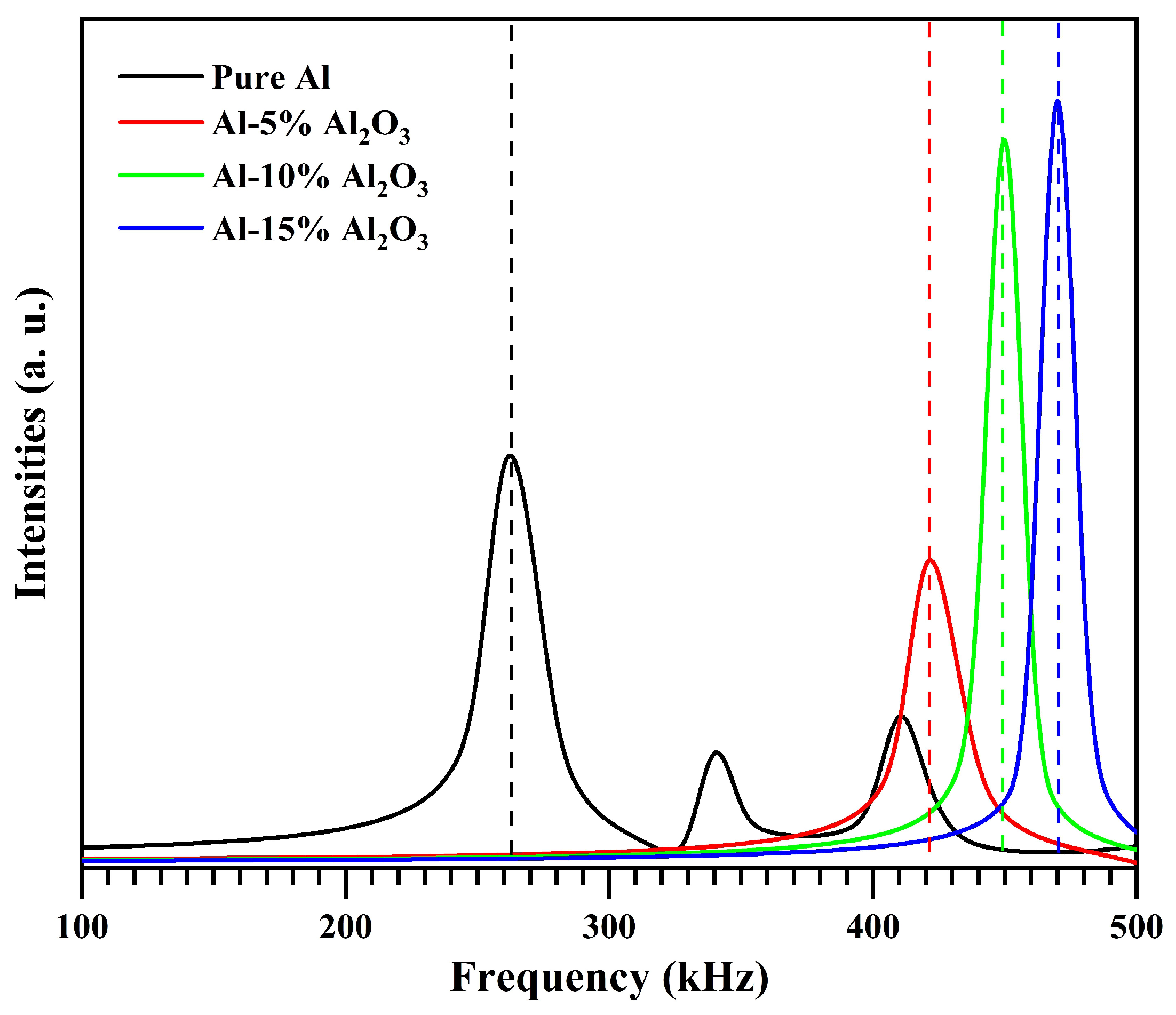
4.4.2. Frequency Response

Frequency domain analysis has been conducted using COMSOL Multiphysics. The peak in Figure 11 represents the natural frequency of the sample. These frequencies are obtained after assigning the corresponding homogenized property to the sample. The obtained natural frequencies of the sample are the same as those obtained from the PSD analysis with an acceptable margin error.

5. Conclusions

The powder metallurgy technique was used to fabricate Al/Al${}_2$O${}_3$ composites. The effect of vol.% variation of the Al${}_2$O${}_3$ NPs content in the composite material was evaluated using a PSD-based non-invasive optical technique. This non-invasive experimental approach helps to determine the dynamic behavior of the composites. The frequency response obtained from the experiments was used further to evaluate Young’s modulus of the composite samples. The significant peaks in the transfer function show the natural frequency at 262 kHz for pure aluminum and at 463 kHz for the composite with 15 vol.% Al${}_2$O${}_3$. Young’s modulus for pure aluminum was evaluated as 70.2 GPa while with 15 vol.% of Al${}_2$O${}_3$ NPs, it increases to 151 GPa. Homogenization optimizes the sample’s material properties, which are then applied to the composite’s model to determine the mechanical response through numerical analysis. A numerical evaluation of the frequency response and Young’s modulus of the composite sample was performed for the experimental comparison. The modulus of elasticity determined by the proposed experimental method and the finite element model are comparable and are within an acceptable margin of error. The modal analysis was performed to determine the natural frequencies and deformation patterns of the sample, while harmonic analysis was conducted to analyze the dynamic behavior of the sample. The sample’s frequency response reveals the damping properties, which characterize the decay of vibration in the sample. SEM and XRD were used to determine the surface morphology and microstructure of the material. This work demonstrates the development of an experimental method for determining the mechanical characteristics of a composite sample. This experimental method may be used on microstructure and biological samples to determine their mechanical response.