Precision and Stability in Hydrostatic Transmissions with Robust H∞ Control Under Parametric Uncertainties
Abstract
1. Introduction
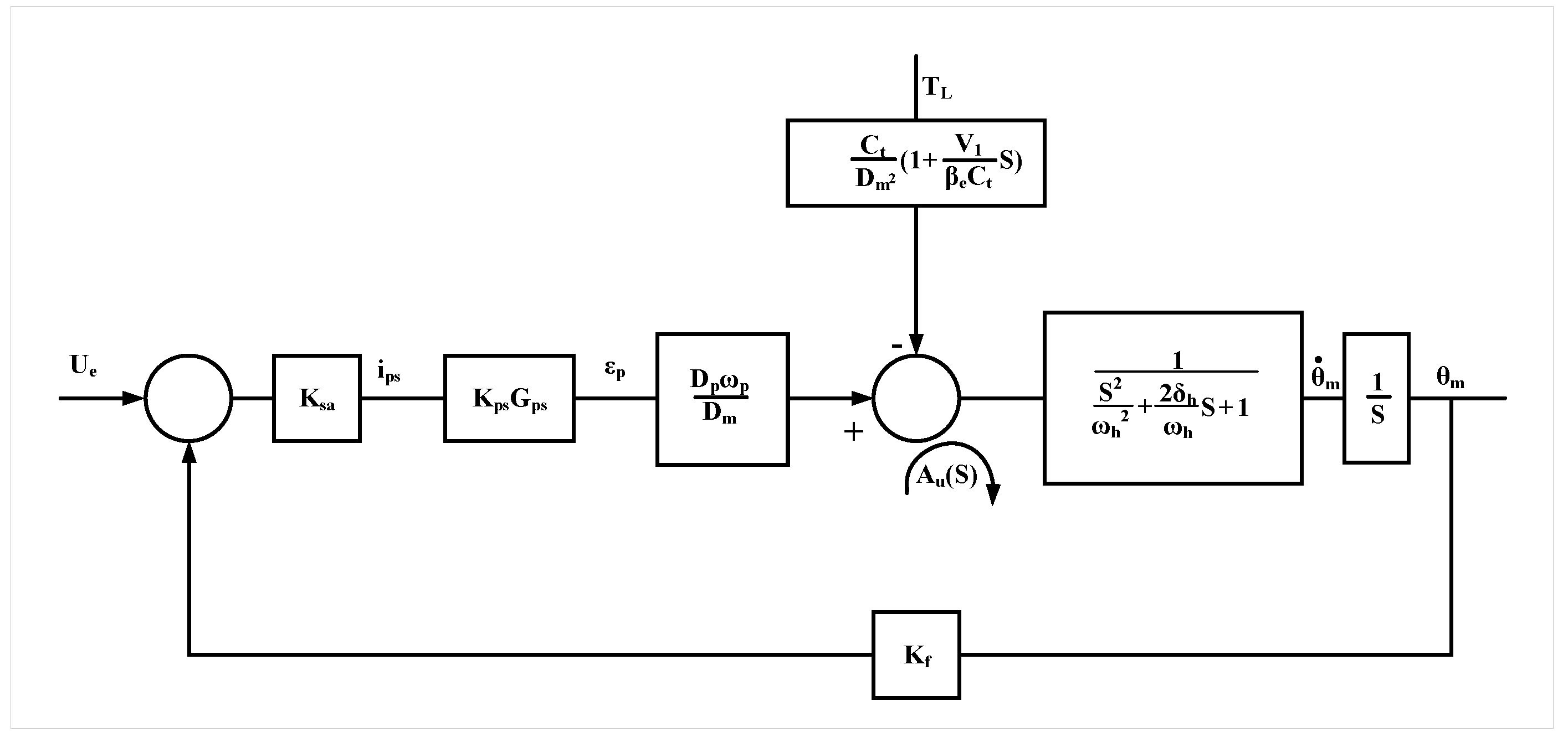
2. Hydraulic System Modeling
- The fluid’s compressibility is taken into account.
- The variation in the valve opening associated with the valve is linear as a function of the pressure differential.
- The inertial as well as the frictional spring loads acting upon the valve are not taken into account.
- The effect arising as a result of flow force is ignored.
- The assumption of constant leakage coefficients is made in this study.
2.1. Pump Servo Dynamics
- is the servo gain of the pump,
- is the time constant of the pump servo system,
- is the input current to the servo.
2.2. Pressure Dynamics
- is the pressure deviation,
- is the pressure generated by the pump,
- represents the leakage flow,
- is the motor flow,
- is the charge flow that offsets the leakage.
2.3. Motor Dynamics
- is the moment of inertia of the motor,
- is the viscous damping coefficient of the motor,
- is the angular velocity of the motor.
2.4. Combining Pressure and Torque Equations
2.5. Hydraulic System Dynamics
- is the natural frequency of the hydraulic system,
- is the damping ratio of the system.
2.6. Incorporating Pump Servo Dynamics
- is the pump servo gain,
- is the time constant of the pump servo system.
2.7. Final Transfer Function
- is the system gain,
- is the servo cutoff frequency,
- and define the hydraulic dynamics.
3. Simulations Result
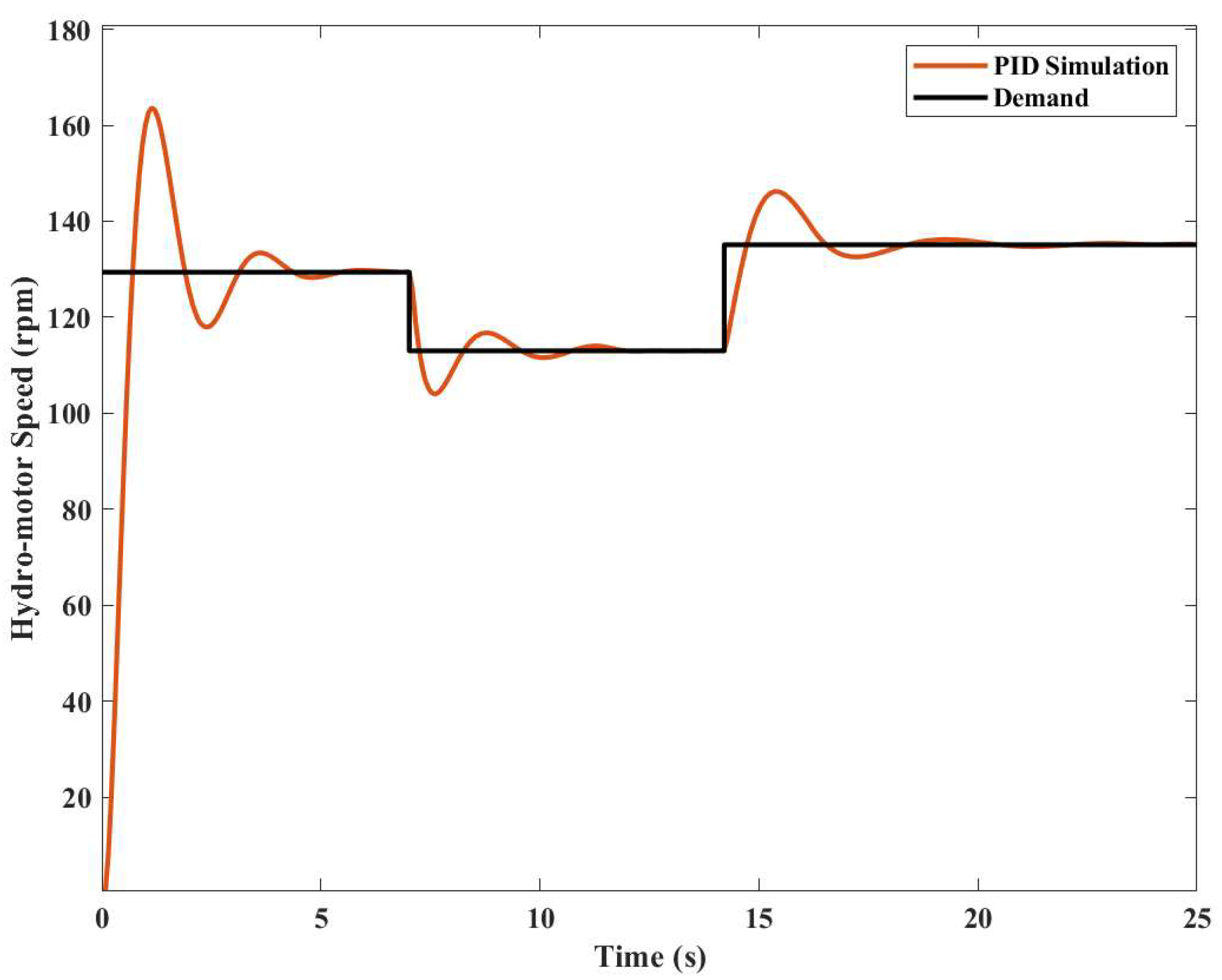
3.1. PID Control of the Closed Loop System
3.2. Controller
3.3. Control Design for the Hydraulic Motor System
3.3.1. System Representation
- : State vector,
- : Control input (pump angular velocity),
- : Disturbance input (external load),
- : Output (motor angular velocity),
3.3.2. Plant Model
- z is the performance output,
- y is the measured output,
- w is the disturbance input,
- u is the control input.
3.3.3. Performance Weights
- Sensitivity weight : Ensures good disturbance rejection and tracking.
- Control effort weight : Limits the control input magnitude.
- Complementary sensitivity weight : Ensures robustness to model uncertainties.
3.3.4. Sensitivity and Complementary Sensitivity Functions
- is the plant transfer function,
- is the controller transfer function.
3.3.5. The Control Problem
3.3.6. State Feedback Controller Design
- X is the solution to the Riccati equation,
- is the performance bound, ensuring that the norm of the transfer function is below a threshold,
- is the state feedback gain.
3.3.7. Output-Feedback Controller Design
- X and Y are the solutions to the Riccati equations,
- The controller is derived from X and Y.
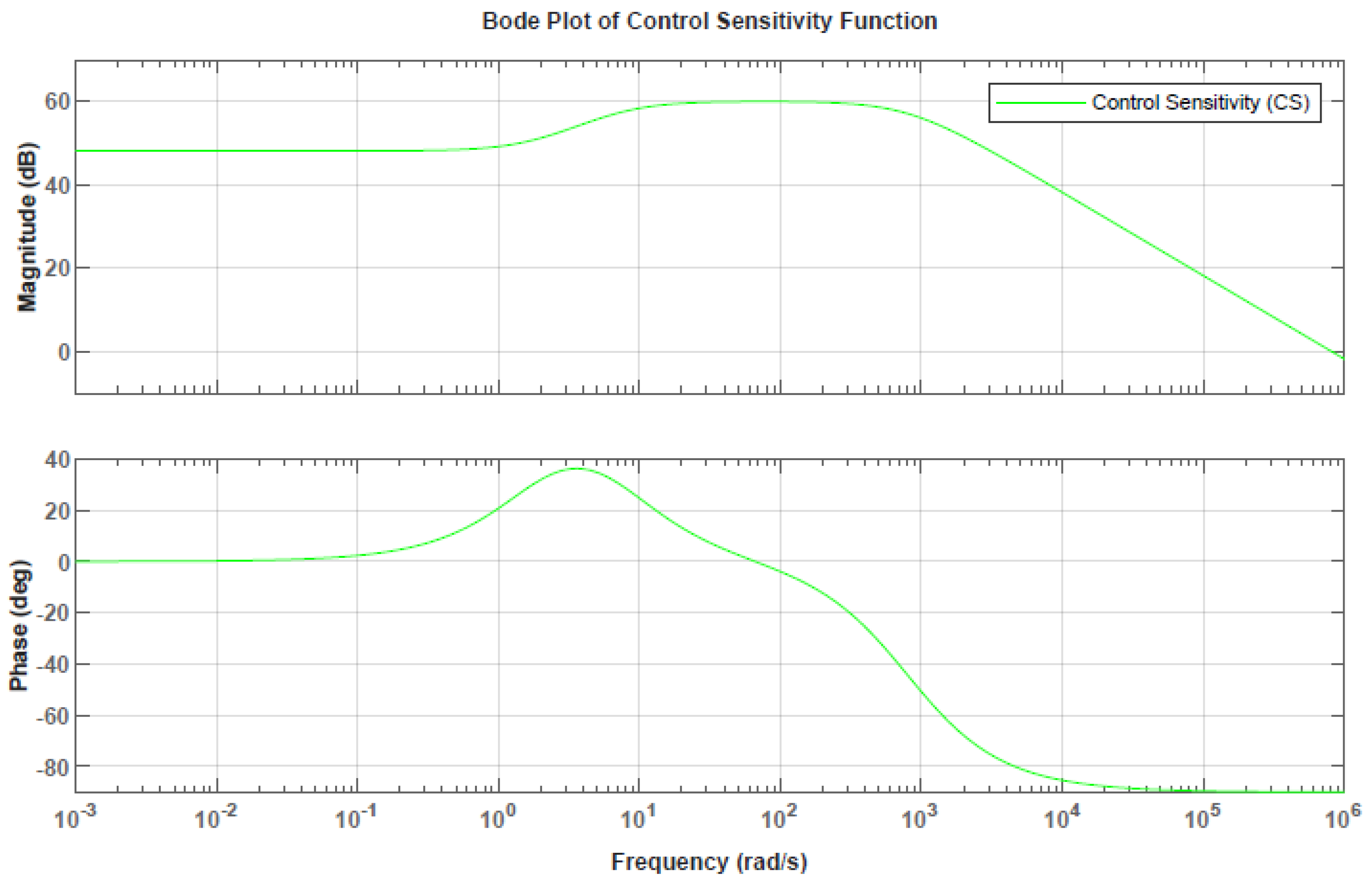
3.3.8. Sensitivity and Complementary Sensitivity Analysis
- measures the system’s ability to reject disturbances,
- measures the system’s robustness to model uncertainties.
3.3.9. Closed-Loop Transfer Functions
- From disturbance w to performance output z:
- From disturbance w to measured output y:
- From control input u to performance output z:
3.3.10. Performance Criteria
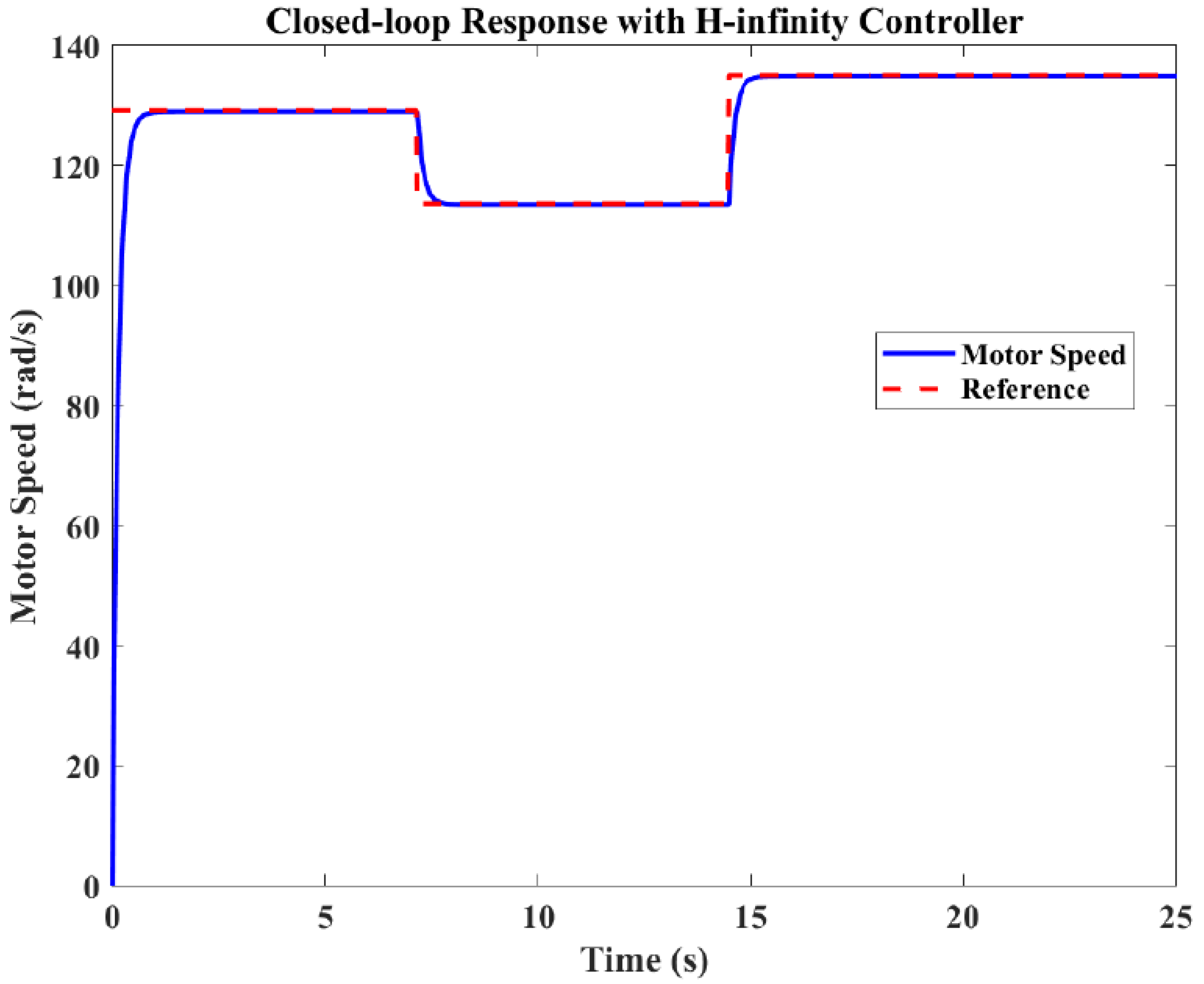
3.3.11. Final Control Implementation
3.4. Performance Metrics
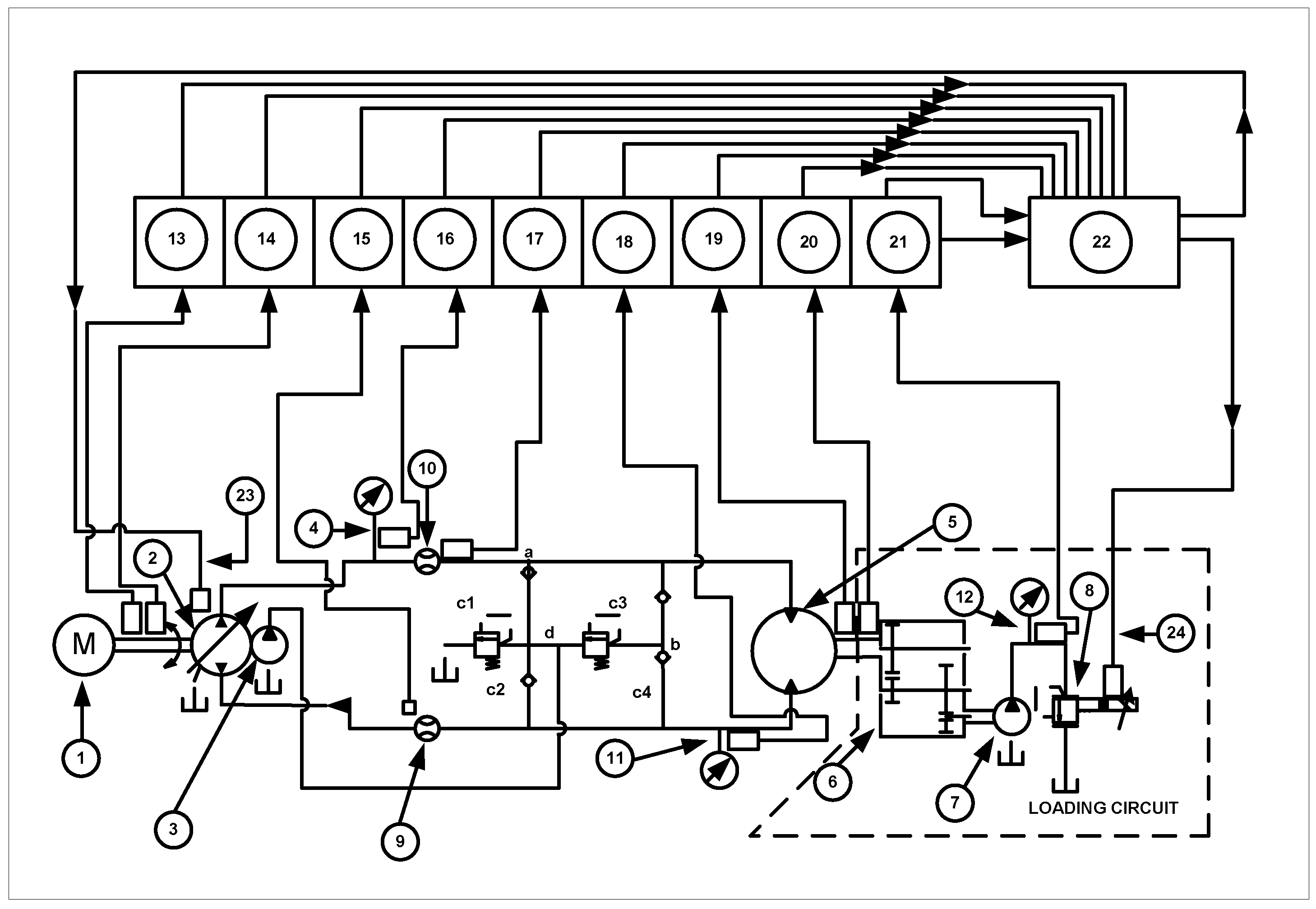
4. System Description
5. Experiment Description
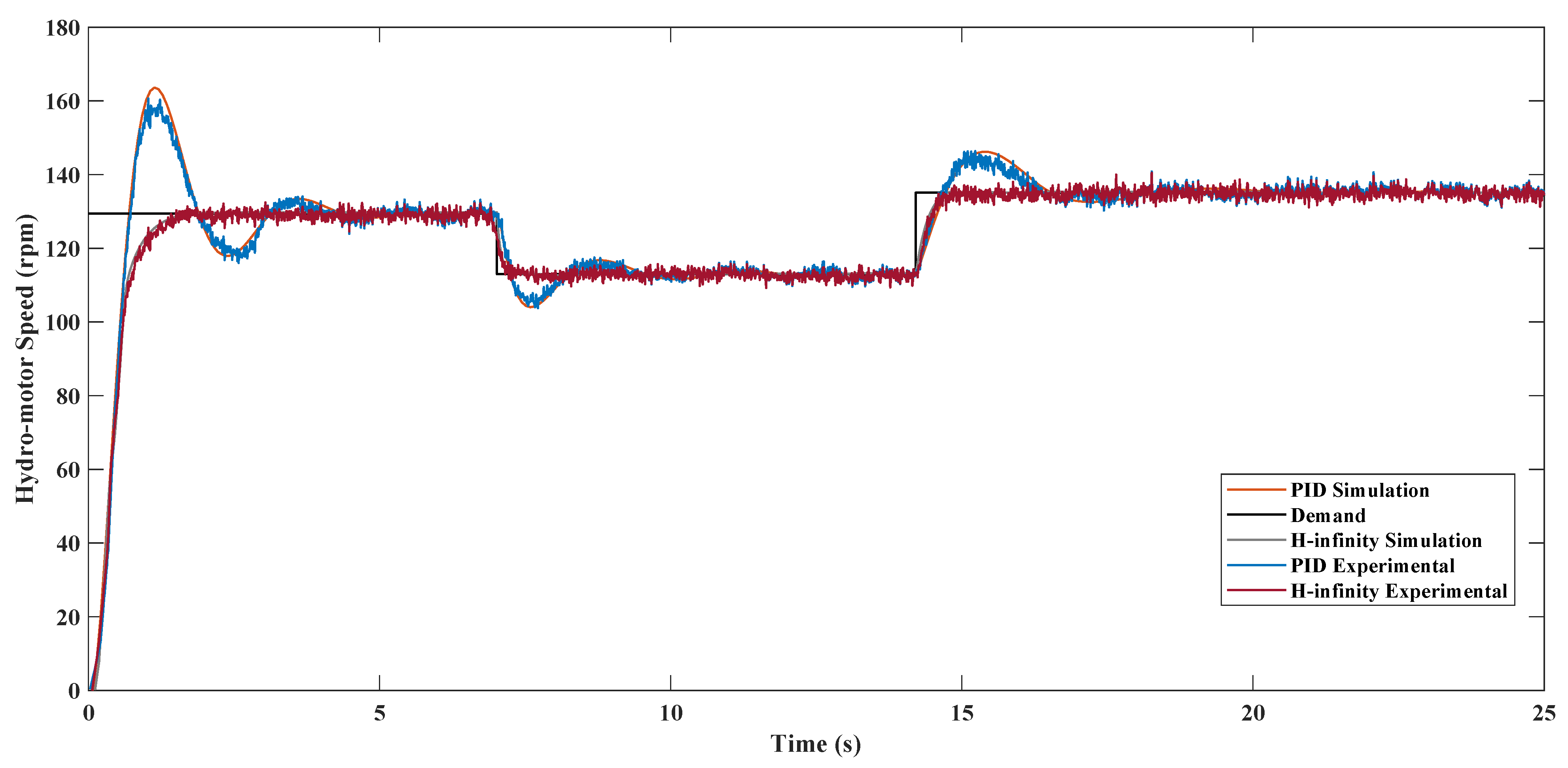
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Costopoulos, T. Hydraulic and Pneumatic Systems; Symeon Publishing Co.: Athens, Greece, 1992. [Google Scholar]
- Kaliafetis, P.; Costopoulos, T. Modelling and simulation of an axial piston variable displacement pump with pressure control. Mech. Mach. Theory 1995, 30, 599–612. [Google Scholar] [CrossRef]
- Karkoub, M.A.; Gad, O.E.; Rabie, M.G. Predicting axial piston pump performance using neural networks. Mech. Mach. Theory 1999, 34, 1211–1226. [Google Scholar] [CrossRef]
- Hu, K.; Zhang, W. Precise control algorithm of rotational speed of the valve-controlled hydraulic motor under load fluctuating conditions. Sci. Prog. 2024, 107, 00368504241296299. [Google Scholar] [CrossRef]
- Wang, W.; Gong, Y.; Bai, X.; Tan, R.; Huang, W. Investigation on operating speed regulation system of mobile straw granulator. Trans. Chin. Soc. Agric. Mach 2021, 52, 186–195. [Google Scholar]
- Kumar, N.; Dasgupta, K.; Ghoshal, S.K. Dynamic analysis of a closed-circuit hydrostatic summation drive using bent axis motors. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2015, 229, 761–777. [Google Scholar] [CrossRef]
- Chen, J.; Luo, Y.; Luo, Y. Co-simulation analysis of synchronization control system on agricultural machinery. Sci. Technol. Eng. 2020, 20, 9362–9366. [Google Scholar]
- Zagar, P.; Kogler, H.; Scheidl, R.; Winkler, B. Hydraulic switching control supplementing speed variable hydraulic drives. Actuators 2020, 9, 129. [Google Scholar] [CrossRef]
- Goman, V.; Oshurbekov, S.; Kazakbaev, V.; Prakht, V.; Dmitrievskii, V. Energy efficiency analysis of fixed-speed pump drives with various types of motors. Appl. Sci. 2019, 9, 5295. [Google Scholar] [CrossRef]
- Çetin, Ş.; Akkaya, A.V. Simulation and hybrid fuzzy-PID control for positioning of a hydraulic system. Nonlinear Dyn. 2010, 61, 465–476. [Google Scholar] [CrossRef]
- Mishra, S.K.; Wrat, G.; Ranjan, P.; Das, J. PID controller with feed forward estimation used for fault tolerant control of hydraulic system. J. Mech. Sci. Technol. 2018, 32, 3849–3855. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, Q.; Niu, H. The research on the position control of the hydraulic cylinder based on the compound algorithm of fuzzy & feedforward-feedback. Sens. Transducers 2014, 162, 314. [Google Scholar]
- Hassan, M.Y.; Kothapalli, G. Interval Type-2 fuzzy position control of electro-hydraulic actuated robotic excavator. Int. J. Min. Sci. Technol. 2012, 22, 437–445. [Google Scholar] [CrossRef]
- Ranjan, P.; Wrat, G.; Bhola, M.; Mishra, S.K.; Das, J. A novel approach for the energy recovery and position control of a hybrid hydraulic excavator. ISA Trans. 2020, 99, 387–402. [Google Scholar] [CrossRef] [PubMed]
- Wrat, G.; Ranjan, P.; Mishra, S.K.; Jose, J.T.; Das, J. Neural network-enhanced internal leakage analysis for efficient fault detection in heavy machinery hydraulic actuator cylinders. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 239, 09544062241289309. [Google Scholar] [CrossRef]
- Milić, V.; Šitum, Ž.; Essert, M. Robust H∞ position control synthesis of an electro-hydraulic servo system. ISA Trans. 2010, 49, 535–542. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Yu, T.; Jiang, D. Robust H∞ positional control of 2-DOF robotic arm driven by electro-hydraulic servo system. ISA Trans. 2015, 59, 55–64. [Google Scholar] [CrossRef] [PubMed]
- Pukpinyo, C.; Assawinchaichote, W. TS fuzzy based H-infinity speed controller design for uncertain surface-mounted permanent-magnet synchronous motor. In Proceedings of the 2016 International Computer Science and Engineering Conference (ICSEC), Chiang Mai, Thailand, 14–17 December 2016; pp. 1–6. [Google Scholar]
- Papkollu, K.; Singru, P.M.; Manajrekar, N. Comparing PID and H-infinity controllers on a 2-DoF nonlinear quarter car suspension system. J. Vibroeng. 2014, 16, 3977–3990. [Google Scholar]
- Péter, G.; Max, G.; Kiss, B. Implementation of a robust electric brake actuator design based on H-infinity control theory. Period. Polytech. Transp. Eng. 2019, 47, 178–185. [Google Scholar] [CrossRef]
- Breganon, R.; Montezuma, M.A.F.; Souza, M.M.d.; Lemes, R.C.; Belo, E.M. A comparative analysis of PID, fuzzy and H infinity controllers applied to a stewart platform. Int. J. Adv. Eng. Res. Sci. 2019, 6, 25–32. [Google Scholar] [CrossRef]
- Wrat, G.; Ranjan, P.; Jose, J.T.; Kumar, R. Modelling and Analysis of the Hydraulic System Parameters Under Different Loading Conditions. In Dynamics of Transportation Ecosystem, Modeling, and Control; Springer: Berlin/Heidelberg, Germany, 2024; pp. 9–21. [Google Scholar]
- Wrat, G.; Das, J. Energy Saving in Off-Road Vehicle Using Leakage Compensation Technique. 2023. Available online: https://www.researchgate.net/publication/374118311_Energy_Saving_in_Off-road_Vehicle_using_leakage_compensation_technique (accessed on 21 October 2024).
- Guo, Q.; Jiang, D. Nonlinear Control Techniques for Electro-Hydraulic Actuators in Robotics Engineering; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Liu, X.; Qin, P. Parameter estimation and model-free multi-innovation adaptive control algorithms. Int. J. Control. Autom. Syst. 2024, 22, 3509–3524. [Google Scholar] [CrossRef]
- Gambhire, S.; Kishore, D.R.; Londhe, P.; Pawar, S. Review of sliding mode based control techniques for control system applications. Int. J. Dyn. Control 2021, 9, 363–378. [Google Scholar] [CrossRef]
- Ali, H.H.; Khafaji, S.O.W.; Al-Bakri, F.F. H∞ loop shaping control design of the rotational velocity of a hydraulic motor. Int. J. Mechatronics Appl. Mech. 2021, 1, 72–79. [Google Scholar]
- Lu, K.; Feng, G.; Ding, B. Robust H-Infinity Tracking Control for a Valve-Controlled Hydraulic Motor System with Uncertain Parameters in the Complex Load Environment. Sensors 2023, 23, 9092. [Google Scholar] [CrossRef] [PubMed]
- Fan, Q.; Zhang, J.; Li, R.; Fan, T. Review of Research on Hydrostatic Transmission Systems and Control Strategies. Processes 2025, 13, 317. [Google Scholar] [CrossRef]
- Njabeleke, I.A.; Pannett, R.F.; Chawdhry, P.K.; Burrows, C.R. Modelling and control of a high speed hydrostatic transmission. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Anaheim, CA, USA, 15–20 November 1998; Volume 15939, pp. 1–10. [Google Scholar]
- Wang, M.; Ren, X.; Chen, Q. Robust tracking and distributed synchronization control of a multi-motor servomechanism with H-infinity performance. ISA Trans. 2018, 72, 147–160. [Google Scholar] [CrossRef] [PubMed]
- Borase, R.P.; Maghade, D.; Sondkar, S.; Pawar, S. A review of PID control, tuning methods and applications. Int. J. Dyn. Control 2021, 9, 818–827. [Google Scholar] [CrossRef]
- Levin, V.M.; Yahya, A.A.; Boyarova, D.A. Predicting the technical condition of the power transformer using fuzzy logic and dissolved gas analysis method. Int. J. Electr. Comput. Eng. 2022, 12, 1139–1146. [Google Scholar] [CrossRef]
- Rahbari, R.; de Silva, C.W. Fuzzy logic control of a hydraulic system. In Proceedings of the Proceedings of IEEE International Conference on Industrial Technology 2000 (IEEE Cat. No. 00TH8482), Goa, India, 19–22 January 2000; Volume 2, pp. 313–318. [Google Scholar]
- Black, W.S.; Haghi, P.; Ariyur, K.B. Adaptive systems: History, techniques, problems, and perspectives. Systems 2014, 2, 606–660. [Google Scholar] [CrossRef]
- Schwenzer, M.; Ay, M.; Bergs, T.; Abel, D. Review on model predictive control: An engineering perspective. Int. J. Adv. Manuf. Technol. 2021, 117, 1327–1349. [Google Scholar] [CrossRef]
- Wu, L.; Liu, J.; Vazquez, S.; Mazumder, S.K. Sliding mode control in power converters and drives: A review. IEEE/CAA J. Autom. Sin. 2021, 9, 392–406. [Google Scholar] [CrossRef]
- Chen, B.M. H∞ Control and Its Applications; Springer: Berlin/Heidelberg, Germany, 2013; Volume 235. [Google Scholar]




| Description | Value | Unit |
|---|---|---|
| Electric motor speed | 1453 | rpm |
| Variable-Displacement Bidirectional Pump | ||
| Maximum displacement | 27.95 | cc/rev |
| Rotational speed | 1453 | rpm |
| Leakage resistance | Pa · s/m3 | |
| Bulk stiffness | Pa/m3 | |
| Hydro Motor | ||
| Maximum displacement | 279.5 | cc/rev |
| Leakage resistance | Pa · s/m3 | |
| Bulk stiffness | Pa/m3 | |
| Charge Pump | ||
| Maximum displacement | 31.42 | cc/rev |
| Rotational speed | 1453 | rpm |
| Coefficient of discharge | 1 | – |
| Gear ratio (Gr) | 0.05 (1:20) | – |
| Nominal fluid density | 900 | kg/m3 |
| Area opening of Proportional PRV | m2 | |
| Port opening area of Proportional PRV | m2 | |
| Atmospheric pressure | Pa | |
| Total equivalent M.I. (motor axis) | 6.18 | kg·m2 |
| Viscous friction coefficient | 11.271 | N·m·s/rad |
| Control Method | Advantages | Disadvantages | Applicability |
|---|---|---|---|
| PID Control [32] | Simple to implement and understand; Effective for stable systems | Performance degrades with non-linearities and disturbances; Requires precise tuning | Suitable for systems with relatively stable dynamics |
| Fuzzy Logic Control (FLC) [34] | Robust to uncertainties and non-linearities; Does not require an accurate mathematical model | Complex design and tuning; May require significant computational resources | Ideal for complex and non-linear systems |
| Adaptive Control [35] | Maintains performance despite changes in system dynamics; Suitable for systems with varying parameters | Complex design and implementation; Requires extensive testing and validation | Best for systems with dynamic changes |
| Model Predictive Control (MPC) [36] | Handles multi-variable control problems; Optimizes performance by considering future states | Computationally intensive; Requires an accurate model | Suitable for systems where future state prediction is crucial |
| Sliding Mode Control (SMC) [37] | Insensitive to matched disturbances; Robust control | Chattering phenomenon; Variable switching frequency | Effective for systems with high robustness requirements |
| Control [38] | Explicitly addresses robust controller problem; Retains computational advantages of state space methods | Complex mathematical formulation; Requires precise system modeling | Ideal for systems requiring robust performance under uncertainty |
| S/n | Item Description | S/n | Item Description |
|---|---|---|---|
| 1 | Electric motor | 2 | Variable displacement pump |
| 3 | Charge pump | 4 | Pressure transducer (system) |
| 5 | LSHT motor | 6 | Gear box (1:20) |
| 7 | Loading pump | 8 | Pressure relief valve |
| 9 | Flow transducer (inlet) | 10 | Flow transducer (outlet) |
| 11 | Pressure transducer (outlet) | 12 | Speed indicator (electric motor) |
| 13 | Torque indicator (electric motor) | 14 | Flow indicator (motor return) |
| 15 | Pressure indicator (system) | 16 | Flow indicator (motor inlet) |
| 17 | Speed indicator (motor) | 18 | Torque indicator (motor) |
| 19 | Computer with cRIO | 20 | Swash plate command signal |
| 21 | Pressure relief valve command | 22 | Computer with DAS |
| 23 | Swash plate command signal | 24 | Pressure relief valve command |
| Type of Controller | Kp | Ki | Kd |
| PID controller | |||
| , | |||
| Type of Controller | Kp | Ki | Kd |
| PID controller | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mishra, S.K.; Wrat, G.; Ranjan, P.; Jose, J.T.; Das, J. Precision and Stability in Hydrostatic Transmissions with Robust H∞ Control Under Parametric Uncertainties. J. Exp. Theor. Anal. 2025, 3, 14. https://doi.org/10.3390/jeta3020014
Mishra SK, Wrat G, Ranjan P, Jose JT, Das J. Precision and Stability in Hydrostatic Transmissions with Robust H∞ Control Under Parametric Uncertainties. Journal of Experimental and Theoretical Analyses. 2025; 3(2):14. https://doi.org/10.3390/jeta3020014
Chicago/Turabian StyleMishra, Santosh Kr., Gyan Wrat, Prabhat Ranjan, Joseph T. Jose, and Jayanta Das. 2025. "Precision and Stability in Hydrostatic Transmissions with Robust H∞ Control Under Parametric Uncertainties" Journal of Experimental and Theoretical Analyses 3, no. 2: 14. https://doi.org/10.3390/jeta3020014
APA StyleMishra, S. K., Wrat, G., Ranjan, P., Jose, J. T., & Das, J. (2025). Precision and Stability in Hydrostatic Transmissions with Robust H∞ Control Under Parametric Uncertainties. Journal of Experimental and Theoretical Analyses, 3(2), 14. https://doi.org/10.3390/jeta3020014







