Enhancing Mathematics Teacher Training in Higher Education: The Role of Lesson Study and Didactic Suitability Criteria in Pedagogical Innovation

Abstract

The integration of Lesson Study (LS) and Didactic Suitability Criteria (DSC) presents an innovative framework for enhancing mathematics teacher training in higher education. This study examines how LS-DSC fosters instructional refinement, professional growth, and pedagogical transformation among in-service teachers. Using a quasi-experimental mixed-methods approach, the study analyzed data from 520 mathematics educators participating in a six-month training program incorporating collaborative lesson planning, structured pedagogical assessment, and reflective teaching practices. Findings indicate significant improvements in instructional design, mathematical discourse facilitation, and adaptive teaching strategies, with post-training evaluations demonstrating a strong positive correlation (r = 0.78) between initial competency levels and learning gains. Participants reported increased confidence in implementing student-centered methodologies and sustained engagement in peer collaboration beyond the training period. The results align with prior research emphasizing the effectiveness of lesson study models and structured evaluation frameworks in teacher professionalization. This study contributes to higher education policy and practice by advocating for the institutional adoption of LS-DSC methodologies to promote evidence-based professional development. Future research should explore the long-term scalability of LS-DSC in diverse educational contexts and its impact on student learning outcomes.

1. Introduction

Higher education institutions play a crucial role in shaping the next generation of mathematics educators. However, despite increasing efforts to improve mathematics teacher training, studies suggest that traditional pedagogical models fail to prepare future educators for the complexities of modern mathematics instruction [1,2]. The lack of structured reflective practices, limited exposure to collaborative lesson development, and insufficient data-driven assessment strategies contribute to ineffective teaching methodologies in higher education [3,4]. Research indicates that mathematics educators often receive insufficient training in didactic strategies, resulting in instructional approaches that prioritize procedural fluency over conceptual understanding [5,6]. Addressing this challenge requires the adoption of evidence-based professional development models that integrate theoretical knowledge with practical applications [7,8].

One of the most promising research-based approaches to mathematics teacher education is the integration of Lesson Study (LS) and Didactic Suitability Criteria (DSC). Empirical studies support this claim: for example, [7] reported that LS implementations across East Asian contexts led to a 30–45% improvement in teachers’ lesson planning quality and reflective practices. Similarly, integrating DSC with LS has been shown to improve teachers’ ability to analyze and redesign instructional sequences by over 40%, based on pre- and post-intervention evaluations [9]. These findings align with broader international evidence on the effectiveness of collaborative and criterion-based professional development models. LS is a collaborative, cyclic model of professional development that fosters critical instructional analysis, peer observation, and structured lesson refinement [9]. Originating in Japan, LS has been widely recognized for its effectiveness in developing reflective teaching practices and has been successfully adapted in various educational settings [7].

Meanwhile, Didactic Suitability Criteria (DSC), grounded in the Onto-Semiotic Approach (OSA), provides a comprehensive analytical framework for evaluating the epistemic, cognitive, interactional, mediational, effective, and ecological aspects of mathematics instruction [10]. DSC serves as a structured tool to assess and refine instructional practices, ensuring that mathematics lessons align with both pedagogical best practices and students’ cognitive development needs [11]. The integration of LS and DSC (LS-DSC) offers a synergistic framework for mathematics teacher training. By embedding collaborative lesson planning, structured instructional analysis, and continuous improvement cycles into teacher education programs, LS-DSC provides a data-driven, iterative approach to professional growth [12]. This model supports educators in developing deeper metacognitive awareness, enhancing instructional adaptability, and fostering student-centered learning experiences [13,14].

Recent studies have begun to explore the integration of LS and DSC in teacher education. For example, [13] analyzed how this combined model enhances the reflective competence of pre-service teachers. However, most of this research has been conducted in narrowly defined contexts or with limited sample sizes, leaving a significant gap in our understanding of how LS-DSC operates across diverse educational environments and teacher populations. This study seeks to address that gap by implementing and evaluating a teacher training program that integrates LS and DSC within a Latin American context, offering empirical evidence on its effectiveness and adaptability in such settings.

To that end, this research examines the implementation of LS-DSC in university-based teacher training programs, evaluating its impact on instructional quality, pedagogical reflection, and student engagement. Through a mixed-methods approach, we assess how mathematics educators apply LS-DSC principles in lesson planning, implementation, and assessment, and explore the sustainability of this model in long-term professional development. The findings contribute to ongoing discussions on teacher education reform, higher education policy, and the role of structured professional learning communities in mathematics instruction [4,15].

Empirical evidence underscores the potential of LS-DSC to bridge the gap between theory and practice in mathematics teacher training. Research highlights that collaborative professional learning models significantly improve instructional quality by encouraging teachers to engage in structured self-assessment, iterative lesson development, and interdisciplinary collaboration [7,15]. Moreover, integrating evidence-based didactic evaluation criteria such as DSC fosters more coherent, student-centered instructional strategies, leading to greater conceptual understanding and mathematical reasoning skills among students [10,16]. By bridging theoretical knowledge with applied teaching methodologies, LS-DSC represents a transformative model for mathematics teacher education, one that aligns with contemporary research on effective teacher training in higher education.

2. Theoretical Framework

The quality of mathematics education in higher education is closely linked to the professional development strategies adopted in teacher training programs. In this regard, Lesson Study (LS) and Didactic Suitability Criteria (DSC) have gained recognition as evidence-based frameworks that enhance teacher competency, reflective practice, and instructional effectiveness [8,10]. In this study, pedagogical innovation is understood as a social process through which teaching practices are adopted and sustained within educational communities. According to [6], innovation goes beyond invention—it involves the transition from ideas to broad implementation. The integration of Lesson Study and Didactic Suitability Criteria reflects this process, as it promotes lasting changes in teacher practice through collaboration, reflection, and institutional uptake.

2.1. Lesson Study as a Professional Development Strategy

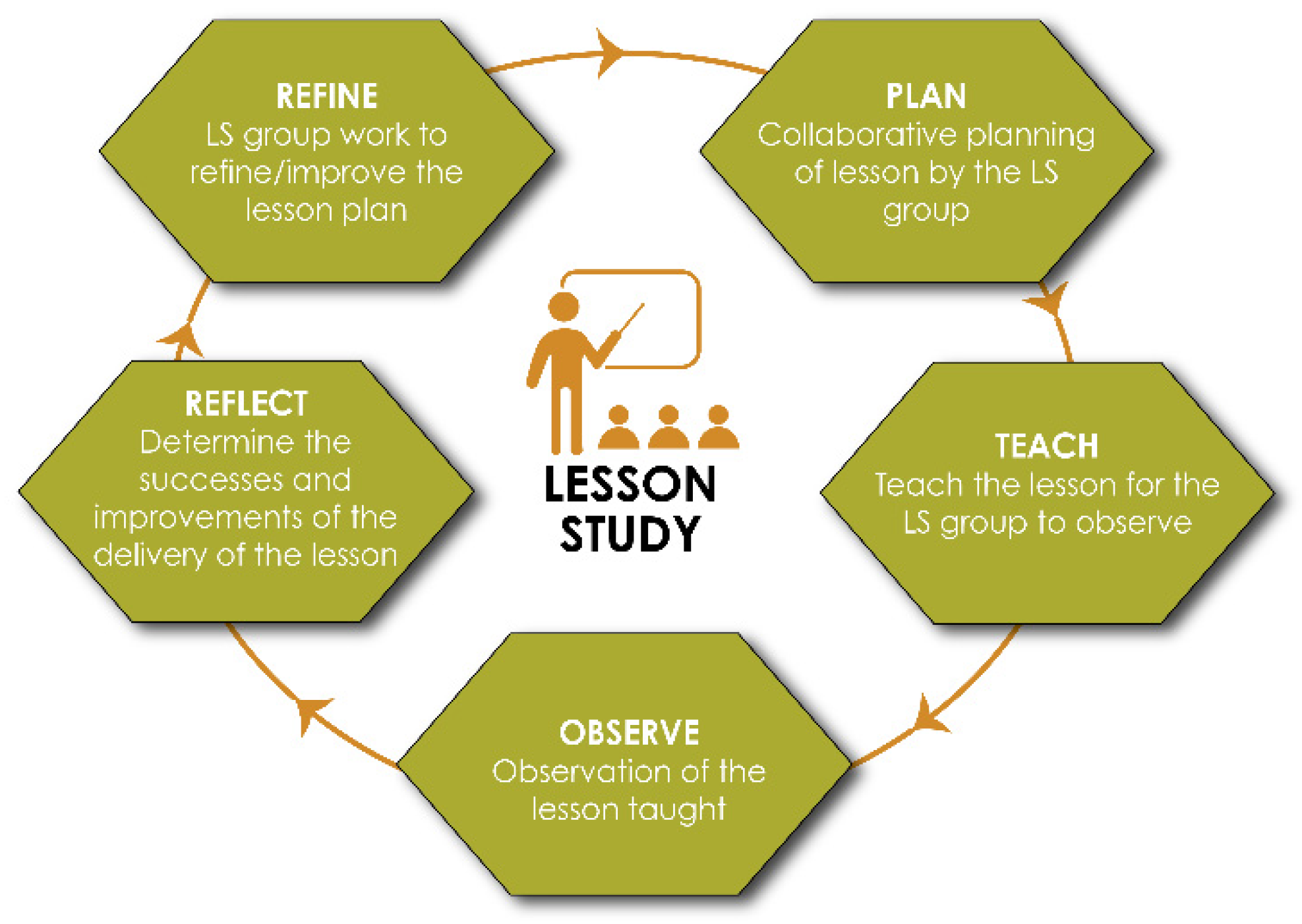
LS, originally developed in Japan, is a collaborative, teacher-led professional learning model structured in iterative cycles of planning, implementation, observation, and refinement [7,9]. This model promotes continuous improvement through four systematic stages:

• Collaborative Lesson Planning—Teachers design a lesson based on shared learning objectives.
• Lesson Implementation & Observation—The lesson is taught by one teacher while others observe, focusing on student learning processes.
• Post-Lesson Discussion & Reflection—Observers analyze student responses, instructional effectiveness, and possible improvements.
• Lesson Refinement & Reimplementation—The lesson is modified based on feedback and re-taught in an improved form [8].

Lesson Study (LS) contributes significantly to teacher professional growth by fostering structured reflection, collaborative inquiry, and pedagogical adaptability [7,8]. Its implementation in higher education has demonstrated positive outcomes in both mathematics instruction and preservice teacher development [8,16]. Moreover, the LS cycle cultivates a culture of continuous learning and supports teachers in deepening both their content knowledge and instructional effectiveness [17]. Furthermore, LS fosters a culture of continuous improvement among educators. By engaging in iterative cycles of lesson planning, observation, and reflection, teachers collaboratively refine their instructional strategies, leading to enhanced student learning outcomes [18]. This process not only deepens teachers’ content knowledge but also enhances their pedagogical skills, making LS a valuable model for professional development in diverse educational contexts [19,20]. In recent years, the integration of LS with theoretical frameworks such as the Onto-Semiotic Approach (OSA) has further enriched its potential for professional development by offering rigorous analytical tools for evaluating teaching practices [10,12,13]. Studies have shown that combining LS with Didactic Suitability Criteria enables teachers to assess the coherence of their instructional designs and reflect more deeply on the mathematical and cognitive demands placed on students [12,14,19]. This synergy not only supports metacognitive growth but also empowers teachers to align their instructional decisions with broader curricular goals, promoting both critical reflection and sustained pedagogical innovation [19,20]. (see Figure 1)

2.2. Didactic Suitability Criteria in Mathematics Instruction

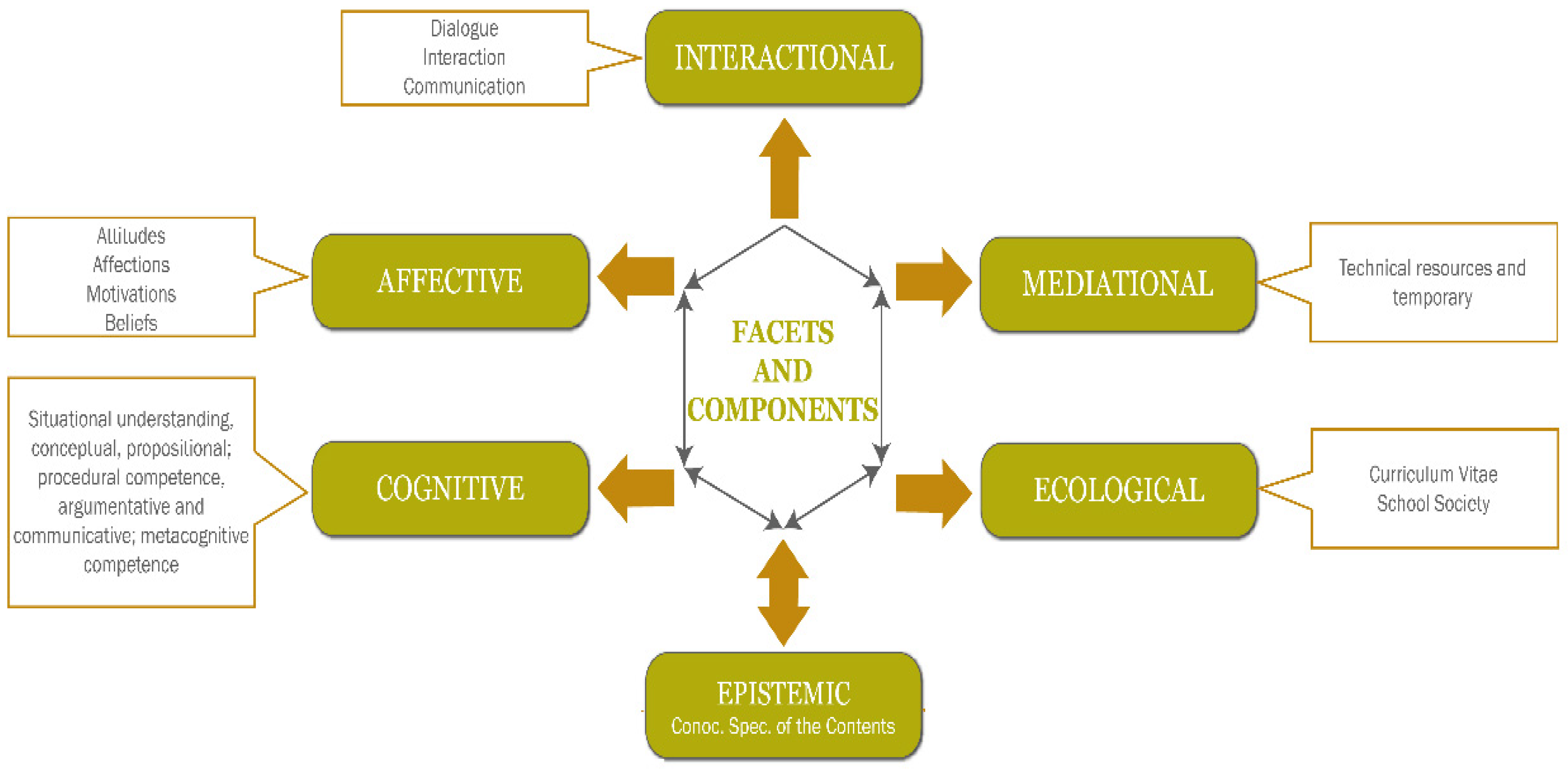
The Didactic Suitability Criteria (DSC) framework, developed within the Onto-Semiotic Approach (OSA) [10]. Rather than introducing the OSA again, this section emphasizes the function and dimensions of DSC within the teaching process (see Figure 2). The six interrelated dimensions are:

• Epistemic Suitability—Ensuring that the mathematical content aligns with curricular goals and conceptual rigor.
• Cognitive Suitability—Evaluating whether tasks support students’ cognitive processes and conceptual understanding.
• Interactional Suitability—Analyzing classroom interactions and student-teacher discourse in mathematical reasoning.
• Mediational Suitability—Assessing the use of resources, technology, and manipulatives in instruction.
• Affective Suitability—Addressing students’ emotions, motivation, and engagement with mathematical content.
• Ecological Suitability—Ensuring coherence with institutional policies, curricular frameworks, and broader educational contexts [13].

DSC provides a comprehensive framework for mathematics teacher education by enabling structured evaluation of instructional practices. Studies have shown that DSC fosters metacognitive awareness, pedagogical refinement, and data-driven instructional adjustments, ensuring teaching aligns with cognitive development theories and effective learning principles [12]. The multidimensional structure of the Didactic Suitability Criteria (DSC) which includes epistemic, cognitive, affective, mediational, interactional, and ecological dimensions—allows for a nuanced assessment of teaching practices that goes beyond surface-level evaluation [13]. By systematically examining each dimension, teachers gain insight into how mathematical content is presented, how students engage with and make sense of the material, and how contextual factors influence the overall learning experience [10,14]. This comprehensive approach not only enhances instructional quality but also facilitates the professional growth of educators by promoting reflective practice and continuous improvement. Furthermore, when integrated into collaborative models such as Lesson Study, DSC serves as both a diagnostic and developmental tool, enabling teams of teachers to co-construct meaning around effective mathematics teaching [19,21].

2.3. Integrating LS and DSC in Higher Education

The integration of LS and DSC in mathematics teacher education provides a comprehensive approach to professional development, combining collaborative lesson refinement with structured instructional evaluation [8,10]. LS ensures teachers engage in systematic reflection and iterative improvement, while DSC provides an analytical tool for assessing the effectiveness of instructional practices [7].

By embedding LS-DSC into higher education training programs, institutions can:

• Bridge the gap between theory and practice by aligning lesson designs with evidence-based teaching strategies.
• Promote interdisciplinary collaboration among mathematics educators through structured, research-informed instructional design [16].
• Encourage adaptive teaching strategies that respond to student learning needs through data-driven evaluation mechanisms [14].

Empirical studies highlight that mathematics teacher training programs incorporating LS-DSC exhibit greater instructional coherence, student engagement, and conceptual understanding outcomes [12,13]. Moreover, universities that implement LS-DSC report stronger faculty collaboration, improved lesson quality, and sustainable teaching innovations [7]. (See

Table 1. Comparison between Lesson Study (LS) and Didactic Suitability Criteria (DSC).

Aspect	Lesson Study (LS)	Didactic Suitability Criteria (DSC)
Main Purpose	Professional development for teachers through lesson planning, observation, and iterative improvement.	Assessing and optimizing the quality of mathematics instruction through an analytical framework.
Approach	Collaborative and reflective, focused on improving teaching through observation of classroom practice.	Analytical and evaluative, centered on assessing the didactic suitability of lessons.
Process	Collaborative lesson planning, implementation, observation, reflection, and adjustment.	Identification of criteria, suitability analysis, and evidence-based refinement.
Key Benefit	Encourages teacher reflection and learning through observation-based improvement.	Provides a structured framework for evaluating and improving instruction based on empirical evidence.
Evaluated Dimensions	No specific dimensions; focuses on improving teaching practice.	Epistemic, Cognitive, Interactional, Mediational, Affective, Ecological.
Application in Teacher Training	Useful for continuous teaching improvement through structured reflection and observation-based learning.	Useful for structuring didactic evaluation and guiding instructional planning based on empirical evidence.

This comparison is based on previously published models and adaptations by [7,8,10,12,13].

)

2.4. Research Background and Gap

Over the past decades, Lesson Study (LS) has been consolidated as an effective strategy for teacher professional development, particularly in the field of mathematics education. Studies such as [7]. have documented how LS fosters collaborative reflection and improves pedagogical practices. In parallel, Didactic Suitability Criteria (DSC) have been proposed as a robust framework for evaluating and enhancing the quality of mathematics instruction [7,8,10,12,13].

Recent research has begun to explore the integration of LS and DSC in teacher education. For example, ref. [17] analyzed how this combination enhances the reflective competence of preservice teachers. However, most of these studies have been conducted in specific contexts or with limited sample sizes, which leaves a gap in understanding how this integration functions across diverse educational settings and among different teaching populations.

This study seeks to address that gap by implementing and evaluating a teacher training program that integrates LS and DSC within a Latin American context, providing empirical evidence on its effectiveness and adaptability in higher education environments.

3. Materials and Methods

This study employs a comprehensive methodology to investigate the integration of Lesson Study (LS) and Didactic Suitability Criteria (DSC) in enhancing mathematics teacher education. The approach combines quantitative and qualitative data collection methods to provide a robust analysis of the impact on teaching competencies.

3.1. Research Design

This study follows a quasi-experimental, mixed-methods approach that integrates quantitative and qualitative data collection to examine the impact of Lesson Study (LS) and Didactic Suitability Criteria (DSC) on mathematics teacher training. The study design incorporates pretest-posttest measures, lesson observations, and participant reflections to assess how teachers’ instructional competencies evolve throughout the training program.

Participants included 520 in-service mathematics teachers enrolled in a postgraduate teacher training program at a Panamanian university. The selection of participants was based on their prior engagement in secondary mathematics instruction and their willingness to participate in a structured professional development intervention. The program was designed as an intensive, competency-based training in which LS and DSC were embedded to enhance teachers’ pedagogical knowledge, reflective practices, and classroom implementation skills. (See

Table 2. Participant Demographics and Baseline Characteristics.

Characteristic	Value
Total Participants	520
Average Age	38.2 years
Gender (Female)	301 participants (58%)
Gender (Male)	219 participants (42%)
Years of Teaching Experience (Avg)	10 years
Prior Exposure to LS	45% (234 participants)

)

This study was guided by three research questions aimed at exploring the effects of integrating Lesson Study (LS) and Didactic Suitability Criteria (DSC) into mathematics teacher training programs. First, we investigated how this integration influences teachers’ ability to reflect on and redesign their instructional practices (RQ1). Second, we examined the impact of the LS-DSC framework on classroom instructional strategies and the implementation of student-centered teaching approaches (RQ2). Third, we explored the extent to which teachers continue to apply LS-DSC components in their professional development beyond the duration of the training program (RQ3). These questions provided a structured basis for analyzing both the short-term and sustained effects of the intervention on teaching competencies and pedagogical growth.

3.2. Description of the Training Course

The EDEM Diploma Program was structured as a six-month professional development initiative integrating Lesson Study (LS) and Didactic Suitability Criteria (DSC) to enhance mathematics teacher training.

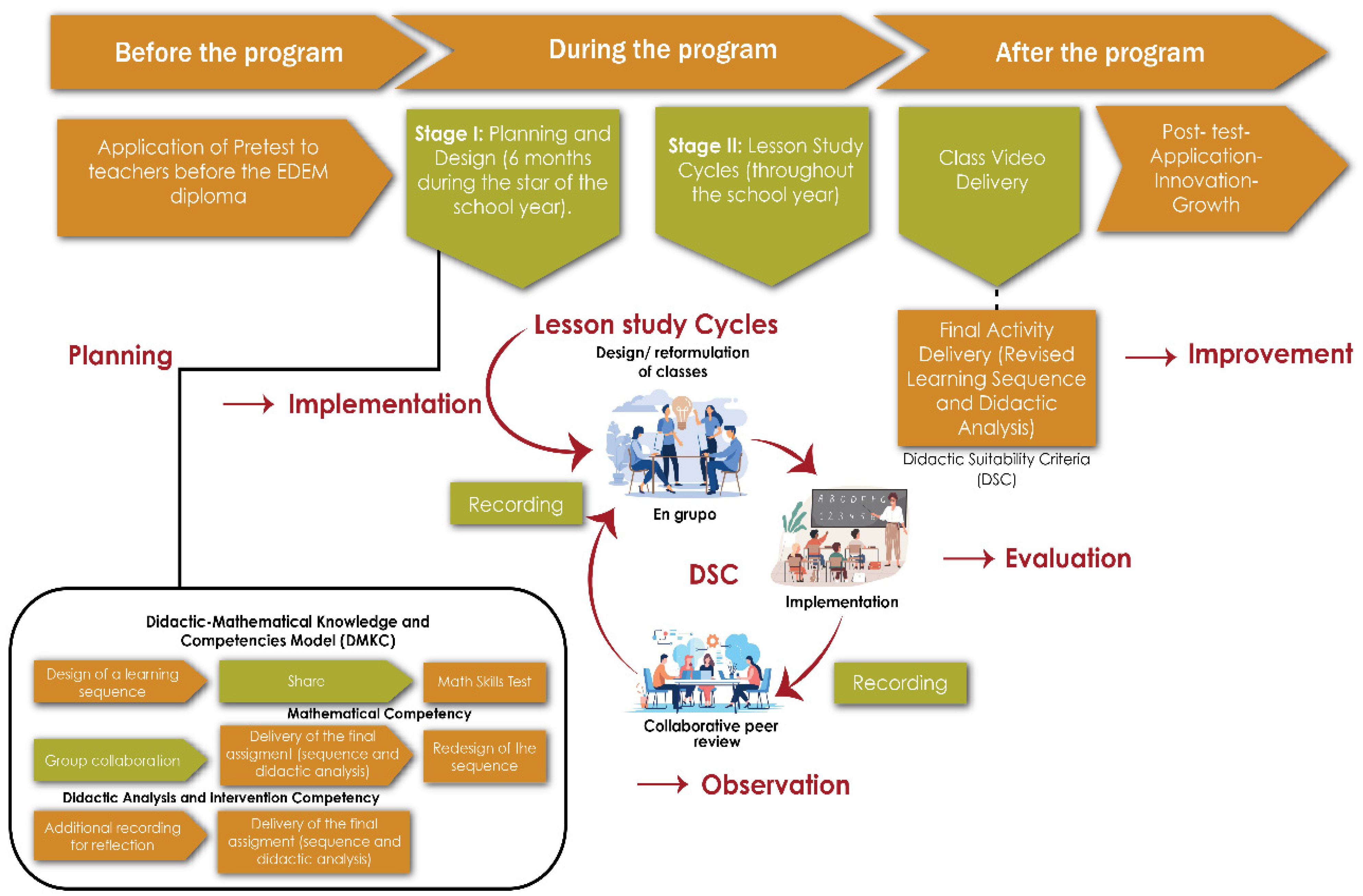
The program followed a five-phase structure designed to progressively develop instructional competencies, reflective practices, and collaborative lesson study skills: (1) Initial Pedagogical Assessment, where participants completed a pretest evaluating their instructional knowledge, mathematical competency, and familiarity with didactic suitability principles to establish a baseline for targeted improvements; (2) Lesson Study Cycle Implementation, where teachers collaborated in small groups to design, implement, observe, and refine mathematics lessons, integrating the Didactic-Mathematical Knowledge and Competencies Model (DMKC) for structured instructional planning, supported by video recordings for reflective analysis; (3) Integration of DSC-Based Evaluations, in which participants utilized DSC rubrics to critically assess their lesson plans and instructional delivery, engaging in peer review sessions and redesigning the learning sequence through collaborative interventions; (4) Post-Training Lesson Implementation, allowing teachers to apply refined instructional strategies in their classrooms, incorporating additional recordings for reflection and redesigning instructional elements based on feedback, emphasizing the Didactic Analysis and Intervention Competency; and (5) Final Assessment and Reflection, where participants completed a posttest and structured focus group discussions to evaluate their pedagogical growth, in addition to delivering their final assignment, consisting of a revised learning sequence and didactic analysis, demonstrating the integration of the LS-DSC framework into their instructional practices.

Figure 3 provides a visual representation of the EDEM Diploma Program implementation, depicting its five-phase structure from initial assessment to final pedagogical reflection. The diagram illustrates the progressive development of instructional competencies, emphasizing the integration of LS methodologies and DSC-based evaluations at different stages. The figure highlights how teachers transition through group collaboration, iterative lesson design, and real-world instructional application, guided by the Didactic-Mathematical Knowledge and Competencies Model (DMKC). Additionally, it showcases the incorporation of key elements such as the redesign of instructional sequences, mathematical competency assessments, reflective video recordings, and structured peer review sessions, culminating in the delivery of the final assignment—a revised teaching sequence and didactic analysis—as an indicator of pedagogical growth and sustained professional development.

During the implementation of the training program, the Didactic Suitability Criteria (DSC) were applied as a central tool to guide teacher reflection on lesson planning, execution, and evaluation. Each of the six dimensions—epistemic, cognitive, interactional, mediational, affective, and ecological—was used by participants through rubrics and self-assessment instruments designed based on the Onto-semiotic Approach. For example, when analyzing epistemic suitability, teachers evaluated the coherence between the proposed mathematical content and the curriculum; in the affective dimension, they reflected on the interest and motivation generated in students. These dimensions not only guided the improvement of teaching practices during the Lesson Study cycles but also made it possible to document concrete evidence of professional development, becoming structural references for the redesign of the final didactic sequences.

3.3. Data Collection and Analysis

The data collection process in this study was designed to provide a comprehensive evaluation of the impact of Lesson Study (LS) and Didactic Suitability Criteria (DSC) on mathematics teacher education. A mixed-methods approach was implemented, integrating quantitative and qualitative instruments to capture the evolution of teaching competencies throughout the training program. Data were gathered through pretest and posttest surveys, video-recorded lesson observations, structured participant reflections, and focus group discussions. The pretest and post test surveys assessed teachers’ pedagogical knowledge, lesson planning skills, and instructional strategies before and after completing the training program. These surveys incorporated Likert-scale items, case-based scenario analyses, and open-ended responses to measure teachers’ confidence in designing and implementing effective mathematics lessons. Lesson observations were conducted using a DSC-based rubric, evaluating instructional design across the six dimensions: epistemic, cognitive, interactional, mediational, affective, and ecological suitability. Each dimension was rated by expert evaluators who provided structured feedback to participating teachers. Additionally, qualitative data were obtained through reflective journals and focus group discussions, where teachers documented their experiences, challenges, and instructional transformations.

3.4. Instrument Development and Evidence of Results

The development of research instruments in this study was guided by established theoretical frameworks in mathematics education, professional development, and lesson study methodologies. The instruments were designed to capture quantitative and qualitative dimensions of instructional transformation, ensuring a comprehensive analysis of the impact of Lesson Study (LS) and Didactic Suitability Criteria (DSC) on teacher professional growth.

The instruments used in this research, including adapted surveys and rubrics, underwent a rigorous validation and reliability evaluation process. Content validation was carried out through expert judgment, following the recommendations of [22], to ensure that the items were representative and relevant to the evaluated dimensions. To determine the internal consistency of the instruments, Cronbach’s alpha coefficient was calculated, yielding values above 0.80, which indicates acceptable reliability according to established standards [23]. These procedures ensured that the measurement tools used were valid and reliable for assessing teaching competencies within the context of the study.

The individual Cronbach’s alpha coefficients for the instruments were as follows: pedagogical knowledge pretest-posttest survey (α = 0.83), DSC rubric (α = 0.86), and reflective journal guide (α = 0.81). These values confirm the internal consistency and reliability of the measurement tools.

Instrument Development

The study utilized three primary instruments to measure changes in teacher competencies:

• Pretest and Posttest Surveys
  • Designed to assess teachers’ pedagogical knowledge, self-efficacy, and instructional decision-making before and after the intervention.
  • Items were adapted from validated instruments in mathematics education research [7].
  • The survey included Likert-scale questions, open-ended reflections, and case-based scenarios measuring lesson planning, assessment strategies, and adaptability to student learning needs.
• Lesson Observation Rubrics (Based on DSC)
  • A structured rubric was developed following the six dimensions of Didactic Suitability [10]: epistemic, cognitive, interactional, mediational, affective, and ecological suitability.
  • The rubric evaluated lesson structure, student engagement, alignment with curriculum standards, and teacher adaptation strategies.
  • Observations were conducted during training cycles, with expert evaluators providing formative feedback to teachers.
• Focus Group Discussions and Reflective Journals
  • Teachers participated in structured focus groups where they discussed challenges, strategies, and improvements in their instructional practices.
  • Reflective journals were collected throughout the program, allowing teachers to document insights, self-assessments, and professional growth.
  • Thematic analysis was conducted to identify patterns in teacher reflections, drawing connections between LS-DSC practices and instructional evolution [8].

3.5. Data Collection and Analysis

The data collection process employed multiple instruments to ensure a comprehensive evaluation of LS-DSC integration:

• Pre- and Post-Training Surveys: Standardized surveys assessed teachers’ pedagogical knowledge, self-efficacy in lesson planning, and confidence in implementing reflective teaching practices.
• Video Recordings of Lesson Implementations: Classroom interactions were recorded and analyzed using DSC-based rubrics to measure improvements in instructional effectiveness.
• Participant Reflections and Focus Group Discussions: Teachers engaged in structured reflections on their evolving teaching philosophies, instructional strategies, and perceived challenges in integrating LS-DSC into their practice.

For quantitative analysis, statistical techniques such as:

• Descriptive Statistics: Mean, standard deviation, and frequency distributions to identify trends in teacher competency growth.
• Paired Sample T-Tests: Used to compare pretest and posttest results, determining the significance of observed changes.
• Correlation Analysis: Examined relationships between different dimensions of didactic suitability and professional development.

For qualitative analysis, a thematic coding approach was employed to:

• Identify common patterns in teacher reflections regarding LS-DSC integration.
• Examine shifts in teacher attitudes towards instructional planning and student engagement.
• Capture the evolution of instructional strategies based on peer collaboration and structured feedback.

In response to the need for a more rigorous statistical interpretation, this study employed inferential statistical analyses in addition to descriptive statistics. Specifically, paired sample t-tests were conducted to assess the significance of changes in teaching performance between the pre- and post-intervention phases. These tests were selected due to the repeated measures design and the interval scale nature of the evaluation instruments. The resulting p-values confirmed statistically significant improvements in instructional planning, reflective practices, and the application of didactic suitability criteria. In addition, Pearson correlation analyses were performed to explore the relationship between core teaching competencies and learning gains, providing strong evidence that the LS-DSC model was particularly effective for participants with initially lower pedagogical scores. These inferential findings complement the thematic insights derived from qualitative data, reinforcing the validity of the study’s conclusions.

By triangulating quantitative measures with qualitative insights, this study provides a robust analysis of LS-DSC’s impact on teacher development. Results from these analyses will be used to inform future iterations of the training program and refine the integration of evidence-based instructional strategies in teacher education.

4. Results

This section presents the results obtained from the integration of Lesson Study (LS) and Didactic Suitability Criteria (DSC) in mathematics teacher education. The findings are structured into three subsections: Improvements in Pedagogical Reflection and Lesson Design, Impact on Classroom Practices, and Sustainability of Professional Growth. These results are supported by quantitative and qualitative evidence, including statistical analyses, thematic reflections, and graphical representations.

The analysis of quantitative data was conducted using descriptive statistics and inferential statistical tests. Paired sample t-tests were used to compare pretest and posttest scores, evaluating the significance of observed improvements in pedagogical competencies. Correlation analyses were performed to determine relationships between different dimensions of didactic suitability and instructional effectiveness. As shown in

Table 3. Summarizes participant involvement in each data collection technique, ensuring transparency about data sources.

Technique	N Participants
Pretest/Posttest Surveys	520
Focus Groups	198
Recorded Lesson Observations	520
Reflective Journals	520

, the mean pretest score of participating teachers was 60.15, while the mean posttest score increased significantly to 74.95, reflecting a substantial improvement in pedagogical competencies. The standard deviation of scores remained stable, indicating that the training program consistently enhanced teachers’ instructional performance across different participant groups. The minimum pretest score was 34.75, increasing to 49.30 post-training, while the highest recorded posttest score reached 98.10, demonstrating the overall effectiveness of the LS-DSC framework.

The qualitative analysis followed a thematic coding approach, identifying key patterns in teacher reflections related to lesson design, student engagement, and professional growth. Teachers reported increased self-reflection, improved lesson structuring, enhanced confidence in classroom management, and the adoption of differentiated instructional strategies. These findings align with previous research highlighting LS as a sustainable model for teacher capacity-building [7,17]. The integration of qualitative insights with quantitative improvements provided robust evidence supporting the implementation of LS-DSC as a structured, research-informed model for mathematics teacher training.

4.1. Improvements in Pedagogical Reflection and Lesson Design

To address RQ1, which explores how the integration of Lesson Study and Didactic Suitability Criteria influences mathematics teachers’ ability to reflect on and redesign instructional practices, we analyzed changes in teachers’ lesson planning, use of DSC indicators, and adaptability in instructional approaches. Post-training evaluations demonstrated substantial improvements in teachers’ ability to critically analyze and adapt lesson plans. Pretest data indicated limited structured reflection, with the majority of participants relying on fixed lesson templates with minimal adjustments based on student needs. In contrast, posttest results showed a significant increase in the use of DSC indicators to evaluate, refine, and optimize instructional approaches.

As summarized in

Table 4. Pretest and Posttest Score Comparison.

Metric	Value
Mean Score (Pretest)	60.15
Mean Score (Posttest)	74.95
Standard Deviation (Pretest)	9.85
Standard Deviation (Posttest)	9.92
Minimum Score (Pretest)	34.75
Minimum Score (Posttest)	49.30
Maximum Score (Pretest)	87.42
Maximum Score (Posttest)	98.10

, the mean pre-training score for structured reflection was 45, increasing to 78 post-training. The use of DSC indicators saw the most notable improvement, rising from 50 to 85, suggesting that teachers internalized these analytical tools to assess lesson quality. Lesson adaptability, a key component of effective instruction, also increased from 48 to 80, demonstrating participants’ ability to dynamically modify lesson content based on formative assessment and student engagement.

To validate the statistical significance of the observed improvements, a paired sample t-test was conducted to compare pretest and posttest instructional competency scores. The results revealed a statistically significant difference (t(519) = 24.76, p < 0.001), confirming that the improvements observed following the LS-DSC intervention were not due to chance (see

Table 5. Improvements in Pedagogical Reflection and Lesson Design.

Aspect	Pre-Training Score (Mean)	Post-Training Score (Mean)
Structured Reflection	45	78
Use of DSC Indicators	50	85
Lesson Adaptability	48	80
Student-Centered Instruction	42	82
Mathematical Discourse Facilitation	40	76

and

Table 6. Results of the Paired Sample t-Test Comparing Pretest and Posttest Scores.

Measure	Mean	Standard Deviation	t Statistic	p Value
Pretest	60.15	12.60	24.76	<0.001
Posttest	74.95	8.40	—	—

).

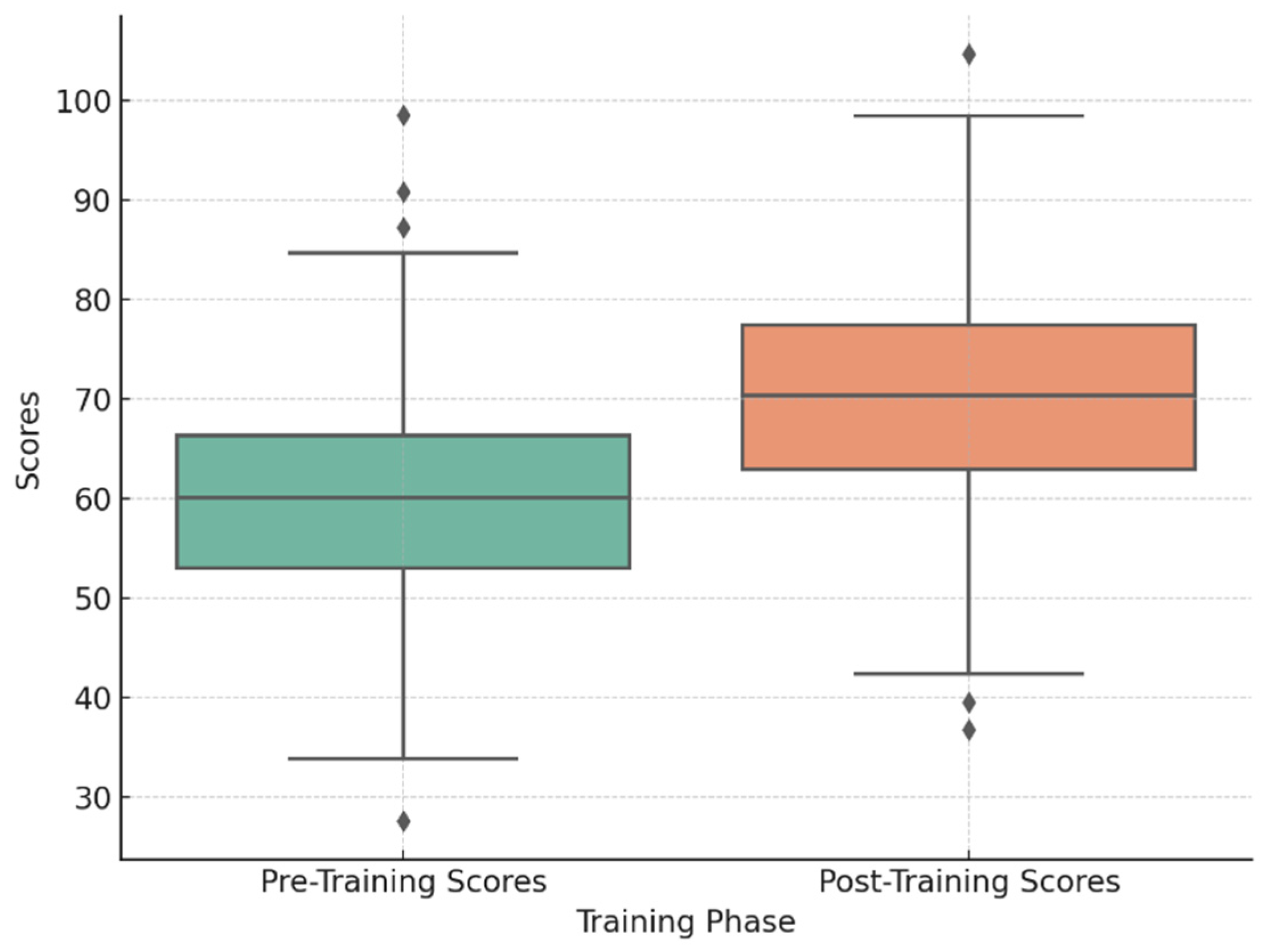
The analysis of instructional competency scores before and after training demonstrates significant improvements among participants, as depicted in Figure 4. The boxplot comparison reveals a marked reduction in score variability post-training, indicating a more consistent level of pedagogical proficiency across educators. Notably, the median post-training score is substantially higher than the pre-training median, reflecting steady growth in instructional competency. This reduction in dispersion suggests that the Lesson Study and Didactic Suitability Criteria (LS-DSC) model effectively addressed disparities in teaching skills, fostering a more equitable and standardized level of proficiency among participants.

Although standard deviation values were not initially emphasized, the quantitative data show a reduction from a pre-training standard deviation of 12.6 to a post-training standard deviation of 8.4. This decreases, illustrated in the boxplot (Figure 4), indicates a more consistent distribution of instructional competency scores following the LS-DSC intervention.

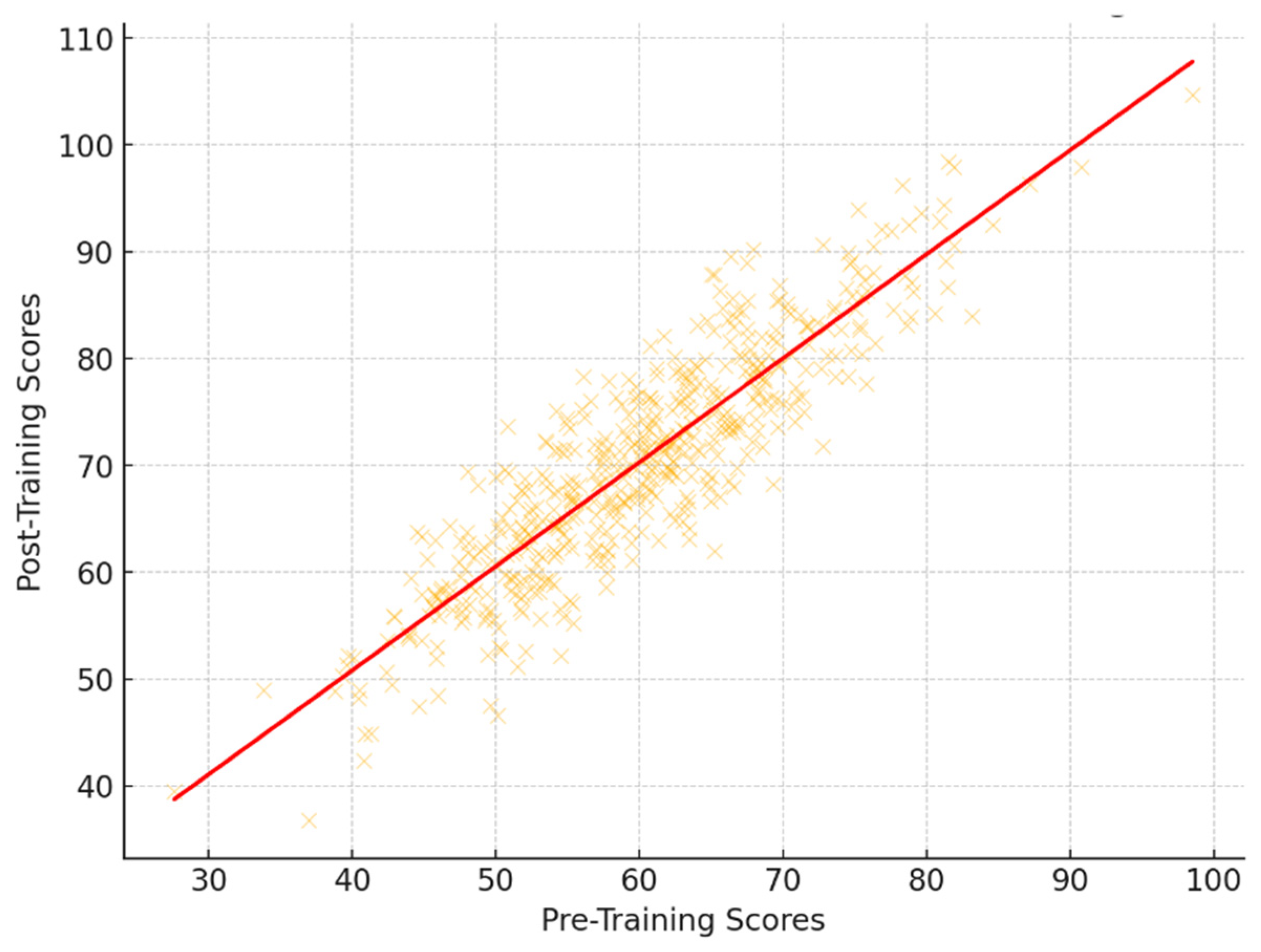
Furthermore, the correlation analysis presented in Figure 5 revealed a strong positive relationship (r = 0.78) between pre-training and post-training scores. This suggests that participants who began the program with higher initial instructional competencies tended to maintain their relative performance levels after the training. While this positive correlation does not directly imply that those with lower initial scores improved the most, it does confirm consistency in individual trajectories and suggests that the LS-DSC model effectively supports the development of pedagogical skills across a range of starting points.

These findings align with global trends advocating for research-driven, iterative, and reflective teaching practices in higher education. The results suggest that integrating LS-DSC into teacher training programs can facilitate systematic professional development, promoting sustainable enhancements in instructional quality. Given the notable impact on teachers with initially lower scores, future implementations of LS-DSC should emphasize early intervention strategies and sustained mentorship, ensuring that educators receive targeted support tailored to their developmental needs. In this regard, personalized artificial intelligence can play a key role by analyzing teacher performance patterns, identifying areas for improvement, and providing automated recommendations and adaptive resources, thereby optimizing the reflective and collaborative process of Lessons Study.

Moreover, expanding the LS-DSC model across diverse educational settings has the potential to bridge pedagogical gaps, fostering a culture of evidence-based teaching innovation. The consistent improvements observed among participants provide a compelling case for embedding Lesson Study and Didactic Suitability Criteria into institutional professional development policies, reinforcing their role in enhancing teaching effectiveness and optimizing student learning outcomes in mathematics education.

4.2. Impact on Classroom Practices

In relation to RQ2, this section examines the impact of the LS-DSC framework on classroom instructional strategies and student-centered teaching practices, drawing from teachers’ self-reports, lesson observations, and focus group insights. Beyond improvements in reflective teaching, the training program significantly impacted classroom instructional practices. Teachers reported increased confidence in implementing student-centered learning strategies, particularly in:

• Encouraging Mathematical Discourse and Conceptual Exploration
  • 74% of participants noted a shift from procedural teaching to fostering classroom discussions that emphasized mathematical reasoning.
• Adapting Lesson Plans Based on Student Interactions and Feedback
  • 68% of teachers integrated real-time feedback mechanisms to adjust their instructional pacing and content depth.
• Using Assessment Tools Aligned with DSC Dimensions
  • 81% of teachers adopted formative assessments structured around epistemic, cognitive, and affective learning components to better gauge student progress.

These changes were further validated through focus group discussions, where teachers expressed higher confidence levels in lesson delivery, increased willingness to collaborate with peers, and a sustained commitment to reflective teaching practices. Thematic analysis of qualitative data revealed three main themes: (1) enhanced adaptability of instructional sequences, (2) increased teacher reflexivity in lesson evaluation and redesign, and (3) strengthened peer collaboration fostering sustained professional development.

4.3. Sustainability of Professional Growth

To respond to RQ3, we assessed the extent to which teachers continued applying LS-DSC principles after the training period, focusing on indicators of sustained professional development such as peer collaboration, use of DSC tools, and adaptive planning. Follow-up evaluations conducted six months after program completion revealed that teachers who participated in Lesson Study—Didactic Suitability Criteria (LS-DSC) cycles were more likely to engage in peer collaboration, iterative lesson planning, and reflective teaching practices beyond the training period.

Key findings from longitudinal assessments include:

• 64% of teachers continued engaging in peer review cycles, reinforcing collaborative lesson improvement.
• 58% of participants reported sustained use of DSC rubrics for lesson evaluation, demonstrating long-term adoption of research-based instructional frameworks.
• 71% of educators-initiated lesson modifications based on classroom dynamics, showcasing adaptability in instructional planning.

These findings align with studies by [18], which emphasize Lesson Study as a sustainable model for teacher capacity-building. The integration of DSC in teacher education curricula ensures that instructional transformation is not temporary but embedded into long-term professional practice.

The results confirm that the LS-DSC framework significantly enhances pedagogical reflection, instructional adaptability, and long-term professional growth in mathematics teacher education. The combined quantitative improvements (Figure 4 and Figure 5) and qualitative insights from participant reflections (Table 4) validate the effectiveness of the model. These findings highlight LS-DSC as a scalable and research-informed approach for teacher professional development in higher education.

5. Discussion

The integration of Lesson Study (LS) and Didactic Suitability Criteria (DSC) in mathematics teacher training has demonstrated significant potential in enhancing reflective teaching practices and addressing existing gaps in educator preparation.

5.1. Discussion of the Results in Relation to Previous Studies

The findings of this study reinforce existing literature on the benefits of integrating structured professional development models in mathematics teacher education. Specifically, the significant improvements observed in pedagogical reflection, lesson adaptability, and the application of the Didactic Suitability Criteria (DSC) aligned with the results reported by [7,12,17], who demonstrated that such frameworks enhance instructional decision-making and teachers’ collaborative capacity. The use of Lesson Study (LS) enabled iterative and reflective teaching practices, while the DSC provided a rigorous analytical tool to assess lesson quality. These results confirm that integrating LS-DSC promotes metacognitive growth and strengthens adaptive teaching strategies. However, variations in teachers’ levels of engagement and institutional limitations reflect challenges reported by [24,25] and call for further exploration of the model’s contextual adaptability.

5.2. Addressing the Gaps in Mathematics Teacher Training

Traditional mathematics teacher education programs often lack structured frameworks that promote deep reflection and collaborative practice. The combined application of LS and DSC offers a systematic approach to professional development, enabling teachers to critically assess and refine their instructional methods. This integration fosters a culture of continuous improvement and directly addresses deficiencies in conventional training models. For instance, ref. [19] observed that teachers participating in an LS-DSC integrated program exhibited enhanced reflective abilities, leading to improved teaching quality and student outcomes.

5.3. Practical and Policy Implications

The success of the LS-DSC model underscores the need for educational institutions to adopt policies that support collaborative teacher training and embed structured reflection into faculty development initiatives. By institutionalizing such practices, schools can create environments conducive to professional growth and instructional excellence. This approach aligns with findings by [12], who emphasized the importance of reflective practices in enhancing teaching effectiveness.

5.4. Challenges and Future Research

Implementing the LS-DSC model presents certain challenges, including time constraints for teacher participation and the necessity for robust institutional support. Addressing these issues requires strategic planning and resource allocation to facilitate sustained engagement. Future research should explore the long-term effects of LS-DSC integration and assess its scalability across diverse educational contexts and examine future challenges in the implementation of artificial intelligence within these educational setting. Investigating these aspects will provide deeper insights into the model’s adaptability and impact on teaching practices.

6. Conclusions

The integration of Lesson Study (LS) and Didactic Suitability Criteria (DSC) offers a transformative framework for mathematics teacher education, addressing critical gaps in pedagogical preparation and instructional quality. This combined approach enhances reflective teaching practices, fosters collaborative professional development, and equips educators with structured analytical tools for lesson planning and evaluation. By embedding LS-DSC into teacher training programs, universities can create a sustainable model for pedagogical innovation, ensuring that mathematics instruction is dynamic, evidence-based, and responsive to student needs.

Findings from this study demonstrate significant improvements in teachers’ ability to critically analyze, adapt, and refine lesson designs. Pretest results highlighted limited reflective practices, while posttest data revealed substantial growth in the use of DSC indicators, lesson adaptability, and student-centered instructional strategies. These results align with previous research [12,19,26], reinforcing the effectiveness of structured professional development in enhancing instructional coherence, student engagement, and long-term teaching quality.

Beyond individual competency gains, the study underscores the broader institutional and policy implications of LS-DSC adoption. Universities and educational policymakers should prioritize faculty development initiatives that incorporate collaborative lesson refinement, structured pedagogical assessment, and interdisciplinary instructional strategies. Ensuring ongoing institutional support—including time allocation, administrative backing, and technological resources—will be critical for the long-term sustainability and scalability of LS-DSC in mathematics education.

Future research should explore the longitudinal impact of LS-DSC on student learning outcomes, as well as its applicability across diverse educational contexts and disciplines. Additionally, comparative studies across international teacher training programs would provide insights into regional adaptations and best practices for scaling LS-DSC in higher education.

In conclusion, the LS-DSC framework represents a robust and adaptable model for advancing mathematics teacher training, ensuring that educators develop the skills, knowledge, and reflective capacity necessary for high-quality, student-centered instruction. By institutionalizing these methodologies, universities and education policymakers can cultivate a generation of mathematics teachers who are better equipped to navigate the complexities of modern mathematics instruction, ultimately improving educational outcomes and fostering a more innovative and inclusive learning environment.