Mathematics Teacher Educators’ Practices to Support Teachers in the Design of Mathematical Tasks
Abstract
:1. Introduction
- What pattern of practices emerges when mathematics teacher educators aim to develop a PDP to support teacher design of mathematical tasks in two different contexts?
- What are the similarities and differences, in terms of practices adopted and results obtained, when a PDP is conducted face-to-face versus through a MOOC?
2. Literature Review
3. Theoretical Framework
4. Methodology and Data Analysis
4.1. Research Contexts
4.1.1. PDP Conducted with Sri Lankan Teachers
4.1.2. PDP Conducted with the Italian Teachers
4.1.3. A Brief Comparison between the Two PDPs
4.2. Data Collection and Analysis
5. Results
5.1. Sri Lankan Experience
5.1.1. The Meta-Didactical Praxeologies of the Educators
5.1.2. Application of the Meta-Didactical Praxeologies
Nimali: We didn’t have an idea about how to write a task. So through this we had a good idea about that
Malka: We can now prepare tasks ourselves for the lessons that students may find difficult.
5.1.3. A Mathematical Task Design Made by a Group of Teachers within the PDP
5.2. The Italian Experience
5.2.1. The Meta-Didactical Praxeologies of the Educators
5.2.2. Application of the Meta-Didactical Praxeologies
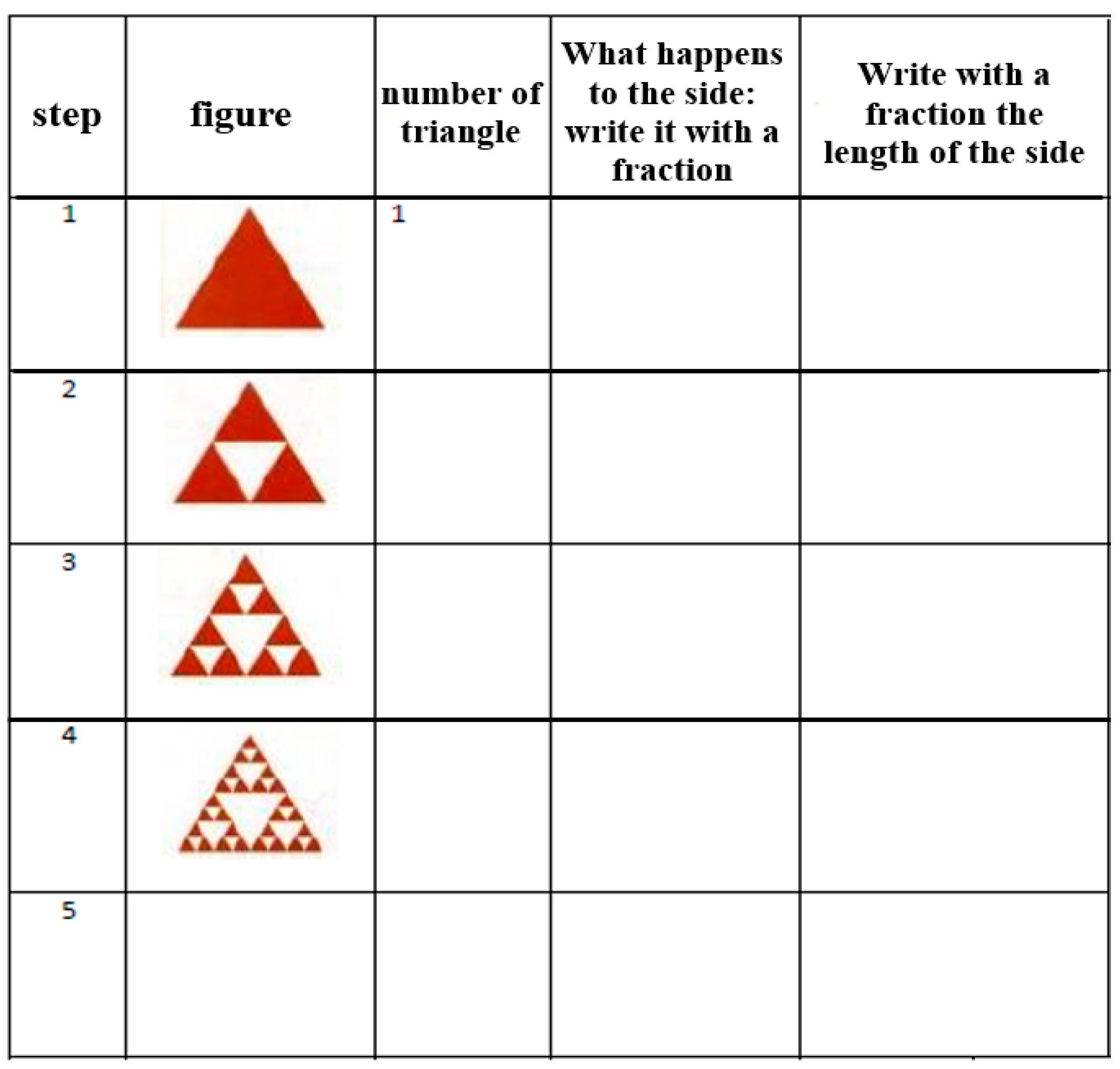
M.C. (high school teacher): I found the proposed activities particularly interesting and especially the way they are presented. […] this year I will propose […] in grade 10 [the activity of] the Sierpinski’s triangle. I think I get the attention and interest of my students, since I have never experienced laboratory activities in class.
V.M. (middle school teacher): I find the proposed activities are very interesting and stimulating. Introducing the principle of induction or recursion is not easy at all, but these ideas are a good starting point. Very nice the activity on the Sierpinski’s triangle.
5.2.3. A Mathematical Task Design Made by a Teacher within the PDP
- It is an example of project work that has taken its cue from the examples proposed by the educators;
- It allows us to observe how a MOOC teacher was able to adapt to her scholastic level the proposals of the educators, even those that could be more difficult to achieve;
- The proposed project work was a DT task design, in line with the intentions of the teachers from Sri Lanka.
The activity proposes a very original and creative work that allows students to recognize geometric figures, properties and their significant elements. Balanced use of manual modelling using plastic strips and modelling using GeoGebra […]. The strengths of the work are: (a) Presentation of a new mathematical concept in a real and original situation; (b) Use of technology; (c) Guided discussion; (d) Propaedeutic modelling for abstraction; (e) Well constructed test worksheet […]. As weaknesses of the work I have identified: (a) The valuation criteria of the asset are not indicated; (b) I would suggest the introduction of a final questionnaire to reflect on the activity.
5.3. A comparison between Sri Lankan Italian Educators’ Meta-Didactical Praxeologies
- i.
- Examples: the examples of activities prepared by educators and proposed to teachers;
- ii.
- Discussions: the teachers’ discussions, (in terms of reflection, modification, change of opinion and ideas), orchestrated by the educators, on the activities;
- iii.
- Design: the task design carried out by the teachers based on (i) and (ii);
- To motivate teachers to discuss and exchange ideas to find answers to issues they face in task design;
- To promote self and peer reflections, and to understand the importance of them in PD;
- To establish communities (among MOOC teachers in the Italian context and having small groups either in the school or in the educational zone in Sri Lanka).
6. Discussion and Conclusions
- What patterns of practices emerge when mathematics teacher educators aim to develop a PDP to support teacher design of mathematical tasks in two different contexts?
- What are the similarities and differences in methods and results if a PDP is conducted face-to-face or through MOOC?
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kieran, C.; Krainer, K.; Shaughnessy, J.M. Linking research to practice: Teachers as key stakeholders in mathematics education research. In Third International Handbook of Mathematics Education; Clements, M.A., Bishop, A.J., Keitel, C., Kilpatrick, J., Leung, F.K.S., Eds.; Springer: London, UK, 2013; pp. 361–392. [Google Scholar]
- Hattie, J. Teachers make a difference: What is the research evidence? In Paper Presented at the Australian Council for Educational Research Annual Conference on Building Teacher Quality; Australian Council for Educational Research: Melbourne, Australia, 2003; Available online: http://research.acer.edu.au/research_conference_2003/4/ (accessed on 28 July 2023).
- Jones, K.; Pepin, B. Research on mathematics teachers as partners in task design. J. Math. Teach. Educ. 2016, 19, 105–121. [Google Scholar] [CrossRef]
- Ratnayake, I.; Thomas, M.O.J. Documentational genesis during teacher collaborative development of tasks incorporating digital technology. In Proceedings of the Re(s)sources 2018 Conference, Lyon, France, 28–30 May 2018. [Google Scholar]
- Sullivan, P.; Knott, L.; Yang, Y.; Askew, M.; Brown, L.; Bussi, M.G.B.; Gimenez, J. The relationship between task design, anticipated pedagogies, and student learning. In Task Design in Mathematics Education; Watson, A., Ohtani, M., Eds.; Springer: London, UK, 2015; pp. 83–114. [Google Scholar]
- Guskey, T.R. Evaluating Professional Development; Corwin Press: Thousand Oaks, CA, USA, 2000. [Google Scholar]
- Shulman, L. Those who understand: Knowledge growth in teaching. Educ. Res. 1986, 15, 4–14. [Google Scholar] [CrossRef]
- Ball, D.L. Bridging practices: Intertwining content and pedagogy in teaching and learning to teach. J. Teach. Educ. 2000, 51, 241–247. [Google Scholar] [CrossRef]
- Hjalmarson, M.A.; Diefes-Dux, H. Teacher as designer: A framework for teacher analysis of mathematical model-eliciting activities. Interdiscip. J. Probl.-Based Learn. 2008, 2, 5. [Google Scholar] [CrossRef]
- Voogt, J.; Laferrière, T.; Breuleux, A.; Itow, R.C.; Hickey, D.T.; McKenney, S. Collaborative design as a form of professional development. Instr. Sci. 2015, 43, 259–282. [Google Scholar] [CrossRef]
- Gueudet, G.; Trouche, L. Teachers’ work with resources: Documentation geneses and professional geneses. In From Text to ‘Lived’ Resources: Mathematics Curriculum Materials and Teacher Development; Gueudet, G., Pepin, B., Trouche, L., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 23–41. [Google Scholar]
- Sardo-Brown, D. Experienced teachers’ planning practices: A US survey. J. Educ. Teach. 1990, 16, 57–71. [Google Scholar] [CrossRef]
- Wanlin, P.; Bodeux, C. Les processus de pensée des enseignants durant la planification et l’implémentation de leur enseignement. In Actes du Colloque International de L’association Pour le Développement des Méthodologies d’Evaluation en Education; E.M.A.C.S: Luxembourg, 2006. [Google Scholar]
- Clark, C.M.; Elmore, J.L. Transforming curriculum in mathematics, science, and writing: A case study of teacher yearly planning. Res. Ser. 1981, 99, 35. [Google Scholar]
- Maher, C. The teacher as designer, implementer, and evaluator of children’s mathematical learning environments. J. Math. Behav. 1988, 6, 295–303. [Google Scholar]
- Kirschner, P.A. Do we need teachers as designers of technology enhanced learning? Instr. Sci. 2015, 43, 309–322. [Google Scholar] [CrossRef]
- George, A.; Sanders, M. Evaluating the potential of teacher-designed technology-based tasks for meaningful learning: Identifying needs for professional development. Educ. Inf. Technol. 2017, 22, 2871–2895. [Google Scholar] [CrossRef]
- Thomas, M.O.J.; Palmer, J.M. Teaching with digital technology: Obstacles and opportunities. In The Mathematics Teacher in the Digital Era; Clark-Wilson, A., Robutti, O., Sinclair, N., Eds.; Springer: London, UK, 2014; Volume 2, pp. 71–89. [Google Scholar]
- Ratnayake, I.; Thomas, M.O.J.; Kensington-Miller, B. Professional development for digital technology task design by secondary mathematics teachers. ZDM—Int. J. Math. Educ. 2020, 52, 1423–1437. [Google Scholar] [CrossRef]
- Clark-Wilson, A.; Aldon, G.; Cusi, A.; Goos, M.; Haspekian, M.; Robutti, O.; Thomas, M.O.J. The challenges of teaching mathematics with digital technologies-The evolving role of the teacher. In 38th Conference of the International Group for the Psychology of Mathematics Education and the 36th Conference of the North American Chapter of the Psychology of Mathematics Education; Liljedahl, P., Nicol, C., Oesterle, S., Allan, D., Eds.; University of British Columbia: Vancouver, BC, Canada, 2014; Volume 1, pp. 87–116. [Google Scholar]
- Arzarello, F.; Robutti, O.; Sabena, C.; Cusi, A.; Garuti, R.; Malara, N.; Martignone, F. Meta-didactical transposition: A theoretical model for teacher education programmes. In The mathematics teacher in the digital era; Clark-Wilson, A., Robutti, O., Sinclair, N., Eds.; Springer: Dordrecht, The Netherlands, 2014; Volume 1, pp. 347–372. [Google Scholar] [CrossRef]
- Chevallard, Y. L’analyse des pratiques enseignantes en théorie anthropologique du didactique. Rech. Didact. Des Mathématiques 1999, 19, 221–265. [Google Scholar]
- García, F.J.; Gascón, J.; Ruiz Higueras, L.; Bosch, M. Mathematical modelling as a tool for the connection of school mathematics. ZDM—Int. J. Math. Educ. 2006, 38, 226–246. [Google Scholar] [CrossRef]
- Aldon, G.; Arzarello, F.; Panero, M.; Robutti, O.; Taranto, E.; Trgalová, J. MOOC for mathematics teacher education to foster professional development: Design principles and assessment. In Technology in Mathematics Teaching. Selected Papers of the 13th ICTMT conference. Mathematics Education in the Digital Era; Aldon, G., Trgalová, J., Eds.; Springer: Cham, Germany, 2019; Volume 13, pp. 223–246. [Google Scholar] [CrossRef]
- Robutti, O. Meta-Didactical Transposition. In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer: Cham, Germany, 2018. [Google Scholar]
- Schoenfeld, A.H. How We Think: A Theory of Goal-Oriented Decision Making and Its Educational Applications; Routledge: New York, NY, USA, 2010. [Google Scholar]
- Choy, B.H. Snapshots of mathematics teacher noticing during task design. Math. Educ. Res. J. 2016, 28, 421–440. [Google Scholar] [CrossRef]
- Taranto, E.; Arzarello, F. Math MOOC UniTo: An Italian project on MOOCs for mathematics teacher education, and the development of a new theoretical framework. ZDM—Int. J. Math. Educ. 2020, 52, 843–858. [Google Scholar] [CrossRef]
- Taranto, E.; Robutti, O.; Arzarello, F. Learning within MOOCs for mathematics teacher education. ZDM – Int. J. Math. Educ. 2020, 52, 1439–1453. [Google Scholar] [CrossRef]
- Kieran, C.; Drijvers, P. The co-emergence of machine techniques, paper-and-pencil techniques, and theoretical reflection: A study of CAS use in secondary school algebra. Int. J. Comput. Math. Learn. 2006, 11, 205–263. [Google Scholar] [CrossRef]
- Leung, A.; Bolite-Frant, J. Designing mathematics tasks: The role of tools. In Task Design in Mathematics Education; New ICMI Study Series; Watson, A., Ohtani, M., Eds.; Springer: New York, NY, USA, 2015; pp. 191–225. [Google Scholar]
- Thomas, M.O.J.; Lin, C. Designing tasks for use with digital technology. In Task Design in Mathematics Education, Proceedings of ICMI Study 22; Margolinas, C., Ainley, J., Frant, J.B., Doorman, M., Kieran, C., Leung, A., Ohtani, M., Sullivan, P., Thompson, D., Watson, A., et al., Eds.; Oxford University Press: Oxford, UK, 2013; pp. 109–118. [Google Scholar]
- Ratnayake, I.; Oates, G.; Thomas, M.O.J. Supporting teachers developing mathematical tasks with digital technology. In Proceedings of the 39th annual conference of the Mathematics Education Research Group of Australasia, Adelaide, Australia; 2016. [Google Scholar]
- Jaworski, B. Research practice into/influencing mathematics teaching and learning development: Towards a theoretical framework based on co-learning partnership. Educ. Stud. Math. 2003, 54, 249–282. [Google Scholar] [CrossRef]
- Jaworski, B. Theory and practice in mathematics teaching development: Critical inquiry as a mode of learning in teaching. J. Math. Teach. Educ. 2006, 9, 187–211. [Google Scholar] [CrossRef]
- Anichini, G.; Arzarello, F.; Ciarrapico, L.; Robutti, O.; Statale, L.S. Matematica 2003; Matteoni Stampatore: Lucca, Italy, 2004. [Google Scholar]
- A Future Full of Badges. Available online: https://www.chronicle.com/article/a-future-full-of-badges/ (accessed on 28 July 2023).
- Bender, W.N. Project-Based Learning: Differentiating Instruction for the 21st Century; Corwin Press: London, UK, 2012. [Google Scholar]
- Laurillard, D. The educational problem that MOOCs could solve: Professional development for teachers of disadvantaged students. Res. Learn. Technol. 2016, 24, 29369. [Google Scholar] [CrossRef]
- Black, P.; Wiliam, D. Developing the theory of formative assessment. Educ. Assess. Eval. Account. 2009, 21, 5. [Google Scholar] [CrossRef]
- Gimenez, J.; Font, V.F.; Vanegas, Y.M. Designing professional tasks for didactical analysis as a research process. In Proceedings of ICMI Study 22; Margolinas, C., Ed.; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Lee, H.; Özgün-Koca, S.A. Professional development for mathematics teachers: Using task design and analysis. J. Curr. Issues Educ. 2016, 2, 1–16. [Google Scholar]
- Huizinga, T.; Handelzalts, A.; Nieveen, N.; Voogt, J.M. Teacher involvement in curriculum design: Need for support to enhance teachers’ design expertise. J. Curric. Stud. 2014, 46, 33–57. [Google Scholar] [CrossRef]





| Sri Lanka | Italy | |
|---|---|---|
| Nature of PDPs | Face-to-face | MOOC (online) |
| Moment of design | Before and after the PD intervention | At the end of the MOOC, after examining a set of examples provided by the educators and after benefiting from other MOOC teachers’ interactions in communication message boards |
| Modality of the design | Teachers wrote their tasks on paper | Teachers had to use Learning Designer |
| Type of design | DT algebra task and planning a lesson to implement such a task | Design a lesson that contains DT or non-DT tasks (arithmetic, algebra) |
| Time devoted to design | 2 days for task design (2 months for the whole process of task design, implementation and modification) | 2 weeks |
| Revision of the design | Teachers design collaboratively (implementation, reflection, and modification) | MOOC teachers design alone but afterwards they received feedback from another teacher (peer review) |
| Teachers’ Discussion during the Initial Task Design Process | |
|---|---|
| Task | To enable teachers to exchange ideas in order to design a task with their existing knowledge |
| Techniques | Dividing teachers in small communities of inquiry (four groups of three) Each group to decide a topic for which they would design a task To exchange teachers’ prior knowledge to design a DT task for their students |
| Argument | To understand what existing knowledge they had in task design |
| Exemplar Task Prepared by the Researchers | |
|---|---|
| Task | To support teachers to design a rich DT task |
| Techniques | Introducing and discussing features of a rich DT mathematical task Showing an exemplar task with these features |
| Argument | To provide teachers with theoretical knowledge on developing DT tasks |
| Teachers’ Discussion during the Task Design Process and after Implementation | |
|---|---|
| Task | To enable teachers to exchange ideas to design a rich task and to reflect on their own work |
| Techniques | Grouping teachers in small communities of inquiry (four groups of three) Each group was to discuss whether to modify the task designed at the beginning or to create a new one in the light of the stimuli received during the PDP Each group was to reflect on the features of a rich task discussed at the PDP when modifying the tasks Supporting teachers to reflect on the tasks themselves Directing teachers to reflect on their task implementation lesson |
| Argument | To have communities of inquiry [34,35] |
| Task Design Carried Out by the Teachers | |
|---|---|
| Task | Allowing teachers to design a DT algebra task |
| Techniques | Suggested they form small groups to work in Directed teachers to design a task based on their existing knowledge Recommended use of GeoGebra as their DT Suggested they either design a new task based on the points discussed at the PD or modify one Suggested further modifications, if necessary, after the implementation |
| Argument | To support teachers to design DT mathematical tasks themselves |
| Principles of Rich Tasks | First Task | Second Task | |||
|---|---|---|---|---|---|
| Scale | Evidence | Score | Evidence | Score | |
| Focuses on mathematical ideas, e.g., epistemological obstacles | 0–4 | ||||
| Considers the role of language and discourse | 0–3 | ||||
| Students give written interpretations and reflections | 0–5 | ||||
| Goes beyond routine methods | 0–4 | ||||
| Encourages student investigation | 0–5 | ||||
| Has multi-representational aspects | 0–4 | ||||
| Appropriate for student instrumental genesis | 0–3 | ||||
| Provides opportunities for instrumental feedback | 0–3 | ||||
| Integration of DT and by-hand techniques | 0–3 | ||||
| Aims for generalization | 0–5 | ||||
| Students think about proof | 0–4 | ||||
| Develops mathematical theory | 0–3 | ||||
| Group | Pre-Intervention (Max 46) | Post-Intervention (Max 46) | t | p |
|---|---|---|---|---|
| A | 18 | 29 | 3.11 | <0.005 |
| B | 12 | 25 | 4.03 | <0.001 |
| C | 12 | 32 | 4.44 | <0.0005 |
| D | 21 | 27 | 1.80 | <0.05 |
| Principles of Rich Tasks | First Task | Final Task | ||
|---|---|---|---|---|
| Evidence | Score | Evidence | Score | |
| Focuses on mathematical ideas, e.g., epistemological obstacles | Behaviour of the graph when delta is negative, completing the square, sign of the function | 3 | Good: Variation of the graph with the sign of a. Sign of the graph when delta is negative. Completing the square. | 4 |
| Considers the role of language & discourse | Words such as behaviour, real values of x, positive and symbols like Δ > 0, a < 0, etc but none of them aimed at the students | 1 | Many mathematical words and symbols such as discriminant, variation, maximum and minimum, touches, sketch, the axis of symmetry, completing the square. All in the context of student direction | 3 |
| Students give written interpretations and reflections | No evidence for students’ interpretations | 0 | Students’ are asked a number of ‘what’ questions and are to fill in blanks but are only required to explain in one question ‘How does the maximum … change?’ | 3 |
| Goes beyond routine methods | Considers the relationship between the sign of a and the sign of f(x). No standard solution methods. | 2 | Students are guided to think logically about the sign of f(x) when delta is negative and when a > 0 and a < 0. Students are guided with given steps in the task. | 2 |
| Encourages student investigation | Students ‘observe the behaviour’ of the graph and investigate the effect of a | 1 | The whole worksheet is structured around student investigation using GeoGebra. Students are asked to observe and answer questions and to find values of b and c that make delta negative. Very directed investigation. | 3 |
| Has multi-representational aspects | Involves mathematical language, graphs and algebra | 2 | Use graphs, algebra and values obtained from the algebra view, along with extensive natural language use. Link the graphs with algebra and graphs with numbers. | 4 |
| Appropriate for student instrumental genesis | Unclear. No mention of how they will observe the graph | 0 | Students need function entry, variation of a, obtain values of b2 − 4ac, draw the axis of symmetry and find the sign of expressions. These seem appropriate and had been covered. | 3 |
| Provides opportunity for instrumental feedback | Students observe the graphs to identify the effect of a | 1 | Graph shape and position relative to axes, sign of discriminant, sign of a, sign of | 3 |
| Integration of DT and by-hand techniques | Not mention of DT techniques present | 0 | Good. Use GeoGebra to draw the graphs and observe the changes of the discriminant. Complete the square and fill the blanks by-hand. | 3 |
| Aims for generalisation | Completing the square for a general quadratic function, but given. Aims to generalise effect of a. | 2 | Completing the square for a general quadratic function. Considers the general effect of a, b and c on the discriminant and the relationship to the graph. Aims to generalise effects of the discriminant and a on the function’s graph. | 4 |
| Students think about proof | No evidence | 0 | No evidence | 0 |
| Develops mathematical theory | No evidence | 0 | No evidence | 0 |
| Totals | 12/46 | 32/46 | ||
| Examples of Activities Prepared by Educators | |
|---|---|
| Task | To propose to MOOC teachers’ activities on the number core (based on arithmetic and algebra) |
| Techniques | To subdivide the activities into one-week modules To choose activities based on laboratory-based methodology and on the use of technology To transpose, in a digital format, materials, and didactical resources for teacher education |
| Argument | To innovate methodology and strategies of teaching mathematics as highlighted in the Italian curriculum and give the MOOC teachers ideas for drawing up their final task design |
| MOOC Teachers’ Discussion on the Activities Examined | |
|---|---|
| Task | To enable MOOC teachers to exchange opinions, reflections, ideas on the MOOC activities |
| Technique | Inserting specific communication message boards in each module Entering a stimulus question or title in order to accompany MOOC teachers in their reading of the materials and identifying their focus Reducing educators’ interventions, but monitoring behind the scenes |
| Argument | To support the establishment of a community made up of only MOOC teachers |
| Task Design Carried Out by MOOC Teachers | |
|---|---|
| Task | To allow MOOC teachers to design a project with arithmetic and algebra content |
| Techniques | MOOC teachers were asked to carry out an individual project work, using Learning Designer software Each project was to be reviewed by another MOOC teacher |
| Argument | Project-based learning [38] |
| Module 1 | Module 2 | Module 3 | Module 4 | Module 5 |
|---|---|---|---|---|
| 15% | 4% | 3% | 8% | 22% |
| Connections to the Real World | Creativity | Collaboration | Use of Technology | General Considerations |
|---|---|---|---|---|
| 4 | 4 | 3 | 3 | 4 |
| Sri Lanka | Italy | |
|---|---|---|
| Task | One exemplar task | Few exemplar tasks |
| DT task | DT tasks and non-DT tasks | |
| Theoretical | Practically used in their classrooms | |
| Techniques | Teachers were directed to discuss the task in terms of features of a rich DT task. | Teachers were invited to use the tasks practically in their classrooms. |
| Argument | To provide teachers with theoretical knowledge on developing DT tasks that they can use in their task design. | To innovate methodology and strategies of teaching mathematics and give ideas for drawing up their final task design. |
| Sri Lanka | Italy | |
|---|---|---|
| Task | A DT algebra task | A project work (including tasks) on arithmetic and algebra content |
| Techniques | In small groups of three | Individual work |
| Using GeoGebra | Using Learning Designer | |
| Directed to design a preliminary task with their existing knowledge and then to modify or re-design after the researcher intervention. | Directed to design tasks after using exemplar tasks. | |
| design, self-reflection as a group, modification, implementation, self-and peer-reflection, modification methodology was applied | practical use of exemplar tasks, design, peer-reflection methodology was applied. | |
| Argument | To support teachers to design DT tasks themselves | Project-based learning |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ratnayake, I.G.; Taranto, E. Mathematics Teacher Educators’ Practices to Support Teachers in the Design of Mathematical Tasks. Trends High. Educ. 2023, 2, 546-569. https://doi.org/10.3390/higheredu2040033
Ratnayake IG, Taranto E. Mathematics Teacher Educators’ Practices to Support Teachers in the Design of Mathematical Tasks. Trends in Higher Education. 2023; 2(4):546-569. https://doi.org/10.3390/higheredu2040033
Chicago/Turabian StyleRatnayake, Iresha Gayani, and Eugenia Taranto. 2023. "Mathematics Teacher Educators’ Practices to Support Teachers in the Design of Mathematical Tasks" Trends in Higher Education 2, no. 4: 546-569. https://doi.org/10.3390/higheredu2040033
APA StyleRatnayake, I. G., & Taranto, E. (2023). Mathematics Teacher Educators’ Practices to Support Teachers in the Design of Mathematical Tasks. Trends in Higher Education, 2(4), 546-569. https://doi.org/10.3390/higheredu2040033






