Numerical Evaluation of Aerosol Propagation in Wind Instruments Using Computational Fluid Dynamics
Abstract
1. Introduction
2. Materials and Methods
2.1. Solver
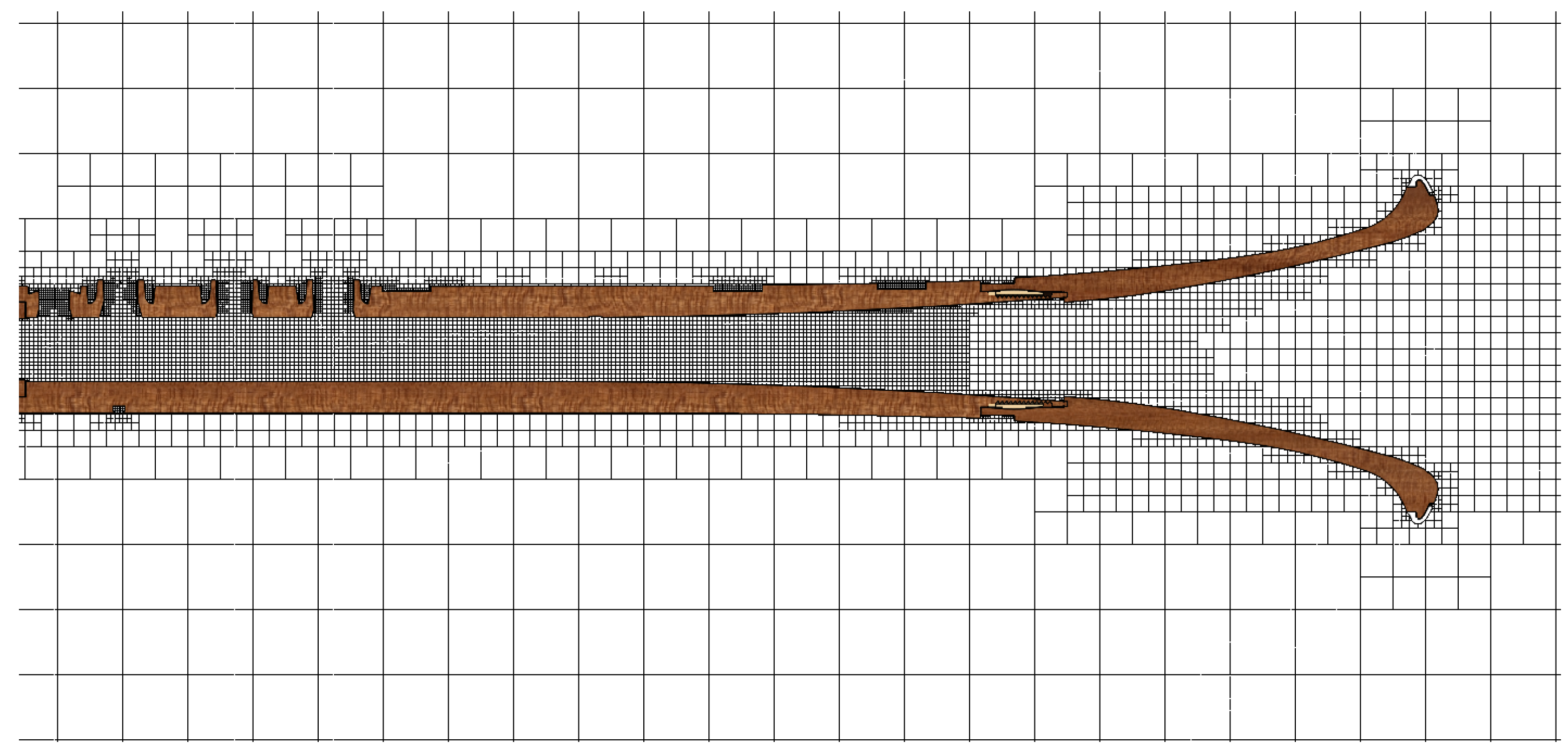
2.2. Computation Set-Up
2.3. Computation Cases
3. Results
3.1. Airflow in the Instrument
3.2. Particle Trajectories
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


Appendix B
| Droplet diameter [µm] | 5 | 20 | 30 | 50 | 80 | 100 |
| Evaporation time [ms] | 10 | 70 | 150 | 410 | 1050 | 1640 |
Appendix C
- average and maximum velocity for each component in the computational domain;
- min, max, and average pressure in the computational domain;
- flow rate and average total pressure through bell exit.
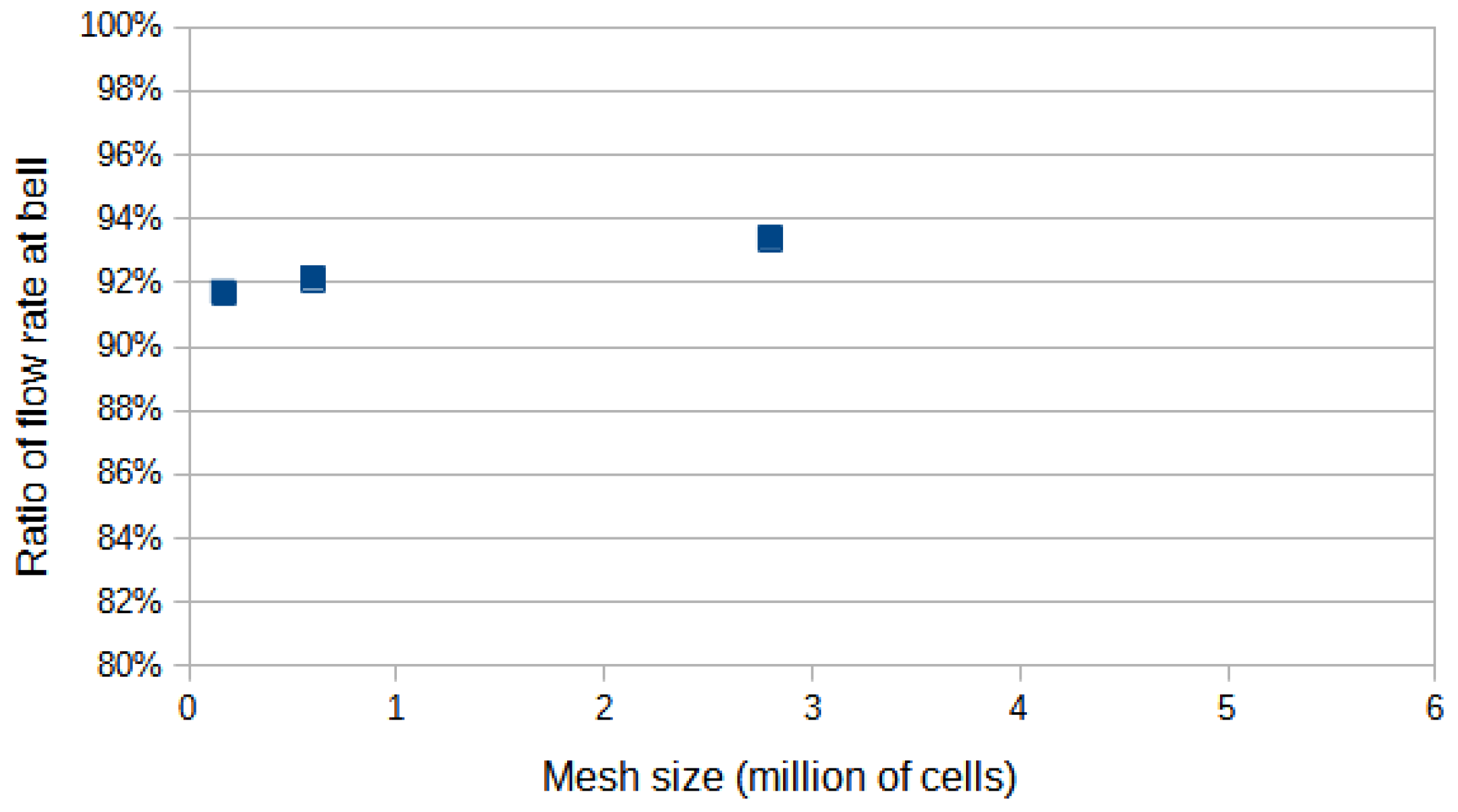
| Level | Total Number of Cells | Number of Partial Fluid/Solid Cells | Cell Size at Wall | Range of |
|---|---|---|---|---|
| Coarse | 170,000 | 90,000 | 0.50 mm | [0.50–4] |
| Nominal | 600,000 | 180,000 | 0.50 mm | [0.50–4] |
| Fine | 2,800,000 | 470,000 | 0.25 mm | [0.25–2] |
References
- Gralton, J.; Tovey, E.; McLaws, M.L.; Rawlinson, W.D. The role of particle size in aerosolised pathogen transmission: A review. J. Infect. 2011, 62, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Drossinos, Y.; Weber, T.P.; Stilianakis, N.I. Droplets and aerosols: An artificial dichotomy in respiratory virus transmission. Health Sci. Rep. 2021, 4, e275. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Marr, L.C. Dynamics of Airborne influenza A viruses indoors and dependence on humidity. PLoS ONE 2011, 6, e21481. [Google Scholar] [CrossRef]
- Lieber, C.; Melekidis, S.; Koch, R.; Bauer, H.J. Insights into the evaporation characteristics of saliva droplets and aerosols: Levitation experiments and numerical modeling. J. Aerosol Sci. 2021, 154, 105760. [Google Scholar] [CrossRef]
- Kähler, C.J.; Hain, R. Singing in Choirs and Making Music with Wind Instruments—Is That Safe during the SARS-CoV-2 Pandemic? University of the Bundeswehr Munich: Neubiberg, Germany, 2020; p. 9. [Google Scholar] [CrossRef]
- Becher, L.; Gena, A.W.; Voelker, C. Risk Assessment of the Spread of Breathing Air from Wind Instruments and Singers during the COVID-19 Pandemic. 2020. Available online: https://www.researchgate.net/profile/Lia-Benetas/publication/343021382_1st_update_Risk_assessment_of_the_spread_of_breathing_air_from_wind_instruments_and_singers_during_the_COVID-19_pandemic_1_Update_Risikoeinschatzung_zur_Ausbreitung_der_Atemluft_beim_Spielen_von_Blasi/links/5f197996a6fdcc9626aa43ca/1st-update-Risk-assessment-of-the-spread-of-breathing-air-from-wind-instruments-and-singers-during-the-COVID-19-pandemic-1-Update-Risikoeinschaetzung-zur-Ausbreitung-der-Atemluft-beim-Spielen-von-B.pdf (accessed on 15 August 2024).
- Viala, R.; Creton, M.; Jousserand, M.; Soubrié, T.; Néchab, J.; Crenn, V.; Léglise, J. Experimental and numerical investigation on aerosols emission in musical practice and efficiency of reduction means. J. Aerosol Sci. 2022, 166, 1–46. [Google Scholar] [CrossRef]
- McCarthy, L.P.; Orton, C.M.; Watson, N.A.; Gregson, F.K.A.; Haddrell, A.E.; Browne, W.J.; Calder, J.D.; Costello, D.; Reid, J.P.; Shah, P.L.; et al. Aerosol and Droplet Generation from Performing with Woodwind and Brass Instruments. Aerosol Sci. Technol. 2021, 55, 1277–1287. [Google Scholar] [CrossRef]
- Firle, C.; Steinmetz, A.; Stier, O.; Stengel, D.; Ekkernkamp, A. Aerosol emission from playing wind instruments and related COVID-19 infection risk during music performance. Sci. Rep. 2022, 12, 8598. [Google Scholar] [CrossRef]
- Abraham, A.; He, R.; Shao, S.; Kumar, S.S.; Wang, C.; Guo, B.; Trifonov, M.; Placucci, R.G.; Willis, M.; Hong, J. Risk Assessment and Mitigation of Airborne Disease Transmission in Orchestral Wind Instrument Performance Risk Assessment and Mitigation of Airborne Disease Transmission in Orchestral Wind Instrument Performance. J. Aerosol Sci. 2020. [Google Scholar] [CrossRef]
- Good, N.; Fedak, K.M.; Goble, D.; Keisling, A.; L’Orange, C.; Morton, E.; Phillips, R.; Tanner, K.; Volckens, J. Respiratory Aerosol Emissions from Vocalization: Age and Sex Differences Are Explained by Volume and Exhaled CO2. Environ. Sci. Technol. Lett. 2021, 8, 1071–1076. [Google Scholar] [CrossRef]
- He, R.; Gao, L.; Trifonov, M.; Hong, J. Aerosol Generation from Different Wind Instruments. J. Aerosol Sci. 2020, 151, 105669. [Google Scholar] [CrossRef] [PubMed]
- Stockman, T.; Zhu, S.; Kumar, A.; Wang, L.; Patel, S.; Weaver, J.; Spede, M.; Milton, D.; Hertzberg, J.; Toohey, D.; et al. Measurements and Simulations of Aerosol Released while Singing and Playing Wind Instruments. ACS Environ. 2021, 1, 71–84. [Google Scholar] [CrossRef]
- Volckens, J.; Good, K.M.; Goble, D.; Good, N.; Keller, J.P.; Keisling, A.; L’Orange, C.; Morton, E.; Phillips, R.; Tanner, K. Aerosol emissions from wind instruments: Effects of performer age, sex, sound pressure level, and bell covers. Sci. Rep. 2022, 12, 11303. [Google Scholar] [CrossRef]
- Archer, J.; McCarthy, L.P.; Symons, H.E.; Watson, N.A.; Orton, C.M.; Browne, W.J.; Harrison, J.; Moseley, B.; Philip, K.E.; Calder, J.D.; et al. Comparing aerosol number and mass exhalation rates from children and adults during breathing, speaking and singing. Interface Focus 2022, 12, 20210078. [Google Scholar] [CrossRef] [PubMed]
- Gregson, F.K.A.; Watson, N.A.; Orton, C.M.; Haddrell, A.E.; Mccarthy, L.P.; Finnie, T.J.R.; Gent, N.; Donaldson, G.C.; Shah, P.L. Comparing the Respirable Aerosol Concentrations and Particle Size Distributions Generated by Singing, Speaking and Breathing. Aerosol Sci. Technol. 2021, 55, 681–691. [Google Scholar] [CrossRef]
- Kähler, C.J.; Fuchs, T.; Hain, R. Can mobile indoor air cleaners effectively reduce an indirect risk of SARS-CoV-2 infection by aerosols? Can mobile indoor air cleaners effectively reduce an indirect risk of SARS-CoV-2 infection by aerosols? MMWR 2020, 70, 972–976. [Google Scholar] [CrossRef]
- De La Cuadra, P.; Vergez, C.; Fabre, B. Visualization and analysis of jet oscillation under transverse acoustic perturbation. J. Flow Vis. Image Process. 2007, 14, 355–374. [Google Scholar] [CrossRef]
- Becher, L.; Gena, A.W.; Alsaad, H.; Richter, B.; Spahn, C.; Voelker, C. The spread of breathing air from wind instruments and singers using schlieren techniques. Indoor Air 2021, 31, 1798–1814. [Google Scholar] [CrossRef] [PubMed]
- Viola, I.M.; Peterson, B.; Pisetta, G.; Pavar, G.; Akhtar, H.; Menoloascina, F.; Mangano, E.; Dunn, K.E.; Gabl, R.; Nila, A.; et al. Face Coverings, Aerosol Dispersion and Mitigation of Virus Transmission Risk. IEEE Open J. Eng. Med. Biol. 2020, 2, 26–35. [Google Scholar] [CrossRef] [PubMed]
- Simcenter. Simcenter FLOEFD Technical Reference, Software version 2020.2; Siemens: Munich, Germany, 2020. [Google Scholar]
- Henderson, C.B. Drag coefficients of spheres in continuum and rarefied flows. AIAA J. 1976, 14, 707–708. [Google Scholar] [CrossRef]
- Gittings, S.; Turnbull, N.; Henry, B.; Roberts, C.J.; Gershkovich, P. Characterisation of human saliva as a platform for oral dissolution medium development. Eur. J. Pharm. Biopharm. 2015, 91, 16–24. [Google Scholar] [CrossRef]
- Duguid, J.P. The Size and Duration of Air-Carriage of Respiratory Droplets and Droplet-Nuclei. J. Hyg. 1946, 44, 471–480. [Google Scholar] [CrossRef] [PubMed]
- Nicas, M.; Nazaroff, W.W.; Hubbard, A. Toward understanding the risk of secondary airborne infection: Emission of respirable pathogens. J. Occup. Environ. Hyg. 2005, 2, 143–154. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Li, Y. Enhanced spread of expiratory droplets by turbulence in a cough jet. Build. Environ. 2015, 93, 86–96. [Google Scholar] [CrossRef]
- Laurent, C. Développement et Validation de Modèles d’évaporation Multi-Composant. Ph.D. Thesis, Université de Toulouse, Toulouse, France, 2008. [Google Scholar]
- Hardy, D.A.; Archer, J.; Lemaitre, P.; Vehring, R.; Reid, J.P.; Walker, J.S. High time resolution measurements of droplet evaporation kinetics and particle crystallisation. Phys. Chem. Chem. Phys. 2021, 23, 18568–18579. [Google Scholar] [CrossRef] [PubMed]
- Alsved, M.; Matamis, A.; Bohlin, R.; Richter, M.; Bengtsson, P.E.; Fraenkel, C.J.; Medstrand, P.; Löndahl, J. Exhaled respiratory particles during singing and talking. Aerosol Sci. Technol. 2020, 54, 1245–1248. [Google Scholar] [CrossRef]
- Mürbe, D.; Fleischer, M.; Lange, J.; Rotheudt, H.; Kriegel, M. Aerosol Emission Is Increased in Professional Singing. OSF Preprints. 2020, pp. 1–10. Available online: https://osf.io/preprints/osf/znjeh (accessed on 15 August 2024).
- Mürbe, D.; Kriegel, M.; Lange, J.; Schumann, L.; Hartmann, A.; Fleischer, M. Aerosol emission of adolescents voices during speaking, singing and shouting. PLoS ONE 2021, 16, e0246819. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Wei, J.; Lei, H.; Xu, P.; Cowling, B.J.; Li, Y. Building ventilation as an effective disease intervention strategy in a dense indoor contact network in an Ideal City. PLoS ONE 2016, 11, e0162481. [Google Scholar] [CrossRef] [PubMed]

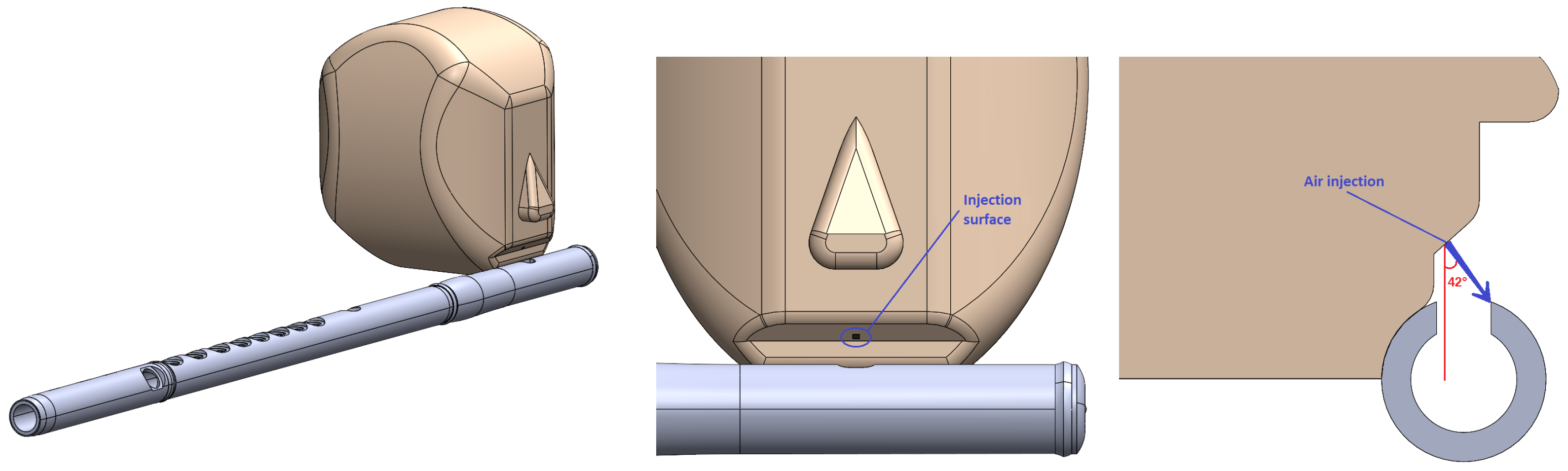

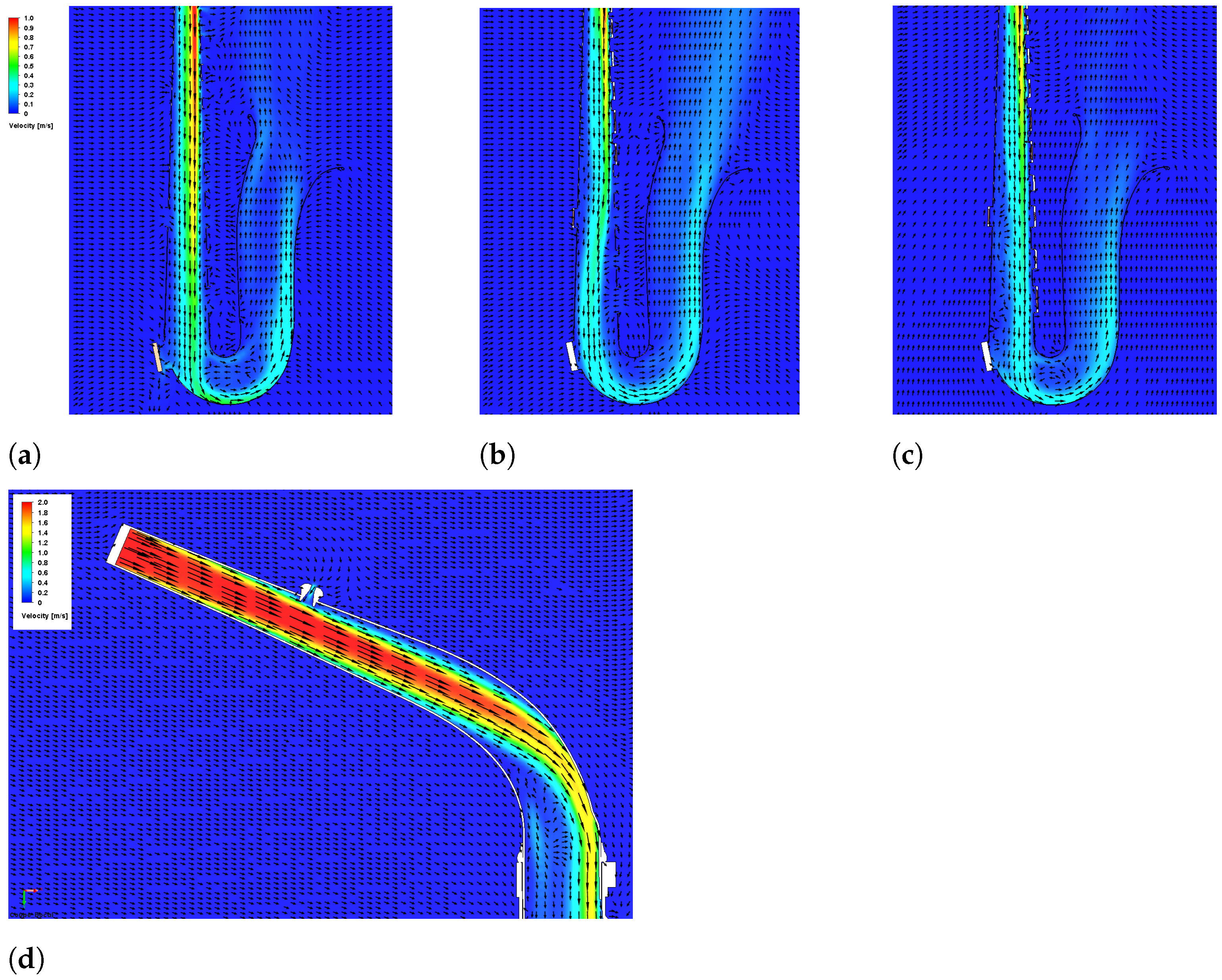

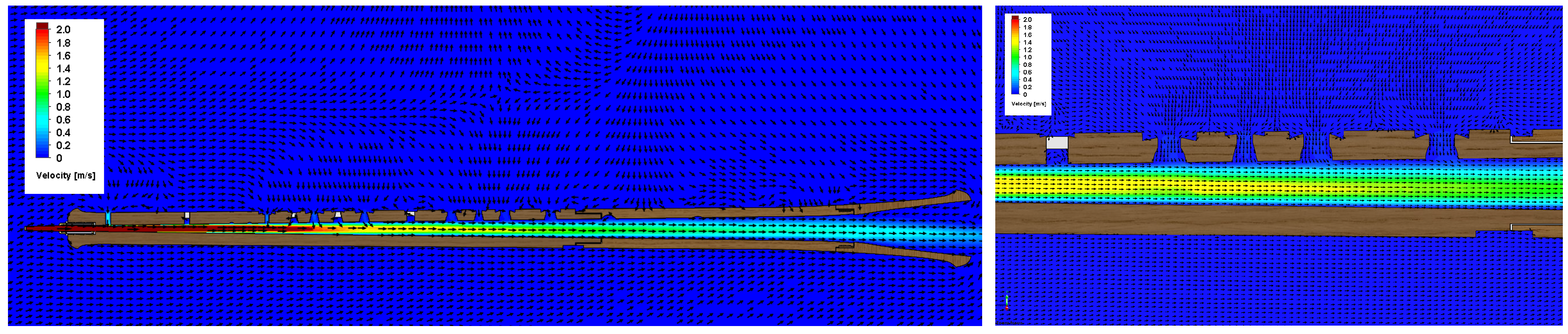

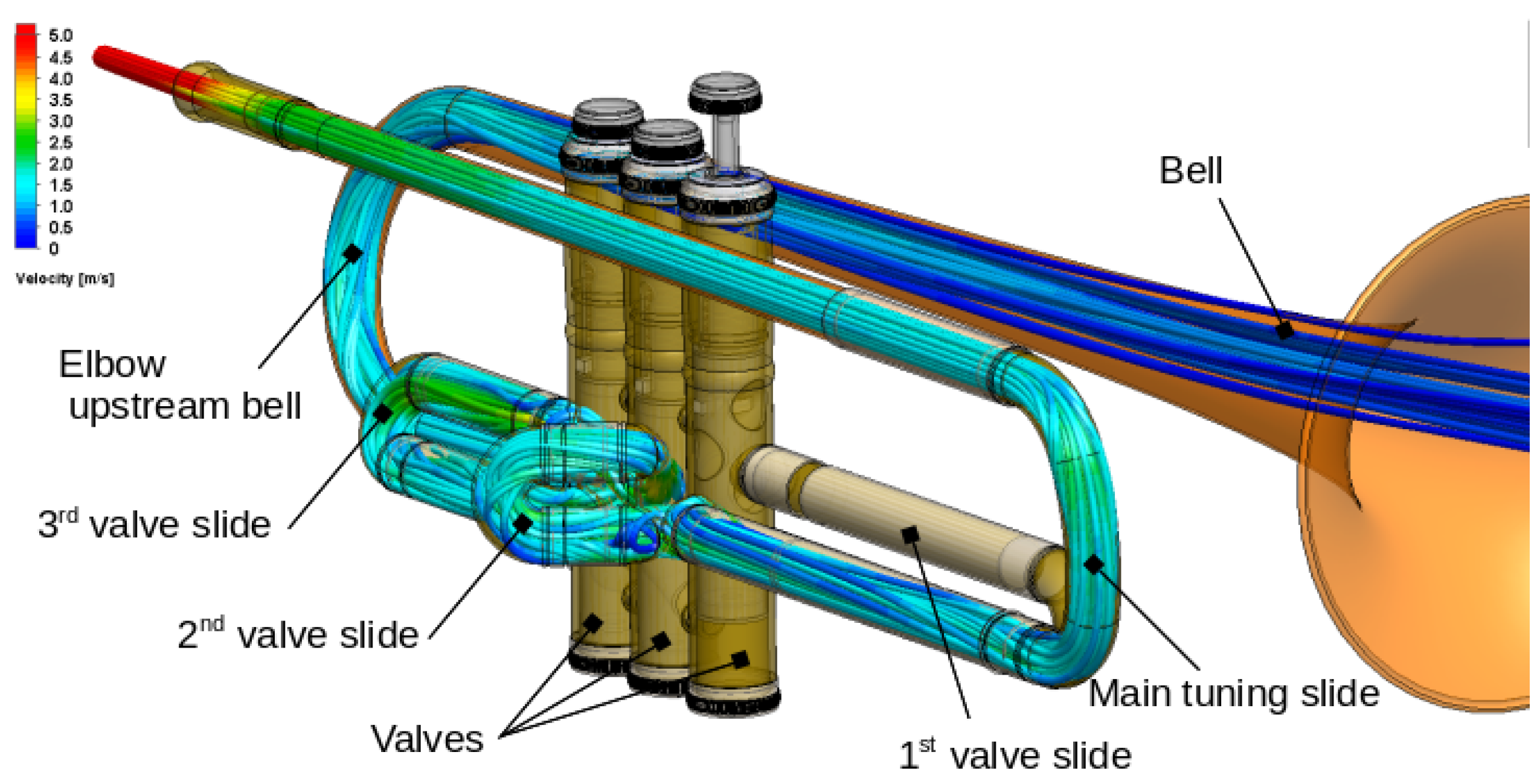
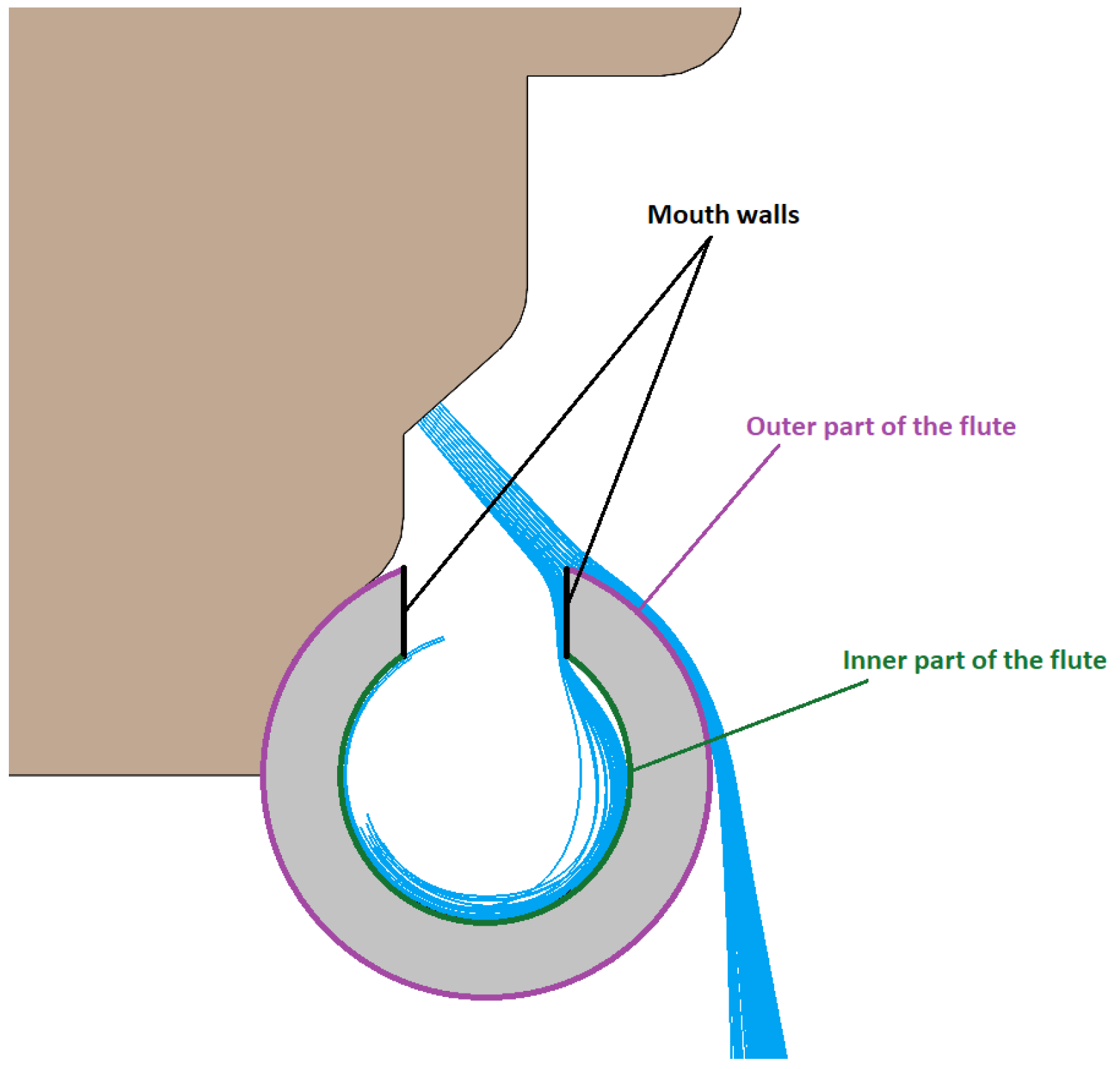
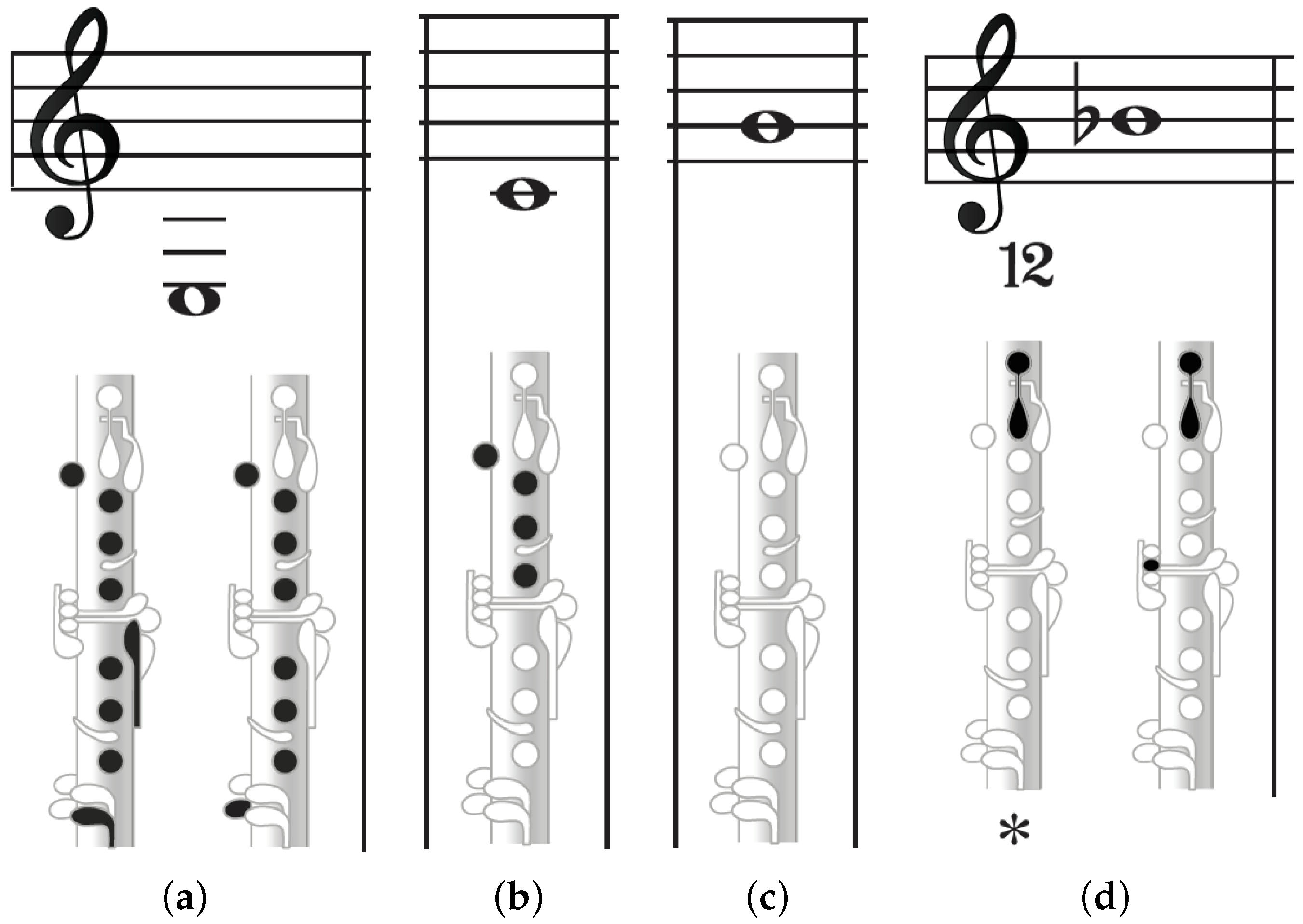
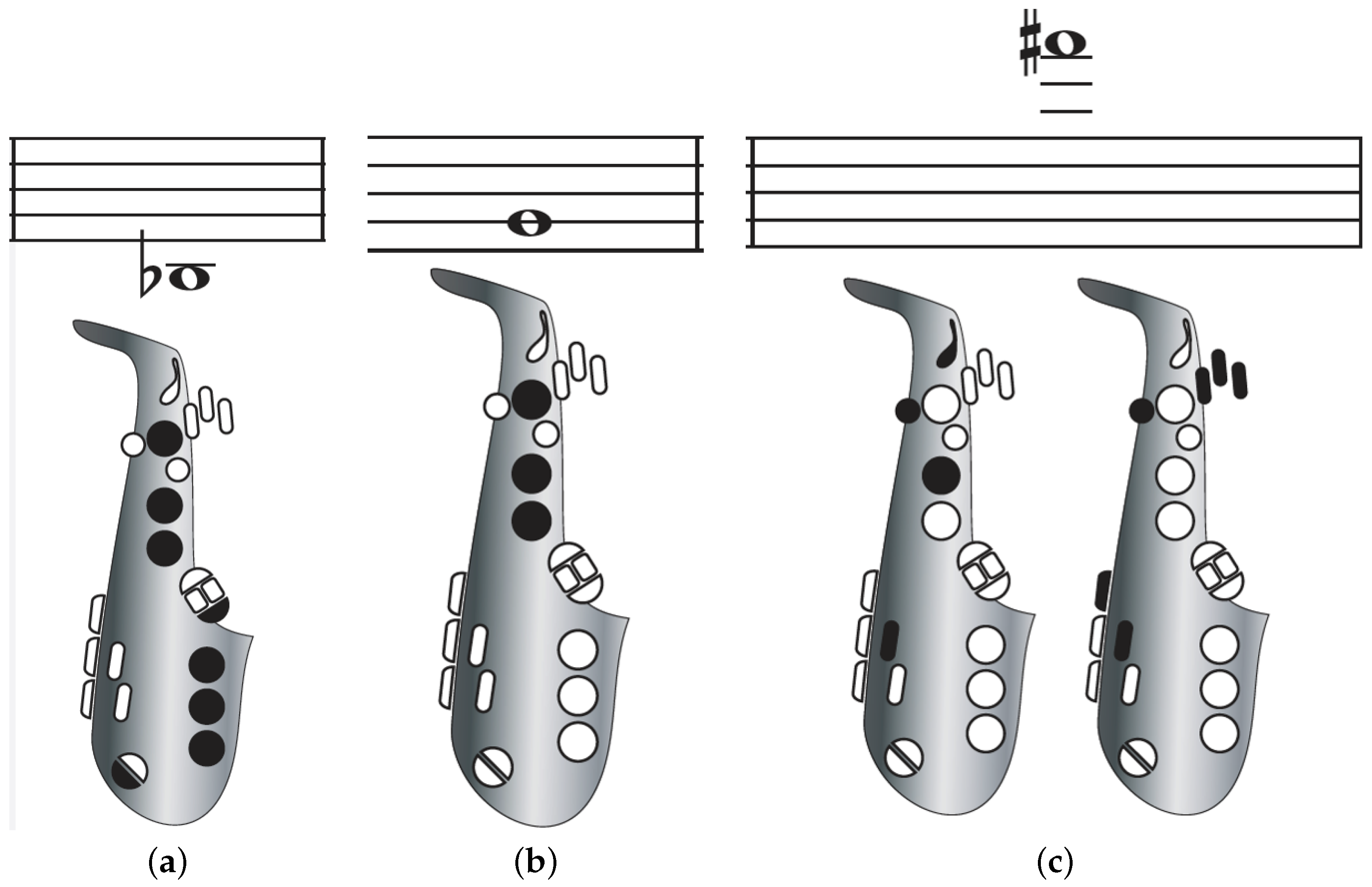
| Instrument | Rate (L/min) | Holes Closed | Intermediate Note (s) | Holes Opened | |
|---|---|---|---|---|---|
| Saxophone | 14 | B♭ | G | F# | |
| Clarinet | 10 | E | C | G | B♭ |
| Oboe | 3 | B | G | C# | |
| Flute | 10 | B | G | C# | |
| Trumpet | 10 | all pistons down | pistons 1 and 2 down, 3 up | all pistons up | |
| a Saxophone | |||||||||
| Instrument fingerings | All closed | Half closed | All opened | ||||||
| Droplet diameter | 0.5 m | 5 m | 50 m | 0.5 m | 5 m | 50 m | 0.5 m | 5 m | 50 m |
| Deposit in neck | 11% | 12% | 68% | 11% | 12% | 68% | 11% | 12% | 68% |
| Deposit in bow | 10% | 11% | 8% | 11% | 13% | 8% | 16% | 18% | 8% |
| Deposit on bow keys | 0% | 0% | 0% | 1% | 1% | 0% | 4% | 3% | 0% |
| Total deposit | 26% | 26% | 100% | 27% | 30% | 99% | 33% | 36% | 100% |
| Exit through keys | 0 | 0 | 0 | 9% | 9% | 1% | 13% | 12% | 0% |
| Exit through bell | 74% | 74% | 0% | 64% | 62% | 0% | 54% | 52% | 0% |
| b Oboe | |||||||||
| Instrument fingerings | Whatever | ||||||||
| Droplet diameter | 0.5–5 m | 50 m | |||||||
| Total deposit | 0% | 100% | |||||||
| Exit through keys | 0% | 0% | |||||||
| Exit through bell | 100% | 0% | |||||||
| c Clarinet | |||||||||
| Instrument fingerings | All closed | Intermediate 1 | Intermediate 2 | All opened | Whatever | ||||
| Droplet diameter | 0.5–5 m | 0.5–5 m | 0.5–5 m | 0.5–5 m | 50 m | ||||
| Total deposit | 1% | 6% | 10% | 11% | 100% | ||||
| Exit through keys | 0 | 5% | 16% | 21% | 0% | ||||
| Exit through bell | 99% | 89% | 74% | 68% | 0% | ||||
| d Flute (instrument fingerings only have influence on exits through keys and main hole) | |||||||||
| Initial angle | Whatever | 42° | 20° | 42° | 20° | ||||
| Droplet diameter | 0.5 m | 5 m | 50 m | ||||||
| Deposit on the internal mouthpiece wall | 21% | 50% | 63% | 47% | 0% | ||||
| Deposit inside flute | 24% | 0% | 29% | 0% | 100% | ||||
| Total internal deposit | 45% | 50% | 92% | 47% | 100% | ||||
| Exit through keys | 2% | 0% | 0% | 0% | 0% | ||||
| Exit through main hole | 2% | 0% | 0% | 0% | 0% | ||||
| Direct to environment | 44% | 31% | 0% | 11% | 0% | ||||
| External deposit | 7% | 19% | 8% | 42% | 0% | ||||
| e Trumpet | |||||||||
| Instrument fingerings | None pushed | Half pushed | All pushed | Whatever | |||||
| Droplet diameter | 0.5 m | 5 m | 0.5 m | 5 m | 0.5 m | 5 m | 50 m | ||
| Deposit in main tuning slide | 6% | 9% | 7% | 9% | 6% | 9% | 7% | ||
| Deposit in valves | 13% | 25% | 16% | 24% | 8% | 14% | 0% | ||
| Deposit in 1st valve slide | 0 | 0 | 10% | 13% | 11% | 14% | 0% | ||
| Deposit in 2nd valve slide | 0 | 0 | 4% | 5% | 4% | 4% | 0% | ||
| Deposit in 3rd valve slide | 0 | 0 | 0 | 0 | 10% | 14% | 0% | ||
| Deposit in tube just downstream valves | 4% | 4% | 0% | 0% | 0% | 0% | 0% | ||
| Deposit in elbow upstream bell | 4% | 7% | 1% | 2% | 2% | 2% | 0% | ||
| Total deposit | 31% | 47% | 40% | 56% | 50% | 68% | 100% | ||
| Exit through bell | 69% | 53% | 60% | 44% | 50% | 32% | 0% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soubrié, T.; Néchab, J.; Viala, R.; Creton, M.; Jousserand, M. Numerical Evaluation of Aerosol Propagation in Wind Instruments Using Computational Fluid Dynamics. Air 2024, 2, 292-310. https://doi.org/10.3390/air2030017
Soubrié T, Néchab J, Viala R, Creton M, Jousserand M. Numerical Evaluation of Aerosol Propagation in Wind Instruments Using Computational Fluid Dynamics. Air. 2024; 2(3):292-310. https://doi.org/10.3390/air2030017
Chicago/Turabian StyleSoubrié, Tristan, Julien Néchab, Romain Viala, Milena Creton, and Michael Jousserand. 2024. "Numerical Evaluation of Aerosol Propagation in Wind Instruments Using Computational Fluid Dynamics" Air 2, no. 3: 292-310. https://doi.org/10.3390/air2030017
APA StyleSoubrié, T., Néchab, J., Viala, R., Creton, M., & Jousserand, M. (2024). Numerical Evaluation of Aerosol Propagation in Wind Instruments Using Computational Fluid Dynamics. Air, 2(3), 292-310. https://doi.org/10.3390/air2030017








