Does “Paper Oil” Matter? Energy Markets’ Financialization and Co-Movements with Equity Markets

Abstract

We revisit, and document new facts regarding, the financialization of U.S. energy markets in 2000–2010. We show that, after controlling for macroeconomic factors and physical energy market fundamentals, the strength of energy markets’ co-movements with the U.S. stock market is positively related to the energy paper market activity of hedge funds that trade both asset classes. This relation weakens when credit risk is elevated. We find, in contrast, no link with the aggregate positions of commodity index traders in energy futures markets. Our findings have implications for the ongoing debate regarding the financialization of commodities.

1. Introduction

In the first decade of this century, a large share of the open interest in energy futures (or “paper”) markets became tied to purely financial firms [1,2]. For commodities overall, [3] document that a key aspect of this so-called financialization was a tripling of the futures commodity open interest share held by hedge funds that also trade equity futures, and that this development was associated with stronger commodity–equity cross-market linkages. We revisit that widely cited paper by specializing its analysis to the specific case of energy markets.

As [4] observe, there are theoretical reasons to expect that financialization might strengthen equity-commodity co-movements. Their arguments run as follows. One, unlike most commodity market participants, financial firms typically trade in other asset markets, so financialization could improve risk sharing and make commodity-specific shocks less important (as in [5,6]) and systemic shocks more important (as in [7]) for the determination of commodity risk premia and returns. Two, institutional financial investors’ risk management practices can amplify price shocks [8] and transmit them across markets, including from financial to commodity markets [9]. Three, even on normal days (when markets are not under stress), the theoretical model of [10] (p. 1511) predicts that an “inflow of institutional funds into commodity futures markets” should boost commodity–equity correlations because financial institutions active in commodity markets rate the performance of their traders versus passive commodity indices. This last insight appears especially relevant in the context of the energy commodities on which the present paper focuses, as they make up a large portion of the major commodity benchmark indices.

As a whole, those three theoretical arguments suggest that not only economic fundamentals (as in [11]) but also “variations in the make-up of the commodity futures open interest (should) help predict long-term fluctuations in commodity–equity return co-movements” (Büyükşahin and Robe [3] (p. 40)). The second theoretical argument, furthermore, suggests that the degree of financialization might matter differentially for cross-market linkages depending on credit market conditions. We provide empirical support for both hypotheses.

We start by estimating weekly dynamic conditional correlations (DCC) between the returns on passive energy and equity investments, using data from 1991 (when the first commodity index products were introduced) to 2020. We find that these DCCs fluctuate substantially over time and increase sharply during recessions. These results extend prior findings in [11,12,13].

Next, we turn to the possible relation between financialization and equity-commodity co-movements that a substantial number of other papers have studied using various methodologies (see [14,15] for recent reviews of that literature). Precisely, we adopt the econometric methodology proposed by Büyükşahin and Robe (2014) [3], and we adapt it to energy markets. While that paper looks at the joint distribution of equity returns with the returns on various portfolios of many heterogenous commodities (including energy together with metals, agriculture, livestock, and softs), our analysis here is specific to energy commodities.

We find that, controlling for physical-market and macroeconomic fundamentals, energy-commodity return DCCs are positively related to greater energy market participation by hedge funds. That relation is especially strong in the case of hedge funds that take positions in both equity and energy futures markets. Interestingly, the intensity of the relation between hedge fund activity and energy–equity return DCCs is lower when credit risk is elevated—a result that does not seem to be driven solely by the financial market freeze during the Great Recession. Those results confirm, for energy markets, the findings of Büyükşahin and Robe [3] for broadly diversified portfolios of commodities.

Importantly for the debate on the impact of commodity index traders (CIT) in commodity markets, we do not find support for the notion that the magnitude of CIT positions is statistically significantly linked to energy–equity return correlations. This result extends to energy markets the conclusion of Büyükşahin and Robe [3] that, unlike active institutional investors (namely, hedge funds), passive institutions (namely, CITs) do not make commodity markets co-move more with equity markets. It also complements evidence, based on intraday data and a very different methodology, that “while the large flows from index traders appear to affect commodity markets, they do not permanently change commodity prices, and smaller flows, such as those from CLNs (commodity-linked notes), appear to negligibly affect prices” ([16] (p. 4753)).

Key to our analysis is a comprehensive dataset of individual positions in the most liquid U.S. futures markets for energy (crude oil, heating oil, natural gas) and equities (S&P 500 e-Mini) that is maintained by the U.S. derivatives market regulator, the Commodity Futures Trading Commission (CFTC). We focus on futures markets in 2000–2010 for three reasons: because that decade is associated with the financialization of commodities [17]; because, in that decade, energy price discovery continued to generally take place on futures exchanges rather than partly over the counter [18]; and because, fifteen years after the end of our sample period, commodities remain “financialized” (using public CFTC data, [15] find that, across all commodities, the non–commercial share of the futures open interest is even higher (almost one third greater) in 2012–2021 than it was in 2006–2011, i.e., in the post-financialization half of our own sample. It is worth noting that part of that non–commercial share increase reflects the fact that, while before 2009 virtually all CITs were classified as (commercial) commodity swap dealers in CFTC reports, many CITs are nowadays classified as non–commercials. In agricultural futures markets, for example, nearly half of CIT positions in 2015–2018 were held by non–commercial traders (mostly managed money funds)—see [19], whose evidence is based on the same non-public CFTC position data as the present paper. Regardless, [15]’s point is valid: first, financial traders’ overall share of the open interest is higher than it was pre–financialization; second, [15] show that equity-commodity return correlations remain higher than in the pre-financialization period). Those facts, combined, mean that the relations that we document and the novel evidence that we provide remain highly relevant today even though they relate specifically to the first decade of financialization.

The CFTC dataset contains detailed information about every large futures trader’s end-of-day futures positions, main line(s) of business, and purpose(s) for trading. Following Büyükşahin and Robe [3], we exploit this regulatory information to construct weekly aggregate measures of index fund, hedge fund, and traditional commercial trader activities in near-dated (three nearest-dated futures maturities) and far-dated (all other maturities) energy futures. Using these measures, we find that the paper market activities of only some groups of traders are statistically related to market co-movements at the weekly frequency.

Formally, we estimate an autoregressive distributed lag (ARDL) model to establish the existence of a long-run relationship between the variables (DCC, macroeconomic conditions, physical oil market fundamentals, trader positions) and to provide “consistent, unbiased estimates of the long run parameters” (Büyükşahin and Robe [3] (p. 64)). In addition, after establishing the existence of a long-run relation, we run an error-correction model (ECM) to analyze the short-term dynamics.

We find that, whereas CIT positions have little explanatory power, hedge fund positions do. Ceteris paribus, a one percent (1%) increase in the overall energy-futures open interest share of hedge funds is associated in equilibrium with an increase in energy–equity return correlations of more than six percent (6%). This figure, which we obtain for a well-defined set of energy commodities using a setup in which we are able to control for physical market fundamentals, exceeds the corresponding percentage (4%) found by Büyükşahin and Robe [3] when looking at a diversified portfolio of 17 commodities for which no such control is possible.

The present paper further extends Büyükşahin and Robe [3] by showing that, in the short term, it is financial variables that drive changes in correlations. Intuitively, the existence of a long-run relationship has implications for the short run behavior of the variables: there must be a mechanism that drives them to their long-run equilibrium relationship. After establishing that the variables are cointegrated, we model this mechanism using an error-correction mechanism (ECM) in which the equilibrium error also drives the short run dynamics of the series. Our ECM analysis buttresses our long-run result by singling out hedge fund activity and credit risk (captured by the TED spread) as the drivers of the short-run dynamics.

As in Büyükşahin and Robe [3] (p. 40), our long-run analysis shows that “it is not just changes in the overall amount of financial activity in commodity futures markets that helps predict the observed correlation patterns”. No, the explanatory power of financial institutions’ energy futures positions relates more narrowly to one type of trader: hedge funds, especially those that hold overnight positions in both equity and energy futures markets. To our knowledge, our findings provide the first empirical evidence of the need to account—not just for commodities in general (Büyükşahin and Robe [3]) but in energy futures markets specifically (the present paper)—for heterogeneity among different sorts of hedge funds (i.e., of market participants that all share the same public CFTC classification of “managed money traders”).

Finally, our analysis confirms the importance of taking into account overall economic and financial conditions when explaining the intensity and the drivers of energy–equity return linkages. On the one hand, energy–equity return DCC are positively related to the TED spread, a proxy for credit risk. On the other hand, over and above that general importance of credit risk, we find that something about the Great Recession is exceptional with respect to energy–equity correlations: the coefficient for a dummy variable capturing that 18-month episode is highly significant and positive even though our regressions also control for the TED spread. This finding confirms the conclusion of Büyükşahin and Robe [3] that the financial crisis of 2008–2011 is qualitatively “different from earlier episodes of financial market stress since 1991 and that this difference is reflected, in part, in an increase in cross-market correlations” ([3] (p. 40)).

The remainder of the paper proceeds as follows. Section 2 provides evidence on return co-movements in energy and equity markets. Section 3 discusses our regulatory data on individual trader positions and documents the financialization of energy markets in 2000–2010. Section 4 ties fluctuations in the strength of energy–equity co-movements to energy market and macroeconomic fundamentals, and to the aggregate positions of commodity futures traders. Section 5 concludes the paper.

2. Three Decades of Energy–Equity Return Correlation

This section describes our sources for energy and equity weekly returns data, how we estimate dynamic conditional correlations between the return series, and how those correlations evolve over time.

Our weekly returns sample covers three decades starting in 1991, when commodity index vehicles first became readily available to investors. This 30-year time interval brackets our sample of trader positions (2000–2010) by one decade on each end. This long period allows us to extend the prior literature documenting changes over time in the degree to which commodities co-move with equities—see, e.g., [11], data from 1959 to 2004 that have been updated through 2014 in [13]; [20], data from 1982 to 2004; [21], data from 1991 to 2006); [3], data from 1991 to 2010; and [15], data from 1986 to 2021; for a detailed survey, see [14]). In the context of energy markets, this section also provides context to numerous studies on the susceptibility of stock markets to oil shocks—see, e.g., [22,23], and references cited in those papers.

2.1. Return Data

We use Bloomberg data from January 1991 to July 2020 to compute weekly Tuesday-to-Tuesday log returns on benchmark passive energy and stock market indices. We follow [3] for the choice of passive investment benchmarks.

For equities, we use Standard and Poor’s S&P 500 index. We find qualitatively similar energy–equity DCC patterns using the Dow-Jones Industrial Average equity index, so there is no loss of generality in discussing only the S&P 500. All of our results are likewise qualitatively robust to using the MSCI World Equity index rather than the S&P 500 U.S. index as the proxy for a passive equity portfolio.

For energy, we use the unlevered total return on the Standard and Poor S&P GSCI-Energy index (GSENTR), i.e., the return on a “fully collateralized energy futures investment that is rolled forward from the fifth to the ninth business day of each month”. The GSENTR averages the nearby prices of six energy futures contracts, using weights based on worldwide production figures. It gives a large weight to crude oil. In unreported robustness checks, we use as an alternative the total (unlevered) returns on the second most widely used investable benchmark, Dow-Jones’s DJAIG (since May 2009, DJ-UBSCI) Total-Return Energy Index. This second index is designed to provide a more “diversified benchmark for the commodity futures market”. We find similar results for both indices, so the remainder of this paper focuses on the GSCI index. This robustness analysis is analogous to the one that [3] carry out to tackle a similar quandary related to the dominance of energy products in the GSCI Total Return index.

2.2. Dynamic Conditional Correlations

In order to estimate the time-varying intensity of commodity–equity return co-movements, we follow [24] and compute dynamic conditional correlations (DCC). First, we estimate time-varying variances using a GARCH(1,1) model. Then, we estimate a time-varying correlation matrix using the standardized residuals from the first-stage estimation.

The above approach is the same as [3], down to the choice of parameter values. This said, [25] caution that conditional variances and correlations (DCC) may exhibit “asymmetric responses”, while those authors’ alternative asymmetric dynamic conditional correlations (ADCC) model “permits conditional asymmetries in correlation dynamics” [25] (p. 537)). For this reason, [4] use ADCC to analyze the financialization of agricultural commodities. In the present paper, we use both approaches and confirm our DCC results using ADCC.

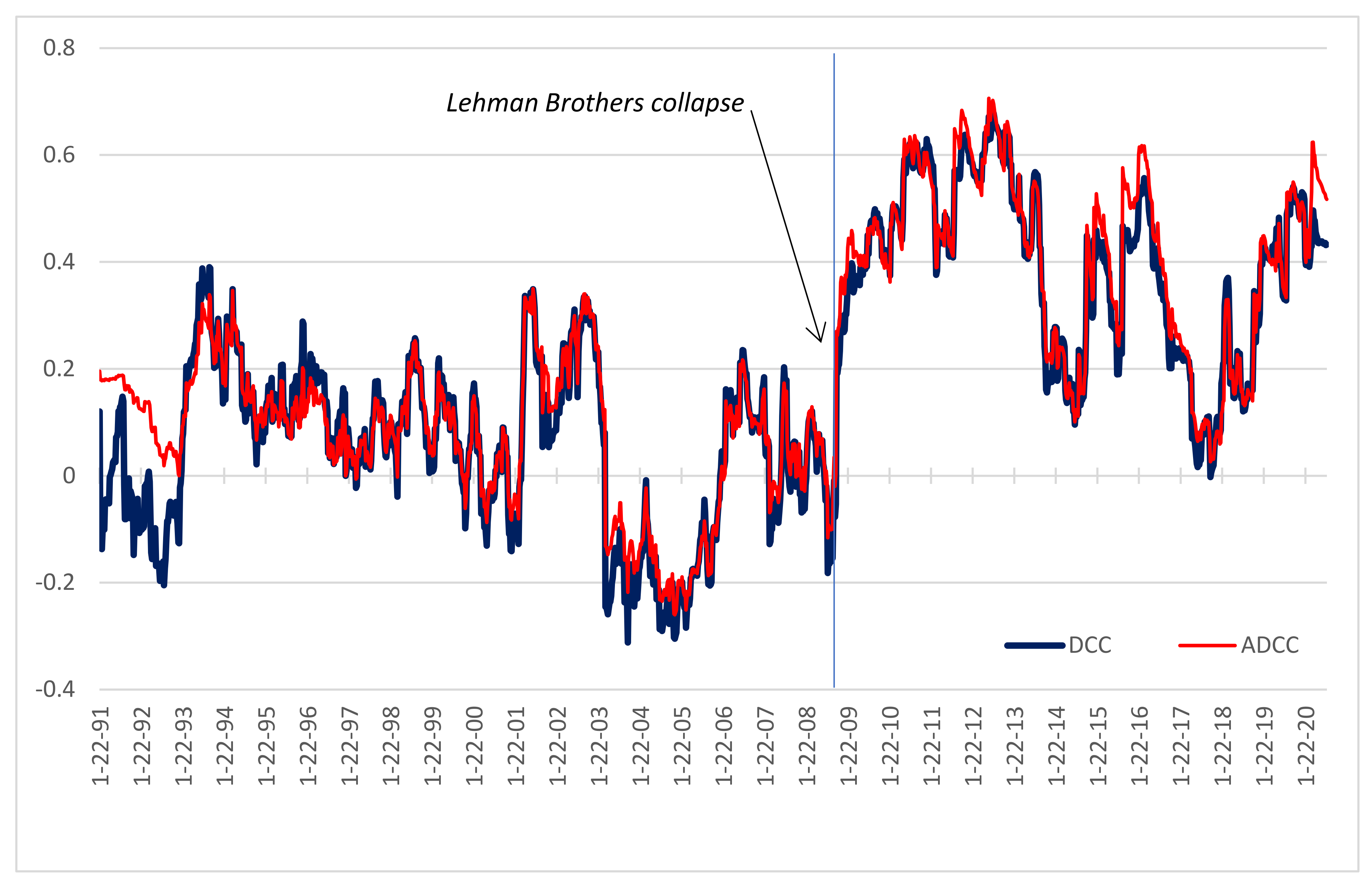
Figure 1 plots, from 22 January 1991 to 28 July 2020, the DCC and the ADCC between the weekly unlevered rates of return on the GSCI-Energy investable index and on the S&P 500 (“SP”) equity index. Several facts emerge from Figure 1.

First, the energy–equity return DCC and ADCC values track one another very closely. The correlation is 0.97 for the whole sample (1991–2020).

Second, both series fluctuate substantially, and both exhibit a sharp increase after a fall in 2008. Prior to Lehman Brothers’ default in 2008, the average for DCC (resp. ADCC) is 0.05 (resp. 0.08) and the range is −0.31 to 0.39 (resp. −0.26 to 0.35), without any obvious trend in the first 18 years of the sample. Strikingly, however, the energy–equity return correlations shoot up in fall 2008. Furthermore, there appears to be a level shift in the mean correlations from that point onward, with DCC (resp. ADCC) averaging 0.38 (resp. 0.41) in the 12 years following that financial catastrophe, with similarly much higher extreme values (−0.08 to 0.68 for DCC and −0.02 to 0.71 for ADCC).

These findings contribute to the ongoing debate about the financialization of commodities in two ways. First, most importantly, they contradict claims in some papers that commodities have started to become “definancialized given that” commodity–equity correlations are down from their 2008–2011 highs (see [14] for a survey of those papers). In reality, well over a decade after the onset of the 2008 Financial Crisis, energy–equity return correlations remain at historically high levels. Second, as a corollary relevant to econometric analyses such as the one that we carry out in Section 3 below, the period after Lehman’s demise should be treated differently than prior years to account for the fact that energy–equity return correlations reach levels unseen in the prior two decades.

3. The Financialization of Energy Futures Markets, 2000–2010

In the first decade of this century, energy futures market activity rose substantially. Using regulatory data on individual trader activity in the three largest U.S. energy (WTI crude oil, natural gas, heating oil) and equity (S&P 500 e-Mini) futures markets, this section documents substantial increases in the aggregate positions of hedge funds and commodity index traders. These findings generalize across multiple energy commodities some of the findings of [2] in the specific case of crude oil. Simultaneously, by providing evidence regarding the extent to which equity futures traders are also active in energy futures markets, this section specializes to energy commodities our more aggregated findings in [3]—which cover a cross-section of 17 diverse commodity futures markets but do not provide results for any subset thereof.

We construct our dataset by aggregating trader-level (non-public) CFTC data from 26 June 2000 to the end of February 2010. That sample period matches the samples of [2,3], allowing for comparisons with those two well-known studies.

Section 3 here closely follows Section 4 in [3] (pp. 45–58) in both structure and wording. Indeed, the present Section 3′s wording mostly paraphrases (when an adaptation is needed, usually due to sample differences) or repeats that companion paper (either with quotation marks for whole sentences, or without quotes when we repeat just a few words at a time). We use the same variable names too, to make obvious the close link with the earlier paper.

3.1. Trader Position Data

The trader-level end-of-day futures position data and the individual trader classifications, that we combine to create aggregate measures of activity by trader type, originate in the CFTC’s Large Trader Reporting System (LTRS). The latter gathers information on every large futures or options-on-futures trader’s positions, business, and purposes for trading, where “large” is defined as holding positions above a certain reporting threshold (which varies by market). Our dataset is limited to those large traders. In practice, it covers 83 percent of the total open interest for our three markets and for our sample period: this figure is slightly lower than the 86 to 93 percent coverage in [19,26] for the four biggest grains or oilseed futures markets in 2015–2018.

The CFTC receives position updates daily. We use Tuesday market-close positions, because they are the data “which the CFTC summarizes in weekly Commitment of Traders (COT) Reports that it publishes every Friday at 3:30 pm EST. Consequently, the information we provide in this section can be contrasted with numerous extant studies of commodity markets that rely on COT data” ([3] (p. 48)).

3.1.1. Public Information

The CFTC has long published weekly COT reports on the composition of the open interest in the markets covered in this paper: WTI light sweet crude oil, Henry Hub natural gas, and New York Harbor No.2 heating oil futures. Prior to September 2009, those reports split traders in a given futures market between just two categories: “commercial” vs. “non-commercial” traders. “Commercials” are traders who use futures contracts for “hedging” their exposures commodity as defined in CFTC regulations. A trading entity generally gets classified as “commercial” by filing a statement with the CFTC that it is commercially “engaged in business activities hedged by the use of the futures or option markets” (to classify traders accurately and consistently, the CFTC staff may exercise judgment in re-classifying a trader in light of additional information about the trader’s use of the markets). All other traders in that given market are “non–commercials”—a group aggregating various types of mostly financial traders, such as hedge funds, mutual funds, floor brokers, etc.

Since 4 September 2009, the COT reports differentiate between four (rather than just two) kinds of energy traders. Those disaggregated COT (DCOT) now split commercial traders between traditional commercials (e.g., natural gas producers, crude oil refiners, petroleum dealers and merchants, powerplants, etc.) and commodity swap dealers (a category that includes commodity index traders in most markets). The DCOT also split the reportable positions of non-commercial traders, between those of managed money traders (MMT, i.e., hedge funds)—see [3] (pp. 69–70) for a more formal discussion of “hedge funds” in U.S. commodity futures markets—and those of other reportable non–commercial traders. The CFTC still “has not indicated plans to make this more detailed information available retroactively prior to 2006 or to break down the aggregate position information by contract maturity” ([3] (p. 49))—a statement that remains true at the time of the present paper’s acceptance for publication.

3.1.2. Non-Public Information

The LTRS data allow for finer groupings than the two (COT) or four broad (DCOT) trader categories. Importantly, the LTRS data allow for classifications in our entire 2000–2010 sample period, not just after 2006. Furthermore, because the LTRS data are not only commodity-, but also maturity-, specific, they “let us disentangle the activities of different traders at the near and far ends of the commodity-futures term structures. In contrast, public COT reports do not separate between traders’ positions at different contract maturities” ([3] (p. 49)). The resulting ability to disaggregate overall trader positions across the futures curves is critical: Section 4 below shows that it is hedge funds’ near-dated energy futures positions that are significantly related to energy–equity return co-movements.

Finally, but crucially, the LTRS dataset follows each large trader’s activities in different futures markets. We use this information in Section 3.3.3 below to provide the first evidence of the extent to which traders are active in both equity and energy paper markets. In Section 4, we will then show that the positions of hedge funds active in both equity and energy markets hold greater explanatory power for cross-market linkages.

3.2. Overall Speculative Intensity

To measure the time-varying intensity of speculative activity in energy futures markets, we use weekly values of Working’s “T” [27] index of “excess speculation”. This provocatively named, yet widely used index, captures the extent to which the positions of non-commercial traders (commodity “speculators”) exceed, in the aggregate, the net demand for hedging originating from commercial traders (as defined above).

In each market, we compute two “T” indices: one for short-term futures only ($SI{S}_{i,t}$), and another for all contract maturities ($SI{A}_{i,t}$). For $SI{S}_{i,t}$, we use position data from the three shortest-maturity contracts with non-trivial open interest. The idea is that it is near-dated futures prices that form the basis of the GSCI Energy Total Return benchmark, so $SI{S}_{i,t}$ is the most natural candidate for the analysis. In addition, we also use $SI{A}_{i,t}$ because “the latter measure can be computed using the publicly–available COT reports, which allows readers without access to the LTRS data to replicate (some) of our results” ([3] (p. 49)).

We then average the weekly index values for each of our three markets to provide a general picture of speculative activity across energy paper markets:

$$WSI{S}_t={{\displaystyle \sum }}_{i=1}^3{w}_{i,t}SI{S}_{i,t} \mathrm{and} WSI{A}_t={{\displaystyle \sum }}_{i=1}^3{w}_{i,t}SI{A}_{i,t}$$

where the weight $w_{i,t}$ for commodity i (WTI, natural gas, heating oil) in a given week t is based on the weight of the commodity in the GSCI-Energy index that year (Source: Standard and Poor), rescaled to account for the fact that we focus on the three U.S. markets (out of six GSCI-Energy markets) for which position data are available.

Table 1. Speculative intensity in energy futures markets (2000–2010).

	Working’s “T”
	All Contract Maturities (WSIA)	Short-Term Contracts (WSIS)
Mean	1.2376	1.2611
Median	1.2581	1.2548
Maximum	1.4639	1.5768
Minimum	1.0547	1.0453
Std. Dev.	0.1154	0.1384
Skewness	0.0656	0.1272
Kurtosis	1.6870	1.7494
Jarque-Bera	36.6388 ***	34.2706 ***
Sum	624.9958	636.8481
Sum Sq. Dev.	6.7067	9.6484
Observations	505	505
ADF (Level)	−1.4100	−1.5807
ADF (1st Diff)	−24.6943 ***	−16.8223 ***

Note: Table 1 provides summary statistics of the intensity of speculative activity in the NYMEX’s WTI light sweet crude oil, New York Harbor No.2 heating oil, and Henry Hub natural gas futures markets. We compute “excess” commodity speculation for the three nearest-term futures (WSIS) and all contract maturities (WSIA) as the weighted–average “excess speculation” index (Working’s “T” index) for the three U.S. energy futures markets in the GSCI-Energy index (Sources: CFTC, S&P and authors’ calculations); annual weights equal the average of the daily GSCI weights that year (Source: Standard & Poor). For the augmented Dickey–Fuller (ADF) tests, *** indicates the rejection of non-stationarity at the 1 percent level of statistical significance; critical values are from [28]. The optimal lag length K is based on the Akaike Information Criterion (AIC). Sample period: 26 June 2000 to 26 February 2010.

provides summary statistics for WSIS and WSIA from late June 2000 to February 2010. The minimum value is approximately 1.05 for short-dated and also for all energy contracts; the maximum is 1.57 in near-term contracts and slightly lower (1.46) across all maturities. Put differently, in U.S. energy markets, speculation in our ten-year sample period exceeds by 5 to 57 percent the minimum required to offset any unbalanced hedging at the market-clearing price.

Figure 2A shows a substantial increase in speculative intensity in 2000–2010. “Excess” speculation (measured using Working’s T index) rises from about 5–10 percent early in the decade to 37–57 percent in 2008. Prior to the Summer of 2006, a comparison of the WSIS and WSIA plots shows similar patterns at the near and far ends of the commodity futures term structure. Between Summer 2006 and Summer 2009, however, “excess” speculation was often 10 percent greater in near-dated contracts than further out on the maturity curve. It falls notably in 2009, especially in near–term contracts (WSIS peaks at 1.57 in April 2008 but falls to 1.34 in late 2009). Put differently, Figure 2A identifies a long-term increase, but also substantial variations, in speculative intensity.

All the above figures exhibit magnitudes similar to those found by Büyükşahin and Robe [3] for corresponding variables in a cross-section of 17 commodities. The patterns over time are also qualitatively similar.

3.3. Breaking down the Overall Increase in Speculation, 2000–2010

We are particularly interested in the roles of several sub-groups of energy futures traders: commodity index traders, hedge funds, and cross-market speculators. Following [3] (p. 52), we therefore compute the respective open-interest or “market” share of each of those groups “of traders, in each commodity futures market each Tuesday, by expressing the average of the long and short positions of all traders from this group in that market as a fraction of the total open interest in that market that same Tuesday. We then average these commodity-specific market shares. We then average these commodity-specific market shares”. As in the previous sub-section for the T indices, we use the annual GSCI index commodity weights to compute weekly average market shares across our three energy futures markets, both for the three nearest-maturity futures with non-trivial open interest and across all contract maturities.

We denote respectively by WMSS_MMT, WMSS_AS, and WMSS_TCOM the weighted-average market shares of hedge funds (“MMT”), commodity swap dealers (“AS”, including commodity index traders—see below), and “traditional” commercial traders (“TCOM”, excluding commodity swap dealers) in short-dated contracts (suffix “SS”). Similarly, we denote each type of traders’ share of the total open interest (i.e., across all contract maturities; suffix “A”) as WMSA_MMT, WMSA_AS, and WMSA_TCOM.

3.3.1. Commodity Index Trading (CIT)

While the LTRS dataset allows for the precise computation of the energy futures open interest shares for many trader types, “it does not identify CIT activity in energy (…) markets at the daily or weekly frequency” ([3] (p. 57)). This limitation stems from the fact that “CIT activity percolates into commodity futures markets partly through index traders’ interactions with commodity swap dealers but, even in the CFTC’s non-public LTRS data, CIT-related positions cannot be identified within the overall positions held by commodity swap dealers” ([3] (p. 58)).

Various approaches have been suggested to circumvent this pitfall using publicly available data. Instead, we exploit our uniquely detailed dataset and the fact that CITs tend to hold short-dated positions 2 to approximate the near-term CIT market share in energy futures by the share of the near-dated open interest held by commodity swap dealers in the three markets that make up our sample (using commodity swap dealers’ long futures positions as a proxy for CIT long positions is appropriate in our 2000–2009 sample period—see [29,30], as discussed in [19]. The same approximation would be poor nowadays, however, because almost half of all CITs are now classified as non-commercial traders and the aggregate long futures positions of commodity swap dealers in the DCOT therefore do not include a substantial part of the total CIT activity—see [19].

Figure 2A plots WMSS_AS (resp. WMSA_AS), i.e., the weighted-average market shares of commodity swap dealers in near-dated (resp. all) energy futures. WMSS_AS and WMSA_AS both peak in the second half of October 2008, before sharply falling in the following two months and then recovering slowly in 2009 and 2010.

Throughout our sample period (2000–2010), commodity swap dealers’ positions contribute to approximately 10 percent more of the overall open interest than to the near-dated open interest. In the case of near-dated energy futures (where, as noted, CIT activity is concentrated during our sample period), Figure 2A shows that swap dealers’ market share grows approximately by two thirds between early 2003 and early 2007. Interestingly, following the dismal last quarter of 2008 and amid a strong rebound of the total energy futures open interest in 2009 and 2010, swap dealers’ positions account for a greater proportion of the long-dated open interest than at any time earlier—suggesting a further lengthening in the aggregate of the maturity structure of their energy exposure, a pattern that was first identified in the crude oil market by [2].

3.3.2. Hedge Fund Activity

“Working’s T lumps together all non-commercial traders: floor brokers and traders, hedge funds, and other non-commercial traders that are not registered as ‘managed money traders’. Yet, there is little reason to believe that floor brokers in a specific commodity market should be relevant to equity–commodity linkages. Hedge funds, in contrast, are plausible candidates for such a role” ([3] (p. 50)).

Figure 2B plots in red (resp. blue) lines the values of WMSS_MMT (resp. WMSA_MMT) over time, i.e., the weighted-average market shares of hedge funds in near-dated (resp. all) energy futures. Together with Panels A and B of

Table 2. Open interest shares of key trader types (2000–2010).

	Panel A: Weighted-Average Market Shares in Short-Term Energy Futures
	Hedge Funds (WMSS_MMT)		Swap Dealers (WMSS_AS)	Traditional Commercials (WMSS_TCOM)
Mean	0.2042		0.2086	0.3669
Median	0.2244		0.2108	0.3435
Maximum	0.3631		0.3008	0.627804
Minimum	0.0460		0.1182	0.1688
Std. Dev.	0.0810		0.0350	0.1144
Skewness	−0.3245		−0.0850	0.4797
Kurtosis	1.8469		2.6898	2.1504
Jarque-Bera	36.8430		2.6331	34.5549
Sum	103.14		105.32	185.28
Sum Sq. Dev.	3.3102		0.6158	6.5960
Observations	505		505	505
ADF (Level)	−1.7212		−2.7133 *	−1.4170
ADF (1st Diff)	−16.5738 ***		−11.5193 ***	−18.6483 ***
	Panel B: Total Open Interest Shares in All Energy Futures
	Weighted-average Market Shares across All energy futures Maturities (WMSA)			Weighted-average OI share of Cross-Market traders across All energy futures maturities (WCMSA)
	Hedge Funds (WMSA _MMT)	Swap Dealers (WMSA _AS)	Traditional Commercials (WMSA _TCOM)	Hedge Funds (WCMSA _MMT)	Swap Dealers (WCMSA _AS)
Mean	0.1736	0.2855	0.3412	0.1015	0.2228
Median	0.2025	0.2928	0.3161	0.1072	0.2239
Maximum	0.3274	0.3715	0.6133	0.2027	0.2934
Minimum	0.0309	0.1826	0.1571	0.0129	0.1548
Std. Dev.	0.0900	0.0393	0.1172	0.0530	0.0237
Skewness	−0.0883	−0.4282	0.4745	−0.0952	−0.3348
Kurtosis	1.6142	2.6932	2.2679	1.6976	3.3322
Jarque-Bera	41.0650	17.4126	30.2299	36.4574	11.7582
Sum	87.66	144.18	172.33	51.23	112.50
Sum Sq. Dev.	4.0814	0.7784	6.9248	1.4181	0.2837
Observations	505	505	505	505	505
ADF (Level)	−1.3245	−1.4956	−0.9740	−1.4659	−1.4956
ADF (1st Diff.)	−22.2460 ***	−10.5792 ***	−21.9711 ***	−20.9203 ***	−10.5792 ***

Notes: In Panel A, WMSS_MMT, WMSS_AS, and WMSS_TCOM stand, respectively, for the weighted-average shares of the short-term open interest in the three nearest-dated futures with non-trivial open interest (for the three U.S. energy commodities in the GSCI-Energy index) of the following types of traders: hedge funds (MMT, “managed money traders” only), commodity swap dealers (AS, including CIT—commodity index traders), and traditional commercial traders (TCOM, excluding commodity swap dealers). In Panel B, WMSA_MMT, WMSA_AS, and WMSA_TCOM stand, respectively, for the MMT, AS, and TCOM weighted-average shares of the open interest across all futures contract maturities, for the same three U.S. energy futures markets (Source: CFTC Large Trader Reporting System (LTRS) and authors’ computations). We set the weights each year equal to the average of the GSCI weights for those three commodities that year and rescale the figures to account for GSCI-Energy markets for which no LTRS position data are available (Source: S&P). For MMT and AS traders, the WCMSA variables in the rightmost two columns of Panel B measure the proportion of energy futures traders who also hold positions in the S&P 500 e-Mini equity futures (“cross-market traders” CM). For the augmented Dickey–Fuller (ADF) tests in both panels of the table, stars (* and ***) indicate the rejection of non-stationarity at standard levels of statistical significance (10% and 1%, respectively); critical values are from [28]. The optimal lag length is based on the Akaike Information Criterion (AIC). Sample period for all statistics: 26 June 2000 to 26 February 2010.

, it highlights several important market transformations.

First, the hedge fund share of the energy futures open interest more than triples between 2000 and 2008. It grows from less than one tenth of the total open interest before 2002 to between a quarter and a third of the total open interest after 2006.

Second, hedge funds’ greater relative contribution to the overall open interest takes place amid a concomitant drop in traditional commercial traders’ market share. Indeed, Table 2—which provide summary statistics about the open interest shares the main kinds of traders in near-term (Panel A) and all (Panel B) futures—show that WMSS_TCOM and WMSA_TCOM both fall from over 60 percent to less than 20 percent of the total open interest in the span of just a decade.

The above findings generalize, to the three biggest U.S. paper markets, some observations that [2] report in the specific case of WTI crude oil. They also confirm, for the three largest U.S. energy futures markets, similar figures and patterns obtained by [3] in the aggregate for a cross-section of 17 diverse commodity markets.

Finally, Figure 2A shows that hedge funds’ overall share of the energy futures open interest starts shrinking in the Spring of 2008 and continues falling through the end of our sample period (late February 2010). In the next sub-section, however, we show that not all hedge funds pull back from energy futures markets at the time. These last two facts will prove critical in Section 4.

3.3.3. Cross-Market Trading

Our goal is to identify the drivers of commodity–equity return correlations. Hence, we use the LTRS information to identify traders holding positions in both energy and equity markets under the assumption that their activities are more likely than other traders’ behaviors to make markets co-move.

• Number of Cross-Market Traders

For each day, we use the unique ID of each trader in the LTRS to identify energy futures traders who also hold positions in the CME’s e-Mini S&P 500 equity futures market at any point in our sample period. We call such traders “cross-market traders” or “cross-traders” for short, as in [3] (p. 53). This exercise, which tells us how many cross-traders hold positions in energy futures markets on a given trading day, is summarized in

Table 3. Cross-market trading activity, 2000–2010.

	Commodity Futures Market Classifications						Equity Futures Classification
Commodity	All Cross-Market Traders		Commodity Swap Dealers		Hedge Funds		Hedge Funds
	Count	Percent of All Traders	Count	Percent of All Cross-Traders	Count	Percent of All Cross-Traders	Count	Percent of All Cross-Traders
Crude Oil	1108	28.0%	63	5.7%	363	32.8%	274	24.7%
Heating Oil	335	8.5%	26	7.8%	170	50.8%	138	41.2%
Natural Gas	743	18.8%	49	6.6%	300	40.4%	235	31.6%

Notes: For the three main energy futures markets for which trader-level position data are available for the entire 2000–2010 period, Table 3 provides information on the number and relative importance of the subset of large commodity futures traders who also held, at some point in the sample period (1 July 2000 through 26 February 2010), positions in the S&P500 e-Mini equity futures contract. Source: CFTC and authors’ computations.

.

In each of the three energy futures markets in our sample period, Table 3 shows that hundreds of traders also take positions in the Chicago Mercantile Exchange’s e-Mini S&P 500 equity futures market (Column 1). Well over a sixth (natural gas) or over a fourth (crude oil) of all large commodity futures traders in 2000–2010 also trade equity futures (Column 2). Table 3 further shows that hedge funds make up a plurality of those cross-market traders, whereas CITs make up a low-single-digit proportion of the total number of cross-market traders. Depending on the market, between 25% and 41% of all cross-market traders are classified as hedge funds in equity futures markets (Column 8).

2.

Open Interest Share of Cross-Market Traders

While the number of cross-market traders is of interest, their market share is of even greater interest. That is because the financial and technical resources available to traders that are active in both equity and commodity markets should intuitively be greater than those available to other, less sophisticated traders. For key groups of traders and for each energy commodity, we therefore compute the collective share of the total energy futures open interest held by cross-market traders in that group for each day in our sample.

We denote by CMSA_MMT_i,t, CMSA _AS_i,t and CMSA _ALL_i,t, respectively, the shares of the open interest (average of long and short positions) in the i^th commodity held by cross-trading hedge funds (MMT), energy swap dealers (AS), and all energy-futures traders (ALL) (i = 1, 2, 3). We then use the annual GSCI index weights to calculate the weighted-average market share of several trader types (xxx = MMT, AS or ALL) across the three energy futures markets in our sample:

$$WCMSA\_{\mathrm{xxx}}_t={\displaystyle \sum }_{i=1}^3{w}_{i,t}CMSA\_{\mathrm{xxx}}_{i,t}$$

We find that the median weighted average share of the energy futures open interest held by all equity-commodity cross-traders was 43 percent in 2000–2010. As we had predicted above, this percentage is much higher than the 28 percent or less of the trader count in Table 3. It is also worth noting that both of those median percentages, which relate to energy markets only, are even larger than the corresponding figures computed across all commodities. Indeed, for all the 17 US futures in the GSCI, the weighted-average median open interest share of “cross-traders was 40.9 percent during the sample period vs. 15 percent of the trader count” ([3] (p. 57)).

The purple line in Figure 2B shows that the market share of hedge funds that also hold equity futures positions increases substantially in our sample period, from under 5 percent of the energy futures open interest in 2000–2001 to around 20 percent by mid-2006. Most striking is the difference in Figure 2B between the behaviors of cross-trading hedge funds (purple line) from that of hedge funds as a whole (blue line). Notably, the market share of commodities-only hedge funds starts to fall several months before the Lehman Brothers collapse—a pattern that accelerates after that event. In sharp contrast, cross-market hedge funds’ energy futures open interest share is not only broadly stable for most of 2008 but also starts to go up after mid-November 2008. These patterns are qualitatively similar to the aggregate patterns documented in Section 4.4 of [3] for a broad cross-section of 17 commodity futures markets.

In sum, our investigation establishes, to our knowledge for the first time in energy futures markets, a clear heterogeneity among two kinds of hedge funds. In the next section, we show that this heterogeneity helps explain the joint distribution of commodity and equity returns.

4. Linking Fundamentals, Speculation, and Commodity–Equity Co–Movements

As discussed in the Introduction, a substantial theoretical literature predicts that the make-up of the commodity futures open interest, macroeconomic conditions, physical energy-market fundamentals, and/or overall financial market stress should affect correlations between commodity and equity prices. Ref. [3] find evidence supporting several such conjectures. However, because they study a cross-section of diverse commodities, they cannot include controls for physical market fundamentals. In this paper, we focus on closely related energy commodities, which allows us to control for the possibility that low energy supplies may impact cross-market linkages. Another difference between the two approaches is that we not only analyze the long-run relation between the various variables but also estimate an error-correction model to look at short-term adjustments.

Similar to our approach in Section 3 above, this section of the present paper hews closely to [3]. Precisely, the structure of our Section 4 follows that of Section 5 in that other paper. We use the same acronyms for all common variables. As well, our wording here paraphrases (when an adaptation is needed due to differences in terms of the relevant literature, commodity samples, or results) or directly repeats that companion paper (either with quotation marks for whole sentences, or without quotes when we repeat just a few words at a time).

Section 4.1 introduces the variables we use to control for financial-sector (4.1.1) and real-sector (4.1.2) factors in assessing the impact of energy markets’ financialization (that we document in Section 3) on energy–equity return correlations (that we document in Section 2).

Table 4. Macroeconomic and market fundamentals, 2000–2010.

	Return Correlations	Macroeconomic Fundamentals		Financial Market Conditions
	DCC S&P500 -GSENTR	REA Index	SPARE (mb/day)	TED (%)	UMD
Mean	0.0486	0.1281	0.9116	0.4877	0.0030
Median	0.0429	0.1561	0.4357	0.2965	0.0900
Maximum	0.5022	0.5530	4.9900	4.3306	4.5500
Minimum	−0.3627	−0.5250	−0.2608	0.0275	−6.5600
Std. Dev.	0.2192	0.2632	1.1531	0.5180	1.1271
Skewness	0.1919	−0.4634	1.6975	2.9511	−0.7008
Kurtosis	2.0384	2.32942	5.1367	14.6372	8.1539
Jarque-Bera	22.5550 ***	27.53235 ***	338.5880 ***	3582.557 ***	600.2571 ***
Sum	24.56	64.69	460.35	246.31	1.52
Sum Sq. Dev.	24.2069	34.9119	670.1042	135.2274	640.2358
Observations	505	505	505	505	505
ADF (Level)	−1.9230	−1.9284	−1.9592	−2.8809 **	−24.2610 ***
ADF (1st Diff.)	−23.0292 ***	−6.6142 ***	−5.7425 ***	−12.8887 ***	−12.6374 ***

Note: We estimate dynamic conditional correlation (DCC) using the Tuesday-to-Tuesday unlevered rates of return (precisely, changes in log prices) on the S&P GSCI Energy Total Return index (GSENTR) and the S&P 500 equity index (SP). We use a log-likelihood for mean-reverting model 24. REA is a measure of worldwide economic activity [31]. ADS is a measure of U.S. economic activity (Aruoba, Diebold and Scotti, 2009). SPARE measures the daily crude oil spare production capacity outside of Saudi Arabia (Source: International Energy Agency). TED is the 90-day annualized Ted spread (Source: Bloomberg). UMD is the [32] momentum factor for U.S. equities. For the augmented Dickey–Fuller (ADF) tests, ** and *** indicate the rejection of non-stationarity at the 5 and 1 percent levels of statistical significance, respectively; critical values are from [28]. The optimal lag length K is based on the Akaike Information Criterion (AIC). Sample period for all statistics: 26 June 2000 to 26 February 2010.

provides summary statistics of the variables described in Section 4.1.

Table 5. Correlation table.

	DCC	REA	TED	SPARE	UMD	WSIA	WSIS	WMSA_AS	WMSA_MMT	WMSA_TCOM	WCMSA_MMT	WCMSA_AS	WMSS_AS	WMSS_MMT	WMSS_TCOM
DCC	1
REA	(0.42)	1
TED	0.06	0.19	1
SPARE	0.45	(0.71)	(0.29)	1
UMD	(0.00)	(0.04)	(0.10)	0.08	1
WSIA	0.20	0.54	0.55	(0.47)	(0.08)	1
WSIS	0.19	0.57	0.55	(0.51)	(0.09)	0.97	1
WMSA _AS	(0.07)	0.54	0.36	(0.50)	(0.11)	0.69	0.68	1
WMSA _MMT	0.13	0.60	0.53	(0.54)	(0.07)	0.98	0.95	0.68	1
WMSA _TCOM	(0.09)	(0.58)	(0.46)	0.50	0.09	(0.94)	(0.91)	(0.86)	(0.93)	1
WCMSA _MMT	(0.01)	0.64	0.20	(0.59)	(0.03)	0.81	0.80	0.52	0.88	(0.79)	1
WCMSA _AS	(0.09)	0.35	0.37	(0.42)	(0.11)	0.52	0.51	0.93	0.50	(0.72)	0.34	1
WMSS _AS	(0.02)	0.50	0.37	(0.42)	(0.08)	0.71	0.69	0.85	0.70	(0.79)	0.59	0.77	1
WMSS _MMT	0.08	0.63	0.47	(0.53)	(0.07)	0.93	0.95	0.69	0.97	(0.92)	0.88	0.51	0.68	1
WMSS _TCOM	(0.05)	(0.63)	(0.45)	0.54	0.09	(0.94)	(0.94)	(0.82)	(0.94)	0.98	(0.83)	(0.67)	(0.81)	(0.96)	1

Note:Table 5 shows the correlations between select variables described in Table 1, Table 2 (Panels A and B), and Table 4. Negative values are indicated by parentheses. Sample period: 26 June 2000 to 26 February 2010.

provides a correlation matrix of our left- and right-hand side variables. Section 4.2 discusses the ARDL regression methodology on which we rely given (i) possible endogeneity issues and (ii) the fact that some of the variables are stationary in levels while others are stationary in first differences only. Section 4.3 discusses our regression results.

4.1. Macroeconomic, Physical-Market and Financial-Market Conditions

Various theoretical models show the importance of macroeconomic and commodity-specific fundamentals for energy price levels and volatility [33] and commodity risk premia (see, e.g., [34,35]). Although there is no unifying theory predicting time-variations in the correlations between the returns on commodity vs. other investments [20], the extant literature suggests several variables for our empirical analysis.

4.1.1. Macroeconomic Fundamentals

Equity and commodity investments perform differentially over the business cycle (see, e.g., [11,13,36]). Furthermore, the response of U.S. stock returns to energy price increases depends on whether the increase is the result of a demand shock or of a supply shock in the energy space [22]. These empirical regularities point to the need to control for the global business cycle when seeking to explain time-variations in the strength of equity-commodity linkages.

To capture the global business cycle at the frequency needed for our analysis, we draw on the Kilian [32] index of real economic activity. That index is based on “dry cargo single voyage ocean freight rates and is explicitly designed to capture shifts in the demand for industrial commodities in global business markets” [32] (p. 1055). The Kilian index is available monthly from 1968: we compute weekly values (which we denote REA) based on Baltic Dry Index quotes following the same procedure as in [3].

4.1.2. Physical-Market Fundamentals

Conditions in physical energy markets could affect equity-energy correlations in two ways. On the one hand, when changes in nearby energy futures prices mostly reflect physical inventory conditions, they are unlikely to be met by contemporaneous changes in equity valuations. To wit, [4] show that the futures returns from grain, oilseed, and livestock markets in 1995 to 2015 are consistent with this intuition, which motivates our approach here (precisely, using a structural vector-autoregression model and weekly data, [4] find no evidence that inventories have a statistically significant impact on commodity–equity correlations). Hence, we refrain from including inventory measures in the econometric analysis. On the other hand, when energy demand increases amid strong economic growth, it can eventually exhaust the crude oil “spare” production capacity that OPEC has historically tried to maintain—leading to a sharp increase in oil prices; conversely, lower energy prices amid greater “surplus” production capacity likely reflect a poor macroeconomic environment. These facts suggest a positive relationship between spare oil output capacity and energy–equity return correlations.

Following [2,37], we use historical data from the International Energy Agency’s (EIA) Oil Market Reports to calculate the total spare crude oil production capacity outside of Saudi Arabia (“SPARE”). We focus on non-Saudi figures because the clearest evidence of changes in energy market fundamentals is evident in this variable (as opposed to world oil consumption, Saudi surplus oil production capacity, OECD stocks of crude oil, etc.).

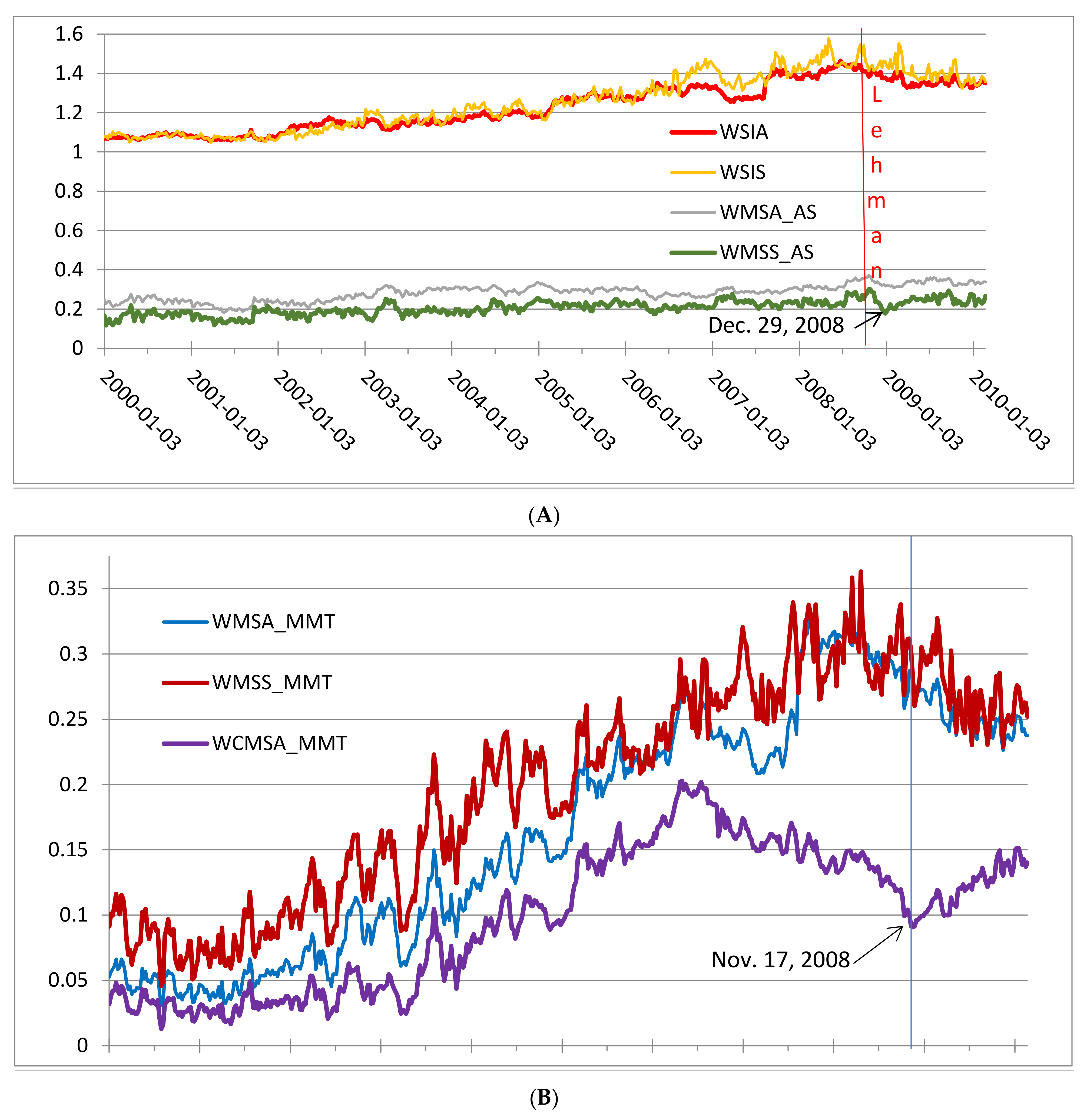
A major change in 2004–2008 is clearly seen in Figure 10 of [2], which provides a scatter plot of the spot WTI crude oil price vs. the non-Saudi spare crude production capacity between 1995 and 2010. From January 1995 to February 2004, when spare capacity was relatively plentiful, prices fluctuated around $29. Likewise, in 2009–2010, spare capacity was non-trivial; again, prices fluctuated in a narrow range (this time around $75). From March 2004 to August 2008, in contrast, SPARE was close to zero and spot oil prices ranged between $27 and $142,

4.1.3. Financial Stress and Lehman Crisis

Following a slump in a major asset market, levered and similarly constrained position holders may face pressures to liquidate other asset holdings. A number of theoretical papers show that those selling pressures may bring about cross-asset contagion even if the fundamental factors driving the returns on different assets are independent—see [38] for a thorough discussion. Refs. [39,40] show that, depending on the make-up of market activity (i.e., who trades) and investor risk appetite, the resulting cross-asset correlations can remain elevated long after the initial shock (a number of empirical studies identify strong cross-market return correlations during crises: for early studies, see [41] in the case of international equity-market linkages; [42] for bond-equity linkages in developed countries; and [12] for equity-commodity linkages).

Those theoretical results suggest that, ceteris paribus, energy–equity correlations should be higher during periods of elevated levels of credit market risk and in the period after a major market crash. As in [3], we include the TED spread to test the first hypothesis, and a time dummy (DUM) for the post-Lehman period (October 2008 to March 2010) to test the second.

4.2. Methodology

Augmented Dickey–Fuller (ADF) unit root tests for the variables used in our estimation equations are summarized at the bottoms of Table 1, Table 2 (Panels A and B), and Table 4. They show that many of the variables are I(1) but that some are I(0).

To examine the link between commodity–equity return correlations, macroeconomic fundamentals, physical market fundamentals, financial market conditions and energy futures traders’ positions, we employ the autoregressive distributed lag (ARDL) approach developed by [43,44]. This approach allows us to “test the existence of a long-run relationship between underlying variables and to provide consistent, unbiased estimators of long-run parameters in the presence of I(0) and I(1) regressors. The ARDL estimation procedure reduces the bias in the long run parameter in finite samples and ensures that it has a normal distribution irrespective of whether the underlying regressors are I(0) or I(1). By choosing appropriate orders of the ARDL(p,q) model, [43] show that the ARDL model simultaneously corrects for residual correlation and for the problem of endogenous regressors” ([3] (p. 64)).

“First, the lag orders of p and q must be selected using some information criterion. Based on Monte Carlo experiments, [43] argue that the Schwarz criterion performs better than other criteria” ([3] (p. 64)). Using model-dependent information criteria, we end up selecting optimal lag lengths p = 1 and q = 1 in all our models—the same values selected in [3] (the Schwarz Information Criterion (SIC) tends to pick a simpler model, resulting in underfitting the model; therefore, we sometimes employ Akaike’s Information Criterion (AIC) to make sure that the errors are serially uncorrelated).

We start with the problem of estimation and hypothesis testing in the context of the following ARDL(p,q) model:

$$y_t=\delta w_t+{\displaystyle \sum }_{i=1}^p{\gamma }_i{y}_{t-i}+{\displaystyle \sum }_{i=0}^q{\alpha }_i{x}_{t-i}+{\epsilon }_t$$

(1)

where p = q = 1; y is a t x 1 vector of the dependent variable, x is a t x k vector of regressors, and ω stands for a t x s vector of deterministic variables such as an intercept, seasonal dummies, time trends, or exogenous variables with fixed lags (the error term is assumed to be serially uncorrelated).

For each of our models, we perform a bounds test of the existence of a long-run relationship between a dependent variable and a set of regressors. The bounds test results, reported in

Table 6. Market fundamentals and GSCI-S&P500 dynamic conditional correlation.

Panel A: Long-Run DCC Determinants.
	Model 1		Model 2
Constant	−0.0244		−0.1775	**
	(0.0682)		(0.0788)
REA	−0.3997	**
	(0.1780)
SPARE			0.0929	**
			(0.0373)
UMD	0.1159	*	0.0998	*
	(0.0663)		(0.0599)
TED	0.4734		0.2142	**
	(0.1380)		(0.1079)
DUM	0.4734	***	0.4630	***
	(0.1380)		(0.1252)
F-Bounds Test	3.7832	**	4.3382	**
Panel B: ECM (Error Correction Model).
	Model 3		Model 4
ECM(-1)	−0.0384	***	−0.0420	***
	(0.0080)		(0.0082)
ΔREA	−0.0922
	(0.0853)
ΔSPARE			0.0008
			(0.0173)
ΔUMD	0.0012		0.0011
	(0.0011)		(0.0011)
ΔTED	0.0154		(0.0142
	(0.0111)		(0.0110)

Notes: The dependent variable is the dynamic conditional correlation (DCC) between passive energy and equity investments. The dependent and explanatory variables are described in Table 4, except for DUM—a time dummy variable equal to 0 prior to 1 September 2008 and 1 afterwards (“Lehman dummy”). Long- and short-run estimates from ARDL(1,1) are based on the two-step approach of [43,44]. Standard errors are in parentheses; statistical significance at the 1, 5, and 10% levels is denoted with ***, **, and * respectively. The critical values for F statistics in the bounds test are taken from [44]. The sample period is = 1 July 2000 to 26 February 2010.

,

Table 7. Speculation and energy–equity dynamic conditional correlation.

Panel A: Long-Run DCC Determinants.
	Model 3		Model 4		Model 5		Model 6
Constant	−3.0125	**	−3.3465	**	−3.6263	**	−3.4924	**
	(1.2545)		(1.4069)		(1.5914)		(1.7288)
REA					−0.3200		−0.3249	*
					(0.2144)		(0.1972)
SPARE	0.1157	***	0.1030	***
	(0.0362)		(0.0341)
UMD	0.0678	*	0.0666	*	0.0865	*	0.0876	*
	(0.0395)		(0.0370)		(0.0503)		(0.0464)
TED	1.5394	***	3.8754	**	1.1266	**	2.9083	*
	(0.5015)		(1.5357)		(0.5547)		(1.6944)
WMSS_MMT	6.0958	***			6.9791	***
	(1.8312)				(2.3462)
WMSS_AS	1.1985		−1.0915		1.9657		−1.1314
	(1.8793)		(1.4069)		(2.3663)		(1.7507)
WMSS_TCOM	3.3910	**	1.0665		4.6530	**	1.4358
	(1.5979)		(1.0069)		(2.0145)		(1.2268)
WSIA			2.3843	***			2.5500	***
			(0.7947)				(0.9788)
INT_TED_MMT	−4.8653	***			−3.5930	*
	(1.6538)				(1.8499)
INT_TED_WSIA			−2.7309	**			−2.0723	*
			(1.0915)				(1.2123)
DUM	0.4817	***	0.3985	***	0.5589	***	0.4347	***
	(0.1056)		(0.0942)		(0.1453)		(0.1265)
F-Bounds Test	4.6189	***	3.9630	***	3.6087	**	3.1871	**
Panel B: ECM (Error Correction Model).
	Model 3		Model 4		Model 5		Model 6
ECM(-1)	−0.0600	***	−0.0663	***	−0.0483	***	−0.0543	***
	(0.0087)		(0.0104)		(0.0080)		(0.0095)
ΔREA					−0.1062		−0.1461	*
					(0.0822)		(0.0829)
ΔSPARE	−0.0164		−0.0094
	(0.0171)		(0.0173)
ΔUMD	0.0010		0.0014		0.0010		0.0015
	(0.0010)		(0.0011)		(0.0011)		(0.0011)
ΔTED	0.1738	***	−0.0061		0.1487	***	−0.1013
	(0.1738)		(0.1551)		(0.0331)		(0.1538)
ΔWMSS_MMT	0.5412	***			0.5082	***
	(0.1646)				(0.1650)
ΔWMSS_AS	−0.1252		−0.2962	**	−0.1123		−0.2807	**
	(0.1267)		(0.1376)		(0.1275)		(0.1380)
ΔWMSS_TCOM	0.0759		−0.0612		0.0884		−0.0500
	(0.1095)		(0.1029)		(0.1104)		(0.1032)
ΔWSIA			−0.0303				−0.0351
			(0.1858)				(0.1864)
ΔINT_TED_MMT	−0.5846	***			−0.4970	***
	(0.1205)				(0.1199)
ΔINT_TED_WSIA			0.0153				0.0842
			(0.1127)				(0.1119)

Notes: The dependent variable is the DCC between the weekly unlevered rates of return on passive equity and energy investments. All variables are described in Table 1, Table 2, Table 3 and Table 4, except for DUM (a “Lehman” time dummy that takes the value 0 prior to 1 September 2008 and 1 afterwards) and INT_TED_xxx (interaction terms of the TED spread with position variables). Long-run (Panel A) and short-run (Panel B) estimates are based on the ARDL(p,q) estimation approach of [43,44]. The Schwarz information criterion suggests optimal lag lengths p = 1 and q = 1. Standard errors are in parentheses; statistical significances at the 1, 5, and 10% levels is denoted with ***, **, and *. The critical values for F statistics in the bounds test are taken from [44]. Sample period: 26 June 2000 through 26 February 2010.

and

Table 8. Cross-market trading as a long-run contributor to the GSCI-S&P500 dynamic conditional correlation.

Panel A: Long-Run DCC Determinants.
	Model 7		Model 8		Model 9		Model 10
Constant	0.3106		−1.0356		0.9441	**	−0.5501
	(0.4612)		(0.9034)		(0.4128)		(0.8844)
REA					−0.3454	*	−0.3595	**
					(0.1861)		(0.1707)
SPARE	0.1253	***	0.0976	***
	(0.0430)		(0.0362)
UMD	0.0674		0.0721	*	0.0715		0.0825	*
	(0.0436)		(0.0395)		(0.0486)		(0.0441)
TED	1.1271	**	3.6601	**	0.5261		2.4862
	(0.4538)		(1.5669)		(0.4447)		(1.5252)
WCMSA_MMT	4.4161	***			2.3962	*
	(1.6648)				(1.4561)
WCMSA_AS	−4.3646	**	−3.2476	*	−5.5186	***	−4.2827	**
	(1.7799)		(1.7119)		(1.9298)		(1.7406)
WSIA			1.2165	**			1.1671	*
			(0.5526)				(0.6097)
INT_TED_CMMTA	−7.8848	**			−3.1154
	(3.5308)				(3.4797)
INT_TED_WSIA			−2.5382	**			−1.7333
			(1.1224)				(1.0980)
DUM	0.3998	***	0.431396	***	0.5283	***	0.4825	***
	(0.1224)		(0.1017)		(0.1242)		(0.1268)
F-Bounds Test	4.5784	***	4.3372	***	3.4774	**	3.7098	**
Panel B: ECM (Error Correction Model).
	Model 7		Model 8		Model 9		Model 10
ECM(-1)	−0.0557	***	−0.0627	***	−0.0510	***	−0.0572	***
	(0.0086)		(0.0100)		(0.0090)		(0.0098)
ΔREA					−0.0658		−0.1361
					(0.0839)		(0.0829)
ΔSPARE	−0.0131		−0.0108
	(0.0171)		(0.0173)
ΔUMD	0.0010		0.0014		0.0008		0.0015
	(0.0010)		(0.0011)		(0.0010)		(0.0011)
ΔTED	0.1591	***	−0.0130		0.1384	***	-0.1005
	(0.0341)		(0.1535)		(0.0343)		(0.1522)
ΔWCMSA_MMT	0.9529	***			0.8632	***
	(0.3072)				(0.3086)
ΔWCMSA_AS	−0.4094	*	−0.5181	**	−0.4273	*	−0.5354	**
	(0.2223		(0.2295)		(0.2239)		(0.2298)
ΔWSIA			−0.0025				−0.0120
			(0.1620)				(0.1621)
ΔINT_TED_CMMTA	−1.2468	***			−1.0851	***
	(0.2930)				(0.2950)
ΔINT_TED_WSIA			0.0220				0.0852
			(0.1116)				(0.1107)

Notes: The dependent variable is the DCC between the weekly unlevered rates of return on passive equity and energy investments. DUM (a “Lehman” time dummy that takes the value 0 prior to 1 September 2008 and 1 afterwards) and INT_TED_xxx (interaction terms of the TED spread with position variables). INT_TED_CMMTA is an interaction terms of the TED spread with the shares of open interest held weekly by cross-market trading hedge funds (MMT). The other variables are described in Table 1, Table 2, Table 4, and Table 7. Long-run (Panel A) and short-run (Panel B) estimates are based on the ARDL(p,q) estimation approach of [43,44]. The Schwarz information criterion suggests optimal lag lengths p = 1 and q = 1 in our case. Standard errors are in parentheses; statistical significance at the 1, 5, and 10% levels is denoted with ***, **, and *. The critical values for F statistics in the bounds test are taken from [44]. The sample period is 26 June 2000 through 26 February 2010.

, suggest the existence of a long-run relationship between our dependent variable and regressors.

After we establish the existence of a long-run relationship between our variables, we estimate long-run coefficients as well as short-run dynamics coefficients. The short-run model coefficient on the error correction term is negative and statistically significant in all our models, consistent with the finding of a long-run relationship.

4.3. Regression Results

Table 6, Table 7, Table 8 and

Table 9. Pre-Lehman LR determinants of equity–energy dynamic conditional correlations.

Variable	Model 3 2000–2008	Model 3b 2000–2008
Constant	−2.4958 **	−4.4461 ***
	(1.205)	(1.491)
REA	−0.7603 ***	−0.6764 ***
	(0.1639)	(0.1446)
UMD	0.0242	0.0184
	(0.0363)	(0.0313)
TED	1.3782 ***	1.0994 ***
	(0.3954)	(0.3476)
WMSS_AS	0.7225	1.2839
	(1.817)	(1.597)
WMSS_MMT	6.7724 ***	6.3014 ***
	(2.000)	(1.710)
WMSS_TCOM	2.5937 *	3.7444 ***
	(1.408)	(1.375)
INT_TED_MMT	−4.3087 ***	−3.5321 ***
	(1.481)	(1.279)
WSIA		1.2395 *
		(0.6362)
Observations	436	436

Notes: Model 3 in Table 9 is the same as Model 3 in Table 7, estimated after excluding the post-Lehman period from the sample. Model 3b is similar but WSIA is added as an explanatory variable. In all models, the dependent variable is the time-varying conditional correlation (DCC) between the weekly unlevered rates of return on the S&P 500 (SP) equity index and the S&P GSCI-Energy total return (GSENTR) index. DCC estimated by log-likelihood for the mean reverting model 24. Explanatory variables are described in Table 1, Table 2, Table 3 and Table 4. Long-run estimates in Table 9 are from the two step ARDL(p,q) estimation approach of [43]. The Schwarz information criterion suggests that the optimal lag lengths are p = 1 and q = 1 in our case. Standard errors are in parentheses; statistical significances at the 1, 5, and 10% levels are denoted with ***, **, and *. The sample period is 4 July 2000 to 11 November 2008.

summarize our regression results. Table 6 establishes the explanatory power of physical market fundamentals (captured by SPARE), macroeconomic fundamentals (captured by REA), and financial market stress (captured by TED) (for completeness, all of our models also include a variable capturing momentum in equity markets (denoted UMD); this variable always has a positive coefficient (consistent with the notion that equity momentum could spill over into other risky assets such as commodities) but we seldom find UMD to be a statistically significant explainer of commodity–equity correlations and, when it is at all statistically significant, the significance level is only 10%). Table 7 establishes the significant additional explanatory power of speculation in general and hedge fund positions in particular. Table 8 shows the relevance of cross-market traders. Table 9 presents some robustness checks. The variables are in levels or in percentages, as discussed in Section 3.

4.3.1. Real Sector and Financial Stress Variables (Table 6)

Long run estimates for Model 1 in Panel A of Table 6 show that, for our sample period (2000–2010), energy–equity DCCs are statistically significantly negatively related to REA. Ref. [45] provide comprehensive evidence that, at least in our sample period, REA is a good “proxy for the state of the global business cycle” [45] (p. 829). To the extent that REA therefore “captures world demand for commodities, (our) finding confirms the intuition that cross-market correlations increase in globally bad economic times” ([3] (p. 64)).

We argued intuitively that, insofar as SPARE measures tightness in the physical crude oil market and as this tightness extends to other energy markets, then DCC and SPARE should be positively related. Model 2 supports this prediction.

In both models, the time dummy for the post-Lehman period (DUM) is always strongly statistically significant and positive. The fact that DUM is significant despite including the TED spread (a measure of financial market stress) supports the “graphical evidence in Section 2 that this sub-period is exceptional” ([3] (p. 65)).

4.3.2. Speculation, including Hedge Funds Activity (Table 7)

Table 7 is one of our main contributions to the literature. It shows that financial activity in energy futures markets is significantly related to long-term variations in energy–equity market linkages.

Intuitively, “there is no reason to expect that traditional commercial traders (…) should matter for co-movements between commodity and equity indices” ([3] (p. 65)). Both panels of Table 7 buttress this intuition in the specific case of energy markets. Panel A seldom finds much long run explanatory power for the WMSS_TCOM variable, and the ECM short run model in Panel B supports this long run finding.

Likewise, “insofar as commodity swap dealing overwhelmingly reflects swap dealers’ over-the-counter relationships with traditional commercials or with unlevered, long-only, passive commodity-index traders (CITs), we would not expect swap dealers’ positions to affect cross-market correlations. This is because CITs do not engage in value-arbitraging and do not alter their positions quickly under financial-market stress” (Büyükşahin and Robe [3] (p. 65)). Table 7 supports this intuition: our variable for swap dealers’ collective share of the short-dated commodity open interest (WMSS_AS)—which captures most CIT positions in our sample period, per [2]—is never statistically significant in the long run (Panel A). This finding presents an interesting counterpoint to the empirical conclusions of [17,46] and the theoretical predictions of [10], regarding the impact of commodity index trading on linkages across commodities or across asset classes.

The main finding in Table 7 is that, after controlling for macroeconomic and physical fundamentals, speculative activity in general (captured by WSIA in Models 4 and 6) and hedge fund positions in energy futures markets particularly (captured by WMSS_MMT in Models 3 and 5) are highly significant in explaining fluctuations in the energy–equity DCC estimates over time. The significance is statistical as well as economic. Ceteris paribus, an increase of 1% in the overall commodity-futures market share of hedge funds (WMSS_MMT) is associated in the long run with dynamic conditional equity-commodity correlations that are approximately 6% to 7% higher (the mean hedge fund market share of about 20%). Again, those results are qualitatively similar to (but quantitatively a bit stronger than) the values estimated on average for a cross-section of 17 commodities [3].

As in [3], Working’s “T” index of overall speculative intensity in energy futures markets (WSIA) “which aggregates the market shares of all non-hedgers across all maturities, has less explanatory power than hedge fund positions in short-dated contracts” ([3] (p. 65)). Going beyond [3], the ECM analysis in Panel B suggests that it is the positions of hedge funds specifically, rather than the activities of non-commercial traders in general, that make the system adjust.

4.3.3. Interaction between Hedge Funds and Financial Stress

Table 7 shows that greater hedge fund participation enhances cross-market linkages. “Yet if the same arbitrageurs or convergence traders, who bring markets together during normal times, face borrowing constraints or other pressures to liquidate risky positions during periods of financial market stress, then their exit from (energy) markets after a major shock in (financial) markets could lead to a decoupling of the markets that they had helped link in the first place” ([3] (p. 66)).

To test this hypothesis, all of our specifications in Table 7 include an interaction term that captures the behavior of hedge funds amid financial stress, as reflected in credit market conditions as proxied by the TED spread. This interaction term is always significant and, as expected, negative. That is, ceteris paribus, the ability of hedge funds’ aggregate energy-futures open interest to explain energy–equity DCCs is lower during periods of stress.

4.3.4. Cross-Market Trading

Table 8 uses specifications similar to Table 7 but focuses on cross-market traders. Two interesting results emerge. First, as intuition would suggest, Models 7 and 9 in Panel A show that the market share of hedge funds that trade in both equity and energy paper markets (WCMSA_MMT) helps explain long-term linkages between equity and energy returns. Second, the market share of commodity swap dealers that are also active in equity markets (WCMSA_AS) is somewhat statistically significant but it has a negative sign in all specifications (Models 7 to 10). These results suggests that “it is value arbitrageurs’ willingness to take positions in both equity and commodity markets, rather than the trading activities of more traditional commodity market participants” ([3] (p. 66)) or of commodity index traders, that help tie energy to equity markets.

4.4. Robustness

The results in Section 4.3 above are all consistent with, and extend, the empirical findings that [3] obtain for financialized commodities in general (but not for any commodity subset in particular). Our results likewise are “qualitatively robust to using additional proxies for energy investment; to introducing dummies to control for unusual circumstances in financial markets; and, to using alternative measures of hedge fund activity in commodity futures markets” ([3] (p. 66)).

4.4.1. Commodity Indexing Activity

“In the past decade, investors have sought an ever greater exposure to commodity prices. Part of this exposure has been acquired through passive commodity index investing. Some of this investment has, in turn, found its way into futures markets through commodity swap dealers” ([3] (p. 66)). However, echoing the latter paper’s findings for a diversified portfolio of 17 commodities, our regressions have the coefficient of the WMSS_AS variable (our proxy for CIT activity) either statistically insignificant or negative. “One possible reason is that, although a part of commodity swap dealers’ positions in short-dated energy futures reflects their over-the-counter interactions with index traders, the rest of their futures positions reflect over-the-counter deals with more traditional commercial commodity traders (so that WMSS_AS) is only an imperfect proxy of commodity index trading activity in commodity futures markets” ([3] (p. 66)).

In unreported results, we tried “another proxy for investor interest in commodities: the post-2004 daily trading volume in the SPDR Gold Shares exchange-traded fund (ETF). Although this volume grew massively between 2004 and 2010” [3], we do not find evidence that it helps explain changes in energy–equity correlations in that period.

Taken together with the results for the WMSS_AS variable, the likely “interpretation is that the activities of passive commodity investors do not explain equity-commodity linkages. This result presents an interesting counterpoint to the findings of [2], who show that increased commodity index trading activity in the WTI crude oil futures market provided additional liquidity that helped integrate crude oil prices across contract maturities” ([3] (p. 67)).

4.4.2. The 2008–2010 Financial Crisis

In Table 6, Table 7 and Table 8, we use a dummy variable (DUM) to account for the uniqueness of the post-Lehman crash period. Table 9 takes a different approach: it repeats the analysis of Table 7 (Panel A), with a sample that ends prior to November 2008. That is “the month when DCC estimates soared upward of 0.4 for the first time since the inception of the investable GSCI commodity index” ([3] (p. 67)).

The results in Table 9 are “qualitatively similar to those” in Table 7. “The main difference is that the statistical significance of the hedge fund variables is stronger pre-crisis. Combined with the strong statistical significance of the post-Lehman dummy (DUM) in every single specification” in Table 7, “as well as with the negative sign of the INT_TED_MMT interaction term” in both Table 7 (Panel A) and Table 9, “this finding suggests that hedge fund activity per se is not responsible for the exceptionally high correlation levels observed from late 2008 to 2010 ([3] (p. 67)).

4.4.3. Hedge Fund Activities in Near-Dated Commodity Futures vs. across the Maturity Curve

Table 10. Pre-Lehman determinants of energy–equity dynamic conditional correlations.

Variable	Model 3c 2000–2008	Model 3d 2000–2008
Constant	0.7722	2.7811
	(1.249)	(2.716)
REA	−0.5934 ***	−0.5889 ***
	(0.1746)	(0.1763)
UMD	0.0325	0.0213
	(0.0380)	(0.0386)
TED	1.1399 ***	1.2577 ***
	(0.3968)	(0.4404)
WMSA_AS	−3.3830 *	−4.6060 *
	(2.178)	(2.571)
WMSA_MMT	1.8172	2.6090
	(1.519)	(1.836)
WMSA_TCOM	−0.7522	−1.7066
	(1.412)	(1.832)
INT_TED_MMTA	−3.4831 **	−3.8345 **
	(1.419)	(1.533)
WSIA		−1.2107
		(1.492)
Observations	436	436

Notes: Model 3c in Table 10 is the same as Model 3 in Table 7, with two differences: it is estimated using trader positions across all maturities, after excluding the post-Lehman period from the sample. Model 3c is similar to Model 3c but WSIA is added as an explanatory variable. In all models, the dependent variable is the time-varying conditional correlation (DCC) between the weekly unlevered rates of return on the S&P 500 (SP) equity index and the S&P GSCI-Energy total return (GSENTR) index. DCC estimated by log-likelihood for mean reverting model [24]. Explanatory variables are described in Table 1, Table 2, Table 3 and Table 4. Long-run estimates in Table 9 are from the two step ARDL(p,q) estimation approach of [43]. The Schwarz information criterion suggests that the optimal lag lengths are p = 1 and q = 1 in our case. Standard errors are in parentheses; statistical significance at the 1, 5, and 10% levels is denoted with ***, **, and * respectively. The sample period is 4 July 2000 to 11 November 2008.

repeats the analysis of Table 9, “except that we measure speculative activity and different traders’ market shares using position information across all maturities (rather than just the three nearest-maturity contracts with non-trivial open interest). The statistical significance of all the position variables drops dramatically, except for the variable capturing hedge fund activity” ([3] (p. 67)), although WMSA_MMT is sometimes significant only at the 10% level. Again, Table 10 “shows little statistical evidence that swap dealers or traditional commercial traders affect the dynamic cross-market correlations” ([3] (p. 67)).

Taken together, Table 7 (Panel A), Table 9 and Table 10 “imply that it is the positions of hedge funds in shorter-dated commodity futures (rather than their activities in commodity markets further along the futures maturity curve) that help predict equity-commodity market linkages. This result is intuitive, in that the GSCI index is constructed using short-dated futures contracts and, hence, “one expects that it is short-dated positions that are relevant for commodity-equity correlations” ([3] (p. 65)).

5. Conclusions

We document that the sign and the strength of the correlation between the returns on passive investments in stock and energy markets fluctuate substantially between 1991 and 2020. Strikingly, the average intensity of this time-varying correlation between energy and equity markets is much higher (0.38) in the dozen years after the start of the Financial Crisis in 2008 than in the two decades prior to that event.

It is by now well known that there was a major upward shift in the commodity futures open interest shares of index funds, hedge funds, and other financial institutions after 2003 [3,17], and that ground zero for this “financialization of commodities” was the WTI crude oil market [1,2]. Thanks to a comprehensive regulatory dataset of all large trader positions in U.S. equity futures and in the three largest U.S. energy futures markets from late June 2000 through February 2010, we provide additional evidence on the financialization of energy paper markets. In particular, we provide novel evidence that their financialization entailed a sharp increase in the energy futures open interest of hedge funds that also invest in other asset classes. This empirical finding establishes that the average financialization patterns documented by [3] for a cross-section of numerous (17) GSCI commodities are especially strong in the specific case of energy markets.

Like Büyükşahin and Robe (2014) [3], we also utilize these data to tease out a possible relation between the financialization and the co-movements of commodity and equity prices. We find that, whereas index fund positions have little explanatory power in this respect, hedge fund positions do. Ceteris paribus, a one percent (1%) increase in the overall energy-futures open interest share of hedge funds is associated in equilibrium with an increase in energy–equity return correlations of over six percent (6%). This figure, which we obtain for three energy commodities using a setup that allows us to control for energy-specific fundamentals, exceeds the corresponding figure (4%) that [3] obtain for a broad portfolio of 17 diverse commodities for which no control for physical market fundamentals is possible.

The present paper further extends Büyükşahin and Robe (2014) [3] by showing that, in the short term, it is financial variables that drive changes in correlations. Intuitively, the existence of a long-run relation has implications for the short run behavior of the variables: a mechanism must exist to drive them to their long-run equilibrium relation. After establishing that the variables are cointegrated, we model this mechanism using an error-correction model (ECM) in which the equilibrium error also drives the short run dynamics of the series. Our ECM analysis supports our long-run results by singling out hedge fund activity, together with credit risk (captured by the TED spread), as the driver of the short-run dynamics.

Finally, we provide empirical evidence that the explanatory power of hedge funds’ energy futures positions relates more narrowly to hedge funds that hold overnight positions in both equity and energy futures markets. To our knowledge, our findings provide the first empirical evidence of the need to account, not just for commodities in general (as shown already in [3]) but in energy futures markets specifically (the present paper), for this heterogeneity among different sorts of hedge funds (i.e., of market participants that all share the same public CFTC classification of “managed money traders”).