Jet Fuel Price Risk and Proxy Hedging in Spot Markets: A Two-Tier Model Analysis

Abstract

This paper applies a two-tier model based on fuel hedging (model 1) and the testing of the impact of commodity risk on airline capacity forecasting, which is based on a system dynamics framework (model 2). Model 1 provides a comprehensive examination of the worldwide airline industry, including an analysis of the statistical impact of oil price fluctuations on the sector and the corresponding hedging strategies employed by airlines. This study examines a sample of North American and European airlines over a 10-year timeframe to assess the degree to which these airlines have engaged in kerosene hedging for future periods and the potential impact of such hedging on their corporate value and performance. In model 2, the author integrates a capacity-forecasting model within the system dynamics framework, drawing upon the theory of capacity forecasting. The study examines the impact of commodity risk by analysing the influence of fluctuations in the jet fuel spot price on the average airfare and its subsequent effects on other interdependent capacity variables. The hypotheses presented in this study were formulated based on a comprehensive review of the relevant literature and a causal feedback loop diagram. The diagram effectively depicts the dynamic interrelationships between capacity forecasting and risk variables. Furthermore, the diagram capturing causal feedback loops was transformed into a stock-flow diagram. This diagram was then utilised to evaluate the hypotheses that were derived using a dataset that pertains to the domestic airline market in the United States. The verification of the qualitative and quantitative models demonstrates the proven impact of commodity risk on capacity forecasting.

1. Introduction

The context of the airline industry is defined by a very cyclical pattern and is very much exposed to exogenous shocks that can have a severe impact on the performance of the airline. Over the last fifty years, there has been a persistent and substantial increase in demand for airline services. However, the industry has only managed to generate a small profit margin. Undoubtedly, the rate of expansion was considerably faster during the 1950s and 1960s, when aviation was still in its early stages, compared to the present, when it has attained a level of maturity. The profit margins of airlines have consistently fallen below the average margins of companies in various other industries.

Furthermore, there have been instances where airlines have incurred substantial losses in certain years. The airline industry is significantly impacted by the volatility of jet fuel prices, which is considered a crucial exogenous factor. This is due to the fact that jet fuel constitutes a substantial portion of an airline’s operating expenses and is highly vulnerable to price fluctuations [1]. Therefore, the factors behind the significant fluctuations in price are analogous to those of any publicly traded commodity, whereby supply, demand, and political factors have a substantial influence. Airlines possess various options to mitigate their exposure to price volatility, as it may not always be feasible to transfer the supplementary expenses to customers owing to the resulting time-related discrepancy between ticket ordering and fuel purchasing for the corresponding flight [2].

This paper incorporates the modelling of a capacity-forecasting model through the system dynamics framework, which is tested for its impact of commodity risk by investigating the effect of changes in the jet fuel spot price on the average airfare and their further impact on the other interrelated capacity variables. However, due to the complexity and the quality of available data, model 2 was simplified to solely focus on the assessment of the impact of commodity risk on the average airfare and its effect on the other main influencing dynamics regarding capacity forecasting. Therefore, some input variables were considered fixed and are provided through a dataset from the Bureau of Transportation Statistics [3].

The literature often questions fuel hedging’s economic sense for airlines or if hedging instruments (derivatives) even positively affect their financial performance at all. There is only one thing that is clear: fuel costs remain a huge chunk of an airline’s overall expenses, and sharp and disruptive swings in prices have a dramatic effect on its financial health.

Since jet fuel is one of the most significant cost factors for an airline, fuel prices may decide whether an airline is successful or not. Rapid or unforeseen changes in fuel prices can be of high risk to airlines if not handled well. Airlines usually hedge 30–60% of their fuel expenses for the next 6 months with the aim of stabilising fuel expenses [4]. The implementation of hedging strategies in the airline industry exhibits variability across different carriers, with a predominant approach being the adoption of short-term contracts typically having a one-year duration. The escalation of oil prices presents a significant challenge for airlines, as it proves difficult to transfer the additional expenses to passengers due to intense competition and the pre-purchase of tickets, which do not accurately reflect the current fuel prices at the time of travel. The financial prospects of airlines engaged in fuel hedging exhibit significant variability that is primarily contingent upon the specific year of hedging [5,6]. Although a permanent fuel hedging policy will not change the long-term profits, it is assumed that fuel hedging reduces volatility in profits, which results in higher share prices [4] and, consequently, higher firm value. Cao and Conlon [7], who explicitly indicated that jet fuel prices are highly volatile and outside airlines’ control, found that incentivizing them to reduce earnings volatility through financial hedging also echoes this view. Due to limited direct hedging options, airlines often resort to cross-hedging of jet fuel requirements.

2. Literature Review

2.1. Hedging

Airlines conduct hedging transactions with commodities whose price movements are highly correlated with the price of oil based on WTI or Brent. According to some publications, heating oil has proven to be particularly suitable for hedging against fluctuations in oil prices.

Airlines normally make an agreement with a refiner on the monthly delivery of a certain number of oil barrels, and the price is usually settled at the end of the month and based on the average price that month. Transportation costs based on the location of the jet fuel delivery site are also included in the billing. Through a swap agreement with a financial institution, an airline can fix the average monthly floating kerosene price for the upcoming month. If the floating price is higher than the agreed fixed price, the financial institution would need to pay the price difference to the airlines. It works the other way around when the floating price is lower than the agreed fixed price. In his works, Schofield [8] explained that airlines often use oil gas to substitute future contracts in order to hedge against jet fuel price risks. Because of jet fuel’s higher quality, an additional premium for quality and transportation charges is factored into the total charges.

Due to this, a jet fuel future contract based on gas oil would look like this:

$$\begin{array}{c}\mathrm{Jet} \mathrm{fuel}=\mathrm{Gas} \mathrm{oil} \mathrm{future} \mathrm{price} \mathrm{at} \mathrm{delivery}+\mathrm{fixed} \mathrm{jet} \mathrm{fuel} \mathrm{differential}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\mathrm{Transport} \cos \mathrm{t} \mathrm{to} \mathrm{delivery} \mathrm{location}\hfill \end{array}$$

In their study “The Systematic Risk Determinants of the US Airline Industry”, Lee and Jang [9] examined which specific airline metrics indicate and contribute to the airline’s systematic and specific risk.

Systematic and firm-specific risks can be avoided through diversification of the stock portfolio [10]. Systematic risks are, in essence, market risk, while an unsystematic risk is firm-specific. The risk factor beta is influenced by financial leverage, firm size, and profitability. A cost structure (e.g., cost per available seat mile) that is more efficient than that of competitors can also influence the risk factor beta.

Ri = Rf + (Rm − Rf)βi

Ri = β0 + βiRm + ԑi

β is derived from a historical dataset and relates the expected return of the single security to the return of a market portfolio (index). β is influenced by the internal and external factors that affect the financial performance of a company and how its overall position in the market—taking into consideration the exogenous events that can affect it (e.g., economic downturn and political crises)—can affect its stock performance.

Lee and Jang [9] identified several factors that can influence the risk factor β. These include the liquidity of a company, its debt leverage, its operating efficiency, its profitability, its firm size, and its growth perspective.

Lee and Jang [9] also examined the type of influence a firm’s size can have on an airline’s systematic risk. They eventually determined that a firm’s size does have a significantly positive link to the proportion of its systematic risks. This means that the bigger the airline, the more it is exposed to airline-specific systematic risks. Managing an airline’s leverage (reducing debt rate) and improving profitability are measures that can be taken to reduce operational cost, wherein fuel is a large chunk of it [9].

Table 1. Synopsis of selected studies on hedging.

Year	Authors	Methodology	Key Findings
2002	Carter, Rogers, and Simkins	Time series regression analysis	Airline stock value negatively correlated to rising jet fuel prices over time. Fuel hedging has a positive and statistically significant impact on airline business value.
2004	Cobbs and Wolf	Analytical model	Optimal hedging strategy for airlines using different derivatives based on price cycles.
2006	Morrell and Swan		Hedging may not significantly impact airline profitability or stock price in the long term.
2007	Lee and Jang	Regression analysis	Firm-specific risk can be reduced through diversification and efficient cost structures. Airline size is positively linked to airline-specific systematic risk.
2008	Maher and Weiss	Regression analysis	Hedge score positively impacts cash flow and equity returns, especially post crisis. Fuel hedging does not fully protect airlines against adverse circumstances (e.g., 9/11).
2012	Cerny and Pelikan	Empirical analysis	The optimal hedge ratio can change during risk management strategy due to correlation shifts.
2013	Gerner and Ronns	Panel data analysis	Airlines with higher credit ratings have more hedging choices and engage in hedging during high fuel demand.
2014	Balu and Morad	Time series analysis	Developed a model to predict crude oil price volatility using historical data.
2015	Lim and Turner	Variance minimisation	The optimal hedge ratio for a portfolio can be determined by minimising variance in returns.
2016	Dafir and Gajjala	Literature review	Identified three types of risks in commodity trading relevant to the spot market.
2017	Jiang et al.	Time series analysis	Oil market recovery after shocks follows established patterns.
2021	Samunderu and Murahwa	Sensitivity analysis	GARCH model sensitivity in measuring risk in oil price distribution.

presents a synopsis of selected studies related to hedging in the airline industry in both American and European markets, which is needed in order to showcase the evolution of research in this field and highlight the soundness of their methodologies and empirical results.

Brandao, Cerqueira, and Nova [11] studied how the usage of derivate hedging against interest rate risks and the usage of derivative hedging against foreign exchange rate risk could affect company value (TobinsQ). For their regression analysis, the authors applied control variables that can influence firm value (leverage, size, dividends paid, investment growth rate, liquidity, profitability, multinational diversification, industry diversification, time effect, and industry effect).

The findings of this research enticed yet another team to provide more detailed insight into the airline industry’s exposure to energy market risks and how they could mitigate these risks through the use of derivative instruments. In their study, Gerner and Ronns [12] tried to determine the circumstances that can prompt airline managers to employ hedging strategies. They noted that airlines with higher credit ratings have more choices of derivative instruments because they can more likely find counterparties that will engage in derivative contracts with them. They also found out that airlines are more engaged in hedging activities in times of high fuel demand to prevent their overall costs from soaring. This is further echoed in the study by Treanor et al. [13], who investigated both the effects of financial and operational hedging in reducing risk exposure. Their findings revealed that both financial and operational hedging are effective at reducing airlines exposure to fuel prices.

Carter, Rogers, and Simkins [14] conducted a study investigating the correlation between fuel derivatives and airlines’ company value. They employed time series regression analyses to assess how changes in oil prices affect returns on airlines’ stock. The study used return on stock as the dependent variable, with the weighted return of the market portfolio and the percentage change in jet fuel price as independent variables. The findings revealed that an airline’s stock value is negatively correlated with rising jet fuel prices over time, but this effect becomes small and insignificant in the short term. The authors further explored the relationship between hedging jet fuel and an airline’s company value, considering the hedging ratio and applying dummies to identify airlines engaged in fuel hedging. Control variables such as dividend, leverage, profitability, and investment were also considered. The study observed that hedging jet fuel had a positive and statistically significant effect on an airline’s business value, while changes in the hedging ratio did not significantly impact the firm’s value. Additionally, hedging kerosene had a positive and statistically significant influence on the overall company value of an airline, whereas changes in the hedging degree (proportion of hedged kerosene) had no statistically significant impact on the firm’s value.

In the literature, several airlines are found to employ a dynamic hedging strategy, taking advantage of price cycles to determine the most beneficial instruments and ratios at different times. Cobbs and Wolf [15] recommended using swap derivatives when prices are at their lowest in the price cycle, as future prices are likely to increase. Collars are suggested when prices are at their average (in the middle) to navigate through potential price increases or decreases, while caps are used as hedging instruments at the highest point of the price cycle to mitigate the effects of price increases. These practices reflect airlines’ efforts to optimise their hedging strategies and manage fuel price risks effectively.

Cobbs and Wolf [15] determined that there is an optimal hedging ratio that can balance the change in jet fuel spot price with a sufficient ratio (H) of future contracts.

$$\Delta \mathrm{Jet} \mathrm{Fuel} \mathrm{Price}-\mathrm{H}*\Delta \mathrm{Future} \mathrm{Contracts}$$

The hedge ratio H is the regression coefficient between the aircraft fuel and the raw material used to hedge the price of the aircraft fuel (e.g., crude oil or heating oil). The coefficient H will determine the number of future contracts, and the price of aviation fuel will be optimally hedged.

H = Ṗ*σ[spot]/σ[future]

The hedge ratio (H) is determined by the correlation between the spot jet fuel price and the price of the future contract (Ṗ) and the standard deviation of the spot price (σ) divided by the standard deviation of the futures price (σ).

By using the formula to determine the hedging ratio, the regression coefficient of aviation gasoline can also be determined with raw materials that are used for price hedging (e.g., how strongly crude oil or heating oil is correlated with aviation gasoline as a measure of the price correlation). The authors compared the price development of aviation gasoline with the price development of crude oil and heating oil over a period of one year and found a correlation of 1.06 between aviation gasoline and crude oil and 1.15 between aviation gasoline and heating oil. If the correlation between the same commodities was compared over a period of 2 years, values of 0.98 and 1.07, respectively, were found [15].

Recently, in their study, Li et al. [16], analysed jet fuel hedging strategies by constructing the Copula-GARCH model to determine the hedging futures products and the hedging ratio. There are two types of hedging strategies that companies can adopt: one is the minimum variance hedging strategy based on risk avoidance purposes, and the other is the maximum utility hedging strategy based on revenue objectives. Their empirical results [16] showed that the correlation between heating oil futures and aviation fuel spot is stronger, and the hedging performance is obviously better than crude oil futures, which can better avoid the risk of jet fuel price fluctuation.

Turner and Lim [17] dealt with the question of determining the optimal hedging ratio for a portfolio.

They suggested that the optimal hedge ratio can be determined by minimising variance in returns.

$$\mathrm{Rt}=\Delta \mathrm{St}-\mathrm{h}\Delta \mathrm{Ft}$$

The variables are defined by Turner and Lim [17] as follows:

Rt = Returns;

∆St = Change in the spot price;

∆Ft = Change in future price;

h = Number of future contracts.

The following formula is presented to minimise the variance of Rt:

$$\frac{\mathrm{dVar}\left(\mathrm{Rt}\right)}{\mathrm{dh}}=2\mathrm{hVar}\left(\Delta \mathrm{Ft}\right)-2\mathrm{Cov}\left(\Delta \mathrm{St},\Delta \mathrm{Ft}\right)=0$$

This produces the minimum variance hedge ratio h*:

$${\mathrm{h}}^{*}=\frac{\mathrm{Cov}\left(\Delta \mathrm{St},\Delta \mathrm{Ft}\right)}{\mathrm{Var}\left(\Delta \mathrm{Ft}\right)}$$

Calculating the correlation coefficient derived from the covariance and the standard deviation obtains the following:

$$\mathsf{\rho }=\frac{\mathrm{Cov}\left(\Delta \mathrm{St},\Delta \mathrm{Ft}\right)}{\mathrm{SD}\left(\Delta \mathrm{St}\right)\mathrm{SD}\left(\Delta \mathrm{Ft}\right)}$$

The optimal hedging ratio h* can also be derived:

$${\mathrm{h}}^{*}=\mathsf{\rho }\frac{\mathrm{SD}\left(\Delta \mathrm{St}\right)}{\mathrm{SD}\left(\Delta \mathrm{Ft}\right)}$$

Tan [18] presents different theories that address the issues of finding the optimal hedging ratio for an airline. Traditional theories propose a ratio of 1 for hedging. This means that the commodity should be hedged by 100% if the airline’s management is certain that hedging is indeed a suitable instrument for adding value to the company. The hedge ratio should always be adjusted to the fluctuations in the price of raw materials (such as crude oil) versus aviation fuel (correlation) so that the idea of risk minimisation and the increase in profits can continue to be optimally realised. According to portfolio theory, several commodities should also be used for hedging if necessary if this helps to further minimise the risk.

Cerny and Pelikan [19] indicated that the optimal hedge ratio could change during the cycle of a risk management strategy because the correlation in prices between the commodity that is hedged and the underlying substitute commodity can change as well.

Naumann, Suhl, and Friedemann [20] advocated the possibility of coordinating the optimal hedging strategy with the fleet planning (procurement of new aircraft and in relation to the existing fleet) to gain the highest profit. The authors thus recommended the integration of operational risk management (fleet planning) with financial risk management (hedging strategy).

In their study, Maher and Weiss [21] investigated the impact of operational and financial hedging, represented as the “hedge score”, on adverse circumstances faced by airlines, specifically focusing on the aftermath of the 11 September terrorist attacks. Their findings revealed that airlines with higher hedge scores experienced better performance in terms of cash flow from operations and equity returns immediately after the attacks. However, this positive effect was limited to a relatively short period, suggesting that hedging can provide some protection against specific events but may not effectively counter overall industry challenges like economic downturns. The study identified various operational and financial factors contributing to the hedge score, with fleet diversification, occupancy rate, aircraft leasing, and cash reserves showing significant correlations. Notably, fuel hedging was not found to be significantly effective in protecting airlines’ performance during adverse circumstances, though it could still be valuable for managing energy market volatility. The last financial hedge variable is leverage, which is negatively and statistically insignificantly correlated with the hedge score [21].

The economic viability of fuel hedging for airlines and the potential impact of hedging instruments such as derivatives on their financial performance are frequently questioned in the literature. Fuel costs continue to constitute a significant portion of an airline’s total expenses, and unexpected and significant fluctuations in prices can have a profound impact on its financial well-being [6].

The primary rationale behind airlines’ practice of fuel price hedging is to mitigate the adverse impacts of fuel price volatility by stabilising and mitigating potential spikes in fuel prices. Consequently, this leads to a decrease in potential hazards since it is perceived as an extra expense. According to Morell and Swan’s [4] computations, an airline’s total expenses are already impacted by 15% when the price of oil reaches USD 25 per barrel. Oil futures are commonly employed by airlines as a hedging mechanism, allowing them to mitigate risk associated with fuel price fluctuations. Typically, airlines maintain a significant portion of their total fuel expenditures, ranging from one-third to two-thirds, through the use of this instrument. Due to the inability of airlines to adjust their cost base in response to fluctuations in demand and revenue, their profitability tends to be unstable. Consequently, airlines often resort to fixing certain variable costs in order to mitigate the effects of this volatility.

However, the effectiveness of hedging as a means to generate profit or increase the stock price of an airline over an extended period of time is weakly established by prior research findings. According to economic theory, the size of airlines is insufficient to exert any significant influence on the oil market through their hedging activities. Additionally, the market is characterised by a high level of depth and participation from numerous professional and speculative traders. Hence, it is unlikely for an airline to pursue profitability through its hedging endeavours; otherwise, the airline would assume the role of a speculative trader. The primary purpose of hedging for airlines is to mitigate the volatility in expenses and thereby achieve greater stability in earnings. The capital assets pricing model highlights a crucial aspect of economics, namely that increased market uncertainties may lead to greater investment returns for investors. However, financial instruments such as futures contracts and swaps can serve to mitigate market risk, thereby causing these instruments to receive the premium. Consequently, the efficacy of financial instruments in mitigating market risk appears to be limited, and investors may persist in paying inflated prices due to a lack of comprehension regarding the underlying mechanics of said instruments.

Dafir and Gajjala [1] identified three types of risks relevant to commodity trading in the spot market. Price risk arises from the volatility of spot prices in long-term contracts, leading to uncertainty about future prices. Counterparty risk refers to uncertainties related to one party’s ability to fulfil contractual obligations. Operational risk encompasses transportation, legal, and documentation risks. As global commodity trade increases, specialised goods like Brent or WTI have emerged, and payment systems have become more sophisticated, leading to the use of financial derivatives in the market.

Regarding fuel expenses, airlines employ three strategies. They try to mitigate fuel cost impact by making operational changes, using more fuel-efficient routes and aircraft, and passing on increased costs to consumers through higher airfare rates [22]. Airlines also use financial instruments or derivatives to manage price fluctuations. According to the capital asset pricing model (CAPM), fuel hedging may have minimal impact on an airline’s overall value since it does not significantly affect long-term stock prices. However, some argue that CAPM may not fully capture real-world factors like asymmetric information, economies of scale, and taxation, which also influence prices.

During periods of economic growth, it is typically anticipated that there will be an increase in oil prices due to heightened demand. Conversely, during economic downturns, there is typically a decrease in demand for oil, resulting in a corresponding drop in prices. This phenomenon is known as the demand-driven economic cycle. Fuel hedging can serve as a viable strategy to safeguard against oil supply crises, which are often characterised by elevated oil prices. This was exemplified by the geopolitical tensions in the Middle East that resulted in the risk of conflict and instability in politics. In the present scenario, characterised by an economic cycle that is supply-driven and marked by an anticipated increase in fuel prices, leading to a corresponding reduction in airline revenues, the adoption of fuel hedging can be considered a selective measure to mitigate the adverse impact on airline profitability and minimise price volatility.

In addition to the aforementioned arguments, the existing literature suggests that the utilisation of hedging strategies is not beneficial to the mitigation of cost and volatility. Rather, it is believed that such strategies are employed to accelerate the transfer of cash flow to earlier periods in the income statement through the sale of oil futures contracts for an earlier date, consequently compensating for declining profits. Furthermore, it has become an approach utilised by airline executives to demonstrate their proficiency in mitigating financial risks. The disclosure of a hedging strategy by an airline company typically leads to an increase in its stock value, while the absence of such disclosure could encourage investors to doubt the company’s commitment to sustaining or improving its financial gains [4].

The measurement of risk is commonly associated with fluctuations in prices, which may occur in diverse forms such as relative, absolute, or log price changes. Jorion [23] emphasised that eliminating all risks entirely is impossible, and the focus should be on taking intelligent risks. Airlines face various internal and external risks, necessitating proactive decisions and strategic responses from management. Shareholders consider companies’ risk profiles crucial in their investment decisions, influencing their expectations and willingness to invest. Due to the cyclicality of the airline industry, fixed capacity, and high debt/lease financing, operating profits are volatile, creating challenges and opportunities [24]. Airlines manage risks through practices such as fuel and financial hedging and insurance. Risk mitigation strategies are developed based on risk assessments to reduce potential risks, but their applicability depends on the organisation’s ability to influence the source of the risk [25].

2.2. Forecasting

The forecasting approach involves predicting future events based on past data, as noted by Bowerman et al. [26]. This methodology can be highly beneficial for facilitating efficient and effective corporate planning, as highlighted by Makridakis et al. [27].

In the context of forecasting, a differentiation between qualitative and quantitative techniques is given due consideration, much like in the case of risk analysis. Makridakis et al. [27] suggested that the selection of a process is dependent upon the availability of quantitative information. In cases where there is a lack of quantitative data, a qualitative methodology may be employed. The process of qualitative forecasting typically involves the formulation of a prediction that is informed by a group of professionals who are tasked with addressing a specific inquiry pertaining to the forecast. The Delphi method is commonly recognised as the above-mentioned process. The methodology of curve fitting, which involves aligning the projection with a pre-existing scenario, is also widely utilised. The product lifecycle is a suitable illustration, as numerous recently launched products undergo this particular sequence.

In the context of analysis, a distinction exists between extrapolative and causative methodologies. The extrapolative method can be founded on either a selective approach, which involves the observation of values at a single point in time, or a serial approach, which involves the analysis of a sequence of events occurring within a defined time period. In the context of time series analysis, the values containing a given dataset are examined with the aim of detecting any noticeable trends within the data. This phenomenon is believed to exhibit a consistent repetition in the future [28], (p. 210). The academic literature primarily differentiates among four distinct patterns. In accordance with the study conducted by Bowerman et al. [26], the constituent elements of a time series are denoted as trend, cycle, seasonal variations, and irregular fluctuations. Conversely, the causative methodology pertains to the correlation between dynamic market structures through the utilisation of instruments such as multiple regression analysis.

In their contribution, Balu and Morad [29] examined the price volatility of crude oil (for the Brent Blend, Dubai Fateh, and WTI Indices) and developed a model for predicting the future volatility of crude oil prices. By analysing the historical data for all three indices, the authors concluded that neither the weather price series nor yield series is normally distributed and that positive and negative price shocks are responsible for this abnormal distribution. They also observed heteroscedasticity for all series.

Different time series models can be applied in forecasting financial and commodity markets. Balu and Morrad [29] suggested three possible methods to use: (1) the naïve model, (2) exponential smoothing models, and (3) the autoregressive models ARIMA and GARCH [1].

Models like the GARCH model often fail to predict oil price developments and its extreme volatility. The GARCH technique, however, is a more sensitive way to measure risk in a distribution [30]. Jiang et al. [31] established that the oil market’s recovery after an endogenous or exogenous shock follows the same pattern, indicating that the global oil market is a mature market in which price adjustments follow established patterns.

Airline capacity management represents a crucial challenge for business operations, as it serves as a major determinant of profit cyclicality. Figure 1 presents an illustrated model that clarifies the dynamics that influence airline flight schedules, which constitute capacity management, without considering the factors that may influence other stakeholders in the aviation value chain. Barnhart et al. [32] posited that the airline flight schedule is subject to various dynamics, including demand, pricing, and schedule design and performance, which are complementary to one another. In order to enhance comprehension of the interrelated dynamics of influence, it may be beneficial to undertake a specific analysis [33].

The complexity of capacity forecasting arises from a multitude of internal and external factors that serve as stimulation. The airline is susceptible to various risks due to uncontrollable external factors, ultimately leading to financial loss.

3. Methodology

This study adopts a two-tier empirical model analysis to evaluate the rationale of fuel hedging (model 1) and system dynamic forecasting (model 2).

The hedging analysis was derived from two sources: the airline share prices were from the Thomson Reuters Datastream, and the WTI oil prices were from the Federal Reserve Bank of St. Louis, and the growth rate of the world economy was depicted from the World Bank.

The present research involved the development of a dynamic model for airline forecasting, which takes into account the various factors that influence demand assessment, airfare pricing, and flight schedules. However, due to the complexity and the quality of available data, the model was simplified to solely focus on the assessment of the impact of commodity risk reflecting the logic of Carter et al. [34] on the average airfare and its effect on the other main influencing dynamics regarding capacity forecasting. Therefore, some input variables were considered fixed and are provided through a dataset from the Bureau of Transportation Statistics [3].

3.1. Empirical Model 1—Fuel Hedging

As the first step, the hedging strategy of the examined airlines and their reported profits and losses from these activities are presented. Firstly, several regression analyses were carried out, covering a sample of airlines over a period from 2008–2017 as panel data. This is to answer the hypothesis that fuel hedging affects the value of the airline (tested on TobinsQ and the share price of the airline). By applying several dummy variables, the extended hypothesis was tested as to whether and how the corporate structure and geographical location of the airline contribute to a different corporate valuation caused by fuel hedging activities.

To determine how airlines are exposed to changes in oil prices and global economic trends, several regression analyses were conducted for several airlines to measure the impact of annual oil price changes (WTI) and adjusted to U.S. consumer prices and annual global economic growth on the development of airlines’ annual share prices (

Table 2. Regression analysis for all companies.

Company	Beta_X1	p-Value_X1	Beta_X2	p-Value_X2	R-Squared
Lufthansa	1.394	0.046 **	0.253	0.654	0.092
Southwest	0.72	0.679	0.177	0.907	−0.052
Air France	−0.653	0.841	−6.733	0.022 **	0.108
Ryanair	−0.084	0.915	0.004	0.995	−0.11
Delta Air Lines	1.86	0.467	−8.814	0.015 **	0.463
United Airlines	4.53	0.09**	−9.941	0.008 **	0.56
Air Canada	1.696	0.134	−2.273	0.105	0.282
Cathay Pacific	0.736	0.072	−6.733	0.000 ***	0.379
Finnair	0.864	0.015**	0.145	0.610	0.15
Qantas	0.186	0.484	−0.109	0.318	−0.013
SAS	15.297	0.289	−5.939	0.685	−0.039
Singapore Airlines	0.264	0.581	1.306	0.003 ***	0.209
WestJet	0.038	0.972	1.064	0.331	−0.058

Note: ** Significant at 95% confidence level (p-value < 0.05). *** Highly significant at 95% confidence level (p-value < 0.01).

).

The airline’s stock price is the dependent variable (Y), while the annual world economic growth rate (X₁) and the annual oil price changes (WTI) adjusted to U.S. consumer prices (X₂) are the two independent variables. The reason for the integration of the economic growth rate into this simple regression analysis is to determine whether there is some multicollinearity that limits the effects of the energy (oil) price development on the shares of the airlines and, in turn, on the performance of the company. In addition, a simple linear regression analysis was performed for each airline if for only one independent variable a significant effect on the airline’s share performance (Y) was detected (Table 2).

Y = Airline’s stock;

X₁ = Annual world economic growth rate;

X₂ = Annual oil price development.

The regression analysis results for all companies are as follows in Table 2:

Based on the analysis, the airlines could be categorised into three groups regarding the response to oil price changes and global economic growth (

Table 3. Airlines Categories.

Group	Airlines	Description
Group 1	Delta Air Lines, United Airlines, Cathay Pacific, Singapore Airlines.	These airlines are significantly affected by changes in oil prices. Delta Air Lines and United Airlines experienced a negative impact, with their stock prices declining as oil prices rose. In contrast, Cathay Pacific and Singapore Airlines have a positive correlation, witnessing stock price increases with higher oil prices.
Group 2	Air France, Finnair.	Airlines in this group are moderately influenced by oil price changes. Air France shows a significant negative correlation between its stock performance and oil price changes. For Finnair, the relationship is less pronounced but still significant.
Group 3	Lufthansa, Southwest, Ryanair, Air Canada, Qantas, SAS, WestJet.	These airlines show no significant correlation between their stock performance and changes in oil prices. Additionally, their stock performance has an insignificant correlation with global economic growth. The impact of oil price changes and global economic growth on these airlines’ stock prices is relatively limited compared to those in group 1 and group 2.

).

Understanding these distinct groups, presented in Table 3, helps to highlight the varied sensitivities of airlines to external economic factors and provides valuable insights for investors and stakeholders in the aviation industry. It is crucial to recognise that each airline’s unique characteristics and strategies contribute to its individual response to market dynamics, including oil price fluctuations and global economic trends.

Lufthansa: (Observation period: 1991–2017; N = 27)

As the largest European airline, the Lufthansa Group carried 130 million passengers in 2017 and comprises a fleet of 728 aircraft. With 130,000 employees, the mother company achieved a turnover of more than EUR 35 billion. The company also divides its business units into network airlines (Lufthansa, Swiss, and Austrian Airlines), point-to-point Airlines (Eurowings, Brussels, and Sunexpress) and aviation service (logistics, catering, maintenance, repair, and overhaul). The hubs used for network airlines are Frankfurt and Munich (for Lufthansa) as well as Zurich (for Swiss Airlines) and Vienna (Austrian Airlines) [35].

Y = 1.394X₁ + 0.253X₂ + 8.833

In total, 9.2% of Lufthansa’s share price performance Y can be attributed to the development of oil prices and global economic growth (R²). The F-test for the overall model is not significant at 0.120 (

Table 4. Lufthansa regression analysis with both variables.

World GDP	1.394 (0.662) **	R2	0.092
Oil price	0.253 (0.558)	F-Statistic	2.322
constant	8.833 (2.596) ***	Significance	0.12

Note: ** Significant at 95% confidence level (p-value < 0.05). *** Highly significant at 95% confidence level (p-value < 0.01). Source: Author.

). This means that the hypothesis that the two independent variables have no influence on the dependent variable cannot be rejected. The p-value for the single independent variable X₂ is not significant (0.654), but the p-value for the economic growth rate X₁ is significant, which is at a confidence level of 95% (0.046) (Table 4). No collinearity can be measured between the two independent variables X₁ and X₂.

Considering the result of the previous analysis that shows that the annual world GDP growth does have a significant influence on Lufthansa’s stock, a single linear regression was performed with the annual world GDP growth variable (X₁) as the only independent variable (

Table 5. Lufthansa regression analysis with world GDP growth.

World GDP	1.394 (0.651) **	R2	0.121
Oil price		F-Statistic	4.584 **
constant	9.564 (2.005) ***	Significance	0.042

Note: ** Significant at 95% confidence level (p-value < 0.05). *** Highly significant at 95% confidence level (p-value < 0.01). Source: Author.

).

Y = 1.394X₁ + 9.564

Overall, 12.1% (R²) of Lufthansa’s share performance Y can be attributed to the annual world economic growth (X₁). This influence is statistically significant (p-value = 0.042) (Table 5).

Southwest: (Observation period: 1980–2017; N = 38)

Southwest Airlines is headquartered in Dallas, Texas, and, after initially concentrating only on the state of Texas, it has now focused on the entire United States as a whole. Southwest is the largest airline in the U.S. in terms of domestic air traffic, and it offers point-to-point connections. The company has 58,000 employees and carries more than 120 million passengers annually, with an annual turnover of over USD 21 million (2017) and a fleet size of 750 aircraft (Boeing 737 type) [36].

Y = 0.72X₁ + 0.177X₂ + 8.546

Overall, −5.2% of the share price development of Southwest’s Y can be attributed to oil price development and the world economic growth (R²) (

Table 6. Southwest regression analysis with both variables.

World GDP	0.72 (0.177)	R2	−0.052
Oil price	0.177 (1.50)	F-Statistic	0.089
constant	8.546 (7.741)	Significance	0.916

Source: Author.

). The F-test for the overall model is clearly not significant at 0.916 (Table 6); i.e., the hypothesis that the two independent variables have no influence on the dependent variable cannot be rejected. The p-value for the two individual independent variables X₁ and X₂ is not significant at a confidence level of 95% (0.679 and 0.907, respectively). No collinearity can be measured between the two independent variables X₁ and X₂.

Air France: (Observation period: 1985–2017; N = 33)

Air France is the former state-owned company of the legacy carrier of France (founded in 1933) and uses Paris-Charles de Gaulle and Paris-Orly as its hubs. Together with the Dutch legacy carrier KLM, it has merged into what is now the Air France-KLM group. With more than 25,000 employees, Air France transports over 100 million passengers a year (airfrance.com, 2019, accessed on 20 May 2020).

Y = −0.653X₁ − 6.733X₂ + 48.163

A total of 10.8% of Air France’s share performance Y can be attributed to the development of oil prices and global economic growth (R²). The F-test for the overall model is not significant at 0.068 (narrow); i.e., the hypothesis that the two independent variables have no influence on the dependent variable cannot be rejected (

Table 7. Air France regression analysis with both variables.

World GDP	−0.653 (3.236)	R2	0.108
Oil price	−6.733 (2.788) **	F-Statistic	2.937 **
constant	48.163 (13.246) ***	Significance	0.068

Note: ** Significant at 95% confidence level (p-value < 0.05). *** Highly significant at 95% confidence level (p-value < 0.01). Source: Author.

). The p-value for the single independent variable X₂ is significant (0.022) at a 95% confidence level, while for the economic growth rate X₁, the p-value at a 95% confidence level (0.841) is not significant. No collinearity can be measured between the two independent variables X₁ and X₂.

After having the result of the previous analysis that shows that the annual oil price development has a significant influence on Air France’s share, a single linear regression analysis—wherein the annual oil price development X₂ is the only independent variable—was carried out.

Y = −6.696X₂ + 46.120

Overall, 13.6% (R²) of Air France’s share price development Y can be attributed to the annual oil price development X₂. This influence is statistically significant (p-value = 0.020) (

Table 8. Air France regression analysis with oil price development.

World GDP		R2	0.136
Oil price	−6.696 (2.729) **	F-Statistic	6.020 **
constant	46.120 (8.413) ***	Significance	0.02

Note: ** Significant at 95% confidence level (p-value < 0.05). *** Highly significant at 95% confidence level (p-value < 0.01). Source: Author.

).

Ryanair: (Observation period: 1997–2017; N = 21)

Ryanair is an Irish-based airline that operates pioneer-to-point flights within Europe. With its 13,000 employees, it carries over 130 million passengers, making Ryanair the largest airline in Europe in terms of intra-European traffic. They achieved a turnover of over EUR 7 billion last year [37] and operate with a fleet size of 430 aircraft (type Boeing 737) [37].

Y = −0.084X₁ + 0.004X₂ + 4.978

In total, −11% of the Ryanair share performance Y can be attributed to the development of oil prices and global economic growth (R²). The F-test for the overall model is clearly not significant at 0.993; i.e., the hypothesis that the two independent variables have no influence on the dependent variable cannot be rejected (

Table 9. Ryanair regression analysis with both variables.

World GDP	−0.084 (0.735)	R2	−0.11
Oil price	0.004 (0.652)	F-Statistic	0.007
constant	4.978 (3.307)	Significance	0.993

Source: Author.

). The p-value for the two individual independent variables X₁ and X₂ is clearly not significant at a confidence level of 95% (0.915 and 0.995, respectively). No collinearity can be measured between the two independent variables X₁ and X₂.

Delta Airlines: (Observation period: 2007–2017; N = 11)

Delta Airlines is an American airline founded in 1928 and has its headquarters in Atlanta, Georgia, where the company also has its largest hub, the Atlanta Hartsfield-Jackson Airport. With 800,000 employees and a fleet of over 800 aircraft, this airline carries 180 million passengers annually (Delta.com, 2019, accessed on 20 May 2020).

Y = 1.86X₁ − 8.814X₂ + 55.201

Overall, 46.3% of the Delta Airlines share performance Y can be attributed to the development of oil prices and global economic growth (R²). The F-test for the overall model is significant at 0.034; i.e., the hypothesis that there is no influence of the two independent variables on the dependent variable can be rejected (

Table 10. Delta Airlines regression analysis with both variables.

World GDP	1.86 (2.438)	R2	0.463
Oil price	−8.814 (2.841) **	F-Statistic	5.313 **
constant	55.201 (14.180) ***	Significance	0.034

Note: ** Significant at 95% confidence level (p-value < 0.05). *** Highly significant at 95% confidence level (p-value < 0.01). Source: Author.

). The p-value for the single independent variable X₂ is significant (0.015) at a 95% confidence level. And as for the economic growth rate X₁, the p-value is not significant at a 95% confidence level (0.467). No collinearity can be measured between the two independent variables X₁ and X₂.

After the result of the previous analysis that shows that the annual oil price development has a significant influence on the Delta Airlines share (Table 10), a single linear regression analysis—wherein the annual oil price development X₂ is the only independent variable—was carried out (

Table 11. Delta Airlines regression analysis with oil price development.

World GDP		R2	0.488
Oil price	−8.979 (2.766) **	F-Statistic	10.534 **
constant	60.661 (11.954) ***	Significance	0.01

Note: ** Significant at 95% confidence level (p-value < 0.05). *** Highly significant at 95% confidence level (p-value < 0.01). Source: Author.

).

Y = −8.979X₂ + 60.661

In total, 48.8% (R²) of the Delta Airlines share performance Y can be attributed to the annual oil price developments X₂. This influence is statistically significant (p-value = 0.010) (Table 11).

United Airlines: (Observation period: 2006–2017; N = 12)

United Airlines is an American carrier operating from its Chicago, Denver, Houston, Los Angeles, Newark, San Francisco, and Washington D.C. hubs. Together with their regional carrier, United Express, they transported 158 million passengers in 2018 [38].

Y = 4.530X₁ − 9.941X₂ + 64.097

In total, 56.0% of the United Airlines share performance Y can be attributed to the development of oil prices and global economic growth (R²). The F-test for the overall model is significant at 0.010; i.e., the hypothesis that there is no influence of the two independent variables on the dependent variable can be rejected at a 95% confidence level (

Table 12. United Airlines regression analysis with both variables.

World GDP	4.530 (2.386) **	R2	0.56
Oil price	−9.941 (2.923) ***	F-Statistic	8.004 **
constant	64.097 (14.514) ***	Significance	0.01

Note: ** Significant at 95% confidence level (p-value < 0.05). *** Highly significant at 95% confidence level (p-value < 0.01). Source: Author.

). The p-value for the single independent variable X₂ is also very significant (0.008), and as for the economic growth rate X₁, the p-value is not significant at a 95% confidence level (0.090).

No collinearity can be measured between the two independent variables X₁ and X₂.

After the result of the previous analysis that shows that the annual oil price development has a significant influence on United Airlines’ share (Table 12), a single linear regression analysis—wherein the annual oil price development X₁ is the only independent variable—was carried out (

Table 13. United Airlines regression analysis with oil price development.

World GDP		R2	0.446
Oil price	−10.724 (3.275) **	F-Statistic	9.838 **
Constant	77.778 (14.146) ***	Significance	0.011

Note: ** Significant at 95% confidence level (p-value < 0.05). *** Highly significant at 95% confidence level (p-value < 0.01). Source: Author.

).

Y = −10.724X₂ + 77.778

Overall, 44.6% (R²) of the United Airlines share performance Y can be attributed to the annual oil price developments X₂. This influence is statistically significant (p-value = 0.011) (Table 13).

Air Canada: (Observation period: 2006–2017; N = 12)

Air Canada is the flag carrier of Canada, and with their 30,000 employees, they transported 51 million in 2018. In addition to its main hub for international flights in Toronto, Air Canada operates from Montreal, Vancouver, Calgary, and other smaller hubs (Aircanada.com, 2019, accessed on 25 April 2020).

Y = 1.696X₁ − 2.273X₂ + 13.071

Overall, 28.2% of Air Canada’s share price development Y can be attributed to the development of oil prices and global economic growth (R²). The F-test for the overall model is not significant at 0.091 (narrow) (

Table 14. Air Canada regression analysis with both variables.

World GDP	1.696 (1.031)	R2	0.282
Oil price	−2.273 (1.263)	F-Statistic	3.163 **
Constant	13.071 (6.270) **	Significance	0.091

Note: ** Significant at 95% confidence level (p-value < 0.05). Source: Author.

); i.e., the hypothesis that there is no influence of the two independent variables on the dependent variable cannot be rejected at a 95% confidence level. The p-values for the two independent variables, X₁ and X₂, are not significant at a 95% confidence level (0.134 and 0.105, respectively).

No collinearity can be measured between the two independent variables X₁ and X₂.

Cathay Pacific: (Observation period: 1986–2017; N = 32)

Cathay Pacific is Hong Kong’s international airline, founded in 1946. It is registered and based in Hong Kong since 1948. With a fleet of 201 aircraft and approximately 20,000 employees, Cathay Pacific operates global flights to and from this special administrative region of China, making the airliner its flag carrier. It has also helped the Hong Kong International Airport become one of the most important hubs in the world (Cathaypacific.com, 2019, accessed on 25 April 2020).

Y = 0.736X₁ + 1.446X₂ + 6.074

A total of 37.9% of Cathay Pacific’s share performance Y can be attributed to oil price developments and global economic growth (R²). The F-test for the overall model is very significant at 0.000 (

Table 15. Cathay Pacific regression analysis with both variables.

World GDP	0.736 (0.394) **	R2	0.379
Oil price	1.446 0.337) ***	F-Statistic	10.452 ***
Constant	6.074 (1.605) ***	Significance	0

Note: ** Significant at 95% confidence level (p-value < 0.05). *** Highly significant at 95% confidence level (p-value < 0.01). Source: Author.

); i.e., the hypothesis that there is no influence of the two independent variables on the dependent variable can be rejected at a 95% confidence level. The p-value for the single independent variable X₂ is also very significant (0.000). And as for the economic growth rate X₁, the p-value is not significant at a 95% confidence level (almost significant at 0.072).

No collinearity can be measured between the two independent variables X₁ and X₂.

After the result of the previous analysis that shows that the annual oil price development has a significant influence on the Cathay Pacific share (Table 15), a single linear regression analysis was carried out, where the annual oil price development X₂ variable is the only independent variable (

Table 16. Cathay Pacific regression analysis with oil price development.

World GDP		R2	0.327
Oil price	1.401 (0.349) ***	F-Statistic	16.086 ***
Constant	8.366 (1.077) ***	Significance	0

Note: *** Highly significant at 95% confidence level (p-value < 0.01). Source: Author.

).

Y = 1.401X₂ + 8.366

In total, 32.7% (R²) of the Cathay Pacific share performance Y can be attributed to the annual oil price developments X₂. This influence is statistically very significant (p-value = 0.000) (Table 16).

Finnair: (Observation period: 1989–2017; N = 29)

Finnair was founded in 1923 and is majority-owned by Finland. It also operates as a network airline from its hub in Helsinki. Finnair employs 5900 people and operates a fleet of over 60 aircraft (Finnair.com, 2019, accessed on 25 April 2020).

Y = 0.864X₁ + 0.145X₂ + 2.022

Overall, 15.0% of Finnair’s stock price performance Y can be attributed to the development of oil prices and global economic growth (R²). The F-test for the overall model is significant at 0.046, which means that the hypothesis that there is no influence of the two independent variables on the dependent variable can be rejected (

Table 17. Finnair regression analysis with both variables.

World GDP	0.864 (0.333) **	R2	0.15
Oil price	0.145 (0.280)	F-Statistic	3.479 **
constant	2.022 (1.311)	Significance	0.046

Note: ** Significant at 95% confidence level (p-value < 0.05). Source: Author.

). The p-value for the single independent variable X₂ is not significant (0.610), and as for the economic growth rate X₁, the p-value is significant at a 95% confidence level (0.015). No collinearity can be measured between the two independent variables X₁ and X₂.

After having the result of the previous analysis that shows that the annual growth in world GDP has a significant impact on Finnair’s share price (Table 17), a single linear regression analysis—wherein the annual oil price development variable X₁ being the only independent variable—was carried out (

Table 18. Finnair regression analysis with world GDP growth.

World GDP	0.861 (0.328) **	R2	0.174
Oil price		F-Statistic	6.878 **
constant	2.441 (1.017) **	Significance	0.014

Note: ** Significant at 95% confidence level (p-value < 0.05). Source: Author.

).

Y = 0.861X₁ + 2.441

In total, 17.4% (R²) of Finnair’s share performance Y can be attributed to the annual world GDP growth X₁. This influence is statistically significant (p-value = 0.014) (Table 18).

Qantas: (Observation period: 1995–2017; N = 23)

Founded in 1920, Qantas is Australia’s largest airline with over 30,000 employees (Qantas.com. 2019, accessed on 25 April 2020).

Y = 0.186X₁ − 0.109X₂ + 2.766

A total of −1.3% of the Qantas stock performance Y is attributed to oil price developments and global economic growth (R²). The F-test for the overall model is not significant at 0.437 (

Table 19. Qantas regression analysis with both variables.

World GDP	0.186 (0.182)	R2	−0.013
Oil price	−0.109 (0.135)	F-Statistic	0.862
constant	2.766 (0.789) ***	Significance	0.437

Note: *** Highly significant at 95% confidence level (p-value < 0.01). Source: Author.

); i.e., the hypothesis that the two independent variables have no influence on the dependent variable cannot be rejected. The p-value for the single independent variable X₂ is not significant, and the p-value for X₁ is also not significant even at a confidence level of 95% (0.318 and 0.484, respectively). No collinearity can be measured between the two independent variables X₁ and X₂.

SAS: (Observation period: 2001–2017; N = 17)

SAS is the largest Scandinavian network carrier, flying 135 aircraft under its banner. It was formed in 1946 from a merger of the Swedish, Norwegian, and Danish state airlines. SAS focuses its business model primarily on Scandinavian businesses and frequent flyers (SAS website, 2019).

Y = 15.297X₁ − 5.939X₂ + 63.147

In total, −3.9% of the SAS share price development Y can be attributed to the development of oil prices and global economic growth (R²). The F-test for the overall model is not significant at 0.514 (

Table 20. SAS regression analysis with both variables.

World GDP	15.297 (13.875)	R2	−0.039
Oil price	−5.939 (14.341)	F-Statistic	0.698
constant	63.147 (68.542)	Significance	0.514

Source: Author.

); i.e., the hypothesis that the two independent variables have no influence on the dependent variable cannot be rejected. The p-value for the two individual independent variables X₁ and X₂ is not significant at a confidence level of 95% (0.289 and 0.685, respectively). No collinearity can be measured between the two independent variables X₁ and X₂.

Singapore Airlines: (Observation period: 1985–2017; N = 33)

Singapore Airlines is the flag carrier of Singapore and serves as a network carrier to all relevant global hubs from its base in Changi International Airport. With a fleet of 107 aircraft and nearly 15,000 employees, Singapore Airlines has flown over 19 million passengers and has generated sales of USD 11.5 million in 2018 [39].

Y = 0.264X₁ + 1.306X₂ + 5.327

A total of 20.9% of the Singapore Airlines share price performance can be attributed to the development of oil prices and global economic growth (R²). The F-test for the overall model is significant at 0.011 (

Table 21. Singapore Airlines regression analysis with both variables.

World GDP	0.264 (0.473)	R2	0.209
Oil price	1.306 (0.406) ***	F-Statistic	5.227 **
constant	5.327 (1.937) **	Significance	0.011

Note: ** Significant at 95% confidence level (p-value < 0.05). *** Highly significant at 95% confidence level (p-value < 0.01). Source: Author.

); i.e., the hypothesis that there is no influence of the two independent variables on the dependent variable can be rejected at a 95% confidence level. The p-value for the single independent variable X₂ is also significant (0.003). As for the economic growth rate X₁, the p-value is not significant at a confidence level of 95% (0.581).

No collinearity can be measured between the two independent variables X₁ and X₂.

After the result of the previous analysis that shows that the annual oil price development has a significant influence on Singapore Airline’s share (Table 21), a single linear regression analysis—wherein the annual oil price development variable X₂ is the only independent variable—was carried out (

Table 22. Singapore Airlines regression analysis with oil price development.

World GDP		R2	0.227
Oil price	1.291 (0.401) ***	F-Statistic	10.373 ***
constant	6.153 (1.235)	Significance	0.003

Note: *** Highly significant at 95% confidence level (p-value < 0.01). Source: See [21,24].

).

Y = 1.291X₂ + 6.153

Overall, 22.7% (R²) of the Singapore Airlines share performance Y can be attributed to annual oil price development X₂. This influence is statistically very significant (p-value = 0.003) (Table 22).

WestJet: (Observation period: 1999–2017; N = 19)

WestJet is a Canada-based, low-cost carrier established in 1996 with a fleet of three aircraft. Today, WestJet has grown to a fleet of more than 150 aircraft serving more than 100 destinations in North and Central America and the Caribbean, and with more than 13,000 employees, it transports 22 million passengers annually (Westjet.com, 2019, accessed on 25 April 2020).

Y = 0.038X₁ + 1.064X₂ + 11.823

In total, −5.8% of WestJet’s share price performance can be attributed to oil price developments and global economic growth (R²). The F-test for the overall model is not significant at 0.613 (

Table 23. WestJet regression analysis with both variables.

World GDP	0.038 (1.082)	R2	−0.058
Oil price	1.064 (1.061)	F-Statistic	0.505
constant	11.823 (5.269) **	Significance	0.613

Note: ** Significant at 95% confidence level (p-value < 0.05). Source: Author.

); i.e., the hypothesis that the two independent variables have no influence on the dependent variable cannot be rejected. The p-value for the two individual independent variables X₁ and X₂ is not significant at a confidence level of 95% (0.972 and 0.331, respectively). No collinearity can be measured between the two independent variables X₁ and X₂.

3.1.1. Interpretation of Findings

The results for the regression analysis of how airline stocks are influenced by oil price movement and overall economic growth are very uneven. The potentially expected outcome that airline stocks are, at least, as a rule, negatively affected by rising oil prices is not reflected in the results at all. The explanatory power of the regression models is often not very convincing, and more importantly for many airlines, the regression model and the influence of the two single independent variables on airline stock is often not significant at all. However, it is worthwhile to have a closer look at the results and to try to analyse certain patterns in the uneven results.

The regression analysis of how the airline’s stocks are influenced by the two independent variables (annual oil price (WTI) changes adjusted to U.S. consumer prices and annual world economic growth rate) is only statistically significant for Delta Airlines, United Airlines, Cathay Pacific, Finnair, and Singapore Airlines (0.034, 0.010, 0.000, 0.046, and 0.011, respectively, on a 95% confidence level). Relatively close to being statistically significant are the results for Lufthansa, Air France, and Air Canada (0.120, 0.068, and 0.091, respectively, on a 95% confidence level). Analysing the single influence of oil price development on airlines stock (simple linear regression), the results are only statistically significant for Delta Airlines, United Airlines, Cathay Pacific, Singapore Airlines, and Air France. Surprisingly, the directions in which airline stocks are influenced by oil price movements are completely different in all these results. The two major U.S. airlines stocks of Delta and United are strongly negatively affected by higher crude oil prices.

Delta Airlines stock reacts by −8.979 if the oil price goes up by one digit (significant with 0.010 on a 95% confidence level). United Airlines stock goes down by −10.724 if oil goes up by one digit (significant with 0.011 on a 95% confidence level). However, this result becomes completely different when analysing the two East Asian carriers Cathay Pacific and Singapore Airlines. Cathay Pacific stock is, in this regression, positively correlated to oil price development by 1.401 if the oil price goes up by one (statistically very significant with 0.000 on a 95% confidence level). The same applies to Singapore Airlines. Their stock goes up by 1.291 if the oil price goes up by one (statistically very significant with 0.003 on a 95% confidence level). As a European carrier, Air France stock is also statistically and significantly affected by the oil price movement. Its stock goes down by −6.696 for every single digit of oil price that moves up (statistically significant with 0.020 on a 95% confidence level). These results raise the question regarding to what extent the performance of an airline is influenced by changes in the oil price. It seems difficult to establish a link between airline performance and oil price developments. One possible answer would be that there are many more influencing factors than oil prices, which have an impact on airline stocks. For this reason, regression analysis was always carried out with overall economic development (annual world economic growth) as a second variable. The results of how these variable influences airline stocks were not clearer than those of oil price developments, and no regression analysis found collinearity between these two independent variables. It is noteworthy that the regression analysis for the low-cost carriers (Ryanair, Southwest, and to a lesser extent WestJet) was too insignificant for both independent variables. A possible explanation (or hypothesis) for this finding could be that the business model of low-cost carriers is relatively independent of external factors and that the drivers for business performance could usually lie within the business model. In the case of Ryanair, one possible explanation could be that they were the first and most aggressive low-cost carrier on the European market and were able to expand rapidly without being significantly influenced by endogenous factors. Moreover, due to their cost and price structure, low-cost carriers may also be able to gain market share. All these factors could explain the different results, often related to the airline’s business model or territory (airline based in East Asia, legacy carrier based in the U.S., low-cost carrier, etc.).

3.1.2. Testing the Hypotheses

In the following section, an OLS regression is presented for the entire airline sample, which determines how TobinsQ is influenced by the hedging ratio of the two previous years and by the application of several control variables that WERE tested for multicollinearity and contribute to a higher validity of the model (i.e., higher R²) (

Table 24. Result panel data regression on TobinsQ.

	All Airlines	Europe	America	Low−Cost	Legacy	Constant	Selective
Model	Panel Data	Panel Data	Panel Data	Panel Data	Panel Data	Panel Data	Panel Data
R2	0.644	0.803	0.5102	0.7774	0.7779	0.8222	0.3897
F-Statistik	12.19 ***	35.35 ***	6.55 ***	34.23 ***	28.97 ***	52.58 ***	8.3 ***
hedge1-lag1	0.0373 (−0.092)	−0.5381 (0.170) ***	0.1225 (−0.131)	0.0382 (−0.078)	−0.1193 (−0.075)	0.0417 (−0.096)	0.0449 (−0.136)
hedge2-lag2	0.2168 (0.104) **	0.3937 (0.168) **	0.2057 (−0.118) **	0.04426 (0.098) ***	0.1427 (−0.094)	0.3488 (0.125) ***	0.0036 (−0.084)
OpMarg	4.3491 (0.0766) **	6.0541 (0.701) ***	3.9798 (1.517) **	5.0856 (0.541) ***		5.1576 (0.430) ***	1.1233 (−0.645) ***
Opln	−0.0001 (0.000) ***		0.0001 (0.000) **		0.0000 (0.000) ***
NetIn	0.0000 (0) **		0.0000 (0.000) ***		−0.0001 (0) **		0.0000 (0.000) ***
RePa	0.0000 (0.0000) **					0.0000 (0.000) ***
Fleet							0.0001 0
CashRa	0.3811 (0.110) ***		0.3369 (0.114) ***		0.2113 (0.098) **
EquityRa	−0.5148 (0.118) ***		0.4826 (0.143) ***		−0.8166 (0.096) ***		0.3942 (0.123) ***
Constant	1.3867 (0.132) ***	1.0236 (0.079) ***	1.2861 (0.102) ***	0.6945 (0.077) ***	1.2749 (0.073) ***	0.8271 (0.094) ***	1.1555 (0.057) ***

Note: ** Significant at 95% confidence level (p-value < 0.05). *** Highly significant at 95% confidence level (p-value < 0.01). Source: Author.

).

Table 25. Model description.

Model	Description
OpMarg	Operating margin of the airlines.
OpLn	Natural logarithm of the airline’s total operating revenue.
hedge1-lag1	This variable is the lagged value of the hedging ratio (hedge1) from the first previous year. In econometrics, lagged variables are used to account for the effect of past values on current outcomes.
hedge2-lag2	Similar to hedge1-lag1, this variable is the lagged value of the hedging ratio (hedge2) from the second previous year. Using lagged variables can help capture the effect of hedging strategies from earlier periods on the current market value (TobinsQ) of the airline.
NetLn	Similar to OpLn, this is the natural logarithm of the airline’s net income, which represents its total earnings after deducting all expenses.
CashRA	Cash return on assets (CashRA) is a financial ratio that measures how efficiently a company generates operating cash flow from its total assets. It indicates the ability of the company to generate cash from its core business operations relative to its total asset base.
EquityRa	Equity return on assets (EquityRa) is a financial ratio that measures the return on assets funded by shareholders’ equity. It indicates how effectively the company utilises its assets to generate returns for its shareholders.
Constant:	This term represents the intercept or constant term in the regression equation. It accounts for the portion of TobinsQ that is not explained by the independent variables included in the model.

presents the regression models included in the panel data regression analysis (Table 24). It attempts to explain their relevance and potential impact on the market valuation of different airlines.

Tested for no multicollinearity for the control variables, the regression explains nearly 65% of the variance of TobinsQ (R² = 0.644) (Table 24). Observing the effect of the two hedging variables on TobinsQ, which only affects the hedging for the second year (hedge2), there is a significant (95% confidence level) positive effect on TobinsQ, and the coefficient for hedge2 is 0.216 (Table 24).

When using Europe (Lufthansa, Ryanair, and Easyjet) as a dummy variable, both hedging variables become significant, and the model registers a high R², but the result should somehow be interpreted suspiciously, as hedge1 has relatively high multicollinearity (32.02). Therefore, the results should be considered invalid. Only testing for North American airlines (Southwest, Westjet, Air Canada, United Airlines, and Delta Air Lines), no significant influence of the hedging ratio on TobinsQ could be proven.

If only low-cost carriers (Ryanair, Easyjet, Westjet, and Southwest) are considered, the result for hedge2 is highly significant (99% confidence level) and positive for TobinsQ with a coefficient of 0.44. The explanatory power of the regression is also relatively high with an R² of 0.77 (Table 24).

In the study of legacy carriers only (Lufthansa, Air Canada, United Airlines, and Delta Airlines), no significant correlation of the two hedging ratios on TobinsQ could be found.

Another dummy variable was introduced for airlines that are relatively constantly hedged (Lufthansa, Southwest, Ryanair, and Easyjet). In this analysis, hedge2 has a significant (95% confidence level) positive impact on TobinsQ with a coefficient of 0.348.

Airlines with a more selective hedging strategy (Westjet, Air Canada, United Airlines, and Delta Airlines) have no significant influence on TobinsQ.

Taxation on fixed effects and the regression for the entire airline sample hedge2 is slightly significant (p value = 0.069) and positively correlated with TobinsQ (coefficient = 0.278). The variable hedge1 is clearly not significant.

In the regression for European airlines with fixed effects, the variable hedge2 has a highly significant (99% confidence level) positive effect on TobinsQ with a coefficient of 1.054. The significance of the model is relatively weak with an R² of 0.115.

With fixed effects, hedge2 also has significant positive effects on TobinsQ for American airlines with a coefficient of 0.131. The significance of regression analysis is very weak with an R² of 0.0184. Checking for low-cost as the dummy variable, the outcome for hedge2 is again highly significant with a positive coefficient of 0.366. R² of 0.748 suggests the high validity of the explanation. No significant influence of hedge1 or hedge2 on TobinsQ is found for legacy carriers, including fixed effects. Applying constantly hedged as a dummy variable for fixed-effects regression analysis, the variable hedge2 again yields a significant and positive effect on TobinsQ (coefficient = 0.363). R² has a high explanatory power at 0.8156 (Table 24).

The hedging ratios have no significant effect on TobinsQ when checking for selectively hedged airlines with fixed effects.

In summary, it can be said that hedging over a longer period (two years in advance, as the variable hedge2 shows) increases the market value of an airline in relation to its book value (measured according to TobinsQ), or at least, potential investors believe it to be so.

These results were even more significant and clear when the analysis was carried out for low-cost carriers and airlines with a constant hedging strategy. The interpretation of this result could be that airlines that pursue a longer-term and constant hedging strategy are rewarded by higher market expectations (higher TobinsQ). This means that the instrument of fuel hedging is used as a permanent risk management strategy and not as a means of counteracting flowing market trends or future oil price expectations.

3.2. Model 2: Dynamic Capacity Forecasting

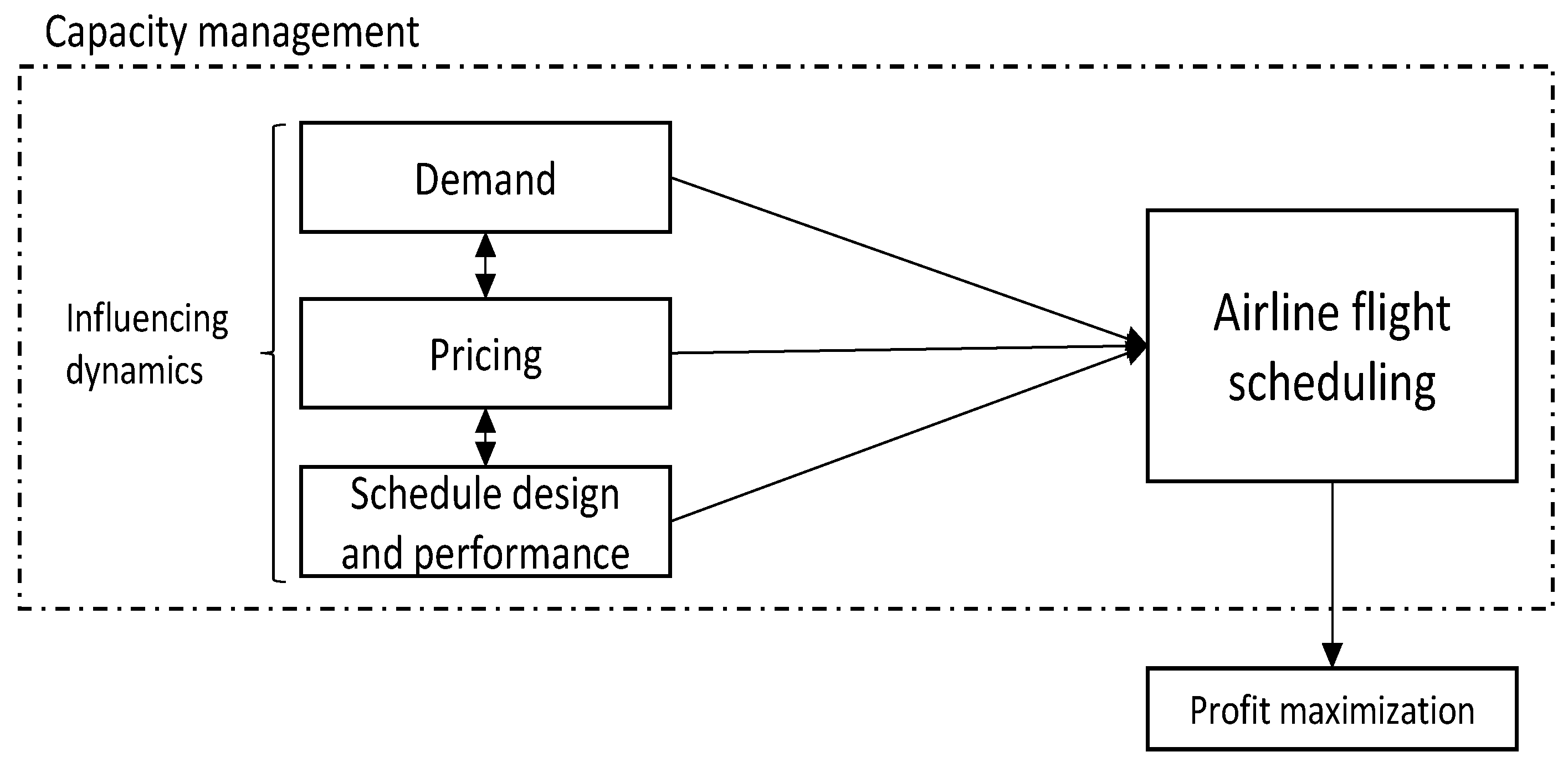
The literature review addresses the dynamics of capacity forecasting that have an influence, involving demand, airfares, and flight schedules. The capacity-forecasting procedure is deconstructed into a dynamic causal feedback loop system, which prioritises the interconnections among the distinct internal and external influencing factors by deriving the hypotheses. Nevertheless, owing to the extent of this study, not all factors that have an influence are encompassed within the framework. Therefore, there exists a possibility for additional exploration with regard to the expansion of the model by incorporating more relevant variables.

Explaining the methodology along the individual steps, it can be stated that the first step considers the identification of the real problem along with critical variables and concepts. Furthermore, it is important to characterise the problem dynamically, as it is essential for the actual model development. The dynamic hypothesis is derived from the second step by investigating the origin of the problem and building linkages between variables in a causal loop diagram, which will be later transformed into a flow diagram. The third step elucidates the definition of the system dynamics model by translating the flow diagram into the stock, rate, and auxiliary equations. Additionally, parameters and behavioural relationships are estimated. The development of the causal loop diagram as well as the flow diagram along with parameter estimations takes place in a computer-simulated model through specific software. Regarding the fourth step of the process, the comparison of the simulated behaviour of the model and the actual behaviour of the system takes place as to validate the model. The fifth and last step considers the interpretation of results as well as evaluating and developing suitable strategies for improvement.

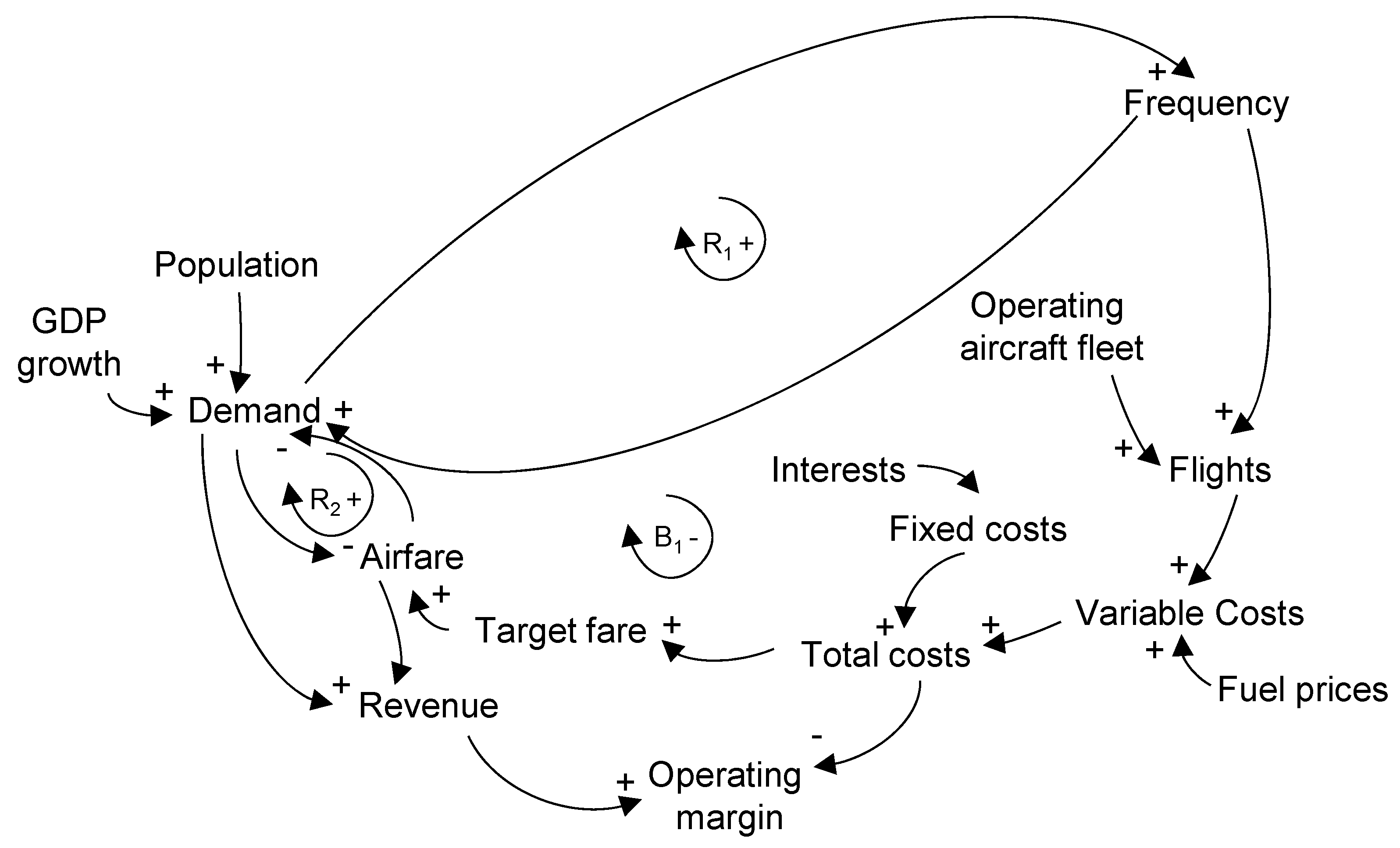
The diagram illustrated in Figure 1 presents a simplified causal feedback loop system associated with the forecasting of airline capacity. The interplay among individual influencing dynamics is depicted using directional arrows (Figure 2). The arrowhead refers to the variable that is being stimulated, while the direction of the relationship signifies the degree to which the parameter is being stimulated. The nature of this association can be described as a causal relationship. A positive polarity denotes that a rise in the output variable results in a corresponding increase in the stimulated variable. With respect to the negative polarity of a relationship, a reduction in the output variable will result in a decrease in the stimulated variable. Furthermore, the interconnectedness of the influencing factors ultimately results in a closed feedback loop.

In Figure 2, three closed feedback loops can be identified. Considering the first closed feedback loop, which is marked as R₁+ within the loop, it describes the inter-causal relationship of demand and frequency of approached routes. As both cause–effect relationships show a positive polarity, the closed feedback loop is characterised as reinforcing, which indicates growth. The second closed feedback loop in Figure 2 is labelled as R₂+ and incorporates the cause–effect relationships of demand and airfare. Both relationships are assessed with a negative polarity. Nevertheless, the polarity of the whole loop is determined by adding the individual relationships. Therefore, in the case of R₂+, the closed feedback loop is considered positive, as the addition of two negative relationships results in a positive loop, and thus, R₂+ is considered a reinforcing loop. The third closed feedback loop, which is marked as B₁-, considers the cause–effect relationship of the main input factors regarding capacity forecasting in Figure 2.

Through the addition of the individual polarities, an overall negative polarity is achieved, which results in a balancing feedback loop. A balancing feedback loop aims to maintain the system stability. There are further cause–effect relationships that stimulate the influencing dynamics. However, these are not considered in the model individually due to the scope and the focus of this study. Nevertheless, these are still involved in the analysis, as they are included in the given dataset.

Given the causal feedback loop diagram in Figure 3, it can already be stated that there is a positive cause–effect relationship of fuel prices, variable costs, total costs, and hence airfare. As fuel price volatility (commodity risk) accounts as the to-be-tested risk factor, the following hypotheses result:

H_1a. 

Commodity risks moderately have a positive effect on costs, hence influencing airfares.

H_1b. 

Commodity risks moderately have a negative effect on costs, hence influencing airfares.

H_1c. 

A strong correlation between risks and airfares has an impact on capacity forecasting.

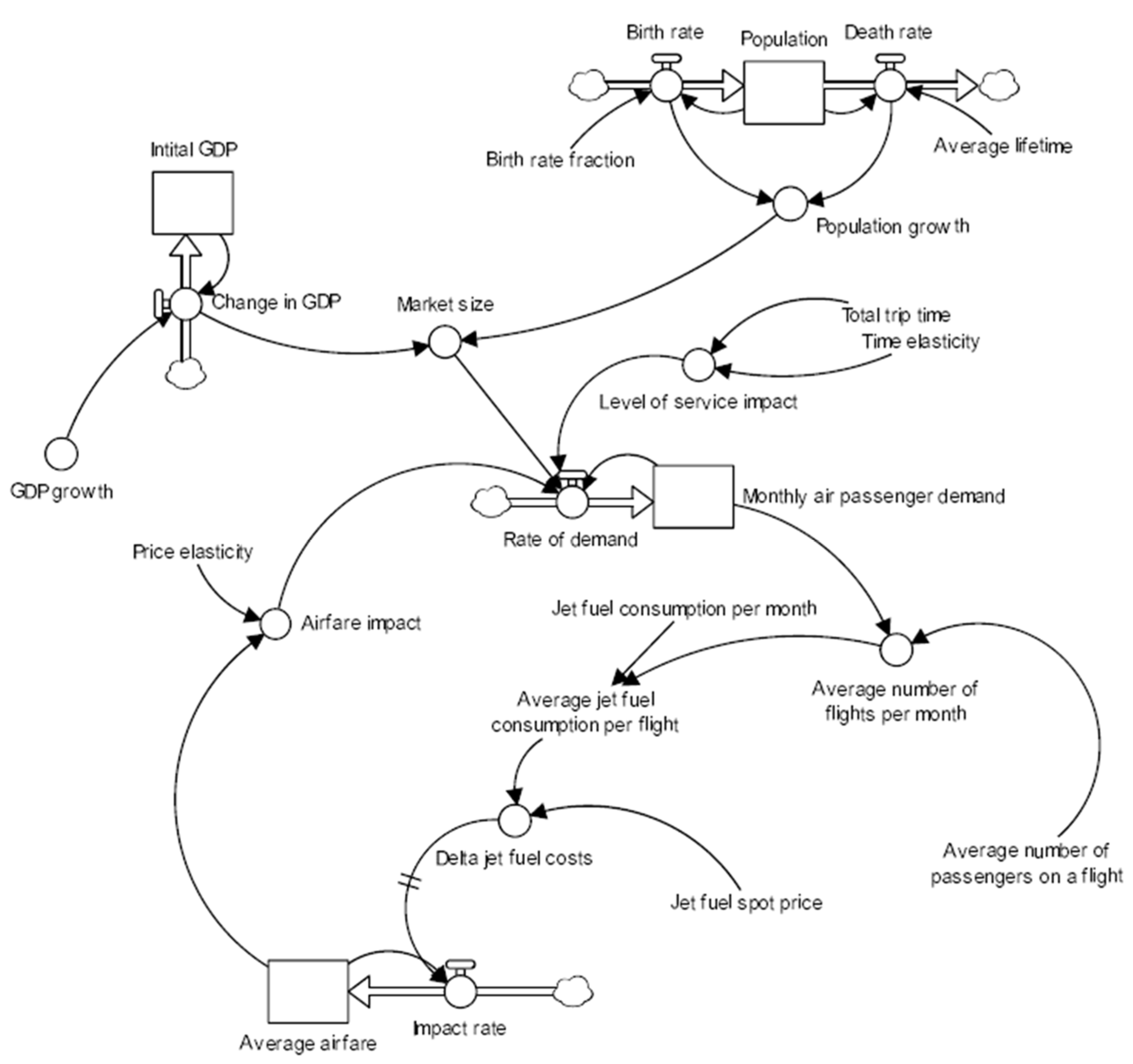
The aforementioned hypotheses were subjected to testing through the employment of the stock and flow diagram, which was derived from the causal feedback loop diagram seen below (Figure 4).

The variables related to market size and service level impact are represented by the growth rate variable, which affects the demand rate in combination with the airfare impact. The rate of demand is used as the input for the stock of monthly air passenger demand (D) over the duration of the model’s operation. The evaluation is conducted via the subsequent mathematical formula.

$${\mathrm{Rate} \mathrm{of} \mathrm{demand}}_{\mathrm{t}} = {\mathrm{D}}_{\mathrm{t}-1} + ({\mathrm{Growth} \mathrm{rate}}_{\mathrm{t}}+{\mathrm{Airfare} \mathrm{impact}}_{\mathrm{t}}) \ast {\mathrm{D}}_{\mathrm{t}}$$

(1)

Equation (1) integrates a specified set of values associated with the monthly mean growth rate of air passenger demand into the growth rate, whereas the airfare impact derives its input parameters from the average airfare of the stock. Moreover, it entails an adjustment of the airfare at a specific point in time, denoted as t.

$${\mathrm{Airfare} \mathrm{impact}}_{\mathrm{t}} = {\mathrm{Airfare}}_{\mathrm{t}}-{ \mathrm{Airfare}}_{\mathrm{t}-1}$$

(2)

Equation (2) represents the average airfare as a variable in the model, which is influenced by the input value for time t1 obtained from the dataset. The calculation of average airfare values is determined by the flow impact rate. The impact rate refers to the proportion of the fluctuation in jet fuel expenditures that is transferred to airfare and, subsequently, to the consumer. The assumption is that other cost factors do not experience comparable volatility; therefore, just the fluctuation in jet fuel expenses is considered to be transferred to the passenger.

The impact rate, which involves cost variations, is influenced by several factors, including the per-gallon spot price of jet fuel (P), the average consumption of jet fuel per flight, and the average seating capacity of an aircraft. Figure 4 displays a connecting arrow that links the airline jet fuel costs and the passing-through rate. This arrow suggests the presence of two horizontal lines, which signify a delay in the impact. Incorporating a time lag into the model is imperative, as the prompt transmission of increased costs is not feasible due to the possibility of cost escalation at a later stage than the actual determination of airfare. The equation that describes the mathematical assessment of the change in jet fuel costs (Δ Jet fuel costs) is as follows:

$$\Delta \mathrm{Jet} \mathrm{fuel} \mathrm{costs} \mathrm{per} \mathrm{seat}=\frac{\left({ \mathrm{P}}_{\mathrm{t}}-{ \mathrm{P}}_{\mathrm{t}-1}\right) \ast \mathrm{Average} \mathrm{jet} \mathrm{fuel} \mathrm{consumption} \mathrm{per} \mathrm{flight}}{\mathrm{Average} \mathrm{number} \mathrm{of} \mathrm{seats}}$$

(3)

$$A\mathrm{verage} \mathrm{jet} \mathrm{fuel} \mathrm{consumption} \mathrm{per} \mathrm{flight}=\frac{\mathrm{Average} \mathrm{jet} \mathrm{fuel} \mathrm{consumption} \mathrm{per} \mathrm{month}}{\mathrm{Average} \mathrm{number} \mathrm{of} \mathrm{flights} \mathrm{per} \mathrm{month}}$$

(4)

The fluctuation in the average airfare depends on the flow impact rate during a given time period t, which is determined by the ratio of the average airfare at that time and the variation in jet fuel prices at a prior time point, t-x, as well as the percentage of pass-through rate. The assessment of the change in jet fuel costs occurs at time t-x due to the consequential effects of delay.

The calculation procedure of the impact rate can be derived from the following mathematical Equation (5):

$${\mathrm{Impact} \mathrm{rate}}_{\mathrm{t}}={\mathrm{Average} \mathrm{airfare}}_{\mathrm{t}}\ast \Delta {\mathrm{Jet} \mathrm{fuel} \mathrm{costs} \mathrm{per} \mathrm{seat}}_{\mathrm{t}-\mathrm{x}}\ast \mathrm{Pass} \mathrm{through} \mathrm{rate}$$

(5)

The calculation of the variable representing the mean monthly frequency of flights involves the correlation between the yearly demand for air travel and the average number of passengers per flight. This value is obtained from the dataset and is expressed mathematically as Equation (6).

$$\mathrm{Average} \mathrm{number} \mathrm{of} \mathrm{flights} \mathrm{per} \mathrm{month}=\frac{\mathrm{Monthly} \mathrm{air} \mathrm{passenger} \mathrm{demand}}{\left(\mathrm{Average} \mathrm{number} \mathrm{of} \mathrm{passengers} \mathrm{in} \mathrm{a} \mathrm{flight}\right)}$$

(6)

A correlation analysis was conducted to determine the statistical significance of the main input variables associated with the relationship between the monthly average jet fuel spot price per gallon (jet fuel spot price p.g. (M)) and the costs of jet fuel per gallon (jet fuel costs p.g.) as well as the quarterly average jet fuel spot price per gallon (jet fuel spot price p.g. (Q)) and the average airfare.

The evaluation involves the utilisation of the covariance, coefficient of correlation, and coefficient of determination to determine the magnitude of the association between two variables. Equation (7) presents the formula for evaluating the covariance of a given sample of data.

$$S_{xy}=\frac{{{\displaystyle \sum }}_{i=1}^N\left(x_i-\overline{x}\right)\ast \left(y_i-\overline{y}\right)}{n-1}$$

(7)

The covariance for a data sample describes mathematically the differences between each independent variable x and each dependent variable y and their mean within the dataset.

The coefficient of correlation is a measure of the strength of the relationship between two variables. It is calculated by dividing the covariance by the standard deviation of the variables. The mathematical representation of the phenomenon is presented in Equation (8), followed by the mathematical derivation of the standard deviation as expressed in Equation (9).

$$r=\frac{S_{xy}}{S_x{S}_y}$$

(8)

$$s_x=\sqrt{s^2{}_x}$$

(9)

The aforementioned method is commonly referred to as Pearson’s correlation coefficient, which assesses the association between variables by establishing upper and lower boundaries. Equation (10) establishes the determination of limits for the variable r, which represents the coefficient of correlation:

$$-1\le r\le 1$$

(10)

The magnitude of the relationship is constrained between −1 and 1 due to the possibility of it being either positive or negative in character. The strength of a relationship is evaluated based on its proximity to the value of 1, indicating a strong relationship, or to the value of 0, indicating a weak relationship. Due to the significant disparity between the upper and lower bounds, the coefficient of correlation is considered imprecise. The coefficient of determination is computed to determine the proportions of the relationship that are explained and unexplained. This provides insight into the degree to which changes in the independent variable account for adjustments in the dependent variable. The quantification of this phenomenon involves the calculation of the square of the correlation coefficient, indicated as r. Moreover, the mathematical expressions for the determination coefficient of a given dataset can be derived using Equation (11).

$$R^2=r^2$$

(11)

The key input parameters represent the jet fuel spot price p.g. (M) and the jet fuel costs as well as the jet fuel spot price p.g. (Q) and the quarterly mean values of the average airfare. The aforementioned delay impact will be incorporated into the correlation analysis. The variable “d” denotes a period of duration measured in months and accounts for a shift in the spot price of jet fuel over time. Thus, the shift can be determined by the correlation coefficient between the mean airfare value at time t and the spot price of jet fuel p.g. (Q) at time t-3. In addition, it is noteworthy that a delay is pertinent not only to the mean airfare but also to the expenses incurred in jet fuel. The results are depicted in

Table 26. Results regression with fixed effects on TobinsQ.

	All Airlines	Europe	America	Low−Cost	Legacy	Constant	Selective
Model	Fixed Effects	Fixed Effects	Fixed Effects	Fixed Effects	Fixed Effects	Fixed Effects	Fixed Effects
R2	0.3942	0.1151	0.0184	0.7494	0.2365	0.8103	0.0185
F-Statistik	8954.49 ***	2612.68 ***	33,49 ***	11,626.74 ***	39,480.28 ***	166.83 ***	7284.66 ***
hedge1-lag1	0.0646 (−0.127)	0.2853 (−0.209)	0.0562 (−0.106)	−0.1208 (−0.246)	−0.0167 (−0.105)	0.1094 (−0.266)	−0.0464 (−0.18)
hedge2-lag2	0.2788 (−0.130) **	1.0547 (0.059) ***	0.1319 (0.036) **	0.3666 (0.055) ***	0.0420 (−0.124)	0.3640 (0.074) **	0.0182 (−0.159)
OpMarg	3.4223 (1.230) **			5.3719 (0.190) ***		5.1708 (0.348) ***
Opln	0.0000 0				0.0000 0
NetIn	0.0000 (0.0000) **		0.0000 (0.000)				0.0000 (0.000) ***
CashRa	−0.3824 (−0.174) **
EquityRa	−0.8833 (0.198) ***		−0.4293 (−0.367)
Constant	1.3677 (0.164) ***	0.8432 (0.170) **	1.3116 (0.079) ***	0.7520 (0.087) ***	1.1455 (0.065) ***	0.7937 (0.131) ***	1.2364 (0.052) ***

Note: ** Significant at 95% confidence level (p-value < 0.05). *** Highly significant at 95% confidence level (p-value < 0.01). Source: Author.

.

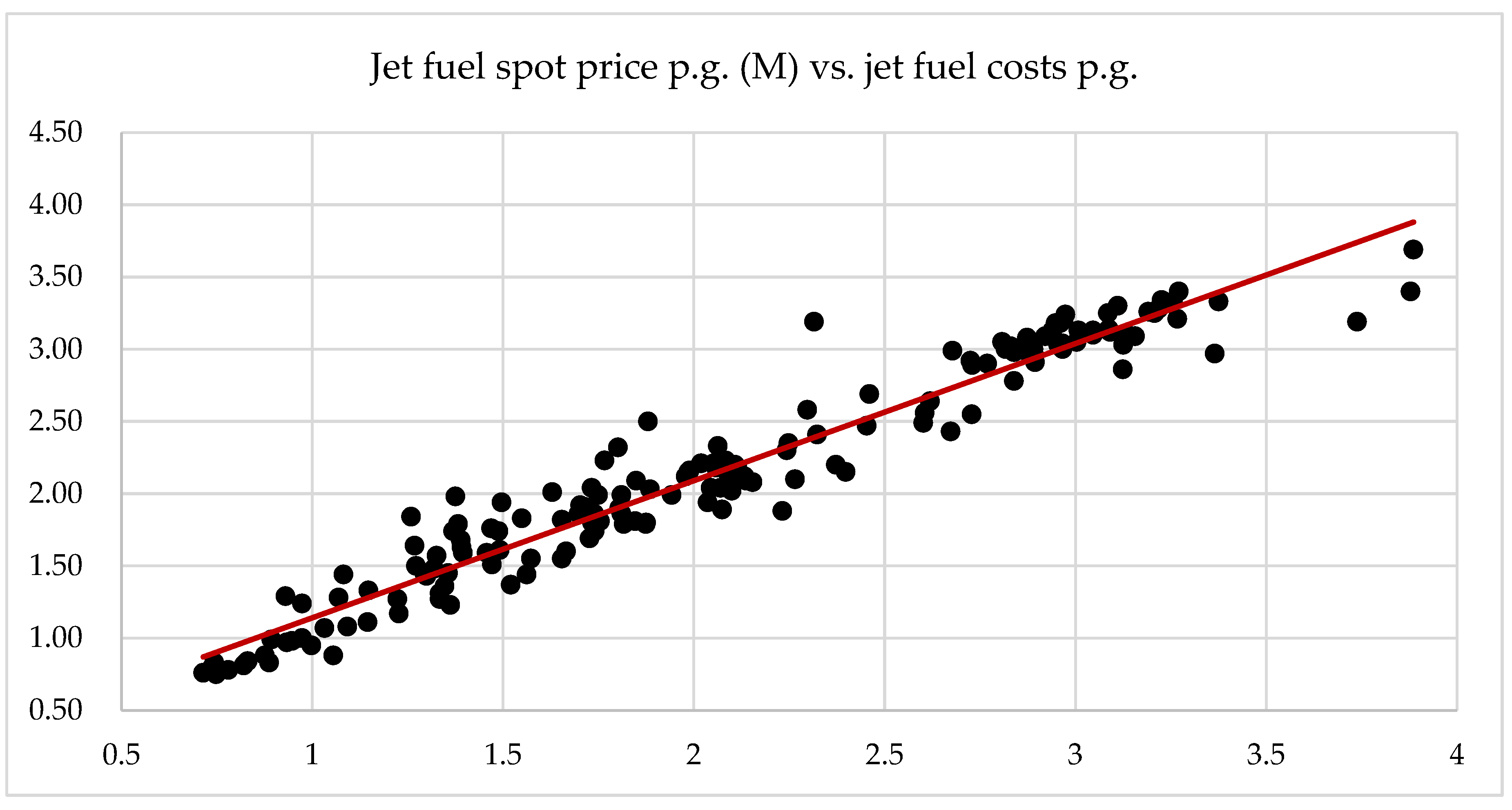
The correlation between the jet fuel spot price p.g. (M) and the jet fuel costs p.g. at d = 0 is highly significant, with 94% of the variance in jet fuel costs p.g. being attributable to the variance in the jet fuel spot price p.g. (M). Figure 5 offers a visual representation in support of the outcome. Thus, it can be assumed that there exists a partial correlation between the jet fuel costs per gallon and the fluctuations in the jet fuel spot price per gallon (M), as both exhibit a similar degree of volatility. Thus, it can be seen that the initial assertion of hypothesis1a is true, while hypothesis1b is rejected.

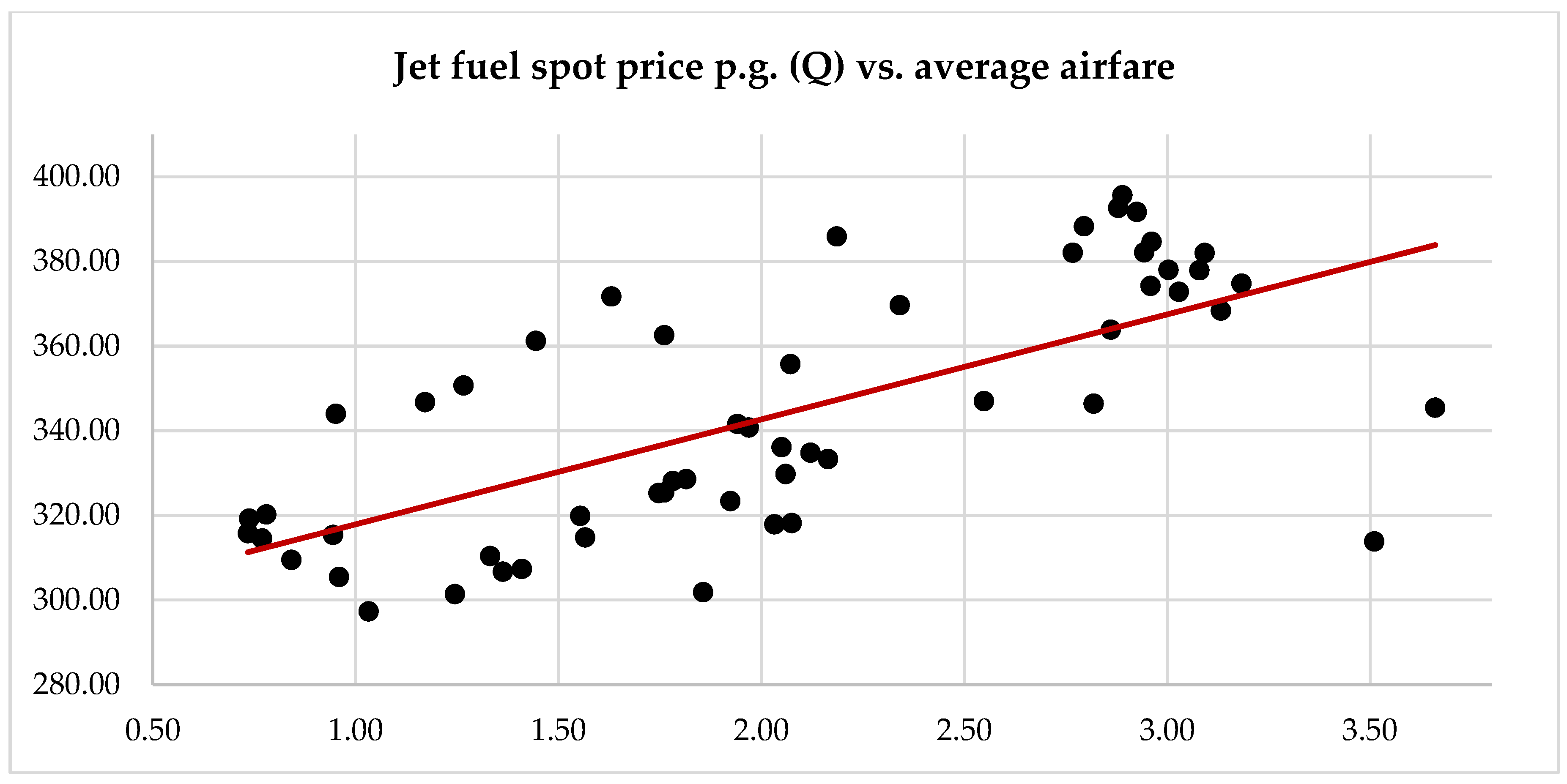
The current study conducted a correlation analysis between the spot price per gallon of jet fuel (Q) and the average airfare (Figure 6). The analysis determined that the most reliable relationship was observed at d = 6, indicating that the impact of the jet fuel spot price at time t on the average airfare was delayed by six months. However, the strength of this relationship is considered to be weak owing to the significant number of outliers and their considerable deviation from the regression line, as depicted in Figure 6. Nevertheless, the hypotheses H_1a and H₂ are thus rejected.

Table 27. Starting Variables for the Testing Procedure of the Stock-Flow Diagram.

Variable	Value
Average airfare at t = 1 (in US-$)	315.77
Monthly air passenger demand at t = 1 (people)	49,757,124.00
Average number of seats on a plane	180
Pass-through rate (in %)	5

Source: Author.

presents the effects of the fluctuation in jet fuel spot price on the mean airfare, along with the essential initial parameters for the model’s execution. The model simulation incorporates a delayed impact of 9 months based on the findings of the correlation analysis. Due to the dataset, which provides monthly data starting from 2003 to 2016, the model runs in total through 168 months.

The examination of the relationship between the jet fuel spot price p.g. (Q) and the average quarterly airfare suggests that there is no significant correlation (

Table 28. The Correlation of the independent variable jet fuel spot price p.g. and the dependent variables jet fuel costs and average airfare.

	Sample Standard Deviation	Sample Covariance	Sample Coefficient of Correlation	Coefficient of Determination
Jet fuel spot price p.g. (M) d = 0	0.784797674
Jet fuel spot price p.g. (Q) d = 0	0.777465358
Jet fuel costs d = 0	0.76770914	0.5847151	0.97048739	0.94184579
Average airfare d = 0	28.99645346	13.216396	0.5862558	0.34369578
Jet fuel spot price p.g. (M) d = 3	0.799174
Jet fuel spot price p.g. (Q) d = 3	0.791104142
Jet fuel costs d = 3	0.76770914	0.575504637	0.93801713	0.879876136
Average airfare d = 3	28.99645346	15.39925295	0.671306901	0.450652955
Jet fuel spot price p.g. (M) d = 6	0.811981982
Jet fuel spot price p.g. (Q) d = 6	0.804338405
Jet fuel costs d = 6	0.76770914	0.521698348	0.836905375	0.700410607
Average airfare d = 6	28.99645346	16.05882491	0.688541426	0.474089296
Jet fuel spot price p.g. (M) d = 9	0.82620344
Jet fuel spot price p.g. (Q) d = 9	0.816916666
Jet fuel costs d = 9	0.76770914	0.474804289	0.748567422	0.560353186
Average airfare d = 9	28.99645346	15.96518357	0.673986624	0.454257969

Source: Author.

). This observation is substantiated by the coefficient of determination, which elucidates that merely 47% of the fluctuations in the average airfare can be attributed to changes in the jet fuel spot price p.g. (Q). This finding underscores the notion that the average quarterly airfare is influenced by a multitude of factors beyond the jet fuel spot price p.g. (Q), indicating a more complex interrelation of variables impacting airfare trends.

Regarding the quantitative evaluation procedure utilising the error rate approach, the subsequent outcomes were computed for the mean monthly airfare, the monthly air passenger demand, and the monthly flight count. These are provided in

Table 29. Quantitative Comparison of actual and simulated Values.

Variable	Actual Value ($\overline{\mathit{A}}$)	Simulated Value ($\overline{\mathit{S}})$	Error Rate
Monthly average airfare	343.7889286	339.770814	0.011687737
Monthly air passenger demand	54.239.240	54.087.453	0.002798481
Monthly number of flights	747.616.46	747.708.13	0.00012261

Source: Author.

.

Interpretation of Findings

The rejection of hypothesis H_1b has already been considered above, as the result of the correlation analysis of the jet fuel costs p.g. and the jet fuel spot price p.g. (M) shows a strong positive correlation, along with 94% of the jet fuel costs p.g. being explained by the jet fuel spot price p.g. (M). The initial segment of hypothesis H_1a has been accepted by correlation analysis. Additionally, based on the outcomes of the stock-flow diagram’s model simulation, it can be entirely accepted. With regards to hypothesis H_1c, it was observed that there is no significant correlation between the jet fuel spot price p.g. (Q) and the average quarterly airfare. This is evident from the coefficient of determination, which indicates that only 47% of the average airfare’s fluctuations can be attributed to the jet fuel spot price p.g. (Q). However, the influence of fluctuations in jet fuel expenses on the mean airfare, as determined by the jet fuel spot price, was validated using the stock-flow diagram. Therefore, the reliability of considering the impact of risk on capacity forecasting is acknowledged. The absence of a notable association between the mean airfare and the spot price of jet fuel could be attributed to the limitations of the dataset employed, which exclusively encompasses quarterly average airfares within the domestic United States market. Consequently, varying outcomes concerning correlation could arise from conducting an analysis utilising an alternative dataset. However, with respect to the investigative methodology and the employed dataset, it is not possible to entirely accept hypothesis H_1c.

4. Conclusions

This paper has made an attempt to elucidate capacity risk management and how airlines use fuel hedging as a buffer against risks of volatility. By employing a two-tier model, it allows the reader to examine how the commodity price of jet fuel influences airline decisions. The framework of system dynamics reveals the interdependent relationships among a diverse range of variables associated with the forecasting of capacity and commodity risk.

The hypotheses were formulated based on a causal feedback loop diagram, which was derived from the concept of system dynamics. Thus, the interrelationships were evaluated by means of connecting arrows and both positive and negative dependencies.

Moreover, the foundational model was expanded through the utilisation of the stock-flow diagram methodology, which enhances the understanding of the interrelationships among capacity prediction factors and commodity risk. The interdependencies in question were expounded upon using mathematical equations and evaluated using a dataset related to the domestic United States airline industry.

The main added value of this paper lies in its comprehensive analysis of the factors influencing airline stocks and capacity forecasting. By examining the impact of oil price movements and economic growth on airline stocks, the study highlights the uneven and sometimes unexpected relationships between these variables. The identification of statistically significant correlations between stock prices and independent variables for certain airlines offers valuable insights for investors and industry stakeholders.

Furthermore, the study delves into the role of hedging strategies on airline market value (TobinsQ) and identifies that longer-term and constant hedging approaches may lead to higher market expectations. This finding has practical implications for airlines’ risk management strategies and provides valuable guidance for industry decision makers.

The dynamic capacity-forecasting model introduced in this paper addresses the intricate interactions among various influencing factors. The incorporation of a time lag in the correlation analysis for jet fuel prices and average airfares provides a nuanced understanding of their relationship, leading to a more accurate simulation model for monthly air passenger demand and flight counts.

4.1. Limitations

Despite its valuable contributions, this study has certain limitations that should be acknowledged. First, the analysis is based on historical data up to 2016, and the dynamic nature of the aviation industry necessitates continuous monitoring and updates. Therefore, future studies should consider incorporating more recent data to capture current market dynamics.

Second, the study’s scope focuses on certain airlines and regions, and variations in industry dynamics across different geographical areas may not be fully captured. Expanding the sample to include a more diverse set of airlines and regions could provide a broader perspective on the studied relationships.

To build on this research, future studies should explore the evolving dynamics of the aviation industry by considering recent data. Examining how airlines have adapted their strategies in response to changing market conditions, technological advancements, and global events (e.g., pandemics and geopolitical shifts) would offer valuable insights into the industry’s resilience and adaptability.

Furthermore, investigating the role of other external factors, such as geopolitical risks, regulatory changes, and environmental concerns, on airline stocks and performance would contribute to a more comprehensive understanding of the industry’s drivers.

4.2. Practical Implications

The findings of this study have several practical implications for airline companies. Firstly, it highlights the importance of considering diverse factors beyond oil price and economic growth when making investment decisions and forecasting capacity. Airlines should adopt a holistic approach to risk management and consider long-term hedging strategies to mitigate market fluctuations effectively.

Secondly, the study emphasises the significance of tailoring strategies to fit the specific characteristics of an airline. Different airlines may be influenced differently by external factors, and understanding these nuances can lead to more informed decision making.

4.3. Proposals and Recommendations for Airlines

Based on the study’s findings, the following proposals and recommendations are offered to airlines:

Diversify Risk Management: Airlines should consider a diversified risk management approach, including hedging strategies, to shield themselves from the impacts of fluctuating oil prices and economic changes. By implementing a mix of long-term and short-term hedges, airlines can manage risks more effectively.

Continuous Monitoring and Adaptation: Airlines should continuously monitor market conditions and industry trends to adapt their strategies promptly. Staying proactive in response to changes can help airlines maintain their competitive edge.

Tailored Forecasting Models: Airlines should develop dynamic capacity-forecasting models that incorporate specific variables and factors relevant to their operations. This customised approach can enhance accuracy and decision making.

4.4. Policy Recommendations for Policymakers

The study’s insights also have implications for policymakers in the aviation sector:

Regulatory Support: Policymakers should consider providing regulatory support to encourage airlines to adopt risk management strategies, including fuel hedging. Promoting stable fuel prices and offering incentives for sustainable practices can foster a resilient industry.

Infrastructure Investment: Policymakers can invest in aviation infrastructure to enhance the industry’s efficiency and capacity. Improving airport facilities and air traffic management can support airlines in managing demand fluctuations.

Research and Development Funding: Policymakers should allocate funding for research and development in aviation technology and alternative fuels. Advancements in these areas can reduce reliance on fossil fuels and improve the industry’s sustainability.

In conclusion, this study contributes to the understanding of the complex relationships within the aviation industry, shedding light on the influences on airline stocks and capacity forecasting. The findings underscore the importance of considering various factors when making investment decisions and offer valuable insights for stakeholders in the aviation sector. To build on this research, continuous monitoring of industry dynamics and the consideration of additional external factors are essential. Airlines should adopt diversified risk management strategies and tailored forecasting models to navigate market fluctuations successfully. Policymakers can support the industry’s resilience by providing regulatory support, investing in infrastructure, and promoting research and development in sustainable aviation practices.