Denoising Stock Price Time Series with Singular Spectrum Analysis for Enhanced Deep Learning Forecasting

Abstract

Aim: Stock price prediction remains a highly challenging task due to the complex and nonlinear nature of financial time series data. While deep learning (DL) has shown promise in capturing these nonlinear patterns, its effectiveness is often hindered by the low signal-to-noise ratio inherent in market data. This study aims to enhance the stock predictive performance and trading outcomes by integrating Singular Spectrum Analysis (SSA) with deep learning models for stock price forecasting and strategy development on the Australian Securities Exchange (ASX)50 index. Method: The proposed framework begins by applying SSA to decompose raw stock price time series into interpretable components, effectively isolating meaningful trends and eliminating noise. The denoised sequences are then used to train a suite of deep learning architectures, including Convolutional Neural Networks (CNN), Long Short-Term Memory (LSTM), and hybrid CNN-LSTM models. These models are evaluated based on their forecasting accuracy and the profitability of the trading strategies derived from their predictions. Results: Experimental results demonstrated that the SSA-DL framework significantly improved the prediction accuracy and trading performance compared to baseline DL models trained on raw data. The best-performing model, SSA-CNN-LSTM, achieved a Sharpe Ratio of 1.88 and a return on investment (ROI) of 67%, indicating robust risk-adjusted returns and effective exploitation of the underlying market conditions. Conclusions: The integration of Singular Spectrum Analysis with deep learning offers a powerful approach to stock price prediction in noisy financial environments. By denoising input data prior to model training, the SSA-DL framework enhanced signal clarity, improved forecast reliability, and enabled the construction of profitable trading strategies. These findings suggested a strong potential for SSA-based preprocessing in financial time series modeling.

1. Introduction

This study investigates how integrating Singular Spectrum Analysis (SSA) with deep learning models can enhance stock price forecasting accuracy and trading performance in noisy financial markets, with a specific focus on the Australian Securities Exchange (ASX)50 index. The Australian equity market offers a valuable yet underexplored environment for testing advanced forecasting models. Unlike major global markets such as in the U.S. or China, the Australian market exhibits distinctive structural characteristics, moderate liquidity, high concentration in resource and financial sectors, and pronounced sensitivity to global commodity price movements. These characteristics introduce complex, non-linear dependencies that pose significant challenges for traditional time-series models. By applying the SSA–DL framework to this unique context, the study extends existing research beyond well-studied markets and demonstrates the model’s robustness and adaptability across diverse economic settings. This focus not only enriches the global literature on financial forecasting but also provides insights applicable to other markets with similar structural profiles.

To date, machine learning algorithms have been extensively applied in stock price prediction studies across global financial markets. Various models, such as Artificial Neural Networks (ANN) and Convolutional Neural Networks (CNN) have demonstrated strong effectiveness in improving predictive accuracy [1]. However, stock market forecasting remains inherently challenging due to the noisy, chaotic, non-stationary, and highly volatile nature of financial time series data [1,2]. To mitigate these challenges, several signal processing and modeling techniques, such as WaveNet and Singular Spectrum Analysis (SSA), have been developed to enhance forecasting reliability [3,4].

While deep learning algorithms integrated with Singular Spectrum Analysis (SSA) have been applied to financial time series in various international markets, there remains a notable gap in the application of these advanced techniques to Australian stock market data. This underrepresentation may stem from competing research interests in other regions, the relatively smaller size of Australian market, and broader global research priorities. To address this gap, the present study focuses on stocks listed on the Australian Securities Exchange (ASX), specifically the ASX50 Index, which comprises the 50 largest and most liquid stocks in the market. In this study, SSA is employed as a preprocessing step to decompose and denoise stock price series, thereby enhancing the quality of inputs for the subsequent deep learning models.

This study makes two key contributions to the existing literature. First, it advances the application of cutting-edge analytics by integrating Singular Spectrum Analysis (SSA) with deep learning architectures, specifically, Convolutional Neural Networks (CNN), Long Short-Term Memory (LSTM), and a hybrid CNN-LSTM model for stock price forecasting. To the best of our knowledge, this integrated approach has not been previously explored in the context of the Australian stock market. Second, while many studies on stock analytics focus primarily on predictive performance, this research extends the scope by developing profitable and reliable trading strategies derived from the model outputs, thereby bridging the gap between predictive modeling and practical financial decision-making.

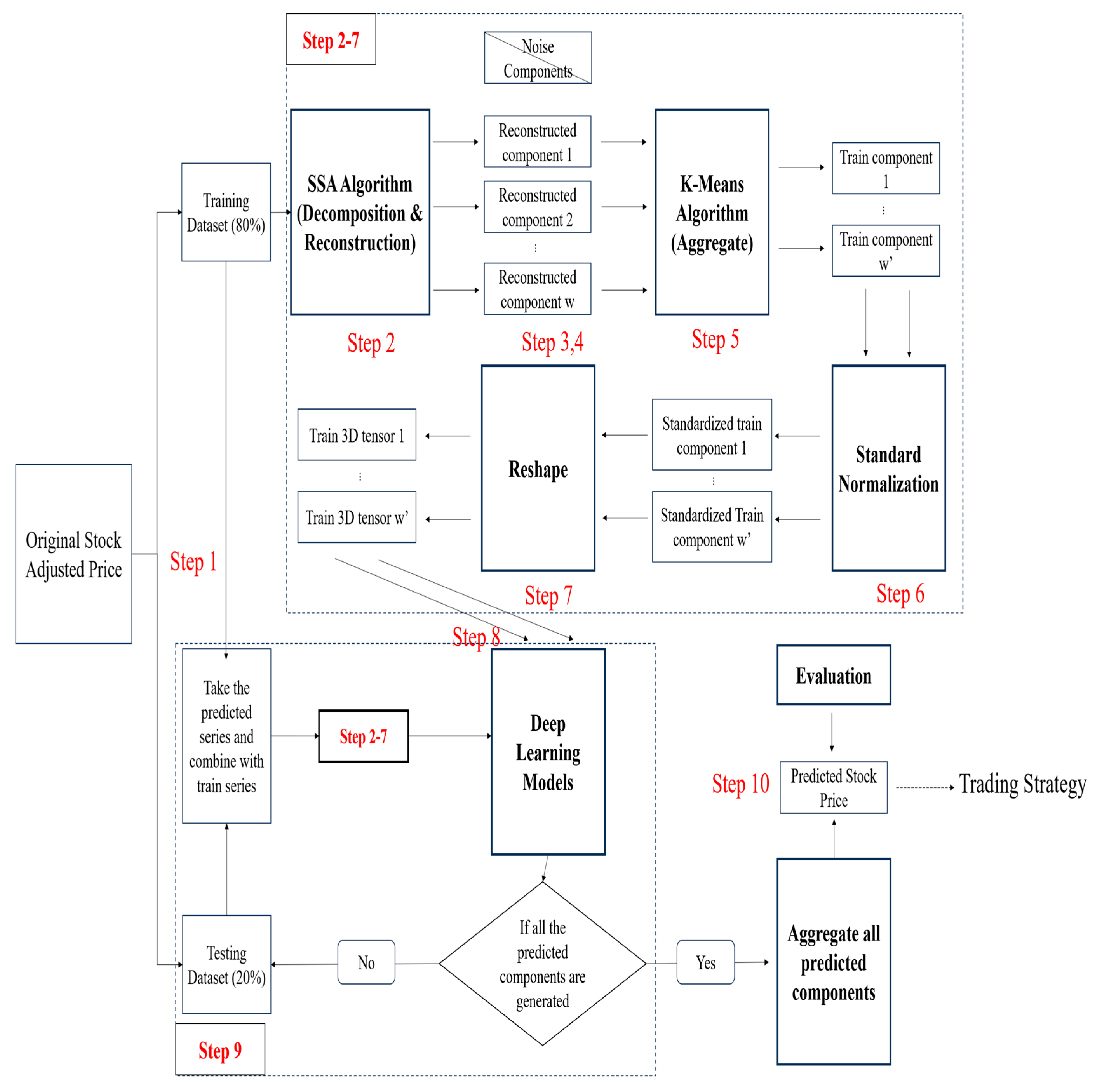
The proposed methodology follows a systematic and structured process. First, the Singular Spectrum Analysis (SSA) algorithm is applied separately to the training and test datasets to generate denoised time series. Second, these denoised training datasets are used to train multiple deep learning models, which are subsequently employed to forecast stock prices during the test period. Third, the predicted stock prices are aggregated and compared with the actual prices to evaluate each model’s forecasting performance. Finally, a trading strategy is developed based on the predicted prices to assess the practical utility and profitability of the proposed SSA-deep learning (SSA-DL) framework.

2. Literature Review

The Efficient Market Hypothesis (EMH), as proposed by Fama, posits that stock prices fully reflect all available market information [5]. According to this theory, when investors attempt to earn excess returns through extensive analysis of historical stock data, the market rapidly incorporates such information, thereby adjusting prices to eliminate any potential profit opportunities. Despite this, many stock investors continue to rely on technical analysis, which seeks to identify empirical patterns and market behaviours based on publicly available price data.

Furthermore, numerous studies have questioned the assumption of market efficiency, presenting evidence that financial markets are not entirely efficient. Recent research, such as that of [2], provides compelling evidence that certain technical trading strategies can still yield significant and consistent returns, particularly in the stock markets of China and South Korea.

Previous research has demonstrated that financial indicators such as the Moving Average (MA) [6], Moving Average Convergence–Divergence (MACD), and the Relative Strength Index (RSI) [7] are statistically significant in predicting stock prices and developing profitable trading strategies. These advantages have been observed across both bull and bear market conditions. Furthermore, various time series models have been employed for stock price forecasting, with notable approaches such as the Autoregressive Moving Average (ARMA) model incorporating past indicators and cyclical factors to enhance predictive accuracy.

Given that many stock price series exhibit non-stationary behavior, often mitigated through differencing, the Autoregressive Integrated Moving Average (ARIMA) model has been widely employed in previous studies. For instance, ref. [8] applied the ARIMA model to forecast stock prices across various sectors of the National Stock Exchange (NSE), reporting high predictive accuracy and robustness as validated through paired t-tests. Another commonly used approach, the Generalized Autoregressive Conditional Heteroskedasticity (GARCH) model, effectively captures stock market volatility dynamics, offering valuable forecasts that serve as key tools for risk management in stock trading strategies [9].

Since the late 20th century, quantitative investing has grown rapidly in popularity, fueled by advances in computing power, analytical methodologies, and the increasing demand from large institutional investors [10]. Today, numerous hedge funds and asset management firms leverage machine learning algorithms for portfolio analysis and management. Given the limitations of traditional time series models in addressing the nonlinear and non-stationary characteristics of financial data, many studies have demonstrated the superior effectiveness of machine learning techniques in predicting stock prices and formulating optimal trading strategies across different markets. Among these methods, supervised learning is the most widely used approach in stock market prediction [11].

Given the nonlinear trends in stock prices and their complex relationships with various influencing factors, several machine learning models employing nonlinear algorithms have been applied to stock price forecasting. These include Support Vector Machines (SVM), Support Vector Regressors (SVR), Random Forests (RF), and Artificial Neural Networks (ANN). For instance, Yu et al. [12] utilized Principal Component Analysis (PCA) to classify stocks based on multiple fundamental indicators and subsequently applied the SVM model for stock selection, achieving superior performance compared to the A-share index on the Shanghai Stock Exchange. Similarly, Kazem et al. [13] proposed an SVR model integrated with a chaotic firefly algorithm and backtested it on three U.S. stock datasets, finding that it outperformed traditional models in terms of Mean Squared Error (MSE) and Mean Absolute Percentage Error (MAPE). Additionally, Polamuri et al. [14] employed RF and Extra Tree Regressor models to forecast stock prices on the S&P 500 index, confirming their superiority over conventional linear models based on Mean Absolute Error (MAE) and MSE metrics.

Vijh et al. [15] constructed technical indicators from stock data and applied Random Forest (RF) and Artificial Neural Network (ANN) models to predict the closing prices of five major U.S. companies. Their results indicated that both RF and ANN achieved strong predictive performance, with ANN generally outperforming RF in terms of Root Mean Square Error (RMSE), Mean Absolute Percentage Error (MAPE), and Mean Bias Error (MBE) metrics [15]. Similarly, Göçken et al. [16] integrated ANN with Genetic Algorithms and Harmony Search to optimize technical indicators and mitigate overfitting and underfitting issues, thereby enhancing stock price prediction accuracy. It is noteworthy that the architecture of the ANN model plays a crucial role in determining predictive performance, as factors such as the number of hidden layers, the number of nodes per layer, the inclusion of dropout layers during training, and other hyperparameter configurations can significantly influence the final outcomes [16].

In recent years, deep learning models with multiple hidden layers, such as Deep Neural Networks (DNN), Convolutional Neural Networks (CNN), and Long Short-Term Memory (LSTM) networks, have proven increasingly effective for stock market forecasting due to their superior ability to extract meaningful features from large datasets [11]. Zhong and Enke [17] employed various DNN models with differing numbers of hidden layers to predict the daily return direction of the SPDR S&P 500 ETF, utilizing Principal Component Analysis (PCA) for feature engineering with 60 financial and economic indicators. While CNNs are well known for their strong performance in image classification task and LSTM networks excel in sequence-to-sequence (Seq2Seq) learning by mitigating the vanishing and exploding gradient problems, both architectures and their hybrid variants have demonstrated superior performance in stock market forecasting due to their ability to learn complex relationships between large sets of input and output variables. Hoseinzade and Haratizadeh [18] further enhanced predictive accuracy by developing fine-tuned 2D-CNNpred and 3D-CNNpred models with kernels designed to mimic image- processing feature extraction, achieving more accurate predictions for six stock index movements compared to a shallow ANN model and a baseline CNN-core model.

Durairaj and Mohan developed two novel chaotic hybrid models, Chaos + CNN and Chaos + CNN + PR, which first reconstructed noisy time series affected by chaotic behaviour and then fit both the original time series and the fitted noise series into CNN models. These hybrid models generally produced more accurate predictions for foreign exchange, commodity, and stock market indices compared to traditional models such as ARIMA, CART, and Random Forest (RF) [19]. However, in certain cases, the hybrid models did not outperform the standalone CNN model, suggesting that the CNN alone could capture intrinsic patterns within the noisy time series. To address the issue of overfitting in stock market forecasting, Beak and Yim proposed a specialized LSTM architecture that combined an overfitting-prevention LSTM module with a prediction LSTM module. This model yielded improved forecasts for the S&P 500 and KOSPI 200 indices [20]. Similarly, Fazeli and Houghten employed an LSTM model enhanced with manually constructed technical indicators to predict the stock trends of major companies such as Apple, Microsoft, Google, and Intel, demonstrating the model’s capability to generate effective buy/sell signals based on historical data [21].

The hybrid CNN-LSTM model has also gained considerable attention in recent research. Livieris et al. utilized a CNN to extract meaningful features and an LSTM to learn the internal representation of time-series data, concluding that the CNN-LSTM model achieved improved predictions for gold market prices [22]. Similarly, Lu et al. incorporated information from the preceding 10 days using a CNN model as input for an LSTM to predict stock prices of the Shanghai Composite Index from 1 July 1991, to 31 August 2020. Their results, compared with models such as MLP, CNN, RNN, and LSTM, demonstrated that the CNN-LSTM combination produced lower RMSE and higher R² values [23]. Song and Choi implemented both CNN-LSTM and GRU-CNN architectures (featuring different configurations of recurrent and convolutional neural networks) for one-step and multi-step predictions of closing prices for the DAX, DOW, and S&P 500 indices [24]. Likewise, Beak applied a CNN-LSTM model using the most recent 20 days of technical data, combined it with Genetic Algorithms (GA) for hyperparameter optimization, and found that this approach achieved higher prediction accuracy for the KOSPI index compared to standalone CNN, LSTM, and CNN-LSTM models [25].

Australia’s equity market is a vital component of global investment management. Research on the Australian market not only uncovers diverse investment opportunities but also enhances market efficiency and transparency. However, most major quantitative studies have primarily focused on regions such as Asia, Europe, North America, and South America, with relatively little attention given to Australia [11]. This gap underscores the need for further exploration of the Australian stock market.

Kwong (2001) conducted a time-series study of selected Australian stocks using neural networks, to uncover patterns between stock movements and influencing factors [26]. Indika Priyadarshani investigated the asymmetry associated with the volatility effects in the Australian stock market compared to other global markets. By modeling covolatility shocks across markets using multivariate generalized autoregressive conditional heteroskedasticity (MGARCH) approach, Priyadarshani demonstrated that the US stock market exerts a dominant influence on the Australian stock market [27]. Hargreaves and Hao applied various machine learning techniques to develop trading strategies based on fundamental factors and concluded that machine-learning-driven equity research can generate superior returns in the Australian market [28]. Hussain et al. employed adaptive neuro-fuzzy inference systems (ANFIS), which integrate the strengths of artificial neural networks (ANNs) and fuzzy systems (FSs) to forecast the performance of Australian stocks listed on the ASX. Their results showed that ANFIS outperformed traditional models such as LSTM and GRU in terms of RMSE, MAE, and MAPE [29].

Due to the random fluctuations or irregularities inherent in both the market and individual stocks, filtering noise becomes a crucial challenge. Singular Spectrum Analysis (SSA) is a non-parametric method that, without many statistical constraints, decomposes a time series into multiple signals, effectively filtering out noise to reconstruct a cleaner time series. This method has a wide range of applications [30]. Wang and Li developed an SSA-NN model that smoothed commodity price series with a threshold of 0.02%, subsequently inputting the results into multiple artificial feed-forward neural networks for prediction purposes [31]. Xiao et al. used SSA to decompose the Shanghai Composite Index into long-term trends, significant event effects, and short-term noise, then applied Support Vector Machines (SVM) to make more accurate predictions than several baseline models [4]. Syukur and Marjuni improved the performance of SSA for forecasting SMS2.SG stock prices over the next 30 days by applying Hadamard transformation to determine the optimal window length for SSA [32].

Fathi et al. employed SSA to decompose price series into various features, which were then used to train non-linear autoregressive neural networks (NARNN) to forecast the performance of 24 stocks in the Egyptian market [33]. While some studies have combined SSA with deep neural networks for forecasting, there has been limited application of this approach to stock markets. For example, Galajit et al. applied SSA to remove noisy components from skewed electrical load series data, using Long Short-Term Memory (LSTM) networks for more accurate electrical load forecasting [34]. Similarly, Wei and Bai integrated SSA with a Convolutional Neural Network (CNN) and a Bidirectional Gated Recurrent Unit (BiGRU) model to forecast non-linear, non-stationary building energy consumption, achieving precise and robust multi-step predictions compared to the individual models [35].

Previous studies have demonstrated the effectiveness of combining Singular Spectrum Analysis (SSA) with deep learning for load and energy forecasting. However, its application in financial markets remains limited. This study advances existing work by extending the SSA–DL framework to sector-level equity forecasting and comparing CNN, LSTM, and CNN–LSTM architectures, each optimized for sector-specific temporal patterns. This approach provides a novel contribution by evaluating the robustness and adaptability of SSA–DL models in complex financial environments.

Existing studies on stock price forecasting have explored a range of traditional and modern techniques, from statistical models such as ARIMA and GARCH to machine learning and deep learning architectures including Support Vector Machines (SVM), Convolutional Neural Networks (CNN), and Long Short-Term Memory (LSTM) networks. While these methods have achieved notable success in various markets, several limitations persist.

First, most deep learning models struggle with the noisy and non-stationary nature of financial time series, often resulting in overfitting and unstable forecasts. Data decomposition methods, such as Empirical Mode Decomposition (EMD) and Wavelet Transforms, have been introduced to address this issue; however, their parameter sensitivity and mode-mixing problems limit their effectiveness. In contrast, Singular Spectrum Analysis (SSA) has shown superior performance in denoising and extracting meaningful patterns from complex signals, yet its integration with deep learning models for stock market forecasting remains scarce [31,32,33,34,35].

Second, the Australian stock market (ASX), despite being one of the most advanced and resource-rich markets globally, has received relatively little attention in data-driven forecasting research compared to the U.S., European, and Asian markets [11,26,27,28,29]. Consequently, there is a pressing need to develop robust forecasting frameworks tailored to the ASX context that can provide both accurate predictions and actionable trading insights.

Finally, existing research tends to focus predominantly on forecasting accuracy metrics, such as MSE or RMSE, without translating predictive results into real-world trading performance. This disconnects between model accuracy and financial utility limits the practical application of predictive models in investment decision-making.

These gaps highlight the opportunity to design a hybrid forecasting and trading framework that integrates advanced signal decomposition, deep learning, and practical trading evaluation, especially in the underexplored ASX market.

3. Contributions

To address these gaps, this study proposes a hybrid Singular Spectrum Analysis–Deep Learning (SSA–DL) framework that integrates Singular Spectrum Analysis (SSA) with Convolutional Neural Networks (CNN), Long Short-Term Memory (LSTM), and a hybrid SSA–CNN–LSTM model to forecast stock prices of companies listed on the ASX50 index. The performance of these models is further evaluated through a back tested trading strategy, linking predictive modeling with investment applicability.

First, stocks from the ASX50 are grouped into three subgroups based on their industrial sectors, and the closing price series of all stocks are decomposed into multiple signals using SSA, with window lengths and criteria optimized for each subgroup. Second, the filtered and denoised signals are used as inputs for deep neural networks to produce rolling forecasts of each signal. These individual forecasts are aggregated into overall stock price predictions, which are evaluated using standard forecasting metrics such as Mean Squared Error (MSE) and Mean Absolute Error (MAE). Finally, a trading strategy based on sector-level stock price forecasts is designed and back tested to assess real-world profitability and robustness.

The key contributions of this research are as follows:

• Novel methodological integration of SSA and deep learning for financial forecasting:

This study introduces a hybrid SSA–DL framework that combines SSA’s noise-reduction capabilities with the pattern recognition power of deep learning architectures (CNN, LSTM, and CNN–LSTM). While SSA has been previously applied to non-financial domains such as energy and commodity forecasting [31,32,33,34,35], its integration with deep learning for stock market prediction—particularly within the Australian context—remains largely unexplored. This approach demonstrates enhanced forecasting accuracy compared to traditional deep learning models trained on raw, noisy data.

2.

Empirical advancement in modeling the Australian stock market:

The study provides one of the first comprehensive deep learning–based analyses of the Australian Securities Exchange (ASX), addressing the lack of research attention to this market [11,26,27,28,29]. By focusing on the ASX50 index, this research offers empirical insights into market dynamics and presents a benchmark for future studies investigating Australian equity behavior using advanced data-driven methods.

3.

Bridging predictive modeling and actionable trading strategies:

Unlike most prior research, which primarily emphasizes predictive accuracy, this study evaluates model performance in terms of real-world trading outcomes. A portfolio-level trading strategy is developed based on the model’s stock price forecasts, and its performance is assessed using profitability metrics such as return on investment (ROI) and Sharpe Ratio. This integration of forecasting and trading evaluation enhances the practical relevance of the proposed models for investors and portfolio managers.

4. Research Methodologies

4.1. Singular Spectrum Analysis (SSA)

Singular Spectrum Analysis (SSA) is a non-parametric method used to analyze time series data, allowing the detection of underlying patterns, trends, and noise [4,30]. The SSA process can be divided into two main stages: decomposition and reconstruction.

• Decomposition: This step involves applying Singular Value Decomposition (SVD) to the trajectory matrix, which helps in breaking down the time series into components that capture its underlying structure.
• Reconstruction: The second stage involves grouping the obtained components and performing anti-diagonal averaging to reconstruct the time series while filtering out noise [33,36,37,38].

Further details on the methodology, including proofs and additional insights, can be found in [36,39].

Step 1: Decomposition Embedding: The first stage of decomposition is to transform the 1-D price series $S=\left[s_1,s_2,s_3,\dots ,s_{N-1},s_N\right]$ into a trajectory matrix, which is composed of various lagged price series created based on the predetermined window length L. The trajectory matrix X is listed below:

$$\mathit{X}=\left[\begin{array}{ccccc}{s}_1& s_2& s_3& \dots & s_K\\ s_2& s_3& s_4& \dots & s_{K+1}\\ s_3& s_4& s_5& \dots & s_{K+2}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ s_L& s_{L+1}& s_{L+2}& \dots & s_N\end{array}\right]\in {\mathit{R}}^{L\times K}$$

where each of the column vector is the corresponding subseries with length L, and $K=N-L+1$.

Singular Value Decomposition, SVD: The next stage is to perform SVD to the trajectory matrix $\mathit{X}$, and we have

$$\mathit{X}=\mathit{U}\mathit{\Sigma }{\mathit{V}}^T$$

where ${\mathit{U}\in \mathit{R}}^{L\times L},\mathit{\Sigma }{\in \mathit{R}}^{L\times K}{,\mathit{V}\in \mathit{R}}^{K\times K}.$

Further, $\mathit{X}$ can be rewritten into

$$\begin{gathered} \mathit{X}=\sum _{i=1}^r{\sigma }_i{\mathit{u}}_i{\mathit{v}}_i^T \\ ={\mathit{X}}_1+{\mathit{X}}_2+\dots +{\mathit{X}}_{\mathit{r}}, \end{gathered}$$

where $r=rank\left(\mathit{X}\right),$ and ${\sigma }_1, {\sigma }_2, \dots , {\sigma }_r$ are the singular values of $\mathit{X}{\mathit{X}}^{\mathit{T}}$ arranged in descending order.

Step 2: Reconstruction Grouping: The grouping stage is to categorize the obtained r-series of X into m disjoint subsets, and series in each subset are summed up. Let $I=\left\{I_1, I_2, \dots ,I_m\right\}(m<r)$, which are the indices of the categorized new subsets. Then, $\mathit{X}$ can be rewritten into:

$$\mathit{X}={\mathit{X}}_{{\mathit{I}}_1}+{\mathit{X}}_{{\mathit{I}}_2}+\dots +{\mathit{X}}_{{\mathit{I}}_{\mathit{m}}}$$

And the contribution of each term is according to its eigenvalues ${\displaystyle \frac{\sum _{i\in I_k}{\lambda }_i}{{\sum }_{i=1}^r{\lambda }_i}}, k\in {\displaystyle (0,m)}$, and the eigenvalues have the correlation with the singular values that ${\sigma }_r=\sqrt{{\lambda }_r}$. In this stage, according to some prespecified criterion such as whether certain numbers of the r-series of X are included in the newly grouped series, which is named by smoothing threshold [31], or whether the increment of singular entropy $∆E$ reaches an asymptotic value [40], $\mathit{X}$ can be partitioned into ${\mathit{X}}_{\mathit{i}\mathit{n}\mathit{f}\mathit{o}\mathit{r}\mathit{m}\mathit{a}\mathit{t}\mathit{i}\mathit{o}\mathit{n}}$ and ${\mathit{X}}_{\mathit{n}\mathit{o}\mathit{i}\mathit{s}\mathit{e}}$, then the noise term can be filtered out. The formula of the singular entropy due to eigentriple $i$ is shown below:

$$∆E=-\left({\displaystyle \frac{{\lambda }_i}{{\sum }_{i=1}^r{\lambda }_i}}\right)log\left({\displaystyle \frac{{\lambda }_i}{{\sum }_{i=1}^r{\lambda }_i}}\right)$$

And we will obtain ${\mathit{X}}_{\mathit{i}\mathit{n}\mathit{f}\mathit{o}\mathit{r}\mathit{m}\mathit{a}\mathit{t}\mathit{i}\mathit{o}\mathit{n}}={\mathit{X}}_{{\mathit{I}}_1}+{\mathit{X}}_{{\mathit{I}}_2}+\dots +{\mathit{X}}_{{\mathit{I}}_{{\mathit{m}}^{\prime }}},m^{\prime }<m$.

Anti-diagonal Averaging: this method is performed to reconstruct the denoised time series based on all the subseries of ${\mathit{X}}_{\mathit{i}\mathit{n}\mathit{f}\mathit{o}\mathit{r}\mathit{m}\mathit{a}\mathit{t}\mathit{i}\mathit{o}\mathit{n}}$. The procedure is performed by the following calculation:

$$\stackrel{~}{{\mathit{X}}_{{\mathit{I}}_{\mathit{k}}}}=\{\begin{array}{c}{\displaystyle \frac{1}{k}}\sum _{m=1}^k{\mathit{X}}_{{{\mathit{I}}_{\mathit{k}}}_{\mathit{m},\mathit{k}-\mathit{m}+1}}, 1\le k<L^{\ast }=min\left\{L,K\right\},\\ {\displaystyle \frac{1}{L^{\ast }}}\sum _{m=1}^{L^{\ast }}{\mathit{X}}_{{{\mathit{I}}_{\mathit{k}}}_{\mathit{m},\mathit{k}-\mathit{m}+1}}, L^{\ast }\le k<K^{\ast }=max\left\{L,K\right\},\\ {\displaystyle \frac{1}{N-k+1}}\sum _{m=k-K^{\ast }+1}^{N-K^{\ast }+1}{\mathit{X}}_{{{\mathit{I}}_{\mathit{k}}}_{\mathit{m},\mathit{k}-\mathit{m}+1}}, K^{\ast }\le k\le N.\end{array}$$

where ${\mathit{X}}_{{{\mathit{I}}_{\mathit{k}}}_{\mathit{i},\mathit{j}}}$ represents of $\left(i,j\right)$ element of ${\mathit{X}}_{{\mathit{I}}_{\mathit{k}}}$.

After performing anti-diagonal averaging to all series in $\{{\mathit{X}}_{{\mathit{I}}_1},{\mathit{X}}_{{\mathit{I}}_2},\dots ,{\mathit{X}}_{{\mathit{I}}_{{\mathit{m}}^{\prime }}}\}$, each of the obtained series has length of $N=L+K-1$, and the final reconstructed denoised series is:

$$\tilde{\mathit{X}}=\sum _{i=k}^{m^{\prime }}\stackrel{~}{{\mathit{X}}_{{\mathit{I}}_{\mathit{k}}}}$$

4.2. Convolutional Neural Network (CNN)

Convolutional Neural Networks (CNNs) are among the most popular deep learning algorithms, particularly renowned for their robustness in image processing tasks. They are capable of automatically extracting important, high-level features from datasets. Recently, CNNs have also found wide applications in stock price prediction tasks.

A typical CNN consists of multiple layers, including Convolutional Layers, Pooling Layers, Dropout Layers, and Fully Connected Layers. Here is how each layer contributes to the model:

• Time Series Data Transformation: Initially, the time series stock price data is transformed into a 3D tensor with the shape (samples, timesteps, features), making it compatible with CNNs.
• Convolutional Layer: The Convolutional Layer uses its kernel (filter) to capture patterns in the lagged series data. This process applies filters to the data to detect relevant features, while activation functions introduce non-linearity between the outputs of different neurons.
• Pooling Layer: The Pooling Layer helps in summarizing the essential features extracted by the Convolutional Layer. It performs down-sampling, reducing the dimensionality of the data while retaining important information.
• Dropout Layer: Dropout is applied to randomly “turn off” certain neurons during training. This regularization technique introduces random noise into the learning process, helping to mitigate the risk of overfitting and ensuring better generalization.
• Fully Connected Layer: After flattening the output from the convolutional and pooling layers into a 1-dimensional vector, the Fully Connected Layer connects all input information from previous layers. This layer is responsible for generating the final output, which is used for prediction or evaluation.

4.3. Long Short-Term Memory (LSTM)

In the realm of neural networks, recurrent models distinguish themselves from Convolutional Neural Networks (CNNs) by employing a recursive approach that propagates hidden state information forward through time. This mechanism allows recurrent models to retain and enhance their knowledge, improving predictions as they process more data over time.

A prominent type of recurrent model is the Long Short-Term Memory (LSTM), designed to address key challenges that traditional Recurrent Neural Networks (RNNs) face, such as the vanishing gradient and exploding gradient problems. LSTMs incorporate a unique mechanism to control how information is retained or discarded across time-steps, allowing them to maintain long-range dependencies in sequential data, which is crucial for time-series analysis.

The LSTM’s core advantage lies in its gates: the input gate, output gate, and forget gate, which are implemented using sigmoid activation functions and element-wise multiplication operations. These gates regulate what information should be remembered or forgotten as the model processes the sequence. This selective memory mechanism makes LSTMs particularly well-suited for tasks such as speech recognition, natural language processing, and financial time-series prediction.

Training an LSTM involves Backpropagation Through Time (BPTT) and the use of gradient descent optimization techniques. These methods enable the model to update its internal weights progressively based on the errors in its predictions, ensuring the model improves its performance over time.

Figure 1 illustrates the detailed structure and functioning of an LSTM model.

Inside the LSTM model, ${\mathit{X}}_{\mathit{t}}$ represents the input information at time $\mathit{t}$, ${\mathit{H}}_{\mathit{t}}$ represents the values in the hidden state at time $\mathit{t}$, and the operators inside the circles are pointwise operators. Initially, the Forget Gate ${\mathit{F}}_{\mathit{t}}$ is to determine what information to forget by the effect of sigmoid activation function.

$$F_t=\sigma \left(W_f\left[H_{t-1},X_t\right]+b_f\right)$$

The next step is to decide what new values to be stored in the Memory Cell, where the Input Gate decides the values to update, and tanh is applied to get the Candidate Memory Cell.

$$I_t=\sigma \left(W_i\left[H_{t-1},X_t\right]+b_i\right)$$

$$\widetilde{C_t}=tanh\left(W_C\left[H_{t-1},X_t\right]+b_c\right)$$

Then the memory cell is updated based on the three prepared functions above.

$$C_t=F_t·C_{t-1}+I_t·\widetilde{C_t}$$

Finally, the Output Gate generates the value from the updated memory cell with the information provided by sigmoid activation function.

$$O_t=\sigma \left(W_o\left[H_{t-1},X_t\right]+b_o\right)$$

$$H_t=O_t\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(C_t\right)$$

Inside all the functions above, $\mathit{W}$ and $\mathit{b}$ represents the weight matrix and bias term, respectively, and they are to be optimized during the backpropagation.

4.4. CNN-LSTM

The CNN-LSTM model is a powerful hybrid deep learning framework that integrates Convolutional Neural Networks (CNNs) with Long Short-Term Memory (LSTM) networks. This model is designed to process sequential data effectively by combining the strengths of both architectures.

• CNNs are used to automatically extract hierarchical and spatial features from the input data. These networks are particularly effective in identifying patterns and key features, such as local dependencies within the data, which are crucial for tasks like image processing and time-series feature extraction.
• LSTM networks, on the other hand, are designed to capture long-range dependencies and temporal relationships within sequential data. LSTMs can learn the context and sequence over time, making them ideal for handling sequential data where previous states influence future ones, such as in time-series forecasting or natural language processing.

By combining CNNs as feature extractors and LSTMs for sequence modeling, the CNN-LSTM model can efficiently process complex data, retain temporal information, and generate more accurate predictions. This hybrid structure allows the model to leverage the strength of CNNs for feature extraction and the power of LSTMs for capturing sequential patterns, making it highly suitable for tasks involving both spatial and temporal data.

5. Experiment Design

5.1. Dataset Description

The ASX50 stock list was sourced from the Market Index website [41] and downloaded from Yahoo Finance [42]. The dataset includes stock data spanning from 12 April 2018, to 31 March 2023, covering a total of 47 companies with consistent trading records and no significant restructuring or delisting during this period. Using the Company Profile information from Yahoo Finance, these 47 companies are divided into three groups based on their respective industrial sectors. Companies within each sector share the same fine-tuned hyperparameters due to the sectoral similarities.

Each deep learning model (CNN, LSTM, and CNN-LSTM) was implemented and fine-tuned separately for each sector group to capture sector-specific temporal and spatial patterns in the data. The CNN architecture consisted of two convolutional layers (kernel size = 3, stride = 1) followed by a max-pooling layer and two fully connected layers. The LSTM model included two LSTM layers (64 and 32 units) with dropout regularization (rate = 0.2). The hybrid CNN-LSTM combined the convolutional layers for feature extraction with an LSTM layer for temporal sequence learning. Model optimization employed the Adam optimizer with an initial learning rate of 0.001, and training was performed with a batch size of 32 for up to 100 epochs using early stopping based on validation loss. Hyperparameters were fine-tuned separately for each sector group using a grid search approach, selecting the configuration that minimized the mean squared error on the validation set.

The chosen CNN configuration emphasizes local temporal feature extraction with an appropriate receptive field to capture short-term price dynamics without excessive model complexity. The LSTM design focuses on preserving sequential dependencies and long-term temporal memory, which is essential for financial time-series prediction. The hybrid CNN-LSTM architecture leverages both short-term pattern extraction and long-term dependency modeling, a structure widely supported in existing financial forecasting literature.

The number of layers, hidden units, kernel sizes, and optimizer settings were determined through preliminary experiments and guided by commonly accepted best practices in deep learning for financial series. These choices balance predictive performance against computational efficiency and overfitting risk. Optimizers were selected based on empirical stability and convergence performance in our datasets.

For two companies that had only one missing value on 29 March 2023, the missing data points were filled using the previous day’s data. To ensure accurate forecasting and account for factors like dividend payments that can distort true stock values, only the adjusted close price series are used. Other data such as Open, High, and Low prices are not considered in the SSA process.

Table 1. Stock Grouping Detail.

Group	Sector	Company Name	Company Code on Yahoo Finance
Industrial and Infrastructure Sectors	Basic Materials	BHP Group Limited	BHP.AX
	Basic Materials	Fortescue Metals Group Limited	FMG.AX
	Basic Materials	IGO Limited	IGO.AX
	Basic Materials	James Hardie Industries plc	JHX.AX
	Basic Materials	Mineral Resources Limited	MIN.AX
	Basic Materials	Newcrest Mining Limited	NCM.AX
	Basic Materials	Northern Star Resources Limited	NST.AX
	Basic Materials	Pilbara Minerals Limited	PLS.AX
	Basic Materials	Rio Tinto Group	RIO.AX
	Basic Materials	South32 Limited	S32.AX
	Energy	Origin Energy Limited	ORG.AX
	Energy	Washington H. Soul Pattinson and Company Limited	SOL.AX
	Energy	Santos Limited	STO.AX
	Energy	Woodside Energy Group Ltd.	WDS.AX
	Industrials	Auckland International Airport Limited	AIA.AX
	Industrials	Brambles Limited	BXB.AX
	Industrials	Qantas Airways Limited	QAN.AX
	Industrials	Reece Limited	REH.AX
	Industrials	Transurban Group	TCL.AX
Consumer and Service Sectors	Communication Services	REA Group Limited	REA.AX
	Communication Services	Telstra Group Limited	TLS.AX
	Communication Services	TPG Telecom Limited	TPG.AX
	Consumer Cyclical	Aristocrat Leisure Limited	ALL.AX
	Consumer Cyclical	The Lottery Corporation Limited	TLC.AX
	Consumer Cyclical	Wesfarmers Limited	WES.AX
	Consumer Defensive	Coles Group Limited	COL.AX
	Consumer Defensive	Endeavour Group Limited	EDV.AX
	Consumer Defensive	Woolworths Group Limited	WOW.AX
Financial, Healthcare, Technology, and Utilities Sectors	Financial Services	ANZ Group Holdings Limited	ANZ.AX
	Financial Services	ASX Limited	ASX.AX
	Financial Services	Commonwealth Bank of Australia	CBA.AX
	Financial Services	Computershare Limited	CPU.AX
	Financial Services	Insurance Australia Group Limited	IAG.AX
	Financial Services	Macquarie Group Limited	MQG.AX
	Financial Services	National Australia Bank Limited	NAB.AX
	Financial Services	QBE Insurance Group Limited	QBE.AX
	Financial Services	Suncorp Group Limited	SUN.AX
	Financial Services	Westpac Banking Corporation	WBC.AX
	Healthcare	Cochlear Limited	COH.AX
	Healthcare	CSL Limited	CSL.AX
	Healthcare	Fisher & Paykel Healthcare Corporation Limited	FPH.AX
	Healthcare	Ramsay Health Care Limited	RHC.AX
	Healthcare	ResMed Inc.	RMD.AX
	Healthcare	Sonic Healthcare Limited	SHL.AX
	Real Estate	Goodman Group	GMG.AX
	Real Estate	Scentre Group	SCG.AX
	Real Estate	Stockland	SGP.AX
	Technology	WiseTech Global Limited	WTC.AX
	Technology	Xero Limited	XRO.AX
	Utilities	APA Group	APA.AX

below outlines the sector grouping of selected companies:

5.2. Experiment Procedure

The training and prediction procedure for each stock is as follows. Stocks in different groups follow this automated process, with different hyperparameters applied based on their sector:

• Split the Data: Divide the daily adjusted close prices into a training dataset (80%) and a testing dataset (20%). The dataset was divided into training (80%) and testing (20%) sets using distinct, non-overlapping time periods to minimize temporal data leakage. This approach ensured comparability across all model architectures while maintaining the chronological integrity of the financial time series data.
• Decompose the Training Series: Use Singular Spectrum Analysis (SSA) to decompose the training data based on the specified window length.
• Calculate Contributions: Compute the contribution of each decomposed term and sort them in descending order. Accumulate the contributions by their order and stop once the cumulative contribution reaches the set criterion.
• Reconstruct Time Series: Reconstruct the time series components using the selected terms from the decomposition.
• Cluster Components: Apply the K-means algorithm to aggregate similar components together.
• Normalize Components: Standardize each reconstructed component by normalizing it.
• Reshape the Data: Reshape the normalized series into 3D tensors according to the optimal rolling window size.
• Build and Train the Model: Construct and train the model using each normalized component.
• Forecast Future Prices: For each point in the testing dataset, forecast the future price by following these steps until all time points are predicted: a. Decompose the previous price series and generate the 3D tensors as described in steps 2–7. b. Perform a one-step prediction for each component. c. Denormalize the predicted components.
• Aggregate and Evaluate: Combine all predicted components into a single price series and evaluate its accuracy using appropriate performance metrics.

Figure 2 below illustrates the training and prediction procedure.

5.3. Trading Strategy

We utilized the model’s predictions to devise a trading strategy, which was tested over 252 trading days from 1 April 2022, to 31 March 2023. The steps of the strategy were as follows:

• Initial Capital and Trade Size:

  ○

  The initial capital was set at 5 million.

  ○

  2 million (40% of the initial capital) was allocated to each daily trade.

  ○

  A maximum cumulative loss of 3 million was set to prevent excessive loss over the trading period.

• Stock Ranking and Investment:

  ○

  Each day, stocks were ranked based on their predicted percentage returns.

  ○

  The top three stocks for the day were selected for investment.

  ○

  An equal amount of 2/3 million (666,666.67 per stock) was allocated to each of the three selected stocks daily, ensuring no short trades were made.

• Closing and Rebalancing:

  ○

  Positions were closed at the end of each trading day.

  ○

  The strategy was rebalanced daily, using fresh predictions and rankings for the next day’s trades.

• Commission Fees:

  ○

  A commission fee of 0.025% was applied for both buying and selling, ensuring the transaction costs were considered in the strategy.

• Percentage Return Calculation:

  ○

  The percentage return for each stock trade was calculated using the formula:

Percentage Return =

$$percentage return={\displaystyle \frac{\widehat{{price}_t}-\widehat{{price}_{t-1}}}{\widehat{{price}_{t-1}}}}$$

(1)

This formula calculates the return based on the change in price relative to the opening price.

6.

Performance Evaluation:

○

The strategy was evaluated based on its cumulative returns, accounting for both transaction costs and predicted stock performance.

6. Results

6.1. Parameters

In the implementation of the Singular Spectrum Analysis method, two key parameters were considered:

• The window length (L) used during the embedding stage, which determines the size of the trajectory matrix constructed from the time series data.
• The contribution threshold for determining which components are retained for reconstruction. This threshold guides the grouping of components based on their relative significance.

The selection of the key parameters in the Singular Spectrum Analysis (SSA) was guided by both theoretical and empirical considerations to ensure a balance between signal fidelity and noise suppression. The window length ($L$) was chosen to be sufficiently large to capture the dominant temporal patterns in the data, while remaining below half of the series length, consistent with established SSA practices. The contribution thresholds of 99.95% and 99.97% were applied to retain the principal components that together explained nearly all the signal variance, effectively filtering out residual noise without over-smoothing the reconstructed series. Preliminary sensitivity analyses confirmed that small variations in $L$ and the threshold values did not materially affect the results, indicating that the decomposition and reconstruction were robust to parameter choice.

In our research, we set the contribution criteria to 99.95% and 99.97%, respectively, meaning that only the components contributing to this cumulative percentage of the signal variance were preserved. The retained components were then grouped using the K-means clustering algorithm into two distinct categories: trend and periodicity [31]. The remaining components, accounting for the last 0.05% (or 0.03%) of the contribution, were classified as noise and deemed non-informative for prediction purposes.

The window length is essential to be tuned for the stocks in different groups, and [37] suggested that the window length should be large enough but no larger than $\lfloor {\displaystyle \frac{N}{2}}\rfloor$, where $N$ is the total length of the series. This problem is also detected in our research, as very low window length will not capture the periodicity effect, causing the contribution value of trend to be larger than the criteria. According to Hassani et al., $L={\displaystyle \frac{N}{4}}$ is a common practice for SSA method [37]. Hence, in our research,

Table 2. SSA’s Values to be tuned.

Contribution Criteria	99.95%		99.97%
Window Length L	63 (Trading days in one quarter)	252 (Trading days in one year)		504 (Trading days in two years)

below, displays the window Length $L$ will be optimized by testing the possible values below for each group:

For the selected deep learning algorithms, several parameters required careful tuning to optimize model performance:

• Time Step for 3D Tensor Formation: This defines the number of lag values used from the time series to form each input sample.
• Neural Network Architecture and Hyperparameters: These include optimizer settings, hidden layer configurations, dropout rates, and activation functions.

In our study, a time step of 5 was chosen to construct each 3D tensor, corresponding to one trading week. For the neural network optimization, we employed the Adam optimizer with a learning rate of 0.001, as implemented in the Keras library. Adam is widely recognized for its adaptive learning capabilities and computational efficiency [43].

Other hyperparameters such as the number of hidden units per layer, dropout rates, and activation functions were fine-tuned separately for each sector group to best fit the characteristics of the grouped stocks.

6.2. Forecasting Results

Similarly, this study initially applies the Singular Spectrum Analysis (SSA) algorithm to decompose each stock’s original price series and reconstruct its Trend and Periodicity components. Based on predefined contribution criteria, SSA identifies and excludes components deemed noise, which are therefore not considered in the K-means clustering stage. The contribution thresholds tested in this study are 99.95% and 99.97%, representing the cumulative variance retained from the original signal.

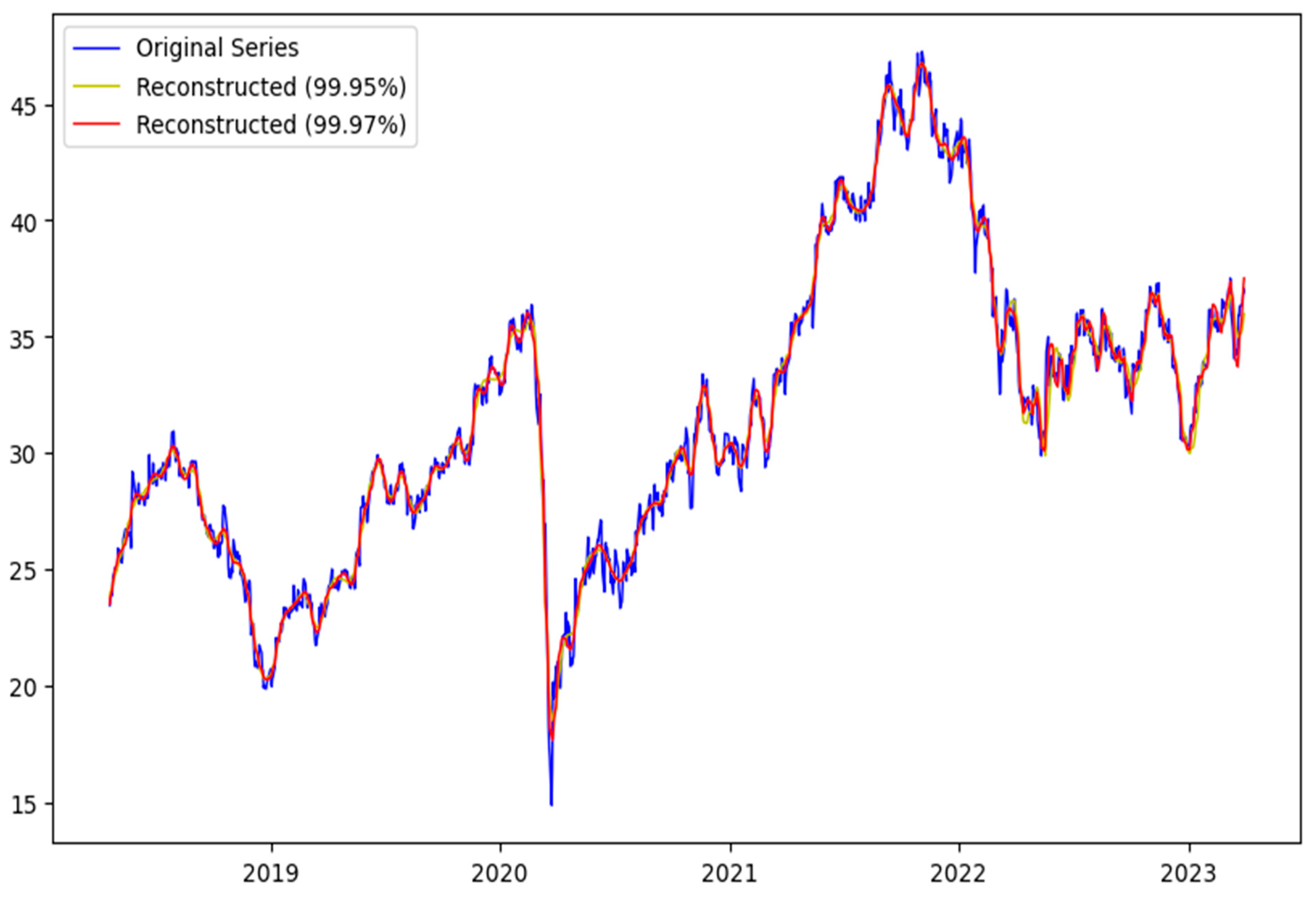
An illustrative example is provided using the stock ALL.AX, with the reconstructed series summarized in

Table 3. Reconstructed Series values of ALL.AX with window_length = 63.

	99.95%			99.97%
Date	Periodicity	Trend	Aggregate	Periodicity	Trend	Aggregate	Actual
12 April 2018	−3.800	26.505	22.704	−4.232	26.505	22.272	21.906
13 April 2018	−3.643	26.575	22.932	−4.088	26.575	22.487	22.512
16 April 2018	−3.500	26.644	23.144	−3.941	26.644	22.703	22.671
17 April 2018	−3.347	26.710	23.363	−3.760	26.710	22.950	22.848
18 April 2018	−3.181	26.773	23.592	−3.543	26.773	23.231	23.407
19 April 2018	−3.025	26.835	23.811	−3.313	26.835	23.522	23.463
20 April 2018	−2.871	26.896	24.025	−3.066	26.896	23.830	23.799
23 April 2018	−2.726	26.956	24.230	−2.815	26.956	24.141	23.892
24 April 2018	−2.585	27.014	24.429	−2.564	27.014	24.450	24.675
26 April 2018	−2.462	27.071	24.609	−2.338	27.071	24.733	24.852
27 April 2018	−2.355	27.128	24.773	−2.143	27.128	24.984	25.076
30 April 2018	−2.261	27.183	24.922	−1.984	27.183	25.199	25.001
1 May 2018	−2.175	27.238	25.064	−1.859	27.238	25.379	25.066
2 May 2018	−2.093	27.294	25.201	−1.768	27.294	25.526	25.905
3 May 2018	−2.018	27.348	25.330	−1.718	27.348	25.630	25.775
4 May 2018	−1.942	27.400	25.458	−1.697	27.400	25.703	25.533
7 May 2018	−1.858	27.451	25.592	−1.692	27.451	25.759	25.803
8 May 2018	−1.770	27.501	25.730	−1.698	27.501	25.803	25.290
9 May 2018	−1.671	27.550	25.879	−1.697	27.550	25.853	25.439
10 May 2018	−1.561	27.598	26.037	−1.681	27.598	25.918	26.157
11 May 2018	−1.446	27.645	26.199	−1.649	27.645	25.995	26.344
14 May 2018	−1.329	27.690	26.360	−1.598	27.690	26.092	26.735

. From the results, it can be observed that the trend components remain consistent across both criteria. However, the periodicity component reconstructed under the 99.97% threshold is smaller compared to that under the 99.95% threshold. This suggests that the trend captures most of the price series’ informational contribution, and the variation in the periodic component is primarily influenced by the stricter criterion.

Importantly, the sequence reconstructed under the 99.97% threshold more closely tracks the original stock price series, as illustrated in Figure 3, where the line labeled “Reconstructed (99.97%)” aligns more accurately with the actual stock prices. This improved alignment is further supported by superior performance in downstream validation. Therefore, subsequent tuning and modeling in this study are conducted primarily under the 99.97% criterion.

The selection of the Window Length (L) in SSA plays a crucial role in effective feature detection and time series reconstruction. An improperly chosen L may hinder the SSA’s ability to accurately capture signal structures. In this study, a range of window lengths from 63 to 504 is explored, corresponding to meaningful temporal intervals such as quarterly (63 days), yearly (252 days), and biannual (504 days) periods.

For each value of L, the original stock price series is decomposed and reconstructed, followed by the construction of various deep learning (DL) models as described previously. These models are then fine-tuned individually within each group using optimized hyperparameters to perform stock price forecasting. The reconstructed trend and periodicity components are aggregated to produce the final predicted stock price series.

To evaluate the accuracy of the predictions, the Mean Squared Error (MSE) and Mean Absolute Error (MAE) are used as performance metrics, comparing the predicted prices to the actual stock prices. The evaluation results for different window lengths and model configurations are summarized in

Table 4. Models’ Performance (window_length = 63).

Company Group	Stocks	CNN		SSA-CNN		SSA-LSTM		SSA-CNN-LSTM
Consumer and Service Sectors		MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
	ALL.AX	0.646	0.643	0.587	0.588	0.976	0.744	0.992	0.773
	REA.AX	11.086	2.509	12.252	2.665	23.058	3.701	18.942	3.346
	TLS.AX	0.021	0.137	0.002	0.040	0.003	0.043	0.003	0.043
	TPG.AX	0.044	0.178	0.011	0.074	0.018	0.101	0.017	0.091
	WES.AX	2.373	1.364	1.183	0.810	1.604	0.947	1.652	0.966
	WOW.AX	0.356	0.485	0.369	0.466	0.487	0.542	0.426	0.503
Financial, Healthcare, Technology, and Utilities Sectors	ANZ.AX	0.216	0.382	0.338	0.440	0.484	0.505	0.431	0.477
	APA.AX	0.185	0.382	0.050	0.175	0.086	0.227	0.128	0.285
	ASX.AX	3.095	1.385	2.349	1.208	3.084	1.368	3.073	1.384
	CBA.AX	36.198	5.672	5.401	1.715	6.745	1.937	5.654	1.858
	COH.AX	20.034	3.451	15.212	2.928	24.616	3.753	18.991	3.269
	CPU.AX	1.986	1.335	0.438	0.476	0.599	0.551	0.478	0.501
	CSL.AX	56.582	6.447	19.564	3.513	25.362	4.013	21.728	3.726
	FPH.AX	0.421	0.523	0.292	0.442	0.711	0.660	0.558	0.587
	GMG.AX	0.769	0.714	0.396	0.475	0.564	0.563	0.516	0.543
	IAG.AX	0.059	0.220	0.008	0.073	0.010	0.082	0.013	0.090
	MQG.AX	97.774	8.960	22.678	3.509	30.687	4.070	22.833	3.588
	NAB.AX	2.740	1.567	0.467	0.512	0.595	0.572	0.501	0.529
	QBE.AX	0.381	0.527	0.071	0.201	0.137	0.280	0.110	0.251
	RHC.AX	4.202	1.383	5.215	1.212	7.481	1.554	5.970	1.359
	RMD.AX	3.529	1.721	0.455	0.518	0.916	0.749	1.055	0.831
	SCG.AX	0.002	0.037	0.004	0.050	0.005	0.059	0.004	0.052
	SGP.AX	0.004	0.050	0.004	0.049	0.006	0.059	0.005	0.055
	SHL.AX	0.939	0.750	0.874	0.705	1.025	0.771	1.075	0.788
	SUN.AX	0.072	0.209	0.058	0.184	0.085	0.237	0.066	0.203
	WBC.AX	0.152	0.326	0.231	0.347	0.329	0.410	0.267	0.374
	WTC.AX	31.246	5.081	4.159	1.584	3.803	1.511	3.685	1.462
	XRO.AX	9.721	2.482	9.961	2.402	16.425	3.191	11.891	2.623
Industrial and Infrastructure Sectors	AIA.AX	0.019	0.107	0.014	0.091	0.020	0.110	0.017	0.102
	BHP.AX	6.377	2.174	1.175	0.838	2.152	1.163	1.630	1.047
	BXB.AX	0.091	0.237	0.070	0.196	0.126	0.264	0.123	0.261
	FMG.AX	4.841	2.051	0.267	0.400	0.364	0.458	0.427	0.497
	IGO.AX	2.605	1.503	0.278	0.410	0.379	0.489	0.292	0.431
	JHX.AX	1.650	0.960	1.266	0.855	2.205	1.152	1.616	0.996
	MIN.AX	115.487	9.971	6.506	2.008	7.589	2.166	15.984	3.215
	NCM.AX	1.583	1.020	0.284	0.415	0.444	0.525	0.487	0.542
	NST.AX	0.244	0.412	0.081	0.223	0.101	0.247	0.089	0.242
	ORG.AX	0.099	0.227	0.049	0.131	0.110	0.242	0.073	0.180
	PLS.AX	0.446	0.603	0.042	0.157	0.043	0.153	0.037	0.146
	QAN.AX	0.046	0.176	0.021	0.111	0.033	0.142	0.028	0.131
	REH.AX	0.199	0.368	0.210	0.360	0.471	0.550	0.296	0.428
	RIO.AX	21.186	3.693	6.640	2.023	11.582	2.752	10.294	2.583
	S32.AX	0.067	0.223	0.017	0.102	0.039	0.149	0.025	0.124
	SOL.AX	0.423	0.547	0.193	0.335	0.341	0.444	0.288	0.400
	STO.AX	0.070	0.225	0.026	0.121	0.042	0.157	0.033	0.143
	TCL.AX	0.068	0.227	0.046	0.171	0.072	0.214	0.057	0.193
	WDS.AX	4.775	1.972	0.904	0.764	1.837	1.103	1.408	0.957

,

Table 5. Models’ Performance (window_length = 252).

Company Group	Stocks	CNN		SSA-CNN		SSA-LSTM		SSA-CNN-LSTM
Consumer and Service Sectors		MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
	ALL.AX	0.646	0.643	0.636	0.627	0.940	0.748	1.016	0.785
	REA.AX	11.086	2.509	15.026	2.994	27.962	4.113	21.090	3.612
	TLS.AX	0.021	0.137	0.004	0.051	0.005	0.059	0.006	0.063
	TPG.AX	0.044	0.178	0.013	0.080	0.026	0.119	0.020	0.104
	WES.AX	2.373	1.364	1.445	0.940	1.583	0.966	1.720	1.032
	WOW.AX	0.356	0.485	0.480	0.500	0.691	0.618	0.753	0.666
Financial, Healthcare, Technology, and Utilities Sectors	ANZ.AX	0.216	0.382	0.341	0.465	0.448	0.519	0.471	0.539
	APA.AX	0.185	0.382	0.052	0.180	0.102	0.258	0.165	0.341
	ASX.AX	3.095	1.385	3.435	1.470	5.279	1.846	5.041	1.796
	CBA.AX	36.198	5.672	5.628	1.854	7.047	2.072	7.382	2.076
	COH.AX	20.034	3.451	19.753	3.563	30.449	4.436	23.945	3.822
	CPU.AX	1.986	1.335	0.654	0.599	1.012	0.741	0.713	0.628
	CSL.AX	56.582	6.447	28.310	4.207	35.103	4.638	40.724	5.028
	FPH.AX	0.421	0.523	0.304	0.429	0.691	0.691	0.369	0.486
	GMG.AX	0.769	0.714	0.534	0.547	0.716	0.635	0.610	0.607
	IAG.AX	0.059	0.220	0.011	0.082	0.015	0.098	0.014	0.096
	MQG.AX	97.774	8.960	24.720	3.744	32.089	4.224	29.218	4.047
	NAB.AX	2.740	1.567	0.476	0.571	0.600	0.625	0.713	0.664
	QBE.AX	0.381	0.527	0.081	0.212	0.166	0.303	0.137	0.275
	RHC.AX	4.202	1.383	4.938	1.317	6.107	1.492	5.785	1.477
	RMD.AX	3.529	1.721	0.620	0.612	0.971	0.781	0.822	0.710
	SCG.AX	0.002	0.037	0.004	0.048	0.006	0.061	0.005	0.058
	SGP.AX	0.004	0.050	0.005	0.055	0.010	0.081	0.007	0.062
	SHL.AX	0.939	0.750	1.374	0.942	1.497	0.979	1.420	0.948
	SUN.AX	0.072	0.209	0.070	0.205	0.098	0.240	0.102	0.249
	WBC.AX	0.152	0.326	0.257	0.398	0.403	0.453	0.395	0.436
	WTC.AX	31.246	5.081	3.765	1.509	3.005	1.323	2.978	1.304
	XRO.AX	9.721	2.482	11.772	2.671	17.526	3.287	12.493	2.816
Industrial and Infrastructure Sectors	AIA.AX	0.019	0.107	0.017	0.100	0.026	0.122	0.027	0.128
	BHP.AX	6.377	2.174	1.549	0.997	2.454	1.232	2.207	1.208
	BXB.AX	0.091	0.237	0.072	0.201	0.124	0.264	0.122	0.256
	FMG.AX	4.841	2.051	0.305	0.418	0.476	0.536	0.397	0.475
	IGO.AX	2.605	1.503	0.253	0.396	0.297	0.430	0.287	0.424
	JHX.AX	1.650	0.960	1.494	0.966	2.503	1.236	2.156	1.113
	MIN.AX	115.487	9.971	6.755	2.035	7.812	2.163	11.370	2.745
	NCM.AX	1.583	1.020	0.263	0.411	0.531	0.595	0.441	0.536
	NST.AX	0.244	0.412	0.069	0.208	0.064	0.202	0.079	0.226
	ORG.AX	0.099	0.227	0.056	0.149	0.086	0.193	0.081	0.190
	PLS.AX	0.446	0.603	0.030	0.134	0.041	0.162	0.033	0.139
	QAN.AX	0.046	0.176	0.024	0.118	0.041	0.157	0.034	0.140
	REH.AX	0.199	0.368	0.274	0.406	0.352	0.478	0.316	0.446
	RIO.AX	21.186	3.693	8.287	2.215	12.546	2.755	12.151	2.765
	S32.AX	0.067	0.223	0.018	0.106	0.028	0.127	0.033	0.144
	SOL.AX	0.423	0.547	0.269	0.404	0.452	0.523	0.423	0.511
	STO.AX	0.070	0.225	0.026	0.125	0.045	0.171	0.038	0.146
	TCL.AX	0.068	0.227	0.040	0.163	0.067	0.207	0.059	0.195
	WDS.AX	4.775	1.972	0.988	0.773	1.333	0.912	1.585	1.008

and

Table 6. Models’ Performance (window_length = 504).

Company Group	Stocks	CNN		SSA-CNN		SSA-LSTM		SSA-CNN-LSTM
Consumer and Service Sectors		MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
	ALL.AX	0.646	0.643	2.212	1.193	1.661	0.962	1.437	0.870
	REA.AX	11.086	2.509	28.166	3.916	24.816	3.616	20.283	3.444
	TLS.AX	0.021	0.137	0.042	0.186	0.010	0.082	0.010	0.084
	TPG.AX	0.044	0.178	0.091	0.252	0.038	0.144	0.032	0.133
	WES.AX	2.373	1.364	3.503	1.588	2.902	1.320	2.266	1.172
	WOW.AX	0.356	0.485	1.327	0.944	1.058	0.830	1.005	0.796
Financial, Healthcare, Technology, and Utilities Sectors	ANZ.AX	0.216	0.382	0.695	0.661	0.882	0.765	0.746	0.682
	APA.AX	0.185	0.382	0.200	0.366	0.079	0.230	0.084	0.235
	ASX.AX	3.095	1.385	7.647	2.213	6.689	2.055	5.787	1.898
	CBA.AX	36.198	5.672	48.577	6.373	9.976	2.429	9.202	2.347
	COH.AX	20.034	3.451	48.952	5.437	33.496	4.533	30.166	4.314
	CPU.AX	1.986	1.335	4.575	1.969	1.039	0.773	0.879	0.712
	CSL.AX	56.582	6.447	219.103	12.274	66.106	6.487	61.242	6.298
	FPH.AX	0.421	0.523	1.191	0.873	0.892	0.728	0.623	0.629
	GMG.AX	0.769	0.714	1.332	0.921	0.647	0.602	0.620	0.595
	IAG.AX	0.059	0.220	0.078	0.249	0.027	0.118	0.026	0.116
	MQG.AX	97.774	8.960	152.101	10.998	42.138	4.564	37.312	4.540
	NAB.AX	2.740	1.567	3.477	1.656	1.814	1.054	1.388	0.910
	QBE.AX	0.381	0.527	0.539	0.622	0.168	0.328	0.158	0.318
	RHC.AX	4.202	1.383	14.492	2.545	8.121	1.643	7.650	1.548
	RMD.AX	3.529	1.721	5.208	2.096	1.205	0.828	0.929	0.727
	SCG.AX	0.002	0.037	0.010	0.076	0.010	0.075	0.010	0.076
	SGP.AX	0.004	0.050	0.014	0.095	0.015	0.092	0.013	0.088
	SHL.AX	0.939	0.750	1.829	1.132	1.186	0.850	1.037	0.786
	SUN.AX	0.072	0.209	0.198	0.371	0.160	0.305	0.142	0.288
	WBC.AX	0.152	0.326	0.698	0.648	0.946	0.659	0.837	0.618
	WTC.AX	31.246	5.081	34.659	5.431	3.316	1.389	2.436	1.192
	XRO.AX	9.721	2.482	15.768	3.189	16.968	3.356	10.183	2.519
Industrial and Infrastructure Sectors	AIA.AX	0.019	0.107	0.059	0.210	0.043	0.171	0.045	0.173
	BHP.AX	6.377	2.174	10.417	2.800	2.411	1.227	1.914	1.099
	BXB.AX	0.091	0.237	0.336	0.470	0.190	0.357	0.181	0.341
	FMG.AX	4.841	2.051	5.904	2.312	0.545	0.580	0.431	0.496
	IGO.AX	2.605	1.503	2.966	1.596	0.365	0.487	0.218	0.364
	JHX.AX	1.650	0.960	3.690	1.459	3.740	1.554	2.357	1.168
	MIN.AX	115.487	9.971	133.294	10.761	8.490	2.196	6.763	1.959
	NCM.AX	1.583	1.020	2.475	1.379	0.837	0.741	0.746	0.684
	NST.AX	0.244	0.412	0.258	0.412	0.105	0.264	0.115	0.275
	ORG.AX	0.099	0.227	0.258	0.371	0.097	0.202	0.087	0.190
	PLS.AX	0.446	0.603	0.468	0.630	0.043	0.159	0.038	0.152
	QAN.AX	0.046	0.176	0.091	0.258	0.044	0.160	0.039	0.148
	REH.AX	0.199	0.368	0.657	0.648	0.338	0.462	0.515	0.564
	RIO.AX	21.186	3.693	31.199	4.718	15.227	3.090	11.924	2.647
	S32.AX	0.067	0.223	0.113	0.299	0.037	0.151	0.032	0.138
	SOL.AX	0.423	0.547	1.632	1.113	0.580	0.605	0.505	0.548
	STO.AX	0.070	0.225	0.107	0.275	0.059	0.187	0.049	0.169
	TCL.AX	0.068	0.227	0.293	0.466	0.115	0.274	0.105	0.265
	WDS.AX	4.775	1.972	4.298	1.709	2.014	1.144	1.690	1.053

, respectively.

Observing the prediction results of different models when the window length of the SSA algorithm is chosen to be 63 to reconstruct the sequence, it can be found that the SSA-CNN provides the most accurate prediction away from the real stock price in most cases, and almost all the best MSEs and MAEs are obtained from this model. The ordinary CNN also gives relatively accurate results, and it should be noted that the ordinary CNN directly uses the original stock price for prediction, independent of the output sequence of the SSA algorithm. SSA-LSTM and SSA-CNN-LSTM hardly provide more accurate results compared to SSA-CNN and CNN, except for the WTC.AX stock, for which the best prediction is obtained by SSA-CNN-LSTM. However, it can be noted that the differences in model performance in terms of the assessment of prediction accuracy are all very small, so it is also necessary to check the empirical analysis provided by the trading strategy.

When analysing the prediction results with larger window lengths of 252 and 504, it becomes apparent that the prediction accuracy of the SSA-CNN model declines significantly. In contrast, the accuracy of SSA-LSTM and SSA-CNN-LSTM remains relatively stable, with only slight decreases observed. Notably, for the WTC.AX stock, the predictive performance even improves as the window length increases. This suggests that as the window length grows, the relative contribution of trend components diminishes, while the influence of periodicity and noise components increases, due to the higher number of decomposed components.

Furthermore, it is observed that the best prediction results for stocks in the Industrial and Infrastructure sectors tend to be achieved by the SSA-CNN-LSTM model rather than the others. This can be attributed to the model’s strength in capturing long-term fluctuations within periodic sequences, whereas SSA-CNN is better suited for non-smooth, trend-dominated sequences. Consequently, the performance of SSA-CNN deteriorates significantly in these cases, occasionally performing worse than the other two models.

Interestingly, CNN-based models (including non-SSA CNN) also demonstrate strong performance. This can be explained by the fact that with larger window lengths, if the same fixed contribution criteria are used to discard noise, there is a greater risk of omitting important information from the original stock price series. As a result, the reconstructed sequences used for training may lack critical signals, leading to less effective predictions.

However, it is important to recognize that the original stock price series inherently contains noise, which may not be informative or actionable for real-world trading strategies. Although CNNs trained on raw data might achieve higher accuracy in terms of price prediction, they might also capture spurious patterns, making them less suitable for practical trading applications. Investors are typically more interested in robust predictions based on the underlying structure of stock movements, rather than predictions influenced by noise.

For this reason, the present study emphasizes the empirical value of SSA-based Deep Learning (SSA-DL) models, aiming to construct more reliable and interpretable trading strategies grounded in the intrinsic properties of stock behaviour.

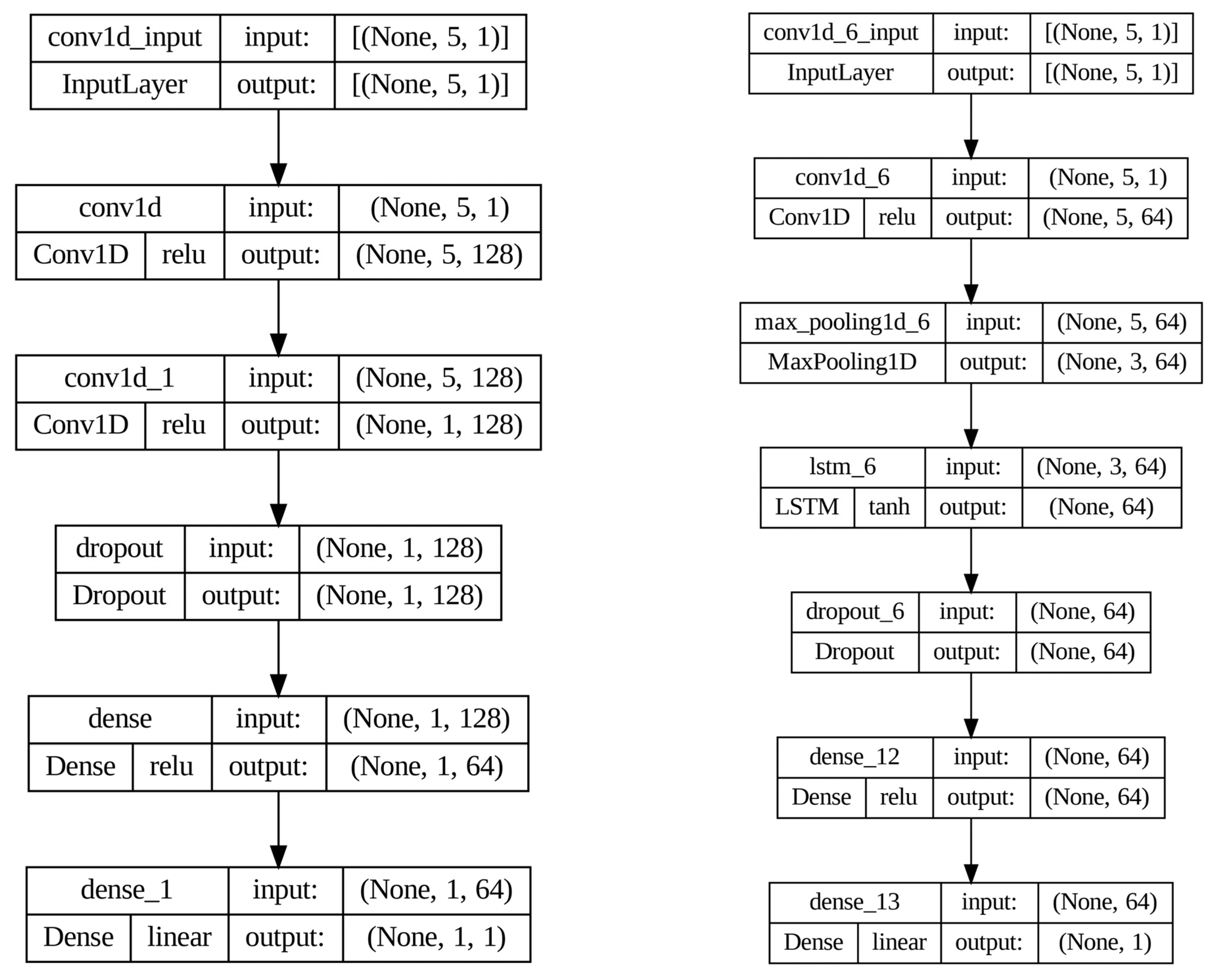
The architecture of the best-performing SSA-CNN model, identified when the window length is set to 63, is illustrated in Figure 4 (left). The model begins with two convolutional layers, each comprising 128 filters with a kernel size of 3 and employing the ReLU activation function. Notably, no pooling layer is applied after the convolutional stages, allowing the model to retain the full granularity of the extracted features. These layers are followed by a Dropout layer with a dropout rate of 0.3 to prevent overfitting. Finally, a fully connected (dense) layer with 64 neurons and ReLU activation is employed to generate the output prediction.

In contrast, the SSA-CNN-LSTM model structure, shown in Figure 4 (right), integrates both convolutional and recurrent layers to leverage spatial and temporal features. The model starts with a convolutional layer consisting of 64 filters and a ReLU activation function, which extracts local spatial patterns from the input sequence. This is followed by a Max Pooling layer to down sample and highlight the most salient features. The resulting feature maps are then passed into an LSTM layer with 64 units and a tanh activation function, designed to capture the temporal dependencies within the sequence. The final prediction is generated through a dense layer with 64 neurons and ReLU activation.

6.3. Trading Strategy Performance

In this study, beyond aiming for more accurate stock price predictions using SSA-DL models, we also emphasize the importance of obtaining noise-filtered forecasts that are practically applicable for real-world trading and profitability. This aligns with the insights from Dessian, who conducted a comprehensive review of over 190 research articles and highlighted that many commonly used evaluation metrics such as MSE and RMSE may be inadequate when the ultimate objective is profit maximization in real financial markets [44].

To assess the practical utility of our models, we constructed daily frequency trading strategies based on the predicted stock prices generated by various models. These strategies were applied to a selection of 47 stocks from the ASX50 index, enabling us to test the extent to which model-driven predictions could inform profitable investment decisions. The performance of each strategy was evaluated using a suite of financial metrics, including Win Rate, Return on Investment (ROI), and the Sharpe Ratio (assuming a risk-free rate of 2%).

The empirical results and comparative analysis across models are presented in the following sections.

As shown in

Table 7. Financial metrics for all models.

Models	Dollar Return (Thousand)	Dollar Gain (Thousand)	Dollar Loss (Thousand)	Win Rate	Lose Rate	ROI	Sharpe Ratio (rf = 0.02)	Max DrawDown
CNN	−$1021	$12,070	−$12,840	0.4669	0.5331	−20.43%	−0.746	−0.410
SSA-CNN (63)	$1121	$14,439	−$13,066	0.5238	0.4762	22.43%	0.546	−0.438
SSA-CNN (252)	$1283	$14,381	−$12,846	0.5053	0.4947	25.66%	0.648	−0.445
SSA-CNN (504)	$2226	$14,733	−$12,255	0.5185	0.4815	44.51%	1.214	−0.473
SSA-LSTM (63)	$1153	$13,824	−$12,419	0.5053	0.4947	23.06%	0.611	−0.359
SSA-LSTM (252)	$3064	$15,701	−$12,385	0.5450	0.4550	61.28%	1.597	−0.473
SSA-LSTM (504)	$1982	$13,701	−$11,467	0.5397	0.4603	39.64%	1.156	−0.390
SSA-CNN-LSTM (63)	$1891	$13,364	−$11,220	0.5317	0.4683	37.82%	1.169	−0.474
SSA-CNN-LSTM (252)	$3328	$14,749	−$11,169	0.5304	0.4696	66.57%	1.878	−0.468
SSA-CNN-LSTM (504)	$3022	$14,328	−$11,053	0.5437	0.4563	60.45%	1.751	−0.458

, the SSA-CNN-LSTM model with a window length of 252 achieves the highest Sharpe Ratio, reaching a value of 1.878. Notably, this model also generates over $3.3 million in cumulative return, based on a daily trading capital of $2 million, significantly outperforming the other models. The SSA-LSTM model (also with a window length of 252) demonstrates similarly strong performance, recording the highest Win Rate and total Dollar Gain among all tested strategies.

Interestingly, while SSA-CNN (window length = 63) and the standard CNN model exhibit relatively higher predictive accuracy in terms of MSE and MAE, their trading strategy performance is notably weaker. In fact, the CNN model results in a substantial financial loss. A closer look at Win Rate and Dollar Loss further underscores that SSA-LSTM and SSA-CNN-LSTM outperform both CNN and SSA-CNN models in risk-adjusted returns. Although SSA-CNN performs comparably to the other two SSA-DL models in terms of total Dollar Gain, its high Dollar Loss reduces its final ROI and Sharpe Ratio.

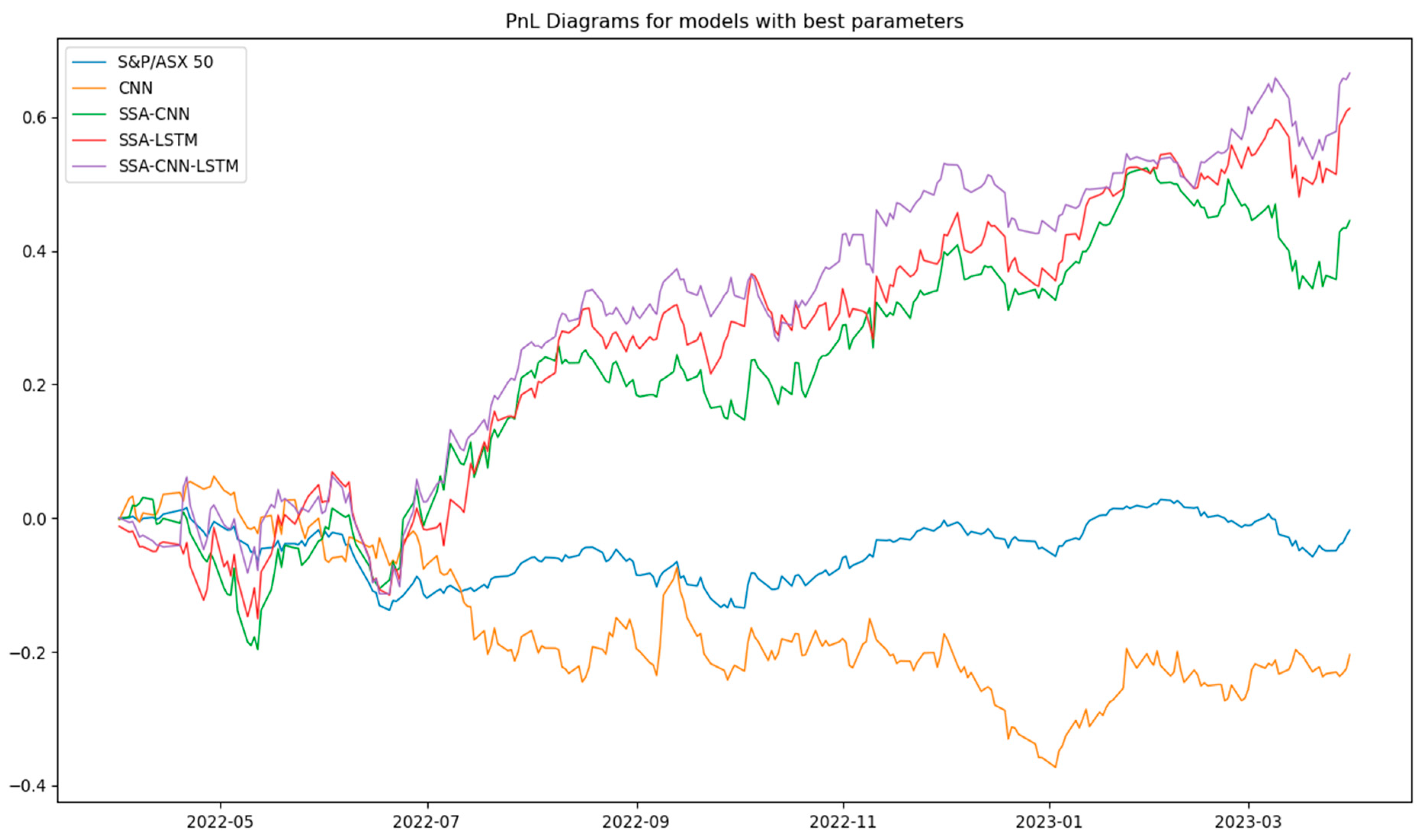
The fact that the two best-performing trading strategies are based on models with a window length of 252 supports the empirical validity of the guideline L = N/4 for selecting the SSA window length. To illustrate these findings visually, Figure 5 presents the PnL (Profit and Loss) curves for CNN and the best-performing models from each SSA-DL variant, compared with the S&P/ASX50 index [45].

The results reveal that the strategies built using SSA-DL models significantly outperform the market baseline. During the one-year evaluation period, the S&P/ASX50 index declined from 7254 to 7049, representing a −2.83% return. Despite the overall market downturn, the SSA-CNN-LSTM model achieved an ROI of 66.58%, while the SSA-LSTM and SSA-CNN models delivered ROIs of 61.28% and 44.51%, respectively. See Figure 5 below. Yan and Ling also integrated their forecasting results with quantitative investing principles and constructed a new strategy that achieved better returns in twelve selected American financial stocks [46]. This validates the practical value of incorporating SSA-DL models into the design of trading strategies, offering substantial alpha generation even in bearish market conditions.

To further investigate the trading behavior of the proposed models, we randomly selected all trading days from 3 January to 31 January for a detailed performance review. The results, summarized in

Table 8. Daily Trading Positions and Dollar Return in January 2023.

Date	SSA-CNN (504)		SSA-LSTM (252)		SSA-CNN-LSTM (252)
	Dollar Return (Thousand)	Long Position	Dollar Return (Thousand)	Long Position	Dollar Return (Thousand)	Long Position
3 January 2023	−$88.0	XRO.AX, BHP.AX, PLS.AX	−$94.2	BHP.AX, FMG.AX, PLS.AX	−$80.6	ANZ.AX, GMG.AX, AIA.AX
4 January 2023	$107.7	IAG.AX, NAB.AX, XRO.AX	$128.4	ANZ.AX, BHP.AX, PLS.AX	$116.8	ANZ.AX, WBC.AX, SOL.AX
5 January 2023	$19.4	TLS.AX, XRO.AX, PLS.AX	$23.2	TPH.AX, PLS.AX, SOL.AX	$11.5	TPG.AX, ANZ.AX, SOL.AX
6 January 2023	$84.6	XRO.AX, PLS.AX, REH.AX	$191.4	TLS.AX, BHP.AX, PLS.AX	$72.2	ANZ.AX, CSL.AX, IGO.AX
9 January 2023	$76.7	XRO.AX, IGO.AX, REH.AX	$8.1	CSL.AX, FPH.AX, XRO.AX	−$27.7	CSL.AX, FPH.AX, RMD.AX
10 January 2023	−$13.1	REA.AX, CPU.AX, IGO.AX	−$45.1	CPU.AX, XRO.AX, PLS.AX	$19.7	CPU.AX, CSL.AX, RMD.AX
11 January 2023	$88.0	REA.AX, CPU.AX, REH.AX	$112.0	CPU.AX, IAG.AX, PLS.AX	$70.8	CPU.AX, IAG.AX, QBE.AX
12 January 2023	$0.5	REA.AX, CPU.AX, JHX.AX	$141.3	CPU.AX, XRO.AX, PLS.AX	$54.3	CPU.AX, SUN.AX, XRO.AX
13 January 2023	$36.8	REA.AX, JHX.AX, PLS.AX	$54.1	REA.AX, CPU.AX, NCM.AX	−$3.2	CPU.AX, SUN.AX, NCM.AX
16 January 2023	$183.1	REA.AX, WTC.AX, REH.AX	$29.5	CPU.AX, NCM.AX, PLS.AX	$7.8	CPU.AX, SUN.AX, NCM.AX
17 January 2023	−$20.6	CPU.AX, WTC.AX, REH.AX	$13.8	CPU.AX, JHX.AX, MIN.AX	$1.8	CPU.AX, SUN.AX, IGO.AX
18 January 2023	−$2.6	XRO.AX, PLS.AX, S32.AX	$45.0	CPU.AX, XRO.AX, JHX.AX	$6.4	CPU.AX, WTC.AX, NCM.AX
19 January 2023	$9.9	ALL.AX, FPH.AX, NCM.AX	−$22.4	CPU.AX, JHX.AX, REH.AX	−$10.0	CPU.AX, NCM.AX, ORG.AX
20 January 2023	$53.2	ALL.AX, FPH.AX, XRO.AX	−$46.4	CPU.AX, XRO.AX, REH.AX	$115.0	CPU.AX, FPH.AX, ORG.AX
23 January 2023	$157.7	ALL.AX, XRO.AX, PLS.AX	$54.8	CPU.AX, XRO.AX, REH.AX	$2.7	XRO.AX, ORG.AX, REH.AX
24 January 2023	$154.1	FPH.AX, IGO.AX, PLS.AX	$149.5	ALL.AX, GMG.AX, REH.AX	$142.6	ALL.AX, TPG.AX, REH.AX
25 January 2023	$18.9	FPH.AX, IGO.AX, PLS.AX	$10.6	COH.AX, CPU.AX, FPH.AX	−$43.7	TPG.AX, COH.AX, FPH.AX
27 January 2023	$16.4	TPG.AX, WES.AX, IGO.AX	$1.7	TPG.AX, CPU.AX, IGO.AX	$20.0	TPG.AX, IGO.AX, SOL.AX
30 January 2023	$17.4	TPG.AX, NCM.AX, REH.AX	−$32.2	TPG.AX, CPU.AX, IGO.AX	−$28.1	TPG.AX, IGO.AX, NCM.AX
31 January 2023	−$41.1	TPG.AX, WES.AX, REH.AX	−$14.1	TPG.AX, CPU.AX, RMD.AX	−$3.7	TPG.AX, RMD.AX, SHL.AX
Total =	$859.0	Total =	$709.2	Total =	444.8

, reveal that during this month, the SSA-CNN model with a window length of 504 achieved the highest cumulative Dollar Gain. Despite this, notable differences in stock selection can be observed among the three models. Interestingly, SSA-LSTM (252) and SSA-CNN-LSTM (252) exhibit greater overlap in daily stock picks, suggesting a similarity in their portfolio construction approach, in contrast to SSA-CNN (504), which tends to diverge significantly in its choices.

Additionally, the analysis shows that on several consecutive trading days, the models, particularly SSA-LSTM and SSA-CNN-LSTM generate portfolios with unchanged or minimally rotated stock selections. This consistency implies that frequent rebalancing is not always necessary, and avoiding unnecessary portfolio turnover could reduce transaction costs, thereby enhancing real-world returns beyond what is reflected in the back-testing results.

A particularly noteworthy observation is that the SSA-LSTM model selects PLS.AX (an Industrial sector stock), 90 times over the course of the year, resulting in substantial representation of the Industrial and Infrastructure sectors within its portfolio. This consistent preference may indicate the model’s sensitivity to long-term cyclical patterns or strong predictive signals inherent in the stock’s behavior.

To examine sectoral tendencies,

Table 9. Frequency of stock selections by each model.

Company Group	Stocks	CNN		SSA-CNN (504)		SSA-LSTM (252)		SSA-CNN-LSTM (252)
Consumer and Service Sectors	ALL.AX	16	Total 67 times	20	Total 104 times	6	Total 109 times	26	Total 132 times
	REA.AX	22		25		46		26
	TLS.AX	0		3		3		0
	TPG.AX	19		10		24		30
	WES.AX	0		39		17		28
	WOW.AX	10		7		13		22
Financial, Healthcare, Technology, and Utilities Sectors	ANZ.AX	9	Total 251 times	18	Total 353 times	10	Total 309 times	28	Total 366 times
	APA.AX	18		8		1		0
	ASX.AX	7		13		24		39
	CBA.AX	0		10		3		6
	COH.AX	12		3		6		5
	CPU.AX	14		26		53		37
	CSL.AX	4		4		2		3
	FPH.AX	18		23		48		19
	GMG.AX	4		37		15		33
	IAG.AX	9		7		13		24
	MQG.AX	0		9		11		19
	NAB.AX	2		12		4		6
	QBE.AX	21		2		3		4
	RHC.AX	15		10		4		9
	RMD.AX	7		25		6		21
	SCG.AX	22		6		1		5
	SGP.AX	15		25		10		6
	SHL.AX	5		20		22		33
	SUN.AX	17		6		4		9
	WBC.AX	9		12		10		12
	WTC.AX	24		26		2		6
	XRO.AX	19		51		57		42
Industrial and Infrastructure Sectors	AIA.AX	12	Total 435 times	1	Total 299 times	1	Total 338 times	3	Total 258 times
	BHP.AX	13		16		28		18
	BXB.AX	16		3		0		1
	FMG.AX	14		12		20		3
	IGO.AX	26		32		22		46
	JHX.AX	12		21		50		25
	MIN.AX	44		21		17		0
	NCM.AX	23		12		26		13
	NST.AX	41		25		2		6
	ORG.AX	26		2		4		10
	PLS.AX	55		59		90		20
	QAN.AX	31		1		4		6
	REH.AX	12		50		24		43
	RIO.AX	21		13		8		24
	S32.AX	21		6		15		4
	SOL.AX	7		0		10		18
	STO.AX	19		5		4		8
	TCL.AX	12		10		0		0
	WDS.AX	30		10		13		10

reports the annual frequency of stock selections made by each model. Relative to the SSA-DL models, the standard CNN model exhibits a pronounced bias towards the Industrial and Infrastructure sectors, while underrepresenting stocks from the Consumer Services, Financials, Healthcare, Technology, and Utilities sectors. In contrast, the SSA-DL models achieve a more balanced sectoral distribution, thereby providing improved diversification.

7. Limitations of Study

While the back testing results demonstrate the potential effectiveness of the proposed trading strategy, it is important to acknowledge that the evaluation was conducted under idealized conditions. Real-world trading involves additional complexities such as transaction costs, liquidity constraints, slippage, and execution delays, which were not explicitly modelled in this study. As the main objective was to assess the predictive capability of the model rather than its operational implementation, these factors were excluded to maintain analytical focus. Future research could extend this work by incorporating realistic trading frictions to better assess the practical performance and robustness of the strategy in live market environments.

In addition, while the proposed SSA-DL framework demonstrates strong predictive potential, this study did not include direct comparisons with classical time-series such as ARIMA or GARCH, or with simple benchmark strategies like buy-and-hold. The omission was deliberate, as the focus of this work was to explore the methodological integration of SSA with deep learning architectures rather than to establish dominance over all alternatives. Future research could extend this work by systematically comparing the SSA-DL framework against both traditional and baseline strategies to provide a broader perspective on its relative advantages and robustness.

Furthermore, the variation in model performance across different window lengths can be attributed to the distinct learning characteristics of the deep learning architectures employed. Specifically, the SSA-CNN model performs better with shorter window lengths, as it effectively captures localized temporal and structural patterns within the decomposed components. In contrast, the SSA-LSTM model tends to excel with longer window lengths, as its recurrent structure enables it to better model long-term dependencies in the financial time series. These complementary strengths highlight the importance of aligning the choice of model architecture and window length with the underlying temporal dynamics of the data.

Note that although the proposed SSA-DL trading framework demonstrated superior returns compared to the ASX50 benchmark, such results should be interpreted cautiously. The high alpha may partially reflect model sensitivity to specific market dynamics during the test period rather than persistent predictive power. Moreover, despite measures taken to mitigate overfitting, the possibility of model over-optimization cannot be fully excluded.

8. Conclusions

This study proposed a novel framework that combines Singular Spectrum Analysis (SSA) with deep learning algorithms to predict stock prices of companies listed on the ASX50 index. The primary objective was to reduce noise in stock price time series, extract meaningful trend and periodicity components, and enhance the accuracy of stock price forecasts. By improving prediction reliability, the proposed approach offers practical guidance for stock selection and portfolio construction in dynamic financial markets. We propose future work to extend the evaluation of the CNN, LSTM, CNN-LSTM and SSA-CNN-LSTM beyond the current dataset to a wide range of financial markets with diverse structural characteristics, including major equity indices such as the S&P 500 (United States), Nikkei 225 (Japan), and ASX200 (Australia), as well as the foreign exchange market (e.g., EUR/USD, USD/JPY), commodity markets (e.g., gold, crude oil), and cryptocurrency markets (e.g., Bitcoin, Ethereum). These markets differ substantially in volatility dynamics, liquidity levels, trading mechanisms, and information efficiency, thereby will provide a robust platform to validate the generality and adaptability of the proposed approach.

To evaluate the model’s performance, we employed Mean Squared Error (MSE) and Mean Absolute Error (MAE) as forecasting accuracy metrics and further validated the models through back tested trading strategies. Results demonstrated that SSA effectively filtered noise and isolated underlying market patterns, enabling deep learning models, specifically CNN, LSTM, and hybrid CNN–LSTM architectures to generate more stable and accurate predictions. Among these, the SSA–CNN–LSTM model with a window length of 252 achieved the best overall performance, yielding a 66% return on investment (ROI) and a Sharpe Ratio of 1.88.

While low-variance SSA components are treated as noise for the current daily/multi-day forecasting horizon, future studies could investigate their potential predictive value for ultra-short-term or intraday strategies, capturing high-frequency market microstructure effects.

These findings have several practical implications. For investors and portfolio managers, the SSA–DL framework provides a data-driven method to improve timing and selection of trades, particularly by filtering out short-term market noise that can distort traditional technical signals. For quantitative analysts and financial engineers, the integration of SSA with deep learning offers a promising pathway for developing robust forecasting engines capable of adapting to volatile, non-stationary financial environments. For trading strategy developers, the study demonstrates how preprocessing techniques can enhance the performance of deep learning-based algorithmic trading systems, leading to superior risk-adjusted returns compared to benchmark models and market indices.

The research also underscores the importance of model configuration, as key hyperparameters such as SSA window length and contribution criteria significantly influenced predictive performance.

9. Future Research Directions

While the proposed SSA–DL hybrid framework has shown promising results, several potential extensions can be explored:

• Hyperparameter Optimization: Future work could employ automated optimization methods, such as Bayesian optimization, grid search, or genetic algorithms, to identify optimal SSA parameters and deep learning architectures, further enhancing model robustness.
• Multimodal Data Integration: Extending the current framework to include fundamental indicators, macroeconomic variables, news sentiment, and social media signals could provide a richer feature set, capturing a more comprehensive view of market dynamics.
• Cross-Market Generalization: Applying the SSA–DL framework to different stock exchanges (e.g., NYSE, NASDAQ, or FTSE) or to other asset classes such as commodities, cryptocurrencies, or exchange-traded funds (ETFs) could test the model’s generalizability across diverse markets.
• Real-Time and High-Frequency Forecasting: Future studies could adapt the model for real-time prediction or high-frequency trading, incorporating adaptive learning mechanisms to respond to rapidly changing market conditions.
• Explainable AI (XAI) and Interpretability: Incorporating interpretability techniques, such as SHAP or LIME, could help explain how the SSA–DL model generates predictions, increasing its transparency and trustworthiness for practitioners and regulators.
• Seasonality: Results from different seasons and diverse datasets to provide a more comprehensive evaluation.
• Experiments using Filtering: A comprehensive comparison with other filtering methods that isolate the effect of each block in the pipeline.
• Extension of framework: Link the framework more explicitly to organizational decision-making processes (such as rebalancing and scaling), using model governance practices, and relevant regulatory considerations
• Future research could employ statistical tests such as the Diebold-Mariano or paired t-tests to confirm whether the observed improvements are statistically meaningful. This addition would enhance the robustness of the performance comparison and provide stronger empirical support for the model’s effectiveness.
• While the current study focuses on 63-day, 252-day and 504-day metrics to provide a clear overview of the strategy’s overall returns and risk, we acknowledge that more detailed temporal analysis such as monthly or quarterly returns and could offer additional insights into performance stability. Examining these intra-year dynamics and their potential correlation with specific market regimes, including bear markets or periods of high volatility, represents a valuable direction for future research.
• While the current study compares the proposed strategy to a passive investment in the ASX50 index, we acknowledge that comparisons with simpler daily selection benchmarks such as a one-day momentum or randomly selected stock portfolio could provide additional insight into the contribution of the predictive model versus the selection mechanism. Exploring such benchmarks represents a valuable direction for future research to further isolate and quantify the “alpha” generated by the model itself.

In summary, this study demonstrates that the SSA–DL hybrid approach not only improves predictive accuracy in noisy financial time series but also translates these improvements into tangible investment benefits, bridging the gap between academic modeling and practical financial decision-making. The future research directions outlined above offer promising avenues for further exploration and refinement of this framework in both academic and professional contexts.