Bayesian Mixture Copula Estimation and Selection with Applications

Abstract

Mixture copulas are popular and essential tools for studying complex dependencies among variables. However, selecting the correct mixture models often involves repeated testing and estimations using criteria such as AIC, which could require effort and time. In this paper, we propose a method that would enable us to select and estimate the correct mixture copulas simultaneously. This is accomplished by first overfitting the model and then conducting the Bayesian estimations. We verify the correctness of our approach by numerical simulations. Finally, the real data analysis is performed by studying the dependencies among three major financial markets.

1. Introduction

Copula functions are important tools for detecting and modeling statistical relations. While the Pearson correlation remains popular among the applied sciences because of its simplicity, its shortcomings become undeniable in the task of constructing nonlinear behavior; see Murphy [1] (Section 2.5.1) for the undesirable results of using the Pearson correlation in the case of non-linearity. On the other hand, copula functions fully describe the connection between random variables by forming their joint distribution from their univariate margins. Mathematically speaking, following from McNeil et al. [2] (p. 221), a d-dimensional copula $C(u_1,u_2,\dots ,u_d)$:${[0,1]}^d\to [0,1]$ is a distribution function with uniform margins. That is, there exists $U_1,U_2,\dots ,U_d$ uniformly distributed such that $C(u_1,u_2,\dots ,u_d)=\mathcal{P}(U_1\le u_1,U_2\le u_2,\dots ,U_d\le u_d)$. The important Sklar theorem [3] guarantees the validity and usefulness of the copula functions in modeling the co-movement among random variables. It states that for the random variables $X_1,X_2,\dots ,X_d$ with the distribution function $F_d(x_1,x_2,\dots ,x_d)$, there exists a copula function, uniquely defined up to Range $\left(F_1\right)$ × Range $\left(F_2\right)$ ×…Range $\left(F_d\right)$ such that $F_d(x_1,x_2,\dots ,x_d)=C(F_1\left(x_1\right),F_2\left(x_2\right),\dots ,F_d\left(x_d\right))$, where $C(·)$ refers to a d-dimensional copula function. See Embrechts [4] for a careful introduction to the concepts and theorems related to the Sklar theorem with applications in financial risk management.

When applying the copula methods to real life, such as modeling the dependence between global trading markets, it is often insufficient to rely on a single parametric copula family because of the data complexity and heterogeneity. A possible remedy is to use mixture modeling; McLachlan et al. [5] give a recent comprehensive review of this classic statistical topic. In terms of the copula functions, we are therefore motivated to write a copula function as the mixture of others:

$$C_{\mathrm{mix}}\left(\mathbf{u}\right)=\sum _{j=1}^K{w}_j{C}_j(\mathbf{u};{\mathit{\alpha }}_j)\mathbf{u}\in {\mathbb{R}}^d,{\mathit{\alpha }}_j\in {\Theta }_j,\sum _j{w}_j=1$$

(1)

where we denote ${\Theta }_j$ to be the parameter space of the copula j and it is straightforward to verify that (1) is also a copula. In most of the research papers regarding the topics of finite mixture models, it is common to assume that the mixed distributions come from the same parametric family. This is also mentioned in [5,6]. However, in the literature on copula methods, mixture copulas consisting of several parametric copula families are also common. Hu [7] is one of a few pioneering works of the mixture copula application in the field of finance. The author used mixed normal Gumbel/survival Gumbel copula with empirical marginal distributions to model the stock dependence between the FTSE 100 of the UK, Nikkei 225 of Japan, S&P 500 of the USA, and Hang Seng of Hong Kong, S.A.R., and quasi-likelihood was used for parameter estimation, and the chi-square test was applied for the goodness of fit. Arakelian and Karlis [8] use the expectation maximization (E.M.) approach to estimate the mixture copula with two components and use them to detect the changing dependence between financial markets, the combination of the Gaussian, Clayton, and Gumbel copulas is mainly considered there, and the model selection criteria is log-likelihood. Vrac et al. [9] combined the dynamic clustering with the gradient ascent to solve the mixture copula; Frank copula family with nonparametric margins are used in their geographical application, and the best model is selected by minimizing the approximate weight of evidence (A.W.E.), which is defined to be $A.W.E.=-\mathrm{MLE}+{\sum }_i^K\dim \left|{\Theta }_i\right|(logN+3/2)$. Given the number of mixture components is correct, the asymptotic convergence of their methods is finally obtained. More recently, Liu et al. [10] proposed constructing the semi-parametric conditional mixture copulas to assess the global currency market; their best models are selected by comparing the Bayes information criterion (B.I.C.), and asymptotic consistency is obtained.

The topics discussed in this essay are mixture copula estimation and selection using the Bayesian approach. Some previous works regarding Bayesian copula selections include [11], where the author treats the copula parameters as a nuisance and selects the copula with the highest posterior. That is, for the model ${\mathcal{M}}_l$ and the data $\mathcal{D}$

$${\mathcal{M}}_{best}={\mathrm{argmax}}_{{\mathcal{M}}_l}\mathcal{P}({\mathcal{M}}_l\mid \mathcal{D})={\mathrm{argmax}}_{{\mathcal{M}}_l}\int \mathcal{P}(\mathcal{D}\mid \mathit{\theta },{\mathcal{M}}_l)dF\left(\mathit{\theta }\right)p\left({\mathcal{M}}_l\right).$$

Their method is free from estimating the copula parameters. However, on the other hand, this selection approach may experience high variance in the case of small data sets with high dimensional copulas, and the computational round-off error becomes significant when we multiply the probability if the data set is large. Silva and Lopes [12] proposed to select the model using deviance information criteria (D.I.C.), expected Bayes information criteria (EBIC), and expected Akaike information criteria (EAIC). They also pointed out the importance of the joint estimation of copula parameters using the Bayesian approach from the perspective of considering parameter dependence. Their work can be viewed as the Bayesian version of the popular frequentist A.I.C. (B.I.C.) approaches. One potential concern here is the trade-off between the computational load and the selection efficiency compared with the classic approach. Wu et al. [13,14] proposed to use the Dirichlet process and select the correct mixture copula from the infinite model. Their methods unify the parameter estimation and the best model selection, and we consider this feature to be convenient and important.

On the other hand, Wu et al.’s [13,14] methods are more suitable for the mixture models where each component is from the same parametric family. For example, $C_{mix}=\sum w_{j}C(u,{\mathit{\theta }}_j)$ with $C(·,{\mathit{\theta }}_j)$ belongs to the normal copula for any j. In copula research, it is interesting and meaningful to consider the mixed model with heterogeneous mixture components because the dependence on real data sets is complex and ever-changing. Therefore, we propose to use the Bayesian Monte Carlo sampling approaches so that the copula parameters and the correct heterogeneous components can be determined at once. This is simply performed by writing out the saturated mixture models with all possible components included and estimating it with the Bayesian approaches, which is expected to have more stable behavior than the maximum-likelihood methods [15].

Following the introduction, we proceed to outline some classic parametric copula families, and in Section 3, we present our sampling methods here, including how we overfit the model first and estimate the parameters by using the Bayesian modeling. Connection of our approach with the penalized likelihood method from Wang [16], Cai, and Wang [17] has also been made through the E.M. method. The last two sections are for numerical simulations and real data analysis.

2. Parametric Copula Families

2.1. Elliptical Copulas

The elliptical copulas are one of the most common choices for modeling the dependence structures among variables, especially in high dimensional settings [18]. From the Sklar theorem, copulas are of the form

$$C(u_1,u_2,\dots ,u_d)=F(F_1^{-1}\left(u_1\right),F_2^{-1}\left(u_2\right),\cdots ,F_d^{-1}\left(u_d\right)).$$

(2)

Since the elliptical distribution is closed under the marginalization, we can therefore get the corresponding parametric copula implicitly defined by (2). For example, by inverting the marginal of the standard multivariate normal distribution, we obtain the normal copula, which is

$$\begin{array}{c}\hfill \begin{array}{c}\hfill C_C(u_1,u_2,\dots ,u_d)={\int }_{-\infty }^{{\varphi }^{-1}\left(u_d\right)}\cdots {\int }_{-\infty }^{{\varphi }^{-1}\left(u_1\right)}{\left({\left(2\pi \right)}^d\left|C\right|\right)}^{-1/2}exp\left(-\frac{1}{2}{\mathit{x}}^{\prime }{C}^{-1}\mathit{x}\right)d\mathit{x},\end{array}\end{array}$$

(3)

where C is the positive definite correlation matrix, and $\mathit{x}={({\varphi }^{-1}\left(u_1\right),{\varphi }^{-1}\left(u_2\right),\dots ,{\varphi }^{-1}\left(u_d\right))}^{\prime }$ with $\varphi (·)$ being the quantile function. On the other hand, taking the same action to the multivariate t distribution yields the t copula,

$$\begin{array}{c}\hfill \begin{array}{c}\hfill C_{v,C}(u_1,u_2,\dots ,u_d)={\int }_{-\infty }^{t_v^{-1}(u_d)}\cdots {\int }_{-\infty }^{t_v^{-1}(u_1)}\frac{\Gamma (\frac{1}{2}(v+d))/\Gamma (\frac{v}{2})}{\sqrt{{(\pi v)}^d\left|C\right|}}(1+\frac{{\mathit{y}}^{\prime }{C}^{-1}\mathit{y}}{v})d\mathit{y},\end{array}\end{array}$$

(4)

$t_v^{-1}\left(u_1\right)$ is the quantile function of the univariate standard t distribution with v degree of freedom and $\mathit{y}={(t_v^{-1}\left(u_1\right),t_v^{-1}\left(u_2\right),t_v^{-1}\left(u_3\right),\dots ,t_v^{-1}\left(u_d\right))}^{\prime }$, C is a correlation matrix. The respective copula density $c(·)$ can be obtained due to the differentiation

$$\begin{array}{c}\hfill f(F_1^{-1}\left(u_1\right),F_2^{-1}\left(u_2\right),\dots ,F_d^{-1}\left(u_d\right))=c(u_1,u_2,\dots ,u_d){\displaystyle \prod _{j=1}^d}{f}_j\left(F_j^{-1}\left(u_j\right)\right).\end{array}$$

(5)

One potential advantage of using the t copula (4) over the normal copula is its ability to model the tail dependence. That is, we wish to measure the degree of dependence on the upper tail ${\rho }_u$ and on the lower tail ${\rho }_l$. Taking two dimensional copulas as examples, we have for the corresponding random vector $(X_1,X_2)$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\rho }_l={\displaystyle \underset{u\to 0}{lim}}\mathcal{P}(X_2<F_2^{-1}\left(u\right)\mid X_1<F_1^{-1}\left(u\right))={\displaystyle \underset{u\to 0}{lim}}\frac{C(u,u)}{u}\hfill \\ \hfill & {\rho }_u={\displaystyle \underset{u\to 1}{lim}}\mathcal{P}(X_2>F_2^{-1}\left(u\right)\mid X_1>F_1^{-1}\left(u\right))={\displaystyle \underset{u\to 1}{lim}}\frac{1-2u+C(u,u)}{u}.\hfill \end{array}\end{array}$$

Calculations lead to ${\rho }_l={\rho }_u=0$ for the normal copula but for the t copula with v degree of freedom we have,

$${\rho }_l={\rho }_u=2F_{v+1;t}(-\sqrt{(v+1)(1-c)/(1+c)}),$$

where $F_{v+1;t}(·)$ is the t distribution function with v degree of freedom. One criticism of the elliptical copula families is their symmetric property $c\left(\mathit{u}\right)=c(1-\mathit{u})$, which might be unrealistic for modeling the asymmetrical correlation that often occurs in the financial market [19]. Therefore, many authors have proposed the skewed elliptical copula. Smith et al. [20] proposed the skew t copula and the estimation of the parameters is performed by MCMC. Wu et al. [13] uses a nonparametric Bayesian approach to construct infinite mixture skew normal copula. Wei et al. [21] explored some theoretical properties of the skew-normal copula. Alternatively, Archimedean families of copulas are another solution for the issue.

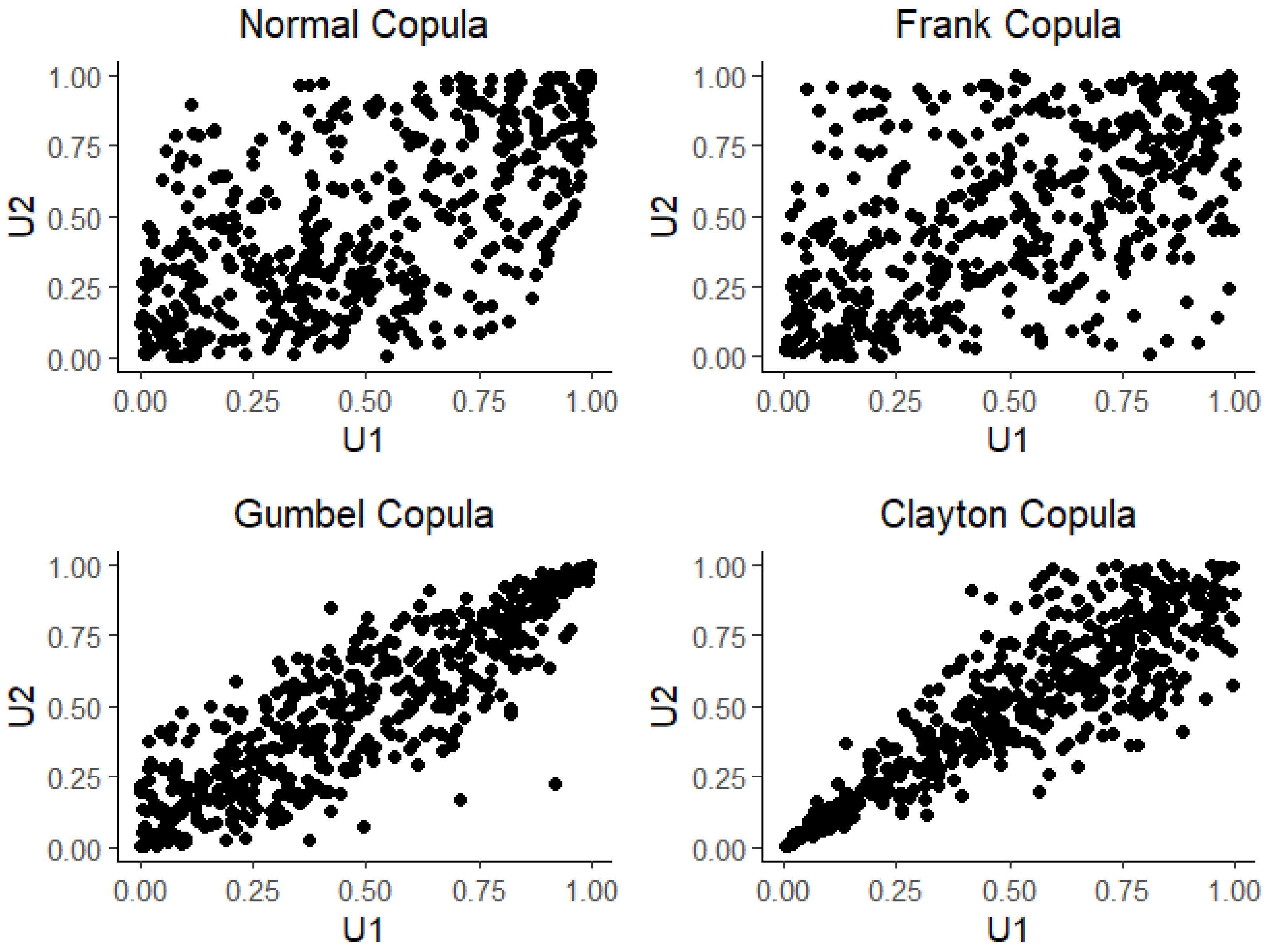
2.2. Archimedean Copulas

Archimedean copulas have been widely researched and applied in the field of credit risk modeling [2]. They can be constructed by satisfying the following linear additive property, that is,

$$\begin{array}{c}\hfill {\phi }^{-1}\left(C(u_1,u_2,\dots ,u_d)\right)={\displaystyle \sum _{i=1}^d}{\phi }^{-1}\left(u_i\right),\end{array}$$

(6)

where $\phi (·):[0,+\infty )\to [0,1]$ is usually called the Archimedean copula generator satisfying convexity, continuity, and completely monotonicity with $\phi \left(0\right)=1$ and ${lim}_{t\to \infty }\phi \left(t\right)=0$. The generator with such properties can be derived from the Laplace transform of the positive random variable X with its distribution function having $F_X\left(0\right)=0$,

$$\phi \left(t\right)={\int }_0^{\infty }exp(-tx)d{F}_X\left(x\right).$$

Taking different forms of $\phi \left(t\right)$ yields different Archimedean families of copulas, a comprehensive table can be found in the textbooks [22] (Table 4.1). We give several copulas that we will use with their generators in

Table 1. Some classic Archimedean families of copulas.

Copula Type	$\mathit{\phi }\left(\mathit{t}\right)$	$\mathit{\theta }$ Range
Frank	${\theta }^{-1}ln\left(\frac{1}{1+(exp(-\theta -t)-exp(-t))}\right)$	$\mathbb{R}\setminus \left\{0\right\}$
Gumbel	$exp(-t^{{\theta }^{-1}})$	$[1,+\infty )$
Clayton $†$	${(1+\theta t)}_{+}^{-{\theta }^{-1}}$	$(0,+\infty )$

^† We denote ${(·)}_{+}:=max(·,0)$.

, and the corresponding distribution function is $C(u_1,\dots ,u_d)=\phi \left({\sum }_{i=1}^d{\phi }^{-1}\left(u_i\right)\right)$.

One noticeable property of the Archimedean copula is its exchangeability. That is, for any permutation $\sigma \left(i\right)$ of $\{1,2,\dots ,d\}$, we have $C(u_1,u_2,\dots ,u_d)=C(u_{\sigma \left(1\right)},u_{\sigma \left(2\right)},\dots ,u_{\sigma \left(d\right)}).$ This characteristic would be attractive for some applications, such as portfolio default modeling in the credit market. However, for the more general purpose, it might be undesirable when we have the copula dimension $d\ge 3$ since this implies that the connection between variables is assumed to be homogeneous. Some improvement has been made on this problem, including nonexchangeable copulas named asymmetric Archimedean copulas [2,23]

$$C^{\mathit{\gamma }}(u_1,u_2,\dots ,u_d)=(\prod _{j=1}^d{u}_j^{{\gamma }_i})C(u_1^{{\gamma }_1},u_2^{{\gamma }_2},\dots ,u_d^{{\gamma }_d}).$$

Otherwise, some amendment in (6) yields so-called nonexchangeable nested Archimedean copula [24].

Different copulas can model different kinds of dependence, and Figure 1 gives us a plot of four different types of copulas. In particular, normal and Frank copulas are symmetric in the sense of $c(1-u_1,1-u_2)=c(u_1,u_2)$ with 0 tail dependence, but the Frank copula was, in addition, proved to be radial symmetric [25]. The Gumbel copula is able to depict the extreme upper tail dependence with $p_u=-2^{{\theta }_{\mathrm{Gumbel}}^{-1}}+2$ but $p_l=0$. Oppositely, the Clayton copula is able to describe the extreme lower tail dependence with $p_l=2^{-{\theta }_{\mathrm{Clayton}}^{-1}}$ for ${\theta }_{\mathrm{Clayton}}>0$, but ${\rho }_u=0$. Hence by mixing those four copulas, setting

$$\begin{array}{c}\hfill C_{\mathrm{mix}}(u_1,u_2)=w_1{C}_{\mathrm{fr}}(u_1,u_2)+w_2{C}_{\mathrm{No}}(u_1,u_2)+w_3{C}_{\mathrm{Cl}}(u_1,u_2)+w_4{C}_{\mathrm{Gu}}(u_1,u_2),\end{array}$$

(7)

We would be able to reconstruct vast amounts of nontrivial dependence from here [17].

3. Estimation and Selection

The main model we use to conduct simulations and real data analysis is (7). We also work with three-dimensional mixture Gaussian copulas in Section 4.3 to demonstrate the application of our approach in the higher dimensional situation. The general starting point is to construct the model by writing out

$$\begin{array}{c}\hfill C_{mix}\left(\mathit{u}\right)={\displaystyle \sum _{j=1}^K}{w}_j{C}_j(\mathit{u};{\mathit{\theta }}_j),\end{array}$$

(8)

with the knowledge that a true model has the form

$$C^0\left(\mathit{u}\right)=\sum _{j=1}^{K^{\prime }}{w}_j{C}_j(\mathit{u};{\mathit{\theta }}_j^0),\mathrm{for}{K}^{\prime }\le K.$$

We then proceed to directly estimate (8) by the Bayesian approach, where $C_j(·), C_k(·)$ for any $j,k\le K$ can either from the same parametric family or not, although for the former case, one needs to take extra measures for the label switching problems [6] (Section 22.3). Rousseau and Mengersen [15] showed that by applying this approach to the standard finite mixture distribution, it would clear out the redundant components asymptotically. In particular, they showed for $\mathit{w}=(w_1,w_2,\dots ,w_K)\sim \mathrm{Dirichlet}({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_K)$ with $\dim \left({\mathit{\theta }}_{\mathit{j}}\right)/2$ plus some other regularity conditions, the posterior estimation of weights has the property ${\sum }_{j=K^{\prime }+1}^{K}E\left[w_j\right|D]=O_P(1/\sqrt{n})$. This result has shown us the extra stability of the Bayesian estimation due to its shrinkage property compared with the maximum likelihood approach (MLE) since the MLE of an over-fitted model only guarantees the convergence to an unidentifiable set with the limiting distribution $C_{\infty }(·)=C^0(·)$ in the domain as $n\to \infty$ [26]. However, the asymptotic results do not guarantee sparsity. This would cause a failure to identify the correct number of components if, for example, $i,j,k\le K$, $w_i{C}_i\left(u\right)+w_j{C}_j\left(u\right)=w_k{C}_k\left(u\right)$ is achievable in the model setting.

On the other hand, Cai and Wang [17] approached the mixed copula estimation and selection problem using penalized MLE approach. In terms of its nature, this approach is quite similar to Bayesian estimation. However, the authors only applied penalties to the weighting parameters, whereas the Bayesian counterpart typically applies penalties to all parameters. The connection between these two approaches is established using the expectation maximization (EM) approach of the posterior, as outlined at the end of Section 3.2, where we compare the maximization form of the posterior mode and the penalized MLE.

3.1. Markov Chain Monte Carlo

We show the sampling algorithm of the model (7), but the spirit of the estimation remains the same for all forms of (8). It is especially straightforward to extend the work to the high dimensional implicit copulas [27], including some skew elliptical copulas by minor modifications. Hence, the validity of the approaches remains valid in high-dimensional settings.

In most cases, for the data $D_n=\{X_1,X_2,\dots ,X_n\}$ where $X_i\in R^d$, we do not have any additional information regarding the marginal distributions. Therefore, it would be necessary to estimate them together or treat them as nuisance parameters using the nonparametric approach. That is, we either specify the marginal parametric model so that the likelihood for the i.i.d data is

$$p(D_n\mid \mathit{\alpha },{\mathit{\theta }}_{mix})=\prod _{i=1}^n{c}_{mix}(F_1(X_{i1};{\mathit{\alpha }}_{\mathbf{1}}),F_2(X_{i2};{\mathit{\alpha }}_{\mathbf{2}}),\dots ,F_d(X_{id};{\mathit{\alpha }}_{\mathit{d}});{\mathit{\theta }}_{mix})\prod _{j=1}^d{f}_j(X_{ij};{\mathit{\alpha }}_{\mathbf{1}}).$$

Or, to avoid misspecification of the marginal models, we use the semiparametric approach. The pseudo-likelihood for the i.i.d data is

$$p\left(D_n\right|{\mathit{\theta }}_{mix})\propto \prod _{i=1}^n{c}_{mix}({\widehat{F}}_{n1}\left(X_{i1}\right),{\widehat{F}}_{n2}\left(X_{i2}\right),\dots ,{\widehat{F}}_{nd}\left(X_{id}\right);{\mathit{\theta }}_{mix})$$

where we have

$${\widehat{F}}_{nj}\left(x\right)=\frac{1}{n+1}\sum _{i=1}^n\mathbb{I}(X_{ij}<x).$$

Other alternatives of the margins ${\widehat{F}}_n=({\widehat{F}}_{n1},{\widehat{F}}_{n2},\dots ,{\widehat{F}}_{nd})$ such as kernel density estimations are also available [28]. Therefore, only ${\mathit{\theta }}_{mix}$ is estimated here. In this paper, we focus on the discussion of semiparametric cases.

We specifying the prior of $\mathit{w}$ and ${\mathit{\theta }}_{mix}$ with

$$\begin{array}{cc}\hfill & \pi \left(\mathit{w}\right)\sim Dir({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_K)\hfill \\ \hfill & \pi \left({\mathit{\theta }}_{mix}\right)\sim N_d(\mathbf{0},I_d)\hfill \end{array}$$

Note that for any copula parameters which do not have the range $(-\infty ,+\infty )$, when convenient, we transfer them from the original parameter space to $\mathcal{R}$ so that $\theta =\varphi \left({\theta }_0\right)\in (-\infty ,+\infty )$. Hence, we will be able to unify the prior to be normal. In case of the model (7), denote ${\mathit{\theta }}_{mix}\in {(-\infty ,+\infty )}^d$, the original parameters can be obtained by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\theta }_{\mathrm{clayton}}^{\mathrm{ori}}=exp\left({\theta }_{\mathrm{mixclayton}}\right)\hfill \\ \hfill & {\theta }_{\mathrm{gumbel}}^{\mathrm{ori}}=exp\left({\theta }_{\mathrm{mixgumbel}}\right)+1\hfill \\ \hfill & {\theta }_{\mathrm{normal}}^{\mathrm{ori}}=\frac{1-exp(-{\theta }_{\mathrm{mixnormal}})}{1+exp(-{\theta }_{\mathrm{mixnormal}})}.\hfill \\ \hfill & {\theta }_{\mathrm{frank}}^{\mathrm{ori}}={\theta }_{\mathrm{mixfrank}}\hfill \end{array}\end{array}$$

(9)

where ${\theta }^{\mathit{o}ri}$ refer to the parameters in the classical copula settings. We augment our data to $(X_i,Z_i)$, where $Z_i$ denotes the cluster of the point i, so that $p(X_i\mid Z_i=k,{\mathit{\theta }}_{mix})\propto c_k(F\left(X_i\right);{\mathit{\theta }}_k)$. The Metropolis–Hasting algorithm of sampling the posterior $p({\mathit{\theta }}_{mix},\mathit{w}\mid D_n)$ follows as:

• Setting initial values ${\mathit{\theta }}_{mix}^{\left(0\right)},{\mathit{w}}^{\left(0\right)}$.
• Denote the current round to be t, iteratively updating $Z_i^{\left(t\right)}$ such that $p(Z_i^{\left(t\right)}\mid {\mathit{Z}}_{\setminus \mathit{i}}^{\left(\mathit{t}\right)},{\mathit{D}}_{\mathit{n}},\mathit{w})$
  $\propto p(X_i\mid {\mathit{Z}}^{\left(t\right)},\mathit{w})p(Z_i^{\left(t\right)}\mid \mathit{w})$ for $i=1,2,\dots ,n$ using Gibbs procedure; this can be sampled from the multinomial distribution with $p_k=\frac{w_k{c}_k({\widehat{F}}_n\left(X_i\right)\mid {\theta }_k)}{{\sum }_i{w}_{i}c({\widehat{F}}_n\left(X_i\right)\mid {\theta }_i)}$ with $k=1,2,\dots ,K$.
• For all $i=1,2,\dots ,K$ , we propose $f({\theta }_i^{*}\mid {\theta }_i^{t-1})\sim N_d({\mathit{\theta }}_i^{t-1},\widehat{\Sigma })$ where $\widehat{\Sigma }$ is updated every 50 iterations from the sample variance of previously accepted points. We accept the ${\theta }_i^{*}={\theta }_i^t$ with the acceptance rate

  $$a_i=\frac{{\prod }_{j=1}^{n_i}{c}_i(X_{ij};{\theta }_i^{*})\pi \left({\theta }_i^{*}\right)f({\theta }_i^{t-1}\mid {\theta }_i^{*})}{{\prod }_{j=1}^{n_i}{c}_i(X_{ij};{\theta }_i^{t-1})\pi \left({\theta }_i^{t-1}\right)f({\theta }_i^{*}\mid {\theta }_i^{t-1})}.$$
• Update $\mathit{w}\sim Dir({\alpha }_1+{\sum }_{i=1}^n\mathbb{I}\left(Z_i^{\left(t\right)}=1\right),\dots ,{\alpha }_K+{\sum }_{i=1}^n\mathbb{I}\left(Z_i^{\left(t\right)}=K\right))$.
• Repeat steps 2–4 until the stopping criteria are reached, for example, after 10,000 iterations. The MCMC method would be sufficient for our purpose. However, by setting up the EM method for the posterior mode, we can bridge between the Bayesian methods and the penalized likelihood methods discussed in [16,17]. In addition, if the gradient information of the copula is available, it would be faster to work with the EM to get the parameter estimations.

3.2. EM Algorithm

Start from the complete data $(X_i,Z_i)$ where $Z_i$ is the cluster label as previously. Therefore, we denote $Q\left(Z\right):=logp(\mathit{w},{\mathit{\theta }}_{mix},Z|X)$; our goal is to work iteratively so that

$$\begin{array}{c}\hfill (w^{t+1},{\theta }^{t+1})={\mathrm{argmax}}_{\theta ,\mathit{w}}\int Q\left(Z\right)p(Z\mid X,{\mathit{\theta }}_{mix}^t,{\mathit{w}}^t)dZ={\mathrm{argmax}}_{\theta ,\mathit{w}}{E}_{p\left(Z\right|X,{\mathit{\theta }}_{mix}^t,{\mathit{w}}^t)}\left(Q\right)\end{array}$$

(10)

In more detail,

$$\begin{array}{cc}\hfill & Q\left(Z\right)=logp(\mathit{w},{\mathit{\theta }}_{mix},Z|X)\hfill \\ & \propto logp\left(X\right|\mathit{w},{\mathit{\theta }}_{mix},Z)+logp\left(Z\right|\mathit{w})+logp(\mathit{w},{\mathit{\theta }}_{mix})\hfill \\ \hfill & \propto log{\displaystyle \prod _{i=1}^n}{\displaystyle \prod _{j=1}^K}{c}_j{(F_n\left(X_i\right);{\theta }_j)}^{\mathbb{I}(Z_i=j)}+log{\displaystyle \prod _{i=1}^n}{\displaystyle \prod _{j=1}^K}{w}_j^{\mathbb{I}(Z_i=j)}\hfill \\ \hfill & +log{\displaystyle \prod _{j=1}^K}{w}_j^{({\alpha }_j-1)}-{\displaystyle \sum _{j=1}^K}\frac{1}{2}\left|\right|{\theta }_j{\left|\right|}^2+C,\hfill \end{array}$$

where we have denoted the irrelevant constant to be C, and $p(\mathit{w},{\mathit{\theta }}_{mix})=p\left(\mathit{w}\right)p\left({\mathit{\theta }}_{mix}\right)$.

Hence, we take the expectation so that the argmax of (10) would be equivalent as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\mathrm{argmax}}_{\mathit{w},{\mathit{\theta }}_{mix}}{\displaystyle \sum _{i,j}}log{c}_j({\widehat{F}}_n\left(X_i\right);{\theta }_j)E\left(\mathbb{I}(Z_i=j)\right)\hfill \\ & +{\displaystyle \sum _{i,j}}E\left(\mathbb{I}(Z_i=j)\right)log{w}_j+{\displaystyle \sum _{j=1}^K}({\alpha }_j-1)log{w}_j-{\displaystyle \sum _{j=1}^K}\frac{1}{2}\left|\right|{\theta }_j{\left|\right|}^2\hfill \\ \hfill & ={\displaystyle \sum _{i,j}}{r}_{ij}^{t}log{c}_j({\widehat{F}}_n\left(X_i\right);{\theta }_j)+n{\displaystyle \sum _{i,j}}{r}_{ij}^{t}log{w}_j-(1-\frac{1}{K}){\displaystyle \sum _j}log{w}_j-{\displaystyle \sum _j}\frac{1}{2}\left|\right|{\theta }_j{\left|\right|}^2,\hfill \end{array}\end{array}$$

(11)

where we have taken ${\alpha }_j=1/K$ to make it less informative while satisfying the regularity condition of [15] and

$$r_{ij}^t=\frac{w_j^t{c}_j\left(y_i\right|{\theta }_j^t)}{{\sum }_j{w}_j^t{f}_j\left(y_i\right|{\theta }_j^t)}$$

To achieve the maximum, we differentiate with respect to $w_j$ while adding the Lagrange multiplier $\lambda (1-\sum w_j)$, we have

$$\begin{array}{c}\hfill w_j^{t+1}=\frac{1}{N+1-K}\left({\displaystyle \sum _i}\frac{w_j^t{c}_j\left(y_i\right|{\theta }_j^t)}{{\sum }_j{w}_j^t{f}_j\left(y_i\right|{\theta }_j^t)}-(1-\frac{1}{K})\right).\end{array}$$

(12)

Differentiate with respect to ${\theta }_j$, and it can be solved numerically using quasi-Newton methods.

We note that the goal of the EM method is to find the mode of the log posterior

$$\begin{array}{cc}\hfill logp(\mathit{w},{\mathit{\theta }}_{mix}|X)& \propto {\displaystyle \sum _i}log{\displaystyle \sum _j}{w}_j{c}_{ij}({\widehat{F}}_n\left(X\right);{\theta }_j)-(1-\frac{1}{K}){\displaystyle \sum _j}log{w}_j-{\displaystyle \sum _j}\frac{1}{2}\left|\right|{\theta }_j{\left|\right|}^2\hfill \\ & ={\displaystyle \sum _i}log{\displaystyle \sum _j}{w}_j{c}_{ij}({\widehat{F}}_n\left(X\right);{\theta }_j)-n{\displaystyle \sum _j}{\Omega }_{(1-1/K)}^{\mathit{w}}\left(w_j\right)-n{\displaystyle \sum _j}{\Omega }_{(1/2)}^{{\mathit{\theta }}_{mix}}\left({\theta }_j\right),\hfill \end{array}$$

(13)

This form shares a similar structure as (3.2) in [16] or (3) in [17] despite the fact that they do not penalize the copula parameters. Intuitively, it would be beneficial to penalize them in order to regularize the parameters of $C_j(·)$ when this copula has 0 weightings. Wang [16] proved the $\sqrt{n}$—asymptotic consistency and sparsity of their semiparametric SCAD-penalized likelihood approaches. The consistency of our Bayesian methods will be tested empirically in the next part. However, the theoretical demonstrations are more challenging to consider with Dirichlet distribution priors due to the singularity of $log{w}_i$ at $w_i=0$ [29].

One shortcoming of using the EM method is the difficulty in obtaining the confidence interval of estimators. Bootstrap could be a very computationally intensive solution. On the other hand, one may consider the fisher information matrix $-\nabla {\nabla }_{\mathit{w},\mathit{\theta }}logp(X\mid \widehat{\mathit{w}},{\widehat{\mathit{\theta }}}_{\mathit{mix}})$ as an asymptotic approximation of the precision matrix. Gelman et al. [6] (p. 324) provide an approach to iteratively calculate the asymptotic variance matrix along with the parameter estimations.

4. Numerical Simulations

4.1. Markov Chain Monte Carlo

We perform two types of numerical simulations. Firstly, we assume that the marginal distributions of the data are perfectly known. Therefore, we focus on the estimation of the copula using the data $(U_{i1},U_{i2},\dots ,U_{id})=(F_{i1}\left(X_1\right),F_{i2}\left(X_2\right),\dots ,F_{id}\left(X_d\right))$ for $i=1,2,\dots ,n$. the dimension d is set to be 2 for our simulation purpose. Our working model is (7). That is,

$$\begin{array}{c}\hfill C_{\mathrm{mix}}(u_1,u_2)=w_1{C}_{\mathrm{fr}}(u_1,u_2)+w_2{C}_{\mathrm{No}}(u_1,u_2)+w_3{C}_{\mathrm{Cl}}(u_1,u_2)+w_4{C}_{\mathrm{Gu}}(u_1,u_2).\end{array}$$

We sample the data from different true models, which are submodels of (7), and we estimate them using the MCMC method of Section 3.1. Secondly, we assume that the marginal distributions are unknown, we hence estimate the margins empirically using ${\widehat{F}}_{np}\left(x\right)=\frac{1}{n+1}{\sum }_{i=1}^n\mathbb{I}(X_{ip}\le x)$. Thus, we have $({\widehat{U}}_{i1},{\widehat{U}}_{i2},\dots ,{\widehat{U}}_{id})=({\widehat{F}}_{i1}\left(X_1\right),{\widehat{F}}_{i2}\left(X_2\right),\dots ,{\widehat{F}}_{id}\left(X_d\right))$ for $i=1,2,\dots ,n$ and the copula parameters can be estimated thereafter.

We simulate 3000 iterations for all models, with the first 2500 points discarded as the burning stage. The number of the sample points is $n=400,800,2000$.

Table 2. MCMC estimations of the copula with the marginal distributions fully known. The numbers inside parentheses indicate standard errors, and estimations of the true components are denoted in bold font.

True Copula (Param)
		MCMC Estimation
	$\mathit{n}$	Clayton		Gumbel		Normal		Frank
		$\mathit{w}$	$\mathit{\theta }$	$\mathit{w}$	$\mathit{\theta }$	$\mathit{w}$	$\mathit{\theta }$	$\mathit{w}$	$\mathit{\theta }$
Normal (0.5)	400	0.089 (0.088)	1.568 (1.670)	0.047 (0.036)	3.801 (2.750)	0.839 (0.105)	0.444 (0.046)	0.025 (0.032)	−0.029 (0.994)
	800	0.0439 (0.066)	1.173 (1.586)	0.007 (0.011)	2.494 (1.370)	0.940 (0.066)	0.514 (0.026)	0.009 (0.014)	0.113 (0.916)
	2000	0.039 (0.049)	1.363 (1.424)	0.028 (0.034)	3.087 (1.968)	0.913 (0.063)	0.494 (0.024)	0.020 (0.038)	0.043 (1.120)
Clayton (5)	400	0.990 (0.011)	4.914 (0.246)	0.005 (0.010)	2.490 (1.612)	0.003 (0.005)	0.526 (0.224)	0.002 (0.003)	0.012 (0.965)
	800	0.992 (0.009)	4.876 (0.185)	0.003 (0.006)	2.641 (1.774)	0.003 (0.005)	0.488 (0.207)	0.002 (0.004)	0.037 (0.944)
	2000	0.996 (0.003)	5.091 (0.133)	0.001 (0.002)	2.411 (1.569)	0.001 (0.002)	0.568 (0.205)	0.001 (0.001)	−0.198 (0.983)
Gumbel (2.5)	400	0.017 (0.027)	1.676 (1.505)	0.957 (0.038)	2.486 (0.105)	0.022 (0.033)	0.530 (0.210)	0.004 (0.007)	0.080 (1.002)
	800	0.002 (0.004)	1.480 (1.593)	0.991 (0.009)	2.701 (0.071)	0.004 (0.007)	0.545 (0.210)	0.002 (0.005)	0.070 (1.051)
	2000	0.006 (0.008)	1.442 (1.268)	0.988 (0.014)	2.470 (0.048)	0.005 (0.011)	0.533 (0.194)	0.001 (0.002)	−0.091 (0.968)
Frank (5)	400	0.061 (0.083)	1.903 (1.512)	0.030 (0.041)	2.386 (2.115)	0.875 (0.087)	0.647 (0.038)	0.033 (0.047)	0.416 (1.037)
	800	0.058 (0.041)	3.774 (2.751)	0.019 (0.039)	2.324 (2.043)	0.899 (0.055)	0.603 (0.031)	0.024 (0.031)	0.280 (0.984)
	2000	0.007 (0.012)	1.358 (1.223)	0.004 (0.007)	2.255 (1.394)	0.205 (0.055)	0.790 (0.041)	0.784 (0.058)	4.408 (0.285)
0.5 Gumbel (2.5) + 0.5 Clayton (5)	400	0.439 (0.057)	6.079 (0.761)	0.533 (0.059)	2.756 (0.242)	0.024 (0.036)	0.569 (0.207)	0.004 (0.007)	0.176 (1.003)
	800	0.567 (0.034)	5.332 (0.390)	0.429 (0.040)	2.328 (0.143)	0.002 (0.004)	0.514 (0.210)	0.002 (0.004)	0.126 (0.976)
	2000	0.509 (0.034)	5.111 (0.356)	0.480 (0.032)	2.505 (0.076)	0.005 (0.008)	0.523 (0.200)	0.006 (0.007)	0.182 (1.005)
0.5 Clayton (5) + 0.5 Normal (0.5)	400	0.513 (0.087)	5.150 (1.054)	0.061 (0.070)	2.606 (2.353)	0.383 (0.095)	0.554 (0.080)	0.044 (0.067)	0.280 (1.036)
	800	0.573 (0.041)	4.107 (0.336)	0.165 (0.079)	1.833 (0.534)	0.191 (0.144)	0.410 (0.126)	0.069 (0.086)	0.365 (1.028)
	2000	0.456 (0.035)	5.500 (0.372)	0.069 (0.046)	2.750 (0.788)	0.473 (0.035)	0.466 (0.035)	0.002 (0.003)	−0.105 (0.941)

and

Table 3. MCMC estimations of the copula with the marginal distributions estimated by empirical distribution. The numbers inside parentheses indicate standard errors, and estimations of the true components are denoted in bold font. The corresponding true marginal distribution is N(1, 1) and N(0.5, 1).

True Copula (Param)
		MCMC Estimation
	$\mathbf{n}$	Clayton		Gumbel		Normal		Frank
		$\mathit{w}$	$\mathit{\theta }$	$\mathit{w}$	$\mathit{\theta }$	$\mathit{w}$	$\mathit{\theta }$	$\mathit{w}$	$\mathit{\theta }$
Normal (0.5)	400	0.003 (0.005)	1.637 (1.785)	0.114 (0.125)	2.015 (1.073)	0.878 (0.124)	0.590 (0.038)	0.005 (0.009)	0.064 (0.993)
	800	0.08 (0.08)	1.543 (1.321)	0.008 (0.011)	2.569 (1.758)	0.886 (0.102)	0.568 (0.033)	0.026 (0.037)	0.246 (1.054)
	2000	0.025 (0.039)	0.845 (1.039)	0.021 (0.021)	1.740 (0.786)	0.952 (0.048)	0.541 (0.022)	0.002 (0.004)	−0.072 (0.951)
Clayton(5)	400	0.987 (0.015)	4.856 (0.240)	0.006 (0.014)	2.648 (1.718)	0.004 (0.007)	0.530 (0.204)	0.002 (0.004)	0.061 (0.929)
	800	0.994 (0.006)	4.733 (0.185)	0.003 (0.005)	2.957 (1.793)	0.001 (0.002)	0.499 (0.226)	0.001 (0.003)	−0.050 (1.023)
	2000	0.996 (0.004)	5.423 (0.130)	0.002 (0.004)	3.438 (2.236)	0.001 (0.002)	0.539 (0.197)	0.001 (0.001)	−0.088 (0.959)
Gumbel (2.5)	400	0.009 (0.018)	1.589 (1.533)	0.971 (0.034)	2.830 (0.122)	0.018 (0.031)	0.554 (0.190)	0.002 (0.004)	−0.104 (1.088)
	800	0.005 (0.007)	2.293 (2.862)	0.981 (0.021)	2.652 (0.084)	0.012 (0.019)	0.484 (0.199)	0.002 (0.003)	0.076 (0.931)
	2000	0.004 (0.008)	2.295 (2.647)	0.993 (0.008)	2.530 (0.044)	0.001 (0.001)	0.522 (0.216)	0.002 (0.004)	0.156 (0.962)
Frank (5)	400	0.012 (0.016)	2.220 (2.809)	0.096 (0.099)	2.333 (1.019)	0.005 (0.010)	0.532 (0.197)	0.887 (0.094)	4.533 (0.376)
	800	0.147 (0.044)	4.664 (1.414)	0.006 (0.011)	2.430 (1.634)	0.836 (0.048)	0.599 (0.028)	0.011 (0.018)	0.145 (1.028)
	2000	0.005 (0.007)	2.334 (3.135)	0.050 (0.028)	2.659 (0.833)	0.016 (0.024)	0.453 (0.208)	0.929 (0.023)	5.107 (0.281)
0.5 Gumbel (2.5) + 0.5 Clayton (5)	400	0.551 (0.085)	4.327 (0.556)	0.363 (0.129)	2.586 (0.276)	0.080 (0.135)	0.603 (0.206)	0.006 (0.009)	0.072 (1.071)
	800	0.413 (0.046)	5.149 (0.526)	0.538 (0.060)	2.645 (0.167)	0.050 (0.050)	0.558 (0.211)	0.003 (0.007)	−0.031 (1.136)
	2000	0.531 (0.030)	4.792 (0.270)	0.464 (0.031)	2.500 (0.089)	0.004 (0.008)	0.508 (0.197)	0.001 (0.002)	0.104 (1.026)
0.5 Clayton (5) + 0.5 Normal (0.5)	400	0.502 (0.082)	4.871 (0.992)	0.044 (0.077)	2.376 (1.230)	0.450 (0.109)	0.488 (0.077)	0.005 (0.009)	−0.122 (0.960)
	800	0.526 (0.042)	5.321 (0.461)	0.015 (0.020)	2.841 (1.888)	0.444 (0.054)	0.485 (0.048)	0.015 (0.026)	0.065 (1.021)
	2000	0.534 (0.034)	4.725 (0.325)	0.106 (0.058)	1.751 (0.353)	0.351 (0.070)	0.512 (0.060)	0.009 (0.011)	0.015 (0.966)

display the simulation results. In general, the weighting parameters as well as the copula parameters of non-zero weighting components approach the truth with decreasing Monte Carlo standard deviation. The mean and error estimations of the copula parameters with zero weightings remain close to its priors, which might be considered as an advantage over the penalized method used in [16,17] as they proved that the zero weighting copula parameters would end up randomly in their parameter spaces by using their penalized likelihood approach. Three major misidentification cases were found in tables, that is, $n=400,800$ of Frank copulas simulations in Table 2 and $n=800$ of Frank copulas in the Table 3. All cases mentioned seem to be misidentified as normal copulas, which are understandable as the normal copula and Frank copula share very similar structures with zero tail dependence.

4.2. Expectaion Maximization

In this part, we investigate the performances of the EM algorithm introduced in Section 3.2. The approach is computationally demanding. Therefore, we only show the results with the sample size of $n=200,400,800$ for one-component copulas. Data are generated directly from the true copula models. More specifically, for each sample size of $n=200,400,800$, we generate 10 batches of data from the true distribution. Every batch is learned by the EM method, and the stopping criteria are 1000 full iterations or the absolute sum of the parameters increase less than $0.001$ for an iteration. We calculate the mean and variance estimators for each sample size.

Table 4. EM estimations of the copula with the marginal distributions fully known. The numbers inside parentheses indicate standard errors, and estimations of the true components are denoted in bold font. The starting value of the $EM$ is $\mathit{w}=(0.25,0.25,0.25,0.25),{\theta }_{mix}=(1,1,1,1)$.

True Copula (Param)
		EM Estimations
	$\mathbf{n}$	Clayton		Gumbel		Normal		Frank
		$\mathit{w}$	$\mathit{\theta }$	$\mathit{w}$	$\mathit{\theta }$	$\mathit{w}$	$\mathit{\theta }$	$\mathit{w}$	$\mathit{\theta }$
Normal (0.5)	200	0.020 (0.060)	1.137 (0.435)	0.035 (0.110)	1.957 (0.135)	0.947 (0.117)	0.509 (0.030)	0 (0)	0.5 (0)
	400	0.031 (0.078)	1.479 (1.661)	0.050 (0.12)	2.031 (0.351)	0.921 (0.129)	0.506 (0.042)	0 (0)	0.5 (0)
	800	0.031 (0.068)	1.021 (0.134)	0 (0)	2 (0)	0.969 (0.068)	0.485 (0.021)	0 (0)	0.5 (0)
Clayton (5)	200	1 (0)	4.955 (0.525)	0 (0)	2 (0)	0 (0)	0.5 (0)	0 (0)	0.5 (0)
	400	0.989 (0.035)	4.972 (0.246)	0.012 (0.036)	2.628 (1.985)	0 (0)	0.5 (0)	0 (0)	0.5 (0)
	800	1 (0)	4.988 (0.162)	0 (0)	2 (0)	0 (0)	0.5 (0)	0 (0)	0.5 (0)
Gumbel (2.5)	200	0 (0)	1 (0)	1 (0)	2.486 (0.177)	0 (0)	0.5 (0)	0 (0)	0.5 (0)
	400	0 (0)	1 (0)	1 (0)	2.500 (0.088)	0 (0)	0.5 (0)	0 (0)	0.5 (0)
	800	0 (0)	1 (0)	0.979 (0.038)	2.562 (0.081)	0.02 (0.04)	0.513 (0.058)	0 (0)	0.5 (0)
Frank (5)	200	0.117 (0.138)	2.182 (1.415)	0.155 (0.268)	2.016 (0.118)	0.723 (0.244)	0.557 (0.102)	0.010 (0.030)	0.498 (0.007)
	400	0.054 (0.087)	1.619 (1.075)	0.184 (0.187)	2.283 (0.383)	0.764 (0.228)	0.555 (0.080)	0 (0)	0.5 (0)
	800	0.075 (0.085)	2.201 (1.456)	0.060 (0.103)	2.249 (0.498)	0.840 (0.089)	0.608 (0.047)	0.030 (0.050)	0.517 (0.029)

displays the results of the EM approach. It shows comparable outcomes with the MCMC. Although all algorithms fail to distinguish the Frank copulas from the normal ones due to their similarities, other copulas are selected with satisfactory accuracy. One clear advantage of using the EM is its convenience in introducing an exit mechanism for unlikely copulas during the training process. That is, due to the shrinkage term of the weight in (12), we can eliminate components when their corresponding weights fall down to non-positive during the training. By adding this procedure, we can automatically consider fewer mixture components at later stages. As we can see from Table 4, there are many components with deterministic 0 weightings. However, the shortcomings of the EM approach are also very clear. It is more computationally demanding especially when we seek to obtain some estimation errors or work with high dimensional copulas. On the other hand, the EM seeks to find the posterior mode which is less favorable than the posterior mean in statistical decision theories, while the MCMC approach gives full posterior distributions, and it is well acknowledged that the performance of the EM could be affected by starting points.

4.3. Higer Dimensional Cases

We proceed to test the effectiveness of our approach in a higher-dimensional case. As the classic Archimedean families of copulas are rarely used in high-dimensional applications due to the restriction of their parameter spaces, we apply the more commonly used Gaussian mixture copulas with 3 components to perform the estimations, while the dimension of the data is set to be 3. That is, we use the MCMC sampler to estimate the model

$$c_{\mathit{NormalMix}}=w_{\alpha }{c}_{\alpha }(\mathit{u};{\Sigma }_{\mathit{\alpha }})+w_{\beta }{c}_{\beta }(\mathit{u};{\Sigma }_{\mathit{\beta }})+w_{\gamma }{c}_{\gamma }(\mathit{u};{\Sigma }_{\mathit{\gamma }}).$$

(14)

A major obstacle to performing MCMC of such type is the sampling of the correlation matrices $({\Sigma }_{\alpha },{\Sigma }_{\beta },{\Sigma }_{\gamma })$. The valid sampler should generate symmetric positive definite matrices every time with every entry from 0 to 1 and 1 in their diagonal. Readers are referred to [30] for a detailed approach. On the other hand, when performing the MCMC sampling with mixture copulas from the same parametric families, it should also be noticed that label-switching problems often occurred. This is because that (14) has $3!$ equivalent forms by just switching the labels; some engineering efforts should be made to mitigate the circumstances. After every round of iteration, one can post-process the model so that the component with the highest weighting always ranks first. In addition, if the weightings are too close to distinguish, further criteria such as $\det |\Sigma |+\mathrm{trace}(\Sigma )$ should be used.

In this study, we use the data sampled from

$$\begin{array}{cc}\hfill & ({\Sigma }_{\alpha }^{12},{\Sigma }_{\alpha }^{23},{\Sigma }_{\alpha }^{13})=(0.7,0.7,-0.6)\hfill \\ \hfill & ({\Sigma }_{\beta }^{12},{\Sigma }_{\beta }^{23},{\Sigma }_{\beta }^{13})=(0.6,0.6,0.6)\hfill \\ \hfill & ({\Sigma }_{\gamma }^{12},{\Sigma }_{\beta }^{23},{\Sigma }_{\gamma }^{13})=(-0.7,0.7,0.7).\hfill \end{array}$$

Additionally, we set the true weighting of the experiments to be $(w_{\alpha },w_{\beta },w_{\gamma })=(1,0,0)$ and $(w_{\alpha },w_{\beta },w_{\gamma })=(0,0.7,0.3)$, respectively. Therefore, the true model lies in the parameter spaces of (14).

Table 5. MCMC estimations of the 3-dimensional mixture Gaussian copulas with the marginal distributions fully known. The numbers inside parentheses indicate standard errors, and estimations of the true components are denoted in bold font. Comp is the abbreviation for component and the components are ordered by their weightings.

True Copula (Param)
		MCMC Estimations
	n	Comp1		Comp2		Comp3
		$\mathit{w}$	$\mathit{\theta }$	$\mathit{w}$	$\mathit{\theta }$	$\mathit{w}$	$\mathit{\theta }$
Normal (0.7, −0.7, −0.6)	400	0.815 (0.160)	0.691 (0.031), −0.676 (0.042), −0.602 (0.048)	0.173 (0.152)	0.685 (0.212), −0.658 (0.278), −0.430 (0.342)	0.019 (0.016)	0.414 (0.306), −0.050 (0.539), −0.152 (0.413)
	800	0.991 (0.014)	0.680 (0.017), −0.715 (0.015), −0.604 (0.023)	0.007 (0.012)	0.371 (0.429),−0.435 (0.318),−0.413 (0.571)	0.002 (0.003)	0.312 (0.445),−0.341 (0.377),−0.308 (0.566)
	2000	0.992 (0.007)	0.70 (0.009),−0.699 (0.010),−0.612 (0.012)	0.007 (0.007)	0.154 (0.350),−0.362 (0.498),−0.336 (0.252)	0.001 (0.001)	−0.225 (0.283),0.303 (0.445),−0.230 (0.239)
0.7 Normal (0.6, 0.6, 0.6) + 0.3 Normal (−0.7, −0.7, 0.7)	400	0.609 (0.097)	0.679 (0.069), 0.616 (0.048), 0.602 (0.043)	0.289 (0.047)	−0.595 (0.310), −0.592 (0.327), 0.713 (0.066)’	0.102 (0.085)	−0.224 (0.387), −0.170 (0.452), 0.468 (0.141)
	800	0.656 (0.074)	0.567 (0.035), 0.599 (0.042), 0.576 (0.038)	0.216 (0.042)	−0.535 (0.326), −0.594 (0.252), 0.687 (0.076)	0.128 (0.054)	−0.331 (0.392), −0.450 (0.342), 0.724 (0.087)
	2000	0.663 (0.030)	0.636 (0.017), 0.607 (0.021), 0.603 (0.014)	0.310 (0.020)	−0.677 (0.030), −0.690 (0.029), 0.740 (0.020)	0.026 (0.027)	0.190 (0.320), 0.138 (0.319), 0.257 (0.193)

displays the results of experiments. It shows good signs of convergence to the truth while we increase the sample size. For the 2000 sample size experiments, the true components are successfully filtered out with low uncertainty, indicating the effectiveness of our proposed approach beyond the classical two-dimensional copula applications.

5. Real Data Analysis

In the real data analysis, we use financial trading data from three major indices, that is, Standard & Poors 500 (SP500), Shanghai Composite Index (SSEC), and Hang Seng Index (HSI). Daily close prices from 9 October 2017 to 29 September 2022 were extracted; we aligned three series with the common trading days among them, and other days were omitted. To ease the analysis of the dependence pattern among them, we take the log returns respectively so that $R_i=log{P}_i-log{P}_{i-1},i=1,2,3$.

Table 6. Pearson and Spearman correlation among three markets from October 2017 to September 2020.

	SSEC	HSI	SP500	SSEC	HSI	SP500
	Pearson Correlation			Spearman Correlation
SSEC	1	0.699	0.18	1	0.679	0.173
HSI	0.699	1	0.25	0.679	1	0.224
SP500	0.18	0.25	1	0.173	0.224	1

shows the Pearson and Spearman correlation among markets. SSEC and HSI display strong levels of dependence, while their connection with SP500 is relatively weak for those two markets. However, as we argued previously, the single metric of correlation does not give the full picture of the dependence. It is therefore reasonable to apply the mixture copula models for further analysis. In addition, the Ljung–Box tests to the absolute values $|R_i|$ of series indicate all series are correlated to themselves through time. Moreover, the augmented Dickey–Fuller tests show that they are covariance stationary. To apply the copula models to the autocorrelated data, we use the standard method of standardizing. That is, the autocorrelation is removed by rescaling the volatility of the GARCH(1,1) model; assume

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & R_t=\mu +{\sigma }_t{z}_t\mathrm{i}.\mathrm{i}.\mathrm{d}{z}_t\sim \mathrm{N}(0,1)\hfill \\ \hfill & {\sigma }_t^2=\alpha {\sigma }_{t-1}^2+\beta z_{t-1}^2+\gamma ,\hfill \end{array}\end{array}$$

(15)

We apply the data $(Z_1,Z_2,\dots ,Z_T)=(\frac{R_1-\mu }{{\sigma }_1},\frac{R_2-\mu }{{\sigma }_2},\dots ,\frac{R_T-\mu }{{\sigma }_T})$ to copula model and use semiparametric approach of Section 3.1 to learn the parameters. The MCMC samplings are performed 5000 times with the last 500 times used for analyzing the parameters.

Table 7. Parameters estimation of the stocks data with mean estimator and $90\%$ credible interval.

		SSEC-HSI	SSEC-SP500	HSI-SP500
Clayton	w	0.280 (0.144, 0.372)	0.685 (0.508, 0.814)	0
	$\theta$	2.53 (1.65, 3.65)	0.168 (0.069, 0.247)
Gumbel	w	0	0	0.104 (0.015, 0.257)
	$\theta$			1.484 (1.130, 2.368)
Normal	w	0.668 (0.587, 0.785)	0.222 (0.062, 0.350)	0.528 (0.350, 0.672)
	$\theta$	0.722 (0.681, 0.764)	0.366 (0.190, 0.563)	0.400 (0.269, 0.561)
Frank	w	0	0	0.33 (0.201, 0.542)
	$\theta$			−0.534 (−1.557, 0.509)

shows the results of the estimation with the insignificant components omitted. We observe the strong Clayton components in the first two columns, but the Gumbel components, on the other hand, are all very weak among the three markets due to the asymmetry nature of the Clayton copula at its left tail, which can be seen in Figure 1. This indicates the existence of asymmetry dependence among markets, especially at the lower left tail, and the dependence on the upper right tail is less obvious. Our finding means that the stock markets usually more easily have a downward co-movement but are much less likely to move upward together. In contrast, the dependence pattern between HSI and SP500 is more symmetrical, with dominating normal and Frank components and a very weak Gumbel component. Given the absence of extreme left tail dependence, a portfolio consisting of HSI and SP500 indexes is less likely to experience significant losses compared to other cross-market portfolios during extreme financial conditions.

6. Conclusions

In this paper, we discuss the method of selecting and estimating the mixture copula simultaneously. This is achieved by first overfitting the model with all potential mixture components and then estimating the parameters by Bayesian methods. The MCMC and EM methods are proposed to learn the parameters, and we have performed numerical simulations to validate the correctness. Furthermore, we apply the methodology to the financial markets to detect the asymmetry dependencies among them. For future research, the effectiveness of this method for general mixture models can be thoroughly investigated and tested. In addition, a full and thorough comparison among various model selection approaches can be studied. We also expect this method to be useful in improving other empirical studies, such as value at risk and conditional value at risk calculations in financial risk management.