Dynamic Skyline Computation with LSD Trees †
Abstract
:1. Introduction
1.1. Dynamic Skylines
1.2. Structure of the Paper
2. Related Work
3. Preliminaries
4. The sLSD Tree
4.1. Dealing with Skewed Distributions
4.2. Complexity Analysis
- finding the bucket in which the element shall be inserted; the time is logarithmic in the depth of the tree; and
- splitting this bucket if it is overfull. The split is done by
- (a)
- sorting the elements in one dimension that takes time, and
- (b)
- creating a new bucket that takes time for moving half of the elements to the new bucket.
Overall, a newly created bucket can take new elements on average before it has to be split. Hence, this step takes amortized time.
- If the sibling is a bucket that has space left, we just shift the parent node’s split position such that the number of elements gets rebalanced.
- If the sibling is a subtree that can adopt a new element without splitting one of its children, we shift again the split position of the bucket’s parent node. This time, however, we also have to recompute the split information of the internal nodes of this subtree.
4.3. Geometrical Characteristics
5. The Algorithm
5.1. The Dynamic Skyline Breaker Algorithm
| Algorithm 1 Dynamic Skyline Breaker: The ternary ? operator has the same semantic as in C/C++, i.e., means if a then b else c. |
| 1: function sbDyn() |
| 2: |
| 3: |
| 4: |
| 5: |
| 6: |
| 7: for do |
| 8: |
| 9: |
| 10: |
| 11: while do |
| 12: |
| 13: |
| 14: if then |
| 15: |
| 16: else |
| 17: |
| 18: |
| 19: |
| 20: clip() |
| 21: return |
| Algorithm 2 Clipping the Tree |
| 1: function clip() |
| 2: |
| 3: |
| 4: |
| 5: if then |
| 6: |
| 7: else |
| 8: |
| 9: |
| 10: |
| 11: if then |
| 12: |
| 13: if then |
| 14: |
| 15: else |
| 16: |
5.2. Skyline in a Bucket
5.3. The Tree Clip Algorithm
6. Analysis and Optimization
7. Comparison to Other Geometrical Data Structures
7.1. Improving the Clipping Condition
7.2. Analysis of Parallelism
7.3. Caching Dynamic Skylines
7.4. Evaluation
8. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Köppl, D. Inferring Spatial Distance Rankings with Partial Knowledge on Routing Networks. Information 2022, 13, 168. [Google Scholar] [CrossRef]
- Sacharidis, D.; Bouros, P.; Sellis, T. Caching Dynamic Skyline Queries. In Scientific and Statistical Database Management; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5069, pp. 455–472. [Google Scholar] [CrossRef]
- Papadias, D.; Tao, Y.; Fu, G.; Seeger, B. Progressive skyline computation in database systems. ACM Trans. Database Syst. 2005, 30, 41–82. [Google Scholar] [CrossRef]
- Köppl, D. Breaking Skyline Computation down to the Metal—The Skyline Breaker Algorithm. In Proceedings of the 17th International Database Engineering & Applications Symposium, IDEAS’13, Barcelona, Spain, 9–13 October 2013. [Google Scholar] [CrossRef]
- Kossmann, D.; Ramsak, F.; Rost, S. Shooting Stars in the Sky: An Online Algorithm for Skyline Queries. In Proceedings of the 28th International Conference on Very Large Databases, VLDB’02, Hong Kong SAR, China, 20–23 August 2002; Morgan Kaufmann: Burlington, MA, USA, 2002; pp. 275–286. [Google Scholar]
- Beckmann, N.; Kriegel, H.P.; Schneider, R.; Seeger, B. The R*-Tree: An Efficient and Robust Access Method for Points and Rectangles. In Proceedings of the 1990 ACM SIGMOD International Conference on Management of Data, SIGMOD ’90, Atlantic City, NJ, USA, 23–26 May 1990; Garcia-Molina, H., Jagadish, H.V., Eds.; ACM Press: New York, NY, USA, 1990; pp. 322–331. [Google Scholar]
- Papadias, D.; Tao, Y.; Fu, G.; Seeger, B. An Optimal and Progressive Algorithm for Skyline Queries. In Proceedings of the 2003 ACM SIGMOD International Conference on Management of Data, SIGMOD ’03, San Diego, CA, USA, 9–12 June 2003; Halevy, A.Y., Ives, Z.G., Doan, A., Eds.; ACM: New York, NY, USA, 2003; pp. 467–478. [Google Scholar]
- Ciaccia, P.; Patella, M.; Zezula, P. M-tree: An Efficient Access Method for Similarity Search in Metric Spaces. In Proceedings of the 23rd International Conference on Very Large Data Bases, VLDB ’97, Athens, Greece, 25–29 August 1997; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1997; pp. 426–435. [Google Scholar]
- Chen, L.; Lian, X. Dynamic Skyline Queries in Metric Spaces. In Proceedings of the 11th International Conference on Extending Database Technology: Advances in Database Technology, EDBT ’08, Nantes, France, 25–29 March 2008; ACM: New York, NY, USA, 2008; pp. 333–343. [Google Scholar] [CrossRef]
- Han, X.; Wang, B.; Lai, G. Dynamic skyline computation on massive data. Knowl. Inf. Syst. 2019, 59, 571–599. [Google Scholar] [CrossRef]
- Tai, L.K.; Wang, E.T.; Chen, A.L.P. Finding the most profitable candidate product by dynamic skyline and parallel processing. Distrib. Parallel Databases 2021, 39, 979–1008. [Google Scholar] [CrossRef]
- Li, Y.; Qu, W.; Li, Z.; Xu, Y.; Ji, C.; Wu, J. Parallel Dynamic Skyline Query Using MapReduce. In Proceedings of the International Conference on Cloud Computing and Big Data, CCBD, Wuhan, China, 12–14 November 2014; pp. 95–100. [Google Scholar] [CrossRef]
- Selke, J.; Lofi, C.; Balke, W.T. Highly Scalable Multiprocessing Algorithms for Preference-Based Database Retrieval. In Database Systems for Advanced Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Heller, S.; Herlihy, M.; Luchangco, V.; Moir, M.; William, S.; Shavit, N. A Lazy Concurrent List-Based Set Algorithm. Parallel Process. Lett. 2007, 17, 411–424. [Google Scholar] [CrossRef]
- Im, H.; Park, J.; Park, S. Parallel skyline computation on multicore architectures. Inf. Syst. 2011, 36, 808–823. [Google Scholar] [CrossRef]
- Essiet, I.O.; Sun, Y.; Wang, Z. A novel algorithm for optimizing the Pareto set in dynamic problem spaces. In Proceedings of the 2018 Conference on Information Communications Technology and Society (ICTAS), Durban, South Africa, 8–9 March 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Hu, X.; Li, H.; Zhou, J.; Zhang, M.; Liao, J. Finding all Pareto Optimal Paths for Dynamical Multi-Objective Path optimization Problems. In Proceedings of the IEEE Symposium Series on Computational Intelligence, SSCI 2018, Bangalore, India, 18–21 November 2018; pp. 965–972. [Google Scholar]
- Gulzar, Y.; Alwan, A.A.; Ibrahim, H.; Turaev, S.; Wani, S.; Soomo, A.B.; Hamid, Y. IDSA: An Efficient Algorithm for Skyline Queries Computation on Dynamic and Incomplete Data With Changing States. IEEE Access 2021, 9, 57291–57310. [Google Scholar] [CrossRef]
- Alami, K. Optimization of Skyline queries in dynamic contexts. Ph.D. Thesis, University of Bordeaux, Bordeaux, France, 2020. [Google Scholar]
- Bentley, J.L. Multidimensional Binary Search Trees Used for Associative Searching. Commun. ACM 1975, 18, 509–517, kd-tree. [Google Scholar] [CrossRef]
- Henrich, A. A Distance Scan Algorithm for Spatial Access Structures. In Proceedings of the 2nd ACM Workshop on Advances in Geographic Information Systems, ACM-GIS, Gaithersburg, MD, USA, December 1994; pp. 136–143. [Google Scholar]
- Henrich, A. The LSDh-Tree: An Access Structure for Feature Vectors. In Proceedings 14th International Conference on Data Engineering, ICDE; Orlando, FL, USA, 23–27 February 1998, Urban, S.D., Bertino, E., Eds.; IEEE Computer Society: Washington, DC, USA, 1998; pp. 362–369. [Google Scholar]
- Henrich, A. Improving the Performance of Multi-Dimensional Access Structures Based on k-d-Trees. In Proceedings of the Twelfth International Conference on Data Engineering, ICDE, New Orleans, LA, USA, 26 February–1 March 1996; Su, S.Y.W., Ed.; IEEE Computer Society: Washington, DC, USA, 1996; pp. 68–75. [Google Scholar]
- Börzsönyi, S.; Kossmann, D.; Stocker, K. The Skyline Operator. In Proceedings of the 17th International Conference on Data Engineering, Heidelberg, Germany, 2–6 April 2001; IEEE Computer Society: Washington, DC, USA, 2001; pp. 421–430. [Google Scholar]
- Guttman, A. R-trees: A Dynamic Index Structure for Spatial Searching. SIGMOD Rec. 1984, 14, 47–57. [Google Scholar] [CrossRef]
- Michael, M.M.; Scott, M.L. Simple, Fast, and Practical Non-blocking and Blocking Concurrent Queue Algorithms. In Proceedings of the Fifteenth Annual ACM Symposium on Principles of Distributed Computing, PODC ’96, Philadelphia PA, USA, 23–26 May 1996; ACM: New York, NY, USA, 1996; pp. 267–275. [Google Scholar] [CrossRef]
- Blumofe, R.D.; Leiserson, C.E. Scheduling Multithreaded Computations by Work Stealing. J. ACM 1999, 46, 720–748. [Google Scholar] [CrossRef]
- Blumofe, R.D. Executing Multithreaded Programs Efficiently; Technical Report; Massachusetts Institute of Technology: Cambridge, MA, USA, 1995. [Google Scholar]
- Cole, M. Bringing skeletons out of the closet: A pragmatic manifesto for skeletal parallel programming. Parallel Comput. 2004, 30, 389–406. [Google Scholar] [CrossRef]
- Blumofe, R.D.; Joerg, C.F.; Kuszmaul, B.C.; Leiserson, C.E.; Randall, K.H.; Zhou, Y. Cilk: An Efficient Multithreaded Runtime System. In Proceedings of the Fifth ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, PPOPP ’95, Santa Barbara, CA, USA, 19–21 July 1995; ACM: New York, NY, USA, 1995; pp. 207–216. [Google Scholar] [CrossRef]
- Henrich, A.; Six, H.W.; Widmayer, P. The LSD tree: Spatial Access to Multidimensional Point and Nonpoint Objects. In Proceedings of the 5th Very Large Databases Conference, VLDB, Amsterdam, The Netherlands, 22–25 August 1989; Apers, P.M.G., Wiederhold, G., Eds.; Morgan Kaufmann: Burlington, MA, USA, 1989; pp. 45–53. [Google Scholar]
- Wiemann, S. Analyse und Auswertung paralleler Skyline-Algorithmen. Bachelor’s Thesis, Technische Universität Dortmund, Dortmund, Germany, 2016. [Google Scholar]
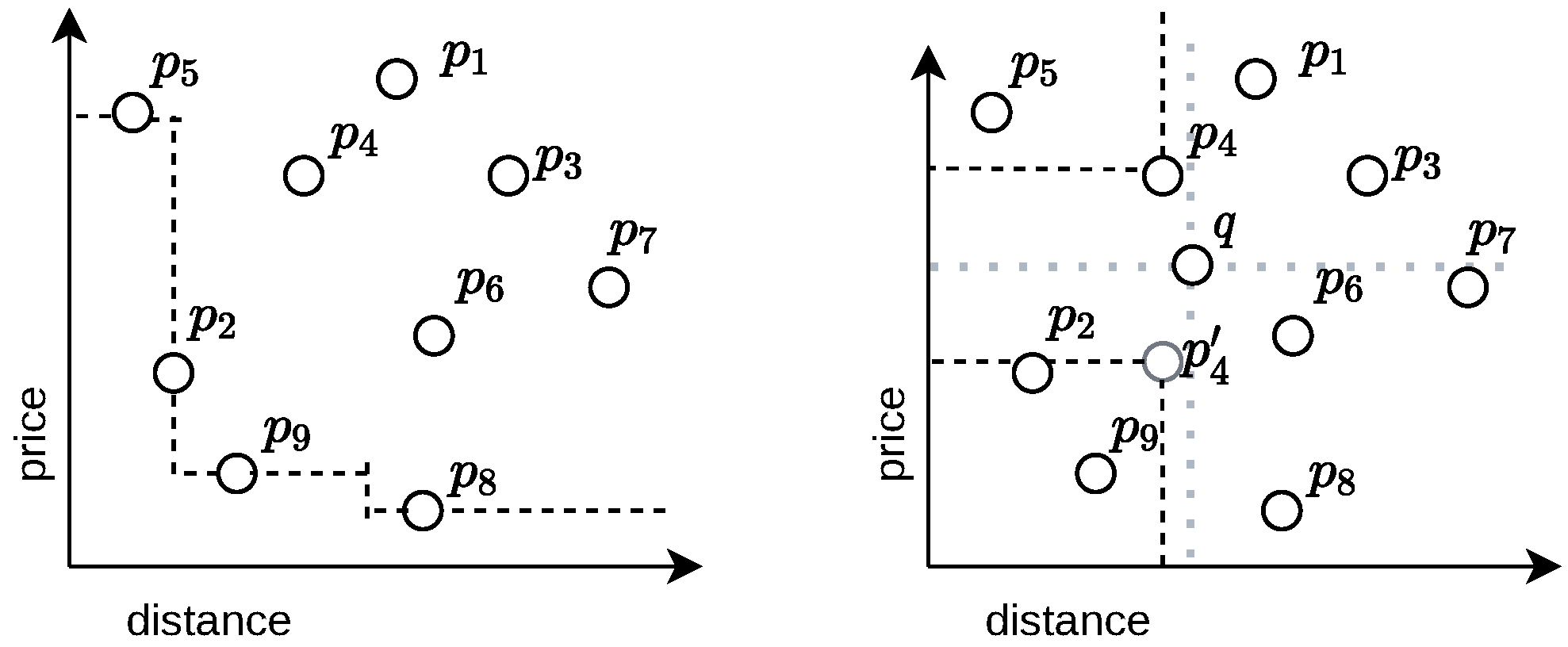


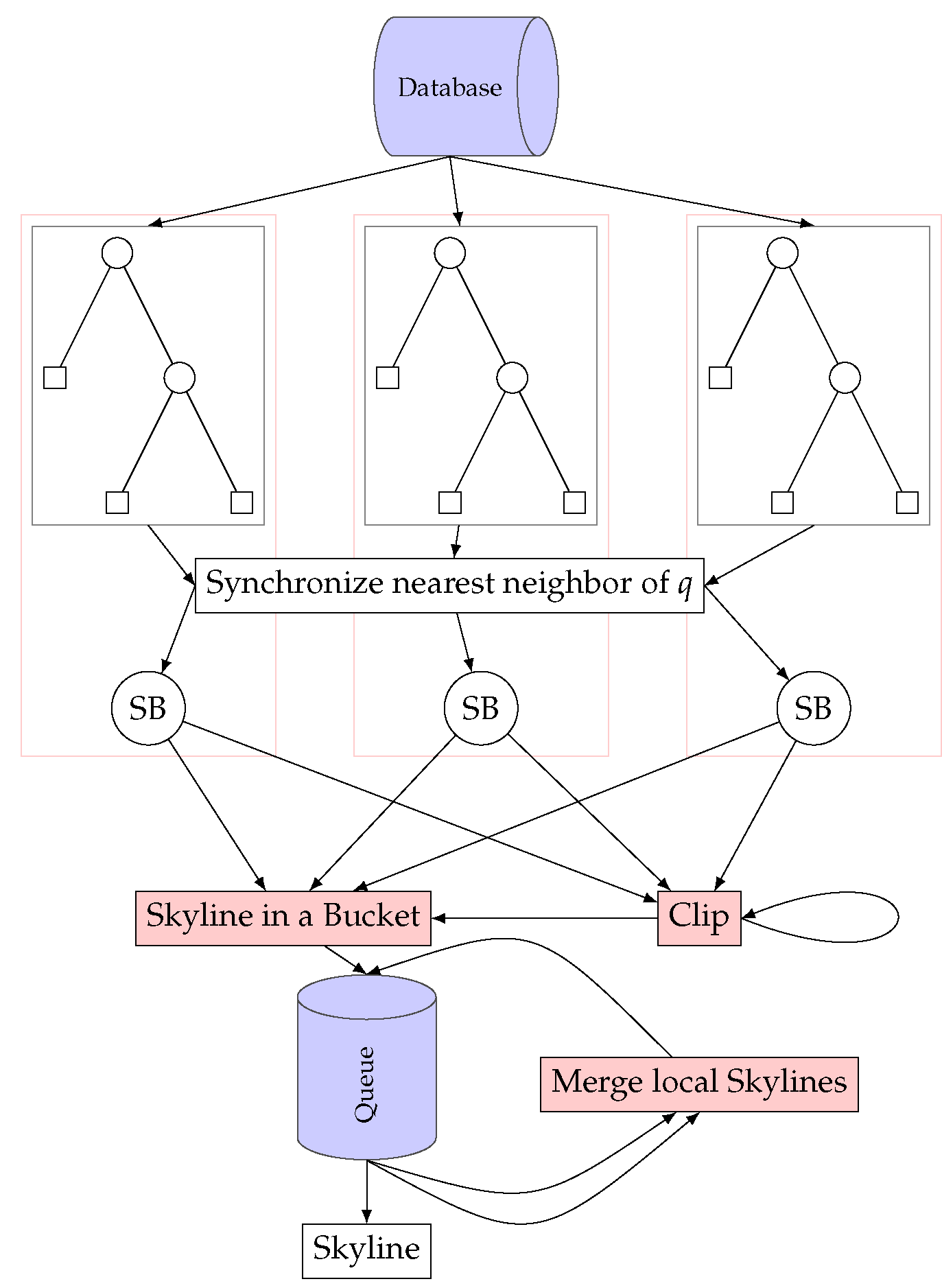



| Vector | |||||||
|---|---|---|---|---|---|---|---|
| dom. | dom. | dom. | dom. | ||||
| = | (10, 35) | (15, 35) | (10, 40) | ||||
| = | − | (35, 25) | (30, 25) | (35, 20) | |||
| = | (25, 15) | (30, 15) | (25, 20) | ||||
| = | (5, 15) | − | (0, 15) | − | (5, 20) | − | |
| = | − | (40, 25) | (35, 25) | (40, 30) | |||
| = | (10, 10) | − | (15, 10) | − | (10, 5) | − | |
| = | (45, 5) | − | (50, 5) | − | (45, 0) | − | |
| = | − | (7, 45) | (12, 45) | (7, 40) | |||
| = | − | (20, 35) | (15, 35) | (20, 30) | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Köppl, D. Dynamic Skyline Computation with LSD Trees. Analytics 2023, 2, 146-162. https://doi.org/10.3390/analytics2010009
Köppl D. Dynamic Skyline Computation with LSD Trees. Analytics. 2023; 2(1):146-162. https://doi.org/10.3390/analytics2010009
Chicago/Turabian StyleKöppl, Dominik. 2023. "Dynamic Skyline Computation with LSD Trees" Analytics 2, no. 1: 146-162. https://doi.org/10.3390/analytics2010009
APA StyleKöppl, D. (2023). Dynamic Skyline Computation with LSD Trees. Analytics, 2(1), 146-162. https://doi.org/10.3390/analytics2010009







