Rationality and Reversibility in Jean Piaget’s Theory of Reasoning

Abstract

Rationality has long been considered the quintessence of humankind. However, psychological experiments revealing reliable divergences in performances on reasoning tasks from normative principles of reasoning have cast serious doubt on the venerable dogma that human beings are rational animals. According to the standard picture, reasoning in accordance with principles based on rules of logic, probability theory, etc., is rational. The standard picture provides the backdrop for both the rationality and irrationality thesis, and, by virtue of the competence-performance distinction, diametrically opposed interpretations of reasoning experiments are possible. However, the standard picture rests on shaky foundations. Jean Piaget developed a psychological theory of reasoning, in which logic and mathematics are continuous with psychology but nevertheless autonomous sources of knowledge. Accordingly, logic, probability theory, etc., are not extra-human norms, and reasoners have the ability to reason in accordance with them. In this paper, I set out Piaget’s theory of rationality, using intra- and interpropositional reasoning as illustrations, and argue that Piaget’s theory of rationality is compatible with the standard picture but actually undermines it by denying that norms of reasoning based on logic are psychologically relevant for rationality. In particular, rather than logic being the normative benchmark, I argue that rationality according to Piaget has a psychological foundation, namely the reversibility of the operations of thought constituting cognitive structures.

1. Reasoning, Logic, and Rationality

Rationality has long been considered to be the quintessence of humanity. However, in the second half of the 20th century, psychological experiments began to reveal robust divergences in performance at reasoning tasks from those expected according the benchmarks of logic, probability theory and decision theory (e.g., [1,2,3,4]), which, pessimistically interpreted, cast serious doubt on the venerable dogma that humans are rational animals [5] (sec. 3) [6]. At first, the findings were disquieting, but, by the 1980s, the disquiet erupted into life [7] (p. 87), and, under the sheer weight of empirical evidence, the rationality debate became a full-blown Kuhnian crisis by the end of the 20th century [7] (p. 95).

The philosophical ramifications of the reasoning experiments were enormous, and philosophers soon became embroiled in the debate. In a survey and philosophical analysis of the debate, well-received for its comprehensiveness, clarity and conceptual contribution [5] (sec. 3.2) [8,9,10], Edward Stein ([11] p. 4 Author’s italics) dubbed the opposing positions in the rationality debate that erupted “rationality” and “irrationality thesis”:

the rationality thesis says that human reasoning competence matches the normative principles of reasoning [logic, probability theory, decision theory, etc.] (that is, the rules embodied in our reasoning competence are the same as those that we ought to follow), while the irrationality thesis says that human reasoning competence diverges from the norms (that is, the rules embodied in our reasoning competence are different from those we ought to follow) [11] (p. 10).

While champions and challengers of the rationality thesis differ in their interpretation of experimental findings, their differences turn on the relationship between reasoning competence and the norms. Both acknowledge a performance-competence distinction, but they differ in their interpretation of the import of the experimentally documented performances that do not conform with the normative principles of reasoning for the underlying competence:

Defenders of the rationality thesis say that all divergences from the norms of reasoning are performance errors and, as such, these divergences are not indicative of an underlying ability to reason. Defenders of the irrationality thesis agree that the competence-performance distinction is applicable to the realm of reasoning, but they deny that our reasoning competence matches the norms of reasoning; they offer alternative accounts of human reasoning competence, accounts according to which we are not rational [11] (p. 10).

The main strategy of champions of the rationality thesis is to immunise rationality against experimental evidence by explaining it away as performance errors via the performance-competence distinction. For champions of the irrationality thesis, in contrast, the results of reasoning experiments reveal the very nature of human reasoning and cannot simply be dismissed as performance errors. However, any argument worthy of consideration must surely be rational; it is therefore debatable whether champions of the irrationality thesis can justify their thesis on the basis of experimental evidence [12,13] (pp. 128–30)!

The competence-performance distinction makes diametrically opposed interpretations of the results of the same reasoning experiments possible. However, the rationality-irrationality debate plays out in front of the same backdrop. According to Stein, the “standard picture of rationality” is as follows:

to be rational is to reason in accordance with principles of reasoning that are based on rules of logic, probability theory, and so forth. If the standard picture of reasoning is right, principles of reasoning that are based on such rules are normative principles of reasoning, namely they are the principles we ought to reason in accordance with ([11] p. 4 Author’s italics).

According to the standard picture, then, reasoning and normative principles of reasoning based on logic, probability theory, etc., comprise rationality, and reasoning in accordance with these norms is rational. However, reasoning has theoretical and practical aspects, and norms of reasoning based on logic are involved in both [7] (p. 87). In this paper, I concentrate on beliefs and belief revision, the primary concern of the theoretical aspect of reasoning.

In contrast to theoretical reasoning, the rules of propositional logic apply to sentences and the relationships between them rather than beliefs. Stein illustrates the difference with modus ponens:

MODUS PONENS: A and if A, then B together entail B [11] (p. 6).

• This is a rule of logic, and Stein formulates the corresponding principle of reasoning as follows:

MODUS PONENS PRINCIPLE: If you believe A and you believe if A then B, you should believe B [11] (p. 6).

The formulations might seem overly pedantic, yet they have consequences. The rules of logic are universal and do not suffer exceptions; reasoning on the other hand is not automatically disqualified as irrational if the corresponding normative principles are violated:

The point then is that, whereas logical principles like modus ponens are exceptionless, corresponding rules of inference are not. Sometimes one should abandon a premise rather than accept a conclusion that follows logically from what one believes [14] (p. 108).

Despite the differences between reasoning and logic, the normative principles of reasoning are based on the rules of logic, according to the standard picture of rationality. However, logic does not suffer contradictions. By dictating that we avoid inconsistency, logic thus appears to tell us what we should not believe. The converse, in contrast, does not hold since consistency is not sufficient grounds to warrant belief. In other words, logic at least appears to play a negative special role in reasoning even if it does not play any positive special role. Nevertheless, Harman points out that no logician has consistently contended that logic has no positive special role to play in reasoning about beliefs, and he feels “perhaps irrationally, that logic must have something special to do with reasoning, even if no one has yet been able to say what this might be” [14] (p. 112).

The mounting weight of experimental evidence against the rationality thesis surely compounds Harman’s feeling of irrationality, yet it is not the only ground. Rational grounds in favour of the rationality thesis are surprisingly thin. Stein sums them up as follows:

The main virtues of the standard picture of rationality are that it accounts for the (seeming) normativity of rationality, that it is intuitively plausible and simple, and that it coheres well with such well-established disciplines as logic and mathematics [11] (p. 247).

• Scaremongery also bolsters the case for the rationality thesis:

Another reply in defence of the standard picture of rationality is to point out that rejecting the standard picture leads to such undesirable results as rampant inconsistency, Dutch-bookability, and so forth. Any picture of rationality that rejects the conjunction principle, the modus ponens principle, and similar principles of reasoning—principles of reasoning that the standard picture says are norms—is sure to run into profoundly problematic results … These results are not just bad in that they fail to fit with our intuitions; they are bad in that they seem to threaten the very practice of reasoning [11] (p. 252).

However, the standard picture is not without problems of its own. It is practically impossible to fulfil all the normative principles of reasoning. For example, rationality requires that our beliefs be consistent; however, it is not possible to check the consistency of a new belief against all the other beliefs we harbour prior to accepting it since these beliefs, both explicit and implicit, are more numerous than the finite resources we have at our disposal. In practice, then, lacking the time, wherewithal or both to suitably modify conflicting beliefs, people often “acquiesce in… contradiction” [14] (p. 108). Acquiescing in contradiction illustrates a coping strategy for the “human finitary predicament” [11] (ch. 4 sec. 5.2), and, just as ought implies can in ethics, it seems unreasonable to require adherence to rules we cannot possibly abide by in practice.

The strongest argument in favour of the standard picture is its intuitive appeal. However, it is notoriously difficult to separate the wheat from the chaff with intuitions, and even the most robust intuitions have proven to be deceptive. Moreover, the roots of our intuitions, robust or otherwise, appear to be quite shallow. They do not appear to reach much deeper than language and culture; thus “[o]ur preferences for the principles that stem from logic, probability, and the like are… the result of epistemic chauvinism” [11] (p. 252). Apart from inciting the ire of bigots, refusing to accept the superiority of a particular language, culture, etc., is therefore not as scary as champions of the rationalist thesis make out.

Though intuitively appealing, the foundations of the standard picture are not as solid as they appear at first blush. Rather than attempting to immunise rationality against empirical evidence by interpreting divergences from the normative principles of reasoning as performance errors, advocates of the rationality thesis could change tack, setting a course that undermines the standard picture [11] (pp. 214–215). However, contemplating other portraits of rationality would require breaking with deep-rooted convictions. Logicism is the philosophical and psychological doctrine that logic is the basis for rational human thought [7] (pp. 87–88) [15] (pp. 979–980). This conviction was the philosophical background of the standard picture and framed the deductive paradigm [15] (p. 979). However, a Kuhnian crisis was looming by the end of the 20th century as research on reasoning and judgment was creaking under the weight of the empirical evidence accumulated on the basis of this paradigm, and desperate times call for desperate measures.

In this paper, I intend to restore the true brilliance of an old masterpiece whose colours have faded in the passage of time, in part due to the harsh light of criticism based on misunderstandings (e.g., [7,16,17,18,19,20])1. Jean Piaget (e.g., [21,22,23,24,25]) developed a psychological theory of reasoning, in which logic and mathematics are developmentally continuous with psychology but nevertheless represent autonomous sources of knowledge. Accordingly, truths of logic, probability theory, decision theory, etc., are neither contingent on the psychological subject nor extra-human norms. Despite the intuitive appeal of the standard picture, I will argue that the ability to reason in accordance with normative principles of reasoning based on logic is accidental in Piaget’s theory of rationality. In particular, I will argue that the picture Piaget painted of rationality undermines the standard picture by denying that the normative principles of reasoning based on logic are psychologically relevant for rationality.

Restoring the brilliance of a masterpiece so that it can be appreciated as intended is perhaps reward enough; however, I also hope to dispel a common misunderstanding of Piaget’s psychological work on rationality. Piaget argued explicitly against the form of logicism, which would have the laws of thought mirror the laws of logic [22] (ch. 2) [26] (sec. 2). He also respected the strict division of labour Frege’s anti-psychologism critique precipitated by clearly demarcating logic, on the one hand, and psychology, on the other [27]. It is therefore highly unlikely, in my opinion, that Piaget, not practicing what he preached, is guilty of committing the logicism often insinuated.

According to Piaget, rationality is based on the reversibility of operations of thought, and Section 2 briefly introduces operations of thought, before going on to illustrate reversibility in intra- and interpropositional operations of thought. Intrapropositional operations of thought are the focus of Section 2.1, and I concentrate on reasoning with classes of objects in classifications to show how the ability to do this adequately is founded on the reversibility of operations of thought. Section 2.2 is devoted to interpropositional operations of thought. It begins with Piaget’s illustration of the propositional reasoning involved in determining a causal relationship between two phenomena and proceeds by setting out the structural possibilities that form the mental framework for reasoning of this kind. The structural possibilities are one aspect of the operational structure interpropositional operations form, and groups of inversions are reversible structures inherent in this operational structure. I wind this subsection up by demonstrating how one of these groups is instrumentalised by propositional reasoners aiming to determine the causal relationship between the phenomena set out in Piaget’s illustration at the beginning of this subsection. Having illustrated the reversibility of operations of thought in intra- and interpropositional reasoning, I return from the psychological excursion to the rationality debate. In Section 3, I set out strategies designed to defend the rationality thesis by undermining the standard picture of rationality before using them to classify Piaget’s theory of rationality. In Section 4, I conclude that by equating rationality with the reversibility of operations of thought Piaget championed the rationality thesis by undermining the standard picture, before considering some ramifications of my conclusion.

2. Reasoning and Reversibility

Operations of thought are key to Piaget’s psychological theory of reasoning. Using propositional connectives, such as “and”, “or”, “if-then” etc., simple propositions can be combined with others to form compound propositions. The meaning of the compound proposition is then constituted by the meanings of the individual propositions combined and the propositional connectives. Just as compound propositions are composed of parts, the propositions themselves are also composite in nature. In contrast to compound propositions, however, the innards of propositions are not also propositions; the sentence “Mammals are vertebrates”, for example, has a subject “mammals”, predicate “vertebrates” and a logical constant, the copula “is”. Other contents can be substituted, and the meaning of the whole proposition is again constituted by the meanings of its parts. Roughly, operations of thought denote the mental activities that compose and decompose such connections between propositions or between the parts of propositions [24] (p. 9). Piaget denotes the former “interpropositional operations” and the latter “intrapropositional operations” [24] (pp. 34–35), and I adopt his terminology in this paper.

2.1. Intrapropositional Operations of Thought

Similarities and differences are the locus of intrapropositional operations of thought, and Piaget discerned and analysed eight distinct kinds [24] (chs. II–III). Since rehearsing them all would be beyond the scope of this paper, I simply illustrate intrapropositional operations with the hierarchical similarities that constitute a classification.

Reasoning with Classes

In nesting inclusions of classes $\mathrm{A}\supset \mathrm{B}\supset \mathrm{C}\supset \mathrm{D}$ etc., like those epitomized by biological taxonomies according to species, genus, family, order, class, phylum, kingdom, etc., (see Figure 1), Piaget [24] (p. 103) calls the classes A, B, C, D, etc., “primary”, and each primary class has a complement. Usually, complements are relative to the universe of discourse; however, Piaget defines relative complements with respect to the proximal primary classes in the nesting hierarchy of inclusions. A class and its relative complement are mutually exclusive and exhaustive with respect to their immediate superclass; using “+” to denote union, a nesting inclusion of classes can therefore be represented by the following series of logical additions: $\mathrm{A}+{\mathrm{A}}^{\prime }=\mathrm{B}$, $\mathrm{B}+{\mathrm{B}}^{\prime }=\mathrm{C}$, $\mathrm{C}+{\mathrm{C}}^{\prime }=\mathrm{D}$, etc.

Complementary to logical addition, Piaget uses logical subtraction “−” to denote the operation that generates the relative complements of classes; for example, ${\mathrm{A}}^{\prime }=\mathrm{B}-\mathrm{A}$; ${\mathrm{B}}^{\prime }=\mathrm{C}-\mathrm{B}$; ${\mathrm{C}}^{\prime }=\mathrm{D}-\mathrm{C}$; etc. [24] (pp. 76–81). By way of contrast, Piaget [24] (p. 103) calls the complementary classes “secondary”.

Operations compose the classes of such nesting hierarchies with each other so that the outcome of a composition is another class of the classification. Some of the operations are as follows:

• The direct operation consists in adding a class of the system to another thus forming the union of these classes; for example, $\mathrm{A}+{\mathrm{A}}^{\prime }=\mathrm{B}$, $\mathrm{B}+{\mathrm{B}}^{\prime }=\mathrm{C}$, etc.
• The inverse operation cancels the outcome of the direct operation by negating a class in a union created by addition so that the relative complement remains; for example, $\mathrm{B}-\mathrm{A}={\mathrm{A}}^{\prime }$; $\mathrm{B}-{\mathrm{A}}^{\prime }=\mathrm{A}$; ${\mathrm{B}}^{\prime }=\mathrm{C}-\mathrm{B}$; ${\mathrm{C}}^{\prime }=\mathrm{D}-\mathrm{C}$; etc.
• The general identity operation simultaneously fulfils the following two criteria: (a) composed with an arbitrary element of the grouping, it leaves it invariant; and (b) it is the outcome of the composition of the direct and inverse operations; for example, (a) $\mathrm{A}+\varnothing =\mathrm{A}$, ${\mathrm{A}}^{\prime }+\varnothing ={\mathrm{A}}^{\prime }$, etc.; and (b) $\mathrm{A}-\mathrm{A}=\varnothing$; $\mathrm{B}-\mathrm{B}=\varnothing$; ${\mathrm{A}}^{\prime }-{\mathrm{A}}^{\prime }=\varnothing$; etc. [23] (sec. 46) [24] (pp. 103–105).

Although this intrapropositional grouping comprises five operations in total, the three listed above encompass its reversibility and are therefore sufficient for the present purposes.

Prior to the formation of such groupings, a period of intuitive thought typically develops between the ages of 4 and 7–8 years [22] (p. 122). Piaget characterises this intermediate stage of thought as “pre-logical” since it supplements incomplete operations with intuitive reasoning so that intuitive regulations rather than operations govern judgments [22] (pp. 128–129). The conservation experiments Piaget conducted together with A. Szeminka illustrate intuitive reasoning:

Two small glasses, A and A2, of identical shape and size, are each filled with an equal number of beads, and this equality is acknowledged by the child, who has filled the glasses himself, e.g., by placing a bead in A with one hand every time he places a bead in A2 with the other hand. Next, A2 is emptied into a differently shaped glass B, while A is left as a standard. Children of 4–5 years then conclude that the quantity of beads has changed, even though they are sure none has been removed or added. If the glass B is tall and thin they will say that there are “more beads than before” because “it is higher”, or that there are fewer because “it is thinner”, but they agree on the non-conservation of the whole [22] (p. 129).

By rational standards, these children are being irrational, and it is Piaget’s enduring contribution to cognitive developmental psychology that he did not simply dismiss their answers as aberrations but asked why children at this stage of cognitive development answer in this way. Piaget explained their behaviour in terms of intuitive regulations involving centralisations and decentralisations as follows:

Suppose a child estimates that there are more beads in B than in A because the level has been raised. He thus “centres” his thought, or his attention, on the relation between the heights of B and A, and ignores the widths. But let us empty B into glasses C or D, etc., which are even thinner and taller; there must come a point at which the child will reply, “there are fewer, because it is too narrow”. There will thus be a correction of centring on height by a decentring of attention on to width. On the other hand, in the case of the subject who estimates the quantity in B as less than that in A on account of thinness, the lengthening of the column in C, D, etc., will induce him to reverse his judgment in favour of height. Now this transition from a single centring to two successive centrings heralds the beginnings of the operation; once he reasons with respect to both relations at the same time, the child will, in fact, deduce conservation. However, in the case we are considering, there is neither deduction nor a true operation; an error is simply corrected, but it is corrected late and as a reaction to its very exaggeration (as in the field of perceptual illusions), and the two relations are seen alternately instead of being logically multiplied. So all that occurs is a kind of intuitive regulation and not a truly operational mechanism [22] (p. 130).

Aiming to pin down the difference between intuitive and operational reasoning more precisely, especially with classes, Piaget conducted the following experiment:

we place about twenty beads in a box, the subject acknowledging that they are “all made of wood”, so that they constitute a whole, B. Most of these beads are brown and constitute part A, and some are white, forming the complementary part A′. In order to determine whether the child is capable of understanding the operation $\mathrm{A}+{\mathrm{A}}^{\prime }=\mathrm{B}$, i.e., the uniting of parts in a whole, we may put the following simple question: In this box (all the beads still being visible) which are there more of—wooden beads or brown beads, i.e., is A<B [22] (p. 132)?

Piaget summarised the results as follows:

Now, up to about the age of 7 years, the child almost always replies that there are more brown beads “because there are only two or three white ones.” We then question further: “Are all the brown ones made of wood?”—“Yes.”—“If I take away all the wooden beads and put them here (a second box) will there be any beads left in the (first) box?”—“No, because they are all made of wood.”—“If I take away the brown ones, will there be any beads left?”—“Yes, the white ones.” Then the original question is repeated and the subject continues to state that there are more brown beads than wooden ones in the box because there are only two white ones, etc. [22] (p. 132–133).

Piaget unravels the children’s seemly irrational answers as follows:

the subject finds no difficulty in concentrating his attention on the whole B, or on the parts A and A′, if they have been isolated in thought, but the difficulty is that by centring on A he destroys the whole, B, so that the part A can no longer be compared with the other part A′. So there is again a non-conservation of the whole for lack of mobility in the successive centralisations of thought [22] (p. 133).

Once again, Piaget’s explanation involves centralisation, decentralisation and conservation; however, it is rather laconic and a comparison with the additive grouping of classes set out above will help explication. Being relative complements, classes A and A’ are related to each other via B; i.e., A is B but not A’ and A’ is B but not A. By focusing their attention on either A or A’, the brown or the white beads, children lose sight of the mediating instance, the wooden beads (class B); they are therefore no longer able to compare classes A and A’ with B. Decentralisation on the other hand leads to the conservation of B whilst focusing on one of its parts.

A variation of this experiment sheds further light on the difficulties children face in transitioning from intuitive to operational reasoning. Asked to imagine making a necklace out of the brown beads or the wooden beads, children will sometimes reply:

If I make a necklace with the brown ones… I could not make another necklace with the same beads and the necklace made of wooden beads would have only white ones! [22] (p. 133).

Piaget explains this type of answer in terms of cognitive inertia as follows:

In so far as [intuitive thought] imitates true actions by imagined mental experiments, it meets with a particular obstacle, namely, that in practice one could not construct two necklaces at the same time from the same elements, whereas in so far as [operational thought] is carried out through internalized actions that have become completely reversible, there is nothing to prevent two hypotheses being made simultaneously and then being compared with each other [22] (p. 133).

In other words, children grown familiar with manipulating objects of the real world manipulate mental phenomena as if they were also objects, and this residue of realism is an impediment to transitioning from intuitive to operational reasoning. However, residual realism is not yet entirely overcome with the advent of the concrete-operational stage of reasoning; in fact, it recurs as the default approach to phenomena that initially resist structuring with the intrapropositional grouping.

In one of the conservation experiments Piaget and his team conducted, two balls of modelling clay with similar dimensions and weight are presented to children before one is moulded before their eyes to look like a sausage or a pancake. The experiment gives rise to three conservation problems: (i) does the altered ball still contain the same quantity of substance as the unaltered one? (ii) does it still have the same weight? and (iii) does it still have the same volume, measured by the amount of water it displaces? Prior to attainment of the concrete-operational stage, children focus on particular aspects of the reconfigured ball and judge on the basis of isolated observations alone: “there is more clay than before because the thing is longer”, “there is less because it is thinner”, etc. From 7–8 onwards, in contrast, there is no doubt in the child’s mind that the substance remains the same despite manifest deformations in appearance, and the grounds they give for their judgements are as follows:

(a) The object has only been lengthened (or shortened), and it is easy to restore it to its former shape (simple reversibility); (b) it has been lengthened; but what it has gained in length it has lost in thickness (composition of relations by reversible composition); (c) nothing has been added or taken away (operation of identity which brings us back to the initial state, the product of direct and inverse operations) [21] (p. 16).

However, children still neither comprehend the conservation of weight nor volume until 9–10 and 11–12 years-of-age, respectively. In analogy to the conservation of substance, the arguments for the non-conservation of weight and volume are again based on particular observations of the reconfigured ball in isolation whilst the same reasons as above are eventually given to justify the conservation first of weight and then of volume. In short, systematic delays in understanding different kinds of conservation still occur although the operational structure essential for understanding conservation has already been constructed. In Piaget’s words:

each field of experience (that of shape and size, weight, etc.) is in turn given a structure by the group of concrete operations, and gives rise in its turn to the construction of invariants (or concepts of conservation). But these operations and invariants cannot be generalized in all fields at once; this leads to a progressive structuring of actual things, but with a time-lag of several years between the different fields or subject-matters [21] (p. 17).

“Horizontal décalage” [28] (p. 374) [29] (p. 816) is the term Piaget coined to denote the systematic delays in structuration, which the conservation experiments eloquently illustrate.

In summary, groupings are cognitive tools, which reasoners deploy to structure subject matters, and rationality is due to the reversibility of operations of thought operating in them. However, subject matters resist reasoners’ structuration attempts to varying degrees; in contrast to Gestalts, which snap into place apparently effortlessly on perception, deployment of groupings thus requires effort. Despite having the capacity to reason rationally, then, it is still possible for reasoners to perform irrationally, especially when coming to grips with difficult content for the first time.

However, cognitive development has not yet come to an end. Besides form and content not yet being sufficiently divorced, operational systems at this stage are restricted in another way—they are fragmentary. With the aid of concrete operations, it is possible to classify, order serially, form equalities or set up correspondences between objects, etc.; however, these operations are not yet combined into a single structured whole. Their fragmentary nature prevents concrete operations from constituting a purely formal logic. From the psychological point of view, on the other hand, this means that operations of thought have not yet completely achieved a state of equilibrium; this equilibrium will only occur at the subsequent stage of cognitive development [21] (p. 18), which is the subject of the next subsection.

2.2. Interpropositional Operations of Thought

The ability to reason hypothetico-deductively is one of the characteristics of the next stage in the psychogenesis of intelligence, and Piaget imagines the following scenario to illustrate how adolescents use their new-found reasoning powers to grasp causal connections between phenomena:

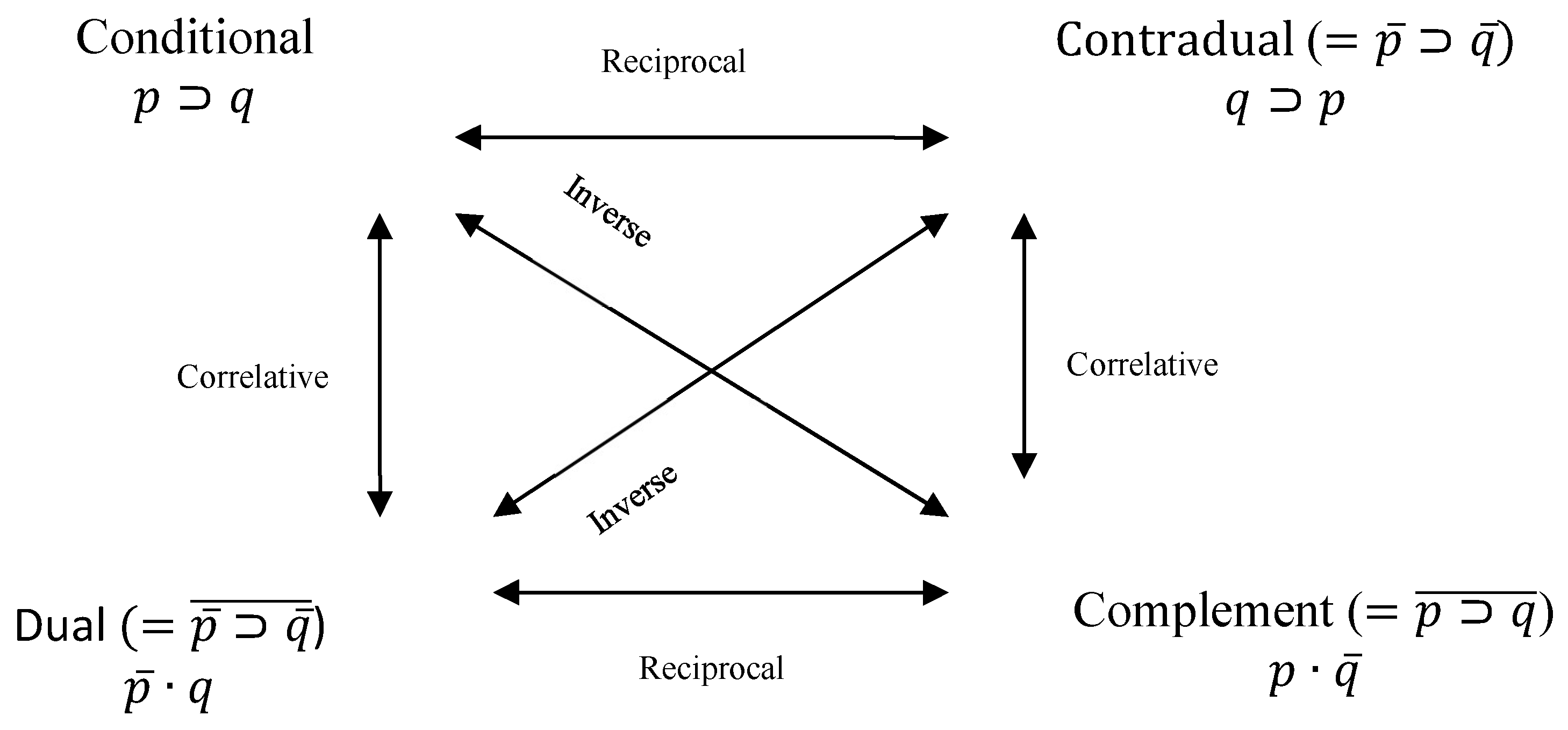
Let us take as an example the implication $p\supset q$, and let us imagine an experimental situation in which a child between twelve and fifteen tries to understand the connections between phenomena which are not familiar to him but which he analyses by means of the new propositional operations rather than by trial and error. Let us suppose then that he observes a moving object that keeps starting and stopping and he notices that the stops seem to be accompanied by lighting of an electric bulb. The first hypothesis he will make is that the light is the cause (or an indication of the cause) of the stops, or $p\supset q$ (light implies stop). There is only one way to confirm the hypothesis, and that is to find out whether the bulb ever lights up without the object stopping, or $p·\overline{q}$($p·\overline{q}$ is the inverse of or negation of $p\supset q$). But he may also wonder whether the light, instead of causing the stop, is caused by it, or $q\supset p$ (now the reciprocal and not the inverse of $p\supset q$). To confirm $q\supset p$ (stop implies light), he looks for the opposite case which would disconfirm it; that is, does the object ever stop without the light going on? This case, $\overline{p}·q$, is the inverse of $q\supset p$. The object stopping every time the light goes on is quite compatible with its sometimes stopping for some other reasons. Similarly, $p·\overline{q}$, which is the inverse of $p\supset q$, is also the correlative of $q\supset p$. If every time there is a stop the bulb lights up ($q\supset p$), there can be lights without stops. Similarly, if $q\supset p$ is the reciprocal of $p\supset q$, then $\overline{p}·q$ is also the reciprocal of $p·\overline{q}$ [30] (p. 139).

More generally, given any two phenomena represented by propositions p and q, it is not immediately obvious how they are in fact related to each other. Nevertheless, the conjunctions $p·q$, $\overline{p}·q$, $p·\overline{q}$ and $\overline{p}·\overline{q}$ represent the four possible associations of these phenomena, and they can be verified by means of observation. Individually each observed association does not allow the relationship between the phenomena to be determined uniquely. Observation of p and q always occurring together $p·q$, for example, means that p and q could actually be related in any of 8 ways (see

Table 1. 16 Structural Possibilities of Two Phenomena. Four distinct conjunctions represent the possible associations of two phenomena expressed by propositions p and q. True conjunctions comprise the columns of this table, and the columns are set out in pairs comprising the full complement of four conjunctions. Connecting the conjunctions in each column disjunctively generates the disjunctive normal form of the binary operators abbreviated and listed in the bottom row. Except for *, w, p[q], and q[p] the binary operators are familiar. * represents the complete affirmation; w, exclusive disjunction; and p[q] as well as q[p] are affirmations of p and q conjointly with either $\overline{q}$ or $\overline{p}$, respectively, Based on [24] (Table 100, p. 214).

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
$p·q$	-	$p·q$	-	-	$p·q$	$p·q$	-	$p·q$	-	$p·q$	-	$p·q$	-	$p·q$	-
$p·\overline{q}$	-	$p·\overline{q}$	-	$p·\overline{q}$	-	-	$p·\overline{q}$	$p·\overline{q}$	-	-	$p·\overline{q}$	$p·\overline{q}$	-	-	$p·\overline{q}$
$\overline{p}·q$	-	$\overline{p}·q$	-	$\overline{p}·q$	-	$\overline{p}·q$	-	-	$\overline{p}·q$	-	$\overline{p}·q$	-	$\overline{p}·q$	$\overline{p}·q$	-
$\overline{p}·\overline{q}$	-	-	$\overline{p}·\overline{q}$	$\overline{p}·\overline{q}$	-	$\overline{p}·\overline{q}$	-	$\overline{p}·\overline{q}$	-	$\overline{p}·\overline{q}$	-	-	$\overline{p}·\overline{q}$	-	$\overline{p}·\overline{q}$
$p\ast q$	o	$p\vee q$	$\overline{p}·\overline{q}$	$p|q$	$p·q$	$p\supset q$	$\overline{p\supset q}$	$q\supset p$	$\overline{q\supset p}$	$p\equiv q$	$p w q$	$p\left[q\right]$	$\overline{p\left[q\right]}$	$q\left[p\right]$	$\overline{q\left[p\right]}$

: $p·q$ occurs in 8 columns). Through observation of all four possible associations of the phenomena, on the other hand, the relationship is uniquely determined. Observation of associations $p·q$ and $\overline{p}·\overline{q}$ occurring but no cases of either $\overline{p}·q$ or $p·\overline{q}$, for example, indicates that the phenomena represented by p and q are equivalent; whereas observation of associations $p·q$, $\overline{p}·q$, and $p·\overline{q}$ but no cases of $\overline{p}·\overline{q}$ indicate $p\vee q$ (see Table 1) [31]. In short, the discovery of factual links between phenomena is mediated by a framework of relations based on possible combinations of associations of the phenomena in question.

The ability to classify is already attained at the intrapropositional stage of reasoning, and a generalisation of this ability is instrumental in the transition to the interpropositional stage of reasoning [21] (p. 33) [31] (pp. 346–350). The existence of structural possibilities constituting such a framework thus distinguishes interpropositional from intrapropositional reasoning [31] (sec. Piaget’s Logic: A Constructivist Interpretation) [32] (chs. 16–17). In fact, the columns of Table 1 represent the subsets of the powerset of the four conjunctions, i.e., $\mathcal{P}\left(\right\{p·q, p·\overline{q}, \overline{p}·q, \overline{p}·\overline{q}\left\}\right)$.

All manner of compound propositions involving propositional variables p, q and propositional connectives exist; it is therefore desirable to be able to compare them. Fortunately, propositions have canonical forms, and those that share the same canonical form are equivalent whereas those with distinct canonical forms are different. In other words, equivalences and differences between propositions can be distinguished via their canonical forms. By disjunctively composing the conjunctions in the columns of Table 1, distinct canonical forms, namely the disjunctive normal forms, are generated, and the binary operators in the bottom row of Table 1 simply represent convenient abbreviations of them. By virtue of the canonical forms, the columns thus represent classes of equivalent propositions; in fact, Table 1 represents a taxonomy of all relations between the propositions p and q [33] (sec. 19) (see also [34] (secs. 13 & 17)).

The structural possibilities set out in the columns of Table 1 give a static impression; however, Piaget’s illustration of causal reasoning reveals a peripatetic moment. Reasoners move between the columns of structural possibilities by means of operations of thought, and Piaget discerned five altogether; for the purposes of this paper, however, only the reversible operations are relevant:

• The direct operation composes combinations of the four conjunctions disjunctively (∨); e.g., $\left(0\right)\vee (p·q)$; $(p·q)\vee (p·\overline{q})$; etc.
• The inverse operation is the negation of combinations of these conjunctions composed conjunctively (∙); e.g., $·\left(\overline{p·q}\right)$; $·\overline{(p·\overline{q})}$; etc.
• The general identity operation ∨(0) leaves the elements it is composed with unaltered, e.g., $(p·q)\vee \left(0\right)=(p·q)$, and it is the product of the direct and inverse operations; e.g., $(p·q)·\overline{(p·q)}=0$ [24] (p. 335).

By virtue of the interpropositional operations, the structural possibilities constitute a closed system of transformations, which Piaget called the “interpropositional grouping” (e.g., [24] (sec. 39 C)).

Before proceeding, potential misunderstandings need to be nipped in the bud. First, the interpropositional grouping has reversible operations like its namesake the group, and they will be the subject of the next section. Nevertheless, it may seem artificial to attribute dynamic and static aspects to propositional reasoning. According to Piaget, natural structures are characterized by ideas of wholeness, transformation and self-regulation, and they are both structured and structuring [35] (ch. I). On the one hand, the operations of the interpropositional grouping form a closed system of transformations on the taxonomy of propositions and thus constitute an operational structure; on the other hand, the structural possibilities are implicitly defined through their relations to each other in this structure [35] (p. 10). The interpropositional grouping is thus the natural structure modelling the dynamic and static characteristics of propositional reasoning; the structured and structuring are therefore simply different aspects of it. Second, reasoning at this stage is propositional, and Piaget found it convenient to adopt the symbolism of propositional logic to model it. In addition, the interpropositional grouping has a very formal appearance. However, caution is advised since it is not a propositional logic in the classical sense. Piaget drew liberally on abstract mathematical tools to construct the interpropositional grouping [36], and the binary operators set out in the bottom row of Table 1 are abbreviations for structural possibilities; they are therefore implicitly defined by the relations they have to each other in the system of compositions as a whole and should not be mistaken for their classical Doppelgänger2. On the other hand, it is not entirely clear what constitutes a logic [39]; nevertheless, by making some broadly accepted assumptions, it is possible to show that Piaget clearly demarcated propositional reasoning and propositional logic despite his choice of symbolism and the formal representation of the interpropositional grouping [27]. For the current purposes, however, an intuitive grasp of propositional reasoning according to the interpropositional grouping will suffice.

Returning to Piaget’s illustration, observation of associations of two phenomena constitute evidence for any suspected relationship between them by virtue of the framework provided by the structural possibilities. In other words, the structural possibilities structure observation by giving the phenomena meaning. In particular, the 16 distinct propositions about the truth and falsity of the conjunctions $p·q$, $\overline{p}·q$, $p·\overline{q}$ and $\overline{p}·\overline{q}$ structure observations of associations of a light going on and an object stopping. Beginning with the complete affirmation $(p·q)\vee (p·\overline{q})\vee (\overline{p}·q)\vee (\overline{p}·\overline{q})$, the outcome of conjunctively composing the negation of the second conjunction according to the operations of the interpropositional grouping is

$$\left[\left(p·q\right)\vee \left(p·\overline{q}\right)\vee \left(\overline{p}·q\right)\vee \left(\overline{p}·\overline{q}\right)\right]·\overline{\left(p·\overline{q}\right)}=\left(p·q\right)\vee \left(\overline{p}·q\right)\vee \left(\overline{p}·\overline{q}\right)=(p\supset q)$$

$p\supset q$ is thus generated by eliminating the possibility $p·\overline{q}$ from all the possibilities of the complete affirmation. Via the interpropositional grouping, it is therefore known that $p·\overline{q}$, in contrast to $p·q$, $\overline{p}·q$, and $\overline{p}·\overline{q}$, represents an impossible observation if $p\supset q$ is the case. Drawing inspiration from the structural possibilities, the hypothesis that the light going on, p, causes the object to stop, q, for example, can thus be formulated, and the significance of the associations of phenomena in question for the hypothesis can be gauged. In particular, $(p\supset q)·(p·\overline{q}) = 0$; no observations can therefore possibly correspond to this composition. Constituting an impossibility from the point of view of the interpropositional grouping, observation of a light going on but the object not stopping, $p·\overline{q}$, under the hypothesis $p\supset q$ is thus a counterexample. On the other hand, $\left[\left(p·q\right)\vee \left(p·\overline{q}\right)\vee \left(\overline{p}·q\right)\vee \left(\overline{p}·\overline{q}\right)\right]·\overline{\left(p·\overline{q}\right)}=T·\overline{\left(p·\overline{q}\right)}=\overline{(p·\overline{q})}$, where, as Piaget was wont to do, T abbreviates the special identity constituted by the complete affirmation. Hence $p\supset q=\overline{(p·\overline{q})}$. Since observation of the light going on but the object not stopping, $p·\overline{q}$, constitutes falsification of the hypothesis whereas ruling out that the light goes on without the object stopping, $\overline{(p·\overline{q})}$, constitutes verification, the kinds of observation on which verification and falsification of the causal hypothesis $p\supset q$ hinge are also anticipated via the interpropositional grouping.

2.2.1. Groups of Inversions

Piaget falsely equates the principle of duality with negation as follows:

Principle of Duality: The negation of a normal form is obtained by substituting the negations for affirmations and vice versa, as well as the conjunctions for disjunctions and vice versa ([24] p. 234 my translation) [cf. 33] (pp. 46–48)3.

Applying the substitutions as prescribed to the normal forms of the binary operators transforms them into their negations; $(p·q)\vee (\overline{p}·q)\vee (\overline{p}·\overline{q})$, for example, is the disjunctive normal form of the conditional operator $p\supset q$, and its negation according to Piaget’s Principle of Duality is $(\overline{p}\vee \overline{q})·(p\vee \overline{q})·(p\vee q) = (p·\overline{q})$. Furthermore, the negation of $(p·\overline{q})$ is $(\overline{p}\vee q)$, which is the conjunctive normal form for the conditional operator. Applying Piaget’s Principle of Duality a second time thus restores the original operator from its negation.

Clearly, the substitutions Piaget’s Principle of Duality prescribe correspond to De Morgen Laws; however, the De Morgan Laws are usually expressed as equivalences. For Piaget, on the other hand, negation is a transformation, and he [24] (p. 257) dubbed the negation of a binary operator via these substitutions “inverse” operation. With this denotation, however, Piaget appears to have introduced a terminological ambiguity since the interpropositional grouping also has an inverse operation.

It will be recalled that the outcome of an inverse operation of the interpropositional grouping such as $·\overline{\left(p·\overline{q}\right)}$ on T is $T·\overline{\left(p·\overline{q}\right)}=\left[\right(p·q)\vee (p·\overline{q})\vee (\overline{p}·q)\vee (\overline{p}·\overline{q}\left)\right]·\overline{\left(p·\overline{q}\right)} =(p·q)\vee (\overline{p}·q)\vee (\overline{p}·\overline{q})=p\supset q$; furthermore, $T·\overline{(p\supset q)}$ = $\left[\right(p·q)\vee (p·\overline{q})\vee (\overline{p}·q)\vee (\overline{p}·\overline{q}\left)\right]·\overline{\left((p·q)\vee (\overline{p}·q)\vee (\overline{p}·\overline{q})\right)}$ = $(p·\overline{q})$. Referring to Table 1, the outcomes of applying these inverse operations to the complete affirmation are the binary operators represented by columns 7 and 8, respectively. Since Piaget’s Principle of Duality also transforms the binary operator of column 7 into 8 and vice versa, there is in reality no ambiguity in Piaget referring to it as an inverse operation as well. In fact, the explication shows that Piaget’s Principle of Duality simply corresponds to a special case of the inverse operation of the interpropositional grouping, namely the inverse operation when applied to the complete affirmation rather than any binary operator of the operational structure. Moreover, taken together, columns 7 and 8 comprise the full complement of four conjunctions, and the columns have no conjunctions in common. Negation of the conditional operator via Piaget’s Principle of Duality therefore corresponds to complementation with respect to the full complement of four conjunctions. In fact, the columns of Table 1 are organised in pairs and transform into each other either through the application of Piaget’s Principle of Duality or, what amounts to the same, the application of the inverse operation to the complete affirmation; in addition, they have no conjunctions in common and comprise the full complement of conjunctions together. Although rehearsed on the conditional, the special case of the inverse operation corresponds to complementation and applies to all 16 binary operators.

Two distinct substitutions are involved in Piaget’s Principle of Duality. They are carried out concurrently in the inverse operation, but they can also be performed separately. By replacing negations for affirmations and vice versa in the normal forms while leaving the conjunctions and disjunctions unchanged, Piaget [24] (p. 257) defined the “reciprocal” operation. By contrast, he [24] (p. 257) defined the “correlative” operation by keeping the negations and affirmations unchanged while substituting disjunctions for conjunctions and vice versa in the normal form of an operator. For example, the reciprocal transforms the conditional $p\supset q$ into $(\overline{p}·\overline{q})\vee (p·\overline{q})\vee (p·q)$, and the correlative transforms it into $(p\vee q)·(\overline{p}\vee q)·(\overline{p}\vee \overline{q}) = \overline{p}·q$. Since the former is the disjunctive normal form of $q\supset p$4, the outcome of the reciprocal operation is the contradual of the conditional, whereas $\overline{p}·q$ is the dual of $p\supset q$ and the complement of $q\supset p$. In addition, the correlative of $q\supset p$ is $(p\vee q)·(p\vee \overline{q})·(\overline{p}\vee \overline{q}) = p·\overline{q}$, which is the dual of $q\supset p$ as well as the complement of $p\supset q$. Besides reproducing the familiar connections between the conditional, its contradual, dual, and complement, the reciprocal, correlative, and inverse operations also show that $p·\overline{q}$ and its contradual $\overline{p}·q$ transform into each other via the reciprocal operation. Like the inverse, all these operations are involutions, and Figure 2 represents their relations to each other diagrammatically.

In conjunction with an identity operation, Piaget [24] (pp. 257–276) showed that the inverse, reciprocal and correlative operations on selected binary operators of the interpropositional grouping, like those in Figure 2, form groups, INCR-groups namely. It will be recalled that the interpropositional grouping also has an identity operation, which is the product of the direct and inverse operation and leaves the binary operator operated on unaltered. In the INCR-group, each operation is its own inverse since they leave operands unaltered when performed twice. Nevertheless, the identity operation of the group corresponds to the identity operation of the interpropositional grouping in the special case in which the inverse operation of the interpropositional grouping corresponds to complementation.

The taxonomy of structural possibilities used to illustrate the interpropositional grouping has 16 distinct binary operators altogether. The operands of the INCR-group set out in Figure 2, on the other hand, only account for a quarter of them. Four further operators constitute the operands of the INCR-group involving disjunction. For the remaining eight operators, there are four further sets of operators since the operations are not all distinct. For the complete affirmation (*) and complete negation (0) as well as the biconditional (≡) and mutual exclusion (w), identity and reciprocal on the one hand and inverse and correlative on the other coincide; whereas reciprocal and inverse, and identity and correlative, coincide for the affirmation and negation of p[q] and q[p]. All told, six INCR-groups are therefore discernible in the operations of the interpropositional grouping, and they constitute reversible structures in the operational structure formed by the interpropositional grouping [24] (sec. 31).

I have already illustrated the role the interpropositional grouping plays in propositional reasoning. In the next section, I rehearse it in terms of the reversible substructures.

2.2.2. Instrumentalization of Structural Possibilities

Returning to the illustration in which Piaget imagined adolescents reasoning propositionally about the causal relationship between a light going on, p, and an object stopping, q, hypotheses about the causal relationship are formulated and then tested by actively searching for counterexamples. In doing so, reasoners instrumentalise particular structural possibilities of the interpropositional grouping [32] (p. 260–263). Propositions about the possible truth and falsity of the four associations of two propositions are propositions like any other; however, it is not immediately obvious what constitutes the negation of such propositions. $p\supset q$, for example, is a proposition about the possible truth and falsity of four propositions, namely, the possible truth of conjunctions $(p·q)$, $(\overline{p}·q)$ and $(\overline{p}·\overline{q})$ but the falsity of $(p·\overline{q})$; however, it is not immediately obvious what $\overline{p\supset q}$ signifies. Referring to columns 7 and 8 in Table 1 again, they are complementaries with respect to the full complement of conjunctions. The outcome of combining $(p·q\vee \overline{p}·q\vee \overline{p}·\overline{q})$ disjunctively with $(p·\overline{q})$ is therefore $(p·q\vee \overline{p}·q\vee \overline{p}·\overline{q})\vee (p·\overline{q})$, the complete affirmation, and the outcome of combining them conjunctively is $(p·q\vee \overline{p}·q\vee \overline{p}·\overline{q})·(p·\overline{q})=(p·q\vee \overline{p}·q\vee \overline{p}·\overline{q})·\overline{(p·q\vee \overline{p}·q\vee \overline{p}·\overline{q})}=0$ or $\overline{(p·\overline{q})}·(p·\overline{q})=0$, the complete negation. The inverse operation of the INCR-group transforms the disjunctive normal form $(p·q)\vee (p·\overline{q})\vee (\overline{p}·\overline{q})$ of the conditional in column 7 directly into its negation, $(p·\overline{q})$, the disjunctive normal form in column 8. Search and recognition of falsifying phenomena is thus facilitated by the anticipatory concepts generated by the inverse operation of the INCR-group.

Thanks to the inverse operation, adolescent reasoners can identify potential counterexamples for hypotheses more directly. However, the INCR-group also saves reasoners from blindly groping in the dark for alternative hypotheses. Returning to the imagined scenario, $p·\overline{q}$ and $\overline{p}·q$, being the complements of $p\supset q$ and $q\supset p$ respectively, anticipate counterexamples for the respective causal hypotheses; however, $p\supset q$ is compatible with $\overline{p}·q$; and $q\supset p$, with $p·\overline{q}$. Having hypothesised and rejected one causal relationship via observation of a counterexample, an alternative hypothesis consistent with the falsifying observation is thus just a reciprocal transformation of the INCR-group away. In other words, formulating alternative hypotheses is far removed from the hit and miss of trial and error thanks to the INCR-group.

3. Alternative Strategies in the Rationality Debate

Champions of the rationality thesis can avail themselves of two alternative strategies: They can either accept the standard picture and explain away the robust findings of psychological experiments as performance errors by appealing to a competence-performance distinction or they can undermine the standard picture. In the standard picture, it will be recalled, the normative principles of reasoning are based on logic, probability theory, decision theory, etc., and Stein distinguishes three arguments for champions of the rationality thesis who wish to undermine the standard picture:

The first… [denies] that there are normative principles of reasoning that apply to everyone; the normative principles of reasoning are indexed to individuals rather than to humans in general. If this is right, then each human thereby reasons in accordance with her own normative principles and hence is rational. The second… [denies] that it is possible for the normative principles of reasoning to diverge from human reasoning competence. In so far as the reasoning experiments show that we diverge from what we think the norms of reasoning are, they show that we must be mistaken about what the norms of reasoning are. According to the second argument, norms of reasoning are not independent of reasoning competence. The third… [denies] that we have access to the norms of reasoning. If we cannot know what the norms of reasoning are, then we cannot reasonably claim that people diverge from them; the irrationality thesis is, on this view, unsupportable [11] (pp. 215–216).

Stein rejects all three arguments. The norms of reasoning being extra-human but inaccessible in the third argument essentially makes a mockery of the reasoning experiments themselves since experimental designs would be based on arbitrarily chosen norms. In the first and second arguments, there are no extra-human norms; however, relativism looms in the first since the norms, being indexed to each individual, are subjective. In the second alternative, the norms are indexed to human reasoning competence rather than individuals. As such they are commensurate with the finitary predicament, but, applying to human reasoning in general, they have intersubjective validity. Nevertheless, Stein [11] (ch. 7 sec. 2.4) rejects the second alternative because evaluation would be impossible with such norms.

For the second alternative, Stein describes a pragmatic strategy for discovering the normative principles imminent in reasoning competence:

when human reasoning competence and a presumed normative principle of reasoning diverge, experimenters reject the norm and say that the principle of reasoning that we use is in fact the normative principle. The no extra-human norm argument suggests that we should always adopt this strategy—which I call the reject-the-norm strategy—when our preconceived idea of what a norm of reasoning is diverges from our actual reasoning competence [11] (p. 233).

According to the reject-the-norm strategy, reasoning competence rather than preconceived norms is the source of the normative principles of reasoning. However, reasoning competence is based on the empirical evidence of reasoning experiments; if competence is indeed derived from the empirical evidence of reasoning experiments, there must therefore be a way of distinguishing competent from erroneous performances. In Stein’s opinion, this constitutes an insurmountable hurdle for pragmatists:

The no extra-human norms argument attempts to undermine the standard picture of rationality and replace it with the pragmatic picture, according to which the normative principles of reasoning are the best possible principles for humans. For this to succeed as an argument for the rationality thesis, the principles in our reasoning competence need to be the best principles we could possibly have… I [have] argued that one initially appealing way of reading what it means to reason as best as we can actually prevents the possibility of evaluation and thus eliminates the normativity of rationality. In so far as a more sophisticated version of the pragmatic picture of rationality can be worked out (that is, in so far as we can develop an account of what it is to reason as best as we can), an argument that the way we in fact reason is the best we can do is still required. The no extra-human norms argument thus does not undermine the standard picture of rationality in a fashion that establishes the rationality thesis ([11] p. 242 my italics).

I have highlighted the crux of the problem with italics. In a nutshell, the challenge is to find a means of demarcating performance in reasoning experiments into the best we can do and the rest.

Piaget’s theory of reasoning is based on the evidence of psychological experiments, and reversibility is a seminal characteristic of the operations of thought constituting the operational structures that characterise the equilibrium states in the development of intelligence. By virtue of the reversibility of the operations of thought constituting operational structures, Piaget’s theory provides a psychological criterion for singling out the best experimental performances from the rest; in other words, the reversibility of operations of thought constituting operational structures allows the demarcation of competent from erroneous performances and thus provides the basis for an account of what it is to reason the best we can.

Moreover, to err is human, and circumstances might contrive to prevent reasoners from reasoning in accordance with normative principles. Nevertheless, a norm based on the reversibility of operations of thought in operational structures is not extra-human; it has an empirical basis, and, given the right circumstances, it must be possible for some reasoners some of the time to reason in accordance with the norm. Reasoning reversibly might therefore be a tall order for most of us most of the time, but it is certainly not impossible for some of us some of the time. Since prescription is indexed to human reasoning competence in Piaget’s theory, basing normative principles of reasoning on reversible operations of thought is thus commensurate with the finitary predicament.

On the other hand, the consequences of the reject-the-norm strategy Stein advocated in cases where preconceptions of the normative principles of reasoning diverge from the robust findings of empirical experiments may not be as radical as they sound. The classical laws of thought, for example, are traditionally associated with rationality, and, corresponding to ontological and logical interpretations, they can be stated as holding for entities or propositions and are set out in

Table 2. Laws of Thought. The laws of thought are set out in the rows, and their ontological and logical forms are presented in the columns [40] (p. 212).

“Ontological” form.	“Logical” form.
Identity.
A is A or A = A	(A true proposition is true, or If a proposition is true it is always true.)
Non-contradiction.
A cannot both be and not be B. A is not non-A. A is not both B and non-B.	No proposition is both true and false.
Excluded Middle.
A is either B or not B. A either is or is not B.	A proposition is either true or false. No proposition is both non-true and non-false.

.

The laws of non-contradiction and excluded middle are usually stated in the logical form, and together they dictate that either the affirmation or negation of a proposition is true but not both and that there are no further possibilities. Piaget based his theory of reasoning on Boolean algebra [35] (p. 31) [38], and, according to Halmos [41] (ch. I), Boolean algebras are embarrassingly rich structures, which can be defined in an almost indefinite number of ways. Although the operations of the interpropositional grouping do not resemble those in typical definitions of a Boolean algebra, they do in fact constitute one [42]. Moreover, “[m]ost logical concepts have an algebraic alter-ego” [41] (p. 18), and the laws of thought in the logical sense are no exception.

Complementation in a Boolean algebra is defined as follows:

$p·q=0$ and $p\vee q=1$ then $q$ is the complement of $p$.

Since $\overline{p}$ satisfies the equations and complementation is unique in a Boolean algebra, $\overline{p}$ is the unique complement of p, so that $p\vee \overline{p}=1$, and $p·\overline{p}=0$. Moreover, $p\vee 0=p$. On the one hand, these are all operations of a Boolean algebra and thus operations of the interpropositional grouping; on the other hand, they correspond to laws of thought—excluded middle, non-contradiction, and identity, respectively5.

Unlike the laws of excluded middle and non-contradiction, the law of identity is generally stated in the ontological form, i.e., each being or object of thought is identical with itself. From a practical viewpoint, this raises the question of how it is possible to establish identity. For the sense of warmth, for example, temperature perception is relative to the temperature of the perceiving hand. Testing the temperature of warmed water thus irrevocably alters subsequent perceptions of temperatures. Restoring the temperature of warmed water to the original state with the sense of warmth alone is thus practically impossible. Analogously, “having made a hypothesis which he subsequently rejects, the child does not return to the original data of the problem, because they remain somewhat distorted by the hypothesis, even though it was discarded.” [22] (p. 42). It will be recalled, for example, that children at the level of intuitive thought cannot yet entertain two hypotheses simultaneously concerning the length of necklaces. Their mental experiments still imitate practice, and, since some wooden beads are brown, it is not possible in practice for these children to mentally construct a necklace of brown beads and one of wooden beads at the same time for the sake of mental comparison. By virtue of the identity operation of the interpropositional grouping, in contrast, propositions are left unaltered; moreover, it is composed of an operation and its inverse. In other words, the identity operation is based on reversibility and ensures that reasoners can still in fact return to the unadulterated starting point of their deliberations despite hypothetical digressions. In short, via complementation and the identity operation, propositional reasoning in accordance with the interpropositional grouping converges with the laws of thought; widely accepted preconceptions of the normative principles of reasoning need not therefore be rejected.

However, logic still seems to have a role to play in reasoning. “Consistency” and “inconsistency” are logical notions used to characterise the relationship between propositions. Semantically, a set of propositions is consistent if it is satisfiable; i.e., if there is at least one interpretation that makes all the propositions in question true and inconsistent if no such interpretation exists. In contrast, logical closure is implicit in the syntactic notion of consistency, and a set of propositions is syntactically consistent if it does not lead to a contradiction; i.e., a proposition and its negation does not follow logically. Syntactically, reasoners need only assume the truth of the set of propositions given and deduce logical consequences until a contradiction arises to establish inconsistency, whereas all consequences of the set of propositions must be checked for contradictions to establish consistency. Practically, it is clearly much easier to establish inconsistency than consistency syntactically. Semantically, in contrast, establishing inconsistency is laborious, requiring a check of all possible interpretations of the set of propositions, whereas discovery of a single interpretation satisfying the set of propositions is all that is required to demonstrate consistency. Practicality aside, however, consistency alone is not sufficient grounds for believing a set of propositions; nevertheless, it does appear to be necessary since reasoners are inclined to reject inconsistent beliefs. In other words, logic, via inconsistency especially, still appears to play a negative special role in reasoning [14].

Like the laws of thought, syntactic and semantic consistency also have algebraic alter egos. Suppose, for example, a theory is syntactically inconsistent. For some sentence p of a theory, both sentences p and $\overline{p}$ would therefore follow, and $p·\overline{p}$ would also be a consequence. Being a tautology, $p\vee \overline{p}$ is always provable, and, for any sentence of the theory q, $(p\vee \overline{p})\vee q$ is also provable.

$$\begin{array}{cc}\mathrm{Since} (p\vee \overline{p})\vee q& \equiv \overline{\overline{(p\vee \overline{p})}}\vee q\hfill \\ & \equiv \overline{(p\vee \overline{p})}\supset q\hfill \\ & \equiv \overline{(\overline{p}\vee p)}\supset q\\ & \equiv \overline{(\overline{p}\vee \stackrel{̿}{p})}\supset q\hfill \\ & \equiv (p·\overline{p})\supset q\hfill \end{array}$$

Now, since $(p·\overline{p})$ and $(p·\overline{p})\supset q$ are provable, any q is also provable. Hence every sentence would be provably equivalent to every other, and the interpropositional grouping would only have one equivalence class of sentences; in other words, it would be trivial. However, the interpropositional grouping has more than one equivalence class of sentences (see for example Table 1)6, and, being non-trivial, there cannot be any sentence p, for which both p and $\overline{p}$ are consequences (compare [33] sec. 21). In other words, reasoning in accordance with the interpropositional grouping is syntactically consistent because the interpropositional grouping is non-trivial. If competent reasoning is reasoning in accordance with the interpropositional grouping, then inconsistency indicates that reasoning has somehow gone awry, i.e., propositions are not being composed in accordance with the interpropositional grouping (compare [24] sec. 40 2). Since it is also a property of the interpropositional grouping, the negative special role consistency plays in reasoning need not therefore be attributed to logic.

Besides capturing the negative special role logic appears to play in reasoning and circumventing the implausibility of rejecting intuitively valid logical norms, Piaget’s theory must also be able to explain the robust body of empirical evidence supporting the irrationality thesis. An in-depth explication would be desirable; however, such an explication would involve too much detail at this late stage in the manuscript. A platitude like “to err is human” on the other hand is definitely too little. By way of compromise, I indicate how Piaget’s psychological theory of reasoning gives plenty of scope for variability in performance at reasoning tasks.

I have already illustrated the development of reasoning with two examples drawn from the psychogenesis of intelligence. Children not yet at the concrete-operational stage are unable to reason reversibly about classes, and, even for those who have reached this stage, the reversibility of their reasoning is still more limited than adolescents already able to reason at the formal-operational stage. One source of performances deviating from the normative principle of reasoning based on logic thus springs from the reasoning competence of the individual. However, even at the formal-operational stage, there are still many cognitive schemata requiring construction [32] (pt. II). Reasoning is far from homogeneous even at the same stage of cognitive development, and the systematic time-lags, horizontal décalage, in solving the conservation experiments show that grasping a subject matter does not depend on reasoning competence alone. Contents also resist structuring, i.e., assimilation to operational structures, to various degrees; reasoners must therefore first overcome this resistance before an adequate grasp of any given subject matter can be acquired. In contrast to logic, reasoning is thus content sensitive. Another source of performances in reasoning tasks deviating from normative principles based on logic thus lies in the subject matter itself. According to Piaget’s theory of reasoning, performance thus depends both on an individual’s cognitive capacity and the contents of reasoning tasks [21] (pp. 15–17). The fact that reasoning experiments show that performance depends on the content of reasoning tasks (e.g., [1,2]), and that reasoners who perform better on accepted measures of intelligence generally perform better at such tasks e.g., [6] (pp. 5–6) [43] are thus in accordance with Piaget’s theory of reasoning.

4. Conclusions

According to Piaget, reversibility is a seminal characteristic of the structured wholes operations of thought form in states of equilibrium. It also allows competent performances in reasoning experiments to be distinguished from erroneous ones. The reversibility of the operations of thought constituting operational structures is thus an empirically based criterion for determining the best we can do in the way we in fact reason. By means of reversibility, a seminal characteristic of operations of thought in states of equilibrium, Piaget thus established the rationality thesis whilst undermining the standard picture. Given the convergence of the principles of reasoning based on reversibility with normative principles of logic, however, Harman’s belief that logic has more than just a negative special role to play in reasoning does not appear to be as irrational as he suspected. Logical knowledge may be autonomous and appear extra-human, but, having an algebraic alter ego, propositional reasoning occurring in accordance with the interpropositional grouping converges, albeit in algebraic guise, with principles of logic. “Logic is the mirror of thought, and not vice versa” [22] (p. 27) is the metaphor Piaget used to express this special relationship.

Returning to the insinuation of logicism, Piaget’s theory is a psychological model of reasoning, and Piaget drew liberally on formal tools from the storehouse of mathematics and logic to construct it [36]. His theory is thus very formal in appearance; amongst other reasons, this has contributed to it being mistaken for a formal logic. However, it is a psychological model based on experimental evidence. Morever, its formality is in my opinion one of its virtues. The truths of logic are a priori; irrespective of the crushing weight of contradictory experimental evidence, their normative appeal will not therefore go away [7] (sec. 6). By demonstrating how the psychological model of reasoning converges with these truths, it is therefore possible to explain a rather exceptional source of knowledge psychologically, and the formality of Piaget’s model actually helps bridge the gap between the descriptive and normative project [5,27]. In other words, Piaget’s theory has unificatory and explanatory epistemic virtues. On the other hand, reasoning in accordance with the interpropositional grouping is a tall order; for most of us most of the time, mistakes are therefore the unfortunate reality. In the sense of convergence of competent reasoning with apodictic truths rather than the latter being constitutive of rationality, I therefore believe it is correct to say that Piaget incorporated the logicist tradition into his theory of reasoning.

The rationality debate precipitated a Kuhnian crisis at the end of the 20th century, and many reasoning researchers abandoned the deductive paradigm as a result. Apart from rejection of the deductive paradigm, however, there is as yet little broad consensus on what constitutes the new paradigm [7] (sec. 5). In this paper, I have argued that Piaget’s theory should have been classified as an alternative strategy according to the taxonomy of a philosophical protagonist writing at the height of the crisis. By indexing rationality to reversibility, Piaget painted an alternative picture to the standard picture of rationality, which does not require the rejection of accepted logical norms and thereby incorporates the logicist tradition. Besides restoring the brilliance of an old masterpiece, which as I said could be deemed reward enough, I believe I have also shown that Piaget’s theory of rationality qualifies for a place in the hegemony of the nascent new paradigm rather than a dusty corner in an exhibition of old classics. Why it is not considered to be a viable contender is a historical question, but on condition my argument is correct, the answer lies in external rather than internal historical factors.