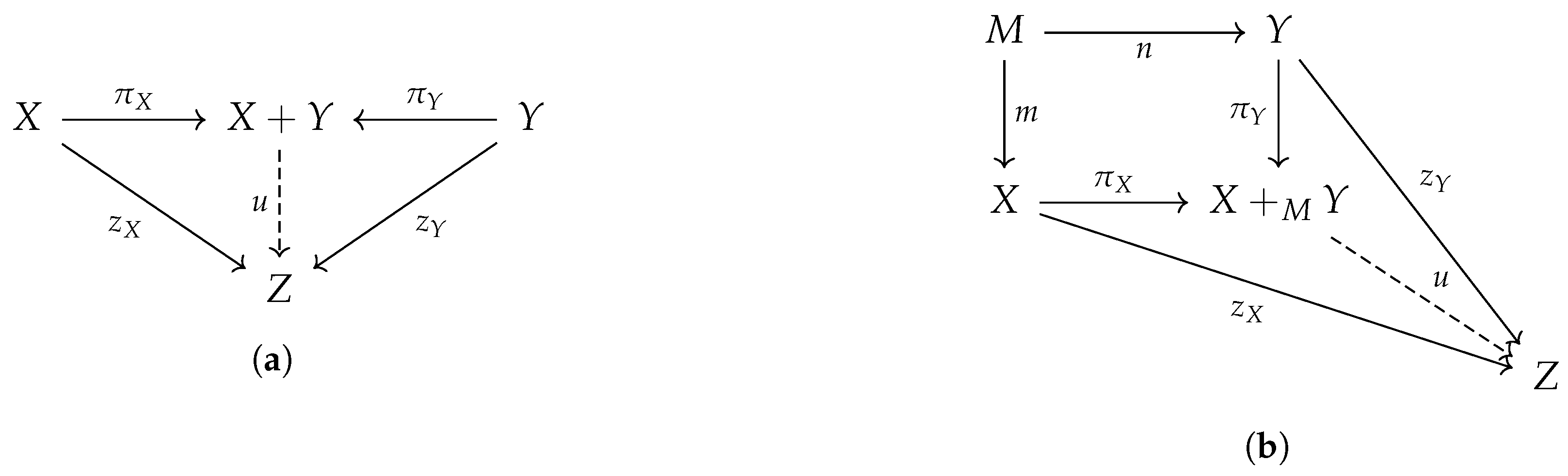Structural Similarity: Formalizing Analogies Using Category Theory

Abstract

Analogies are an important part of human cognition for learning and discovering new concepts. There are many different approaches to defining analogies and how new ones can be found or constructed. We propose a novel approach in the tradition of structure mapping using colored multigraphs to represent domains. We define a category of colored multigraphs in order to utilize some Category Theory (CT) concepts. CT is a powerful tool for describing and working with structure-preserving maps. There are many useful applications for this theory in cognitive science, and we want to introduce one such application to a broader audience. CT and the concepts used in this paper are introduced and explained. We show how the category theoretical concepts product and pullback can be used with the category of colored multigraphs to find possible analogies between domains using different requirements. The dual notion of a pullback, the pushout, is then used as conceptual blending to generate a new domain.

1. Introduction

Analogies are seen as a staple of human cognition because they play an important part in teaching, learning, and developing new concepts [1,2]. Similarities between two domains can be used to transfer knowledge from one domain to another to gain new insights or explain complex concepts. There are many questions concerning analogies, like how they are best defined, how they can be constructed from two domains, and what a good analogy is. These questions are also important when incorporating analogies in artificial reasoning to improve it or make it more interpretable. A key part of any approach to analogies is the representation of the involved knowledge and concepts [3]. Liu et al. [4], for example, embed knowledge graphs in an abstract linear space to transfer relations from one domain to another. The structure mapping theory by Gentner [5] focuses on mappings between domains based solely on their structure and has been used to automatically generate analogies in the structure mapping engine [6].

In this paper we use Category Theory (CT), a mathematical field concerned with general and specific properties of structure-preserving maps, to define domains as objects in the category of colored multigraphs and analogies as maps between them. This category theoretic view on analogies allows us to use CT concepts to analyze these maps and what information is contained in them.

In the remainder of this section, we will introduce our concept of analogies together with a specific example and basic concepts of CT. The main section contains a definition of analogies as morphisms in the category of colored multigraphs and shows how the CT concepts pullback and pushout can be used to form new colored graphs representing possible analogies and blends between two domains.

1.1. Analogies

An analogy consists of two domains, the base and the target, and a mapping between them [5]. This mapping gives rise to a generalization of their common structure and can be used to transfer knowledge from the base domain to the target domain or to generate a new concept that contains properties of both (concept blending). Structure mapping [5] is a classic approach to finding the commonalities between two domains, which focuses on the shared structure of each domain, rather than the properties of involved objects. A common example is to say that the solar system is like the Bohr model of the hydrogen atom because certain relations between the Sun and planets are similar to relations between the nucleus and the electron [5].

In examples, domains are often shown as directed multigraphs, whose nodes are objects and whose edges are relations between these objects (see example in Figure 1). We introduce a formalization of domains that is based on these directed multigraphs. Each node and edge of a domain has a name to differentiate them, and there may be several edges between two nodes. A multigraph consists of two sets, the set of nodes N and the set of edges E, and two functions $s,t$ from E to N, mapping each edge e to its source ($s\left(e\right)$) and target node ($t\left(e\right)$). In structure mapping, relations between objects are the defining characteristics that guide which objects are seen as similar, while properties of objects are not. We add a coloring to the edges of the directed multigraph to capture that some relations are the same or similar. A coloring is described by a set C of possible colors and a function c that maps each edge to its color. In the example of Figure 1, the attraction between the Sun and planets can be related to the attraction between the nucleus and electron, but there are no distinctive similarities between the properties of the Sun and the nucleus.

Edges in graphs are binary relations, so we can only describe domains with binary and, using loops, unary relations as multigraphs. We will also not cover higher-order predicates here. Higher-order predicates and n-ary relations can be included in a different representations of domains using categories and types as described in Ott and Jäkel [7].

We use a category of colored graphs to formalize analogies and determine possible maps.

1.2. Category Theory

CT is a theory that bridges many mathematical fields. An abstract description of mathematical objects, which focuses on their relations, is used to show and leverage commonalities and differences between these objects. CT can therefore be seen as a theory of analogies between mathematical objects. Using CT in cognitive science in general and to model analogy making in particular has been suggested before, for example by using commutative diagrams to analyze an analogy and coequalizers to describe re-representation [8] or by using functors to describe the instantiation of an abstract concept to the base and target domain and a natural transformation of these functors to describe an analogy [9]. The structure-preserving morphisms of a category can be used with most formalizations, for example with Heuristic-Driven Theory Projection [10].

We will give definitions of a category and some concepts that are needed for our use case. For a more detailed introduction, we refer the reader to introductory textbooks [11,12].

CT deals with categories, which consist of objects and arrows, so-called morphisms, between these objects. These morphisms are usually written as $f:X\to Y$ for the morphism f from object X to object Y. For example, the category $\mathbf{Set}$ consists of sets as objects and functions as morphisms. Functions behave nicely in the sense that the combination of two functions is again a function and each set has an identity function such that its composition with another function yields again that other function. These properties are general for each category and included in the following definition.

Definition 1

(Category). A category $\mathcal{C}$ consists of a set or class of objects $\mathrm{Ob}\left(\mathcal{C}\right)$ and for each pair of objects $X,Y\in \mathrm{Ob}\left(\mathcal{C}\right)$ a set of morphisms between these objects ${\mathrm{Mor}}_{\mathcal{C}}(X,Y)$. Morphisms can be concatenated if one has the same source as the other’s target. The composition of two morphisms is marked by ∘ and has the following properties:

1. 

For every object $X\in \mathrm{Ob}\left(\mathcal{C}\right)$ there exists an identity morphism $i{d}_X:X\to X$ such that for any object $Y\in \mathrm{Ob}\left(\mathcal{C}\right)$ and any morphism $f:X\to Y$, $f\circ i{d}_X=f$ and $i{d}_Y\circ f=f$ holds.

2. 

For any objects $X,Y,Z,W\in \mathrm{Ob}\left(\mathcal{C}\right)$ and morphisms $f:X\to Y$, $g:Y\to Z$ and $h:Z\to W$ the compositions $g\circ f$ and $h\circ g$ exist and it holds that $h\circ (g\circ f)=(h\circ g)\circ f$.

The category of directed multigraphs (not colored), based on the standard definition of the category of undirected graphs [13], contains multigraphs as objects and all structure-preserving maps as morphisms. Structure preserving in this context means that a morphism $f=(f_E,f_N):G_1\to G_2$ consists of a map of nodes ($f_N$) and one of edges ($f_E$) that are consistent with the graph structure; i.e., the source $s_1\left(e\right)$ of an edge e is mapped to the source of its image ($f_N\left(s_1\left(e\right)\right)=s_2\left(f_E\left(e\right)\right)$) and the target $t_1\left(e\right)$ is mapped to the target of its image ($f_N\left(t_1\left(e\right)\right)=t_2\left(f_E\left(e\right)\right)$) for all edges $e\in E$. The identity morphism maps each node and edge to itself and fulfills the first property of a category. The composition of two morphisms $f:G_1\to G_2$ and $g:G_2\to G_3$ is defined by the composition of the single components. For example $g\circ f\left(n\right)=g\left(f\right(n\left)\right)$ for any $n\in N_1$. This composition is also a morphism in the category of directed multigraphs and fulfills the second property.

When talking about morphisms, a key question is whether certain morphisms or combinations are equal to each other. Certain parts of a category can be nicely drawn as a diagram, using arrows to represent morphisms, and such a diagram is called commuting if all directed paths with the same start and end points, i.e., compositions of morphisms with the same domain and codomain, are equal.

We can now define the category of colored multigraphs and demonstrate how the CT concepts pullback and pushout can be used to describe analogies.

2. Formalizing Analogies

In this section, we formalize analogies using the category of colored directed multigraphs. We will first define the respective category and then show how some concepts central to the theory of analogies can be formalized using the CT concepts pullbacks and pushouts.

2.1. Category of Domains

We want to focus on the relational mapping between domains as a basis for finding and constructing analogies. Each domain consists of objects (e.g., sun and planets) and relations between these object (e.g., the Sun attracts a planet). A relation always has a direction (the Sun is bigger than a planet is not the same as a planet is bigger than the Sun) and each pair of objects can have multiple relations. As mentioned before, domains are modeled as directed multigraphs with loops. Colors are added to edges to show similarities between various edges. The attracts relations in Figure 1 have, for example, more in common with each other than with the hotter relations. From here on, colored directed multigraphs will be just called colored graphs.

We now want to formally define a category $\mathbf{ColG}$ of colored graphs in order to better analyze the structure of maps between colored graphs. We expand the definition from Section 1.2 to include colors. Each object in $\mathbf{ColG}$ is a colored graph that consists of three sets, the set of nodes N, the set of edges E, and the set of colors C. In addition to the function mapping each edge to a source node ($s:E\to N$) and a target node ($t:E\to N$), there is one for color as well ($c:E\to C$). Color is here not restricted to classic colors but can be seen as general labeling.

For example the graph for the atom in Figure 1 can be formalized as object $\mathcal{A}=\{N_{\mathcal{A}},E_{\mathcal{A}},C_{\mathcal{A}},s_{\mathcal{A}},t_{\mathcal{A}},c_{\mathcal{A}}\}$ in $\mathbf{ColG}$ with $N_{\mathcal{A}}=\{$ nucleus, electron}, $C_{\mathcal{A}}=\{$ more massive, attracts, revolves around}, a set $E_{\mathcal{A}}$ of four distinct edges, and the respective maps $s_{\mathcal{A}}$, $t_{\mathcal{A}}$, and $c_{\mathcal{A}}$ to build the graph in the figure.

A category is defined not only by its objects, but also by its morphisms. A morphism $f=(f_E,f_N,f_C)$ in our category $\mathbf{ColG}$ consists of three structure-preserving functions. The first, $f_E:E_B\to E_T$, maps all edges from the base graph B to edges of the target graph T. The second map, $f_N:N_B\to N_T$, maps all nodes from the base graph B to nodes of the target graph T in a way that preserves source and target nodes of the mapped edges. The third map, $f_C:C_B\to C_T$, maps colors to colors, meaning that all edges that have the same color in the base graph must have the same color in the target graph. This may be a different color. This map makes the left square in Figure 2 commute.

In our example of Figure 1, there are many valid morphisms from the solar system graph $\mathcal{S}$ to the atom graph $\mathcal{A}$. The two planets have to be mapped to a different node from the node sun, because there are no loops in $\mathcal{A}$. The color ‘attracts’ is the only color with edges in all directions, so it can only be mapped to ‘attracts’ in $\mathcal{A}$. However, there are not the same restrictions on morphisms for the other colors. Morphisms between sets can be easily composed, and each colored graph has an identity function, so $\mathbf{ColG}$ indeed fulfills all properties of a category.

So far we have encoded important structural information of domains in colored graphs and defined morphisms that preserve this structure. However, there can be many morphisms between two graphs, and not every morphism gives rise to a good analogy. There is also the additional concern that a morphism maps the whole graph. The ‘hotter’ edges in $\mathcal{S}$, for example, have no match in $\mathcal{A}$ but will be mapped to some other edges by a morphism. We now want to use the concepts product and pullback to construct possible mappings between two domains that are more restricted but also allow a partial correspondence.

2.2. Pullbacks with Possible Analogies

The next concept we introduce is the product, which is a generalization of the Cartesian product of sets. A product of two objects in a category is another object in that category that contains all information of the two factors. Figure 3a shows the product in a commutative diagram.

Definition 2

(Product). The product $X\times Y$ of two objects $X,Y\in \mathrm{Ob}\left(\mathcal{C}\right)$ is equipped with two projection morphisms ${\pi }_X:X\times Y\to X$ and ${\pi }_Y:X\times Y\to Y$ such that for any object $Z\in \mathrm{Ob}\left(\mathcal{C}\right)$ and pair of morphisms $z_X:Z\to X$ and $z_Y:Z\to Y$ there exists a unique morphism $u:Z\to X\times Y$ such that $z_X={\pi }_X\circ u$ and $z_Y={\pi }_Y\circ u$.

A product is unique up to isomorphisms. The category $\mathbf{Set}$ contains for every pair of sets their Cartesian product and the respective projections, which fulfill the properties of the product defined above. So $\mathbf{Set}$ has all products. This is not necessarily true for every category.

A product of two colored graphs shows all possible mappings between the edges of the two graphs at once. For two colored graphs $G_i=(N_i,E_i,C_i,s_i,t_i,c_i)$ for $i\in \{1,2\}$, the product $G_1\times G_2$ has the node set $N_{1\times 2}=N_1\times N_2$, edge set $E_{1\times 2}=E_1\times E_2$, and a color set $C_{1\times 2}$ isomorphic to $C_1\times C_2$. The maps are defined as $f_{1\times 2}\left((e_1,e_2)\right)=(f_1\left(e_1\right),f_2\left(e_2\right))$ for $f\in \{s,t,c\}$. The projections ${\pi }_1$ and ${\pi }_2$ map each element of $N_{1\times 2}$, $E_{1\times 2}$, and $C_{1\times 2}$ to their first or second component. See Figure 4 for an example.

For the solar system example above, the product results in a large graph with many edges because any combination of edge mappings is considered. We will now define pullbacks and look at how a pullback over a simple graph can be used to force edges of certain colors to be only combined with other edges of these colors.

A pullback can be seen as a restricted product. The pullback in $\mathbf{Set}$ over two morphisms $f:X\to M$ and $g:Y\to M$ consists, for example, of the set $\left\{\right(x,y)\in X\times Y|f\left(x\right)=g\left(y\right)\}$ and the respective projections. Figure 3b shows the following definition as a commutative diagram.

Definition 3

(Pullback). A pullback $X{\times }_{M}Y\in \mathrm{Ob}\left(\mathcal{C}\right)$ over two morphisms $f:X\to M$ and $g:Y\to M$ is equipped with the morphisms ${\pi }_X:X{\times }_{M}Y\to X$ and ${\pi }_Y:X{\times }_{M}Y\to Y$ such that $f\circ {\pi }_X=g\circ {\pi }_Y$ and for any other object $Z\in \mathrm{Ob}\left(\mathcal{C}\right)$ and morphisms $z_X:Z\to X$ and $z_Y:Z\to Y$ with $f\circ z_X=g\circ z_Y$ there exists a unique morphism $u:Z\to X{\times }_{M}Y$ such that ${\pi }_X\circ u=z_X$ and ${\pi }_Y\circ u=z_Y$.

As mentioned above, a pullback can be used to restrict the product. This construction of seeing a product as all possibilities and using the pullback to sort by an inert structure has been used before in a paper on artificial perception [14]. The pullback $G_1{\times }_G{G}_2$ over two morphisms $f:G_1\to G$ and $g:G_2\to G$ consists of the node set $N_{1\times 2}=\left\{(n_1,n_2)\right|f\left(n_1\right)=g\left(n_2\right)\}$, edge set $E_{1\times 2}=\left\{(e_1,e_2)\right|f\left(e_1\right)=g\left(e_2\right)\}$, a color set $C_{1\times 2}=\left\{(c_1,c_2)\right|f\left(c_1\right)=g\left(c_2\right)\}$, and the respective maps s (for source nodes), t (for target nodes), and c (for colors).

The graph G, which we call a middle graph here, is used to encode some prior information or restriction regarding the possible maps. For example, Figure 5 shows a pullback for the graphs from Figure 1 over a middle graph with a single node and one edge for each color that occurs in at least one of the two graphs. This graph and the morphisms f and g that map edges to edges of the same color encodes the prior knowledge that possible matches should only match edges of the same color with each other. For space reasons, the graphs of the solar system and the atom are shown at a smaller scale. For reference, we can compare this diagram to the one in Figure 3b. The object X is replaced by the graph describing the solar system and Y by the graph describing the atom; the small graph has the same function as M and the large graph is the pullback and therefore replaces $X{\times }_{M}Y$.

All possible analogies that adhere to the graph colors are superimposed in the pullback. The example pullback in Figure 5 does not contain the hotter relation between the Sun and planets because there is no equivalent edge in the hydrogen atom. We can now look for each possible combination of pairing the nodes mars, venus, and sun with the the nodes electron and nucleus in the respective subgraph. There are six possible combinations of matches for injective mappings between the nodes of the two domains. Each match consists of one node of the graph $\mathcal{S}$ and one of $\mathcal{A}$ and a subgraph consists of two of these matches. The respective subgraph of the pullback contains all edges between these two node pairs. Figure 6 shows the six resulting subgraphs. There are two subgraphs without any edges (a, b), two with only two edges (c, d), and two with four (e, f). The last two contain the most structure and are therefore the preferred mappings. These correspond to matching the Sun with the nucleus and one planet with the electron and are equally valid.

We could loosen the requirement on the color matching by changing the maps f and g. If edges of two colors are mapped to the same edge, all their combinations occur in the pullback. Another option is to force certain nodes or edges to be matched by adding edges and nodes to the middle graph. Hence, the pullback can be used to obtain a graph with all possible analogies superimposed based on prior knowledge. We can then reconstruct all possible matches and use the number of edges in the subgraphs as a preference order.

Figure 7 shows another pullback over a different graph. The middle graph now has three instead of one node and four edges with the same color black. This graph encodes different restrictions than the one in Figure 5. Here, the nodes are already paired. The morphism f maps the node mars to m, sun to s,n and venus to v,e, respectively, while g maps nucleus to s,n and electron to v,e. However, each edge is mapped to the one edge that has the correct source and target to fulfill the condition of a graph morphism without adhering to any color conditions because the middle graph does not encode any differentiation between colors. The resulting pullback contains only the two nodes sun, nucleus and venus, electron because the node m was only matched by one of the two original graphs. However, because there was no differentiation between edge colors, each combination of two edges in $\mathcal{S}$ and $\mathcal{A}$ with the right source and target has a representation in the pullback graph.

In this example, the differentiation contained in the colors was lost in the maps to the uni-colored graph, resulting in many possible edges. In this case, it is more difficult to decide which edges should be used in a subgraph to describe the analogy.

2.3. Blending Using Pushouts

We can use a partial map from one domain to another to construct a new combined domain, the so-called conceptual blend. We build on the idea of using a pushout for this conceptual blending [15,16] to define the asymmetric transfer from the base domain to the target domain.

Many CT concepts have a dual in which the morphisms are reversed. The dual of a product is called a coproduct and is a generalization of a disjoint union of two sets. Figure 8a shows the diagram describing a coproduct.

Definition 4

(Coproduct). The coproduct $X+Y$ of two objects $X,Y\in \mathrm{Ob}\left(\mathcal{C}\right)$ is equipped with two morphisms ${\pi }_X:X\to X+Y$ and ${\pi }_Y:Y\to X+Y$ such that for any object $Z\in \mathrm{Ob}\left(\mathcal{C}\right)$ and pair of morphisms $z_X:X\to Z$ and $z_Y:Y\to Z$ there exists a unique morphism $u:X+Y\to Z$ such that $z_X=u\circ {\pi }_X$ and $z_Y=u\circ {\pi }_Y$.

In the category of multigraphs introduced above, a coproduct of two graphs is given by a disjoint union of these graphs and the morphisms mapping each graph to its respective subgraph. The dual of a pullback is called a pushout.

Definition 5

(Pushout). A pushout $X{+}_{M}Y\in \mathrm{Ob}\left(\mathcal{C}\right)$ over two morphisms $m:M\to X$ and $n:M\to Y$ is equipped with the morphisms ${\pi }_X:X\to X{+}_{M}Y$ and ${\pi }_Y:Y\to X{+}_{M}Y$ such that ${\pi }_X\circ m={\pi }_Y\circ n$ and for any other object $Z\in \mathrm{Ob}\left(\mathcal{C}\right)$ and morphisms $z_X:X\to Z$ and $z_Y:Y\to Z$ with $z_X\circ m=z_Y\circ n$ there exists a unique morphism $u:X{+}_{M}Y\to Z$ such that $u\circ {\pi }_X=z_X$ and $u\circ {\pi }_Y=z_Y$.

We have started by constructing a graph of possible analogies using the pullback, as shown in Figure 5. The resulting subgraphs in Figure 6 describe different analogies and can be used to create a blended graph via pushout. For the example in Figure 9, the subgraph (f) in Figure 6 was chosen because it is one of the subgraphs with the most edges. The resulting graph describing the blend contains this common graph and additionally all nodes and edges that occur in one of the two graphs, but not in the common graph.

The pushout over this graph matching sun to the nucleus and venus to the electron yields a graph with these two combined nodes and their combined edges and one additional node for Mars and some additional edges. This positioning of mars in the combined graph can be seen as the idea of having more than one revolving object in such a system and therefore having more than one electron in an atom. The hotter relation, which is also transferred, can lead to the realization that an explanation using this analogy has to point out this difference to avoid a wrong transfer or confusion.

Starting with a simple graph to match the colors of the two domain graphs, we constructed a pullback to find all possible matches for an analogy. One of these matches was chosen in the form of a subgraph of the pullback and used for a pushout to generate a blended graph.

3. Discussion

We have formalized knowledge domains as colored multigraphs and used CT to show how this structure can be used to describe and find possible analogies between two domains. We used pullbacks over a graph describing prior knowledge to generate a new graph of possible maps. A subgraph of this pullback that describes one of those possible matches was used in a pushout to construct a blend of the two domains.

We do not assume that humans actually use CT when finding, teaching, or learning analogies, but we know that some kind of mapping between relations can be performed and this is one way of describing this process. We demonstrated the usefulness of CT for such considerations.

Colored graphs are a common visualization of domains and the category $\mathbf{ColG}$ includes the basic tools to form matches and blends, but this formalization works best for binary and first-order relations. A second, more abstract approach building on the same ideas is presented by Ott and Jäkel [7] to include n-ary and higher-order relations.

This is only a small demonstration of the possibilities, and a next step could be to better define which of the possible analogies should be used. This could be guided by endowing the domain graphs with further information, for example which relations are the most important for defining a domain. The methods used could also be implemented in automatic analogy forming. A good formalization of domains and analogies between them can help us further understand human reasoning and can be used to improve artificial reasoning in a way that is interpretable and understandable for human users.