A Fundamental Non-Classical Logic
Abstract
1. Introduction
Without going nearly so far as to claim that the ability to follow the introduction and elimination rules is all there is to grasping the meaning of ’and’, one can still appreciate that the validity of the introduction and elimination rules is a central semantic fact about ’and’.If we are asked what is the meaning of the word ’and’, at least in the purely conjunctive sense (as opposed to, e.g., its colloquial use to mean ’and then’), the answer is said to be completely given by saying that (i) from any pair of statements P and Q, we can infer the statement formed by joining P to Q with ’and’ (which statement we hereafter describe as ’the statement P-and-Q’), that (ii) for any conjunctive statement P-and-Q we can infer P, and (iii) from P-and-Q we can always infer Q. Anyone who has learnt to perform these inferences knows the meaning of ’and’, for there is simply nothing more to knowing the meaning of ’and’ than being able to perform these inferences. (p. 38)
- (1)
- It’s raining but it might not be raining ()
- (2)
- either it’s raining or it’s not, and it might be raining and it might not be raining ()
- (3)
- it’s raining and it might not be, or it’s not raining and it might be(),
- if and , then ,
- if and , then , or
- if and , then .

2. Fitch-Style Natural Deduction
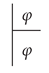 We allow proofs that do not end with a conclusion formula (which could be called “partial proofs”) but we define the provability relation as follows: if there exists a proof beginning with and ending with . For those familiar with Fitch-style natural deduction, the rules of our system are shown in Figure 2.
We allow proofs that do not end with a conclusion formula (which could be called “partial proofs”) but we define the provability relation as follows: if there exists a proof beginning with and ending with . For those familiar with Fitch-style natural deduction, the rules of our system are shown in Figure 2.- If is a proof and is a proof, then is a proof.
- If is a proof and are formulas, then is a proof (∧I).
- If is a proof and is a formula of the form , then and are proofs (∧E).
- If is a proof and is a formula, then for any formula , bothand are proofs (∨I).
- If is a proof, is a formula of the form , is a sequence beginning with and ending with , and is a sequence beginning with and ending with , then is a proof (∨E).
- If is a proof, is a formula , and is a sequence beginning with and ending with , then is a proof (¬I).
- If is a proof and and are formulas of the form and , respectively, then for any formula , is a proof (¬E).
This formulation of ¬ introduction is admissible in Fitch’s system, thanks to his Reiteration rule; but Fitch [14] states his ¬ introduction rule in a way that requires a pair of contradictory formulas to appear in the subproof that starts with .4 To accomplish what we accomplish with ¬I, Fitch would reiterate into the subproof beginning with to obtain a contradiction between and within the subproof. But we can disassociate Reiteration, which we do not allow (recall the cautionary Figure 1), from ¬ introduction. The idea of Reiteration is that if was derived just before a subproof beginning with , then ψ still holds under the assumption of φ. By contrast, when applying our ¬I rule, we prove that the negation of holds under the assumption of φ, and then since we know that ψ holds prior to the assumption of φ, we deduce .5if from the assumption of φ, you derive the negation of another formula derived just before the assumption, then conclude .

| 1. | 8. if and , then |
| 2. | |
| 3. | 9. if and , then |
| 4. | |
| 5. | 10. if and , then |
| 6. | |
| 7. | 11. if , then . |
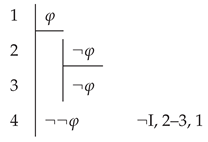 Next is the property that if , then . Assuming we have a proof from to , we construct a proof from to as follows:
Next is the property that if , then . Assuming we have a proof from to , we construct a proof from to as follows: 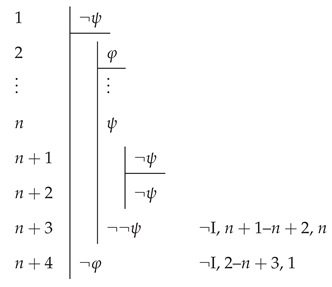 Proving 8–10 of Definition 2.1 for also involves gluing together proofs. For 8, given proofs and , it is easy to see that is also a proof. For 9, given proofs and , the sequence is a proof. For 10, given proofs and , the sequence is a proof.
Proving 8–10 of Definition 2.1 for also involves gluing together proofs. For 8, given proofs and , it is easy to see that is also a proof. For 9, given proofs and , the sequence is a proof. For 10, given proofs and , the sequence is a proof.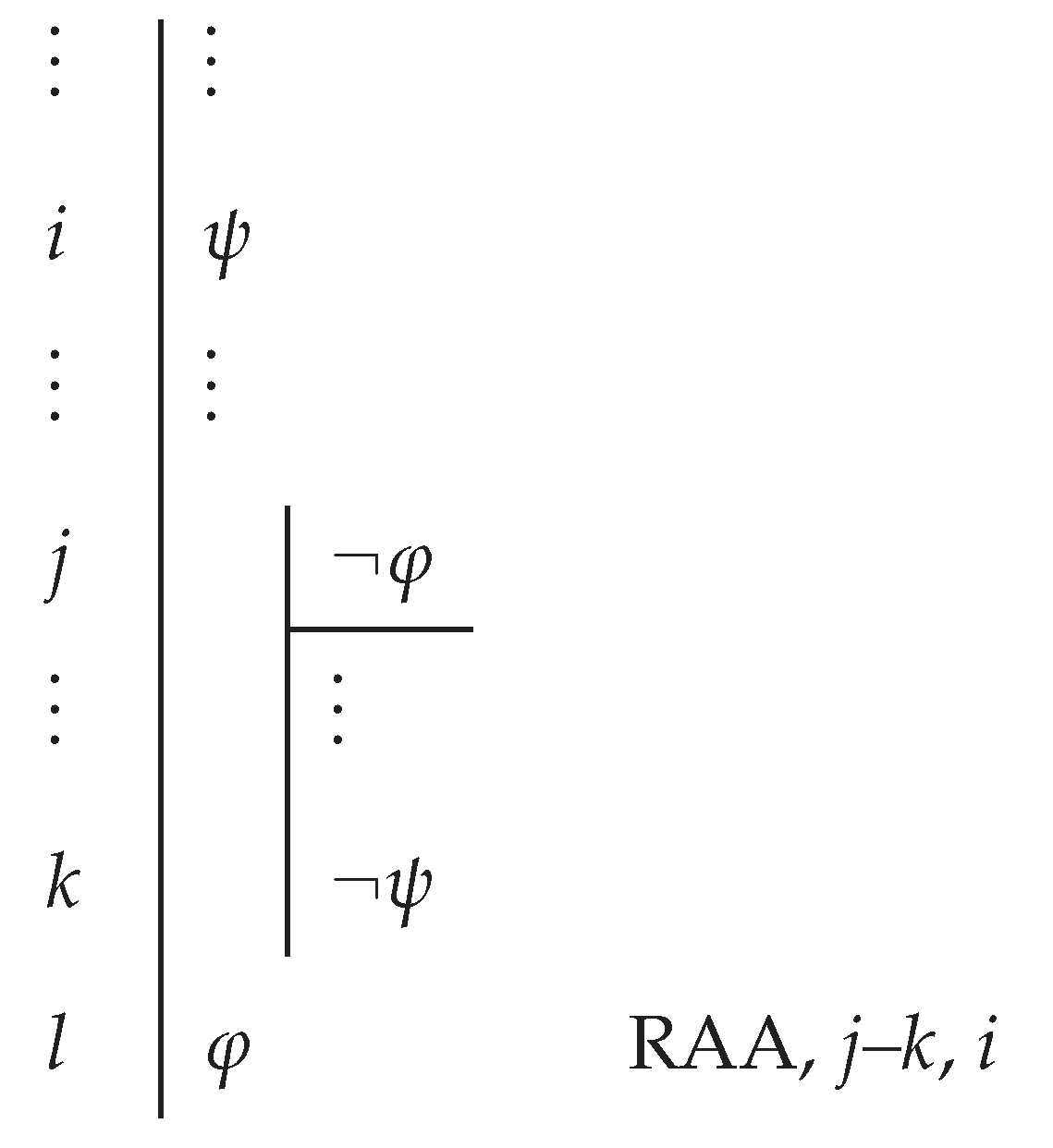

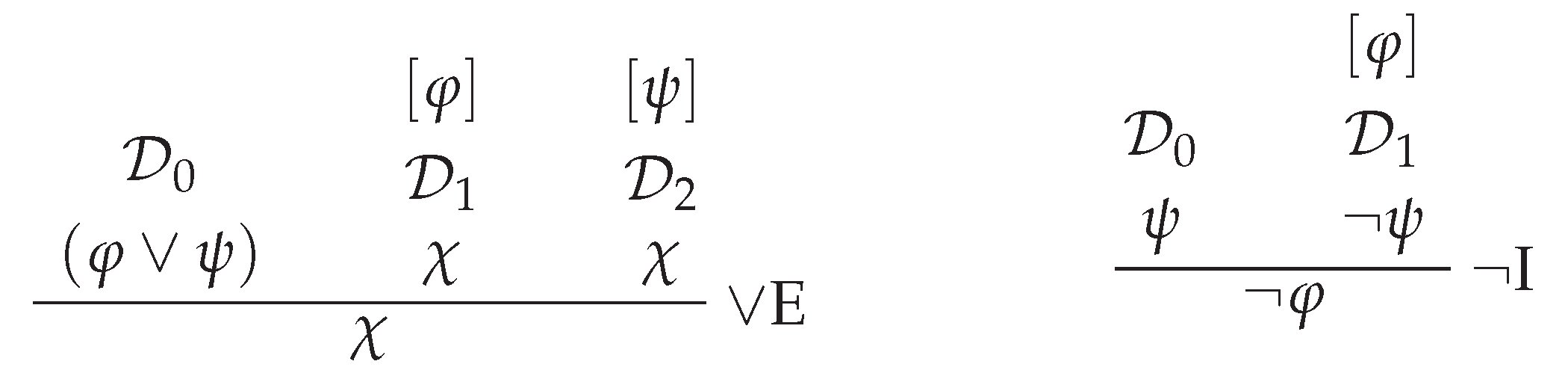
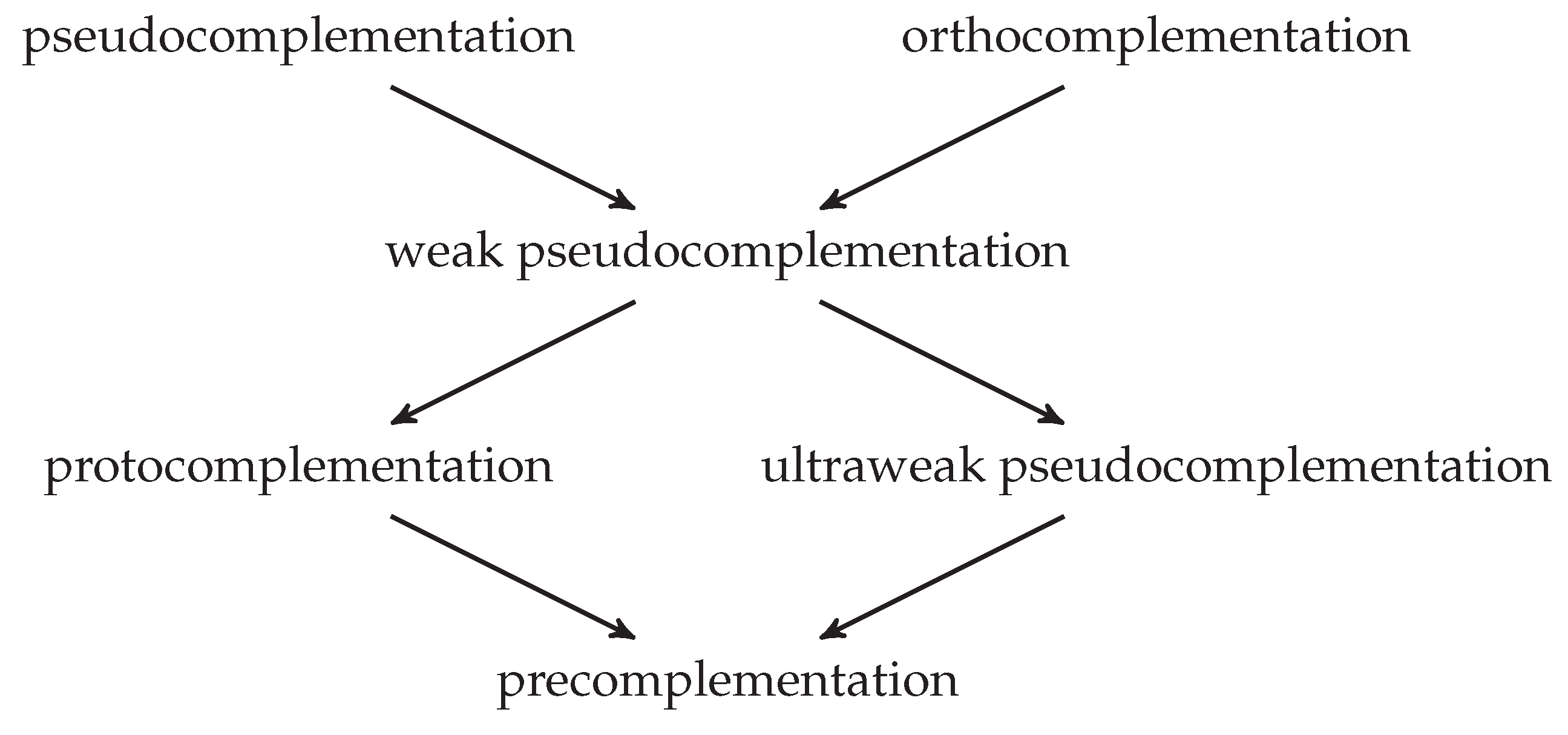
3. Algebras
| pre | proto | ultraweak pseudo | weak pseudo | pseudo | ortho | |
|---|---|---|---|---|---|---|
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| ✓ | ✓ | ✓ | ✓ | ✓ | ||
| ✓ | ✓ | ✓ | ✓ | |||
| ✓ | ✓ | ✓ | ✓ | |||
| ✓ | ||||||
| ✓ |
- 1.
- If ¬ is a semicomplementation, then ¬ is anti-inflationary: for all nonzero . If ¬ is antitone and anti-inflationary, then ¬ is a semicomplementation.
- 2.
- ¬ satisfies antitonicity and double negation introduction iff for all , implies .
- 3.
- ¬ is an orthocomplementation iff ¬ is a weak pseudocomplementation satisfying double negation elimination: for all .

4. Relational Representation and Semantics
4.1. From Relational Frames to Lattices with Negation
- 1.
- the operation defined byis a closure operator on ;
- 2.
- the operation defined bysends -fixpoints to -fixpoints.
- 1.
- the -fixpoints ordered by ⊆ form a complete lattice with meet and join calculated as in Proposition 4.3;
- 2.
- is a precomplementation on ;
- 3.
- if ⊲ is reflexive, then is a protocomplementation on .
- 1.
- the 0 of is the set of absurd states, also equal to ;
- 2.
- iff there is no and absurd with .
- from any , you can step forward along an arrow to a state that cannot step backward along an arrow into A.

- 1.
- x pre-refines y if for all , implies ;
- 2.
- x post-refines y if for all , implies ;
- 3.
- x refines y if x pre-refines and post-refines y;
- 4.
- x is compossible with y if there is a non-absurd that refines x and pre-refines y.
- 1.
- is a complete Heyting algebra with pseudocomplementation ¬ iff is isomorphic to for a relational frame in which ⊲ is reflexive and compossible.
- 2.
- is a complete ortholattice with orthocomplementation ¬ iff is isomorphic to for a relational frame in which ⊲ is reflexive and symmetric.
- 3.
- is a complete Boolean algebra with Boolean negation ¬ iff is isomorphic to for a relational frame in which ⊲ is reflexive, symmetric, and compossible.
- (a) for all -fixpoints A, we have ;(b) for all non-absurd , there is a that pre-refines x.
- (a) for all -fixpoints A, we have ;(b) pseudosymmetry: for all and , there is a that pre-refines x.
- (a) for all -fixpoints , if , then .(b) weak compossibility: for all and , there is a non-absurd z that pre-refines y and x.
- (a) for all -fixpoints A, we have ;(b) for all and , there is a such that for all , if then .
- 1.
- iff ;
- 2.
- iff for all , ;
- 3.
- iff and ;
- 4.
- iff : or .
4.2. Discrete Representation of Lattices with Negation
- 1.
- if , then there is a with and ;
- 2.
- for all , if , then there is a such that for all, we have .
- 1.
- f is a complete embedding of L into ;
- 2.
- if L is complete, then f is an isomorphism from L to .
- 1.
- If ¬ is a precomplementation on L, then wherethere is a complete embedding of into .
- 2.
- If ¬ is a protocomplementation on L, then wherethere is a complete embedding of into , and ⊲ is reflexive.
- 3.
- If ¬ is an ultraweak pseudocomplementation on L, then wherethere is a complete embedding of into , and ⊲ is pseudosymmetric (and strongly pseudosymmetric if ).
- 4.
- If ¬ is a weak pseudocomplementation on L, then wherethere is a complete embedding of into , and ⊲ is reflexive and pseudosymmetric (and strongly pseudosymmetric if ). Moreover, if ¬ is a pseudocomplementation, then ⊲ is weakly compossible.
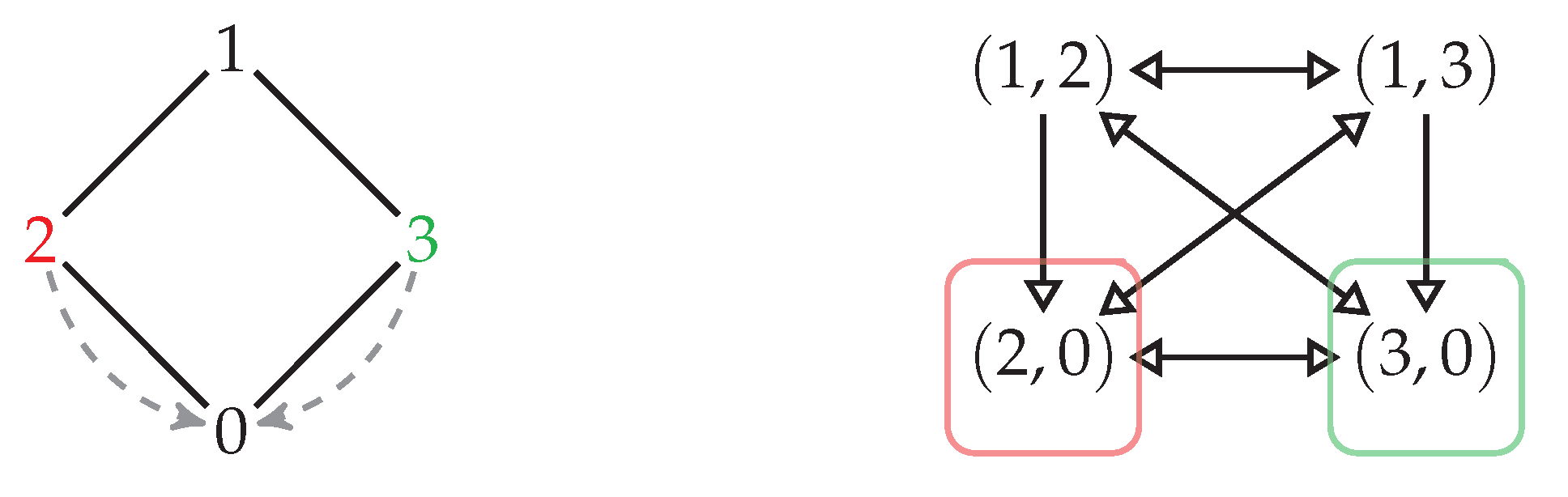
- 1.
- if and only if ;
- 2.
- if and only if ;
- 3.
- if and only if (resp. );
- 4.
- if and only if (resp. );
- 5.
- if and only if .
4.3. Topological Representation of Lattices with Negations
- 1.
- an embedding of into and
- 2.
- an isomorphism from L to the subalgebra of consisting of -fixpoints that are compact open in the space .
4.4. Modal Translations
5. Quantification
- If is a proof, is a formula , and v does not occur free in , then is a proof (∀I).
- If is a proof, is a formula of the form , and u is substitutable for v in , then is a proof (∀E).
- If is a proof, is a formula of the form , and u is substitutable for v in , then is a proof (∃I).
- If is a proof, is a formula of the form , is a proof beginning with and ending with , and v does not occur free in , then is a proof (∃E).
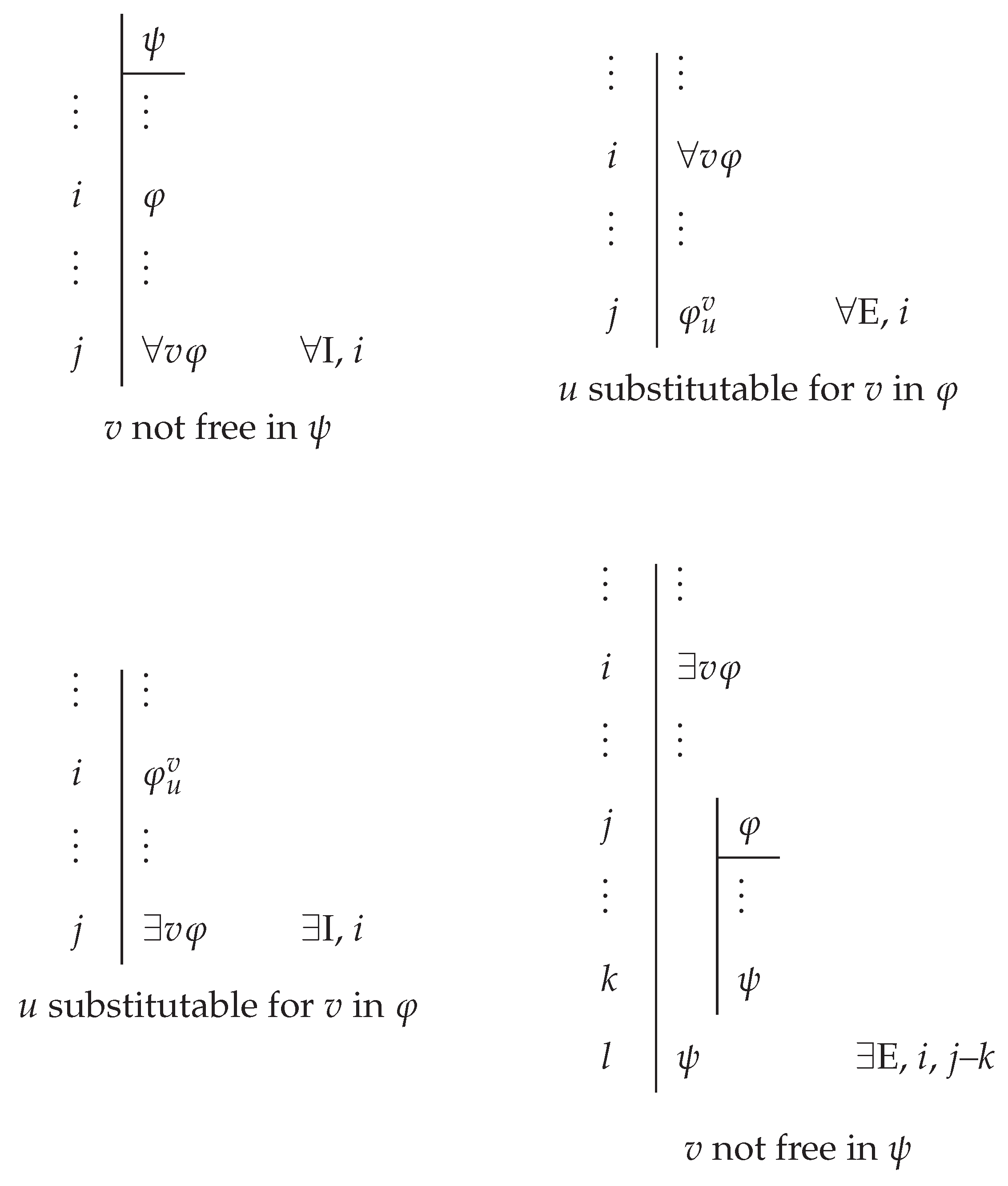
- iff ;
- clauses for ¬, ∧, and ∨ as before;
- iff , ;
- iff : .
6. Comments on Conditionals
- 1.
- ;
- 2.
- : ;
- 3.
- : ;
- 4.
- : ;
- 5.
- : .
- 1.
- ;
- 2.
- ;
- 3.
- ;
- 4.
- if , then ;
- 5.
- if , then .

7. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- If is a proof given R and is a proof given , then is a proof given R.
- If is a proof given R and , then is a proof given R (Reiteration).
- closure conditions for ∧I, ∧E, ∨I, ∨E, ¬I, and ¬E as in Section 2 with ’proof’ replaced by ’proof given R’.
- If is a proof given R, is a formula of the form , and is a sequence beginning with and ending with , then is a proof given R (RAA).
Appendix B
- turns into ;
- turns into ;
- turns into ;
- turns into .
- (a) for all -fixpoints B, we have ;(b) for all and , there is a that pre-refines y.
- (a) for all -fixpoints , we have ;(b) right pre-interpolation: for all and , there is a that post-refines y and pre-refines x.
- (a) for all -fixpoints , we have ;(b) left pre-interpolation: for all and , there is a that post-refines y and pre-refines x.
- (a) for all -fixpoints , if , then ;(b) left post-extendability: for all and , there is a that pre-refines y and x.
- 1.
- ;
- 2.
- ;
- 3.
- if , then ;
- 4.
- if , then .
- 1.
- for all , ;
- 2.
- for all , if , then .
- 1.
- If → is a preimplication on L, then wherethere is a complete embedding of into . Moreover, if ¬ is an ultraweak pseudocomplementation, then ¬ is strongly pseudosymmetric (recall Definition 4.17).
- 2.
- If → is a protoimplication on L, then wherethere is a complete embedding of into , and ⊲ is reflexive and satisfies right pre-interpolation. Moreover, if ¬ is a weak pseudocomplementation, then ⊲ is strongly pseudosymmetric.
- 3.
- If → is an ultraweak pseudoimplication on L, then wherethere is a complete embedding of into , and ⊲ satisfies left pre-interpolation.
- 4.
- If → is a weak pseudoimplication on L, then wherethere is a complete embedding of into , and ⊲ is reflexive and satisfies right pre-interpolation and left pre-interpolation. Moreover, if ¬ is a pseudocomplementation, then ⊲ is weakly compossible (recall Proposition 4.14.3).
- 5.
- If → is a relative pseudocomplementation on L, then wherethere is a complete embedding of into , and ⊲ is reflexive and compossible (recall Definition 4.11).
- 1.
- an embedding of into and
- 2.
- an isomorphism from L to the subalgebra of consisting of -fixpoints that are compact open in the space .
| 1 | This is in contrast to ’It’s raining but I don’t know it’, which is infelicitous to assert but does not embed like a contradiction; e.g., it is fine in the antecedent of a conditional such as ’If it’s raining but I don’t know it, I’ll be surprised when I get wet’. For a review of evidence that the badness of (1) is not merely pragmatic, see [8] (Section 2.1). |
| 2 | On the importance of this distinction concerning side assumptions in relation to the idea that the introduction and elimination rules for ∨ should be in “harmony” with each other, see [12] (p. 229). |
| 3 | To avoid ambiguity, assume formulas are constructed in such a way that no formula is a sequence beginning with a formula. |
| 4 | Note that if one does derive a pair of contradictory formulas in a subproof that starts with , then by ¬E one can derive the negation of a formula derived just before the assumption of the subproof, so our ¬I rule is applicable. |
| 5 | Note that our ¬I rule produces proofs of the form but not (where is not an element of the subproof beginning with ). If we were to strengthen ¬I so as to allow the intervention of the additional assumption as in the preceding sequence, then we could commit the same mistakes to which Reiteration leads as in Section 1. Indeed, we could reiterate any negated formula into a subproof: given a formula immediately preceding a subproof beginning with , to reiterate into , create a subproof inside such that begins with , from which we can prove , contradicting the occurring before the assumptions of and , in which case the strengthened rule would allow us to conclude after . Then a restricted version of pseudocomplementation would hold: if , then . But then from the fact that (“It might be that it isn’t raining, but it’s not the case that it isn’t raining”) is contradictory, we could prove using the restricted version of pseudocomplementation and other properties of negation that . |
| 6 | |
| 7 | We do not have ⊥ as a primitive in our language, so we formulate ¬E as follows: proofs of and may be joined with a new root labeled by any formula , forming a proof that inherits all the open assumptions of the two proofs. |
| 8 | |
| 9 | Ultraweak pseudocomplementations are equivalent to what Dunn and Zhou [44] call quasi-minimal negations with the added assumption that (see Remark 3.3). |
| 10 | |
| 11 | Another definition of c, building in monotonicity, is . |
| 12 | |
| 13 | It follows that accepting A entails rejecting . The ideas that accepting A is inconsistent with rejecting A and that accepting entails rejecting A will follow from the key conditions on frames for fundamental logic. |
| 14 | If and y accepts A, so , then x does not reject A by definition. Conversely, if , then using Proposition 4.4, y accepts the proposition but x rejects it given . |
| 15 | Given this definition of the closure operation, a candidate definition of morphism between and is a map such that (i) implies , and (ii) if , then . Condition (ii) guarantees that if is a fixpoint of , then is a fixpoint of . For suppose , so . Then since is a fixpoint of , there is a such that for all , we have . By (ii), , which by the previous sentence implies and hence . This shows that is a fixpoint of . If we want morphisms that also preserve negation, then follows from (i), and follows from the additional condition (iii) that if , then . For if , so , then there is a with . Then we claim for the given by (iii) that ; for by (iii), , and since , we have . Hence . |
| 16 | |
| 17 | Note that in this setting, ’⊥’ and ’⊤’ are arguably no longer appropriate symbols to abbreviate and . |
| 18 | This shows that is complete with respect to bounded lattices with precomplementations satisfying . This depends on the fact that we do not have primitive symbols ⊥ and ⊤ interpreted as 0 and 1 in our language. If we had such symbols in a language with corresponding rules and in the definition of , then would not be complete with respect to lattices with precomplementations satisfying , and the Lindenbaum-Tarski algebra of would be bounded in the first place. |
| 19 | When defining a proof given a set R of reiterables as in Appendix A, ∀I states that if is a proof given R, is a formula , and v does not occur free in or in any formula in R, then is a proof given R. |
| 20 | Recall Theorem 4.13.1. In compossible reflexive frames, a definition used in [21] (Thm. 2.21(i)) that is equivalent to options 3 and 5 is that iff for every y that pre-refines x, if , then . Toward proving the equivalence, first a lemma about Modus Ponens under option 3: if and , then . For if , then by compossibility, there is a z that refines y and pre-refines x; since ⊲ is reflexive and z pre-refines x, we have and by Lemma 4.12. Given , , and , there is a with . Then since z post-refines y, we have . Thus, we have shown that : , so . Now for the equivalence, suppose according to option 3. Further suppose that y pre-refines x, and . Then by Lemma 4.12, so by the Modus Ponens lemma, so according to the definition from [21]. Conversely, suppose according to that definition, which obviously validates Modus Ponens. Further suppose and . Then by compossibility, there is a z that refines y and pre-refines x, and by reflexivity, . Hence , , and , so by Modus Ponens, so according to options 3 and 5. |
| 21 | By contrast, we note that the implication in algebras for Visser’s [102] basic propositional logic is not necessarily a preconditional or preimplication, since it can violate . |
| 22 | The equivalent condition is that if , then : z pre-refines y. To see this is sufficient, suppose , so there is a with . Then by the condition, : z pre-refines y. Since z pre-refines y and A is a -fixpoint, by Lemma 4.12, so . Thus, assuming , we have , , which shows that is a -fixpoint. For necessity, suppose the condition does not hold. Let , which is the set of states that pre-refine y. Then but : , so is not a -fixpoint. |
| 23 | Applying the discrete representation of Section 4.2 to complete lattices with modalities raises additional issues, such as the requirement that □ (resp. ) be completely multiplicative (see [21] (Section 4)). |
| 24 | The introduction and elimination rules for the intuitionistic implication → can obviously be added in the same style. |
| 25 | Returning to the issue of morphisms broached in Note 15, a candidate notion of morphism between relational frames that also preserves is a map f that satisfies (i) and (ii) from Note 15 plus two extra conditions for . First recall (iii) from Note 15, expressed in the language of Definition 4.11: if , then : pre-refines . This ensures . To ensure , we strengthen (iii) to (iii): if , then : refines . For suppose . To show , suppose and . Then picking y as in (iii), since pre-refines , we have by Lemma 4.12. Hence , which with and implies there is a with , so . Then from we have by (i), and then since post-refines , we have . Thus, we have shown that for all with , there is a with , so . Finally, to ensure , consider (iv) (and compare it with (iii)): if , then : pre-refines . We will apply (iv) with a change of variables: if , then : pre-refines . Now suppose . To show , suppose and , so . By (i), we have . Then since , there is a such that . Then taking z as in (iv), we have by Lemma 4.12, so . Thus, we have shown that for all with , there is a with , so . |
| 26 | A referee informed me that this idea is what led Meyer and Slaney [109] to their Abelian Logic by generalizing the classical axiom to . |
| 27 | For parts 2 and 4 when , we can take , in which case pre-refines and vice versa, so a strong right pre-interpolation property holds. |
| 28 | For parts 3 and 4 when , we can take , in which case pre-refines and vice versa, so a strong left pre-interpolation property holds. |
References
- Gentzen, G. Untersuchungen über das logische Schließen. Math. Z. 1935, 39, 176–210, 405–431. [Google Scholar]
- Prawitz, D. Towards a foundation of a general proof theory. In Logic, Methodology and Philosophy of Science IV; Suppes, P., Henkin, L., Joja, A., Moisil, G.C., Eds.; North-Holland: Amsterdam, The Netherlands, 1973; pp. 225–250. [Google Scholar]
- Dummett, M. The Logical Basis of Metaphysics; Harvard University Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Schroeder-Heister, P. Proof-Theoretic Semantics. In The Stanford Encyclopedia of Philosophy, Spring 2018 ed.; Zalta, E.N., Ed.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2018. [Google Scholar]
- Prior, A.N. The Runabout Inference-Ticket. Analysis 1960, 21, 38–39. [Google Scholar] [CrossRef]
- Dummett, M. Elements of Intuitionism, 2nd ed.; Clarendon Press: Oxford, UK, 2000. [Google Scholar]
- Mandelkern, M. Bounded Modality. Philos. Rev. 2019, 128, 1–61. [Google Scholar] [CrossRef]
- Holliday, W.H.; Mandelkern, M. The Orthologic of Epistemic Modals. arXiv 2022, arXiv:2203.02872. [Google Scholar]
- Groenendijk, J.; Stokhof, M.; Veltman, F. Coreference and Modality. In Handbook of Contemporary Semantic Theory; Lappin, S., Ed.; Blackwell: Oxford, UK, 1996; pp. 179–216. [Google Scholar]
- Aloni, M. Conceptual Covers in Dynamic Semantics. In Logic, Language and Computation; Cavedon, L., Blackburn, P., Braisby, N., Shimojima, A., Eds.; CSLI Publications: Stanford, CA, USA, 2000; Volume III, pp. 23–48. [Google Scholar]
- Yalcin, S. Epistemic Modals. Mind 2007, 116, 983–1026. [Google Scholar] [CrossRef]
- Rumfitt, I. Against Harmony. In A Companion to the Philosophy of Language, 2nd ed.; Hale, B., Wright, C., Miller, A., Eds.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2017; Volume 1, pp. 225–249. [Google Scholar]
- Fitch, F.B. Symbolic Logic: An Introduction; The Ronald Press Company: New York, NY, USA, 1952. [Google Scholar]
- Fitch, F.B. Natural Deduction Rules for Obligation. Am. Philos. Q. 1966, 3, 27–38. [Google Scholar]
- Dalla Chiara, M.L.; Giuntini, R. Quantum logics. In Handbook of Philosophical Logic; Gabbay, D., Guenthner, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 129–228. [Google Scholar] [CrossRef]
- Goldblatt, R.I. Semantic Analysis of Orthologic. J. Philos. Log. 1974, 3, 19–35. [Google Scholar] [CrossRef]
- Troelstra, A.S.; van Dalen, D. Constructivism in Mathematics; North-Holland: Amsterdam, The Netherlands, 1988; Volume 1. [Google Scholar]
- Wright, C. On being in a quandary: Relativism, vagueness, logical revisionism. Mind 2001, 110, 45–98. [Google Scholar] [CrossRef]
- Field, H. No Fact of the Matter. Australas. J. Philos. 2003, 81, 457–480. [Google Scholar] [CrossRef]
- Bobzien, S.; Rumfitt, I. Intuitionism and the Modal Logic of Vagueness. J. Philos. Log. 2020, 49, 221–248. [Google Scholar] [CrossRef]
- Holliday, W.H. Compatibility and accessibility: Lattice representations for semantics of non-classical and modal logics. In Advances in Modal Logic; Duque, D.F., Palmigiano, A., Eds.; College Publications: London, UK, 2022; Volume 14. [Google Scholar]
- Burgess, J.P. Which Modal Models are the Right Ones (for Logical Necessity)? Theoria 2003, 18, 145–158. [Google Scholar] [CrossRef]
- Battilotti, G.; Sambin, G. Basic Logic and the Cube of its Extensions. In Logic and Foundations of Mathematics; Cantini, A., Casari, E., Minari, P., Eds.; Springer: Berlin, Germany, 1999; Volume 280, pp. 165–186. [Google Scholar]
- Kolmogorov, A.N. O principe tertium non datur. Mat. Sb. 1925, 32, 646–667. [Google Scholar]
- Jaśkowski, S. On the rules of suppositions in formal logic. Studia Logica 1934, 1, 5–32. [Google Scholar]
- Geuvers, H.; Nederpelt, R. Rewriting for Fitch Style Natural Deductions. In Rewriting Techniques and Applications. RTA 2004, Aachen, Germany, 3–5 June 2004; Lecture Notes in Computer Science; Oostrom, V., Ed.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3091, pp. 134–154. [Google Scholar] [CrossRef]
- Hazen, A.P.; Pelletier, F.J. Gentzen and Jáskowski Natural Deduction: Fundamentally Similar but Importantly Different. Stud. Log. 2014, 102, 1103–1142. [Google Scholar] [CrossRef]
- Cutland, N.J.; Gibbins, P.F. A regular sequent calculus for quantum logic in which ∧ and ∨ are dual. Log. Anal. 1982, 25, 221–248. [Google Scholar]
- Gödel, K. Zur intuitionistischen Arithmetik und Zahlentheorie. Ergeb. Eines Math. Kolloquiums 1933, 4, 34–38. [Google Scholar]
- Gentzen, G. Die Widerspruchsfreiheit der reinen Zahlentheorie. Math. Ann. 1936, 112, 493–565. [Google Scholar]
- Glivenko, V. Sur quelques points de la logique de M. Brouwer. Acad. R. Belg. Bull. Cl. Des Sci. 1929, 15, 183–188. [Google Scholar]
- Rebagliato, J.; Verdú, V. On the Algebraization of Some Gentzen Systems. Fundam. Informaticae 1993, 17, 319–338. [Google Scholar] [CrossRef]
- Chiswell, I.; Hodges, W. Mathematical Logic; Oxford Texts in Logic; Oxford University Press: Oxford, UK, 2007; Volume 3. [Google Scholar]
- Aguilera, J.P.; Bydžovský, J. Fundamental Logic is Decidable. Unpublished Manuscript. Available online: https://juan.ag/research (accessed on 18 January 2023).
- Mönting, J.S. Cut elimination and word problems for varieties of lattices. Algebra Universalis 1981, 12, 290–321. [Google Scholar] [CrossRef]
- Egly, U.; Tompits, H. On different proof-search strategies for orthologic. Stud. Log. 2012, 73, 131–152. [Google Scholar] [CrossRef]
- Dzik, W.; Orlowska, E.; van Alten, C. Relational Representation Theorems for General Lattices with Negations. In Proceedings of the Relations and Kleene Algebra in Computer Science. RelMiCS 2006, Manchester, UK, 29 August–2 September 2006; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4136, pp. 162–176. [Google Scholar] [CrossRef]
- Dzik, W.; Orlowska, E.; van Alten, C. Relational Representation Theorems for Lattices with Negations: A Survey. Lect. Notes Artif. Intell. 2006, 4342, 245–266. [Google Scholar] [CrossRef]
- Almeida, A. Canonical extensions and relational representations of lattices with negation. Stud. Log. 2009, 91, 171–199. [Google Scholar] [CrossRef]
- Dunn, J.M.; Hardegree, G.M. Algebraic Methods in Philosophical Logic; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Horn, L.R.; Wansing, H. Negation. In The Stanford Encyclopedia of Philosophy, Spring 2020 ed.; Zalta, E.N., Ed.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2020. [Google Scholar]
- Humberstone, L. The Connectives; MIT Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Priest, G.; Tanaka, K.; Weber, Z. Paraconsistent logic. In The Stanford Encyclopedia of Philosophy, Spring 2022 ed.; Zalta, E.N., Ed.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2022. [Google Scholar]
- Dunn, J.M.; Zhou, C. Negation in the Context of Gaggle Theory. Stud. Log. 2005, 80, 235–264. [Google Scholar] [CrossRef]
- Kleene, S.C. On notation for ordinal numbers. J. Symb. Log. 1938, 3, 150–155. [Google Scholar] [CrossRef]
- Johansson, I. Der Minimalkalkül, ein reduzierter intuitionistischer Formalismus. Compos. Math. 1937, 4, 119–136. [Google Scholar]
- Bezhanishvili, G.; Holliday, W.H. A semantic hierarchy for intuitionistic logic. Indag. Math. 2019, 30, 403–469. [Google Scholar] [CrossRef]
- McCune, W. Prover9 and Mace4. Available online: http://www.cs.unm.edu/~mccune/prover9 (accessed on 29 October 2022).
- Ploščica, M. A natural representation of bounded lattices. Tatra Mt. Math. Publ. 1995, 5, 75–88. [Google Scholar]
- Urquhart, A. A topological representation theory for lattices. Algebra Universalis 1978, 8, 45–58. [Google Scholar] [CrossRef]
- Allwein, G.; Dunn, J.M. Kripke models for linear logic. J. Symb. Log. 1993, 58, 514–545. [Google Scholar] [CrossRef]
- Birkhoff, G. Lattice Theory; American Mathematical Society: New York, NY, USA, 1940. [Google Scholar]
- Birkhoff, G.; von Neumann, J. The Logic of Quantum Mechanics. Ann. Math. 1936, 37, 823–843. [Google Scholar] [CrossRef]
- Dishkant, H. Semantics of the Minimal Logic of Quantum Mechanics. Stud. Log. 1972, 30, 23–30. [Google Scholar] [CrossRef]
- Dummett, M.A.E.; Lemmon, E.J. Modal logics between S4 and S5. Z. Fur Math. Log. Und Grund. Der Math. 1959, 5, 250–264. [Google Scholar] [CrossRef]
- Grzegorczyk, A. A Philosophically Plausible Formal Interpretation of Intuitionistic Logic. Indag. Math. 1964, 26, 596–601. [Google Scholar] [CrossRef]
- Kripke, S.A. Semantical analysis of intuitionistic logic I. In Formal Systems and Recursive Functions; Crossley, J.N., Dummett, M.A.E., Eds.; North-Holland: Amsterdam, The Netherlands, 1965; pp. 92–130. [Google Scholar]
- Došen, K. Negative modal operators in intuitionistic logic. Publ. L’Institut MathéMatique Nouv. SéRie 1984, 35, 3–14. [Google Scholar]
- Došen, K. Negation as a modal operator. Rep. Math. Log. 1986, 20, 15–27. [Google Scholar]
- Došen, K. Negation in the Light of Modal Logic. In What Is Negation? Gabbay, D.M., Wansing, H., Eds.; Kluwer: Dordrecht, The Netherlands, 1999; pp. 77–86. [Google Scholar]
- Vakarelov, D. Consistency, Completeness and Negation. In Paraconsistent Logic: Essays on the Inconsistent; Priest, G., Routley, R., Norman, J., Eds.; Philosophia Verlag: Munich, Germany, 1989; pp. 328–368. [Google Scholar]
- Dunn, J.M. Star and perp: Two treatments of negation. Philos. Perspect. 1993, 7, 331–357. [Google Scholar] [CrossRef]
- Dunn, J.M. Generalized ortho negation. In Negation. A Notion in Focus; Wansing, H., Ed.; de Gruyter: Berlin, Germany, 1996; pp. 3–26. [Google Scholar]
- Dunn, J.M. A comparative study of various model-theoretic treatments of negation: A history of formal negation. In What Is Negation? Gabbay, D.M., Wansing, H., Eds.; Kluwer: Dordrecht, The Netherlands, 1999; pp. 23–51. [Google Scholar]
- Berto, F. A Modality called ’Negation’. Mind 2015, 124, 761–793. [Google Scholar] [CrossRef]
- Berto, F.; Restall, G. Negation on the Australian Plan. J. Philos. Log. 2019, 48, 1119–1144. [Google Scholar] [CrossRef]
- Zhong, S. A General Relational Semantics of Propositional Logic: Axiomatization. In Proceedings of the 27th International Workshop, WoLLIC 2021, Virtual Event, 5–8 October 2021; Silva, A., Wassermann, R., Queiroz, R., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2021; Volume 13038, pp. 82–99. [Google Scholar] [CrossRef]
- Scott, D. Advice on Modal Logic. In Philosophical Problems in Logic: Some Recent Developments; Lambert, K., Ed.; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1970; Volume 29, pp. 143–173. [Google Scholar]
- Montague, R. Universal Grammar. Theoria 1970, 36, 373–398. [Google Scholar] [CrossRef]
- Pacuit, E. Neighborhood Semantics for Modal Logic; Short Textbooks in Logic; Springer: Dordrecht, The Netherlands, 2017. [Google Scholar] [CrossRef]
- Burris, S.; Sankappanavar, H.P. A Course in Universal Algebra; Springer: New York, NY, USA, 1981. [Google Scholar]
- van Fraassen, B. Identity in Intensional Logic. Versus 1986, 44/45, 201–219. [Google Scholar]
- Goldblatt, R. Cover semantics for quantified lax logic. J. Log. Comput. 2011, 21, 1035–1063. [Google Scholar] [CrossRef]
- Dragalin, A.G. Matematicheskii Intuitsionizm: Vvedenie v Teoriyu Dokazatelstv; Matematicheskaya Logika i Osnovaniya Matematiki; Nauka: Moscow, Russia, 1979. [Google Scholar]
- Dragalin, A.G. Mathematical Intuitionism: Introduction to Proof Theory; Translations of Mathematical Monographs; American Mathematical Society: Providence, RI, USA, 1988; Volume 67. [Google Scholar]
- Bezhanishvili, G.; Holliday, W.H. Locales, Nuclei, and Dragalin Frames. In Advances in Modal Logic; Beklemishev, L., Demri, S., Máté, A., Eds.; College Publications: London, UK, 2016; Volume 11, pp. 177–196. [Google Scholar]
- Holliday, W.H. Three roads to complete lattices: Orders, compatibility, polarity. Algebra Universalis 2021, 82, 26. [Google Scholar] [CrossRef]
- Conradie, W.; Palmigiano, A.; Robinson, C.; Wijnberg, N. Non-distributive logics: From semantics to meaning. In Contemporary Logic and Computing; Landscapes in Logic; Rezus, A., Ed.; College Publications: New York, NY, USA, 2020; pp. 38–86. [Google Scholar]
- Davey, B.A. On the Lattice of Subvarieties. Houst. J. Math. 1979, 5, 183–192. [Google Scholar]
- Ganter, B. Two Basic Algorithms in Concept Analysis. In Proceedings of the 8th International Conference, ICFCA 2010, Agadir, Morocco, 15–18 March 2010; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 5986, pp. 312–340. [Google Scholar] [CrossRef]
- MacLaren, M.D. Atomic Orthocomplemented Lattices. Pac. J. Math. 1964, 14, 597–612. [Google Scholar] [CrossRef]
- Massas, G. B-frame duality. Ann. Pure Appl. Log. 2023, 174, 103245. [Google Scholar] [CrossRef]
- Restall, G. An Introduction to Substructural Logics; Routledge: New York, NY, USA, 2000. [Google Scholar]
- Craig, A.P.K.; Haviar, M.; Priestley, H.A. A Fresh Perspective on Canonical Extensions for Bounded Lattices. Appl. Categ. Struct. 2013, 21, 725–749. [Google Scholar] [CrossRef]
- Allwein, G.; Hartonas, C. Duality for Bounded Lattices; Preprint Series, IULG-93-25; Indiana University Logic Group: Bloomington, IN, USA, 1993. [Google Scholar]
- Bezhanishvili, N.; Holliday, W.H. Choice-free Stone duality. J. Symb. Log. 2020, 85, 109–148. [Google Scholar] [CrossRef]
- Goldblatt, R.I. The Stone Space of an Ortholattice. Bull. Lond. Math. Soc. 1975, 7, 45–48. [Google Scholar] [CrossRef]
- McDonald, J.; Yamamoto, K. Choice-free duality for orthocomplemented lattices by means of spectral spaces. Algebra Universalis 2022, 83, 37. [Google Scholar] [CrossRef]
- Bimbó, K. Functorial duality for ortholattices and De Morgan lattices. Log. Universalis 2007, 1, 311–333. [Google Scholar] [CrossRef]
- Dmitrieva, A. Positive Modal Logic beyond Distributivity: Duality, Preservation and Completeness. Master’s Thesis, University of Amsterdam, Amsterdam, The Netherlands, 2021. [Google Scholar]
- Gehrke, M.; Harding, J.; Venema, Y. MacNeille completions and canonical extensions. Trans. Am. Math. Soc. 2005, 358, 573–590. [Google Scholar] [CrossRef]
- Gehrke, M.; Harding, J. Bounded Lattice Expansions. J. Algebra 2001, 238, 345–371. [Google Scholar] [CrossRef]
- Craig, A.; Haviar, M. Reconciliation of approaches to the construction of canonical extensions of bounded lattices. Math. Slovaca 2014, 64, 1335–1356. [Google Scholar] [CrossRef]
- Gödel, K. Eine Interpretation des intuitionistischen Aussagenkalküls. Ergeb. Eines Math. Kolloquiums 1933, 4, 39–40. [Google Scholar]
- McKinsey, J.C.C.; Tarski, A. Some theorems about the sentential calculi of Lewis and Heyting. J. Symb. Log. 1948, 13, 1–15. [Google Scholar] [CrossRef]
- Blackburn, P.; de Rijke, M.; Venema, Y. Modal Logic; Cambridge University Press: New York, NY, USA, 2001. [Google Scholar]
- Enderton, H.B. A Mathematical Introduction to Logic; Harcourt Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Chen, Z. A unified relational semantics for intuitionistic logic, basic propositional logic and orthologic with strict implication. arXiv 2022, arXiv:2207.07306. [Google Scholar]
- Kawano, T. Sequent Calculi for Orthologic with Strict Implication. Bull. Sect. Log. 2022, 5, 73–89. [Google Scholar] [CrossRef]
- Stalnaker, R.C. A Theory of Conditionals. In Studies in Logical Theory; Rescher, N., Ed.; Blackwell: Oxford, UK, 1968; pp. 98–112. [Google Scholar]
- Edgington, D. On Conditionals. Mind 1995, 104, 235–329. [Google Scholar] [CrossRef]
- Visser, A. A propositional logic with explicit fixed points. Stud. Log. 1981, 40, 155–175. [Google Scholar] [CrossRef]
- Lewis, D. Counterfactuals; Basil Blackwell: Oxford, UK, 1973. [Google Scholar]
- McGee, V. A Counterexample to Modus Ponens. J. Philos. 1985, 82, 462–471. [Google Scholar] [CrossRef]
- Santorio, P. Trivializing Informational Consequence. Philos. Phenomenol. Res. 2022, 104, 297–320. [Google Scholar] [CrossRef]
- Veltman, F. Logics for Conditionals. Ph.D. Thesis, University of Amsterdam, Amsterdam, The Netherlands, 1985. [Google Scholar]
- Yalcin, S. A Counterexample to Modus Tollens. J. Philos. Log. 2012, 41, 1001–1024. [Google Scholar] [CrossRef]
- Kolodny, N.; MacFarlane, J. Ifs and Oughts. J. Philos. 2010, 107, 115–143. [Google Scholar] [CrossRef]
- Meyer, R.K.; Slaney, J.K. Abelian Logic (From A to Z). In Paraconsistent Logic: Essays on the Inconsistent; Priest, G., Norman, J., Routley, R., Eds.; Philosophia Verlag: Munich, Germany, 1989; pp. 245–288. [Google Scholar]


| lattices with weak pseudocomplementation | 1 | 1 | 3 | 9 | 38 | 187 | 1130 | 7914 | 63,782 |
| lattices | 1 | 1 | 2 | 5 | 15 | 53 | 222 | 1078 | 5994 |
| pseudocomplemented lattices | 1 | 1 | 2 | 4 | 10 | 29 | 99 | 391 | 1357 |
| distributive lattices | 1 | 1 | 2 | 3 | 5 | 8 | 15 | 26 | 47 |
| ortholattices | 1 | 0 | 1 | 0 | 2 | 0 | 5 | 0 | 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Holliday, W.H. A Fundamental Non-Classical Logic. Logics 2023, 1, 36-79. https://doi.org/10.3390/logics1010004
Holliday WH. A Fundamental Non-Classical Logic. Logics. 2023; 1(1):36-79. https://doi.org/10.3390/logics1010004
Chicago/Turabian StyleHolliday, Wesley H. 2023. "A Fundamental Non-Classical Logic" Logics 1, no. 1: 36-79. https://doi.org/10.3390/logics1010004
APA StyleHolliday, W. H. (2023). A Fundamental Non-Classical Logic. Logics, 1(1), 36-79. https://doi.org/10.3390/logics1010004






