Logics for Strategic Reasoning of Socially Interacting Rational Agents: An Overview and Perspectives

Abstract

This paper is an overview of some recent and ongoing developments of formal logical systems designed for reasoning about systems of rational agents who act in pursuit of their individual and collective goals, explicitly specified in the language as arguments of the strategic operators, in a socially interactive context of collective objectives and attitudes which guide and constrain the agents’ behavior.

1. Introduction

The concepts of agency and rationality are fundamental for describing and understanding the modern society. Rational agents can be humans, intelligent robots, automated devices, or other autonomous entities that act and interact in pursuit of their individual and collective preferences and goals. In accordance with their various essential attributes, such as beliefs, knowledge, and abilities to observe, learn, remember, reason and communicate, rational agents plan and execute strategies (in AI, often also called “policies”) to achieve their goals. The common environment in which agents act and interact is commonly called a multiagent system. This generic concept covers a variety of entities, including teams of agents, social groups and networks, organizations, markets, and entire societies. Nowadays, the modeling and analysis of systems of rational agents is a broad interdisciplinary field of extensive research, bringing together ideas, approaches, and methods from humanities, social sciences, artificial intelligence, decision and game theory, mathematics, and computer science.

Agents and groups (also often called “coalitions”) of rational agents in multiagent systems typically have competing, sometimes adversarial to each other, interests and goals. When the goals are purely quantitative, such systems are modeled as multiplayer games, studied in game theory, where rational players act so as to optimize their payoffs. Agents may also have purely qualitative (“win–lose”) or combined goals. A fundamental aspect of reasoning both within and about multiagent systems is the reasoning about abilities of agents and coalitions to design and execute strategies to achieve their goals, or to prevent others from achieving theirs, hereafter called (multiagent) strategic reasoning.

Importantly, the behavior of rational agents is usually guided not only by their individual and group goals, but also by those of the others, as well as by common (e.g., societal) goals. Furthermore, their behavior is constrained by various individual, collective, and societal norms (such as rights, obligations, and prohibitions). The totality of common goals, attitudes, norms, and other constraints under which agents act and interact I will call socially interactive context. That context leads to a complex interplay of cooperation and competition between the agents in the system.

Since the 1980s, formal logic has emerged as a useful and efficient methodological and technical tool for modeling, analysis, and reasoning about multiagent rational interaction. A rich variety of logical frameworks for strategic reasoning in, and about, multiagent systems have been developed. Early formal logical systems capturing agents’ abilities were developed with philosophical motivations and applications in mind, including Parikh’s Game Logic [1], where he also suggested perhaps the first applications of logic to multiagent social scenarios, such as cake-cutting, exchanging secrets (see further Example 10), etc.; Brown’s modal logic of ability [2]; and Belnap and Perloff’s STIT logics [3]. In the late 1990s–early 2000s, two important logical systems for multiagent strategic reasoning were introduced independently: Pauly’s coalition logic $\mathsf{CL}$, introduced in [4,5], and Alur, Henzinger, and Kupferman’s alternating time temporal logic $\mathsf{ATL}$, introduced first in [6], and then, in its final version, in [7] (cf. [8,9] for more recent and detailed discussion on these and related works).

Some remarks1 are due on conceptual issues arising in regards to the terminology used in this paper, and also generally adopted in the literature on the topic. To begin with, let me emphasize that other, not discussed in the present work important concepts related to rational agency, such as beliefs, desires, intentions, goals, and commitments have been extensively explored in the philosophy and AI literature. Among the most influential such approaches are [10,11,12], where (especially in the latter) agents’ goals and what they imply are explicitly indicated in the language. While being important and influential, these works are not about strategic reasoning regarding the agents’ goals and their achievement which is the focus of the present paper, so they will not be discussed further here.

Now, let me explain the meaning and use of some key concepts and terms used in this paper, to avoid possible misunderstandings, especially on the background of the alternative approaches mentioned above. First, the use of the word “goal” in the context of these logical frameworks and formal systems should be understood in a precise and possibly somewhat narrow sense. Agents’ goals are not some intentional objects permanently or temporarily ascribed to the agents, or intrinsically associated with them. The agents’ goals in the present work are not explicitly specified as such in the language, but are determined by the context and identified with properties (respectively, sets) of states in the model—or, more generally, with properties (respectively, sets) of plays in that model—which the agents are assumed to pursue to realize with their strategic behavior. These sets of states, or plays, are represented in the language by formulae which extensionally specify them by means of their formal semantics. Thus, the logical languages considered here cannot express statements such as “the agent $\mathsf{a}$ has as its goal to realize G”, nor even “the goal of agent $\mathsf{a}$ is to realize G”, but rather “the agent $\mathsf{a}$ has a strategy that guarantees (under the assumed interactive context) the truth of the formula G”, where G is regarded as “$\mathsf{a}$’s goal” in this context. “Coalitional goals” should be understood likewise. Thus, agents’ goals are only contextually specified and can freely change, even within the same formalized statement, but this should be taken only as a terminological choice, rather than a conceptual commitment to what “goal” means. Next, “rationality” of agents here should also be understood in a concrete and precise sense: once a goal (in the sense described above) is assigned to a rational agent, that agent is assumed to act in pursuit of that goal, and that assumption naturally constrains the agent’s behavior. This is all that “rationality” is assumed to mean here. Lastly, the phrase “socially interactive context” should also be considered merely as a convenient and sufficiently intuitive term, rather than a precise social concept. Though not precisely defined, that term is hopefully well illustrated in the various logical frameworks presented here.

There are other interesting and important approaches to logics for games and strategic behavior, which—mostly for practical reasons—I will only mention here, but will not be discussed further in this paper:

• The STIT-based approach, building on the theory of “Seeing To It That” (STIT), originating from the seminal work of Belnap and Perloff [3]. For exploring the closer links of the present paper with STIT, the reader is referred to [13] and the overview chapter [14] on using STIT for strategic reasoning, as well as to [15] for temporal extensions of STIT and applications to normative reasoning, to [16] for using STIT for reasoning about social influence, and to [17] for providing semantics of temporal STIT in concurrent game models used in this paper.
• The dynamic logic based approach, originating from Parikh’s Game Logic [1], and more recently explored further in [18,19] and other related works.

For further references and a broader view on logics for analyzing games, I also refer the reader to [20].

Now, a few words about the main precursors of the logics presented here. The logic $\mathsf{CL}$ was introduced in [4,5] with the explicit intention to formalize reasoning about one-step (local) strategic abilities of agents and coalitions, i.e., strategic abilities to guarantee the achievement of their explicitly specified goals in the immediate outcome of their (individual or collective) action, regardless of the respective actions of all remaining agents. The logic $\mathsf{ATL}$ was initially introduced in [6,7] as a logical formalism for formal specification and verification of open (interacting with environment) computer systems where the agents represent concurrently executed processes. Still, it was gradually adopted as one of the most popular and standard logical systems for reasoning about long-term strategic abilities of agents and coalitions in extended concurrent multiplayer games. Technically, $\mathsf{ATL}$ can be described as an extension of $\mathsf{CL}$ with the long-term temporal operators $\mathsf{G}$, $\mathsf{F}$, and $\mathsf{U}$, which were previously adopted, inter alia, in the branching-time temporal logic $\mathsf{CTL}$ (which can be regarded as a single-agent fragment of $\mathsf{ATL}$). Both $\mathsf{CL}$ and $\mathsf{ATL}$ feature a special type of modal operators, denoted by ${\left[C\right]}_{{}_{}}$ in $\mathsf{CL}$, respectively by $\langle \langle \mathrm{C}\rangle \rangle$ in $\mathsf{ATL}$, parameterized with a coalition of agents C, such that, given a coalitional goal of C formalized as (ensuring the truth of) a formula $\varphi$, the formula ${\left[C\right]}_{{}_{}}\varphi$ intuitively says that the coalition C has a collective strategy ${\sigma }_C$ that guarantees the satisfaction of $\varphi$ in every outcome state (for $\mathsf{CL}$), respectively, in every outcome play (for $\mathsf{ATL}$) that can occur when the agents in C execute their strategies in ${\sigma }_C$, regardless of the choices (strategic or not) of actions of the agents that are not in C.

Thus, both $\mathsf{CL}$ and $\mathsf{ATL}$ capture reasoning about unconditional strategic abilities of agents within coalitions, acting in full cooperation with each other in pursuit of their coalitional goals, aiming to succeed against any possible behavior of their opponents, which are thus regarded as their complete adversaries (in the context of $\mathsf{CL}$) or as randomly behaving environment (in the original context of $\mathsf{ATL}$). This, however, is a rather narrow and extreme perspective, as agents in the real world are seldom either complete allies or complete adversaries to each other. In reality, all agents acting in the system (except for the environment, or absolute adversaries) have their own goals and act in pursuit of their fulfillment, rather than just to prevent the proponents from achieving their goals. Thus, the strategic interactions of rational agents usually involve a complex interplay of cooperation and competition, both driven by the individual and collective goals of all agents, which may be partly or fully allied or adversarial to each other. To adequately model and capture the behavior and interactions of rational agents within a socially interactive context requires much richer and more versatile formal logical frameworks than those provided by the logics $\mathsf{CL}$, $\mathsf{ATL}$ and their close variations. Several richer frameworks have been proposed more recently, including strategy logics [21,22,23,24]; the socially friendly coalitional logic $\mathsf{SFCL}$ and the group protecting coalitional logic $\mathsf{GPCL}$ [25], with the latter subsequently extended with temporal operators for long-term goals to the temporal logic of coalitional goal assignments $\mathsf{TLCGA}$ in [26]; the logic for conditional strategic reasoning $\mathsf{ConStR}$ (cf. [27,28]); and several recently proposed more special-purpose logics for strategic reasoning, focusing on know-how strategies [29], ethical dilemmas [30], responsibility [31], blameworthiness [32], etc.

This paper aims to provide an accessible and not too technical, yet fairly detailed, overview of the recent developments in the area and to outline some perspectives and challenges for further research. To keep the paper within reasonable scope and size, I will not discuss here the aspects of socially interactive context related to agents’ knowledge, nor to normative constraints, but will focus on the strategic reasoning guided only by various patterns of cooperation and competition between agents and coalitions. I will usually assume here complete knowledge of the agents about the system and their full observability (with or without memory) and ability to communicate and coordinate during the “play”. These assumptions are sometimes not justified, and then substantial further complications arise, both conceptual and computational, with respect to analyzing the agents’ strategic abilities and designing their strategies in the context of agents’ incomplete or imperfect information. For more on these issues, the reader is referred to, e.g., [8,9,33], and the entire volume [34], where the latter is published.

Structure of the paper

Section 2 provides some technical preliminaries on concurrent game models, including plays and strategies in them, and provides an illustrative example. Then, Section 3 presents a brief informal preview of the main logical systems presented in the next five sections: the basic coalition logic $\mathsf{CL}$ in Section 4, its temporal extension $\mathsf{ATL}$ in Section 5, the logic of conditional strategic reasoning $\mathsf{ConStR}$ in Section 6, the socially friendly coalition logic $\mathsf{SFCL}$ in Section 7, and the logic of local coalitional goal assignments $\mathsf{LCGA}$ and its temporal extension $\mathsf{TLCGA}$ in Section 8. Eventually, Section 9 proposes a uniform logical framework, called basic strategy logic, which involves variables over strategies and quantification over them, and thus enables uniform embedding of all other strategic operators mentioned here. I end with brief concluding remarks in Section 10.

2. Technical Preliminaries

The reader is expected to have a basic background in propositional classical and modal logics, within the introductory chapters of, e.g., [35]. In addition, this section provides technical preliminaries needed for the definitions and understanding of the formal semantics of the various strategic operators and logics presented and discussed further. Most of it can be omitted by a reader who is only interested in the informal aspects of the topics, and can be consulted only if, and when, necessary for understanding the further content. For more technical details on these preliminaries, the reader is referred to [8,9], as well as [36] (Chapter 9) on concurrent game models and $\mathsf{ATL}$.

2.1. Concurrent Game Models

Consider a fixed finite nonempty set of agents $\mathsf{Agt}=\{{\mathsf{a}}_1,\dots ,{\mathsf{a}}_n\}$, also called here players, and a fixed countable set of atomic propositions $\mathsf{Prop}$. Subsets of $\mathsf{Agt}$ will also be called coalitions. The Cartesian product of a family of sets ${\left\{X_{\mathsf{a}}\right\}}_{\mathsf{a}\in \mathsf{Agt}}$ is the set of tuples $(x_1,\dots ,x_n)$ where $x_i\in X_{{\mathsf{a}}_i}$ or each $i=1,\dots ,n$, denoted, as usual, by ${\mathsf{\Pi }}_{\mathsf{a}\in \mathsf{Agt}}{X}_{\mathsf{a}}$.

Definition 1. 

Let $\mathsf{O}$ be any nonempty set. A (strategic) game form for the set of agents $\mathsf{Agt}$ over the set of outcomes $\mathsf{O}$ is a tuple

$$\mathcal{G}=(\mathsf{Act},\mathsf{act},\mathsf{O},\mathsf{out})$$

 where

• $\mathsf{Act}$ is a nonempty set of actions;
• $\mathsf{act}:\mathsf{Agt}\to {\mathcal{P}}^{+}\left(\mathsf{Act}\right)$ is a mapping assigning to each $\mathsf{a}\in \mathsf{Agt}$ a nonempty set $\mathsf{act}\left(\mathsf{a}\right)$ of actions available to the player $\mathsf{a}$;
• $\mathsf{out}:{\mathsf{\Pi }}_{\mathsf{a}\in \mathsf{Agt}}\mathsf{act}\left(\mathsf{a}\right)\to \mathsf{O}$ is a map assigning to every action profile $\zeta \in {\mathsf{\Pi }}_{\mathsf{a}\in \mathsf{Agt}}\mathsf{act}\left(\mathsf{a}\right)$ a unique outcome in $\mathsf{O}$.

Definition 2. 

A concurrent game model (CGM) is a tuple

$$\mathcal{M}=(\mathsf{Agt},\mathsf{S},\mathsf{Act},\mathfrak{g},\mathsf{Prop},\mathsf{L})$$

 where

• $\mathsf{S}$ is a nonempty set of (game) states;
• $\mathsf{Act}$ is a nonempty set of actions;
• $\mathfrak{g}$ is a game map, assigning to each state $w\in \mathsf{S}$ a strategic game form
  $\mathfrak{g}\left(w\right)=(\mathsf{Act},{\mathsf{act}}_w,\mathsf{S},{\mathsf{out}}_w)$ over the set of outcomes $\mathsf{S}$;
• $\mathsf{Prop}$  is a countable set of atomic propositions;
• $\mathsf{L}:\mathsf{S}\to \mathcal{P}\left(\mathsf{Prop}\right)$ is a labeling function, assigning to every state in $\mathsf{S}$ the set of atomic propositions true at that state.

Thus, for each $\mathsf{a}\in \mathsf{Agt}$ and $w\in \mathsf{S}$, the set ${\mathsf{act}}_w\left(\mathsf{a}\right)$ consists of the locally available actions for $\mathsf{a}$ in w. We can now define the global action function $\mathsf{act}:\mathsf{Agt}\times \mathsf{S}\to {\mathcal{P}}^{+}\left(\mathsf{Act}\right)$ by setting $\mathsf{act}(\mathsf{a},w)⩴{\mathsf{act}}_w\left(\mathsf{a}\right)$. We also define the set ${\mathsf{Act}}_{\mathsf{a}}⩴{\bigcup }_{w\in \mathsf{S}}{\mathsf{act}}_w\left(\mathsf{a}\right)$ of possible actions for $\mathsf{a}$.

Given a concurrent game model $\mathcal{M}=(\mathsf{Agt},\mathsf{S},\mathsf{Act},\mathfrak{g},\mathsf{Prop},\mathsf{L})$, we define the following.

• An action profile $\zeta \in {\mathsf{\Pi }}_{\mathsf{a}\in \mathsf{Agt}}{\mathsf{Act}}_{\mathsf{a}}$ is available at the state w if it consists of locally available actions, i.e., if $\zeta \in {\mathsf{\Pi }}_{\mathsf{a}\in \mathsf{Agt}}{\mathsf{act}}_w\left(\mathsf{a}\right)$.
  The set of all action profiles that are available at w will be denoted by ${\mathsf{ActProf}}_w$.
• ${\mathsf{out}}_{\mathcal{M}}$ is the global outcome function assigning to every state w and an action profile $\zeta \in {\mathsf{ActProf}}_w$ the unique outcome ${\mathsf{out}}_{\mathcal{M}}(w,\zeta )⩴{\mathsf{out}}_w\left(\zeta \right)$.
  When $\mathcal{M}$ is fixed by the context, it will be omitted from the subscript.
• More generally, given a coalition $C\subseteq \mathsf{Agt}$, a joint action for C in $\mathcal{M}$ is a tuple of individual actions ${\zeta }_C\in {\prod }_{\mathsf{a}\in C}\mathsf{act}\left(\mathsf{a}\right)$. In particular, for any action profile $\zeta \in {\mathsf{\Pi }}_{\mathsf{a}\in \mathsf{Agt}}\mathsf{act}\left(\mathsf{a}\right)$, ${\zeta |}_C$ is the joint action obtained by restricting $\zeta$ to C. The joint action ${\zeta |}_C$ is locally available at the state w iff every individual action in it is locally available for the respective agent in w.
• For any $w\in \mathsf{S}$, $C\subseteq \mathsf{Agt}$, and joint action ${\zeta }_C$ that is available at w, we define the set of possible outcomes from the application of the joint action ${\zeta }_C$ at the state w:

  $$\mathsf{Out}[w,{\zeta }_C]=\left\{u\in \mathsf{S}\mid \mathrm{there}\mathrm{exists}\zeta \in {\mathsf{ActProf}}_w{\mathrm{such}\mathrm{that}\zeta |}_C={\zeta }_C \mathrm{and}\mathsf{out}(w,\zeta )=u\right\}.$$
  In the special case when $C=\mathsf{Agt}$, ${\zeta }_{\mathsf{Agt}}$ is a full available action profile, so $\mathsf{Out}[w,{\zeta }_{\mathsf{Agt}}]$ consists of the single outcome $\mathsf{out}(w,{\zeta }_{\mathsf{Agt}})$.

Remark 3. 

Note that we only consider deterministic models, where every available action profile produces a single outcome. This is not an essential restriction, because every nondeterministic model can be made deterministic by adding a fictitious additional agent (say, nature) that settles the nondeterminism with its actions which settle the outcome. However, it should be noted that whether nondeterministic models are considered or not will make a difference on the validities of coalition logic $\mathsf{CL}$, as shown in Section 4.4, and in the various other logics where strategic abilities of coalitions can be expressed.

It is sometimes more convenient to eliminate the “local view” from the definition of concurrent game models, given by the game map assigning the local strategic game forms, and to redefine these models globally, as follows:

$$\mathcal{M}=(\mathsf{Agt},\mathsf{S},\mathsf{Act},\mathsf{act},\mathsf{Out},\mathsf{Prop},\mathsf{L})$$

where the components are defined as above. Clearly, the two definitions are equivalent and will be used interchangeably.

Example 4 

(Concurrent game model: Adam and Eve in hotel Life). Figure 1 pictures a concurrent game model formalizing the following story, which the reader is advised to take at face value and with a grain of salt. While it has a clearly allegoric flavor, it is not meant to formalize some meaningful (real or fiction) life story, but just to give an intuitively appealing and sufficiently nontrivial, yet not too complicated, example of a concurrent game model on which to illustrate the components of that concept. Thus, questions about the meaning or idea behind this or that state or transition do not necessarily have good answers.

Two agents, Adam and Eve, live in hotel “Life”. It has (at least) three rooms: $R1,R2,and R3$. Initially, both Adam and Eve are in room $R1$. Every day, each of them is able to choose either to stay in the same room (action $\mathsf{stay}$, denoted by $\mathsf{s}$), or to move to another room (action $\mathsf{move}$, denoted by $\mathsf{m}$), with some restrictions described further. Whichever room each of them chooses, they stay there for the night, and then each chooses again to either stay in the same room, or move to another room, as specified in the model. In some cases, they also have the option to “retreat” (action $\mathsf{retreat}$, denoted by $\mathsf{r}$).

Here are the formal components of the model, with some brief explanations:

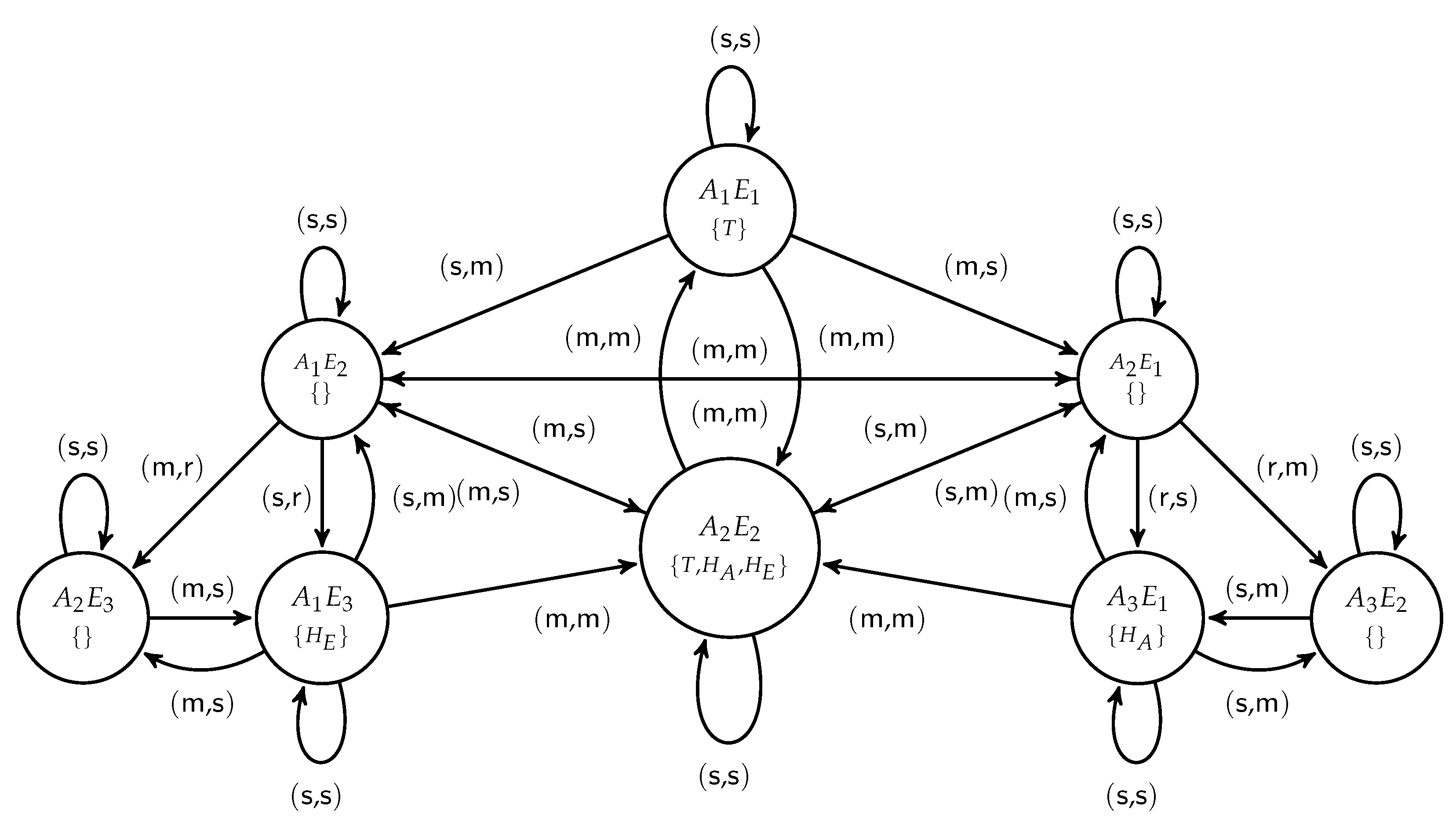
• The set of agents is $\mathsf{Agt}=\{\mathit{Adam},\mathit{Eve}\}$.
• The set of game states is $\mathsf{St}=\{A_1{E}_1,A_1{E}_2,A_2{E}_1,A_2{E}_2,A_3{E}_1,A_1{E}_3,A_3{E}_2,A_2{E}_3\}$ and the names of the states represent the current locations of the agents, e.g., $A_1{E}_2$ means that Adam is in $R1$ and Eve is in $R2$, etc. Thus, the names of the states can also be interpreted as pairs of atomic propositions saying “Adam is in room X” and “Eve is in room Y”. These atomic propositions, however, will not feature in the example.
• There are three atomic propositions of interest for us: $\mathsf{Prop}=\{T,H_A,H_E\}$, where:

  -

  T, which is true in a state iff Adam and Eve are in the same room (“together”), i.e., in $A_1{E}_1$ and $A_2{E}_2$, as indicated in their labels;

  -

  $H_A$, meaning “Adam is happy”, true in the states where $H_A$ is listed in the label;

  -

  $H_E$, meaning “Eve is happy”, true in the states where $H_E$ is listed in the label.

• The global set of actions is $\mathsf{Act}=\{\mathsf{stay},\mathsf{move},\mathsf{retreat}\}$, denoted in the figure, respectively, by  $\mathsf{s},\mathsf{m},\mathsf{r}$. The transitions caused by the respective ordered pairs of actions are indicated on the figure (the first for Adam, and the second for Eve). For example, if at state $A_1{E}_1$ both Adam and Eve choose to stay, then the transition, labeled with (s,s), is looping back to the same state, whereas if Adam chooses to stay and Eve chooses to move, the transition, labeled with (s,m), leads to the state  $A_1{E}_2$, etc. These transitions also define the global outcome function $\mathsf{Out}$.
• The global action function $\mathsf{act}$ (defining the available actions to every agent at every state) can be readily extracted from the figure. For example, $\mathsf{act}(\mathit{Adam},A_1{E}_2)=\{\mathsf{s},\mathsf{m}\}$,  $\mathsf{act}(\mathit{Eve},A_1{E}_2)=\{\mathsf{s},\mathsf{m},\mathsf{r}\}$, etc.
• Lastly, the labeling function $\mathsf{L}:\mathsf{St}\to \mathcal{P}\left(\mathsf{Prop}\right)$ is explicitly given in the figure, where the label of each state is given in $\{\dots \}$.

2.2. Plays and Strategies in Concurrent Game Models

Given a (globally defined concurrent game model $\mathcal{M}=(\mathsf{Agt},\mathsf{S},\mathsf{Act},\mathsf{act},\mathsf{Out},\mathsf{Prop},\mathsf{L})$, a partial play, or a history in $\mathcal{M}$ is either an element of $\mathsf{S}$ or a finite word of the form:

$$h=w_0{\zeta }_0{w}_1\dots w_{n-1}{\zeta }_{n-1}{w}_n$$

where $w_0,\dots ,w_n\in \mathsf{S}$ and for each $i<n$, ${\zeta }_i$ is a locally available action profile in ${\mathsf{ActProf}}_{w_i}$.

Some partial plays in Example 4 are:

$A_1{E}_1$; $A_1{E}_1(\mathsf{s},\mathsf{m})A_1{E}_2$; $A_1{E}_1(\mathsf{s},\mathsf{m})A_1{E}_2(\mathsf{m},\mathsf{m})A_2{E}_1(\mathsf{s},\mathsf{m})A_2{E}_2$; etc.

The last state in a history h will be denoted by $\mathit{l}\left(h\right)$. The set of histories in $\mathcal{M}$ is denoted by $\mathsf{Hist}\left(\mathcal{M}\right)$. The sequence of states $w_0{w}_1\dots w_n$ obtained by forgetting the action profiles in the history h is called the (initial) path induced by h and denoted $\mathsf{path}\left(h\right)$.

A (memory-based) strategy for player $\mathsf{a}$ is a map ${\sigma }_{\mathsf{a}}$ assigning to each history $h=w_0{\zeta }_0\dots {\zeta }_{n-1}{w}_n$ in $\mathsf{Hist}\left(\mathcal{M}\right)$ an action ${\sigma }_{\mathsf{a}}\left(h\right)$ from $\mathsf{act}(\mathsf{a},w_n)$. A strategy ${\sigma }_{\mathsf{a}}$ is path-based, if it assigns actions only based on the path generated by the history (not taking into account the intermediate action profiles), i.e., ${\sigma }_{\mathsf{a}}\left(h\right)={\sigma }_{\mathsf{a}}\left(h^{\prime }\right)$ whenever $\mathsf{path}\left(h\right)=\mathsf{path}\left(h^{\prime }\right)$. A strategy ${\sigma }_{\mathsf{a}}$ is memoryless, or positional, if it assigns actions only based on the current (last) state, i.e., ${\sigma }_{\mathsf{a}}\left(h\right)={\sigma }_{\mathsf{a}}\left(h^{\prime }\right)$ whenever $\mathit{l}\left(h\right)=\mathit{l}\left(h^{\prime }\right)$.

Given a coalition $C\subseteq \mathsf{Agt}$, a joint strategy for C in the model $\mathcal{M}$ is a tuple ${\mathsf{\Sigma }}_C$ of individual strategies, one for each player in C. For every joint strategy ${\mathsf{\Sigma }}_C$ and a history h, we denote by ${\mathsf{\Sigma }}_C\left(h\right)$ the joint action prescribed by ${\mathsf{\Sigma }}_C$ on h.

A (global) strategy profile $\mathsf{\Sigma }$ is a joint strategy for the grand coalition $\mathsf{Agt}$, i.e., an assignment of a strategy to each player. We denote the set of all strategy profiles in the model $\mathcal{M}$ by ${\mathsf{StratProf}}_{\mathcal{M}}$ and the set of all joint strategies for a coalition C in $\mathcal{M}$ by ${\mathsf{StratProf}}_{\mathcal{M}}\left(C\right)$. Thus, ${\mathsf{StratProf}}_{\mathcal{M}}={\mathsf{StratProf}}_{\mathcal{M}}\left(\mathsf{Agt}\right)$.

Given a strategy profile $\mathsf{\Sigma }$, the play induced by $\mathsf{\Sigma }$ at $w\in \mathsf{S}$ is the unique infinite word

$$\mathsf{play}(w,\mathsf{\Sigma })=w_0{\zeta }_0{w}_1{\zeta }_1{w}_2{\zeta }_2\dots$$

such that $w_0=w$ and, for each $n<\omega$ we have $w_{n+1}=\mathsf{out}(w_n,{\zeta }_n)$, and

$${\zeta }_{n+1}=\mathsf{\Sigma }(w_0{\zeta }_0\dots {\zeta }_n{w}_{n+1})$$

The infinite word $w_0{w}_1{w}_2\dots$ obtained by forgetting the action profiles in this infinite play is called the path induced by $\mathsf{\Sigma }$ at w, denoted $\mathsf{path}(\mathsf{\Sigma },w)$.

Here are some simple, informally described, positional strategy profiles and the plays induced by them in Example 4:

• Consider the strategy ${\sigma }_1$ which prescribes the action $\mathsf{s}$ if Adam and Eve are currently together, or else $\mathsf{m}$, if possible, otherwise, again, $\mathsf{s}$. If both Adam and Eve follow that strategy starting from $A_1{E}_1$, the induced play is
  $\mathsf{play}(A_1{E}_1,({\sigma }_1,{\sigma }_1))=A_1{E}_1(\mathsf{s},\mathsf{s})A_1{E}_1(\mathsf{s},\mathsf{s})\dots$
  Respectively, the induced play starting from $A_1{E}_2$ is
  $\mathsf{play}(A_1{E}_2,({\sigma }_1,{\sigma }_1))=A_1{E}_2(\mathsf{m},\mathsf{m})A_2{E}_1(\mathsf{m},\mathsf{m})A_1{E}_2(\mathsf{m},\mathsf{m})\dots$
• Consider the strategy ${\sigma }_2$ which prescribes the action $\mathsf{s}$ if the player is currently happy, or else $\mathsf{r}$ if possible, otherwise $\mathsf{m}$, if possible, otherwise, $\mathsf{s}$.
  If both Adam and Eve follow ${\sigma }_2$ starting from $A_1{E}_1$, the induced play is
  $\mathsf{play}(A_1{E}_1,({\sigma }_2,{\sigma }_2))=A_1{E}_1(\mathsf{m},\mathsf{m})A_2{E}_2(\mathsf{s},\mathsf{s})A_2{E}_2(\mathsf{s},\mathsf{s})\dots$
• If Adam follows ${\sigma }_1$ and Eve follows ${\sigma }_2$, the induced play starting from $A_1{E}_1$ is
  $\mathsf{play}(A_1{E}_1,({\sigma }_1,{\sigma }_2))=A_1{E}_1(\mathsf{s},\mathsf{m})A_1{E}_2(\mathsf{m},\mathsf{r})A_1{E}_3(\mathsf{m},\mathsf{s})A_2{E}_3(\mathsf{m},\mathsf{s})A_1{E}_3(\mathsf{m},\mathsf{s})\dots$
• Lastly, if Adam follows ${\sigma }_1$ and Eve follows the strategy ${\sigma }_3$ which prescribes the action $\mathsf{s}$ only if both players are currently happy or if no other action is available, or else $\mathsf{r}$ if possible, otherwise $\mathsf{m}$, then the induced play starting from $A_1{E}_1$ is this happy ending:
  $\mathsf{play}(A_1{E}_1,({\sigma }_1,{\sigma }_3))=A_1{E}_1(\mathsf{s},\mathsf{m})A_1{E}_2(\mathsf{m},\mathsf{r})A_1{E}_3(\mathsf{m},\mathsf{m})A_2{E}_2(\mathsf{s},\mathsf{s})A_2{E}_2(\mathsf{s},\mathsf{s})\dots$

More generally, given a coalition $C\subseteq \mathsf{Agt}$, a state $w\in \mathsf{S}$, and a joint strategy ${\mathsf{\Sigma }}_C$ for C, the set of outcome plays induced by the joint strategy ${\mathsf{\Sigma }}_C$ at w is the set of plays

$$\mathsf{Plays}(w,{\mathsf{\Sigma }}_C)=\left\{\mathsf{play}(w,\mathsf{\Sigma })\mid \mathsf{\Sigma }\in {\mathsf{StratProf}}_{\mathcal{M}}\mathrm{such}\mathrm{that} \mathsf{\Sigma }\left(\mathsf{a}\right)={\mathsf{\Sigma }}_C\left(\mathsf{a}\right)\mathrm{for}\mathrm{all} \mathsf{a}\in C\right\}$$

Given a strategy profile $\mathsf{\Sigma }$, we also denote $\mathsf{Plays}(w,\mathsf{\Sigma },C)⩴\mathsf{Plays}(w,\mathsf{\Sigma }{|}_C)$. We will likewise use the notation $\mathsf{paths}(w,\mathsf{\Sigma },C)$ for the set of paths obtained from the plays in $\mathsf{Plays}(w,\mathsf{\Sigma },C)$. Since these only depend on the strategies assigned to players in C, I shall freely use the notation $\mathsf{Plays}(w,\mathsf{\Sigma },C)$ and $\mathsf{paths}(w,\mathsf{\Sigma },C)$, even when $\mathsf{\Sigma }$ is defined for all members of C, but not necessarily for all other players.

3. A Variety of Strategic Abilities

This short section is a brief informal preview of the types of strategic abilities and logical operators and systems formalizing them that will be presented further in the paper.

Most of the natural claims about strategic abilities of agents and coalitions (for convenience, hereafter I will often treat individual agents as singleton coalitions) can be stated in terms of existence of a strategy profile $\mathsf{\Sigma }$ (in particular, an action profile $\zeta$) that satisfies certain requirements formalizing these abilities. Here is a natural hierarchy of types of strategic abilities and associated claims about them, which will be discussed further.

• Strictly competitive and unconditional, where all agents, respectively, coalitions, act only in pursuit of their own goals and can be assumed to regard all others either as adversaries, or as behaving randomly. An alternative way of thinking here is that these are abilities of a given agent, respectively, coalition, to achieve goals independently of the actions of all other agents. Both interpretations make good sense in the context of this paper. The typical claim for such kind of local (immediate, one step) abilities is:

  “The coalition A has a joint action to ensure satisfaction of the coalitional goal of A in every outcome state that may result from that joint action”.

  This is the informal semantic reading of the strategic operator ${\left[A\right]}_{{}_{}}$ in the coalition logic $\mathsf{CL}$ [4,5], which will be presented in Section 4.
  Respectively, here is a typical long-term strategic ability claim:

  “The coalition A has a joint strategy to ensure satisfaction of the coalitional goal of A in every outcome play resulting from A following that strategy”.

  This is the informal reading of the strategic operator $\langle \langle \mathrm{A}\rangle \rangle$ in the alternating time temporal logic $\mathsf{ATL}$ and family [7], which will be presented in Section 5.
• Competitive, but conditional on the other agents’ expected actions, where coalitions (respectively, agents) still act only in pursuit of their own goals, but, when deciding on their course of action, they take into account the goals and the respective expected actions of the other players, so they are not treated as adversaries (or, behaving randomly), but as rational agents pursuing their own goals. Here is a typical such claim expressing conditional strategic ability:

  “For some (or, every) joint action of the coalition A that ensures satisfaction of its goal ${\gamma }_A$, the coalition B has a joint action of its own to ensure satisfaction of its goal ${\gamma }_B$.

  There are (at least) two naturally arising readings of such conditional claims, as “proactive ability” and as “reactive ability”, and two respective versions of local strategic operators formalizing them. These were first introduced in [27] (respectively, as “de dicto” and “de re” abilities) and further studied in [28]. Conditional abilities will be discussed in more detail in Section 6.
• Socially cooperating abilities, where agents and coalitions still act in pursuit of their own goals, but when deciding on their course of action take into account the goals of other agents in the system and make allowance, if possible, for their satisfaction, too. Thus, agents and coalitions are assumed, i.e., not only rational but also cooperative, whenever possible to reconcile their interests with those of the others. Two natural examples of strategic operators formalizing such abilities are:

  (a)

  the “cooperative ability” operator ${\mathsf{O}}_c$, again introduced and studied in [27,28], which, when applied to (disjoint) coalitions A and B with respective goals $\varphi$ and $\psi$, formalizes the statement saying that

  “$\mathrm{A}$ has a joint action ${\sigma }_{\mathrm{A}}$ which guarantees the satisfaction of $\varphi$ and enables $\mathrm{B}$ to also apply a joint action ${\sigma }_{\mathrm{B}}$ that guarantees $\psi$”.

  This will be presented in more detail in Section 6.

  (b)

  The “socially friendly” coalitional operator SF, introduced and studied in [25], which is a somewhat more general version of ${\mathsf{O}}_c$, informally says that

  “A has a joint action ${\sigma }_A$ that guarantees satisfaction of its goal and also enables the complementary coalition $\overline{A}$ to realize any one of a list of secondary goals by applying a respectively suitable joint action”.

  The operator SF and the logic $\mathsf{SFCL}$ built on it will be presented in more detail in Section 7.

• Abilities for cooperation, protecting the interests of agents and coalitions. These capture the idea, complementary to that of $\mathsf{SFCL}$, that, while socially responsible rational agents and coalitions contribute with their individual and collective actions to the society of all agents, they wish to perform that in a way that protects their individual and collective interests and goals. Such abilities are expressed by means of the coalitional goal assignment operator$\langle [·]\rangle$, introduced in [25] as a local operator and extended with temporalized long-term goals in [26]. A coalitional goal assignment $\gamma$ is a mapping which assigns a goal formula to each possible coalition, and the operator $\langle \left[\gamma \right]\rangle$ formalizes the claim that there is a strategy profile $\sigma$ of $\mathsf{Agt}$, the restriction of which to every coalition $\mathrm{C}$ is a joint action ${\sigma }_{\mathrm{C}}$ that guarantees the satisfaction of its goal $\gamma \left(\mathrm{C}\right)$ regardless of any possible behavior of the remaining agents. The coalitional goal assignment operator and the logics $\mathsf{LCGA}$ and $\mathsf{TLCGA}$ built on it will be presented in more detail in Section 8.

4. Coalition Logic and Unconditional Local Strategic Reasoning

The case of strictly competitive (noncooperative) and unconditional abilities, presented in this section, is the extreme case of strategic abilities, where agents, respectively, coalitions, act only in pursuit of their own goals and regard all others either as adversaries or as behaving randomly. In this section, I will present briefly the basic multiagent logic $\mathsf{CL}$ formalizing these abilities and will illustrate its use with some examples.

4.1. The Basic Logic for Coalitional Strategic Reasoning $\mathsf{CL}$

As noted earlier, a typical claim for such kind of local strategic abilities is of the following type: “The coalition C has a joint action to guarantee satisfaction of the coalitional goal of C in every outcome state that may occur as a result from that joint action”.

This is the informal semantic reading of the strategic operator ${\left[C\right]}_{{}_{}}$ in the coalition logic $\mathsf{CL}$ introduced in [4]; cf. also [5,37]. $\mathsf{CL}$ extends the classical propositional logic with coalitional strategic modal operators $\left[\mathrm{C}\right]$, for any coalition of agents $\mathrm{C}$. The formulae of $\mathsf{CL}$ are defined by the following formal grammar:

$$\phi ⩴p|\top |\neg \phi \left|(\phi \vee \phi )\right|\left[\mathrm{C}\right]\phi$$

All other standard propositional connectives and constants, including ⊥, ∧, →, and ↔, are defined as usual. I will write $\left[\mathsf{i}\right]$ instead of $\left[\left\{\mathsf{i}\right\}\right]$.

4.2. Expressing Claims about Strategic Abilities in $\mathsf{CL}$

Here are some examples of formalizing statements about agents’ strategic abilities in $\mathsf{CL}$, based on the story in Example 4. The reader may wish to check whether they are all intuitively true in the model in Figure 1, say, at state $A_1{E}_1$.

1.

$$\left[\mathbf{Eve}\right]H_E\to \neg \left[\mathbf{Adam}\right]\neg H_E$$

If Eve has an action ensuring that she becomes happy, then

Adam cannot prevent Eve from reaching a state where she is happy.

2.

The statement above naturally generalizes (with $\mathrm{Win}$ being an atomic proposition) to

$$\left[\mathsf{i}\right]\mathrm{Win}\to \neg \left[\mathsf{Agt}\backslash \left\{\mathsf{i}\right\}\right]\neg \mathrm{Win}$$

If the agent $\mathsf{i}$ has an action to guarantee reaching a “winning” outcome, then the coalition of all other agents cannot prevent $\mathsf{i}$ from reaching a “winning” outcome.

It should be intuitively clear that this statement expresses a valid principle of $\mathsf{CL}$. Indeed, we will see shortly that this is the case.

3.

$$\neg \left[\mathbf{Adam}\right]T\wedge \neg \left[\mathbf{Eve}\right]T\wedge \left[\{\mathbf{Adam},\mathbf{Eve}\}\right]T$$

Neither Adam nor Eve has an action ensuring that they stay together, but they have a joint action ensuring that.

4.

$$\neg \left[\mathbf{Adam}\right]H_A\wedge \neg \left[\mathbf{Eve}\right]H_E\wedge \left[\{\mathbf{Adam},\mathbf{Eve}\}\right](H_A\wedge H_E)$$

Neither Adam nor Eve has an action ensuring happiness for himself/herself but they have a joint action ensuring happiness for both.

5.

$$\neg \left[\mathbf{Adam}\right](H_A\wedge \neg \left[\mathbf{Eve}\right]H_E)$$

Adam cannot act so as to ensure at the outcome state that both Adam is happy and Eve does not have an action to ensure reaching her happiness.

6.

$$\left[\{\mathbf{Adam},\mathbf{Eve}\}\right](\left[\mathbf{Adam}\right]H_A\to \left[\mathbf{Eve}\right]H_E)$$

Adam and Eve can act jointly so that at the outcome state Adam has an action to ensure reaching his happiness only if Eve has an action to ensure reaching her happiness.

7.

$$\left[\mathbf{Adam}\right]\left[\mathbf{Eve}\right](H_A\wedge H_E\wedge \left[\mathbf{Adam}\right]H_E\wedge \left[\mathbf{Eve}\right]H_A)$$

Adam can act to ensure (at the outcome state), that Eve can then act to ensure that they are both happy and that each of them can act so as to keep the other happy.

Thus, we see that the language of $\mathsf{CL}$ allows expressing meaningful and nontrivial claims about agents’ local (immediate) strategic abilities. However, $\mathsf{CL}$ does not allow expressing long-term (temporal) goals and claims, e.g., that Adam and Eve have a joint strategy to stay together forever, or to eventually reach happiness. For that, a more expressive logic is needed, also involving temporal operators. It is introduced in Section 5.

4.3. Formal Semantics of CL

The formulae of $\mathsf{CL}$ are interpreted in concurrent game models. Consider a CGM $\mathcal{M}=(\mathsf{Agt},\mathsf{S},\mathsf{Act},\mathsf{act},\mathsf{Out},\mathsf{Prop},\mathsf{L})$. Truth of a CL-formula $\psi$ at a state s in $\mathcal{M}$, denoted $\mathcal{M},s\vDash \psi$, as in modal logic, is defined by structural induction on formulae via the clauses:

• $\mathcal{M},s\vDash p$ iff $p\in \mathsf{L}\left(s\right)$, for $p\in \mathsf{Prop}$.
• $\mathcal{M},s\vDash \neg \varphi$ iff $\mathcal{M},s⊭\varphi$.
• $\mathcal{M},s\vDash ({\varphi }_1\vee {\varphi }_2)$ iff $\mathcal{M},s\vDash {\varphi }_1$ and $\mathcal{M},s\vDash {\varphi }_2$.
• $\mathcal{M},s\vDash \left[C\right]\varphi$ iff there exists a joint action ${\sigma }_C$ available at s,
  such that $\mathcal{M},u\vDash \varphi$ for each $u\in \mathsf{Out}[s,{\sigma }_C]$.

Note that this definition makes no implicit assumption that the agents in $\mathrm{C}$ know the goals of the remaining agents, nor the actions that they may possibly use to achieve these goals.

Here are examples of truth of some of the $\mathsf{CL}$ formulae listed in Section 4.2 in the CGM for Example 4, given in Figure 1, which are left for the reader to formally verify.

• $\mathcal{M},A_1{E}_1\vDash \neg \left[\mathbf{Adam}\right]T$; $\mathcal{M},A_1{E}_1\vDash \neg \left[\mathbf{Eve}\right]T$.
• $\mathcal{M},A_1{E}_1\vDash \left[\{\mathbf{Adam},\mathbf{Eve}\}\right]T$.
• $\mathcal{M},A_1{E}_1\vDash \neg \left[\mathbf{Adam}\right]H_A\wedge \neg \left[\mathbf{Eve}\right]H_E\wedge \left[\{\mathbf{Adam},\mathbf{Eve}\}\right](H_A\wedge H_E)$.
• $\mathcal{M},A_1{E}_1\vDash \left[\{\mathbf{Adam},\mathbf{Eve}\}\right](\left[\mathbf{Eve}\right]H_E\wedge \neg \left[\mathbf{Adam}\right]H_A\wedge \left[\{\mathbf{Adam},\mathbf{Eve}\}\right](H_A\wedge H_E))$.

4.4. Axiomatizing the Validities of $\mathsf{CL}$

A CL formula $\varphi$ is called:

• (Logically) valid if $\mathcal{M},s\vDash \varphi$ for every CGM $\mathcal{M}$ and a state $s\in \mathcal{M}$.
• Satisfiable if $\mathcal{M},s\vDash \varphi$ for some CGM $\mathcal{M}$ and a state $s\in \mathcal{M}$.

Pauly [4,5] obtained a complete axiomatization of the valid formulae of $\mathsf{CL}$, by extending the classical propositional logic $\mathsf{PL}$ with the following axiom schemes and rule:

• $\mathsf{Agt}$-maximality: $\neg \left[Ø\right]\neg \phi \to \left[\mathsf{Agt}\right]\phi$
  This axiom says that the grand coalition $\mathsf{Agt}$ can act collectively so as to guarantee any goal that is satisfied in at least one outcome state. Note that the validity of this axiom presupposes that the models are deterministic, implying that the coalition of all agents $\mathsf{Agt}$ can enforce any particular possible outcome.
• Safety: $\neg \left[C\right]\perp$
  No coalition has the ability to ensure the falsum will become true.
• Liveness: $\left[C\right]\top$
  Every coalition has the ability to ensure the truth will become true.
• Superadditivity: for any $C_1,C_2\subseteq \mathsf{Agt}$ such that $C_1\cap C_2=Ø$:

  $$(\left[C_1\right]{\phi }_1\wedge \left[C_2\right]{\phi }_2)\to \left[C_1\cup C_2\right]({\phi }_1\wedge {\phi }_2)$$
  This axiom scheme says that two disjoint coalitions, each of which has a joint action to guarantee satisfaction of their own goal, can join forces (simply by each of them following their respective joint action) to guarantee satisfaction of both goals.
• $\left[C\right]$-monotonicity Rule:

  $$\frac{{\phi }_1\to {\phi }_2}{\left[C\right]{\phi }_1\to \left[C\right]{\phi }_2}$$

Some important derivable validities include:

• Outcome Monotonicity: $\left[C\right]({\phi }_1\wedge {\phi }_2)\to \left[C\right]{\phi }_1$.
  This is derived directly by applying the $\left[C\right]$-monotonicity rule.
• Coalition Monotonicity: $\left[C_1\right]\phi \to \left[C_1\cup C_2\right]\phi$.
  This is derived by applying the superadditivity axiom scheme to the coalitions $C_1$ and $C_2\backslash C_1$ with respective goals $\phi$ and ⊤. Note that this validity together with $\mathsf{Agt}$-maximality also implies the validity of $\left[\mathsf{Agt}\right]\phi \vee \left[\mathsf{Agt}\right]\neg \phi$, for any formula $\phi$.
• Coalition complementarity: $\left[C\right]\phi \to \neg \left[\overline{C}\right]\neg \phi$, where $\overline{C}=\mathsf{Agt}\backslash C$.
  This is derived by applying the superadditivity axiom scheme to the coalitions C and $\overline{C}$ with respective goals $\phi$ and $\neg \phi$, and then the safety axiom scheme.

The problem of deciding whether a given formula in the logic $\mathsf{CL}$ is valid, respectively, satisfiable, is decidable [4,5]. This and other technical results about $\mathsf{CL}$ are subsumed by respective results for the more expressive logic $\mathsf{ATL}$, presented in the next section.

5. Logics for Unconditional Long-Term Strategic Reasoning

The logic $\mathsf{CL}$ can only capture strategic reasoning about abilities to achieve local, i.e., one-step goals. It can be naturally extended with temporal operators to reason about long-term unconditional strategic abilities, of the type:

“The coalition C has a joint strategy to guarantee achievement of the coalitional goal of C in every outcome play resulting from C following that strategy”.

This is the informal reading of the strategic operator $\langle \langle \mathrm{C}\rangle \rangle$ in the alternating time temporal logic $\mathsf{ATL}$ and family, introduced (independently from the logic $\mathsf{CL}$) in [7].

I will present and illustrate here the family of $\mathsf{ATL}$-related logics. For more detailed and technically involved surveys on these logics, see [8,9].

5.1. The Alternating-Time Temporal Logic ${\mathsf{ATL}}^{*}$

The full alternating-time temporal logic ${\mathsf{ATL}}^{*}$, introduced in [7], involves long-term temporal operators, the standard repertoire being “next-time” $\mathsf{X}$, “always” $\mathsf{G}$, and “until” $\mathsf{U}$.

The strategic operator in ${\mathsf{ATL}}^{*}$ is $\langle \langle \mathrm{C}\rangle \rangle \varphi$, denoting the claim that

“The coalition $\mathrm{C}$ has a joint strategy that guarantees the satisfaction of the goal $\varphi$ on every outcome play induced by that joint strategy“,

where $\varphi$ is any formula of ${\mathsf{ATL}}^{*}$. The language of ${\mathsf{ATL}}^{*}$ is formally defined as follows. It involves two sorts of formulae: state formulae, that are evaluated at game states, and path formulae, that are evaluated on game plays. These are, respectively, defined by the following grammars, where $p\in \mathsf{Prop}$ and $\mathrm{C}\subseteq \mathsf{Agt}$:

State formulae:	$\phi$	$⩴$	$p\mid \top \mid \neg \phi \mid (\phi \vee \phi )\mid \langle \langle \mathrm{C}\rangle \rangle \gamma$.
Path formulae:	$\gamma$	$⩴$	$\phi \mid \neg \gamma \mid (\gamma \vee \gamma )\mid \mathsf{X}\gamma \mid \mathsf{G}\gamma \mid (\gamma \cup \gamma )$.

Thus, the path formulae are used to formalize goals.

The language of ${\mathsf{ATL}}^{*}$ is too expressive, and that both creates problems with its intuitive interpretation (see discussions on [38,39,40]) and raises the complexity cost of computing the truth of an ${\mathsf{ATL}}^{*}$ to 2EXPtime (cf. [7]). To alleviate these, the fragment $\mathsf{ATL}$ was also introduced in [7], which only contains state formulae, defined by the grammar:

$$\phi ⩴p\mid \neg \phi \mid (\phi \vee \phi )\mid \langle \langle \mathrm{C}\rangle \rangle \mathsf{X}\phi \mid \langle \langle \mathrm{C}\rangle \rangle \mathsf{G}\phi \mid \langle \langle \mathrm{C}\rangle \rangle (\phi \cup \phi ),$$

Thus, the coalitional goals in $\mathsf{ATL}$ only involve simple patterns with a single temporal operator, which will be called simple temporal goals. We define $\langle \langle \mathrm{C}\rangle \rangle \mathsf{F}\phi$ as $\langle \langle \mathrm{C}\rangle \rangle (\top \cup \phi )$.

The logic $\mathsf{CL}$ embeds into $\mathsf{ATL}$ as the fragment where the goals can only be of the type $\mathsf{X}\phi$, for a state formula $\phi$ (cf. [41]), i.e., $\left[C\right]\phi ⩴\langle \langle \mathrm{C}\rangle \rangle \mathsf{X}\phi$.

Hereafter, in this section, I will focus on the logic $\mathsf{ATL}$.

5.2. Formal Semantics of $\mathsf{ATL}$

Similar to $\mathsf{CL}$, the formulae of ${\mathsf{ATL}}^{*}$ are interpreted in concurrent game models. To keep the presentation less technical, I will only give the formal semantics for the fragment $\mathsf{ATL}$, which consists only of state formulae; for full details of the semantics of ${\mathsf{ATL}}^{*}$, see, e.g., [8].

Consider a CGM $\mathcal{M}=(\mathsf{Agt},\mathsf{S},\mathsf{Act},\mathsf{act},\mathsf{Out},\mathsf{Prop},\mathsf{L})$. Truth of an $\mathsf{ATL}$-formula $\psi$ at a state s in $\mathcal{M}$, denoted $\mathcal{M},s\vDash \psi$, is defined by structural induction on formulae. The propositional cases are similar to in $\mathsf{CL}$, and the only new clauses are those for the strategic operators. They all follow the same pattern, which is essentially the semantic clause for $\langle \langle \cdots \rangle \rangle$ in ${\mathsf{ATL}}^{*}$:

$\mathcal{M},s\vDash \langle \langle \mathrm{C}\rangle \rangle \gamma$ iff there exists a joint strategy ${\mathsf{\Sigma }}_C$ for C such that $\gamma$ is true on every play in $\mathsf{Plays}(s,{\mathsf{\Sigma }}_C)$, i.e., every play starting at s and induced by ${\mathsf{\Sigma }}_C$.

The specific clauses for the temporal operators defining the goal $\gamma$ are as follows, where $s_0=s$:

• $\mathcal{M},s\vDash \langle \langle \mathrm{C}\rangle \rangle \mathsf{X}\phi$ iff there exists a joint strategy ${\mathsf{\Sigma }}_C$ such that $\mathcal{M},s_1\vDash \phi$ for every play $s_0,s_1,\dots \in \mathsf{Plays}(s,{\mathsf{\Sigma }}_C)$.
• $\mathcal{M},s\vDash \langle \langle \mathrm{C}\rangle \rangle \mathsf{G}\phi$ iff there exists a joint strategy ${\mathsf{\Sigma }}_C$ such that $\mathcal{M},s_i\vDash \phi$ for every play $s_0,s_1,\dots \in \mathsf{Plays}(s,{\mathsf{\Sigma }}_C)$ and $i\ge 0$.
• $\mathcal{M},s\vDash \langle \langle \mathrm{C}\rangle \rangle \left(\phi \mathsf{U}\psi \right)$ iff there exists a joint strategy ${\mathsf{\Sigma }}_C$ such that for every play $s_0,s_1,\dots \in \mathsf{Plays}(s,{\mathsf{\Sigma }}_C)$ there is $i\ge 0$ for which $\mathcal{M},s_i\vDash \psi$ and $\mathcal{M},s_j\vDash \phi$ for all j such that $0\le j<i$.

Satisfiability and validity in $\mathsf{ATL}$ are defined similar to in $\mathsf{CL}$.

It can be shown (cf., e.g., [36]) that memoryless strategies suffice for the semantics of $\mathsf{ATL}$ formulae, but that is no longer the case even when conjunctions of simple temporal goals are allowed. Indeed, consider the ${\mathsf{ATL}}^{*}$ formula $\varphi =\langle \langle \mathsf{a}\rangle \rangle (\mathsf{F}p\wedge \mathsf{F}q)$ and a concurrent game model in Figure 2 for the only agent $\mathsf{a}$. Clearly, there is no positional strategy to satisfy $\varphi$ at $s_0$, as it must always prescribe the same action, L or R, there, so either $s_1$ or $s_2$, but not both, will always be visited. On the other hand, there is a simple strategy for $\mathsf{a}$ using a bit of memory that can satisfy $\varphi$, e.g., prescribing the first time when $s_0$ is visited the action L, and the next time—the action R.

5.3. Expressing Claims about Strategic Abilities in $\mathsf{ATL}$

Here are some examples of formalizing in $\mathsf{ATL}$ statements about agents’ long-term strategic abilities.

1.

$$\langle \langle \mathbf{Eve}\rangle \rangle \mathsf{F}{H}_E\to \neg \langle \langle \mathbf{Adam}\rangle \rangle \mathsf{G}\neg H_E$$

If Eve has an action ensuring that she eventually becomes happy, then Adam cannot prevent Eve forever from reaching a state where she is happy.

It should be intuitively clear that this statement expresses a valid principle of $\mathsf{ATL}$. Indeed, this is the case.

2.

$$(\langle \langle \mathbf{Yin}\rangle \rangle \mathsf{G}\mathrm{Safe}\wedge \langle \langle \mathbf{Yin}\rangle \rangle \mathsf{F}\mathrm{Goal})\to \langle \langle \mathbf{Yin}\rangle \rangle (\mathrm{Safe}\cup \mathrm{Goal})$$

If $\mathbf{Yin}$ has a strategy to keep the system in safe states forever and has a strategy to eventually achieve its goal, then $\mathbf{Yin}$ has a strategy to keep the system in safe states until it achieves its goal.

The formula above is not logically valid. Indeed, the strategies of $\mathbf{Yin}$ to keep the system in safe states forever and to eventually achieve its goal may be incompatible.

3.

$$(\langle \langle \mathbf{Yin}\rangle \rangle \mathsf{G}\mathrm{Safe}\wedge \langle \langle \mathbf{Yang}\rangle \rangle \mathsf{F}\mathrm{Goal})\to \langle \langle \{\mathbf{Yin},\mathbf{Yang}\}\rangle \rangle (\mathrm{Safe}\cup \mathrm{Goal})$$

If $\mathbf{Yin}$ has a strategy to keep the system in safe states forever and $\mathbf{Yang}$ has a strategy to eventually reach a goal state, then $\mathbf{Yin}$ and $\mathbf{Yang}$ together have a strategy to stay in safe states until a goal state is reached.

Assuming that $\mathbf{Yin}$ and $\mathbf{Yang}$ are distinct agents, the formula above is logically valid, unlike the previous one. Indeed, this is due to the independence of the actions of the two agents, and hence of their abilities to execute their respective strategies.

4.

$$\langle \langle \mathrm{A}\rangle \rangle \mathsf{F}\langle \langle \mathrm{B}\rangle \rangle \mathsf{G}\neg \phi$$

The coalition A has a joint strategy to eventually ensure that the coalition B has a strategy to prevent φ from ever happening.

This example raises the question of how the semantics works in the case of nested strategic operators. Suppose, the coalitions A and B intersect and $\mathsf{a}$ is an agent in both of them. Then, the claim of the external strategic operator $\langle \langle \mathrm{A}\rangle \rangle$ requires, inter alia, existence of a strategy for the agent $\mathsf{a}$ within a joint strategy ${\sigma }_A$ for A that guarantees the eventual satisfaction of the subformula $\langle \langle \mathrm{B}\rangle \rangle \mathsf{G}\neg \phi$. However, when evaluating that subformula, to justify its truth, one has to identify a respective joint strategy ${\sigma }_B$ for $\langle \langle \mathrm{B}\rangle \rangle$. Now, the question arises whether the strategy of $\mathsf{a}$ within ${\sigma }_B$ should not be assumed to be already fixed by ${\sigma }_A$ or, conversely, whether the strategy of $\mathsf{a}$ within ${\sigma }_A$ should not be assumed to be already fixed by ${\sigma }_B$. Note that the standard formal semantics for ${\mathsf{ATL}}^{*}$ (in particular, of $\mathsf{ATL}$) presented here does not impose any such constraints, but, rather, treats these strategies independently. That is, the standard semantics of ${\mathsf{ATL}}^{*}$does not commit the agents in A to the strategies they adopt in order to bring about the truth of the formula $\langle \langle \mathrm{A}\rangle \rangle \gamma$. That creates some conceptual issues with the very concept of “strategy”, independently addressed in different ways in [38,39,42,43], where several proposals were made in order to incorporate strategic commitment or uncommitment and persistent strategies in the syntax and semantics of ${\mathsf{ATL}}^{*}$. These raise a number of still open technical problems regarding constructing provably complete axiomatizations, proving decidability, and designing decision procedures for the variations of $\mathsf{ATL}$ and ${\mathsf{ATL}}^{*}$ mentioned above.

6. The Logic of Conditional Strategic Reasoning ConStR

Let us now look at the reasoning of (and about) an agent, conditional on that agent’s knowledge of the goals and choices of actions of the other agents. Note that, while knowledge is not explicitly included in the syntax of the logics considered here, it is implicit in their reasoning, or in the reasoning of the external observers reasoning about the agents’ abilities, and it is also implicitly assumed in the formal semantics.

6.1. Conditional Strategic Reasoning: An Informal Discussion

I first focus on a simple case: two agents, Alice and Bob, acting independently, and possibly concurrently with other agents. Alice has a goal, ${\gamma }_A$, to achieve. Suppose that Alice has several possible choices of action that would possibly, or certainly, ensure the achievement of her goal. Bob also has a goal, ${\gamma }_B$, of his own and has several possible actions (there may be other agents, besides Alice and Bob, also acting in pursuit of their own goals, but we will ignore them here). Now, based on his knowledge about Alice’s goal and possible choices of actions she may take towards that goal, Bob decides on his own choice of action in pursuit of his goal.

Here is a simple illustrating scenario, discussed in [27]. Alice and Bob are students at Downtown University. Alice is coming to campus today, to meet with her supervisor. Bob wants to meet with Alice somewhere on campus today. Alice may not know that, and they may have no direct communication. In turn, Bob may, or may not, know what Alice is going to do on campus. Now, using his knowledge of what, where, and when Alice intends to do, Bob wants to come up with a plan of where and how to meet her.

This calls for a conditional strategic reasoning with statements of the type:

For some/every action of Alice that guarantees achievement of her goal ${\gamma }_A$,

Bob has/does not have an action of his own to guarantee achievement of his goal ${\gamma }_B$.

I will focus here on local conditional strategic reasoning, which only refers to the immediate actions of the agents, not to their long-term global strategies.

As we will see further, the standard logics for multiagent strategic reasoning, such as $\mathsf{CL}$ and $\mathsf{ATL}$, cannot capture this type of conditional reasoning. A more expressive logic for conditional strategic reasoning is needed here.

Depending on Bob’s knowledge about Alice’s goal and of her possible or expected choices of action, there can be several possible cases for Bob’s reasoning.

6.1.1. Case 1: Bob Does Not Know Alice’s Goal or Actions

The simplest case is when Bob does not know Alice’s goal, or her available actions, and therefore has no a priori expectations about her choice of action. Then, Bob can only ensure that ${\gamma }_B$ will occur if he has an action to make ${\gamma }_B$ true, regardless of how Alice (and all others) act. For instance, in our scenario, suppose the campus has only one entrance. If Bob is standing by the only entrance of the campus, then he is sure to meet Alice when she comes, no matter what she will do there. This can be simply expressed in coalition logic as $\left[B\right]{\gamma }_B$.

6.1.2. Case 2: Bob Knows Alice’s Goal and Possible Actions

Suppose now, that Bob knows Alice’s goal, as well as all possible actions of Alice that can ensure the satisfaction of her goal. Thus, Bob knows that Alice will perform one of these actions, but possibly does not know which one. For instance, in our scenario, Bob knows that Alice is coming to campus to meet with her supervisor and she can meet with him either in his office, or in the lecture room, or in the café.

We can express Bob’s conditional ability to achieve his goal as follows:

“Whichever way Alice acts towards achieving her goal ${\gamma }_A$,

Bob can act so as to ensure achievement of his goal ${\gamma }_B$”.

This claim can no longer be expressed in coalition logic, except in the special case when the satisfaction of Alice’s goal guarantees satisfaction of Bob’s goal, too (thus, Bob need not do anything about that). That can again be simply expressed in $\mathsf{CL}$ as $[Ø]({\gamma }_A\to {\gamma }_B)$.

6.1.3. Reactive and Proactive Ability

This case above admits two essentially different readings, discussed further: as a reactive ability, and as a proactive ability. (In [27], these were called ability de dicto and ability de re.)

Bob’s reactive ability. Suppose first, that Bob will know Alice’s choice of action when he is to choose his action. Then, Bob’s ability to achieve his goal is reactive, meaning that for every action of Alice that ensures her goal ${\gamma }_A$, Bob has an action of his, possibly dependent on Alice’s action, that would also ensure his goal, ${\gamma }_B$. For instance, in our scenario, suppose that Alice’s supervisor tells Bob where and when he is going to meet with Alice. Then Bob can wait for Alice at the respective place. This claim cannot be expressed in $\mathsf{CL}$, so a new operator is needed for it.

Bob’s proactive ability. Suppose now that Bob will not know Alice’s action when he is to choose his. For instance, in our scenario, suppose all that Bob knows is that Alice will meet with her supervisor either in his office, or in the lecture room, or in the café, but does not know where. Now, for Bob to ensure that his goal will be achieved, he must have a uniform choice of action to make ${\gamma }_B$ true, when applied with any action of Alice that ensures the truth of her goal, ${\gamma }_A$. For instance, in our scenario, suppose that all meeting places for Alice and her supervisor are in the same building, so Bob can wait for her at the only entrance of that building. That is, Bob must have a proactive ability to achieve his goal.

This cannot be expressed in $\mathsf{CL}$, either, so a new operator is needed again.

Remark 5. 

The notions of proactive and reactive ability, respectively, generalize the notions of $\alpha$-effectivity and $\beta$-effectivity in game theory (cf., e.g., [44]). Indeed, in the context of the Alice and Bob story above, proactive and reactive ability of Bob correspond precisely, respectively, to α-effectivity and β-effectivity when either ${\gamma }_A\equiv \top$ (so, any action of Alice is equally good for achieving ${\gamma }_A$) or when Bob does not know ${\gamma }_A$ and hence can expect any action from Alice. Furthermore, one can still associate proactive and reactive ability with α-effectivity and β-effectivity if one explicitly assumes individual rationality of Alice, implying that she would only choose actions that would ensure ${\gamma }_A$. Thus, one can regard proactive and reactive ability, respectively, as conditional $\alpha$-effectivity and $\beta$-effectivity, terminology which will be used further.

Lastly, an important point: even though knowledge of the agent (here, Bob) about the other’s goals and possible actions is essential, it will not feature in our formal logical language, nor in the formal semantics, but only in the external reasoner’s analysis, in which case conditional strategic ability applies.

6.1.4. Case 3: Assuming Alice’s Cooperation

Suppose now that Alice also knows Bob’s goal and can choose to cooperate with Bob by selecting a suitable action ${\sigma }_{\mathrm{A}}$, that would not only guarantee achievement of her goal ${\gamma }_A$, but will also enable Bob to supplement ${\sigma }_{\mathrm{A}}$ with an action ${\sigma }_{\mathrm{B}}$ of his, which would then also guarantee achievement of his goal ${\gamma }_B$ (we also assume that Alice knows enough about Bob’s possible actions). This scenario cannot be formalized in $\mathsf{CL}$, either.

6.2. Modal Operators for Conditional Strategic Reasoning

I will now present three new binary modal operators for conditional strategic reasoning, for any coalitions $\mathrm{A}$ and $\mathrm{B}$, with intuitive semantics corresponding to the three reasoning cases in Section 6.1, i.e., formalizing, respectively, reactive abilities, proactive abilities, and abilities under cooperation.

Below, $\mathrm{A}$ and $\mathrm{B}$ are coalitions and ${\gamma }_{\mathrm{A}}$ and ${\gamma }_{\mathrm{B}}$ are their respective goals. In the special case when $\mathrm{A}$ and $\mathrm{B}$ are singletons, they are assumed to be different agents.

(${\mathsf{O}}_{\alpha }$)

${\left[\mathrm{A}\right]}_{\alpha }({\gamma }_{\mathrm{A}};\langle \mathrm{B}\rangle {\gamma }_{\mathrm{B}})$ means that the coalition $\mathrm{B}\backslash \mathrm{A}$ of agents who are in $\mathrm{B}$ but not in $\mathrm{A}$ has a joint action ${\sigma }_{\mathrm{B}\backslash \mathrm{A}}$ such that if $\mathrm{A}$ applies any joint action that guarantees the truth of ${\gamma }_{\mathrm{A}}$, then $\mathrm{B}\backslash \mathrm{A}$ can ensure the truth of ${\gamma }_{\mathrm{B}}$ by applying ${\sigma }_{\mathrm{B}}$.

This operator formalizes the notion of a coalition’s proactive ability, discussed in the special case of single-agent coalitions in Section 6.1.3, respectively, to the game-theoretic notion of conditional α-effectivity, hence the notation. Note that the agents in $\mathrm{B}\cap \mathrm{A}$ (if any) are assumed to act on behalf of $\mathrm{A}$ in its pursuit of ${\gamma }_{\mathrm{A}}$.

(${\mathsf{O}}_{\beta }$)

${\left[\mathrm{A}\right]}_{\beta }({\gamma }_{\mathrm{A}};\langle \mathrm{B}\rangle {\gamma }_{\mathrm{B}})$ means that for any joint action ${\sigma }_{\mathrm{A}}$ of $\mathrm{A}$ that guarantees the truth of ${\gamma }_{\mathrm{A}}$, when applied by $\mathrm{A}$ there is a joint action ${\sigma }_{\mathrm{B}\backslash \mathrm{A}}$ that guarantees ${\gamma }_{\mathrm{B}}$ when additionally applied by $\mathrm{B}\backslash \mathrm{A}$. Note that ${\left[\mathrm{A}\right]}_{\beta }(\perp ;\langle \mathrm{B}\rangle {\gamma }_{\mathrm{B}})$ is vacuously true for any $\mathrm{A}$, $\mathrm{B}$, and ${\gamma }_{\mathrm{B}}$, as then there cannot be such joint actions ${\sigma }_{\mathrm{A}}$ that enable satisfying ⊥. This may sounds odd, but it is no special phenomenon in $\mathsf{ConStR}$, as the same effect occurs in FOL with universal quantification over an empty set of objects.

This operator formalizes a claim of the ability of the coalition $\mathrm{B}$ to choose a suitable joint action so as to achieve the goal ${\gamma }_{\mathrm{B}}$ assuming that $\mathrm{A}$ acts so as to achieve the goal ${\gamma }_{\mathrm{A}}$, if $\mathrm{B}$ is to choose their joint action after $\mathrm{B}$ learns the joint action of $\mathrm{A}$. In this case, the actions of the agents in $\mathrm{B}\cap \mathrm{A}$ (if any) are assumed to be already fixed by ${\gamma }_{\mathrm{A}}$.

This corresponds to the notion of agents’ reactive ability discussed in Section 6.1.3, respectively, to the game-theoretic notion of conditional β-effectivity, hence the notation.

(${\mathsf{O}}_c$)

${\langle \mathrm{A}\rangle }_{\mathsf{c}}({\gamma }_{\mathrm{A}};\langle \mathrm{B}\rangle {\gamma }_{\mathrm{B}})$ means that $\mathrm{A}$ has a joint action ${\sigma }_{\mathrm{A}}$ which, when applied, guarantees the truth of ${\gamma }_{\mathrm{A}}$ and enables $\mathrm{B}\backslash \mathrm{A}$ to apply a joint action ${\sigma }_{\mathrm{B}\backslash \mathrm{A}}$ that guarantees ${\gamma }_{\mathrm{B}}$ when additionally applied by $\mathrm{B}\backslash \mathrm{A}$.

This operator formalizes Case 3 discussed in Section 6.1, where $\mathrm{A}$ knows the goal of $\mathrm{B}$ and can choose to cooperate with $\mathrm{B}$ by selecting an action among those that ensure satisfaction of ${\gamma }_{\mathrm{A}}$ which is also suitable for $\mathrm{B}$.

6.3. The Logic $\mathsf{ConStR}$: Language and Some Definable Operators

We fix a finite nonempty set of agents $\mathsf{Agt}$ and a countable set of atomic propositions $\mathsf{Prop}$. The formulae of $\mathsf{ConStR}$, where $p\in \mathsf{Prop}$ and $\mathrm{A},\mathrm{B}\subseteq \mathsf{Agt}$ are defined as follows:

$$\varphi ⩴p\mid \top \mid \neg \varphi \mid (\varphi \vee \varphi )\mid {\left[\mathrm{A}\right]}_{\alpha }(\varphi ;\langle \mathrm{B}\rangle \varphi )\mid {\left[\mathrm{A}\right]}_{\beta }(\varphi ;\langle \mathrm{B}\rangle \varphi )\mid {\langle \mathrm{A}\rangle }_{\mathsf{c}}(\varphi ;\langle \mathrm{B}\rangle \varphi )$$

Here are some definable operators and expressions in $\mathsf{ConStR}$, which can be easily seen from the informal semantics above, and can also be easily verified with the formal semantics introduced further.

• The coalitional operator from $\mathsf{CL}$ is definable by means of each of ${\mathsf{O}}_c$, ${\mathsf{O}}_{\alpha }$, ${\mathsf{O}}_{\beta }$ as follows:

  (${\mathsf{O}}_{\alpha }$)

  $\left[\mathrm{C}\right]\varphi ⩴{[Ø]}_{\alpha }(\top ;\langle \mathrm{C}\rangle \varphi )$.

  This claims an unconditional ability of $\mathrm{C}$ to choose an action that guarantees $\varphi$.

  (${\mathsf{O}}_{\beta }$)

  $\left[\mathrm{C}\right]\varphi ⩴{[Ø]}_{\beta }(\top ;\langle \mathrm{C}\rangle \varphi )$, or $\left[\mathrm{C}\right]\varphi ⩴{\left[\overline{\mathrm{C}}\right]}_{\beta }(\top ;\langle \mathrm{C}\rangle \varphi )$.

  The only strategy of the empty coalition guarantees the satisfaction of ⊤.

  (${\mathsf{O}}_c$)

  $\left[\mathrm{C}\right]\varphi ⩴{\langle \mathrm{C}\rangle }_{\mathsf{c}}(\varphi ;\langle \mathrm{C}\rangle \varphi )$ or $\left[\mathrm{C}\right]\varphi ⩴{\langle \mathrm{C}\rangle }_{\mathsf{c}}(\varphi ;\langle \mathrm{C}\rangle \top )$.

• ${\langle \mathrm{A}\rangle }_{\mathsf{c}}({\gamma }_{\mathrm{A}};\langle \mathrm{B}\rangle {\gamma }_{\mathrm{B}})$ is equivalent to $\langle \langle \mathrm{A}\rangle \rangle ({\gamma }_{\mathrm{A}}\wedge \langle \langle \mathrm{B}\backslash \mathrm{A}\rangle \rangle {\gamma }_{\mathrm{B}})$ in ${\mathsf{ATL}}^{*}$.
• The negated ${\mathsf{O}}_c$ operator $\neg {\langle \mathrm{A}\rangle }_{\mathsf{c}}(\varphi ;\langle \mathrm{B}\rangle \psi )$ says that every joint action of $\mathrm{A}$ that, when applied, guarantees the truth of $\varphi$, would prevent $\mathrm{B}$ from acting additionally so as to guarantee $\psi$. This formalizes the conditional reasoning scenario where the goals of $\mathrm{A}$ and $\mathrm{B}$ are conflicting, so whichever way $\mathrm{A}$ acts towards its goal would block $\mathrm{B}$ from acting to guarantee achievement of $\mathrm{B}$’s goal.
• ${\left[\mathrm{A}\right]}_{\beta }(\top ;\langle \mathrm{B}\rangle \psi )$ essentially formalizes the case when the agents in $\mathrm{B}$ are not informed about the goal of $\mathrm{A}$, but have to choose their action after learning the action of $\mathrm{A}$.
• On the other hand, $\left[\mathrm{A}\right]\left(\varphi \right|\psi )⩴{\left[\mathrm{A}\right]}_{\beta }(\varphi ;\langle Ø\rangle \psi )$, also equivalent to ${\left[\mathrm{A}\right]}_{\alpha }(\varphi ;\langle Ø\rangle \psi )$, says that any joint strategy of $\mathrm{A}$ that guarantees $\varphi$ to be true also guarantees $\psi$ to be true. That formalizes the claim of an observer who knows both the goal $\varphi$ and the possible joint actions of $\mathrm{A}$, that the outcome from the joint action of $\mathrm{A}$ will also satisfy $\psi$.
• $\langle \mathrm{A}\rangle \left(\varphi \right|\psi )⩴\neg [\mathrm{A}\left]\right(\varphi |\neg \psi )$ says that there is a joint strategy of $\mathrm{A}$ that ensures the truth of $\varphi$ and also enables the satisfaction of $\psi$.
  $\langle \mathrm{A}\rangle \left(\varphi \right|\psi )$ is also definable as ${\langle \mathrm{A}\rangle }_{\mathsf{c}}(\varphi ;\langle \overline{\mathrm{A}}\rangle \psi )$, where $\overline{\mathrm{A}}=\mathsf{Agt}\backslash \mathrm{A}$.
• The coalitional operator $\left[\mathrm{A}\right]$ from $\mathsf{CL}$ is a special case of the above: $\left[\mathrm{A}\right]\varphi ⩴\langle \mathrm{A}\rangle \left(\varphi \right|\top )$.

6.4. Formal Semantics of $\mathsf{ConStR}$

Given coalitions $\mathrm{A},\mathrm{B}\subseteq \mathsf{Agt}$ and joint actions ${\sigma }_{\mathrm{A}}$ for $\mathrm{A}$ and ${\sigma }_{\mathrm{B}}$ for $\mathrm{B}$, we define the ordered join of ${\sigma }_{\mathrm{A}}$ and ${\sigma }_{\mathrm{B}}$ to be the joint action ${\sigma }_{\mathrm{A}}\uplus {\sigma }_{\mathrm{B}}$ for $\mathrm{A}\cup \mathrm{B}$ which equals ${\sigma }_{\mathrm{A}}$ when restricted to $\mathrm{A}$ and equals to ${\sigma }_{\mathrm{B}}$ when restricted to $\mathrm{B}\backslash \mathrm{A}$. Thus, in particular, ${\sigma }_{\mathrm{A}}\uplus {\sigma }_{\mathrm{B}}={\sigma }_{\mathrm{A}}$ for any $\mathrm{B}\subseteq \mathrm{A}\subseteq \mathsf{Agt}$ and ${\sigma }_{\mathrm{A}}\uplus {\sigma }_{\mathrm{B}}={\sigma }_{\mathrm{A}}\cup {\sigma }_{\mathrm{B}}$ when $\mathrm{A}$ and $\mathrm{B}$ are disjoint.

Now, let $\mathcal{M}=(\mathsf{Agt},\mathsf{S},\mathsf{Act},\mathfrak{g},\mathsf{Prop},\mathsf{L})$ be a concurrent game model.

The formal semantics of $\mathsf{ConStR}$ extend the semantics of $\mathsf{CL}$ to the new operators as follows (recall the definition of $\mathsf{Out}[s,\sigma ]$ from Section 2):

• $\mathcal{M},s\vDash {\left[\mathrm{A}\right]}_{\alpha }(\varphi ;\langle \mathrm{B}\rangle \psi )$ iff

        

  $\mathrm{B}$ has a joint action ${\sigma }_{\mathrm{B}}$ such that for every joint action ${\sigma }_{\mathrm{A}}$ of $\mathrm{A}$,

  if $\mathcal{M},u\vDash \varphi$ for every $u\in \mathsf{Out}[s,{\sigma }_{\mathrm{A}}]$, then $\mathcal{M},u\vDash \psi$ for every $u\in \mathsf{Out}[s,{\sigma }_{\mathrm{A}}\uplus {\sigma }_{\mathrm{B}}]$.

• $\mathcal{M},s\vDash {\left[\mathrm{A}\right]}_{\beta }(\varphi ;\langle \mathrm{B}\rangle \psi )$ iff

        

  for every joint action ${\sigma }_{\mathrm{A}}$ of $\mathrm{A}$ such that $\mathcal{M},u\vDash \varphi$ for every $u\in \mathsf{Out}[s,{\sigma }_{\mathrm{A}}]$,

  $\mathrm{B}$ has a joint action ${\sigma }_{\mathrm{B}}$ (generally, dependent on ${\sigma }_{\mathrm{A}}$) such that

  $\mathcal{M},u\vDash \psi$ for every $u\in \mathsf{Out}[s,{\sigma }_{\mathrm{A}}\uplus {\sigma }_{\mathrm{B}}]$.

• $\mathcal{M},s\vDash {\langle \mathrm{A}\rangle }_{\mathsf{c}}(\varphi ;\langle \mathrm{B}\rangle \psi )$ iff

        

  $\mathrm{A}$ has a joint action ${\sigma }_{\mathrm{A}}$, such that $\mathcal{M},u\vDash \varphi$ for every $u\in \mathsf{Out}[s,{\sigma }_{\mathrm{A}}]$ and

  $\mathrm{B}$ has a joint action ${\sigma }_{\mathrm{B}}$ such that $\mathcal{M},u\vDash \psi$ for every $u\in \mathsf{Out}[s,{\sigma }_{\mathrm{A}}\uplus {\sigma }_{\mathrm{B}}]$.

Remark 6. 

The semantics of each of the operators above can be restated to consider joint actions for $\mathrm{B}\backslash \mathrm{A}$ rather than the whole $\mathrm{B}$. For instance, it can be easily verified for the latter operator, that $\mathcal{M},s\vDash {\left[\mathrm{A}\right]}_{\alpha }(\varphi ;\langle \mathrm{B}\rangle \psi )$ iff $\mathrm{B}\backslash \mathrm{A}$ has a joint action ${\sigma }_{\mathrm{B}\backslash \mathrm{A}}$ such that for every joint action ${\sigma }_{\mathrm{A}}$ of $\mathrm{A}$, if $\mathcal{M},u\vDash \varphi$ for every $u\in \mathsf{Out}[s,{\sigma }_{\mathrm{A}}]$, then $\mathcal{M},u\vDash \psi$ for every $u\in \mathsf{Out}[s,{\sigma }_{\mathrm{A}}\uplus {\sigma }_{\mathrm{B}\backslash \mathrm{A}}]$.

As usual, formula $\varphi$ of $\mathsf{ConStR}$ is called valid in $\mathsf{ConStR}$, denoted ${\vDash }_{\mathsf{ConStR}}\varphi$, iff $\mathcal{M},u\vDash \varphi$ for every concurrent game model $\mathcal{M}$ and state $u\in \mathcal{M}$; $\varphi$ is satisfiable in $\mathsf{ConStR}$, iff $\mathcal{M},u\vDash \varphi$ for some concurrent game model $\mathcal{M}$ and state $u\in \mathcal{M}$.

Here are some easy observations on the relationships between the operators in $\mathsf{ConStR}$:

Proposition 7. 

The following validities and nonvalidities in $\mathsf{ConStR}$ hold:

1. 

${\vDash }_{\mathsf{ConStR}}{\left[\mathsf{a}\right]}_{\alpha }(p;\langle \mathsf{b}\rangle q)\to {\left[\mathsf{a}\right]}_{\beta }(p;\langle \mathsf{b}\rangle q)$.

2. 

${⊭}_{\mathsf{ConStR}}{\left[\mathsf{a}\right]}_{\beta }(p;\langle \mathsf{b}\rangle q)\to {\left[\mathsf{a}\right]}_{\alpha }(p;\langle \mathsf{b}\rangle q)$.

3. 

${⊭}_{\mathsf{ConStR}}{\langle \mathsf{a}\rangle }_{\mathsf{c}}(p;\langle \mathsf{b}\rangle q)\to {\left[\mathsf{a}\right]}_{\beta }(p;\langle \mathsf{b}\rangle q)$.

4. 

${⊭}_{\mathsf{ConStR}}{\langle \mathsf{a}\rangle }_{\mathsf{c}}(p;\langle \mathsf{b}\rangle q)\to {\left[\mathsf{a}\right]}_{\alpha }(p;\langle \mathsf{b}\rangle q)$.

5. 

${⊭}_{\mathsf{ConStR}}{\left[\mathsf{a}\right]}_{\alpha }(p;\langle \mathsf{b}\rangle q)\to {\langle \mathsf{a}\rangle }_{\mathsf{c}}(p;\langle \mathsf{b}\rangle q)$.

6. 

${⊭}_{\mathsf{ConStR}}{\left[\mathsf{a}\right]}_{\beta }(p;\langle \mathsf{b}\rangle q)\to {\langle \mathsf{a}\rangle }_{\mathsf{c}}(p;\langle \mathsf{b}\rangle q)$.

7. 

${\vDash }_{\mathsf{ConStR}}(\left[\mathrm{A}\right]p\wedge {\left[\mathsf{a}\right]}_{\beta }(p;\langle \mathsf{b}\rangle q))\to {\langle \mathsf{a}\rangle }_{\mathsf{c}}(p;\langle \mathsf{b}\rangle q)$.

Proof. 

• Immediately from the semantic definitions, as $\exists \forall$ implies $\forall \exists$.
• A counter-model is shown further, in Example 8.
• A counter-model is shown in Example 8.
• Follows from 1 and 3 above.
• This holds for the trivial reason that if in a given model the agent $\mathsf{a}$ has no action that ensures the truth of p in the given state, then the antecedent is vacuously true, whereas the consequent is false there.
• Likewise.
• An easy semantic exercise.

□

Example 8. 

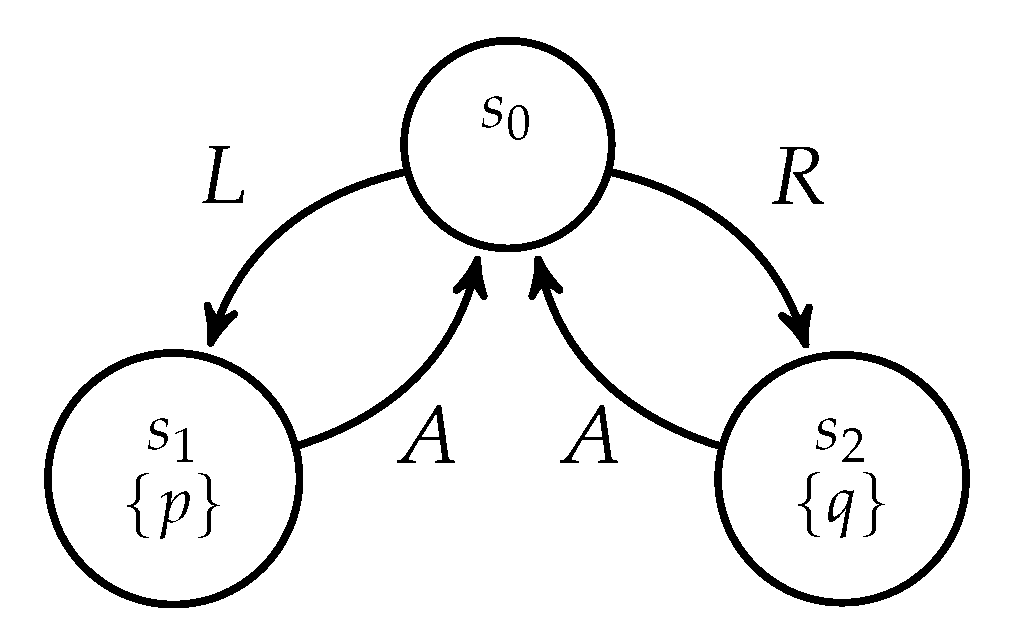
Consider the game model $\mathcal{M}$ in Figure 3, with two players, $\mathsf{a}$ and $\mathsf{b}$, where at state $s_0$ $\mathsf{a}$ has 3 actions, $a_1,a_2,and a_3$, and $\mathsf{b}$ has 2 actions, $b_{1}and b_2$.

Note that:

1. 

$\mathcal{M},s_0⊭\left[\mathsf{b}\right]q$, whereas $\mathcal{M},s_0\vDash {\langle \mathsf{a}\rangle }_{\mathsf{c}}(p;\langle \mathsf{b}\rangle q)$.

Thus, an agent may have only conditional ability to achieve its goal.

2. 

$\mathcal{M},s_0⊭{\left[\mathsf{a}\right]}_{\alpha }(p;\langle \mathsf{b}\rangle q)$. Indeed, neither $b_1$ nor $b_2$ ensures q against both choices $a_1$ and $a_2$ of $\mathsf{a}$. Thus, $\mathsf{b}$ does not have a uniform action to ensure q against any action of $\mathsf{a}$that ensures p.

3. 

$\mathcal{M},s_0\vDash {\left[\mathsf{a}\right]}_{\beta }(p;\langle \mathsf{b}\rangle q)$. Indeed, $\mathsf{a}$ has two actions at state $s_0$ to ensure p: $a_1$ and $a_2$. For each of them, $\mathsf{b}$ has an action to ensure q: choose $b_2$ if $\mathsf{a}$ chooses $a_1$, and choose $b_1$ if $\mathsf{a}$ chooses $a_2$.

Therefore, ${⊭}_{\mathsf{ConStR}}{\left[\mathsf{a}\right]}_{\beta }(p;\langle \mathsf{b}\rangle q)\to {\left[\mathsf{a}\right]}_{\alpha }(p;\langle \mathsf{b}\rangle q)$. Thus, the claim made by the proactive ability operator ${\mathsf{O}}_{\alpha }$ is stronger than the claim made by the reactive ability operator ${\mathsf{O}}_{\beta }$.

4. 

On the other hand, if the outcomes of $(a_2,b_1)$ and $(a_2,b_2)$ are swapped, then ${\left[\mathsf{a}\right]}_{\alpha }(p;\langle \mathsf{b}\rangle q)$ becomes true at $s_0$in the resulting model.

5. 

Furthermore, clearly, ${\left[\mathsf{a}\right]}_{\alpha }(p;\langle \mathsf{b}\rangle q)\to {\left[\mathsf{a}\right]}_{\beta }(p;\langle \mathsf{b}\rangle q)$ is a valid formula in $\mathsf{ConStR}$.

6. 

If the model is modified by making p true also at $s_6$, then in the resulting model ${\mathcal{M}}^{\prime }$ we have ${\mathcal{M}}^{\prime },s_0\vDash {\langle \mathsf{a}\rangle }_{\mathsf{c}}(p;\langle \mathsf{b}\rangle q)$ and ${\mathcal{M}}^{\prime },s_0⊭{\left[\mathsf{a}\right]}_{\beta }(p;\langle \mathsf{b}\rangle q)$.

Therefore, ${⊭}_{\mathsf{ConStR}}{\langle \mathsf{a}\rangle }_{\mathsf{c}}(p;\langle \mathsf{b}\rangle q)\to {\left[\mathsf{a}\right]}_{\beta }(p;\langle \mathsf{b}\rangle q)$.

7. 

Note also that$(\mathcal{M},s_0)$ does not satisfy the $\mathsf{ATL}$ formula $\left[\right[\mathsf{a}\left]\right](\mathrm{X}p\to \langle \langle \mathsf{b}\rangle \rangle \mathrm{X}q)$ (where $\left[\right[\mathrm{C}\left]\right]\varphi ⩴\neg \langle \langle \mathrm{C}\rangle \rangle \neg \varphi$); hence, it is not equivalent to ${\left[\mathsf{a}\right]}_{\beta }(p;\langle \mathsf{b}\rangle q)$.

For more examples and observations on the mutual nonexpressiveness of the operators in $\mathsf{ConStR}$, see [28]. Moreover, using the notions of bisimulation defined there for each of these operators, one can show that none of the three binary operators in $\mathsf{ConStR}$ can be defined in terms of the other two.

6.5. On the Axiomatization and Decidability for $\mathsf{ConStR}$

A system of axioms ${\mathsf{Ax}}_{\mathsf{ConStR}}$ for $\mathsf{ConStR}$ is presented in [28]. It involves lists of axioms for each of the operators ${\mathsf{O}}_c$, ${\mathsf{O}}_{\alpha }$, and ${\mathsf{O}}_{\beta }$, as well the following two interaction axiom schemes:

($\mathsf{ConStR}$ 1) 

${\left[\mathrm{A}\right]}_{\alpha }(\varphi ;\langle \mathrm{B}\rangle \psi )\to {\left[\mathrm{A}\right]}_{\beta }(\varphi ;\langle \mathrm{B}\rangle \psi )$.

($\mathsf{ConStR}$ 2) 

$(\left[\mathrm{A}\right]\varphi \wedge {\left[\mathrm{A}\right]}_{\beta }(\varphi ;\langle \mathrm{B}\rangle \psi )\to {\langle \mathrm{A}\rangle }_{\mathsf{c}}(\varphi ;\langle \mathrm{B}\rangle \psi )$.

These schemes are generated by uniform substitutions in the respective validities 1 and 7 in Proposition 7. Notably, the only axiom scheme identified there which distinguishes the operators ${\mathsf{O}}_{\alpha }$ and ${\mathsf{O}}_{\beta }$ is the following antimonotonicity (with respect to $\mathrm{A}$) scheme:

$${[\mathrm{A}\cup \mathrm{C}]}_{\alpha }(\varphi ;\langle \mathrm{B}\rangle \psi )\to {\left[\mathrm{A}\right]}_{\alpha }(\varphi ;\langle \mathrm{B}\rangle \psi ) \mathrm{for}\mathrm{any} \mathrm{C}\subseteq \mathsf{Agt},$$

which is valid for ${\mathsf{O}}_{\alpha }$ but not ${\mathsf{O}}_{\beta }$. For proof of this claim, and for the other axiom schemes and inference rules for each of the operators of $\mathsf{ConStR}$, see [28].

The only additional (to modus ponens) inference rules are the O-monotonicity rules, for O being each of ${\mathsf{O}}_{\alpha }$, ${\mathsf{O}}_{\beta }$, and ${\mathsf{O}}_c$. For instance, here is the ${\mathsf{O}}_c$ -monotonicity rule:

$$\frac{\varphi \to {\varphi }^{\prime },\psi \to {\psi }^{\prime }}{{\langle \mathrm{A}\rangle }_{\mathsf{c}}(\varphi ;\langle \mathrm{B}\rangle \psi )\to {\langle \mathrm{A}\rangle }_{\mathsf{c}}({\varphi }^{\prime };\langle \mathrm{B}\rangle {\psi }^{\prime })}$$

The completeness proof for ${\mathsf{Ax}}_{\mathsf{ConStR}}$ is currently still under development, so its completeness is currently still a conjecture, and so is even the completeness of each of the three main subsystems, one for each of the respective operators. For all that I currently know, these seem to be quite challenging problems.

Another conjecture is the decidability of satisfiability in $\mathsf{ConStR}$, even in each of its three main subsystems. Here, I only claim that it can be proved by a model-theoretic argument, based on the bounded tree-model property, meaning that every satisfiable formula of $\mathsf{SFCL}$ is satisfiable in a finite tree-like model of height and branching factor effectively bounded above in terms of the size of the formula. (Detailed proof of this claim is currently under construction, so the claim is, at present, still a working conjecture.)

7. The Socially Friendly Coalition Logic SFCL

The “socially friendly coalition logic” $\mathsf{SFCL}$ was introduced in [25] with the aim to capture and formalize the idea that, while socially responsible (or, “friendly”) rational agents and coalitions act in pursuit of their own goals, when deciding on their course of action they can take into account the goals of other agents in the system and make allowance for cooperation enabling their satisfaction, too, whenever it is possible, to reconcile their goals with those of the others. Formally, the idea is implemented by introducing in the formal language a “socially friendly coalitional operator”, presented here.

7.1. Socially Friendly Coalitional Operators

SF 

The socially friendly coalitional operator SF takes any positive number of formulae $\varphi ,{\psi }_1,\dots ,{\psi }_k$ as arguments and places them together into a single formula as follows:

$$\left[C\right](\varphi ;{\psi }_1,\dots ,{\psi }_k).$$

I will call the formula $\varphi$ above the primary goal of the formula (and of the coalition C) and the formulae ${\psi }_1,\dots ,{\psi }_k$—the secondary goals of the formula.

The intuitive meaning of the formula $\left[C\right](\varphi ;{\psi }_1,\dots ,{\psi }_k)$ is that

“C has a joint action ${\sigma }_C$ that guarantees satisfaction of ϕ and also enables the complementary coalition $\overline{C}$ to satisfy any one of the goals ${\psi }_1,\dots ,{\psi }_k$ by applying a respectively suitable joint action”.

The operator SF is a multiagent extension of the modal operator $\square ({\psi }_1,\dots ,{\psi }_k;\varphi )$ (note the different order of the arguments) in the instantial neighborhood logic (INL) introduced and studied in [45].

The special case of the “socially friendly coalitional operator” with a single secondary goal ${\left[\mathrm{A}\right]}_{{}_{}}(\varphi ;\psi )$ is equivalent to the operator $\langle \mathrm{A}\rangle \left(\varphi \right|\psi )$ defined in Section 6.

In particular, the strategic operator of $\mathsf{CL}$ is also definable here, as $\left[C\right]\varphi ⩴\left[C\right](\varphi ;\top )$.

SF1 

A refinement of SF: $\left[C;C_1,\dots ,C_n\right](\varphi ;{\varphi }_1,\dots ,{\varphi }_n)$, meaning:

“C has a collective action ${\sigma }_C$ that guarantees ϕ, and is such that, when fixed,

each $C_i$ has a collective action that guarantees ${\varphi }_i$”.

This definition presumes that if C intersects with $C_i$, then the agents in $C\cap C_i$ are already committed to ${\sigma }_C$. On the other hand, the collective actions claimed to exist for each $C_i$ need not be compatible, similar to in the intuitive semantics of $\left[C\right](\varphi ;{\psi }_1,\dots ,{\psi }_k)$, which is a special case of SF1, where $C_1=\dots =C_n=\mathsf{Agt}\backslash C$.

SF2 

$\left[\langle C_1\rangle {\varphi }_1;\dots ;\langle C_k\rangle {\varphi }_k\right]$ meaning: “$C_1$ has a collective action to guarantee ${\varphi }_1$, and given that action… $C_k$ has a collective action to guarantee ${\varphi }_k$”.

This is a sequential version of SF1 where the coalitions $C_1,...,C_k$ are arranged in decreasing priority order.

Hereafter, I will consider SF only.

7.2. Syntax and Semantics of the Logic $\mathsf{SFCL}$

The formulae of $\mathsf{SFCL}$ are defined by the following grammar:

$$\varphi ⩴p\mid \top \mid \neg \varphi \mid (\varphi \vee \varphi )\mid \left[C\right](\varphi ;\varphi ,\dots ,\varphi )(p\in \mathsf{Prop})$$

The standard definitions of the other propositional connectives apply.

In addition, I define $\left[C\right]\varphi ≔\left[C\right](\varphi ;\top )$. Given a finite list of formulae $\mathsf{\Psi }={\psi }_1,\dots ,{\psi }_k$, I will write $\left[C\right](\varphi ;\mathsf{\Psi })$.

The fragment of $\mathsf{SFCL}$ containing only formulae $\left[C\right](\varphi ;\psi )$ where $\psi$ is a single formula will be denoted by ${\mathsf{SFCL}}_{\mathsf{1}}$.

The formal semantics of $\mathsf{SFCL}$ is given in terms of truth of an $\mathsf{SFCL}$-formula at a state s of a concurrent game model $\mathcal{M}$ inductively, as in $\mathsf{CL}$, with the following main clause:

• $\mathcal{M},s\vDash \left[\mathrm{C}\right](\varphi ;\mathsf{\Psi })$ iff

      

  there exists a joint action ${\sigma }_C$ of $\mathrm{C}$ available at s,

      

  such that $\mathcal{M},u\vDash \varphi$ for each state u in its outcome set $O[s,{\sigma }_C]$,

      

  and for each $\psi \in \mathsf{\Psi }$ there is a state $v\in O[s,{\sigma }_C]$ such that $\mathcal{M},v\vDash \psi$.

7.3. Example 1: Negotiating the Family Budget

Example 9. 

This example is an adapted and extended version of one from [25]. Consider the family couple Ann and Bill and their son Charlie. Each of them has saved some money. Now, they are sitting in a family meeting and negotiating on how to spend their savings. Ann wishes for a complete kitchen renovation, Bill wants a new car, and Charlie dreams of a holiday trip to Disneyland.

Ann considers two options for a kitchen: a cheaper IKEA version, or a designer’s luxury version. Bill thinks of three options for a car: a cheap used black Ford, a more expensive new green Tesla, or an even more expensive, vintage pink Cadillac. As for Charlie, he would prefer the whole family to go for an expensive week-long family excursion to Disneyland in Paris, but could also settle for a cheaper 2-day car trip to Disneyland Park in California.

The possible actions of every family member or a group are to pay for any option of their wish that they can afford, and then leave the rest of their savings in the family money pool for the other(s) to use. Let us denote the respective goals by:

• $CK$ (cheap kitchen), $EK$ (expensive kitchen), $K=CK\vee EK$ (any kitchen);
• $CC$ (cheap car), $AC$ (average car), $EC$ (expensive car), $C=CC\vee AC\vee EC$ (any car);
• $CT$ (cheap trip), $ET$ (expensive trip), $T=CT\vee ET$ (any trip).

Calculations show that Ann’s choices and money produce the following strategic powers:

• Ann can afford to pay for an expensive kitchen and then let the others choose some car or some trip, formally: $\left[\mathsf{Ann}\right](EK;C,T)$.
• Alternatively, Ann can settle with a cheap kitchen, and then let the others choose between some car plus some trip, or an expensive car, or an expensive trip; formally: $\left[\mathsf{Ann}\right](CK;CC\wedge CT,EC,ET)$.
• However, if Ann opts for an expensive kitchen, then the family cannot afford an average car plus a trip; formally: $\neg \left[\mathsf{Ann}\right](EK;AC\wedge T)$.

Likewise, it turns out that Bill has the following strategic powers:

• $\left[\mathsf{Bill}\right](C;K,T)$;
• $\left[\mathsf{Bill}\right](CC;EK,ET)$.
• However, $\neg \left[\mathsf{Bill}\right](EC;AK\wedge T)$.

Charlie alone cannot afford to pay in full for any trip, but can only leave his savings in the family pool and try to negotiate some trip with his parents. Formally: $\neg \left[\mathsf{Charlie}\right](T;\top )$.

Lastly, here are some coalitional powers:

• $\left[\right\{\mathsf{Ann},\mathsf{Bill}\left\}\right](C\wedge EK;CT)$;
• $\left[\right\{\mathsf{Ann},\mathsf{Charlie}\left\}\right](CK\wedge ET;CC)$;
• $\left[\right\{\mathsf{Bill},\mathsf{Charlie}\left\}\right](AC\wedge CT;K)$.

Now, one may ask, for instance, whether it can be derived from all of the above whether the whole family can afford to buy the pink Cadillac and also drive with it to Disneyland in California, i.e., whether $\left[\right\{\mathsf{Ann},\mathsf{Bill},\mathsf{Charlie}\left\}\right](EC\wedge CT;\top )$; or whether Ann can obtain her dream designer’s kitchen and still enable Bill to buy a new Tesla or the family to go to Disneyland in Paris, i.e., $\left[\mathsf{Ann}\right](EK;AC,ET)$, etc.

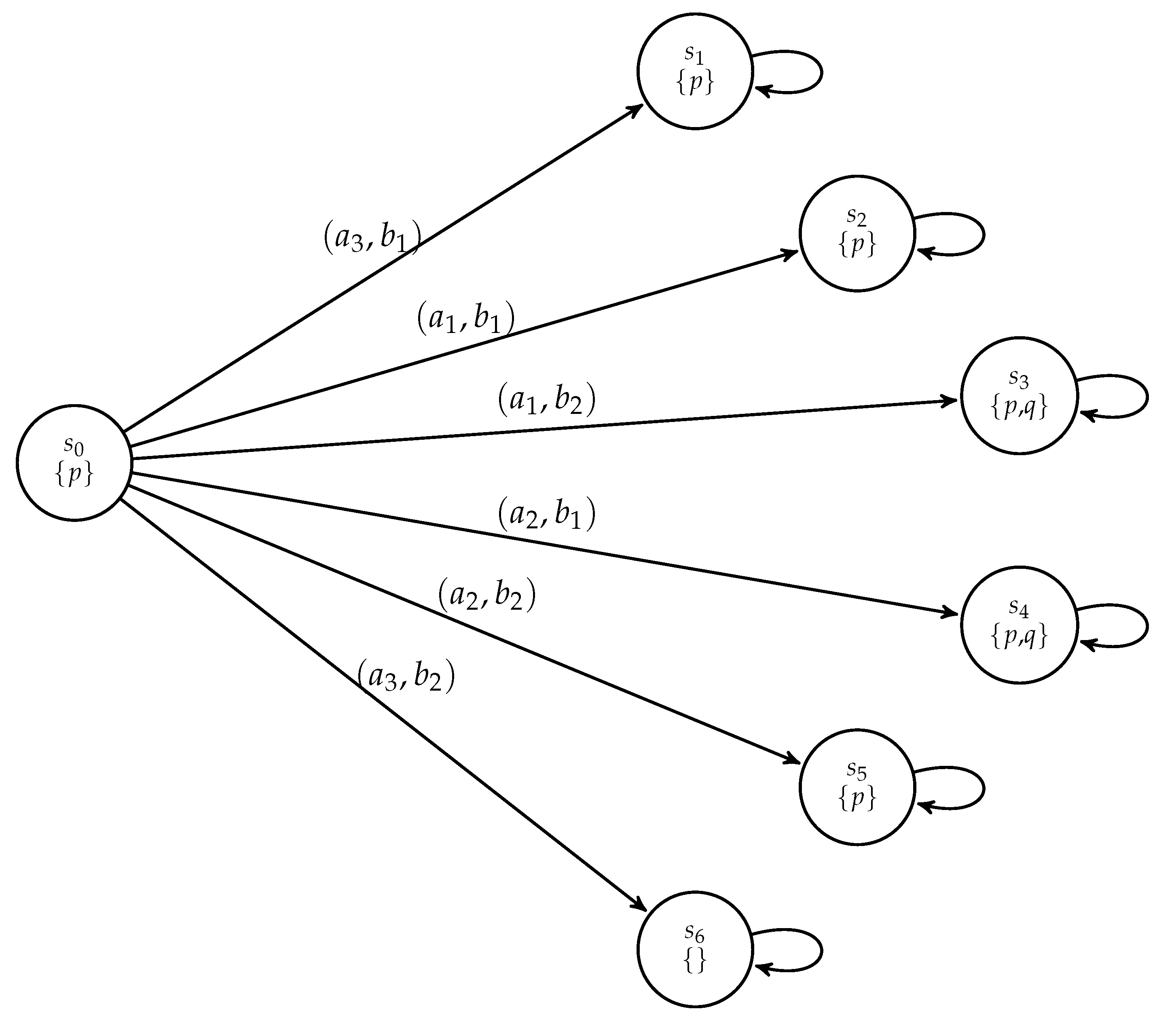
7.4. Example 2: Job Applicants

Consider four job candidates, Alice, Bob, Carl, and Diana, who have applied to three companies: Banana, Megasoft, and Fakebook, each advertising one position.

Suppose no candidate has strong preferences between these jobs.

All candidates have been interviewed by each of the companies.

Each company has selected and ranked in a priority order some of them, in which order they are offered the job and have to accept it or not. If an offer is not accepted, it goes to the next-ranked candidate, until the position is filled (if at all).

The rankings have been communicated to the candidates, as follows:

Banana:		Megasoft:		Fakebook:
1. Alice, 2. Bob, 3. Carl.		1. Diana, 2. Bob.		1. Alice, 2. Diana.

Each of the candidates must now make their strategic choice of which offer to accept, if and when given the option. Suppose the candidates can communicate with each other.

Here are some true statements formalized in $\mathsf{SFCL}$, where Alice, Bob, Carl, and Diana are labeled as $A,B,C,D$ and $e_X$ means “X obtains a job”:

• $\left[A\right](e_A;e_B\wedge e_D,e_C\wedge e_D,e_B\wedge e_C)$
  Indeed, Alice can take the offer from Fakebook and leave it to the others to decide on the other two positions. Note that Bob can then choose either offer and enable either Carl or Diana to obtain a job, but can also decline both offers and thus enable both of them to obtain a job.
• $\left[A\right](\top ;e_B\wedge e_C\wedge e_D)$
  Alternatively, Alice can act selflessly by declining both offers, and thus enable all others to obtain a job (by Bob choosing Fakebook).
• $\neg \left[C\right](e_C;\top )\wedge \left[C\right](\top ;e_C)$
  Carl cannot be sure to obtain a job, but all others can be sure of this.
• $\neg \left[D\right](e_D;e_B\wedge e_C)\wedge \left[D\right](e_D;e_B,e_C)$
  Diana cannot be sure to obtain a job and enable the others to see to it that both Bob and Carl obtain a job, but she can ensure that she obtains a job (by accepting the offer from Megasoft) and then the others ensure that either Bob or Carl obtains a job, too.
• $\left[\{A,D\}\right](e_A\wedge e_D;e_B,e_C)$
  Alice and Diana together can ensure that they both obtain a job and then either of the other two can obtain a job, too, up to their choice.
• $\left[\{A,D\}\right](e_A\wedge e_D\wedge \neg e_B\wedge \neg e_C)$
  Alice and Diana can also be mean and act together so that only they obtain jobs, by accepting the respective offers from Banana and Megasoft and leaving the Fakebook position unfilled.

7.5. Socially Friendly Coalition Logic SFCL: A System of Axioms

The system of axioms $A{x}_{\mathsf{SFCL}}$ for $\mathsf{SFCL}$, proposed in [25], combines $A{x}_{\mathsf{CL}}$ with a multiagent extension of the axiomatization of the instantial neighborhood logic (INL) [45], plus some additional axiom schemes. Here is just one of these additional schemes from $A{x}_{\mathsf{SFCL}}$, where $\mathsf{\Psi }$ is a finite list of $\mathsf{SFCL}$-formulae and $\mathsf{\Psi },\theta$ is the list obtained by appending $\theta$ to $\mathsf{\Psi }$:

(INL5) 

$\left[C\right](\varphi ;\mathsf{\Psi })\to \left[C\right](\varphi \wedge \neg \theta ;\mathsf{\Psi })\vee \left[C\right](\varphi ;\mathsf{\Psi },\theta )$

This is a valid scheme. Indeed, for any formula $\mathsf{\theta }$, the strategy for C that ensures $\varphi$ and enables each formula in the list $\mathsf{\Psi }$ either also ensures $\neg \theta$, in which case it can be added conjunctively to $\varphi$, or else enables $\theta$, in which case it can be added to the list $\mathsf{\Psi }$.

The only additional (to modus ponens) inference rule is $\left[C\right]$-monotonicity:

$$\frac{\varphi \to {\varphi }^{\prime },{\psi }_1\to {\psi }_1^{\prime },\dots ,{\psi }_k\to {\psi }_k^{\prime }}{\left[C\right](\varphi ;{\psi }_1,\dots ,{\psi }_k)\to \left[C\right]({\varphi }^{\prime };{\psi }_1^{\prime },\dots ,{\psi }_k^{\prime })}.$$

Note that the rule RE in the axiomatic system for INL in [45] is an admissible rule here, and that can be proved by a routine induction on the structure of $\phi$ in that rule. For the Boolean cases, that is due to the completeness of the purely propositional fragment (where MP suffices), and the case of $\phi =\left[C\right](\dots )$ is handled by using the $\left[C\right]$-monotonicity rule.

A completeness proof for $A{x}_{\mathsf{SFCL}}$ was presented in [25], but an error was subsequently found in it (on which an erratum has been posted). The correct proof of completeness is currently still under development, and therefore the completeness claim is currently only a working conjecture.

Another conjecture is the decidability of satisfiability in $\mathsf{SFCL}$. Here, I only claim that it can be proved by a model-theoretic argument, similar to the decidability of $\mathsf{ConStR}$, based on the bounded tree-model property, meaning that every satisfiable formula of $\mathsf{SFCL}$ is satisfiable in a finite tree-like model of height and branching factor effectively bounded above in terms of the size of the formula. A proof of this claim, which is, at present, formally still a working conjecture, will be presented in a subsequent work.

Further open problems and directions for further research are related to various natural generalizations of SF, including SF1 and SF2. To my knowledge, they have not been explored and no technical results are even conjectured for them yet, except for some special cases explored in the context of conditional strategic reasoning in Section 6.

8. The Logic of Local Coalitional Goal Assignments (LCGA)

The logic $\mathsf{LCGA}$ was introduced in [25] as the “group protecting coalition logic ($\mathsf{GPCL}$)”, with the aim to formalize the idea, complementary to that of $\mathsf{SFCL}$, that, while socially responsible rational agents and coalitions contribute with their individual and collective actions to the society of all agents, they wish to achieve that in a way that protects their individual and collective interests and goals. Formally, the idea is implemented by introducing in the formal language a “coalitional goal assignment operator” (called “group protecting coalitional operator” in [25]), presented here.

8.1. The Coalitional Goal Assignments Operator

The coalitional goal assignments operator takes a list of coalitions $C_1,\dots ,C_k$ and a list of formulae representing their goals ${\varphi }_1,\dots ,{\varphi }_k$ and produces a formula of the type:

$$\langle [C_1▹{\varphi }_1,\dots ,C_k▹{\varphi }_k]\rangle .$$

The intuitive meaning of the claim formalized by the formula above is that there is an action profile $\sigma$ of $\mathsf{Agt}$, such that for each i, the restriction of $\sigma$ to the coalition $C_i$ is a joint action ${\sigma }_i$ that guarantees the satisfaction of ${\varphi }_i$, even if some, or all, other agents deviate from the action profile $\sigma$. In particular, $\left[C\right]\varphi$ is equivalent to $\langle [C▹\varphi ]\rangle$.

Now, I will define a more general and succinct representation of that operator. First, a coalitional goal assignment is a mapping $\gamma :\mathcal{P}\left(\mathsf{Agt}\right)\to \mathsf{\Gamma }$, where $\mathsf{\Gamma }$ is a set of goal formulae (which may, but need not be, the full logical language under consideration). Thus, for every coalition C, $\gamma \left(C\right)$ expresses the goal of C.

Usually, most of the possible coalitions do not have coalitional goals and hence do not form. That can be formalized by assigning the “truth” ⊤ as a goal to each of them.

Now, the operator defined above naturally generalizes to one expressed simply as $\langle \left[\gamma \right]\rangle$, which is a concise representation of $\langle [C_1▹\gamma \left(C_1\right),\dots ,C_{2^n}▹\gamma \left(C_{2^n}\right)]\rangle$, where $C_1,\dots ,C_{2^n}$ is a (fixed) canonical enumeration of the set $\mathcal{P}\left(\mathsf{Agt}\right)$ of all subsets (coalitions) of $\mathsf{Agt}$.

8.2. Syntax and Semantics of the Logic $\mathsf{LCGA}$

The formulae of $\mathsf{LCGA}$ are given by the following grammar:

$$\varphi ⩴p\mid \top \mid \neg \varphi \mid (\varphi \vee \varphi )\mid \langle \left[\gamma \right]\rangle (p\in \mathsf{Prop})$$

where $p\in \mathsf{Prop}$ and $\gamma$ is a coalitional goal assignment. All other standard propositional connectives are defined as usual.

I will use the notation $\langle [C_1▹{\varphi }_1,\dots ,C_k▹{\varphi }_k]\rangle$ as an explicit record of $\langle \left[\gamma \right]\rangle$ where $\gamma$ is the (unique) coalitional goal assignment defined by $\gamma \left(C_1\right)={\varphi }_1,\dots ,\gamma \left(C_k\right)={\varphi }_k$, and $\gamma \left(C\right)=\top$ for every other $C\in \mathcal{P}\left(\mathsf{Agt}\right)$. Clearly, both notations for the coalitional goal assignment operator are expressively equivalent. Furthermore, while the alternative option seems generally more succinct, that gain vanishes if $\langle \left[\gamma \right]\rangle$ is defined as a partial goal assignment, assigning only the nontrivial goals.

The semantics of $\mathsf{LCGA}$ is given in terms of truth of an $\mathsf{LCGA}$-formula at a state s of a concurrent game model $\mathcal{M}$. The only new semantic clause is the one for $\langle [·]\rangle$:

$\mathcal{M},s\vDash \langle \left[\gamma \right]\rangle$ iff there exists an action profile $\sigma \in {\mathsf{\Sigma }}_{\mathsf{Agt}}$, available at s

and such that $\mathcal{M},u\vDash \gamma \left(C\right)$ for every $C\subseteq \mathsf{Agt}$ and every $u\in O[s,\sigma {|}_C]$.

The intuitive reading is spelled out in more detail as follows:

“There is a strategy profile of the grand coalition in which all agents participate with their individual strategies in such a way that, each agent or coalition guarantees the satisfaction of its own goal against any possible deviations of all other agents, thus protecting its individual (respectively, coalitional) interests.”

The clause for $\langle \left[\gamma \right]\rangle$ can also be given in terms of extensions, where ${\mathsf{\Sigma }}_{\mathsf{Agt}}={\prod }_{a\in \mathsf{Agt}}{\mathsf{\Sigma }}_a$:

$${\left[\left[\langle \left[\gamma \right]\rangle \right]\right]}_{\mathcal{M}}=\left\{s\in S\mid \exists \sigma \in {\mathsf{\Sigma }}_{\mathsf{Agt}}:O[s,{\sigma }_C]\subseteq {\left[\left[\gamma \left(C\right)\right]\right]}_{\mathcal{M}}\mathrm{for}\mathrm{all}C\subseteq \mathsf{Agt}\right\}$$

8.3. Some Observations and Examples of the Expressiveness of $\mathsf{LCGA}$

• The operator ${\langle \mathrm{A}\rangle }_{\mathsf{c}}(\varphi ;\langle \mathrm{B}\rangle \psi )$, introduced in Section 6, is definable in terms of $\langle [·]\rangle$: ${\langle \mathrm{A}\rangle }_{\mathsf{c}}(\varphi ;\langle \mathrm{B}\rangle \psi )=\langle [A▹\varphi ,\mathrm{A}\cup \mathrm{B}▹\psi ]\rangle$. Nevertheless, it has a different motivation and intuitive interpretation there.
• The fragment ${\mathsf{SFCL}}_{\mathsf{1}}$ of $\mathsf{SFCL}$ (subsuming $\mathsf{CL}$) embeds into $\mathsf{LCGA}$ by defining $\left[C\right](\varphi ;\psi )$ equivalently as $\langle [C▹\varphi ,\mathsf{Agt}▹\psi ]\rangle$.
  However, this does not generalize to ${\left[C\right]}_{{}_{}}(\varphi ;{\psi }_1,\dots ,{\psi }_k)$ for $k\ge 2$.
  Conversely, the operator $\langle [C_1▹{\varphi }_1,\dots ,C_n▹{\varphi }_n]\rangle$ cannot be expressed in terms of the $\mathsf{SFCL}$ operators ${\left[C\right]}_{{}_{}}(\varphi ;{\psi }_1,\dots ,{\psi }_k)$, either.
  These nonexpressiveness claims can be proved by using the respective notions of bisimulations introduced for each of these operators in [25].
• $\langle [C_1▹{\varphi }_1,C_1\cup C_2▹{\varphi }_2,\dots ,C_1\cup \dots \cup C_k▹{\varphi }_k]\rangle$ is equivalent to the sequential version SF2 of the operator SF, mentioned in Section 7.1 as ${\left[\langle C_1\rangle {\varphi }_1;\dots ;\langle C_k\rangle {\varphi }_k\right]}_{{}_{}}$, where the coalitions $C_1,...,C_k$ and their goals are arranged in decreasing priority order.
• On the other hand, $\langle [C_1▹{\varphi }_1,C_1▹{\varphi }_2,\dots ,C_k▹{\varphi }_k]\rangle$ is essentially expressible, up to a natural transformation of the models and semantics, in the group strategic STIT (cf. [13,14]), as $\diamond (\left[C_1\mathsf{stit}\right]\mathsf{X}{\varphi }_1\wedge ...\wedge \left[C_k\mathsf{stit}\right]\mathsf{X}{\varphi }_k)$. This observation (suggested by a reviewer) leads to a new computationally well-behaved fragment of the group strategic STIT, which is known to be not only undecidable, but even nonaxiomatizable; cf. [14].

The following example is from [25], where it was adapted from [1].

Example 10. 

[password protected data sharing] Consider a scenario involving two players, Alice (A) and Bob (B). Each of them owns a server storing some data, to which access is password-protected. The two players want to exchange passwords, but neither player is sure whether to trust the other. Thus, their common goal is to successfully cooperate and exchange passwords, but each player also has the private goal not to give away their password in case the other one turns out to be untrustworthy and refuses access to their data (a side remark: nowadays, such deals are arranged by smart contracts).

Let us write $H_A$ for “Alice has access to the data on Bob’s server” and $H_B$ for “Bob has access to the data on Alice’s server”. Thus, the best possible outcome for $\mathsf{Alice}$ is $H_A\wedge H_B$ and the worst possible outcome is $\neg H_A\wedge H_B$; symmetrically for Bob. Therefore, can the two players cooperate to exchange passwords in a way that satisfies the provisos above? Clearly, we cannot answer that question in any definitive way without having the precise details of the actual setup.

For example, suppose we define the game as follows: each player chooses a password, which may or may not be the correct one, and sends it to the other player, and they perform that simultaneously. Then, the game ends. In this game, the coalition $\{A,B\}$ can certainly force an outcome where each player has the other’s password, i.e., the $\mathsf{LCGA}$-formula

$$\langle \left[\{A,B\}(H_A\wedge H_B)\right]\rangle$$

 holds true. However, the strategy profile satisfying this goal assignment does not satisfy the players’ individual private goals, since each runs the risk of giving away their password without obtaining the other’s in return, if the other deviates. Therefore, the problem is more correctly described by the following stronger formula of $\mathsf{LCGA}$:

$$\langle [\{A,B\}▹H_A\wedge H_B,A▹H_B\to H_A,B▹H_A\to H_B]\rangle$$

Clearly, in the simple setup above, such a strategy profile does not exist, but suppose we add a second round to the game, in which each player can first verify the other’s password received in the first round (without being able to access the data yet) and then can either confirm their own password they have sent, if the other’s password is correct, or else change their password (thus making the shared one useless) if the other’s is not correct. Then, there is a strategy profile that satisfies the specification above, and thus enables the players to exchange passwords in a way that protects their individual interests, too.

8.4. Axiomatic System for $\mathsf{LCGA}$

The axiomatic system $A{x}_{\mathsf{LCGA}}$ for the logic $\mathsf{LCGA}$ presented here was first proposed in [25] (for the logic $\mathsf{GPCL}$) and then refined in the present form in [26]. Note, however, that the notation $\langle [C▹\varphi ]\rangle$ here corresponds to the notation used in [25], not the one in [26].

In addition, I will use further the following notation from [26]:

$\gamma [C▹\psi ]$, to denote the coalitional goal assignment obtained from $\gamma$ by reassigning the goal of the coalition C to be $\psi$, and

${\gamma |}_C$, to denote the coalitional goal assignment obtained from $\gamma$ by “restricting it to C”, meaning reassigning the trivial goal ⊤ to all coalitions not included in C.

Here are the axiom schemes of $A{x}_{\mathsf{LCGA}}$ with brief explanations:

• (Triv) $\langle \left[{\gamma }^{\top }\right]\rangle$, where ${\gamma }^{\top }$ is the trivial goal assignment, mapping each coalition to ⊤.
• (Safe) $\neg \langle [\mathsf{Agt}▹\perp ]\rangle$
  Even the grand coalition of all agents cannot ensure the falsum to become true.
• (Merge) $\langle [C_1▹{\theta }_1]\rangle \wedge \dots \wedge \langle [C_n▹{\theta }_n]\rangle \to \langle [C_1▹{\theta }_1,...,C_n▹{\theta }_n]\rangle$,
  where $C_1,\dots ,C_n$ are pairwise disjoint.
  This axiom scheme generalizes the superadditivity axiom of coalition logic (cf. Section 4.4.) It is valid, because, if the coalitions $C_1,\dots ,C_n$ are pairwise disjoint, then they can join together their collective strategies for their respective coalitional goals into one strategy profile that ensures satisfaction of all these collective goals.
• (GrandCoalition) $\langle \left[\gamma \right]\rangle \to (\langle [\gamma [\mathsf{Agt}▹(\phi \wedge \psi \left)\right]]\rangle \vee \langle [\gamma [\mathsf{Agt}▹(\phi \wedge \neg \psi \left)\right]]\rangle )$, where $\gamma \left(\mathsf{Agt}\right)=\phi$.
  This axiom scheme is valid because any strategy profile for $\mathsf{Agt}$ generates a unique successor state. If a state formula $\psi$ is true in it, then it can be added to the coalitional goal of $\mathsf{Agt}$, otherwise its negation can be added to it.
• (Case) $\langle \left[\gamma \right]\rangle \to (\langle \left[\gamma [C▹(\phi \wedge \psi )]\right]\rangle \vee \langle [\gamma {|}_C\left[(\mathsf{Agt}▹\neg \psi ]\right]\rangle )$, where $\gamma \left(C\right)=\phi$.
  This scheme says that for any coalition C, state formula $\psi$, and a strategy profile $\mathsf{\Sigma }$, either its projection ${\mathsf{\Sigma }}_C$ to C ensures the truth of $\psi$ in all successor states enabled by ${\mathsf{\Sigma }}_C$—in which case $\psi$ can be added to the goal of C enforced by $\mathsf{\Sigma }$—or, otherwise, $\neg \psi$ is true in some of these successor states, in which case it can be added to ${\gamma |}_C$ as the goal of the grand coalition $\mathsf{Agt}$ enforced by $\mathsf{\Sigma }$.
• (Con) $\langle \left[\gamma \right]\rangle \to \langle \left[\gamma \right[C▹(\phi \wedge \psi )\left]\right]\rangle$ where $\gamma \left(C\right)=\phi$ and $\gamma \left(C^{\prime }\right)=\psi$ for some $C^{\prime }\subseteq C$.
  Given any coalition C and subcoalition $C^{\prime }$, this scheme says that the goal of $C^{\prime }$ can be added for free to the goal of C. Indeed, if there is any strategy profile $\mathsf{\Sigma }$ that ensures that C and $C^{\prime }$ can force their respective goals, then $\mathsf{\Sigma }$ also ensures that C can force the conjunction of these goals.

The rules of inference are modus ponens (MP) and goal monotonicity (G-Mon):

$$\frac{\gamma \left(C\right)\to \psi }{\langle \left[\gamma \right]\rangle \to \langle \left[\gamma \right[C▹\psi \left]\right]\rangle }$$

The axiomatic system $A{x}_{\mathsf{LCGA}}$ was first proved sound and complete in [25] (for the logic $\mathsf{GPCL}$) and in the present form in [26]. Moreover, the satisfiability problem for $\mathsf{LCGA}$ is decidable, which follows from completeness results together with the finite model property, as shown in [25,26].

8.5. The Temporal Logic of Coalitional Goal Assignments $\mathsf{TLCGA}$

$\mathsf{LCGA}$ can only express local goals, referring to the immediate outcomes states. Usually, however, agents and coalitions have long-term goals, which need explicit temporal operators to be formalized. This was the motivation to introduce and study the temporal extension $\mathsf{TLCGA}$ of $\mathsf{LCGA}$ in [26]. It uses the standard temporal operators $\mathsf{X},\mathsf{U},\mathsf{G}$ to express temporalized goals, similarly to $\mathsf{ATL}$ (Section 5).

It is convenient to classify the formulae of $\mathsf{TLCGA}$ in two sorts, state formulae and path formulae, and to define their sets by mutual induction, as follows:

$\mathsf{StateFor}:\phi ⩴p\mid \top \mid \neg \phi \mid (\phi \vee \phi )\mid \langle \left[\gamma \right]\rangle$

$\mathsf{PathFor}:\theta ⩴\mathsf{X}\phi \mid (\phi \cup \phi )\mid \mathsf{G}\phi$

where $p\in \mathsf{Prop}$ and $\gamma :\mathcal{P}\left(\mathsf{Agt}\right)\to \mathsf{PathFor}$ is a coalitional goal assignment.

Thus, the path formulae are auxiliary, used to express temporalized goals. As before, I will use $\langle [C_1▹{\varphi }_1,\dots ,C_k▹{\varphi }_k]\rangle$ as an explicit notation for $\langle \left[\gamma \right]\rangle$ with support $\{C_1,\dots ,C_k\}$.

Note the change in the notation from $\mathsf{LCGA}$: the goals ${\varphi }_1,\dots ,{\varphi }_k$ from now on, refer to the current state, not to a successor. Thus, $\mathsf{LCGA}$ is embedded in $\mathsf{TLCGA}$ as its $\mathsf{X}$-fragment $\mathsf{XCGA}$, where the path formulae are only of the type $\mathsf{X}\phi$.

$\mathsf{TLCGA}$ also extends $\mathsf{ATL}$: $\langle \langle \mathrm{C}\rangle \rangle \theta \equiv \langle [C▹\theta ]\rangle$, for any $\theta \in \mathsf{PathFor}$.

8.6. An Aside: Equilibria and Co-Equilibria

The logic $\mathsf{TLCGA}$ can be used to express (see [26]) the fundamental game-theoretic concept of Nash equilibrium: a strategy profile ensuring that no player can deviate to improve the outcome with respect to his/her private goal. This concept is good for quantitative goals, but not for qualitative (win/lose) ones, because rational players whose goals are not satisfied (the “losers”) can still deviate in weak equilibria. Thus, the arguably more suitable for qualitative goals concept of co-equilibrium was proposed in [26], meaning a strategy profile ensuring that every player (and coalition) achieves their private goal, even if all other agents deviate. Existence of a co-equilibrium is expressed precisely by the $\mathsf{TLCGA}$ formula $\langle [{\mathsf{a}}_1▹{\varphi }_1,\dots ,{\mathsf{a}}_k▹{\varphi }_k]\rangle$.

8.7. An Example

The following example, illustrating the use of $\mathsf{TLCGA}$ to express natural statements, is adapted from [26].

Example 11. 

Three sheep and three wolves are standing on a river bank and all animals want to cross the river (say, because a pride of lions is approaching). There is just one boat, which takes up to two animals. There is no boatman, but the animals can sail the boat across the river. However, if on either side of the river, at any time the wolves outnumber the sheep, then they eat them up there. Of course, the sheep do not want that to happen. Therefore, do the animals have a “safe” strategy to cross the river without any being eaten?

Let us first look at a simple specification in $\mathsf{ATL}$ of the claim that such strategy exists:

$$\langle \langle \mathsf{Sheep}\cup \mathsf{Wolves}\rangle \rangle (\neg e\cup c)$$

where

• c is the atomic proposition “all animals have crossed the river”.
• e is the atomic proposition “some sheep are eaten”.

Thus, the formula above says that all animals have a strategy to eventually all cross the river and meanwhile no sheep are eaten. Is this what we want? Not quite, as the strategy may be such that the wolves can deviate from it at an opportune moment and eat some of the sheep. Thus, here is a better specification, in $\mathsf{TLCGA}$:

$$\langle [\mathsf{Sheep}\cup \mathsf{Wolves}▹\mathsf{F}c,\mathsf{Sheep}▹\mathsf{G}\neg e]\rangle ,$$

 saying “all animals have a collective goal to cross the river, but the coalition of sheep have their coalitional goal that no sheep is ever eaten”, and this is what we really want. Therefore, is there a solution—a strategy profile—satisfying this specification? Well, it depends on a subtle but crucial detail: if all animals act simultaneously, where each animal can either stay on the river bank or board the boat (but if more than two animals board the boat, the boat cannot sail), then it is not difficult to see that such strategy does not exist. However, if at every round the wolves act first, and then the sheep act, then such strategy exists, and I leave the fun to the reader to design such strategy. Note that the strategy of each sheep will now depend also on how the wolves have just acted, so any deviation of the wolves from the agreed-upon “safe” strategy can be counteracted by the strategies of the sheep, and this is the key point.

9. Basic Strategy Logic: A Unifying Formalism for Strategic Reasoning

The semantics of all strategic operators introduced here are defined in terms of quantification in the metalanguage over actions and strategies of the agents and coalitions involved. Thus, the natural idea arises to add explicit quantification over strategies in the object language and have all these operators definable there. That idea was realized in the family of strategy logics, the first (two-agents) version of which was introduced in [21], and later extended and further studied in [22,23,24]. The common feature of these strategy logics is that they formally treat strategies as primitive objects, similar to elements of standard structures for first-order logic. I will refer to these generically as standard strategy logic, denoted $\mathsf{SSL}$.

Since quantification over strategies is essentially a second-order quantification over functions, the language of $\mathsf{SSL}$ is very expressive and it should not be surprising that the standard systems of $\mathsf{SSL}$ are not recursively axiomatizable in general. Still, even some restricted fragments of $\mathsf{SSL}$ are quite expressive and enable specifying important properties of non-zero-sum games in a simple and natural way. In particular, the “one-alternation” fragment of $\mathsf{SSL}$ already subsumes, by expressiveness, the logic ${\mathsf{ATL}}^{*}$ and is strong enough to express, inter alia, the existence of Nash equilibria and secure equilibria (cf. [21]).

I will define and use here a simple generic version of a strategy logic, which I call basic strategy logic, further denoted $\mathsf{BSL}$. It builds on some temporalized language for expressing goals, such as $\mathsf{LTL}$ (cf., e.g., [36] (Chapter 6)) that defines a set of goal formulae $\mathsf{\Gamma }$ which are evaluated on plays in concurrent game models. $\mathsf{BSL}$ extends $\mathsf{\Gamma }$ with standard Boolean connectives, with variables associated with agents and ranging over strategies for them, by means of strategy assignments, and with quantification over such variables within the formulae. More precisely, with each agent $\mathsf{a}$, the language of $\mathsf{BSL}$ associates a strategy variable for $\mathsf{a}$, denoted by ${\mathsf{x}}_{\mathsf{a}}$. Let $\mathsf{StrVar}$ be the set of strategy variables for all agents. Then, for every nonempty coalition of agents $C=\{{\mathsf{c}}_1,...,{\mathsf{c}}_m\}$, I will use ${\mathsf{x}}_C$ to denote the tuple of variables $({\mathsf{x}}_{{\mathsf{c}}_1},...,{\mathsf{x}}_{{\mathsf{c}}_m})$. Furthermore, I will write $\forall {\mathsf{x}}_{\mathrm{C}}$ as a shorthand for the string $\forall {\mathsf{x}}_{{\mathsf{c}}_1}...\forall {\mathsf{x}}_{{\mathsf{c}}_m}$, and likewise for $\exists {\mathsf{x}}_{\mathrm{C}}$.

Formally, the language of $\mathsf{BSL}$ involves two sets of formulae: a set of goal formulae $\mathsf{\Gamma }$ and a set of state formulae $\mathsf{StateFor}$, defined as follows:

$$\mathsf{StateFor}:\phi ⩴p\mid \top \mid \psi \mid \neg \phi \mid (\phi \vee \phi )\mid \exists {\mathsf{x}}_{\mathsf{a}}\phi ,$$

where $p\in \mathsf{Prop}$, $\psi \in \mathsf{\Gamma }$, and ${\mathsf{x}}_{\mathsf{a}}\in \mathsf{StrVar}$. All other standard propositional connectives and constants, including ⊥, ∧, →, ↔, are defined as usual. In addition, $\forall {\mathsf{x}}_{\mathsf{a}}⩴\neg \exists {\mathsf{x}}_{\mathsf{a}}\neg$.

The semantics of $\mathsf{BSL}$ is given in concurrent game models, using, additionally, strategy assignments, which are functions defined on $\mathsf{StrVar}$ and assigning to every strategy variable ${\mathsf{x}}_{\mathsf{a}}$ a strategy of the respectively specified in the semantics type (e.g., memory-based or positional) for the agent $\mathsf{a}$. Given such strategy assignment $\mathbf{v}$ and a strategy ${\sigma }_{\mathsf{a}}$ for agent $\mathsf{a}$, I will denote by $\mathbf{v}[{\mathsf{x}}_{\mathsf{a}}⩴{\sigma }_{\mathsf{a}}]$ the modified strategy assignment which reassigns the value of ${\mathsf{x}}_{\mathsf{a}}$ to be ${\sigma }_{\mathsf{a}}$. Likewise, $\mathbf{v}[{\mathsf{x}}_{\mathrm{C}}⩴{\sigma }_{\mathrm{C}}]$ is defined for any coalition $\mathrm{C}$.

Given a state s in a CGM $\mathcal{M}$, every strategy assignment $\mathbf{v}$ in $\mathcal{M}$ defines the strategy profile $\mathsf{\Sigma }\left(\mathbf{v}\right)$, where $\mathsf{\Sigma }{\left(\mathbf{v}\right)}_{\mathsf{a}}=\mathbf{v}\left({\mathsf{x}}_{\mathsf{a}}\right)$, and therefore determines the unique play in $\mathcal{M}$, generated by $\mathsf{\Sigma }\left(\mathbf{v}\right)$, which will be denoted by $\mathsf{play}(s,\mathbf{v})$. Then, the truth of any goal formula can be evaluated on that play.

The semantics of $\mathsf{BSL}$ can now be defined in terms of truth of a formula at a state s in a given CGM $\mathcal{M}$, for a given strategy assignment $\mathbf{v}$, through the clauses:

• $\mathcal{M},s,\mathbf{v}{\vDash }_{}\psi$, for $\psi \in \mathsf{\Gamma }$ iff $\mathcal{M},\mathsf{play}(s,\mathbf{v}){\vDash }_{}\psi$
  (assuming that truth of the goal formulae in $\mathsf{\Gamma }$ on plays has already been defined).
• $\mathcal{M},s,\mathbf{v}{\vDash }_{}\exists {\mathsf{x}}_{\mathsf{a}}\phi$ iff $\mathcal{M},s,\mathbf{v}[{\mathsf{x}}_{\mathsf{a}}⩴{\sigma }_{\mathsf{a}}]{\vDash }_{}\phi$ for some strategy ${\sigma }_{\mathsf{a}}$ for $\mathsf{a}$.

The latter clause extends in a straightforward way to $\exists {\mathsf{x}}_{\mathrm{C}}\phi$ and $\forall {\mathsf{x}}_{\mathrm{C}}\phi$, for any coalition $\mathrm{C}$.

Note that, similar to the classical first-order logic, every bound occurrence of a variable ${\mathsf{x}}_{\mathsf{a}}$ is bound by the innermost occurrence of a quantifier binding ${\mathsf{x}}_{\mathsf{a}}$, so in quantification patterns such as $Q_1{\mathsf{x}}_{\mathsf{a}}...Q_k{\mathsf{x}}_{\mathsf{a}}...\varphi$, where each $Q_i$ is ∃ or ∀, all occurrence of $Q_i{\mathsf{x}}_{\mathsf{a}}$ containing the innermost one in its scope are vacuous.

Now, one can uniformly translate the semantic conditions of the various strategic operators introduced here into formulae in the language of $\mathsf{BSL}$, by using a uniform compositional translation $\tau$, as follows:

• $\mathsf{CL}$/${\mathsf{ATL}}^{*}$
  $$\tau \left(\left[\mathrm{C}\right]\phi \right)⩴\exists {\mathsf{x}}_{\mathrm{C}}\forall {\mathsf{x}}_{\overline{\mathrm{C}}}\tau \left(\phi \right),$$

           where $\overline{\mathrm{C}}=\mathsf{Agt}\backslash \mathrm{C}$; likewise, for $\langle \langle \mathrm{C}\rangle \rangle \phi$.
• $\mathsf{ConStR}$ (${\mathsf{O}}_{\alpha }$) 
  $$\tau \left({\left[\mathrm{A}\right]}_{\alpha }(\varphi ;\langle \mathrm{B}\rangle \psi )\right)⩴\exists {\mathsf{x}}_{\mathrm{B}\backslash \mathrm{A}}\forall {\mathsf{x}}_{\mathrm{A}}(\forall {\mathsf{x}}_{\overline{\mathrm{A}}}\tau \left(\varphi \right)\to \forall {\mathsf{x}}_{\overline{\mathrm{A}\cup \mathrm{B}}}\tau \left(\psi \right)).$$

      

  Note that the joint strategy for $\mathrm{B}\backslash \mathrm{A}$ assigned to ${\mathsf{x}}_{\mathrm{B}\backslash \mathrm{A}}$ is supposed to ensure, together with the joint strategy for $\mathrm{A}$ assigned to ${\mathsf{x}}_{\mathrm{A}}$, the truth of the (translation of the) goal formula $\psi$ whenever the joint strategy for $\mathrm{A}$ assigned to ${\mathsf{x}}_{\mathrm{A}}$ ensures the truth of the (translation of the) goal formula $\varphi$ against any joint strategy of the agents in $\overline{\mathrm{A}}$, including those in $\mathrm{B}\backslash \mathrm{A}$.

• $\mathsf{ConStR}$ (${\mathsf{O}}_{\beta }$) 
  $$\tau ({\left[\mathrm{A}\right]}_{\beta }(\varphi ;\langle \mathrm{B}\rangle \psi ))⩴\forall {\mathsf{x}}_{\mathrm{A}}(\forall {\mathsf{x}}_{\overline{\mathrm{A}}}\tau \left(\varphi \right)\to \exists {\mathsf{x}}_{\mathrm{B}\backslash \mathrm{A}}\forall {\mathsf{x}}_{\overline{\mathrm{A}\cup \mathrm{B}}}\tau \left(\psi \right)).$$

      

  Note the difference with the previous translation, reflecting the difference between the semantics of (${\mathsf{O}}_{\alpha }$) and (${\mathsf{O}}_{\beta }$): the joint strategy for $\mathrm{B}$ now depends on the joint strategy for $\mathrm{A}$, and the strategies of the agents in $\mathrm{B}\cap \mathrm{A}$ may not differ from those already fixed in the latter.

• $\mathsf{ConStR}$ (${\mathsf{O}}_c$) 
  $$\tau \left({\langle \mathrm{A}\rangle }_{\mathsf{c}}(\varphi ;\langle \mathrm{B}\rangle \varphi )\right)⩴\exists {\mathsf{x}}_{\mathrm{A}}(\forall {\mathsf{x}}_{\overline{\mathrm{A}}}\tau \left(\varphi \right)\wedge \exists {\mathsf{x}}_{\mathrm{B}\backslash \mathrm{A}}\forall {\mathsf{x}}_{\overline{\mathrm{A}\cup \mathrm{B}}}\tau \left(\psi \right)).$$

      

  This formula captures the semantics of ${\mathsf{O}}_c$ in a straightforward way.

• $\mathsf{SFCL}$ (SF) 
  $$\tau \left(\left[C\right](\varphi ;{\psi }_1,\dots ,{\psi }_k)\right)⩴\exists {\mathsf{x}}_{\mathrm{C}}\left(\forall {\mathsf{x}}_{\overline{\mathrm{C}}}\tau \left(\varphi \right)\wedge \underset{m=1}{\overset{k}{\bigwedge }}\exists {\mathsf{x}}_{\overline{\mathrm{C}}}\tau \left({\psi }_m\right)\right).$$

      

  Likewise, the formula above formalizes precisely the semantic definition of SF.

• $\mathsf{SFCL}$ (SF1) 
  $$\tau \left(\left[C;C_1,\dots ,C_k\right](\varphi ;{\varphi }_1,\dots ,{\varphi }_k)\right)⩴\exists {\mathsf{x}}_{\mathrm{C}}\left(\forall {\mathsf{x}}_{\overline{\mathrm{C}}}\tau \left(\varphi \right)\wedge \underset{m=1}{\overset{k}{\bigwedge }}\exists {\mathsf{x}}_{{\mathrm{C}}_m\backslash \mathrm{C}}\forall {\mathsf{x}}_{\overline{\mathrm{C}\cup {\mathrm{C}}_m}}\tau \left({\varphi }_m\right)\right).$$

      

  This formula says that C has a collective strategy (in particular, a collective action) assigned to ${\mathsf{x}}_{\mathrm{C}}$ that guarantees (the translation of) $\varphi$, and is such that, when fixed,

  each $C_m$ has a collective action (already fixed for the agents in ${\mathrm{C}}_m\cap \mathrm{C}$) that guarantees (the translation of) ${\varphi }_m$ against any behavior of the noncommitted agents, i.e., those in $\overline{\mathrm{C}\cup {\mathrm{C}}_m}$. This is precisely the semantics of SF1, defined in Section 7.1.

• $\mathsf{SFCL}$ (SF2) $\tau \left(\left[\langle C_1\rangle {\varphi }_1;\dots ;\langle C_k\rangle {\varphi }_k\right]\right)⩴$

      

  (for simplicity, assuming that $C_1,...,C_k$ are pairwise disjoint)

  $$\exists {\mathsf{x}}_{C_1}\left(\forall {\mathsf{x}}_{\overline{C_1}}\tau \left({\varphi }_1\right)\wedge \exists {\mathsf{x}}_{C_2\backslash C_1}\left(\forall {\mathsf{x}}_{\overline{C_1\cup C_2}}\tau \left({\varphi }_2\right)\wedge \dots \wedge \exists {\mathsf{x}}_{C_k\backslash (C_1\cup ...\cup C_{k-1})}\forall {\mathsf{x}}_{\overline{C_1\cup ...\cup C_k}}\tau \left({\varphi }_k\right)\right)\dots \right).$$

  This formula likewise expresses the semantics of the sequential version SF2 of SF1, defined in Section 7.1. To achieve this, every time it claims existence of a joint strategy of $C_i$ it assumes that the strategies of all agents in the already previously mentioned coalitions are already fixed, and that joint strategy must succeed against any behavior of the not-yet-committed agents only.

• $\mathsf{LCGA}$
  $$\tau \left(\langle \left[\gamma \right]\rangle \right)⩴\exists {\mathsf{x}}_{\mathsf{Agt}}\underset{\mathrm{C}\subseteq \mathsf{Agt}}{\bigwedge }\forall {\mathsf{x}}_{\overline{\mathrm{C}}}\tau \left(\gamma \left(\mathrm{C}\right)\right).$$

      

  Again, this formula captures the formal semantics of $\langle \left[\gamma \right]\rangle$ in a straightforward way.

Thus, the logic $\mathsf{BSL}$ is more expressive than any of the other logics introduced here. Still, it is not as expressive as the versions of $\mathsf{SSL}$ introduced in [23,24], which decouple the strategy variables and quantification over them from the agents to which they are assigned, and thus enable assigning the same strategy to different agents, which (in my view, is unnatural and) $\mathsf{BSL}$ cannot do. Still, the second-order quantification over strategies is fully enabled in $\mathsf{BSL}$, so it is to be expected that $\mathsf{BSL}$ is not recursively axiomatizable in general. However, in the natural special case where only finite models over a fixed finite set of agents and with positional strategies are considered, there are clearly only finite such strategies in the model, so model checking of $\mathsf{BSL}$ in such models is decidable, whereas satisfiability is recursively enumerable. The complexity of model checking, as well as the questions of axiomatizability and decidability, of the validities of $\mathsf{BSL}$ in semantics restricted to such models are left to future work.

10. Concluding Remarks: Outlook and Perspectives

Logic-based strategic reasoning in socially interactive context is still in its relatively early stage of development, and the logical systems presented in this paper are just a representative sample of such special-purpose driven developments. While these systems were introduced with different motivations, they share the common purpose of formalizing natural and important patterns of strategic interaction between rational agents. Furthermore, as seen in the previous section, these can all be treated as fragments of the basic strategy logic $\mathsf{BSL}$, so the natural question arises: why, instead of the many bespoke alternatives presented here, is $\mathsf{BSL}$ not adopted as a uniform logical language for formalizing strategic reasoning? Of course, that can be achieved, and the study of some fragments of strategy logic have shown that to be a viable approach. However, as I indicated earlier, there are computational reasons in favor of staying within the purely modal framework of the logics introduced here, where actions and strategies are not explicitly referred to and quantified over in the language, but are only present in the semantics. There are many aspects of strategic reasoning, and a logical language that can adequately capture them all would be too heavy to use, so if one only wants to reason about some such specific aspects, then one can naturally look for a minimal language that suffices for that purpose. The standoff between the two approaches—propositional modal logics vs. quantified strategy logics—is quite analogous to the standoff between plain modal logic and first-order logic, and the pros and cons for one over the other approach in both cases are very similar. Still, it would be interesting and useful to compare in deeper detail the expressiveness and the tradeoff between it and the computational complexity of these two approaches in the case of logics for strategic reasoning, to a degree closer to the very-well-explored parallels between modal logic and first-order logic (cf. relevant chapters in [46] for ample details and further references.)

Some major open problems and directions of further exploration of the logic-based strategic reasoning in socially interactive context include:

• Adding agents’ knowledge in the semantics, and explicitly in the language, by assuming that the agents reason and act under imperfect information.
• Taking into account the normative aspects and constraints of the socially interactive context, including obligations, permission, and prohibitions, which socially responsible rational agents must respect in their strategic behavior.
• Analysis of the expressiveness and computational complexity of the basic strategy logic $\mathsf{BSL}$ which should eventually determine whether and to what extent $\mathsf{BSL}$ may be regarded as a viable alternative to the propositional modal approach behind the logical systems for strategic reasoning presented here.
• In particular, an interesting currently open question is whether there is a finite set of modal strategic operators with semantics that can be translated to $\mathsf{BSL}$ which provide expressive completeness, if not for the full language of $\mathsf{BSL}$, then at least for natural and reasonably expressive fragments of it.
• Completeness results for some of the systems of axioms mentioned here, including the three main fragments of $\mathsf{ConStR}$, the entire $\mathsf{ConStR}$, and $\mathsf{SFCL}$. Ultimately, a complete axiomatic system for $\mathsf{BSL}$, if possible, or for substantially rich fragments of it.
• Finite tree-model property and decidability results for the logical systems presented here, as well as other fragments of $\mathsf{BSL}$. In particular, it would be tableaux-based deductive systems and decision methods for the logics studied here, by adapting such systems developed in, e.g., [47,48].

From a more general perspective, this work can be regarded as a step towards developing a unifying and optimally rich, yet computationally feasible, technical framework for logic-based strategic reasoning of rational agents in a socially interactive context.