Concepts of Interpolation in Stratified Institutions
Abstract
1. Introduction
1.1. Stratified Institutions
1.2. Institution Theoretic Interpolation
1.3. Our Contributions
2. Preliminaries
- category theory;
- institution theory; and
- stratified institution theory.
2.1. Categories
2.2. Institutions
- a category whose objects are called signatures,
- a sentence functor defining for each signature a set whose elements are called sentences over that signature and defining for each signature morphism a sentence translation function,
- a model functor defining for each signature the category of Σ-models and -model homomorphisms, and for each signature morphism the reduct= functor ,
- for every signature , a binary Σ-satisfaction relation ,

| if for each then | union |
| if then | monotonicity |
| if and then | transitivity |
| if then | translation. |
2.3. Stratified Institutions
- category of signatures,
- a sentence functor ;
- a model functor ;
- a “stratification” lax natural transformation , where is a functor mapping each signature morphism to the identity functor on ; and
- a satisfaction relation between models and sentences which is parameterized by model states, where such that the following satisfaction conditionholds for any signature morphism , , , .
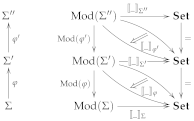

- –
- for each signature , denotes the set of all the mappings such that ; and
- –
- for each signature morphism

- In modal propositional logic () the category of the signatures is , is the set of the usual modal sentences formed with the atomic propositions from P, and the P-models are the Kripke structures where consists of a set of “possible worlds” and an accessibility relation , and . The stratification is given by .
- In first order modal logic () the signatures are first-order logic () signatures consisting of sets of operation and relation symbols structured by their arities. The sentences extend the usual construction of sentences with the modal connectives □ and ⋄. The models for a signature are Kripke structures where W is like in but subject to the constraint that the carrier sets and the interpretations of the constants are shared across the possible worlds. The stratification is like in .
- Hybrid logics refine modal logics by adding explicit syntax for the possible worlds such as nominals and @. Stratified institutions of hybrid logics upgrade the syntactic and the semantic components of the stratified institutions of modal logics accordingly. For instance, in the stratified institution of hybrid propositional logic () the signatures are pairs of sets , the -models are Kripke structures like in , but where W adds interpretations of the nominals, i.e., , and at the level of the syntax, for each we have a new sentence , a new unary connective , and existential quantifications over nominals variables. Then , etc.
- Multi-modal logics exhibit several modalities instead of only the traditional ⋄ and □ and, moreover, these may have various arities. If one considers the sets of modalities to be variable then they have to be considered as part of the signatures. Each of the stratified institutions discussed in the previous examples admit an upgrade to the multi-modal case.
- In a series of works on modalization of institutions [38,39,40] modal logic and Kripke semantics are developed by abstracting away details that do not belong to modality, such as sorts, functions, predicates, etc. This is achieved by extensions of abstract institutions (in the standard situations meant in principle to encapsulate the atomic part of the logics) with the essential ingredients of modal logic and Kripke semantics. The result of this process, when instantiated to various concrete logics (or to their atomic parts only) generate a uniformly wide range of hierarchical combinations between various flavours of modal logic and various other logics. Concrete examples discussed in [38,39,40] include various modal logics over non-conventional structures of relevance in computing science, such as partial algebra, preordered algebra, etc. Various constraints on the respective Kripke models, many of them having to do with the underlying non-modal structures, have also been considered. All of these arise as examples of stratified institutions like the examples presented above in the paper. An interesting class of examples that has emerged quite smoothly out of the general works on hybridization (i.e., modalization including also hybrid logic features) of institutions is that of multi-layered hybrid logics that provide a logical base for specifying hierarchical transition systems (see [41]).
- Open first order logic (). This is a instance of , the “internal stratification” abstract example developed in [5]. An signature is a pair consisting of signature and a finite block of variables. To any signature it corresponds a signature that adjoins X to as new constants. Then, , , , i.e the set of the “valuations” of X to M and for each -model M, each , and each -sentence we define where is the expansion of M to such that (i.e., the new constants of X are interpreted in according to the “valuation” w).
- Various kinds of automata theories can be presented as stratified institutions. For instance, the deterministic automata (for regular languages) have the set of the input symbols as signatures, the automata A are the models, and the words are the sentences. Then, is the set of the states of A and if and only if is recognized by A from the state s.
- In [10], there is a development of a general representation theorem of -institutions as stratified institutions. The theory of -institutions [11] is an extension of ordinary institution theory that accommodates the partiality of the signature morphisms and its syntactic and semantic effects, motivated by applications to conceptual blending and software evolution. The representation theorem is based, for each -model M, on setting to the set its -reducts. This is possible because in -institutions, unlike in ordinary institution theory, a model may have more than one reduct with respect to a fixed signature morphism, this being the semantic effect of the (implicit) partiality of the signature morphisms.
2.4. Flattening Stratified Institutions to Ordinary Institutions
- –
- the objects of are the pairs such that and ;
- –
- the -homomorphisms are the pairs such that and ;
- –
- for any signature morphism and any -model
- –
- for each -model M, each , and each
2.5. Nominals in Stratified Institutions

- a -sentence is an i-sentence when
- for any -sentence , a -sentence is the satisfaction of ρ at i whenfor each -model M and for each .
2.6. Quantifications in Stratified Institutions
if and only if for each -expansion of M.
2.7. Concepts of Model Amalgamation in Stratified Institutions
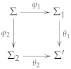
- is a model amalgamation square when for each -model , such that there exists an unique -model such that , , and
- is a stratified model amalgamation square when for each -model and each , , such that and there exists an unique -model and a unique such that and , .
3. Two Concepts of Interpolation
3.1. Two Semantic Consequence Relations
- the local semantic consequence relation is the semantic consequence relation of the institution , and
- the global semantic consequence relation is the semantic consequence relation of the institution .
- if and only if for each Σ-model M and each ,
- if and only if for each Σ-model M,
3.2. Local Versus Global Interpolation in Stratified Institutions

- With ordinary interpolation, the diagram (7) is restricted to an intersection-union square consisting of signature inclusions, i.e., and .
- Concrete interpolation considers single sentences rather than sets of sentences. In the presence of logical conjunctions, there is no difference between these two approaches. However, there are important logics that lack conjunctions, such as equational and Horn logics, and many more. In these logics, interpolation is traditionally considered as failed. But works such as [29,48,49] show that this is a misunderstanding due to the rather faulty import of the single-sentence formulation of interpolation from some very prominent logics (such as classical propositional or first order logic) to other logical systems.
4. When Local Interpolation Causes Global Interpolation
4.1. Signature Extensions with Nominals
- 1.
- is the extension of with one new constant i, and,
- 2.
- for each Σ-model M and each there exists a ι-expansion of M such that
- 3.
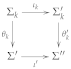
- For each signature morphism and each signature extension with one nominal there exists a signature extension with one nominal i and signature morphism such thatis a stratified model amalgamation square.
- is the set inclusion .
- Let be any -model. For any we define the -expansion of by .
- Let , . Then we consider , , and that just extends by letting . Note that in this case the commutative square Equation (8) yields a pushout square in . Since is semi-exact (cf. [9]) this is a model amalgamation square. Furthermore, since is strictly stratified this is also a stratified model amalgamation square.
4.2. Interpolation in Stratified Institutions with Universal Nominals
- it has signature extensions with nominals;
- it has universal quantifications corresponding to the signature extensions with nominals; and
- it has explicit local satisfaction.
- if and only if .
- if and only if .
- implies .
- implies .
- implies .
- For the implication from the left to the right we consider that . Let be any -expansion of M and let such that . We have to prove that . We have that
The latter satisfaction holds because .definition of local explicit satisfaction satisfaction condition in . For the implication from the right to the left we assume . Let be arbitrary. We have to prove that . Let us consider a -expansion of M such thatThenfor any definition of univ.
quantificationdefinition of local explicit satisfaction satisfaction condition. - Follows from 1. because is arbitrary.
- Let . By 1. it follows that hence . By 1. (again) we obtain .
- Let . By 2. it follows that . Hence .
- Let . Then . By 2. it follows .

- On the one hand, meanswhich by the definition of universal -quantification means that for all -expansions ofwhich is successively equivalent to:
Because is a homomorphism of -models, because its underlying function is , and because , we have that1 definition of explicit local satisfaction 2 satisfaction condition in 3 definition of reducts in 4 5 definition of reducts in . which makes the satisfaction 5 above equivalent to6 . - On the other hand, is equivalent to the following satisfactions:
By the definition of universal -quantifications the satisfaction 9 means that for all -expansions of7 satisfaction condition in 8 definition of reducts in 9 definition of .
which is successively equivalent to the following satisfactions:10 11 definition of explicit local satisfaction 12 satisfaction condition in 13 definition of reducts in .

5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goguen, J.; Burstall, R. Institutions: Abstract Model Theory for Specification and Programming. J. Assoc. Comput. Mach. 1992, 39, 95–146. [Google Scholar] [CrossRef]
- Sannella, D.; Tarlecki, A. Foundations of Algebraic Specifications and Formal Software Development; Springer: Berlin, Germany, 2012. [Google Scholar]
- Diaconescu, R. Institution-Independent Model Theory; Birkhäuser: Basel, Switzerland, 2008. [Google Scholar]
- Diaconescu, R.; Stefaneas, P. Modality in Open Institutions with Concrete Syntax. Bull. Greek Math. Soc. 2004, 49, 91–101. [Google Scholar]
- Aiguier, M.; Diaconescu, R. Stratified institutions and elementary homomorphisms. Inf. Process. Lett. 2007, 103, 5–13. [Google Scholar] [CrossRef]
- Diaconescu, R. Implicit Kripke Semantics and Ultraproducts in Stratified Institutions. J. Log. Comput. 2017, 27, 1577–1606. [Google Scholar] [CrossRef]
- Aiguier, M.; Bloch, I. Logical dual concepts based on mathematical morphology in stratified institutions: Applications to spatial reasoning. J. Appl. Non-Class. Logics 2019, 29, 392–429. [Google Scholar] [CrossRef]
- Găină, D. Forcing and Calculi for Hybrid Logics. J. Assoc. Comput. Mach. 2020, 67, 25:1–25:55. [Google Scholar] [CrossRef]
- Diaconescu, R. Decompositions of stratified institutions. J. Log. Comput. 2022. [Google Scholar] [CrossRef]
- Diaconescu, R. Representing 3/2-Institutions as Stratified Institutions. Mathematics 2022, 10, 1507. [Google Scholar] [CrossRef]
- Diaconescu, R. Implicit Partiality of Signature Morphisms in Institution Theory. In Hajnal Andréka and István Németi on Unity of Science: From Computing to Relativity Theory Through Algebraic Logic; series Outstanding Contributions to Logic; Madarász, J., Székely, G., Eds.; Springer: Berlin, Germany, 2021; Volume 19, pp. 81–123. ISBN 978-3-030-64186-3. [Google Scholar]
- Bergstra, J.; Heering, J.; Klint, P. Module Algebra. J. Assoc. Comput. Mach. 1990, 37, 335–372. [Google Scholar] [CrossRef]
- Diaconescu, R.; Goguen, J.; Stefaneas, P. Logical Support for Modularisation. In Logical Environments; Proceedings of the Workshop Held in Edinburgh, Scotland, May 1991; Huet, G., Plotkin, G., Eds.; Cambridge University Press: Cambridge, UK, 1993; pp. 83–130. [Google Scholar]
- Dimitrakos, T. Formal Support for Specification Design and Implementation. Ph.D. Thesis, Imperial College, London, UK, 1998. [Google Scholar]
- Bicarregui, J.; Dimitrakos, T.; Gabbay, D.; Maibaum, T. Interpolation in practical formal development. Log. J. IGPL 2001, 9, 231–243. [Google Scholar] [CrossRef]
- Veloso, P. On pushout consistency, modularity and interpolation for logical specifications. Inf. Process. Lett. 1996, 60, 59–66. [Google Scholar] [CrossRef]
- Borzyszkowski, T. Logical systems for structured specifications. Theor. Comput. Sci. 2002, 286, 197–245. [Google Scholar] [CrossRef]
- Kutz, O.; Mossakowski, T. Modules in Transition. Conservativity, Composition, and Colimits. In Proceedings of the Second International Workshop on Modular Ontologies, Whistler, BC, Canada, 28 October 2007. [Google Scholar]
- Nelson, G.; Oppen, D. Simplication by cooperating decision procedures. ACM Trans. Program. Lang. Syst. 1979, 1, 245–257. [Google Scholar] [CrossRef]
- Oppen, D. Complexity, convexity and combinations of theories. Theor. Comput. Sci. 1980, 12, 291–302. [Google Scholar] [CrossRef]
- Jhala, R.; Majumdar, R.; Xu, R.G. State of the Union: Type Inference Via Craig Interpolation. In Lecture Notes in Computer Science. Proceedings of the Tools and Algorithms for the Construction and Analysis of Systems: 13th International Conference on Tools and Algorithms for the Construction and Analysis of Systems, TACAS 2007, Braga, Portugal, 24 March–1 April 2007; Springer: Berlin, Germany, 2007; Volume 4424, pp. 553–567. [Google Scholar]
- McMillan, K. Applications of Craig interpolants in model checking. In Lecture Notes in Computer Science, Proceedings TACAS’2005, Edinburgh, UK, 4–8 April 2004; Springer: Berlin, Germany, 2005; Volume 3440, pp. 1–12. [Google Scholar]
- Amir, E.; McIlraith, S. Improving the Efficiency of Reasoning Through Structure-Based Reformulation. In Lecture Notes in Artificial Intelligence. Proceedings of the Symposium on Abstraction, Reformulation and Approximation (SARA’2000), Horseshoe Bay, TX, USA, 26–29 July 2000; Choueiry, B., Walsh, T., Eds.; Springer: Berlin, Germany, 2000; Volume 1864, pp. 247–259. [Google Scholar]
- McIlraith, S.; Amir, E. Theorem Proving with Structured Theories. In Proceedings of the 17th International Conference on Artificial Intelligence (IJCAI-01), Seattle, WA, USA, 4–10 August 2001; pp. 624–631. [Google Scholar]
- Tarlecki, A. Bits and Pieces of the Theory of Institutions. In Lecture Notes in Computer Science. Proceedings of the Summer Workshop on Category Theory and Computer Programming Guildford, UK, 16–20 September 1985; Pitt, D., Abramsky, S., Poigné, A., Rydeheard, D., Eds.; Springer: Berlin, Germany, 1986; Volume 240, pp. 334–360. [Google Scholar]
- Borzyszkowski, T. Generalized Interpolation in CASL. Inf. Process. Lett. 2001, 76, 19–24. [Google Scholar] [CrossRef]
- Dimitrakos, T.; Maibaum, T. On a Generalized Modularization Theorem. Inf. Process. Lett. 2000, 74, 65–71. [Google Scholar] [CrossRef]
- Găină, D.; Popescu, A. An institution-independent proof of Robinson Consistency Theorem. Stud. Log. 2007, 85, 41–73. [Google Scholar] [CrossRef]
- Diaconescu, R. An institution-independent proof of Craig Interpolation Theorem. Stud. Log. 2004, 77, 59–79. [Google Scholar] [CrossRef]
- Diaconescu, R. Interpolation in Grothendieck Institutions. Theor. Comput. Sci. 2004, 311, 439–461. [Google Scholar] [CrossRef]
- Diaconescu, R. Borrowing interpolation. J. Log. Comput. 2012, 22, 561–586. [Google Scholar] [CrossRef]
- Diaconescu, R. Interpolation for predefined types. Math. Struct. Comput. Sci. 2012, 22, 1–24. [Google Scholar] [CrossRef]
- Găină, D. Downward Löwenheim-Skolem theorem and interpolation in logics with constructors. J. Log. Comput. 2017, 27, 1717–1752. [Google Scholar] [CrossRef]
- Blackburn, P. Representation, Reasoning, and Relational Structures: A Hybrid Logic Manifesto. Log. J. IGPL 2000, 8, 339–365. [Google Scholar] [CrossRef]
- Blackburn, P.; Seligman, J. Hybrid Languages. J. Logic, Lang. Inf. 1995, 4, 251–272. [Google Scholar] [CrossRef]
- Areces, C.; Blackburn, P.; Delany, S.R. Bringing them all together. J. Log. Comput. 2001, 11, 657–669. [Google Scholar] [CrossRef]
- Mac Lane, S. Categories for the Working Mathematician, 2nd ed.; Springer: Berlin, Germany, 1998. [Google Scholar]
- Diaconescu, R.; Stefaneas, P. Ultraproducts and Possible Worlds Semantics in Institutions. Theor. Comput. Sci. 2007, 379, 210–230. [Google Scholar] [CrossRef]
- Martins, M.A.; Madeira, A.; Diaconescu, R.; Barbosa, L. Hybridization of Institutions. In Lecture Notes in Computer Science. Proceedings of the Algebra and Coalgebra in Computer Science, Winchester, UK, 30 August–2 September 2011; Corradini, A., Klin, B., Cîrstea, C., Eds.; Springer: Berlin, Germany, 2011; Volume 6859, pp. 283–297. [Google Scholar]
- Diaconescu, R. Quasi-varieties and initial semantics in hybridized institutions. J. Log. Comput. 2016, 26, 855–891. [Google Scholar] [CrossRef]
- Madeira, A. Foundations and Techniques for Software Reconfigurability. Ph.D. Thesis, Universidades do Minho (Braga), Aveiro, Portugal, Porto, Portugal, 2014. [Google Scholar]
- Blackburn, P.; de Rijke, M.; Venema, Y. Modal Logic; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Tarlecki, A. Quasi-Varieties in Abstract Algebraic Institutions. J. Comput. Syst. Sci. 1986, 33, 333–360. [Google Scholar] [CrossRef]
- Sannella, D.; Tarlecki, A. Specifications in an Arbitrary Institution. Inf. Control 1988, 76, 165–210. [Google Scholar] [CrossRef]
- Tarlecki, A. On the Existence of Free Models in Abstract Algebraic Institutions. Theor. Comput. Sci. 1986, 37, 269–304. [Google Scholar] [CrossRef]
- Meseguer, J. General Logics. In Studies in Logic and the Foundations of Mathematics. Proceedings of the Logic Colloquium, Granada, Spain, 20–25 July 1987; Ebbinghaus, H.-D., Fernandez-Prida, J., Garrido, M., Lascar, D., Artalejo, M.R., Eds.; Elsevier: Amsterdam, The Netherlands, 1989; pp. 275–329. [Google Scholar]
- Diaconescu, R.; Ţuţu, I. On the Algebra of Structured Specifications. Theor. Comput. Sci. 2011, 412, 3145–3174. [Google Scholar] [CrossRef]
- Rodenburg, P.H. A Simple Algebraic Proof of the Equational Interpolation Theorem. Algebra Universalis 1991, 28, 48–51. [Google Scholar] [CrossRef]
- Roşu, G.; Goguen, J. On Equational Craig Interpolation. Univers. Comput. Sci. 1999, 5, 482–493. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diaconescu, R. Concepts of Interpolation in Stratified Institutions. Logics 2023, 1, 80-96. https://doi.org/10.3390/logics1020005
Diaconescu R. Concepts of Interpolation in Stratified Institutions. Logics. 2023; 1(2):80-96. https://doi.org/10.3390/logics1020005
Chicago/Turabian StyleDiaconescu, Răzvan. 2023. "Concepts of Interpolation in Stratified Institutions" Logics 1, no. 2: 80-96. https://doi.org/10.3390/logics1020005
APA StyleDiaconescu, R. (2023). Concepts of Interpolation in Stratified Institutions. Logics, 1(2), 80-96. https://doi.org/10.3390/logics1020005





