Abstract
The definition and description of the dynamics of a predator–prey system are some of the fundamental problems of population biology. Since 1925, several models have been introduced. Although they are highly effective, most of them neglect certain relevant criteria such as the spatial and temporal distribution of the studied species. We introduced these criteria by coupling two models designed initially for collective dynamics. The first is for predator mobility and is a Vicsek-type model, and the second is a Brownian particle (BP) model for prey. We observed, as occurs in the classical models, periodic cycles of the densities of predators and prey. In this case, the period of oscillations depends on the collective dynamics parameters.
1. Introduction
The study of population dynamics is a subject of multidisciplinary research involving ecology, biology, mathematics and physics. It is sometimes oriented specifically in the dynamics of two species: predators and prey. In this perspective, the model developed independently by A. J. Lotka (1925) [1] and V. Volterra (1926) [2] provides a satisfactory explanation of observed phenomena such as the periodic variation in species density.
Since then, several variants of this model (called LV) have been derived. They are discrete or continuous dynamical systems whose qualitative study most often shows the existence of a steady state and periodic solutions around it [3,4]. Some variants of these models incorporate the mobility (spatio-temporal distribution) of the studied species, they are known as reaction–diffusion systems [5]. The commonality between the above-mentioned approaches is that they are Eulerian, deterministic and known as the mean-field approach. There are still some stochastic formulations studied in [6,7].
Recently, agent-based models (ABMs) have also been used to interpret predator–prey dynamics [8]. This concept was first introduced to study the collective behavior of a given species. These are self-propelled particle models (SPP); they are presented in two- or three-dimensional space and have undergone extensive investigations [9,10,11,12,13]. The central issues here include the mechanisms by which autonomous agents interact to exhibit emergent collective behavior and the properties of the resulting behavior. On the other hand, the mobility of certain species such as bacteria or phytoplankton is not a coherent collective dynamic but rather a random walk. Individuals from these species are generally considered as Brownian particles (BPs) [14,15,16]. In summary, self-propelled particle models were introduced to study the collective dynamics of a single species but never considered for the simultaneous description of two species and even less so for two species of predator and prey. If so, what about the basic properties deduced from these models such as orientation ordering, cluster formation, etc.?
Our approach consists of constructing a framework interpreting a predator–prey-type dynamic. Individuals are considered as material points inside the domain, a periodic box of size , and located by their positions on the Cartesian plane and animated with some velocity.
To implement this approach, we develop in the first section two separate models to simulate the mobility of prey and predators. For this purpose, we use the SPP and BP models, respectively. Then, we mix the two with assumptions of living interactions to illustrate via flowcharts and equations a prey–predator-type dynamic. We then make a python program to incorporate the global model.
Throughout the analysis of this model, we look for a range of standard parameters for which periodic oscillations between the densities of species can be found. This is followed by an underlying analysis of the characteristics of collective behavior.
2. Models and Simulation Setting
We designed separate prey and predator models describing their motions. Then, we constructed a predator–prey model which takes into account their living interactions.
2.1. Prey’s Motion
For the prey’s motion, particles are randomly uniformly distributed inside the domain and their density by unit area is . , , which represents, respectively, the position and velocity of particle i at time t, where the index p is set for prey. A complex type of this model using thrust force and interactions between particles is studied in [16].
In the beginning of the simulation , we set the prey’s velocities from a Gaussian distribution with zero mean and standard deviation (i.e., each particle has a random normal velocity in and is chosen to have values in ). After the first time step, each particle undergoes the action of a total force , denoted as , and moves according to the Langvin Equation (1) [16]:
where M is the mass of the prey and is set to 1 for simplicity; is the velocity of the prey i; is the coefficient of viscous friction, which is set by the properties of the environment and the particle geometry; and is a random force given by where , T and are, respectively, the Boltzmann constant, temperature and Gaussian white noise with zero mean and unit variance. is called the Boltzmann temperature. We used a Box–Muller transformation to compute the components of , consisting of choosing two elements and from a uniform distribution from and mapping them to two standard, normally distributed samples: Thus, we used the Verlet algorithm to calculate the prey’s position and the Störmer–Verlet method for their velocities (cf. [17]): .
In this system, each particle has a Brownian trajectory (random walk) and the average velocity of all particles depends closely on two parameters and (cf. Additional Materials) (Table 1).

Table 1.
Global and predator parameters.
2.2. Predator’s Motion
To describe the predator’s motion in the domain, we used a variant of the Vicsek model and added a repulsion rule (cf. [9,12,18]). Thus, predator particles are distributed inside the domain and move with a constant speed . Their density is and and represent, respectively, the position and velocity vectors for the particle at time t, where the subscript q denotes predator. For initial conditions, we set each particle with a uniform random position and velocity (cf. [16]). Then, in any time step , the position changes according to the equation and the velocity depends on the position of the particle which is either in the area of repulsion (zor) or alignment (zoa). These areas are defined by circles whose radii are denoted for zor and for zoa with . The first behavioral zone, represented by a circle of smaller radius , is responsible for the maintenance of a minimum distance between neighboring particles, while the second one with a grater radius is used for aligning the particle velocities (Figure 1a).
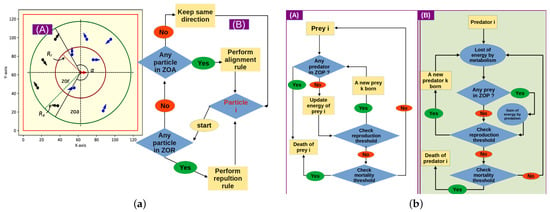
Figure 1.
Diagram of interactions. (a) (A) Schema of interactions between particles in the Vicsek-type model. The central particle (red arrow) turns away from the nearest neighbors (blue arrows) within the zone of repulsion (the inner circle of radius , zor) to avoid collisions and aligns itself with the neighbors (blue arrows) within the zone of alignment (the outer circle of radius , zoa). The alignment excludes particles (black arrows) within a blind angle (), where [13]. (B) Flowchart illustrating movement choices of a predator i. (b) Flowchart illustrating living interaction between prey (A) and predators (B). ZOP denotes the zone of the predators and the equations satisfying the different conditions are shown in the underlying section.
In the same figure, we demonstrate a flowchart illustrating the movement choices of a predator i whose rules are described as follows:
(a) Repulsion rule: If there are neighbors around i in zor, the velocity is given by the equation where is the desired direction of particle i and is given by the equation where is a constant speed for all particles; is the vector in the direction of neighbor j and is the rotation matrix. is the random angular noise obtained from by a Gaussian distribution, where represents the noise strength. The standard deviation is then around .
(b) Alignment rule: If there are no neighbors in the zone of repulsion, the individual i responds to others which are in the zone of alignment with:
where b is the cosine of the angle measured between and . It is evaluated to check if particle i sees particle j. has a fixed value which is the cosine of the half angle of perception , and the blind angle should be . Thus, if , the central particle i interacts with all particles inside the zone of alignment. The desired direction of particle i in the zoa is where is the number of particles in the zone of alignment; is the polar order (or polarization), given by and is the degree of polarization.
(c) Absolute rule: If repulsion occurs, the alignment is neglected.
(d) Alternative rule: If there are no individuals in the both zones, the particle i maintains its previous direction and thus
Finally, the parameters involved in this model for predators are shown in Table 2. Thus, in the next section, we will model the vital interactions simulating a prey–predator dynamic.

Table 2.
Parameters of the predator model.
2.3. The Predator–Prey Model
In addition to previous models describing the movement of prey and predators (Section 2.1 and Section 2.2), in this section, we are interested in their dynamics of evolution as two species living in a common environment (the domain). To describe this dynamic, we introduced a predator–prey model by coupling these two models through underlining assumptions.
Firstly, we treated the prey as living agents with the principal idea that any prey has some energy state which varies according to its position with respect to the predators. It features the life states of all individuals, i.e., survival, reproduction and mortality. Then, at , we set as the initial size of the prey population and an initial energy to each one. This is a random value obtained from a Gaussian distribution with zero mean and standard deviation (i.e., ).
Therefore, after each time step, i prey survive when they are outside the predatory area of all predators. They gain a survival bonus, an energy , which can increase or decrease their next state of energy. This models the fact that each prey can survive by potentially endangering another one or just die. thus Consequently, if the energy state reaches some certain reproduction threshold , the individual will be able to reproduce by cloning. Then, a new prey k born inside a birth zone of radius inherits similar movement abilities from their ancestor: Subsequently, its mortality is due to predators or a deficiency of energy, and occurs when the energy become less than a fixed mortality threshold :
With the same order of ideas, we approached in the second instance the dynamics of predators. Thus, for an initial size of population , we assumed that predators will need energy to survive. It is also a normal distribution with zero mean and standard deviation.
Therefore, in each time step, predator use amount of energy for metabolism (2). Predators derive energy from predation of prey present in their predatory zone zop (a circle of radius ). Thus, its state of energy decreases by the metabolism cost or increases by the predatory bonus:
Following this energy update, a predator dies when its state of energy decreases below the mortality threshold . Otherwise, if its energy level reaches more than the reproduction threshold , a new predator k will be born with a random normal energy and a random uniform velocity inside the zone of birth of radius . This is the cloning reproduction principle that we used for prey, i.e.,
Finally, after recapping the parameters involved in the model described above in Table 3, we designed a python program for simulations. The files are available on this link, where “main.py” generates the data and “anim.py” simulates interactions between the species.

Table 3.
Parameters of the predator–prey model. The standard values are those who create a pseudo-periodic regime.
3. Results and Discussion
We performed computer simulations to analyze the predator–prey model. Unless explicitly stated, we kept all parameters standard as indicated in Table 1. The standard parameters provide a regime where the density of species oscillates over time, inferring a pseudo-periodic regime for all trials performed. However, by varying certain parameters, one can have other types of regime such as the simultaneous extinction of two species or the survival of one and the extinction of the other.
We began with running the model by focusing mainly on three characteristic times [3 × 10, 8 × 10]. We chose the characteristic times with respect to predator density as , and , where the subscripts , and denote, respectively, the minimum, middle and maximum densities. Note that in this notation, might be greater than , etc., because the subscripts here are only attached to density values. These three cases typically represent the different phases of predators’ collective dynamics. In this sense, we illustrated the spatial distribution of species in snapshots in Figure 2A(a–c), i.e., the locations inside the domain of predators (blue) and preys (orange) at a specific time (, or ). We noticed that the prey density is less important and that of predators is elevated and vice versa. Such a fact infers a cyclic evolution of the species, which is represented in Figure 2A(d). For global picture, we recorded the range of densities for predators and prey, respectively, in and . The corresponding characteristic densities are . Hence, we observed that density variations have an impact on the collective dynamics, notably on the particle orientation ordering and cluster formation groups. This result is also found in many studies of Viscek-type models.
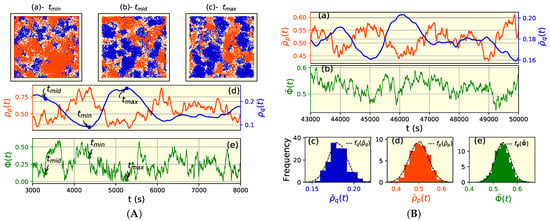
Figure 2.
Snapshots of particles and related indicators. (A) Snapshots of particle distributions in the predator (blue) and prey (brown) domains, respectively, for three cases of predator density: (a) minimum density , (b) maximum density and (c) medium density . (B) Subfigures (d,e) show, respectively, the density evolution of species and the polar order parameter (green) versus time. , and indicate the three cases mentioned above. (a) Average density evolution of predators (blue) and prey (brown) and (b) the corresponding average polar order parameter (green). The average is taken from 18 independent runs within standards parameters with a total time equal to . Subfigures (c–e) show, respectively, the distribution of , and . The dashed lines are the corresponding fitted functions of , , and .
For this, we investigated particle orientation ordering by evaluating the polar order parameter , which quantifies the alignment of predator particles to the average instantaneous velocity vector . This parameter ranges from zero in the case of a disordered phase to one in the case of a completely ordered phase. We have shown in Figure 2A(e) the evolution of the polar order parameter , where particles seem less ordered at a low density. A correlation between the variation in particle density and the polar order parameter is not obvious because the appearance of newborns disturbs the alignment of particles, and we observe the emergence of a spontaneous local phase transition.
To further understand the evolution of predator–prey densities and the equivalent predator polar ordering , we ran 18 trials with a total time of . The results were very similar, i.e., the density of predators oscillates in and that of prey oscillates in . The results show that in the first trial, increases when decreases and vice versa. Thus, there is an equilibrium point and a limited cycles around it. We also highlight that the curve of is smoother than the curve of , this is due to the height impact of randomness in prey dynamics assumptions. This randomness effect appears also in the polar order parameter , which is bounded in . Therefore, predators could be completely disordered for some time, and they cannot reach a degree of order more than . This indicates that the presence of prey has an impact on predator collective dynamics as a disordering factor.
We continued our analysis by looking at histograms of , which denote the instantaneous average (quadratic mean) of , where [4.3 × 10, 5 × 10]. We found approximate functions , and to fit, respectively, predator and prey density distributions and the polar order parameter distribution (subfigures (c–e) in Figure 2), where
Since only the evolution of the predator density does not follow a Gaussian distribution, we are interested in the fluctuation in the number of predator particles in the system: , where denotes the number of predators in a box of linear size l. is in general proportional to . corresponds to normal fluctuation, while is a significant fluctuation. In our system, the extent of fluctuation of predator particles was estimated for the three density cases. For minimum and middle densities, the critical exponent is , this corresponds to a significant fluctuation. For the maximum density, the fluctuation is normal because (Figure 3a).
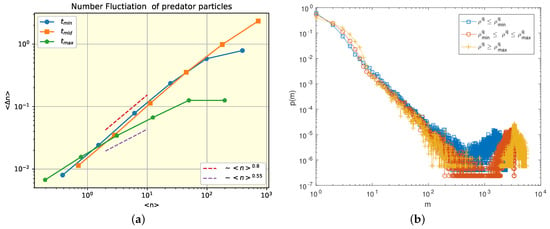
Figure 3.
Number fluctuation and cluster statistics. (a) Fluctuation in the number of predator particles for three characteristic times: minimum density , middle density and maximum density . The critical exponent is in . (b) Cluster statistics for three ranges of predator density: , and . and . and the rest of the parameters are standard.
We finally examined the cluster distribution of predator particles. Formally, the cluster dynamics of the SPP system can be described by deriving a master equation for the evolution of the probability , where , with being the number of isolated particles, being the number of two-particle clusters, being the number of three-particle clusters, etc. Clusters in our model are defined as a group of particles with a distance between neighbors smaller or equal to the radius of alignment zone , i.e., particles interacting directly or via neighboring agents are included in one cluster ([13]).
4. Conclusions
In summary, we built a predator–prey model from a collective dynamics and self-propelled particles approach. Despite the plethora of assumptions, stability of the system is possible with appropriate parameters which give a quasi-periodic regime.
The main results related to SPP and BP models are maintained with the particularity that the densities are dynamic here. Let us note, however, the difficulty in the design of the algorithm caused by the large sizes of parameters.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
This paper and the research behind it would not have been possible without the exceptional support of M. Romenskyy and David J. T Sumpter from Uppsala University. Their enthusiasm, knowledge and exacting attention to detail have been an inspiration and kept my work on track from my first visit to their lab to the final draft of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- James Lotka, A. Elements of Physical Biology; Williams & Wilkins Company: Baltimore, MD, USA, 1925; p. 460. [Google Scholar]
- Voterra, V. Fluctuations in the abundance of a species considered mathematically. Nature 1926, 118, 558–560. [Google Scholar] [CrossRef]
- May, R.M. Limit Cycle in Predator-Prey Communities. Science 1972, 177, 900–902. [Google Scholar] [CrossRef] [PubMed]
- Arditi, R.; Ginzeburg, L.R. Coupling in Predator-Prey Dynamics: Ratio-Dependence. J. Theor. Biol. 1989, 139, 311–326. [Google Scholar] [CrossRef]
- Ainseba, B.; Bendahmane, M.; Noussair, A. A reaction–diffusion system modeling predator–prey with prey-taxis. Nonlinear Anal. Real World Appl. 2008, 9, 2086–2105. [Google Scholar] [CrossRef]
- Rodrigues, A.L.; Tomé, T. Reaction-diffusion stochastic lattice model for a predator-prey system. Braz. J. Phys. 2008, 38, 87–93. [Google Scholar] [CrossRef]
- Liu, M.; Fan, M. Permanence of Stochastic Lotka–Volterra Systems. J. Nonlinear Sci. 2017, 27, 425–452. [Google Scholar] [CrossRef]
- Lin, Y.; Abaid, N. Collective behavior and predation success in a predator-prey model inspired by hunting bats. Phys. Rev. E 2013, 88, 062724. [Google Scholar] [CrossRef] [PubMed]
- Vicsek, T.; Czirók, A.; Ben-Jacob, E.; Cohen, I.; Shochet, O. Novel Type Of phase Transition in a System of Self-Driven Particles. Phys. Rev. Lett. 1995, 75, 1226–1229. [Google Scholar] [CrossRef]
- Sumpter, D.J.T. The principles of collective animal behaviour. Phil. Trans. R. Soc. B 2006, 361, 5–22. [Google Scholar] [CrossRef]
- Buhl, J.; Sumpter, D.J.T.; Couzin, I.D.; Hale, J.J.; Despland, E.; Miller, E.R.; Simpson, S.J. From Disorder to Order in Marching Locusts. Science 2006, 312, 1402–1406. [Google Scholar] [CrossRef] [PubMed]
- Vicsek, T.; Zafeiris, A. Collective motion. Phys. Rep. 2012, 517, 71–140. [Google Scholar] [CrossRef]
- Romenskyy, M.; Lobaskin, V. Statical properties of swarms of self-propelled particles with repultions across the order-disorder transition. Eur. Phys. J. B 2013, 86, 91. [Google Scholar] [CrossRef]
- Ebeling, W.; Schweitzer, F.; Tilch, B. Active Brownian particles with energy depots modeling animal mobility. BioSystems 1999, 49, 17–29. [Google Scholar] [CrossRef] [PubMed]
- Romanczuk, P.; Bär, M.; Ebeling, W.; Lindner, B.; Schimansky-Geier, L. Active Brownian particles. Eur. Phys. J. Spec. Top. 2012, 202, 1–162. [Google Scholar] [CrossRef]
- Lobaskin, V.; Romenskyy, M. Collective dynamics in system of Brownian particles with dissipative interactions. Phys. Rev. E 2013, 87, 052135. [Google Scholar] [CrossRef] [PubMed]
- Verlet, L. Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Phys. Rev. E 1967, 159, 98. [Google Scholar] [CrossRef]
- Cousin, I.D.; Krause, J.; James, R.; Ruxton, G.D.; Franks, N.R. Collective memory and spatial sorting in animal group. J. Ther. Biol. 2002, 218, 1–11. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).