Finite Difference Method for Intuitionistic Fuzzy Partial Differential Equations ^†

Abstract

In this paper, we investigate an intuitionistic fuzzy Poisson equation with uncertain parameters, considering the parameters as intuitionistic fuzzy numbers. We apply a finite difference method to solve the ‘Intuitionistic fuzzy Poisson equation’. The continuity of the membership and non-membership functions (which imply the continuity of the hesitancy function) is used to obtain qualitative properties on regular $\alpha$-cut and $\beta$-cut of the intuitionistic fuzzy solution. The fuzzification of the deterministic $\alpha$-cut and $\beta$-cut solutions obtained lead to the intuitionistic fuzzy solution. Finally, an example is presented to illustrate the proposed methodology, as well as to show a graphical representation of its corresponding intuitionistic fuzzy solution.

1. Introduction

One of the fruitful ways of modelling uncertainty and imprecision in particular quantities for certain real-life problems, is Intuitionistic Fuzzy Partial Differential Equations (IFPDEs). IFPDEs have essential applications in diverse fields, such as physics, biology, chemistry, and engineering. We propose a method for the approximate solution of IFPDE using a Finite Difference Method. In [1], J. Buckley and T. Feuring introduced a method for the solution of the fuzzy partial differential equation. In [2], T. Allahvironloo used a numerical method to solve the Fuzzy Partial differential equation that was based on the Seikala derivative. C. Samuel and V. Stefen used a numerical method to solve elliptic FPDE using a polynomial Galerkin approximation. In [3], Man et al. applied the finite difference method to solve an intuitionistic fuzzy heat equation. A. Kermani et al. Numerical methods for fuzzy linear partial differential equations applied by Kermani et al. [4]. An intuitionistic fuzzy set introduced by K.T. Atanassov [5,6]. Intuitionistic fuzzy number and its arithmetic operations discussed by [7,8]. An intuitionistic fuzzy set is an extension of the fuzzy set defined in a domain of discourse. We may obtain better results using IFPDEs rather than FPDEs.

This paper presents a new approach to finding the numerical solution of the intuitionistic fuzzy elliptic equation. We solve the Poisson equation using the finite difference method with intuitionistic fuzzy parameters.

2. Materials and Methods

In the following we consider the Poisson equation

$$\begin{array}{c}\hfill (D_x^2+D_y^2)\tilde{U}=\tilde{F}(x,y,\tilde{K}),\end{array}$$

(1)

Let us consider $\tilde{U}$ and $\tilde{F}$ to be a fuzzy function of the independent crisp variables x and y. We define the domain

$$\begin{array}{c}\hfill R=[(x,y):(x,y)\in I_{1}X{I}_2]\end{array}$$

(2)

A($\alpha ,\beta$)-cuts of $\tilde{U}(x,y)$ and its parametric form will be

$$\begin{array}{c}\hfill \tilde{U}(x,y)[\alpha ,\beta ]=<[\underline{U}(x,y;\alpha ),\overline{U}(x,y;\alpha )],[\underline{U^{\prime }}(x,y;\beta ),\overline{U^{\prime }}(x,y;\beta )]>.\end{array}$$

(3)

We suppose that $\underline{U}(x,y;\alpha ),\overline{U}(x,y;\alpha )),\underline{U^{\prime }}(x,y;\beta )$ and $\overline{U^{\prime }}(x,y;\beta ))$ have continuous partial derivatives with respect to x and y, therefore $(D_x^2+D_y^2)\underline{U}(x,y;\alpha ),(D_x^2+D_y^2)\overline{U}(x,y;\alpha )),(D_x^2+D_y^2)\underline{U^{\prime }}(x,y;\beta )$ and $(D_x^2+D_y^2)\overline{U^{\prime }}(x,y;\beta ))$ are continuous for all $(x,y)\in R$, for all $\alpha \in [0,1]$, for all $\beta \in [0,1]$.

Equation (1) can be decomposed as

$$\begin{array}{c}\hfill \left(D_x^2\right)\underline{U}+\left(D_y^2\right)\underline{U}=\underline{F}(x,y,\tilde{K}),\end{array}$$

(4)

$$\begin{array}{c}\hfill \left(D_x^2\right)\overline{U}+\left(D_y^2\right)\overline{U}=\overline{F}(x,y,\tilde{K}),\end{array}$$

(5)

$$\begin{array}{c}\hfill \left(D_x^2\right)\underline{U^{\prime }}+\left(D_y^2\right)\underline{U^{\prime }}=\underline{F}(x,y,\tilde{K}),\end{array}$$

(6)

$$\begin{array}{c}\hfill \left(D_x^2\right)\overline{U^{\prime }}+\left(D_y^2\right)\overline{U^{\prime }}=\overline{F}(x,y,\tilde{K}),\end{array}$$

(7)

for all $(x,y)\in I_1\times I_2$, for all $\alpha \in [0,1]$ and for all $\beta \in [0,1]$.

We subdivide the intervals $I_1=[0,1]$, $I_2=[0,1]$ into N equal subintervals of length $h=\frac{1}{N}$ then the points $x_i=ih,i=0,1,2,\cdots ,N-1$ and $y_j=jh,j=0,1,2,\cdots ,N-1$.

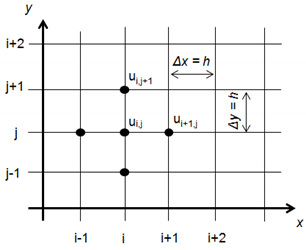
Denote the value of $\tilde{U}$ at the representative mesh point $P(ih,jh)$ by

$$\begin{array}{c}\hfill \widetilde{U_P}=\tilde{U}(ih,jh)={\tilde{U}}_{i,j}\end{array}$$

(8)

and also denote the parametric form of intuitionistic fuzzy number ${\tilde{U}}_{i,j}$, involving the parameters $\alpha$ and $\beta$, as

$$\begin{array}{c}\hfill {\tilde{U}}_{i,j}=<[{\underline{u}}_{i,j}\left(\alpha \right),{\overline{u}}_{i,j}\left(\alpha \right)],[{\underline{u^{\prime }}}_{i,j}\left(\beta \right),{\overline{u^{\prime }}}_{i,j}\left(\beta \right)]>.\end{array}$$

(9)

Then, we have

$$\begin{array}{c}\hfill \left(D_x^2\right)\tilde{U}(x,y)=<[D_x^2\underline{U}(x,y;\alpha ),D_x^2\overline{U}(x,y;\alpha )],[D_x^2\underline{U^{\prime }}(x,y;\beta ),D_x^2\overline{U^{\prime }}(x,y;\beta )]>,\end{array}$$

(10)

$$\begin{array}{c}\hfill \left(D_y^2\right)\tilde{U}(x,y)=<[D_y^2\underline{U}(x,y;\alpha ),D_y^2\overline{U}(x,y;\alpha )],[D_y^2\underline{U^{\prime }}(x,y;\beta ),D_y^2\overline{U^{\prime }}(x,y;\beta )]>,\end{array}$$

(11)

Following [2], using Taylor’s theorem and definition of standard difference formula we obtain

$$\begin{array}{c}\hfill D_x^2\underline{U}{(x,y;\alpha )|}_{i,j}\simeq \frac{{\underline{u}}_{i+1,j}-2{\underline{u}}_{i,j}+{\underline{u}}_{i-1,j}}{h^2},\end{array}$$

(12)

$$\begin{array}{c}\hfill D_x^2\overline{U}{(x,y;\alpha )|}_{i,j}\simeq \frac{{\overline{u}}_{i+1,j}-2{\overline{u}}_{i,j}+{\overline{u}}_{i-1,j}}{h^2},\end{array}$$

(13)

$$\begin{array}{c}\hfill D_x^2\underline{U^{\prime }}{(x,y;\beta )|}_{i,j}\simeq \frac{{\underline{u^{\prime }}}_{i+1,j}-2{\underline{u^{\prime }}}_{i,j}+{\underline{u^{\prime }}}_{i-1,j}}{h^2},\end{array}$$

(14)

$$\begin{array}{c}\hfill D_x^2\overline{U^{\prime }}{(x,y;\beta )|}_{i,j}\simeq \frac{{\overline{u^{\prime }}}_{i+1,j}-2{\overline{u^{\prime }}}_{i,j}+{\overline{u^{\prime }}}_{i-1,j}}{h^2},\end{array}$$

(15)

with a leading error of $O\left(h^2\right)$. Similarly, using the notation of forward difference approximation for $\left(D_y^2\right)\tilde{U}$ at P, we have

$$\begin{array}{c}\hfill D_y^2\underline{U}{(x,y;\alpha )|}_{i,j}\simeq \frac{{\underline{u}}_{i,j+1}-2{\underline{u}}_{i,j}+{\underline{u}}_{i,j-1}}{h^2},\end{array}$$

(16)

$$\begin{array}{c}\hfill D_y^2\overline{U}{(x,y;\alpha )|}_{i,j}\simeq \frac{{\overline{u}}_{i,j+1}-2{\overline{u}}_{i,j}+{\overline{u}}_{i,j-1}}{h^2},\end{array}$$

(17)

$$\begin{array}{c}\hfill D_y^2\underline{U^{\prime }}{(x,y;\beta )|}_{i,j}\simeq \frac{{\underline{u^{\prime }}}_{i,j+1}-2{\underline{u^{\prime }}}_{i,j}+{\underline{u^{\prime }}}_{i,j-1}}{h^2},\end{array}$$

(18)

$$\begin{array}{c}\hfill D_y^2\overline{U^{\prime }}{(x,y;\beta )|}_{i,j}\simeq \frac{{\overline{u^{\prime }}}_{i,j+1}-2{\overline{u^{\prime }}}_{i,j}+{\overline{u^{\prime }}}_{i,j-1}}{h^2},\end{array}$$

(19)

with a leading error of $O\left(h^2\right)$.

Using (12)–(19) the finite difference scheme for Poisson equation reads as

$$\begin{array}{c}\hfill \frac{{\underline{u}}_{i,j+1}-2{\underline{u}}_{i,j}+{\underline{u}}_{i,j-1}}{h^2}+\frac{{\underline{u}}_{i+1,j}-2{\underline{u}}_{i,j}+{\underline{u}}_{i-1,j}}{h^2}=\underline{F}(x,y,\tilde{K}),\end{array}$$

(20)

$$\begin{array}{c}\hfill \frac{{\overline{u}}_{i,j+1}-2{\overline{u}}_{i,j}+{\overline{u}}_{i,j-1}}{h^2}+\frac{{\overline{u}}_{i+1,j}-2{\overline{u}}_{i,j}+{\overline{u}}_{i-1,j}}{h^2}=\overline{F}(x,y,\tilde{K}),\end{array}$$

(21)

$$\begin{array}{c}\hfill \frac{{\underline{u^{\prime }}}_{i,j+1}-2{\underline{u^{\prime }}}_{i,j}+{\underline{u^{\prime }}}_{i,j-1}}{h^2}+\frac{{\underline{u^{\prime }}}_{i+1,j}-2{\underline{u^{\prime }}}_{i,j}+{\underline{u^{\prime }}}_{i-1,j}}{h^2}=\underline{F}(x,y,\tilde{K}),\end{array}$$

(22)

$$\begin{array}{c}\hfill \frac{{\overline{u^{\prime }}}_{i,j+1}-2{\overline{u^{\prime }}}_{i,j}+{\overline{u^{\prime }}}_{i,j-1}}{h^2}+\frac{{\overline{u^{\prime }}}_{i+1,j}-2{\overline{u^{\prime }}}_{i,j}+{\overline{u^{\prime }}}_{i-1,j}}{h^2}=\overline{F}(x,y,\tilde{K}).\end{array}$$

(23)

This can be written as

$$\begin{array}{c}\hfill {\underline{u}}_{i,j}=\frac{1}{4}[{\underline{u}}_{i+1,j}+{\underline{u}}_{i-1,j}+{\underline{u}}_{i,j+1}+{\underline{u}}_{i,j-1}-h^2\underline{F}(x,y,\tilde{K})]\end{array}$$

(24)

$$\begin{array}{c}\hfill {\overline{u}}_{i,j}=\frac{1}{4}[{\overline{u}}_{i+1,j}+{\overline{u}}_{i-1,j}+{\overline{u}}_{i,j+1}+{\overline{u}}_{i,j-1}-h^2\overline{F}(x,y,\tilde{K})]\end{array}$$

(25)

$$\begin{array}{c}\hfill {\underline{u^{\prime }}}_{i,j}=\frac{1}{4}[{\underline{u^{\prime }}}_{i+1,j}+{\underline{u^{\prime }}}_{i-1,j}+{\underline{u^{\prime }}}_{i,j+1}+{\underline{u^{\prime }}}_{i,j-1}-h^2\underline{F}(x,y,\tilde{K})]\end{array}$$

(26)

$$\begin{array}{c}\hfill {\overline{u^{\prime }}}_{i,j}=\frac{1}{4}[{\overline{u^{\prime }}}_{i+1,j}+{\overline{u^{\prime }}}_{i-1,j}+{\overline{u^{\prime }}}_{i,j+1}+{\overline{u^{\prime }}}_{i,j-1}-h^2\overline{F}(x,y,\tilde{K})]\end{array}$$

(27)

3. Results

Consider the fuzzy Poisson’s equation. This example can be found in [2]

$$\frac{{\partial }^2\tilde{U}}{\partial x^2}(x,y)+\frac{{\partial }^2\tilde{U}}{\partial y^2}(x,y)=\tilde{F}(x,y,\tilde{K}),0<x<2,0<y<1,$$

(28)

where

$$\begin{array}{c}\hfill \tilde{F}(x,y,\tilde{K})=\tilde{k}x{e}^y,\end{array}$$

(29)

and

$$\begin{array}{c}\hfill \tilde{k}[\alpha ,\beta ]=<[\underline{k}\left(\alpha \right),\overline{k}\left(\alpha \right)],[\underline{k}\left(\beta \right),\overline{k}\left(\beta \right)]>=<[0.75+0.25\alpha ,1.25-0.25\alpha ],[1-0.5\beta ,1+0.5\beta ]>.\end{array}$$

(30)

with the boundary conditions

$$\begin{array}{c}\hfill \tilde{U}(0,y)=0,\tilde{U}(2,y)=2\tilde{k}{e}^y,0\le y\le 1,\end{array}$$

(31)

$$\begin{array}{c}\hfill \tilde{U}(x,0)=\tilde{k}x,\tilde{U}(x,1)=\tilde{k}ex,0\le x\le 2.\end{array}$$

(32)

The exact solutions for

$$\begin{array}{c}\hfill \frac{{\partial }^2\underline{U}}{\partial x^2}(x,y;\alpha )+\frac{{\partial }^2\underline{U}}{\partial y^2}(x,y;\alpha )=\underline{k}\left(\alpha \right)x{e}^y,0<x<2,0<y<1,\end{array}$$

(33)

$$\begin{array}{c}\hfill \frac{{\partial }^2\overline{U}}{\partial x^2}(x,y;\alpha )+\frac{{\partial }^2\overline{U}}{\partial y^2}(x,y;\alpha )=\overline{k}\left(\alpha \right)x{e}^y,0<x<2,0<y<1,\end{array}$$

(34)

$$\begin{array}{c}\hfill \frac{{\partial }^2\underline{U^{\prime }}}{\partial x^2}(x,y;\beta )+\frac{{\partial }^2\underline{U^{\prime }}}{\partial y^2}(x,y;\beta )=\underline{k}\left(\beta \right)x{e}^y,0<x<2,0<y<1,\end{array}$$

(35)

$$\begin{array}{c}\hfill \frac{{\partial }^2\overline{U^{\prime }}}{\partial x^2}(x,y;\beta )+\frac{{\partial }^2\overline{U^{\prime }}}{\partial y^2}(x,y;\beta )=\overline{k}\left(\beta \right)x{e}^y,0<x<2,0<y<1,\end{array}$$

(36)

are, respectively,

$$\begin{array}{c}\hfill \underline{U}(x,y;\alpha )=\underline{k}\left(\alpha \right)x{e}^y,\end{array}$$

(37)

$$\begin{array}{c}\hfill \overline{U}(x,y;\alpha )=\overline{k}\left(\alpha \right)x{e}^y,\end{array}$$

(38)

$$\begin{array}{c}\hfill \underline{U^{\prime }}(x,y;\beta )=\underline{k}\left(\beta \right)x{e}^y,\end{array}$$

(39)

$$\begin{array}{c}\hfill \overline{U^{\prime }}(x,y;\beta )=\overline{k}\left(\beta \right)x{e}^y,\end{array}$$

(40)

4. Discussion

We have used Equations (24)–(27) to approximate the exact solutions with $h=0.025$ and $k=0.01$. Figure 1 shows the approximate and exact solution at the point $(0.5,0.25)$ for each $\alpha \in (0,1)$.

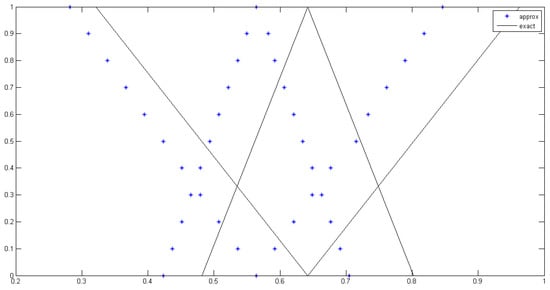
Figure 1. The intuitionistic fuzzy solution of Poisson equation.

5. Conclusions

The intuitionistic fuzzy partial differential equation can be applied for modelling in physics, engineering, and mechanical system. In this paper, we have developed a finite difference method to solve the intuitionistic fuzzy Poisson equation. Future work may focus on intuitionistic fuzzy partial differential equations to more realistic applications from practice.