Fractional Approach to the Study of Damped Traveling Disturbances in a Vibrating Medium ^†

Abstract

The Cauchy problem of a time–space fractional partial differential equation which has as a particular case the damped wave equation is solved for the Dirac delta initial condition. The solution is obtained in terms of H-Fox functions and models the travel of a disturbance in a vibrating medium.

1. Introduction

In previous works [1,2,3], the fractional space–time partial linear differential equation $D_t^{\alpha }u(x,t)=v_{\alpha ,\beta }^2{\mathbb{D}}_x^{\beta }u(x,t)$ has been solved. In such an expression, $D_t^{\alpha }$ indicates the time fractional derivative in the sense that Caputo (see Ref. [4]), ${\mathbb{D}}_x^{\beta }$ represents the space fractional operator in the sense of Riesz (see Ref. [5]) and $v_{\alpha ,\beta }$ is a constant such that $\left[v_{\alpha ,\beta }\right]={\left[L\right]}^{\beta /2}{\left[T\right]}^{-\alpha /2}$, where $\left[L\right]$ and $\left[T\right]$ stand for the units of length and time, respectively. This equation includes as particular cases the heat equation [6] for $(\alpha ,\beta )=(1,2)$, for which $v_{1,2}^2=k$, where k stands for the thermometric conductivity, and the wave equation [7,8,9,10], for $(\alpha ,\beta )=(2,2)$, for which $v_{2,2}=v$, where v represents the velocity of propagation of the wave. The Cauchy problem of such an equation with the Dirac delta initial condition is solved by means of Laplace and Fourier methods in Refs. [1,2,3]. In Ref. [1], the equation was solved in terms of generalized Wright functions [11]. The solution has different representations depending on which of the three cases $\alpha >\beta$, $\alpha =\beta$ or $\alpha <\beta$ is fulfilled. In Ref. [2], a unified representation of the solution was obtained for all possible combinations of $\alpha$ and $\beta$ by solving the problem in terms of H-Fox functions. Furthermore, in Ref. [2], a Gaussian initial condition was also considered, leading to a series of H-Fox functions as a solution, where, in the appropriate limit, the solution for the Dirac delta initial condition is recovered. In Ref. [3], attention is paid to the particular case $\alpha =\beta$. The solution is obtained in terms of the well-known sine and cosine trigonometric functions. In the first two cases (Refs. [1,2]), the solution depends on the parameters $\alpha$ and $\beta$. Its solution enables on to recover the heat and wave equation solutions for $(\alpha ,\beta )=(1,2)$ and $(\alpha ,\beta )=(2,2)$, respectively. In the last case, (Ref. [3]), the main results depend on $\alpha$ and enable one to recover the wave equation solution for $\alpha =2$. In addition, the integro-differential equations of integer order arise as particular cases of the mentioned equation: the first is obtained for $(\alpha ,\beta )=(1,1)$ (see Refs. [1,2]) and the second for $(\alpha ,\beta )=(2,1)$ (see Ref. [2]). The last is introduced in Ref. [2] as a complementary equation, a broader analysis of an such equation is made in Ref. [12].

In a recent work [13], the Cauchy problem of the more general fractional differential expression $\left[D_t^{\alpha }+a^{\alpha }\right]u(x,t)=v_{\alpha ,\beta }^2{\mathbb{D}}_x^{\beta }u(x,t)$ ($a>0$) that includes as a particular case the Klein–Gordon equation [14] (for its classical applications see, e.g., [15]), is solved in terms of a series of H-Fox functions. The solution is reduced to that of the equation $D_t^{\alpha }u(x,t)=v_{\alpha ,\beta }^2{\mathbb{D}}_x^{\beta }u(x,t)$ in the limit $a=0$.

Numerical techniques to solve space–time fractional differential equations were proposed in Refs. [16,17,18,19]. In [16], they aimed to solve the equations of the wave type and in Ref. [17], they aimed to solve the equations of the telegraph form, in both cases with constant coefficients. In Ref. [18], they aimed to solve equations of the Klein–Gordon-type and in Ref. [19], of a more general form, in these two last cases with variable coefficients.

Motivated by those previous works, we consider now the study of a fractional differential equation that includes as a limit case the damped wave equation. Such an equation has the form $[D_t^{\alpha }+{\gamma }^{\frac{\alpha }{2}}{D}_t^{\frac{\alpha }{2}}]u(x,t)=v_{\alpha ,\beta }^2{\mathbb{D}}_x^{\beta }u(x,t)$ with $\gamma >0$. This work is addressed to solve the Cauchy problem of such a fractional differential equation for Dirac delta initial condition.

2. Problem Formulation

Let us consider the one-dimensional damped wave equation

$$\left[\frac{{\partial }^2}{\partial t^2}+\gamma \frac{\partial }{\partial t}\right]u(x,t)=v^2\frac{{\partial }^2}{\partial x^2}u(x,t).$$

(1)

In Equation (1), $\gamma >0$ represents the damping parameter and the constant v the velocity of the damped wave. By replacing the time derivative operators $\frac{{\partial }^2}{\partial t^2}$ and $\frac{\partial }{\partial t}$ in Equation (1) with the Caputo fractional derivative operators $D_t^{\alpha }$ and $D_t^{\frac{\alpha }{2}}$, respectively, (see its definition in Appendix A). We obtain the equation

$$\left[D_t^{\alpha }+{\gamma }^{\frac{\alpha }{2}}{D}_t^{\frac{\alpha }{2}}\right]u(x,t)=v_{\alpha }^2\frac{{\partial }^2}{\partial x^2}u(x,t).$$

(2)

In Equation (2), $\alpha \in [1,2]$ and the constant $v_{\alpha }$ fulfills $\left[v_{\alpha }\right]=\left[L\right]{\left[T\right]}^{-\frac{\alpha }{2}}$.

A more general expression of Equation (2) can be obtained by replacing the space-derivative operator $\frac{{\partial }^2}{\partial x^2}$ in Equation (2) with the Riesz fractional operator ${\mathbb{D}}_x^{\beta }$ (see its definition in Appendix A). We arrive at the expression

$$\left[D_t^{\alpha }+{\gamma }^{\frac{\alpha }{2}}{D}_t^{\frac{\alpha }{2}}\right]u(x,t)=v_{\alpha ,\beta }^2{\mathbb{D}}_x^{\beta }u(x,t).$$

(3)

In Equation (3), $\beta \in [1,2]$ and the constant $v_{\alpha ,\beta }$ fulfills $\left[v_{\alpha ,\beta }\right]={\left[L\right]}^{\frac{\beta }{2}}{\left[T\right]}^{-\frac{\alpha }{2}}$. Additionally, $v_{\alpha ,2}=v_{\alpha }$ and $v_{2,2}=v_2=v$.

Let us consider a fractional $\eta$-order differential equation with $1\le \eta \le 2$, derivatives defined in the sense of Caputo and solution $y\left(t\right)$. The Caputo fractional derivative is reduced to the first and second derivative operators for $\eta =1$ and $\eta =2$, respectively; this permits the equation to transit from a first-order differential equation for $\eta =1$ to a second-order one for $\eta =2$. For $1<\eta \le 2$, this equation requires two initial conditions to have a completely determined solution. For $\eta =1$, the equation requires one initial condition for such purposes. To obtain a solution that permits to transit between the solution to the fractional differential equation for $\eta =1$ to that of $\eta =2$ through the parameter $\eta$, we may impose the initial condition $\frac{dy}{dt}{|}_{t=0}=0$ for $1<\eta \le 2$. Taking into account the last considerations, we may impose the following initial conditions into Equation (3)

$$u(x,0)=\phi \left(x\right),\frac{\partial u}{\partial t}{(x,t)|}_{t=0}=0.$$

(4)

Equations (3) and (4) constitute the Cauchy problem to be solved. In this work, we consider the Dirac delta initial condition $u(x,0)=\phi \left(x\right)=\mu \delta \left(x\right)$ and no boundary conditions.

3. Solution of the Problem

The Laplace transform $\mathcal{L}$ of Equation (3) is

$$(s^{\alpha }+{\gamma }^{\frac{\alpha }{2}}{s}^{\frac{\alpha }{2}})U(x,s)-(s^{\alpha -1}+{\gamma }^{\frac{\alpha }{2}}{s}^{\frac{\alpha }{2}-1})\phi \left(x\right)=v_{\alpha ,\beta }^2{\mathbb{D}}_x^{\beta }U(x,s).$$

(5)

In the above equation, $U(x,s)=\mathcal{L}\left[u\right(x,t\left)\right]$. The Fourier transform $\mathcal{F}$ of Equation (5) is

$$(s^{\alpha }+{\gamma }^{\frac{\alpha }{2}}{s}^{\frac{\alpha }{2}})\overline{U}(k,s)-(s^{\alpha -1}+{\gamma }^{\frac{\alpha }{2}}{s}^{\frac{\alpha }{2}-1})\varphi \left(k\right)=-v_{\alpha ,\beta }^2{\left|k\right|}^{\beta }\overline{U}(k,s),$$

(6)

where $\overline{U}(k,s)=\mathcal{F}\left[\mathcal{L}\left[u(x,t)\right]\right]$ and $\mathcal{F}\left[\phi \right(x\left)\right]=\varphi \left(k\right)$. The algebraic expression (6) is solved by

$$\overline{U}(k,s)=\frac{(s^{\alpha -1}+{\gamma }^{\frac{\alpha }{2}}{s}^{\frac{\alpha }{2}-1})\varphi \left(k\right)}{s^{\alpha }+{\gamma }^{\frac{\alpha }{2}}{s}^{\frac{\alpha }{2}}+v_{\alpha ,\beta }^2{\left|k\right|}^{\beta }}.$$

(7)

To obtain the solution $u(x,t)$, we first recover $U(x,s)$ by taking the inverse Fourier transform ${\mathcal{F}}^{-1}$ of $\overline{U}(k,s)$. From the definition of inverse Fourier transform, we have

$$U(x,s)=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }\frac{(s^{\alpha -1}+{\gamma }^{\frac{\alpha }{2}}{s}^{\frac{\alpha }{2}-1})\varphi \left(k\right)e^{ikx}dk}{s^{\alpha }+{\gamma }^{\frac{\alpha }{2}}{s}^{\frac{\alpha }{2}}+v_{\alpha ,\beta }^2{\left|k\right|}^{\beta }}.$$

(8)

Setting the initial condition $\phi \left(x\right)=\mu \delta \left(x\right)$ into Equation (8) gives

$$U(x,s)=\frac{\mu {\lambda }^{\beta }}{2\pi s}{\int }_{-\infty }^{\infty }\frac{e^{ikx}dk}{{\lambda }^{\beta }+{\left|k\right|}^{\beta }},\lambda ={\left(\frac{s^{\alpha }+{\gamma }^{\frac{\alpha }{2}}{s}^{\frac{\alpha }{2}}}{v_{\alpha ,\beta }^2}\right)}^{\frac{1}{\beta }}.$$

(9)

In Ref. [20], the integral in Equation (9) was calculated (as can also be seen in Ref. [2]), and the result leads to the following expression for $U(x,s)$

$$U(x,s)=\frac{\mu \lambda }{\beta s}{H}_{2,3}^{2,1}\left[\lambda \left|x\right||\begin{array}{c}\left(1-\frac{1}{\beta },\frac{1}{\beta }\right),\left(\frac{1}{2},\frac{1}{2}\right)\\ (0,1),\left(1-\frac{1}{\beta },\frac{1}{\beta }\right),\left(\frac{1}{2},\frac{1}{2}\right)\end{array}\right],$$

(10)

where $H_{p,q}^{m,n}\left[x\right|-]$ is the H-Fox function [21,22] (as can also be seen in Appendix A). The inverse Laplace transform ${\mathcal{L}}^{-1}$ of $U(x,s)$ is calculated in the Appendix B and gives the solution $u(x,t)$ as follows

$$u(x,t)=\frac{\mu }{\beta t^{\frac{\alpha }{\beta }}{v}_{\alpha ,\beta }^{\frac{2}{\beta }}}\sum _{n=0}^{\infty }{\left(\gamma t\right)}^{\frac{\alpha n}{2}}{\mathrm{\Theta }}_n(x,t;\alpha ,\beta ),$$

(11)

where

$${\mathrm{\Theta }}_n(x,t;\alpha ,\beta )=H_{4,4}^{2,2}\left[\frac{\left|x\right|}{t^{\frac{\alpha }{\beta }}{v}_{\alpha ,\beta }^{\frac{2}{\beta }}}|\begin{array}{c}\left(1-\frac{1}{\beta },\frac{1}{\beta }\right),\left(-\frac{1}{\beta },\frac{1}{\beta }\right),\left(\frac{1}{2},\frac{1}{2}\right),(1-\frac{\alpha }{\beta }+\frac{\alpha n}{2},\frac{\alpha }{\beta })\\ (0,1),\left(1-\frac{1}{\beta },\frac{1}{\beta }\right),\left(\frac{1}{2},\frac{1}{2}\right),(-\frac{1}{\beta }+n,\frac{1}{\beta })\end{array}\right].$$

(12)

4. Discussion of Results

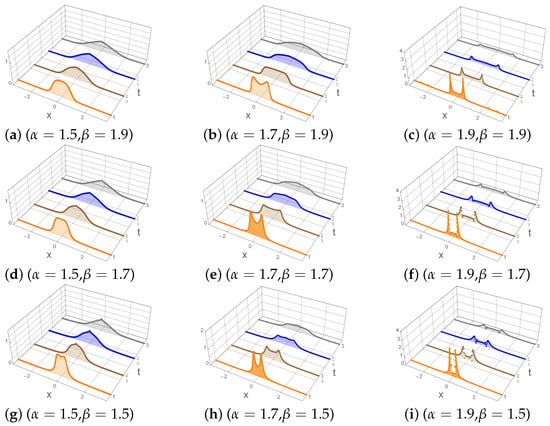
In Figure 1, the graphic representation of the solution is depicted in Equations (11) and (12) for some combinations of $(\alpha ,\beta )$. According to the graphics contained in the panel, the solution to Equation (3) can be studied in terms of a disturbance propagating in a vibrating medium. In all the cases presented herein, a mixture of diffusive and wave-like behavior can be observed in the traveling disturbances. As $\alpha$ becomes smaller, the diffusive behavior becomes more predominant. As $\alpha$ approaches 2, the wave-like behavior is predominant over the diffusive one and the effects of the reduction in the parameter $\beta$ become notorious, as can be observed in the third column with the change in the shape in the center of the traveling disturbances, in contrast to the first and second columns where such changes are not evident. Such a phenomenon may be associated with the presence of jump processes (as can be seen in [23,24,25]) into the traveling disturbance; as $\beta$ is reduced, its effects become more significant.

5. Conclusions

The Cauchy problem for a fractional differential equation with the damped wave equation as a particular case was solved with the Dirac delta initial condition, and its solution was obtained in terms of series of H-Fox functions. According to the graphic representation of the solution, the fractional differential equation models traveling disturbances, where a mixture of wave-like and diffusive behavior is observed. Future work is addressed to the study of a fractional differential equation with the telegrapher equation as a particular case. Such an equation also contains the fractional expressions $\left[D^{\alpha }+a^{\alpha }\right]u(x,t)=v_{\alpha ,\beta }^2{\mathbb{D}}^{\beta }u(x,t)$ and $\left[D^{\alpha }+{\gamma }^{\frac{\alpha }{2}}{D}^{\frac{\alpha }{2}}\right]u(x,t)=v_{\alpha ,\beta }^2{\mathbb{D}}^{\beta }u(x,t)$ as limit cases, which are the second object of study in this work. Work in this direction is in progress and will be reported elsewhere.