Electricity Consumption Forecasting for Out-of-Distribution Time-of-Use Tariffs †
Abstract
:1. Introduction
- We consider the problem of electricity consumption forecasting under new tariff profiles not encountered previously. This is then used for tariff profile allocation to optimize electricity broker’s profits.
- We note that the forecasting problem can be seen as an out-of-distribution (OOD) generalization problem with bias in the training data consisting of temporal and confounding bias.
- To achieve OOD generalization, we leverage the logic behind how consumers respond to tariff profiles in order to shift load, and propose a novel neural network architecture to achieve better OOD generalization.
2. Problem Formulation
- IID Scenario: when the profiles to be allocated to the consumers in future are from the same set of profiles used historically, i.e., .
- OOD Scenario: when the tariff profiles to be allocated to the consumers in future belong to , where is a new set of profiles not previously seen in , i.e., are out-of-distribution with respect to the training data, and not previously allocated to any consumer by the broker who wants to consider these new profiles to improve future gains, i.e., .
3. Related Work
4. The Learning Problem
- Step 1: For each consumer, forecast/estimate the consumption under each potential tariff profile allocation. Given features (including ), history of allocated tariffs , and values of potential future tariff , the goal is to estimate . This can be seen as a multi-step time series forecasting problem with exogenous variables. We provide the details of our proposed approach for this in the next section.
- Step 2: Compute the profit usingfor each tariff in for OOD scenario ( for IID scenario). Allocate the tariff profile to consumer c which results in maximum . Note that, in practice, the future wholesale rates () are also not known and might need to be estimated. In this work, we assume that s are known in advance or estimable accurately and focus on estimating s which are the only terms controllable via s.
4.1. Biased and Scarce Data
4.2. How Consumers Respond to Tariffs
- Independent processing: Here, the tariff at each hour is processed independently [16,17] and used to estimate the consumption at that hour. Of course, since the consumer’s decision making is based on comparison of tariff rates across hours, such a processing of tariff profiles will not be effective.
- All considered together or fully connected: Here, tariffs at all hours (the entire tariff profile) are processed simultaneously, e.g., through a fully connected layer in a feed-forward neural network. We argue that such processing of tariff profiles will be able to effectively learn a good function approximator for the profiles in . However, it will be highly biased to the profiles in since it does not effectively learn the way consumers are processing the tariff rates for shifting the loads. This leads to biased tariff profile processing modules due to the temporal bias in the historical profiles, as discussed above.
- Focusing on relevant information or Attention: Here, the tariffs rates in a day are considered as tokens and hours of a day are used as a positional information. This information is processed through a self-attention layer. We argue that such processing of tariff profiles will mimic the logic of how consumers respond to a tariff profile. However, it will be biased towards the profiles in since the tariffs and hour of the day are correlated (due to temporal bias in the historical tariff profiles).
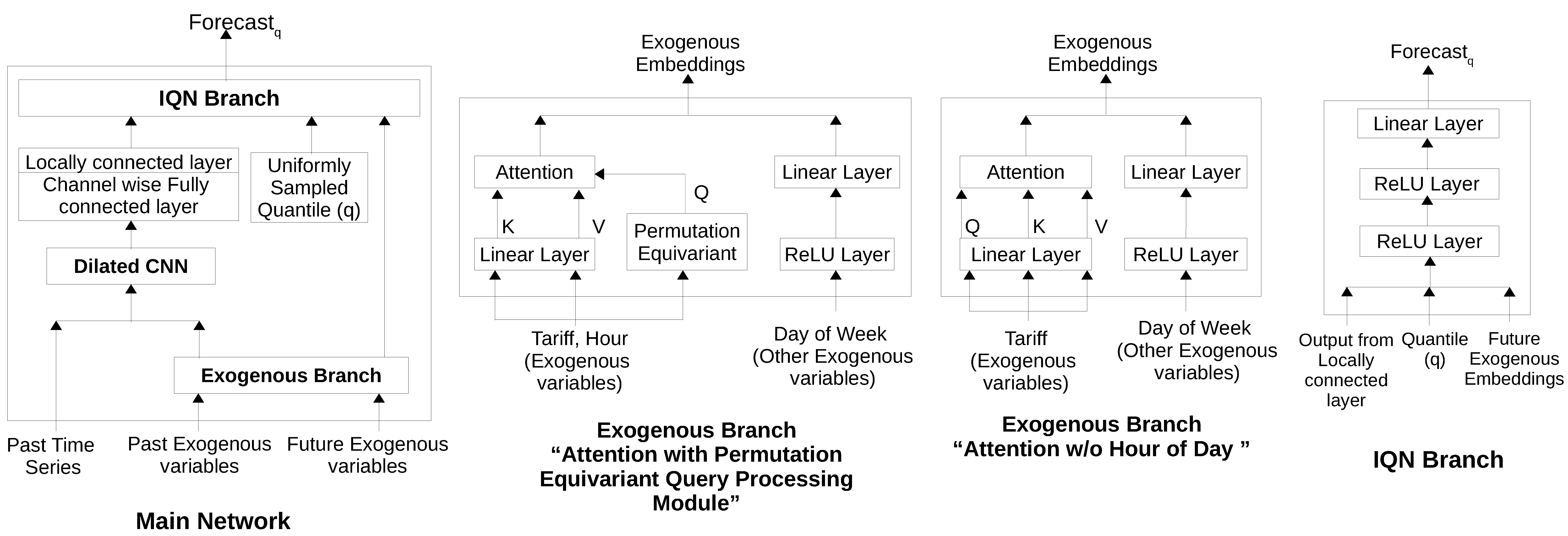
- Permutation Equivariance: As discussed earlier, permutation equivariance is an important aspect of the consumer decision-making logic. To mimic the same in the processing of tariffs by the neural networks, we expect that if trained on one of the tariff sequences, say, HHMMLL in the earlier example), it should perform equally well on other sequence (i.e., HHLLMM). In other words, processing of tariffs by neural networks should be Permutation Equivariant. We propose two ways to achieve approximate permutation equivariance:
- −
- Attention w/o Hour of Day (Att.-HOD): As explained above, the standard self-attention method can mimic the logic of how consumers respond to tariffs, but due to temporal bias in the data, the attention method does not generalize well to . We propose a simple variant that does not take HOD as input in the self-attention module to obtain the permutation equivariance property.
- −
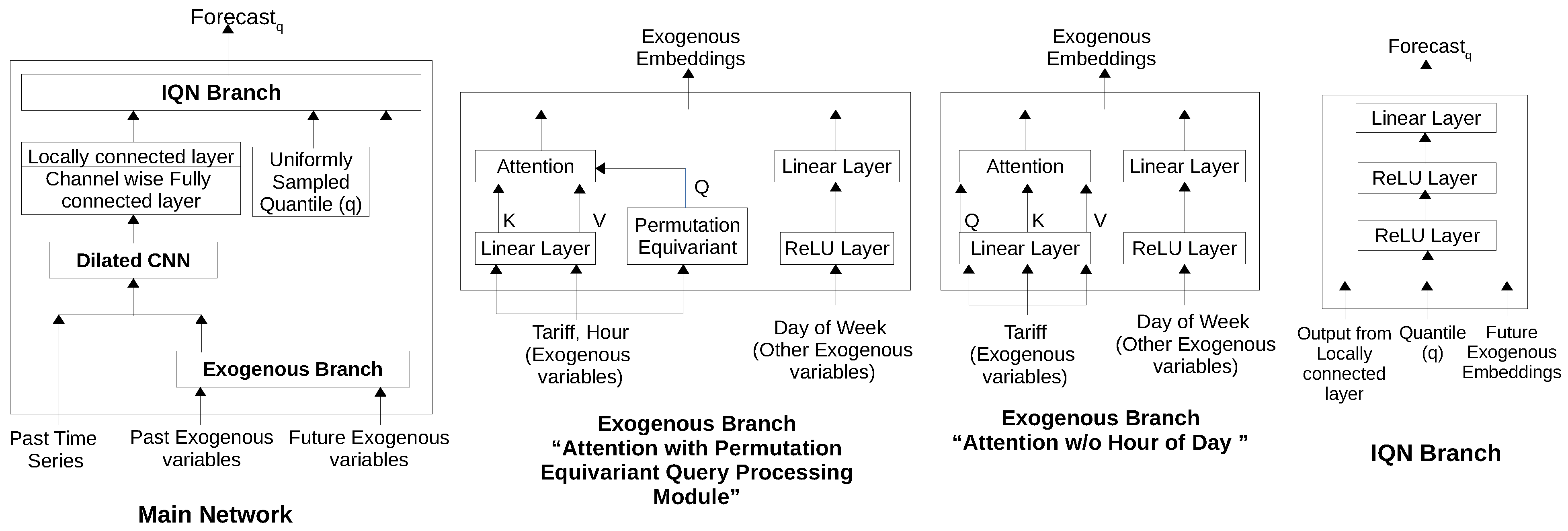
5. Forecasting Architecture
- Dilated Convolutional Neural Networks (DCNN) branch for processing of past consumption time series. (Since we have large input time series (t = 168 in our case), we consider 1D-Convolution Neural Networks for computational efficiency instead of Recurrent Neural Networks based architecture such as LSTMs [20].)
- Exogenous branch: This branch consists of Attention with Permutation Equivariant Query Processing Module (Att.+PE) branch for processing of tariff rates, and other modules for processing of features like hour of day, day of week, etc.
- Implicit Quantile Network (IQN) branch for generating the quantile estimates for future consumption.
6. Experimental Evaluation
6.1. Baselines Considered
- No future exogenous variable (NoX) is the simple univariate time series forecasting approach which uses only history of aggregated consumption without any additional future information. This can be considered as a lower bound in the sense that the network does not have access to any future tariff rates to estimate where a consumer will shift the load.
- Independent tariff-based method (Ind.) is an approach that treats each tariff rate independently, and uses the tariff at time to estimate the aggregated consumption at that time. Importantly, this approach has no means to capture comparison of the tariff rates in order to figure out whether the tariff at time is high or low in comparison to another timestep.
- Fully-Connected Approach (FC) utilizes the information of all timesteps to estimate the aggregated consumption at each timestep. As explained previously, we expect such an approach to perform well in the IID scenario but struggle in the OOD scenario where new profiles are included.
- Permutation Equivariant (PE) method uses only the permutation equivariance idea from our approach and ignores the attention mechanism. This method can be thought of as an ablation over our approach.
- Attention (Att.): This is another ablation over our approach which uses standard attention module for processing the tariffs along with hour of the day information without any permutation equivariance property.
- Upper Bound (UB): This is an oracle approach that assumes knowledge about the hours at which the consumer is going to shift the load. In this, a binary value indicating whether the shiftable load will be shifted to this hour or not is passed as an additional feature to the exogenous branch of the Att.+PE network.
6.2. Hyperparameters Used
6.3. Results and Observations
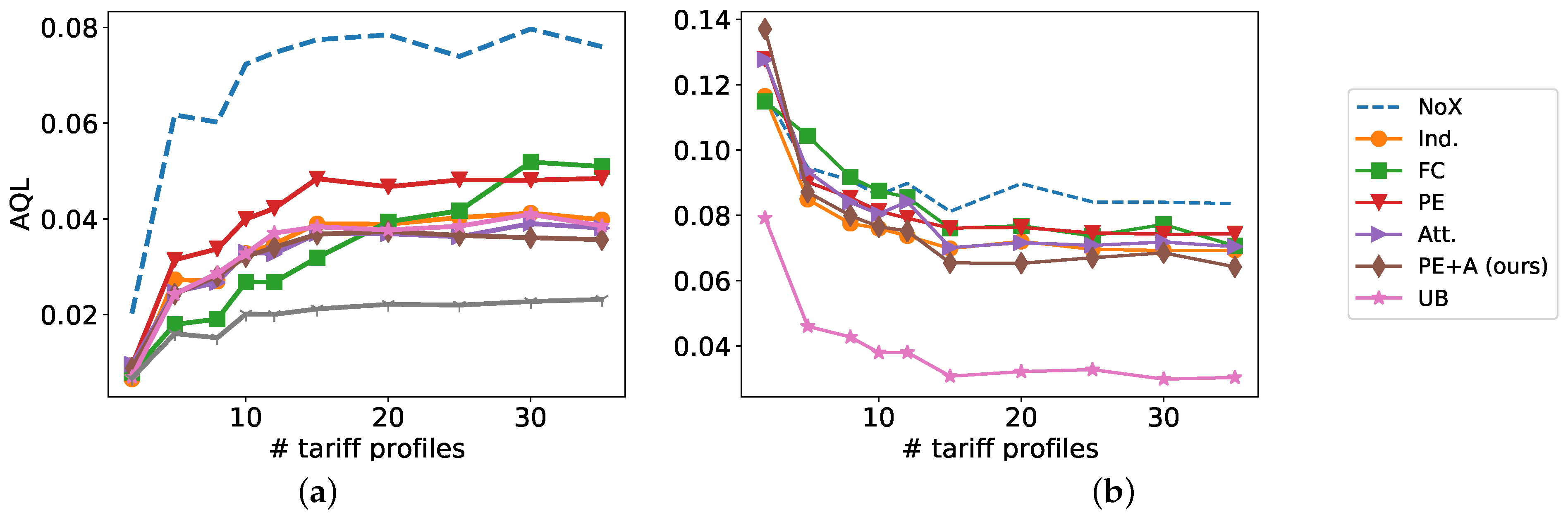
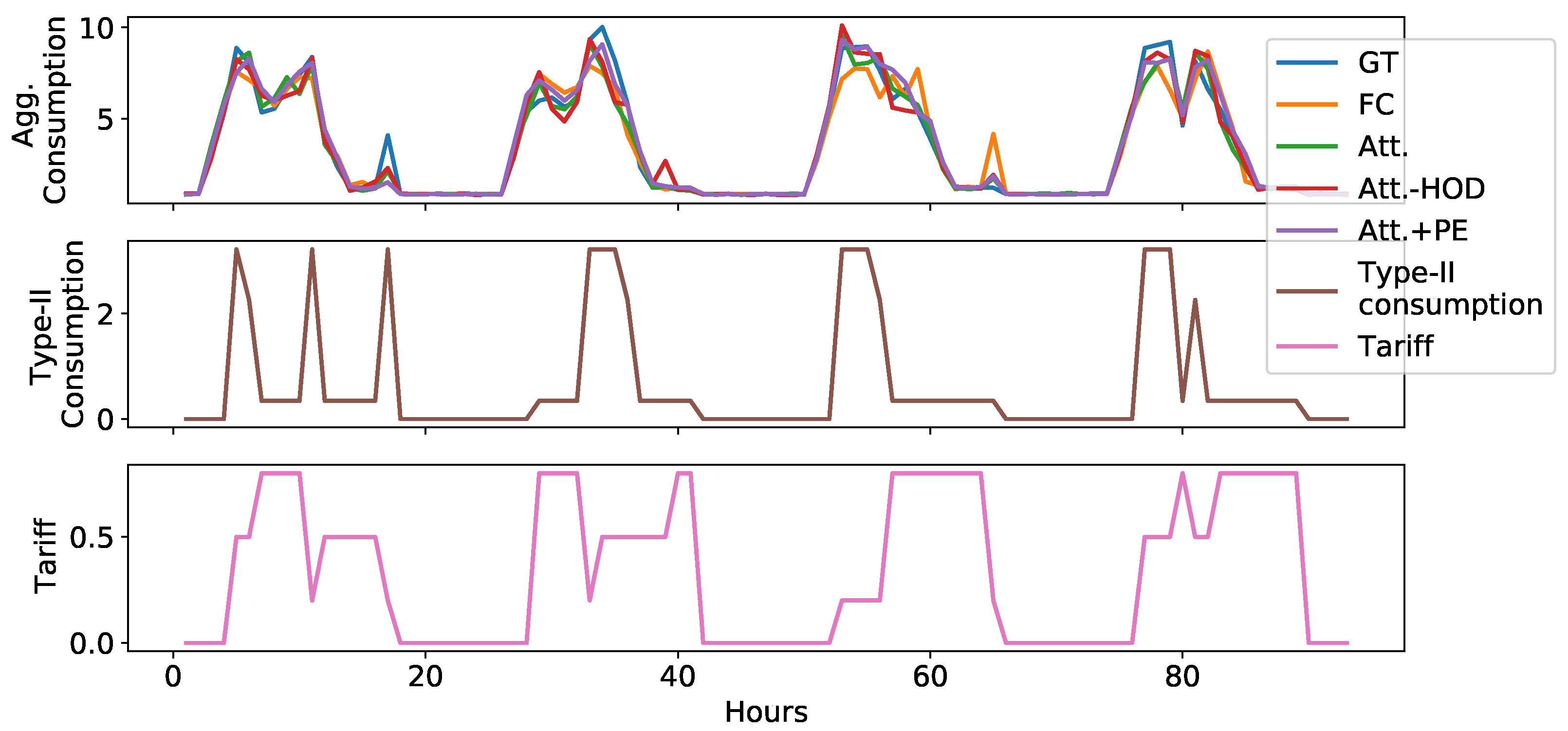
- Observations from forecasting results as shown in Figure 6:
- −
- In the IID scenario, the average quantile loss (AQL) for all approaches increases with increasing number of tariff profiles as the complexity of the dataset increases. The FC approach performs better than other approaches for , indicating higher expressivity of the FC approach to fit to a smaller number of IID profiles, indicating potential overfitting.
- −
- On the other hand, for the OOD scenario, the performance of all approaches improves with increasing number of IID profiles which is expected as more IID profiles implies less bias and better generalization to OOD profiles as well. Interestingly, the FC approach which was the best approach for the IID profiles for , is the worst approach (except the lower bound NoX) in the OOD setting, because it uses a fully connected layer to process the tariffs of the day, and due to temporal bias in the data, the weights of fully connected layer will try to overfit on and thus not generalize to OOD profiles .On the other hand, our proposed approaches Att.+PE and Att.-HOD are consistently better than FC for all values of , which shows that FC struggles with the temporal bias in the historical data. We also analyze that Att.-HOD as well as Att.+PE are also consistently better than Att. for all values of , which shows that permutation equivariant way of handling tariff profiles provide better generalization on OOD profiles.
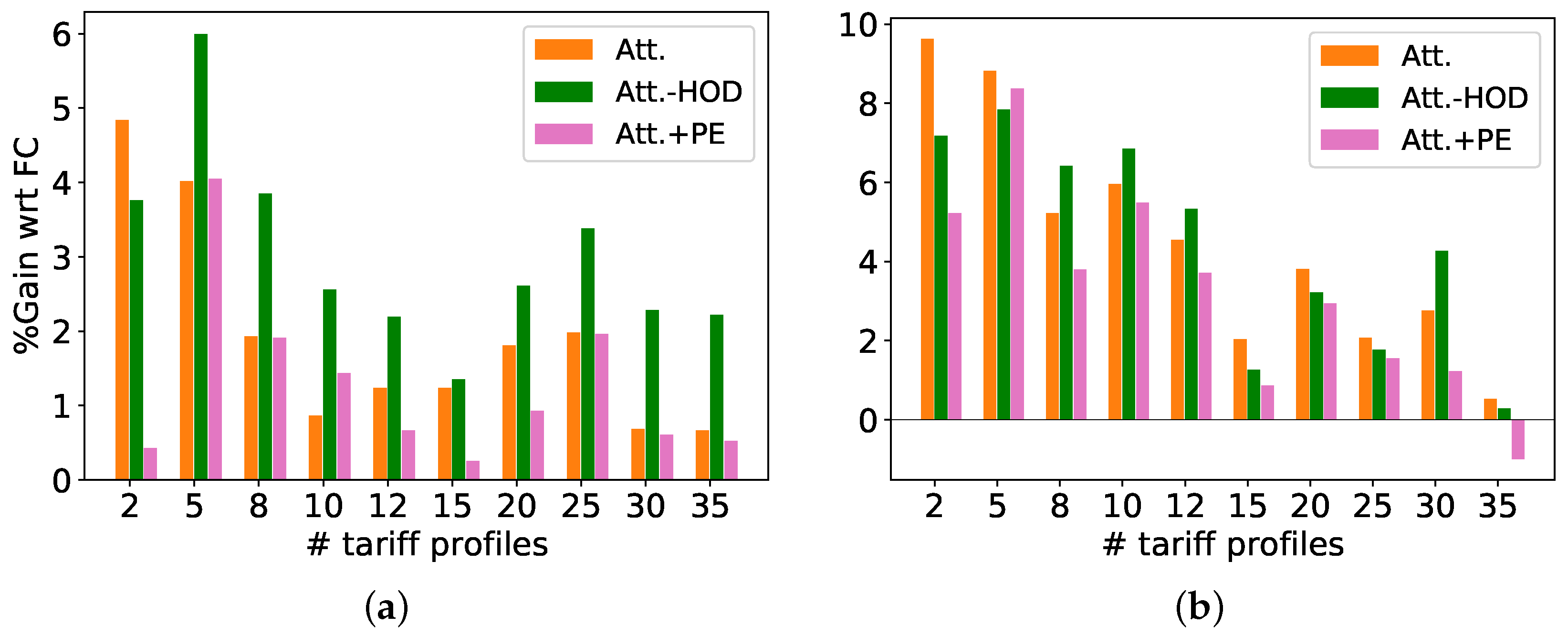
- We further analyze whether the gains of Att.+PE and Att.-HOD over other methods on the OOD scenario translate into more profitable tariff profile allocation for the retailer. We compare the gain G of Att.+PE, Att.-HOD, and Att. in comparison to FC. We consider two kinds of profiles for wholesale prices p, one with two values (0.2 and 0.8, referred to as Option-1) and one with three values (0.2, 0.5, and 0.8, referred to as Option-2).
- −
- Comparison with FC: We observe that all attention-based proposed approaches Att., Att.-HOD, and Att.+PE depict significant positive gains over FC. We also observe that Att., Att.-HOD, and Att.+PE approaches have higher positive gain in fewer IID tariff profiles scenarios (except , where data is too little to claim any generalization), and the gains tend to diminish as increases.
- −
- As expected, we note that it is not important that the gains in forecasting translate directly into monetary profits, as the optimization objective involves other terms such as wholesale costs p. Therefore, the best approach on forecasting (Att.+PE) in the OOD scenario is not necessarily the best approach in terms of profit always.
- −
- Comparison with Att.: For Option-1, Att.-HOD has significantly better gains than Att. for all values of except , which shows that the permutation equivariant way of handling tariff profiles is helpful. For Option-2, the gains of Att.-HOD are better or close to the gains of Att. approach (except ).
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Siano, P. Demand response and smart grids—A survey. Renew. Sustain. Energy Rev. 2014, 30, 461–478. [Google Scholar] [CrossRef]
- Lu, R.; Hong, S.H. Incentive-based demand response for smart grid with reinforcement learning and deep neural network. Appl. Energy 2019, 236, 937–949. [Google Scholar] [CrossRef]
- Lu, R.; Hong, S.H.; Zhang, X. A dynamic pricing demand response algorithm for smart grid: Reinforcement learning approach. Appl. Energy 2018, 220, 220–230. [Google Scholar] [CrossRef]
- Yang, P.; Tang, G.; Nehorai, A. A game-theoretic approach for optimal time-of-use electricity pricing. IEEE Trans. Power Syst. 2012, 28, 884–892. [Google Scholar] [CrossRef]
- Hendrycks, D.; Basart, S.; Mu, N.; Kadavath, S.; Wang, F.; Dorundo, E.; Desai, R.; Zhu, T.; Parajuli, S.; Guo, M.; et al. The many faces of robustness: A critical analysis of out-of-distribution generalization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 8340–8349. [Google Scholar]
- Arjovsky, M. Out of Distribution Generalization in Machine Learning. Ph.D. Thesis, New York University, New York, NY, USA, 2020. [Google Scholar]
- Krueger, D.; Caballero, E.; Jacobsen, J.H.; Zhang, A.; Binas, J.; Zhang, D.; Le Priol, R.; Courville, A. Out-of-distribution generalization via risk extrapolation (rex). In Proceedings of the International Conference on Machine Learning. PMLR, Virtual Event, Switzerland, 7–8 June 2021; pp. 5815–5826. [Google Scholar]
- Sun, Y.; Wang, X.; Liu, Z.; Miller, J.; Efros, A.A.; Hardt, M. Test-time training for out-of-distribution generalization. In Proceedings of the Eighth International Conference on Learning Representations (ICLR 2020), Virtual Conference, 26 April–1 May 2020. [Google Scholar]
- Hospedales, T.; Antoniou, A.; Micaelli, P.; Storkey, A. Meta-learning in neural networks: A survey. arXiv 2020, arXiv:2004.05439. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Liao, R.; Ba, J.; Fidler, S. Nervenet: Learning structured policy with graph neural networks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Narwariya, J.; Malhotra, P.; TV, V.; Vig, L.; Shroff, G. Graph Neural Networks for Leveraging Industrial Equipment Structure: An application to Remaining Useful Life Estimation. arXiv 2020, arXiv:2006.16556. [Google Scholar]
- Andreas, J.; Rohrbach, M.; Darrell, T.; Klein, D. Neural module networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2016; pp. 39–48. [Google Scholar]
- Bansal, H.; Bhatt, G.; Malhotra, P.; Prathosh, A. Systematic Generalization in Neural Networks-based Multivariate Time Series Forecasting Models. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–8. [Google Scholar]
- Liu, T.; Lu, J.; Yan, Z.; Zhang, G. Statistical generalization performance guarantee for meta-learning with data dependent prior. Neurocomputing 2021, 465, 391–405. [Google Scholar] [CrossRef]
- Pearl, J.; Glymour, M.; Jewell, N.P. Causal Inference in Statistics: A Primer; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Salinas, D.; Flunkert, V.; Gasthaus, J.; Januschowski, T. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. Int. J. Forecast. 2020, 36, 1181–1191. [Google Scholar] [CrossRef]
- Liu, X.; Yin, J.; Liu, H.; Liu, J. DeepSSM: Deep State-Space Model for 3D Human Motion Prediction. arXiv 2020, arXiv:2005.12155. [Google Scholar]
- Zaheer, M.; Kottur, S.; Ravanbakhsh, S.; Poczos, B.; Salakhutdinov, R.; Smola, A. Deep sets. arXiv 2017, arXiv:1703.06114. [Google Scholar]
- Lee, J.; Lee, Y.; Kim, J.; Kosiorek, A.; Choi, S.; Teh, Y.W. Set transformer: A framework for attention-based permutation-invariant neural networks. In Proceedings of the International Conference on Machine Learning. PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 3744–3753. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Ketter, W.; Collins, J.; Reddy, P. Power TAC: A competitive economic simulation of the smart grid. Energy Econ. 2013, 39, 262–270. [Google Scholar] [CrossRef]

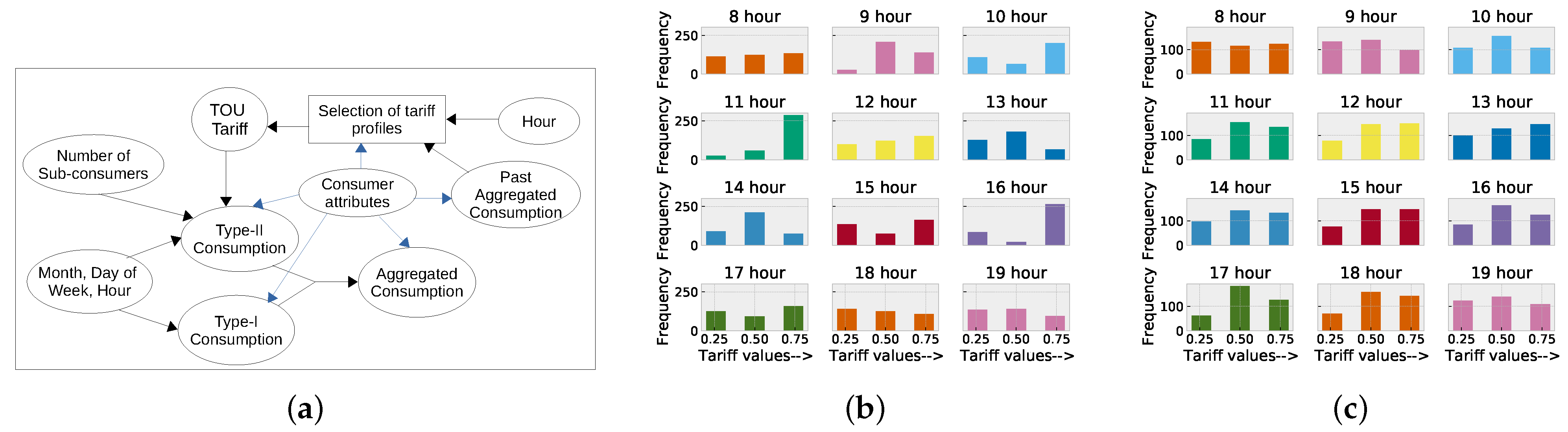


| S.N. | Properties of Consumers | Value(s) |
|---|---|---|
| 1 | Number of consumers | 12 |
| 2 | Number of sub-consumers | 3, 5 |
| 3 | Working days | 3, 4 |
| 4 | Work Start hour | {8, 9, 10} (+/−) 1 h |
| 5 | Break Start hour | {13, 14} (+/−) 1 h |
| 6 | Work duration | 8 (+/−) 1 h |
| 7 | Shiftable consumption( in KW) | 600, 2400 |
| 8 | Total data duration (in months) | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Narwariya, J.; Verma, C.; Malhotra, P.; Vig, L.; Subramanian, E.; Bhat, S. Electricity Consumption Forecasting for Out-of-Distribution Time-of-Use Tariffs. Comput. Sci. Math. Forum 2022, 3, 1. https://doi.org/10.3390/cmsf2022003001
Narwariya J, Verma C, Malhotra P, Vig L, Subramanian E, Bhat S. Electricity Consumption Forecasting for Out-of-Distribution Time-of-Use Tariffs. Computer Sciences & Mathematics Forum. 2022; 3(1):1. https://doi.org/10.3390/cmsf2022003001
Chicago/Turabian StyleNarwariya, Jyoti, Chetan Verma, Pankaj Malhotra, Lovekesh Vig, Easwara Subramanian, and Sanjay Bhat. 2022. "Electricity Consumption Forecasting for Out-of-Distribution Time-of-Use Tariffs" Computer Sciences & Mathematics Forum 3, no. 1: 1. https://doi.org/10.3390/cmsf2022003001
APA StyleNarwariya, J., Verma, C., Malhotra, P., Vig, L., Subramanian, E., & Bhat, S. (2022). Electricity Consumption Forecasting for Out-of-Distribution Time-of-Use Tariffs. Computer Sciences & Mathematics Forum, 3(1), 1. https://doi.org/10.3390/cmsf2022003001






