Abstract
Multi-commodity flow problems concerned with the transshipment of more than one commodity from respective sources to the corresponding sinks without violating the capacity constraints on the arcs. If the objective of the problem is to send the maximum amount of flow within a given time horizon, then it becomes the maximum flow problem. In multi-commodity flow problems, the flow of different commodities departing from their sources arriving at the common intermediate node have to share the capacity through the arc. The sharing of the capacity in the common arc (bundle arc) is one of the major issues in the multi-commodity flow problems. In this paper, we introduce the maximum static and maximum dynamic multi-commodity flow problems with proportional capacity sharing and present polynomial time algorithms to solve the problems. Similarly, we investigate the maximum dynamic multi-commodity flow problems with flow-dependent capacity sharing and present a pseudo-polynomial time solution strategy.
1. Introduction
A topological structure with links and crossings, known as arcs and nodes, respectively, is a network in which entities are transshipped from one point to another. The initial and the final points are termed as source and sink nodes, respectively. In a multi-terminal network, the transshipment of more than one commodity from the respective sources to the corresponding sinks satisfying the capacity constraints on the arcs is a multi-commodity flow (MCF) problem. Supply chain networks, message routine in telecommunication, and transportation networks are some examples of multi-commodity network topology.
Ford and Fulkerson [1] introduced the concept of the static multi-commodity flow problem, and thereafter many researchers have contributed to the different aspects of the multi-commodity flow problems [2,3,4,5]. If the demand and supply of each commodity is to be maximized in the given time horizon, then the problem becomes a maximum dynamic multi-commodity flow problem. The static multi-commodity flow problem is polynomial time solvable by using the ellipsoid or interior point method, whereas the dynamic multi-commodity flow problem is NP-hard [6]. Kappmeier [7] provided the solution to the maximum dynamic multi-commodity flow problem using a time-expanded network in a pseudo-polynomial time complexity. Pyakurel et al. [8] presented a polynomial time algorithm for the maximum static flow problem and pseudo-polynomial algorithms for the earliest arrival transshipment and maximum dynamic flow problems with partial contraflow. A priority based multi-commodity flow problem can be found in Khanal et al. [9]. Using the concept of intermediate storage introduced by Pyakurel and Dempe [10], Khanal et al. [11] presented a polynomial time algorithm for the maximum static—and a pseudo-polynomial time algorithm for the maximum dynamic—multi-commodity flow problems with intermediate storage.
The sharing of the bundle arc capacity is one of the major issues in the multi-commodity flow problems. For each commodity, if the sharing of the capacity of the bundle arc is set in proportion to the bottleneck capacity of path from their respective sources to the tail node of the bundle arc, then it is known as proportional capacity sharing. In this case, the shared capacity of the bundle arc for each commodity is fixed and the multi-commodity flow problem is reduced to an independent single commodity flow problem. To avoid the fractional flow, we can use ceiling and floor functions with an appropriate manner. Similarly, if the sharing of the capacity of the bundle arc is made according to the inflow rate of the flow of each commodity, then it is termed as flow-dependent capacity sharing. In this method, the shared capacity of the bundle arc may not always be the same as the flow on the arc may vary over the time. We investigate these two sharing techniques hereafter in Section 2.1 and Section 2.2.
In this paper, we introduce the maximum multi-commodity flow problem using proportional as well as flow-dependent capacity sharing on the bundle arcs. We present the polynomial time algorithms for the static as well as the dynamic multi-commodity flow problems, using proportional capacity sharing in Section 3. Similarly, in Section 4 a pseudo-polynomial time algorithm for the dynamic multi-commodity flow problem with flow-dependent capacity sharing is presented. The paper is concluded in Section 5.
2. Basic Terminologies
Consider a network topology G = (N, A, K, u, , di, S, D, T) with commodity iK = {1, 2, …, k}, set of nodes N and set of arcs A. Here, di represents the demand/supply of each commodity iK which is routed through a unique source–sink pair si-ti, where siS N and tiD N. Each arc e = (v, w) A with head(e) = w and tail(e) = v is equipped with a capacity function u:A + that restricts the flow of the commodity and a non-negative transit time function + that measures the time to transship the flow from node v to node w. Let (v) and (v) be the set of outgoing arcs from node v and the incoming arcs to node v, respectively. We denote Pi as the set of all paths of the commodity i such that P Pi is a si-ti path and P[si,v] Pi represents the path from si to the intermediate node v. The time horizon is denoted by T = {0, 1,…, T} in discrete time settings and T = [0, T + 1) in continuous time settings. In case of static flow, the time parameters T and are absent.
2.1. Proportional Capacity Sharing
The multi-commodity flow problem differs from the single commodity flow problem due to the bundle constraints and the unique source–sink flow for each commodity. Our assumption is that the nature of flows inside the same commodity group are homogeneous and between the commodity groups are heterogeneous yet uniform in the occupancy rate of the arc capacity. To share the capacity of the bundle arc, we propose a proportional capacity sharing technique depending on the minimum of the arc capacity of paths P[si,v], (that is, bottleneck capacity of path P[si,v]) for each commodity i from their respective sources si to the tail v of bundle arc e = (v, w) as follows: Let ue be the capacity of a bundle arc e, then proportional sharing of capacity ue for each commodity iK is,
where P[si,v] is the path from si to the tail v of bundle arc e, for all iK and is an arc in P[si,v] with minimum capacity. Here, represents the portion of the capacity of the arc e allocated for the commodity i. Clearly, the sum of the shared capacities over each commodity is equal to the original arc capacity, i.e., ue.
The shared capacity may be in fraction, i.e., = int+ fra, the sum of the integral part and the fractional part, respectively. The fractional capacities can be converted into the integral capacities as follows:
- Find the sum fra(). If fra() = p, then the first p fractional capacities with the greatest fractional part (with descending order of the fractional part) are rounded up using the ceiling function and the remaining capacities are rounded below by the floor function .
- If the same fractional part occurs in more than one commodity then priority is given to the capacity with the greatest integral part among them.
- In case of equal integral parts, priority goes to the commodity with the higher demand among them. If the demand values are also the same, then either of them can be rounded up.
It is to be noted that if < 1 and has no alternative path for commodity i, then it may block the transshipment of the flow. In such a case, the fractional capacity is to be accepted.
2.2. Flow-Dependent Capacity Sharing
In the proportional capacity sharing technique the shared capacity of each commodity remains fixed at each time step . In this subsection, we present the flow-dependent capacity sharing technique, where the share of the capacity for each commodity depends on the inflow rate of the flow f in the predecessor arcs. At any instance of time , if a bundle arc e = (v, w) with the capacity ue holds more than one commodity i K, then the flow-dependent capacity sharing of ue for each commodity i K is,
where is the set of the predecessor arcs of bundle arc e so that head() = tail(e) and is the portion of the capacity of arc e for the commodity i at time . For each time , the sum of the portion of the shared capacities over all the commodities i K is equal to the original arc capacity, i.e., = . If the shared capacities are in fraction, we can convert them into integer values as described in Section 2.1.
3. Maximum MCF with Proportional Capacity Sharing
3.1. Maximum Static Multi-Commodity Flow
In the static network G = (N, A, K, u, di, S, D) the multi-commodity flow with proportional capacity sharing is the sum of the non-negative flows + for each i with demand di satisfying the proportional capacity sharing Equation (1) together with the conditions (3) and (4).
The constraints in (3) represent the supply/demand at the source/sink nodes and the flow conservation constraints at the intermediate nodes, whereas the constraints in (4) represent the boundedness of the flow on the arcs by their capacities. By taking the sum over each commodity in the later equation, we get the bundle constraints for all . For a maximum static multi-commodity flow problem with proportional capacity sharing the objective is to maximize the total flow value subject to the constraints (1), (3) and (4).
We now introduce the maximum static multi-commodity flow problem with proportional capacity sharing as follows:
Problem 1.
For the given static multi-commodity network G = (N, A, K, u, di, S, D) the maximum static multi-commodity flow problem with proportional capacity sharing is to transship the maximum flow from si to ti, where the shared capacity for each commodity i K on the bundle arc is depending on the minimum capacity of paths from the respective source to the tail node of the bundle arc.
To solve the problem, we first reduce the multi-commodity flow problem into k independent single commodity flow problems by sharing the capacity of the bundle arc using Equation (1). For each commodity i maximum static flow is obtained and the sum of the flows for the commodities is the maximum static flow value . We now present the algorithm to solve Problem 1.
Theorem 1.
Algorithm 1 solves the maximum static MCF problem correctly in polynomial time complexity.
| Algorithm 1: Maximum static MCF algorithm with proportional capacity sharing |
| Input: Given static multi-commodity flow network G = (N, A, K, u, di, S, D). |
|
| Output: Maximum static MCF on G with proportional capacity sharing. |
3.2. Maximum Dynamic Multi-Commodity Flow
For a given dynamic network G with constant transit times on arc e, the MCF over time function f with proportional capacity sharing is the sum of the flows +, satisfying the proportional capacity sharing Equation (1) together with the constraints (5) and (7).
Here, the constraints in (5) represent the supply/demand at the sources/sinks and the flow conservation at the intermediate nodes on time horizon T. The non-conservation of the flow at the intermediate nodes in any time step in T = {0, 1, …, T} are represented by the constraints in (6). Similarly, (7) represents that the flows on the arcs are bounded above by their capacities. With these constraints, together with Equation (1), we introduce the maximum dynamic MCF problem with proportional capacity sharing, which maximizes the total flow value within the given time horizon T as follows:
Problem 2.
For given dynamic multi-commodity network G = (N, A, K, u, , di, S, D, T), the maximum multi-commodity flow problem with proportional capacity sharing is to transship the maximum amount of flow from si to ti within the given time horizon T, where the shared capacity for each on the bundle arc is depending on the minimum capacity of paths from the respective source to the tail node of the bundle arc.
We now present an algorithm to solve Problem (2).
Theorem 2.
Algorithm 2 provides the feasible solution to the maximum dynamic MCF problem with proportional capacity sharing in polynomial time.
| Algorithm 2: The maximum dynamic MCF algorithm with proportional capacity sharing |
| Input: Given static multi-commodity flow network G = (N, A, K, u, di, S, D). |
|
| Output: Maximum dynamic MCF on G with proportional capacity sharing. |
4. Maximum MCF with Flow-Dependent Capacity Sharing
For a given dynamic network G with constant transit times on arc e, the multi-commodity flow over time function f with flow-dependent capacity sharing is the sum of flows +, satisfying the constraints (8)–(12).
Here, the constraints in (8) and (9) have the usual meanings as represented in Section 3.2. The bundle constraints bounded by the arc capacities are presented by (10). The constraints in (11) represent the flow-dependent capacity sharing and the non-negativity of flows are represented by the constraints in (12). We now present the maximum dynamic MCF problem with flow-dependent capacity sharing satisfying the above constraints as follows:
Problem 3.
For a given multi-commodity network G = (N, A, K, u, , di, S, D, T), the maximum multi-commodity flow problem with flow-dependent capacity sharing is to transship the maximum amount of flow from si to ti within the given time horizon T, where shared capacity for each on the bundle arc is depending on the inflow of incoming arcs of the bundle arc.
To solve the problem, we use a time-expanded layer graph.
Multi-Commodity Time-Expanded Layer Graph
The multi-commodity time-expanded layer graph is a three-dimensional graph that contains the copy of nodes from the underlying static network for every discrete time step and for each commodity. It is applicable to solve the variety of flow over time problems by applying the algorithms and techniques developed for the static network flows. For a given network G with integral transit time on the arcs and the time horizon T, the T-time-expanded layer graph GT is obtained by creating T + 1 copies of node set N, which are labeled as N(0), N(1), …, N(T), together with an copy of node v labeled as v(), and the commodities . For every arc e = (v, w) A and , there is an arc from to with the same capacity of arc e for a single commodity arc and the sharing capacity for bundle arc e. If intermediate storage is allowed at node v, then the arc from to represents the holdover arc with infinite capacity that is used to hold the flow for the unit time interval for all , T}.
For the graphical representation, we present a three-dimensional layer graph GT with the set of node N, time T, and commodity K as the coordinate axes (see Figure 1). Each commodity preforms the layers of the graphs in a vertical line. In Figure 1, network (a) represents a two-commodity network in which commodity-1 is transshipped from s1 to t1 and commodity-2 from s2 to t2. Arc (x, y) is the bundle arc, which carries both commodities. Figure 1b represents the time-expanded layer graph of Figure 1a with the time horizon T = 6, where parallel arcs on (x, y) share the capacity for each commodity with the flow-dependent capacity sharing technique. At time step and , no flow of commodity-1 reaches arc (x, y), so only commodity-2 is transshipped on it; however, the capacity is shared after among the commodities. Similarly, the bundle arc transships only commodity-1 at time due to the absence of commodity-2.
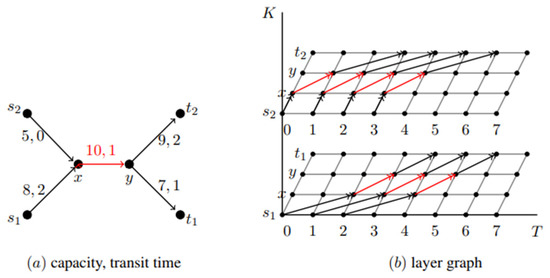
Figure 1.
(b) represents the time-expended layer graph GT of given network (a).
Depending on the time-expanded layer graph, we now present the algorithm to solve Problem 3.
Theorem 3.
A feasible solution to the maximum dynamic MCF problem with flow-dependent capacity sharing can be obtained by using Algorithm 3 in pseudo-polynomial time.
| Algorithm 3: Maximum dynamic MCF algorithm with flow-dependent capacity sharing |
| Input: Given dynamic multi-commodity flow network G = (N, A, K, u, τ, di, S, D, T). |
|
| Output: Maximum dynamic MCF on G with proportional capacity sharing. |
5. Conclusions
The maximum MCF problem deals with the transshipment of the maximum amount of flow of more than one different commodity from respective sources to the corresponding sinks within the given time horizon. Allocation of the capacity of the bundle arc to each commodity is one of the major issues in the multi-commodity flow problem. To deal with this problem we have proposed proportional capacity sharing and flow-dependent capacity sharing. We have presented polynomial time solutions for the static—as well as the dynamic—maximum MCF problems with proportional capacity sharing and a pseudo-polynomial time algorithm with flow-dependent capacity sharing. To the best of our knowledge these solution strategies for the maximum MCF problems are introduced for the first time.
Author Contributions
D.P.K.—conceptualization, investigation and documentation, U.P., T.N.D. and S.D.—formal analysis, editing and supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research work received no specific grants from any funding in the public, commercial or non-profit organizations.
Data Availability Statement
The authors have not used any additional data in this article.
Acknowledgments
The first author (Durga Prasad Khanal) thanks to the German Academic Exchange Service—DAAD for research grants—Bi-nationally Supervised Doctoral Degree/Cotutelle, 2021/2022 and the second author (Urmila Pyakurel) thanks the Alexander von Humboldt Foundation for Digital Cooperation Fellowship (1 August 2021–31 January 2022).
Conflicts of Interest
Authors have no any conflict of interest regarding the publication of the paper.
References
- Ford, L.R.; Fulkerson, D.R. Flows in Networks; Princeton University Press: Princeton, NJ, USA, 1962. [Google Scholar]
- Ahuja, R.K.; Magnanti, T.L.; Orlin, J.B. Network Flows: Theory, Algorithm and Applications; Englewood Cliffs: Bergen, NJ, USA, 1993. [Google Scholar]
- Ali, A.; Helgason, R.; Kennington, J.; Lall, H. Computational comparison among three multi-commodity network flow algorithms. Oper. Res. 1980, 28, 995–1000. [Google Scholar] [CrossRef] [Green Version]
- Assad, A. Multi-commodity network flows—A survey. Networks 1978, 8, 37–91. [Google Scholar] [CrossRef]
- Kennington, J. A survey of linear cost multi-commodity network flows. Oper. Res. 1978, 26, 209–236. [Google Scholar] [CrossRef]
- Hall, A.; Hippler, S.; Skutella, M. Multi-commodity flows over time: Efficient algorithms and complexity. Theor. Comput. Sci. 2007, 379, 387–404. [Google Scholar] [CrossRef] [Green Version]
- Kappmeier, P.W. Generalizations of Flows Over Time with Application in Evacuation Optimization. Ph.D. Thesis, Technical University, Berlin, Germany, 2015. [Google Scholar]
- Pyakurel, U.; Gupta, S.P.; Khanal, D.P.; Dhamala, T.N. Efficient algorithms on multicommodity flow over time problems with partial lane reversals. Int. J. Math. Math. Sci. Hindawi 2020, 2020, 2676378. [Google Scholar] [CrossRef]
- Khanal, D.P.; Pyakurel, U.; Dhamala, T.N. Prioritized multi-commodity flow model and algorithm. In Proceedings of the International Symposium on Analytic Hierarchy Process 2020, ISAHP 2020, Web Conference, 3–6 December 2020. [Google Scholar] [CrossRef]
- Pyakurel, U.; Dempe, S. Network flow with intermediate storage: Models and algorithms. SN Oper. Res. Forum 2020, 2020, 37. [Google Scholar] [CrossRef]
- Khanal, D.P.; Pyakurel, U.; Dhamala, T.N. Maximum multicommodity flow with intermediate storage. Math. Probl. Eng. Hindawi 2021, 2021, 5063207. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).