Abstract
This research focuses on the study of stochastic processes with irregularly spaced time intervals, which is present in a wide range of fields such as climatology, astronomy, medicine, and economics. Some studies have proposed irregular autoregressive (iAR) and moving average (iMA) models separately, and moving average autoregressive processes (iARMA) for positive autoregressions. The objective of this work is to generalize the iARMA model to include negative correlations. A first-order moving average autoregressive model for irregular discrete time series is presented, being an ergodic and strictly stationary Gaussian process. Parameter estimation is performed by Maximum Likelihood, and its performances are evaluated for finite samples through Monte Carlo simulations. The estimation of the autocorrelation function (ACF) is performed using the DCF (Discrete Correlation Function) estimator, evaluating its performance by varying the sample size and average time interval. The model was implemented on real data from two different contexts; the first one consists of the two-week measurement of star flares of the Orion Nebula in the development of the COUP and the second pertains to the measurement of sunspot cycles from 1860 to 1990 and their relationship to temperature variation in the northern hemisphere.
1. Introduction
Time-varying data are present in a wide variety of fields, such as economics [1], engineering [2], climatology [3], astronomy [4], and ecology [5], among others. The importance of modeling the behavior of these data is critical to generate predictions and anticipate their outcomes. Although most studies have focused on the analysis of data observed at regular time intervals, this approach does not always reflect the reality of many environments. Consequently, research has been encouraged in the development of models for time series observed at specific moments and not necessarily equidistantly.
In the literature, several alternatives are available to address the treatment of time series whose observations have been recorded at irregular time intervals. These proposals usually seek to adjust these irregular intervals to regular ones and make use of conventional models [6], or manipulate them as regular series with missing data [7,8]. These techniques work well as an approximation; however, they generally have a higher degree of bias in model fit than a model that accounts for the irregular nature of the sampling.
For the treatment of irregular series, studies have developed models with moving average structures, iMA [9]; with autoregressive structures, iAR [4,10,11]; and moving average autoregressives structures for discrete time series observed at irregular time intervals, iARMA(1,1) [12]. However, these models are proposed under the assumptions that their parameters must be positive, taking values among 0 and 1, which limits their application in time series that may have negative correlation structures. In this paper, the iARMA(1,1) model is made more flexible by extending the parameter space of (, ), so it is possible to model negative correlations.
Once the model is proposed, ACF estimators are evaluated in the context of irregular time series, which allow, from the data, the identification of whether the model is a suitable candidate, as happens in the MA(p) models, where the ACF behavior is cancelled from (), and in the AR(q) models, with decreasing exponential behavior. In their work, Ref. [13] present the algorithm BINCOR (BINned CORrelation) to estimate the correlation between two unequally spaced climate time series that are not necessarily sampled at identical points in time, which will contribute to the identification of the ACF for the proposed model.
The remainder of this paper is organized as follows. Section 2 introduces the model definition and its properties. Also, this section provides the one-step linear predictors and their mean squared errors. The maximum likelihood estimation and bootstrap method are introduced in Section 3. The finite-sample behavior of this estimator is studied via the Monte Carlo method in Section 4. Two real-life data applications are presented in Section 5. Finally, conclusions are given in Section 6.
2. The Model
The construction of a model of a stationary stochastic process with an autoregressive moving average structure considering irregularly spaced time (iARMA) is performed, where is the set of times, such that the consecutive differences , for all .
2.1. iARMA Model
Let be a sequence of uncorrelated random variables with mean 0 and variance 1, where (when ), , and
with and . The process is said to be an iARMA process if and
Note that this model allows both coefficients to take positive and negative values as long as . This condition allows the model to consider both positive and negative autocorrelation structures.
2.2. Properties
Let be a random vector of an iARMA process. Let , for all n, be a sequence of uncorrelated normal random variables; then is a normally distributed random vector with and covariance matrix
where and , for . Thus, the iARMA process is an ergodic and weakly stationary Gaussian process and, hence, strictly stationary.
Another property of the iARMA model is that it is a more general process, since when , an iMA process is obtained [9,14], while when , an iAR process is obtained [10]. Likewise, when , for all n, the traditional ARMA(1,1) model is obtained [12].
2.3. Prediction
Using the innovations algorithm [8], the one-step linear predictors are and
with mean square error and
2.4. Theoretical ACF
Taking the covariance matrix presented in Section 2.2, the theoretical ACF of the iARMA model is determined as
where .
The behavior of the ACF for the iARMA model depends on both the Lag (k) and the time intervals between observations; so, a three-dimensional representation is presented for a case where both parameters are negative in Figure 1a and another for the case where both parameters are positive in Figure 1b.

Figure 1.
(a) Theoretical ACF when and . (b) Theoretical ACF when and .
As expected, as the lag increases, the correlation between the variables decreases. The same happens as the time interval increases. On the basis of this, it can be said that an expected behavior of the ACF is obtained. The behavior of a regular ARMA(1,1) model can be visualized by taking a cross-sectional view at .
3. Estimation
3.1. Maximum Likelihood Estimation Method
MLE is used from the one-step linear predictors (Equation (3)) with distribution N(). Let be observed at points , the log-likelihood is
Concentrated criterion function was used in order to optimize the process and estimate and by minimizing the expression (5), replaced with (the optimum of ), which results in the reduced likelihood [8], . Thus, must be minimised with respect to and and then must be plugged in for the sigma estimation.
3.2. Bootstrap Method
The bootstrap method in time series is based on obtaining the residuals of a model fitted to the data, and then generating a new series including random samples of the residuals to the fitted model. The estimated standardized innovations for the iARMA model (assuming ) are , where and are the MLE estimates of the process observed at points . Normally, the residuals are centered to have the same mean as the model innovations, so model-based resampling is given by equiprobable sampling with replacement of the centered residuals , where , obtaining the simulated innovations , considering the same times of the observations, in order to define
as the bootstrapped sequence. In this way, the parameters of the sequence can be estimated through MLE. This process is repeated B times, generating a collection of bootstrapped parameter estimates that allow an estimation of the finite sample distribution of the and estimators.
4. Simulation
In this study, trajectories of size are simulated from the iARMA model (Equation (2)), considering , and , using the combinations in which both parameters have the same sign.
For each simulated series, the parameters and are estimated through the MLE, and their variances by bootstrap with resamples (methods described in Section 3.1 and Section 3.2), respectively. For this study, irregular time sequences are generated for .
4.1. ML Estimator
We define and as the ML estimates for the mth trajectory obtained by minimizing . The standard errors are estimated via the curvature of the likelihood surface in and . The calculated quantities of the M trajectories are summarized with an average and their variances
4.2. Bootstrap Estimator
In order to determine the behavior of the estimators and and to estimate their respective variances, B resamplings are performed for each mth MLE trajectory, defining them as bootstrap estimators and their variances: and , respectively, in which the behavior of the variances obtained by bootstrap is compared with the variances of the estimators by MLE.
4.3. Performance Measures
The root mean square error (RMSE) and the coefficient of variation (CV) are proposed as performance measures of the estimators by MLE. Taking as , we define and .
4.4. Simulation Results
The bootstrap method is useful to identify the variance of ML estimators, since in reality there is usually only one path, so the variance cannot be obtained from the result of many ML estimates. As we see in Table 1, the performance of bootstrap variance estimates improves when the sample size is large, so if the sample size is not large enough in real data, there is a greater likelihood of high variability in the estimates of the parameters of the data. Bias, RMSE, and CV are smaller when N increases as expected. Although better results are obtained for than for , the values obtained are consistent.

Table 1.
Monte Carlo results for the ML estimator with irregularly spaced times for different values of , , and N.
4.5. ACF Estimation
The DCF estimator was used to estimate the autocorrelation function of the proposed model and to analyse its behavior. ACF is fundamental to obtain key information on the temporal dependencies between the values of the time series and facilitates the choice of an appropriate model that can also generate a good forecast by identifying whether there are cyclical behaviors or important dependencies.
The DCF estimator proposed by [15] was applied, following the algorithm outlined in [13]. The approach relies on transforming an irregularly spaced series into a regular one using an average time interval .
Trajectories were generated by changing the sample size for , , , and , , analysing the first ten lags. These estimates are compared with the theoretical ACF (Equation in Section 2.4), revealing that the theoretical ACFs in Figure 2a,b perform better than the positive parameter scenarios (Figure 3a,b), as these series have smoother fluctuations allowing several points in the primary series to be replaced with a single value in the binned series. Consequently, the differs significantly from that of the irregular series in these cases, impacting their theoretical ACF.

Figure 2.
Comparison between theoretical ACF (right) and ACF estimated with DCF (left) for a binned serie with y . (a) . (b) .

Figure 3.
Comparison between theoretical ACF (right) and ACF estimated with DCF (left) for a binned serie with y . (a) . (b) .
5. Applications
Two application cases with real data are presented. The first one corresponds to the two-week measurement of starbursts from the Orion Nebula in the development of the Chandra Orion Ultradeep Project (COUP) and the second one case is related to the measurement of solar cycles and their relationship with temperature variation in the northern hemisphere.
5.1. Chandra Orion Ultradeep Project
For two weeks, the most extensive data collection in the field of X-ray astronomy was carried out through the COUP, where observations of the amount of energy released as flares in the young star region of the Orion Nebula were made from NASA’s Chandra X-ray Observatory. From this study, Ref. [16] resulted in the detection of 1616 X-ray sources, of which one (COUP263) was taken for the analysis of interest in this study. The simplified information consists of the photon arrival time (measured in seconds) and the photon energy (measured in kiloelectronvolts, keV); however, because the measurement in seconds generates very large time intervals between each observation (values among 19 and 24,537 s, with an average of 4071 s, Figure 4a), it was chosen to analyse them as the . The results of the estimation of the and parameters by MLE, and of their respective bootstrap variances (B = 500) are presented in Table 2, where it is identified that a strong autoregressive structure is suggested.
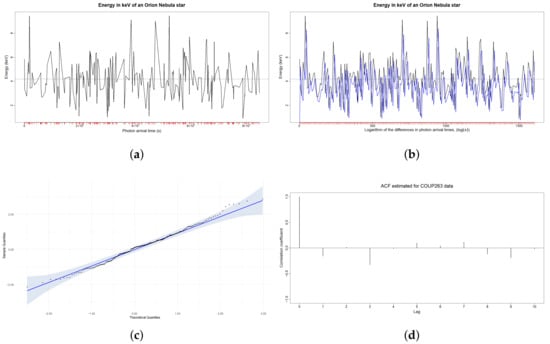
Figure 4.
(a) COUP263 trajectory in seconds. (b) In blue, COUP263 data forecast from the iARMA model. In black, the original data with the logarithm of the differences in photon arrival times, . (c) QQ-plot of residuals with normality bands. (d) ACF estimated from COUP263 data.

Table 2.
iARMA model estimates for COUP263 data.
Figure 4b presents the trajectory of COUP263, with the transformed times in a black line. Good estimation behavior is observed (blue line), obtaining normality in the residuals in Figure 4c, and a p-value = in the Shapiro–Wilk test. However, the estimation of the ACF did not have the expected behavior, since having an average time interval of 7.71, it is expected that the first coefficient is very close to 1 as a consequence of the obtained estimations, but had a negative value. When analysing the behavior of the estimation, it became evident that the DCF adjustment created a binned series with a size of 42 observations, which generated an average time much longer than the original (38.44), which affects the behavior of the ACF.
5.2. Sunspot Cycle
Ref. [17] identified a direct influence between the Earth’s climate and the variation of the solar cycle length through measurements of air temperature in the northern hemisphere from 1860 to 1990, and their comparison with sunspot cycles in the same period. The information analysed is based on 24 data with sunspot cycle lengths (years) from 1860 to 1990, with a mean of 5.35 years. By examining the trajectory of the analyzed data (Figure 5a), two pronounced trends of mean decrease and increase are identified, indicating that stationarity is not guaranteed. To address this, the series is differentiated to ensure a constant mean. In Table 3, the values of the and estimators are presented, having a case in which both parameters are negative.
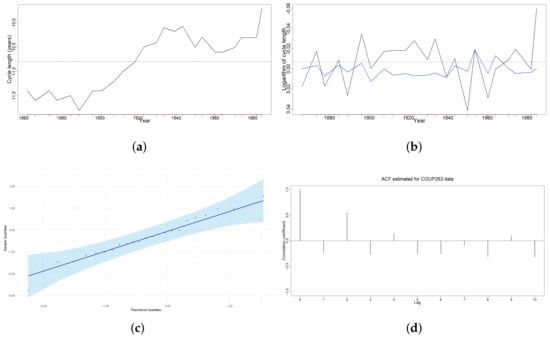
Figure 5.
(a) Transformation of the logarithm of the sunspot cycle length from 1860 to 1990. (b) In blue, the sunspot cycle length forecast from the iARMA model. In black, the original data. (c) QQ plot of residuals with normality bands. (d) ACF estimated from transformed solar cycle length data.

Table 3.
iARMA model estimates for sunspot cycle data.
The residuals are tested for normality with a value- 0.8647 in the Shapiro–Wilk test. It shows that despite being a much smaller sample than the previous example, a good prediction of the model is maintained. In this case, the ACF (Figure 5d) correctly estimates the trajectory behavior with a negative and alternating sign in the following correlation coefficients, approximating the values of the correlation coefficients quite well. This optimal behavior is due to the fact that the average time interval handled in the binned series was not significantly affected, so it is close to that expected.
6. Conclusions
A first-order moving average autoregressive model for irregularly spaced time intervals is presented, based on the proposal of [12], extending the correlation structure for both negative and positive parameters, limited to cases where the parameters have the same sign. The model is an ergodic and strictly stationary Gaussian process.
The use of Maximum Likelihood estimation showed good results for both positive and negative structures; however, the result improves as the sample size increases. The best results were obtained when positive coefficients were used. The estimates for were better than those for , showing lower dispersion (smaller CV) and values closer to the true value (lower bias and RMSE). This can be analysed as an effect of the correlation structure, since relates to the autoregressive structure, where the data at time n is correlated with all past data for which information is available, while the moving average structure () is only correlated with the immediately previous data, which generates a greater variability effect at the time of estimating .
The estimation of the variance of the ML estimators was performed by bootstrap, identifying better behavior as the sample size increases. Good performance for both positive and negative scenarios was obtained. In general terms, the estimates of were better than those of as they presented lower dispersion even with a small sample size.
The DCF estimator had good results for estimating the ACF and identifying whether it is a scenario with parameters with positive or negative signs; however, as the average distance of the times increases, the estimation does not present the best results, mainly when the coefficients are very close to 0, with a greater probability of obtaining results with the opposite sign. This is a sparse result as a consequence of the weakness of the autocorrelation when the observations are further apart.
Finally, the practical application of the proposed model was exemplified by means of two real cases related to astronomical and climatic time series.
The model obtained had the limitation of being applied only in cases where the signs of both parameters are equal (). It is proposed for future research to include correlations when the parameters have different signs, which can be widely found in real fields of application.
Author Contributions
Conceptualization, D.A.G.P. and C.A.O.E.; Data curation, D.A.G.P.; Formal analysis, D.A.G.P.; Methodology, D.A.G.P. and C.A.O.E.; Software, D.A.G.P.; Supervision, C.A.O.E.; Validation, D.A.G.P. and C.A.O.E.; Visualization, D.A.G.P.; Writing–original draft, D.A.G.P.; Writing–review and editing, D.A.G.P. and C.A.O.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are available in this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Franses, P.H. Estimating persistence for irregularly spaced historical data. Qual. Quant. 2021, 55, 2177–2187. [Google Scholar] [CrossRef]
- Coelho, M.; Fernandes, C.V.S.; Detzel1, D.H.M.; Mannich, M. Statistical validity of water quality time series in urban watersheds. Braz. J. Water Resour. 2017, 22, e51. [Google Scholar] [CrossRef]
- Ólafsdóttir, K.B.; Schulz, M.; Mudelsee, M. REDFIT-X: Cross-spectral analysis of unevenly spaced paleoclimate time series. Comput. Geosci. 2016, 91, 11–18. [Google Scholar] [CrossRef]
- Elorrieta, F.; Eyheramendy, S.; Palma, W. Discrete-time autoregressive model for unequally spaced time-series observations. Astron. Astrophys. 2019, 627, A120. [Google Scholar] [CrossRef]
- Liénard, J.F.; Gravel, D.; Strigul, N.S. Data-intensive modeling of forest dynamics. Environ. Model. Softw. 2015, 67, 138–148. [Google Scholar] [CrossRef]
- Shukla, S.N.; Marlin, B.M. A survey on principles, models and methods for learning from irregularly sampled time series. arXiv 2020, arXiv:2012.00168. [Google Scholar]
- Erdogan, E.; Ma, S.; Beygelzimer, A.; Rish, I. Statistical Models for Unequally Spaced Time Series; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2005. [Google Scholar]
- Brockwell, P.J.; Davis, R.A. Time Series: Theory and Methods; Springer Science & BUSINESS Media: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Ojeda, C.; Palma, W.; Eyheramendy, S.; Elorrieta, F. Extending time-series models for irregular observational gaps with a moving average structure for astronomical sequences. RAS Tech. Instrum. 2023, 2, 33–44. [Google Scholar] [CrossRef]
- Eyheramendy, S.; Elorrieta, F.; Palma, W. An irregular discrete time series model to identify residuals with autocorrelation in astronomical light curves. Mon. Not. R. Astron. Soc. 2018, 481, 4311–4322. [Google Scholar] [CrossRef]
- Rumyantseva, O.; Sarantsev, A.; Strigul, N. Time series analysis of forest dynamics at the ecoregion level. Forecasting 2020, 2, 20. [Google Scholar] [CrossRef]
- Ojeda, C.; Palma, W.; Eyheramendy, S.; Elorrieta, F. A Novel First-Order Autoregressive Moving Average Model to Analyze Discrete-Time Series Irregularly Observed. In Theory and Applications of Time Series Analysis and Forecasting; Springer: Cham, Switzerland, 2023; pp. 91–103. [Google Scholar]
- Polanco-Martinez, J.M.; Medina-Elizalde, M.A.; Sanchez Goni, M.F.; Mudelsee, M. BINCOR: An R package for estimating the correlation between two unevenly spaced time series. R J. 2019, 11, 170–184. [Google Scholar] [CrossRef]
- Ojeda, C.; Palma, W.; Eyheramendy, S.; Elorrieta, F. An irregularly spaced first-order moving average model. arXiv 2021, arXiv:2105.06395. [Google Scholar] [CrossRef]
- Edelson, R.; Krolik, J. The discrete correlation function-A new method for analyzing unevenly sampled variability data. Astrophys. J. Part 1 1988, 333, 646–659. [Google Scholar] [CrossRef]
- Getman, K.V.; Flaccomio, E.; Broos, P.S.; Grosso, N.; Tsujimoto, M.; Townsley, L.; Garmire, G.P.; Kastner, J.; Li, J.; Harnden, F.R., Jr.; et al. Chandra Orion Ultradeep Project: Observations and Source Lists. Astrophys. J. Suppl. Ser. 2005, 160, 319–352. [Google Scholar] [CrossRef]
- Friis-Christensen, E.; Lassen, K. Length of the Solar Cycle: An Indicator of Solar Activity Closely Associated with Climate. Science 1991, 254, 698–700. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).