Benchmarking Foundation Models for Time-Series Forecasting: Zero-Shot, Few-Shot, and Full-Shot Evaluations ^†

Abstract

Recently, time-series forecasting foundation models trained on large, diverse datasets have demonstrated robust zero-shot and few-shot capabilities. Given the ubiquity of time-series data in IoT, finance, and industrial applications, rigorous benchmarking is essential to assess their forecasting performance and overall value. In this study, our objective is to benchmark foundational models from Amazon, Salesforce, and Google against traditional statistical and deep learning baselines on both public and proprietary industrial datasets. We evaluate zero-shot, few-shot, and full-shot scenarios using metrics such as sMAPE and NMAE on fine-tuned models, ensuring reliable comparisons. All experiments are conducted with onTime, our dedicated open-source library that guarantees reproducibility, data privacy, and flexible configuration. Our results show that foundation models often outperform traditional methods with minimal dataset-specific tuning, underscoring their potential to simplify forecasting tasks and bridge performance gaps in data-scarce settings. Additionally, we address non-performance criteria, such as integration ease, model size, and inference/training time, which are critical for real-world deployment.

1. Introduction

The ability to forecast is one of the most prevalent uses of modeling. From weather forecasting to anomaly detection for specific industrial machines, accurately predicting the next few data points can significantly impact outcomes. Therefore, to be able to choose the right predictor is of critical importance.

In this paper, we explore some of the most recent modeling methods used to predict time series. These models are called foundation models and are becoming gradually more prevalent in the literature. For instance, notable examples include Chronos by Amazon, Moirai by Salesforce, and TimesFM by Google [1,2,3]. These models are based on methods similar to those used in foundation models for other applications, such as NLP.

Today, data scientists can rely on existing benchmarks such as GIFT-Eval or ProbTS to guide the selection of foundation models [4,5]. However, when applying these models to their own datasets, the results may differ from those reported. Furthermore, the benchmarks often consider the zero-shot scenario of those models, whereas the latter models can be trained and used in few-shot or full-shot scenarios as well, leaving practitioners with an incomplete view of the models’ true potential.

Therefore, our research question revolves around the use of time series with foundation models and is as follows: “What is the performance of foundation models for time series forecasting and analysis on industrial datasets, particularly in the context of few-shot and zero-shot learning for specific use cases?”

Given the modernity of these models, this task involves challenges. Each model is rather large, requires significant computational power, has no unified interface, can treat time-series differently (e.g., as uni- or multi-variate, etc.), and the models’ metrics are difficult to choose.

In summary, the ability to position the performance of a given model on a specific dataset is of utmost importance. It enables practitioners to leverage these models and accelerates the technological transfer from academia to industry.

The outline of our paper is structured within the framework of the scientific method. First, we explain the method based on a benchmarking tool that we developed. Second, we present the results of our benchmark. Finally, we discuss the implications of these results.

2. Materials and Methods

Our work’s objective is to evaluate the performance of recent foundation models in comparison with traditional methods. The following sections introduce our method, which aims to be as fair as possible. First, we present the choice of datasets, models, and metrics. Then, we introduce our method, which fits different training and evaluation scenarios.

2.1. Datasets

Our dataset selection, presented in

Table 1. All datasets used to train the models. These datasets cover a wide range of use cases.

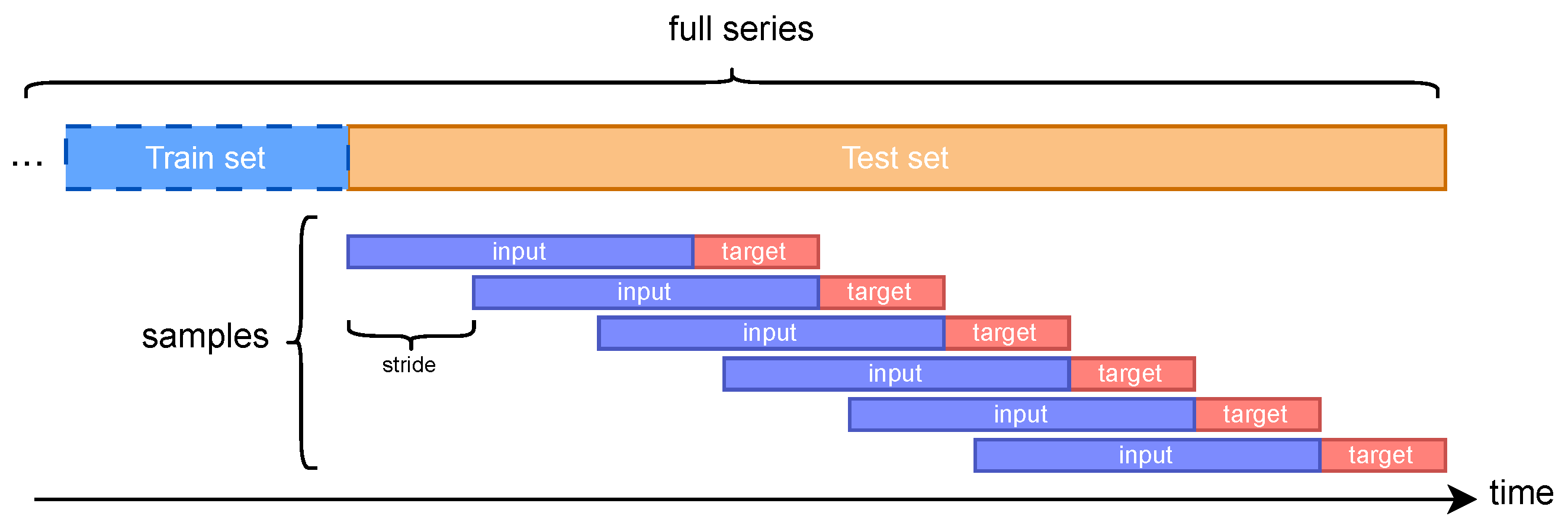
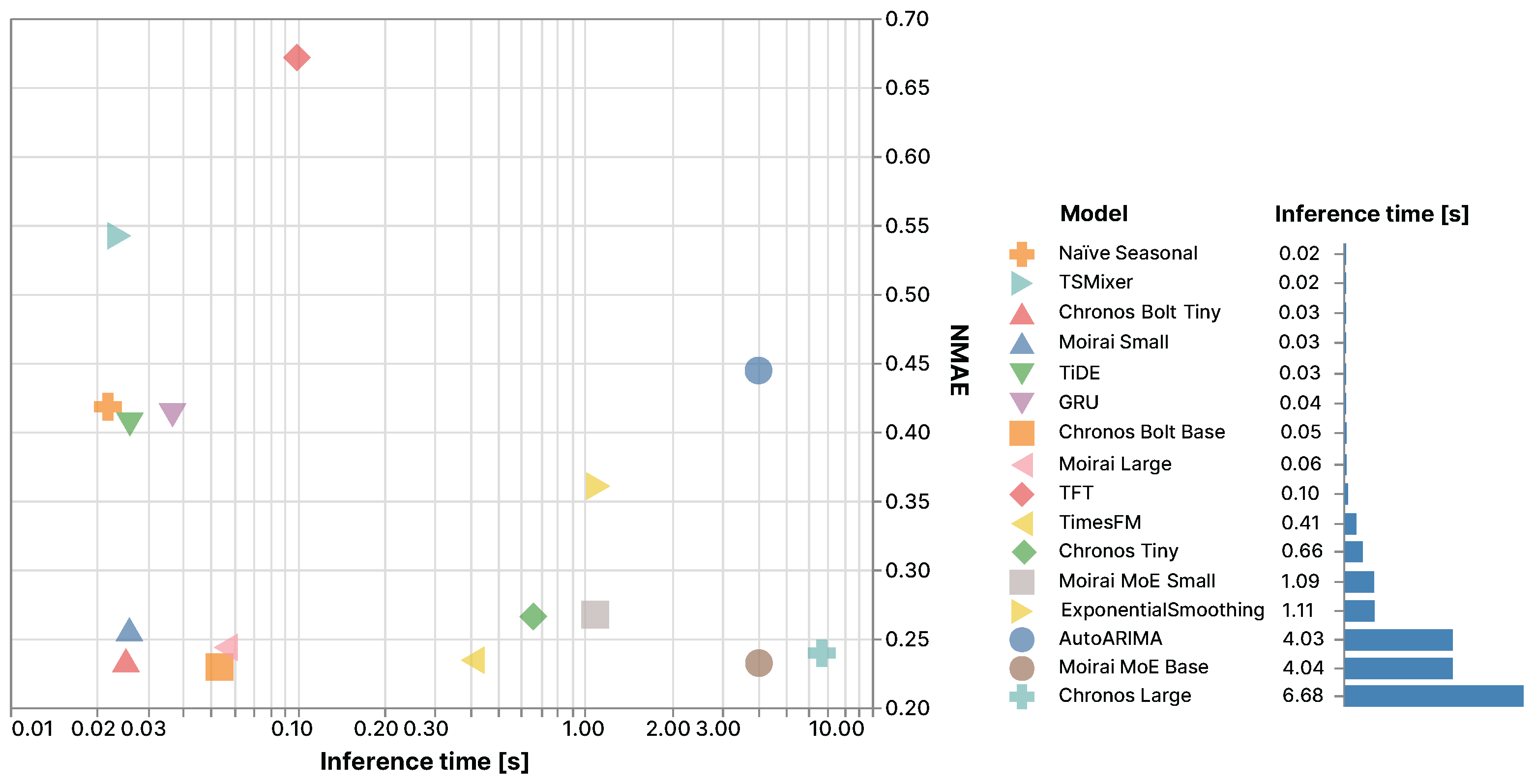
Dataset	Type	# Features	Resolution	# Target Features	Size
Energy [7]	Academic	20	1 h	1 (Total load)	35,064
ETTh1 [8]	Academic	7	1 h	1 (Oil temp.)	17,420
ETTm1 [8]	Academic	7	15 min	1 (Oil temp.)	69,680
ExchangeRate [9]	Academic	8	1 day	8 (All)	7588
Weather [10]	Academic	21	10 min	21 (All)	52,704
ZurichElectricity [11,12]	Academic	10	15 min	2 (Consumption)	93,409
HEIA1h	Industrial	8	1 h	8 (All)	11,664
MeteoSwiss [13]	Industrial	8	10 min	24 (All)	105,264

, aims to represent both reference data frequently used in academia and industrial data that no model has ever seen during training. All academic datasets were sourced through the Darts Python library [6]. For consistency, a context window of 512 time steps is used across all datasets. We evaluate forecasting performance at horizons of 24, 48, 96, and 192 time steps, with a particular focus on the 96-step horizon in most experiments.

The energy dataset covers hourly energy generation and weather in Spain from 2015 to 2018; eight constant features were removed. ETTh1 and ETTm1 contain hourly and 15-minute multivariate data from an electricity transformer, used to forecast oil temperature based on power load features. ExchangeRate contains daily exchange rates for eight countries from 1990 to 2016. Weather includes 21 weather indicators, such as temperature and humidity, recorded every 10 min in Germany during 2020. ZurichElectricity reports 15-minute resolution electricity consumption in Zurich up to 2022, combining household and business usage with interpolated weather data. HEIA reports hourly electricity consumption from eight buildings at our engineering school in Fribourg, Switzerland. Finally, MeteoSwiss provides 10 min meteorological data from Fribourg/Grangeneuve, with features like pressure, wind, and humidity.

The datasets are split in a standard way, with 80% used for training and 20% for testing. For the deep learning models presented in the next section, the data are standardized to zero mean and unit variance using z-score normalization. In contrast, no normalization is applied to the statistical models, while for the foundation models, data normalization is handled internally by their respective implementations.

2.2. Models

Table 2. Overview of all models used for the benchmark.

Model	Type	Prediction Type	# Parameters
NaïveSeasonal	Statistical	Univariate	Not applicable
AutoARIMA [14]	Statistical	Univariate	<100
ExpotentialSmoothing	Statistical	Univariate	Not applicable
GRU [15]	Deep learning	Multivariate	3–160 K
TiDE [16]	Deep learning	Multivariate	285 K–8.5 M
TFT [17]	Deep learning	Multivariate	3–36 K
TSMixer [18]	Deep learning	Multivariate	19–931 K
Chronos Tiny † [1]	Foundation	Univariate	8 M
Chronos Large † [1]	Foundation	Univariate	710 M
Chronos Bolt Small [1]	Foundation	Univariate	48 M
Chronos Bolt Base [1]	Foundation	Univariate	205 M
Moirai small † [19]	Foundation	Multivariate	14 M
Moirai large † [19]	Foundation	Multivariate	311 M
Moirai MoE Small [2]	Foundation	Multivariate	117 M
Moirai MoE Base [2]	Foundation	Multivariate	935 M
TimesFM [3]	Foundation	Univariate	500 M

^† These models are also finetuned.

presents all models we considered for our benchmark. The 16 models can be split into three categories: (1) statistical, (2) deep learning, and (3) foundational. Those models have different characteristics: some are able to model multivariate data, while others focus on univariate series; the number of parameters varies; and one statistical model is included as a naive baseline for reference.

The hyperparameters of the deep learning models are optimized using the Optuna library in Python [20]. While each model has its own specific set of tunable parameters, several common hyperparameters—such as output chunk length, learning rate and its scheduler, dropout rate, and batch size—were consistently optimized across all models.

2.3. Metrics

The different metrics chosen for this benchmark must enable comparison across datasets and model characteristics (for instance, uni- vs. multivariate output). Therefore, scale-independent metrics such as sMAPE and NMAE were chosen over traditional metrics like MSE or MAE.

sMAPE (Symmetric Mean Absolute Percentage Error) evaluates the relative error as a percentage, symmetrically penalizing over- and under-predictions. sMAPE is calculated as shown in Equation (1). Unlike traditional MAPE, sMAPE avoids division by zero and ensures that the metric remains bounded, making it well-suited for datasets with values near zero.

NMAE (Normalized Mean Absolute Error) expresses the total absolute error relative to the total magnitude of the true values. It provides an interpretable, scale-independent measure of forecast accuracy, which is particularly useful for comparing performance across datasets with different units or scales. NMAE is computed as shown in Equation (2).

$$\mathrm{sMAPE}=200\times {\displaystyle \frac{1}{T}}\sum _{t=1}^T{\displaystyle \frac{|y_t-{\widehat{y}}_t|}{\left(\right|y_t|+|{\widehat{y}}_t\left|\right)}}$$

(1)

$$\mathrm{NMAE}={\displaystyle \frac{{\sum }_{t=1}^T\left|y_t-{\widehat{y}}_t\right|}{{\sum }_{t=1}^T\left|y_t\right|}}$$

(2)

By normalizing the absolute error by the total observed magnitude, NMAE avoids scale-related issues and allows a fair evaluation across different datasets or targets.

For multivariate forecasting, metrics are computed per component and averaged to yield a single aggregated performance score across all target variables.

2.4. Scenarios

Once the trio of models, datasets, and metrics is defined, different training scenarios are tested along two dimensions: (1) the amount of training data and (2) the prediction length.

The amount of training data can vary from none (zero-shot) to a little (few-shots) and to most of the dataset (full-shot). Statistical and deep-learning models have been trained in full-shot setting on the datasets from Section 2.1. Foundation models are first evaluated in a zero-shot setting, then fine-tuned for few-shot scenarios of varying training data proportion, and finally for full-shot scenarios. This dimension allows us to understand how effectively a model can capture patterns or characteristics within the data.

Regarding the prediction length, the lengths mentioned in Section 2.1 are considered (24, 48, 96, and 192 time-steps). This allows us to evaluate the ability of a model to capture dependencies as a function of time.

2.5. Evaluation Framework and Infrastructure

To create this benchmark, we developed an evaluation framework based on the onTime library [21]. This tool eases the development of all scenarios while increasing the certainty that experiments are executed in the exact same way. To define such experiments, the trio datasets, models, and metrics can be defined easily in a Python file. This framework is extensible via abstract classes, which allows a practitioner to specify a custom implementation.

While training is handled by each model’s implementation, evaluation is performed in a unified way across all models to ensure fair comparison. Specifically, a sliding window with a stride equal to the prediction horizon is used to generate multiple input–target samples from the test set. These are provided to the model after training, or directly in the case of zero-shot foundation models. Figure 1 illustrates this sampling process.

In terms of infrastructure, all experiments are performed on a Slurm cluster in version 24.05.3 with the following NVIDIA GPUs (NVIDIA Corporation, Santa Clara, CA, USA): (1) RTX A6000 with 48 GB, (2) A40 with 48 GB, and (3) TITAN RTX with 24 GB. Once all models are trained, a single GPU (A40) is used to compute all inference times, thus allowing a fair comparison.

3. Results

In this section, we present the results of the benchmark described in Section 2. First, we report the performance of the baseline models and compare them to the foundation models in a zero-shot setting (Section 3.1). Next, we analyze the performance of the foundation models across varying prediction horizons (Section 3.2). Finally, we evaluate the foundation models in few-shot settings, considering different proportions of the training data (Section 3.3).

3.1. Predictions Across Models

The baseline results from

Table 3. Forecasting performance of baseline models on a prediction horizon of 96 time steps. The best score per row is shown in bold; the second-best is underlined.

		Deep Learning				Statistical
	Metrics	GRU	TFT	TiDE	TSMixer	Naive Seasonal	AutoARIMA	ES †
Energy	sMAPE	13.49	15.25	8.102	9.724	20.56	13.34	22.67
	NMAE	0.1332	0.1507	0.0825	0.0952	0.1946	0.1318	0.2215
ETTh1	sMAPE	35.00	47.15	40.11	38.13	34.49	33.60	35.80
	NMAE	0.4003	0.6310	0.4097	0.5261	0.3627	0.3526	0.3781
ETTm1	sMAPE	32.11	41.53	55.02	26.05	22.27	23.59	24.55
	NMAE	0.3190	0.6568	1.040	0.2950	0.2325	0.2369	0.2462
ExchangeRate	sMAPE	15.55	18.06	11.45	15.34	2.336	2.514	2.537
	NMAE	0.1428	0.1631	0.1049	0.1416	0.0234	0.0249	0.0252
Weather	sMAPE	79.09	81.48	62.53	65.67	54.58	61.77	66.82
	NMAE	250.0	223.5	50.21	39.41	1.073	10.85	38.16
ZurichElectricity	sMAPE	14.20	21.87	5.395	8.260	18.53	18.49	23.39
	NMAE	0.1401	0.2160	0.0548	0.0835	0.1871	0.1858	0.2416
HEIA	sMAPE	42.26	52.47	29.56	39.48	39.99	41.65	31.28
	NMAE	0.5380	0.6706	0.3240	0.5422	0.4182	0.4445	0.3606
MeteoSwiss	sMAPE	75.64	89.08	64.64	80.11	68.98	71.96	72.76
	NMAE	1.641	2.170	1.085	1.810	2.152	1.768	2.664

^† ES = Exponential Smoothing.

feature deep learning and statistical models. The results are consistent across metrics, and TiDE provides the best predictions in most cases, followed by Naïve Seasonal and AutoARIMA.

In

Table 4. Forecasting performance of foundation models on a prediction horizon of 96 time steps, evaluated in a zero-shot setting. The best baselines scores from Table 3 are also reported. The best score per row is in bold; the second best is underlined.

		Moirai		Moirai-MoE		Chronos		Chronos Bolt		TFM †	BB ‡
	Metrics	Small	Large	Small	Base	Tiny	Large	Tiny	Base
Energy	sMAPE	7.360	7.134	7.088	7.062	7.508	4.854	6.183	5.095	7.035	8.102
	NMAE	0.0744	0.0718	0.0719	0.0718	0.0751	0.0491	0.0622	0.0511	0.0708	0.0825
ETTh1	sMAPE	32.64	34.61	33.25	34.04	31.15	30.68	31.95	30.56	31.40	33.60
	NMAE	0.3382	0.3344	0.3333	0.3370	0.3242	0.3217	0.3408	0.3334	0.3231	0.3526
ETTm1	sMAPE	23.66	24.64	24.78	23.64	22.95	21.61	21.58	22.40	22.45	22.27
	NMAE	0.2461	0.2658	0.2569	0.2488	0.2347	0.2303	0.2346	0.2329	0.2521	0.2325
ExchangeRate	sMAPE	2.505	2.687	2.470	2.535	2.714	2.583	2.412	2.552	2.565	2.336
	NMAE	0.0251	0.0273	0.0248	0.0255	0.0270	0.0260	0.0242	0.0255	0.0256	0.0234
Weather	sMAPE	64.20	64.43	62.01	59.47	63.47	61.83	62.40	61.81	45.05	54.58
	NMAE	2.663	9.052	11.05	5.192	13.03	0.4987	6.455	4.629	1.243	1.073
ZurichElectricity	sMAPE	17.92	18.06	17.30	15.63	8.368	6.119	5.635	4.177	7.292	5.395
	NMAE	0.1769	0.1804	0.1727	0.1540	0.0872	0.0639	0.0592	0.0440	0.0768	0.0548
HEIA	sMAPE	22.74	20.89	23.31	20.20	23.33	20.73	20.37	19.71	20.67	29.56
	NMAE	0.2570	0.2423	0.2670	0.2321	0.2687	0.2411	0.2343	0.2294	0.2343	0.3240
MeteoSwiss	sMAPE	67.72	66.98	66.14	66.49	67.99	62.95	67.58	65.18	62.74	64.64
	NMAE	0.8146	1.488	2.442	1.173	1.657	1.662	0.9932	1.377	0.9777	1.085

^† TFM = TimesFM, ^‡ BB = Best baselines.

, we observe that foundation models perform better than the best baseline from Table 3. The best foundation models are Chronos Bolt Base and Chronos Large, followed by Chronos Tiny and TimesFM. For some datasets, the performance across metrics shows a slight instability.

Figure 2 illustrates the trade-off between inference efficiency and forecasting error on the HEIA dataset. The bar chart (on the right) shows large differences in inference time across models: deep learning models are generally faster than foundation models, although lightweight variants like Chronos Bolt Tiny and Moirai Small also exhibit low inference times. In contrast, larger models such as Chronos Large and Moirai MoE Base are slower, as are AutoARIMA and Exponential Smoothing.

The scatter plot (on the left) highlights that foundation models offer the best accuracy while maintaining competitive latency. Chronos Bolt and Moirai models represent a favorable trade-off, achieving both low error and fast inference.

3.2. Predictions Horizons

In terms of prediction horizon,

Table 5. Forecasting performance of foundation models on different prediction horizons, evaluated in a zero-shot setting. NMAE is reported. The best score per row is in bold; the second-best is underlined.

		Moirai		Moirai-MoE		Chronos		Chronos Bolt		TFM †
	Horizons	Small	Large	Small	Base	Tiny	Large	Tiny	Base
Energy	24	0.0643	0.0592	0.0591	0.0528	0.0563	0.0338	0.0503	0.0385	0.0589
	48	0.0719	0.0678	0.0678	0.0628	0.0678	0.0414	0.0587	0.0442	0.0676
	96	0.0744	0.0718	0.0719	0.0718	0.0751	0.0491	0.0622	0.0511	0.0708
	192	0.0773	0.0755	0.0746	0.0802	0.0754	0.0529	0.0646	0.0556	0.0734
ETTh1	24	0.2048	0.2104	0.1970	0.2021	0.2011	0.2074	0.1999	0.1944	0.2077
	48	0.2619	0.2713	0.2503	0.2547	0.2447	0.2490	0.2495	0.2517	0.2536
	96	0.3382	0.3344	0.3333	0.3370	0.3242	0.3217	0.3408	0.3334	0.3231
	192	0.2883	0.2969	0.3063	0.2905	0.2849	0.2838	0.3070	0.2870	0.2784
ETTm1	24	0.1616	0.1967	0.1752	0.1755	0.1796	0.1446	0.1479	0.1443	0.1643
	48	0.2515	0.2742	0.2574	0.2571	0.2382	0.2166	0.2397	0.2307	0.2594
	96	0.2461	0.2658	0.2569	0.2488	0.2347	0.2303	0.2346	0.2329	0.2521
	192	0.2917	0.3094	0.3055	0.3007	0.2950	0.2870	0.3008	0.3017	0.2977
ExchangeRate	24	0.0138	0.0133	0.0128	0.0130	0.0140	0.0136	0.0131	0.0136	0.0132
	48	0.0177	0.0179	0.0171	0.0174	0.0186	0.0184	0.0170	0.0182	0.0180
	96	0.0251	0.0273	0.0248	0.0255	0.0270	0.0260	0.0242	0.0255	0.0256
	192	0.0350	0.0472	0.0394	0.0397	0.0406	0.0375	0.0340	0.0343	0.0346
Weather	24	0.8605	0.4102	0.5990	0.8083	2.260	0.3976	2.760	0.6189	0.6271
	48	2.915	1.317	6.538	7.237	1.779	0.9095	6.655	1.919	1.834
	96	2.663	9.052	11.05	5.192	13.03	0.4987	6.455	4.629	1.243
	192	0.5276	0.6359	0.8007	0.7821	0.7816	0.5519	0.6735	0.5559	0.6298
ZurichElectricity	24	0.0883	0.0758	0.0721	0.0596	0.0339	0.0244	0.0292	0.0233	0.0316
	48	0.1576	0.1413	0.1403	0.1076	0.0501	0.0297	0.0348	0.0289	0.0441
	96	0.1769	0.1804	0.1727	0.1540	0.0872	0.0639	0.0592	0.0440	0.0768
	192	0.1757	0.1838	0.1752	0.1621	0.1056	0.0825	0.0667	0.0501	0.0926
HEIA	24	0.2220	0.1959	0.2131	0.1924	0.2123	0.1837	0.1998	0.1937	0.2013
	48	0.2459	0.2177	0.2479	0.2111	0.2322	0.2086	0.2173	0.2098	0.2206
	96	0.2570	0.2423	0.2670	0.2321	0.2687	0.2411	0.2343	0.2294	0.2343
	192	0.2687	0.2659	0.2807	0.2467	0.2762	0.2540	0.2437	0.2408	0.2507
MeteoSwiss	24	0.6949	0.8155	0.8457	0.6222	0.7558	0.7167	0.6576	0.8176	0.6057
	48	1.153	1.441	1.771	1.016	1.457	1.297	1.045	1.346	0.9871
	96	0.8146	1.488	2.442	1.173	1.657	1.662	0.9932	1.377	0.9777
	192	1.226	1.530	1.850	1.898	1.584	1.374	1.295	1.231	1.336

^† TFM = TimesFM.

showcases the ability of models to predict different horizons. The best models align with the results from the previous Table 4. The awaited result is that the longer the prediction horizon, the more difficult it is to predict. However, when looking at the scores, the aforementioned statement is not always confirmed, and the scores can be interpreted as instabilities that are difficult to characterize.

3.3. Few-Shot Learning with Various Data Proportions

Finally, we test the gain in score as a function of the proportion of the data seen by the model.

Table 6. Forecasting performance of fine-tuned foundation models using different proportions of available training data from 0% (zero-shot) to 100% (full-shot). NMAE is reported. The best score for a given dataset and model is shown in bold. The overall best score for each dataset across all models is highlighted in bold red, and the second-best is underlined in red.

		Moirai		Chronos
	Proportions	Small	Large	Tiny	Large
Energy	0%	0.0744	0.0718	0.0751	0.0491
	33%	0.0727	0.0704	0.0649	0.0549
	67%	0.0667	0.0658	0.0594	0.0495
	100%	0.0687	0.0661	0.0599	0.0445
ETTh1	0%	0.3382	0.3344	0.3242	0.3217
	33%	0.3146	0.3307	0.3315	0.3161
	67%	0.3173	0.3167	0.3157	0.3272
	100%	0.3127	0.3346	0.3099	0.3460
ETTm1	0%	0.2461	0.2658	0.2347	0.2303
	33%	0.2404	0.3616	0.2459	0.2540
	67%	0.2686	0.3693	0.2484	0.2754
	100%	0.2437	0.2558	0.2198	0.2308
ExchangeRate	0%	0.0251	0.0273	0.0270	0.0260
	33%	0.0282	0.0694	0.0319	0.0319
	67%	0.0250	0.0360	0.0285	0.0299
	100%	0.0285	0.0779	0.0251	0.0302
Weather	0%	2.663	9.052	13.03	0.4987
	33%	3.793	6.041	2.053	0.9532
	67%	6.670	2.425	1.670	3.274
	100%	2.459	3.703	8.644	5.433
ZurichElectricity	0%	0.1769	0.1804	0.0872	0.0639
	33%	0.0482	0.0475	0.0326	0.0295
	67%	0.0419	0.0526	0.0323	0.0277
	100%	0.0499	0.0535	0.0333	0.0265
HEIA	0%	0.2570	0.2423	0.2687	0.2411
	33%	0.2631	0.2736	0.3271	0.2574
	67%	0.2991	0.2920	0.2981	0.2488
	100%	0.2653	0.2728	0.2494	0.2420
MeteoSwiss	0%	0.8146	1.488	1.657	1.662
	33%	0.5650	0.6690	0.6111	0.9706
	67%	0.4954	0.4532	1.446	0.7739
	100%	0.5396	0.5316	0.7382	0.6285

reports forecasting performance for 0% (zero-shot), 33%, 67%, and 100% (full-shot) scenarios. The results indicate that fine-tuning provides added value in most cases. However, Chronos Large appears to benefit less from fine-tuning compared to other models. Additionally, fine-tuning does not yield improvements when the data presents a more random character, which could indicate a data issue.

4. Discussion

In the context of this benchmark, we asked ourselves the following questions: “What is the performance of foundation models for time series forecasting and analysis on industrial datasets, particularly in the context of few-shot and zero-shot learning for specific use cases?”. To answer this question, we performed an extensive analysis of the models listed in Table 2 with an evaluation procedure testing cases such as datasets, prediction length, and data quantity.

The results presented in the previous section show the superiority of foundational models when compared with traditional methods in various contexts. First, as seen in Table 4, the latter models mostly provide better resulting metrics on prediction tasks. Second, as seen on Figure 2, when their size remains small, their inference speed is on par with the fastest traditional models. Third, when used in zero-shot settings, they do not require model-specific retraining.

However, such models are not a solution to all predictive needs. Having sizes varying from 8M to 700M parameters, their larger versions are computationally intensive and slow, limiting applications in resource-constrained contexts. Albeit, the smallest versions provide great predictive performances compared to most baseline models (see Figure 2) within a very portable model, thus allowing for numerous applied usages.

When benchmarking, we noted interesting features of foundation models regarding (1) their prediction stability, (2) their prediction length performance, and (3) their fine-tuning process.

Regarding the prediction stability, when looking at the metrics across datasets, it seems like foundation models are more frequently specialized for some datasets (see Chronos Bolt Base), whereas baseline models (see TiDE and NaiveSeasonal) obtained great performance for 50% of the datasets. This seems slightly counterintuitive, since one of the basic concepts of foundation models is to perform well across different datasets.

Concerning prediction performance, irregular behaviors have been observed across different prediction lengths. Indeed, longer predictions are usually harder to make, and when looking at Table 5, some errors did decrease. The case of the weather dataset is particularly special, which may be due to the sampling length resulting in samples that are difficult to predict.

With respect to fine-tuning, such a process requires quite extensive knowledge and computation, and can deliver a wide range of results depending on the chosen dataset; e.g., marginal gains on the HEIA dataset and significant ones on the MeteoSwiss and ZurichElectricity datasets. Therefore, such a process should be conducted carefully and is, for now, limited to practitioners who have access to great computational resources.

Finally, we cannot say that one foundation model is better than all others, but given our quantitative evaluation, Chronos generally seems to perform better. However, the testing of such models should also be conducted with a qualitative mindset and visual analysis, for instance, to validate their performance together with applied experts.

5. Conclusions

This study benchmarks foundation models for industrial time-series forecasting, highlighting their superior zero-shot accuracy compared to traditional methods. Compact models, such as Chronos Bolt Tiny, provide an optimal balance of speed and performance suitable for resource-constrained scenarios. However, larger models require substantial computational resources, and their performance varies across datasets and prediction horizons. Future work should focus on improving model stability, simplifying fine-tuning processes, and incorporating qualitative assessments to enhance practical usability.