Drift and Diffusion in Panel Data: Extracting Geopolitical and Temporal Effects in a Study of Passenger Rail Traffic †
Abstract
1. Introduction
2. Previous Work, Materials, and Methods
2.1. Economic Determinants of European Railway Traffic
2.2. Drift and Diffusion in Geospatial Econometrics
- Data engineering of predictive variables as a prelude to predictive methods;
- Two-stage least-squares (2SLS) regression of residuals;
- Iterative local regression of instances defined by unsupervised k-nearest neighbors.
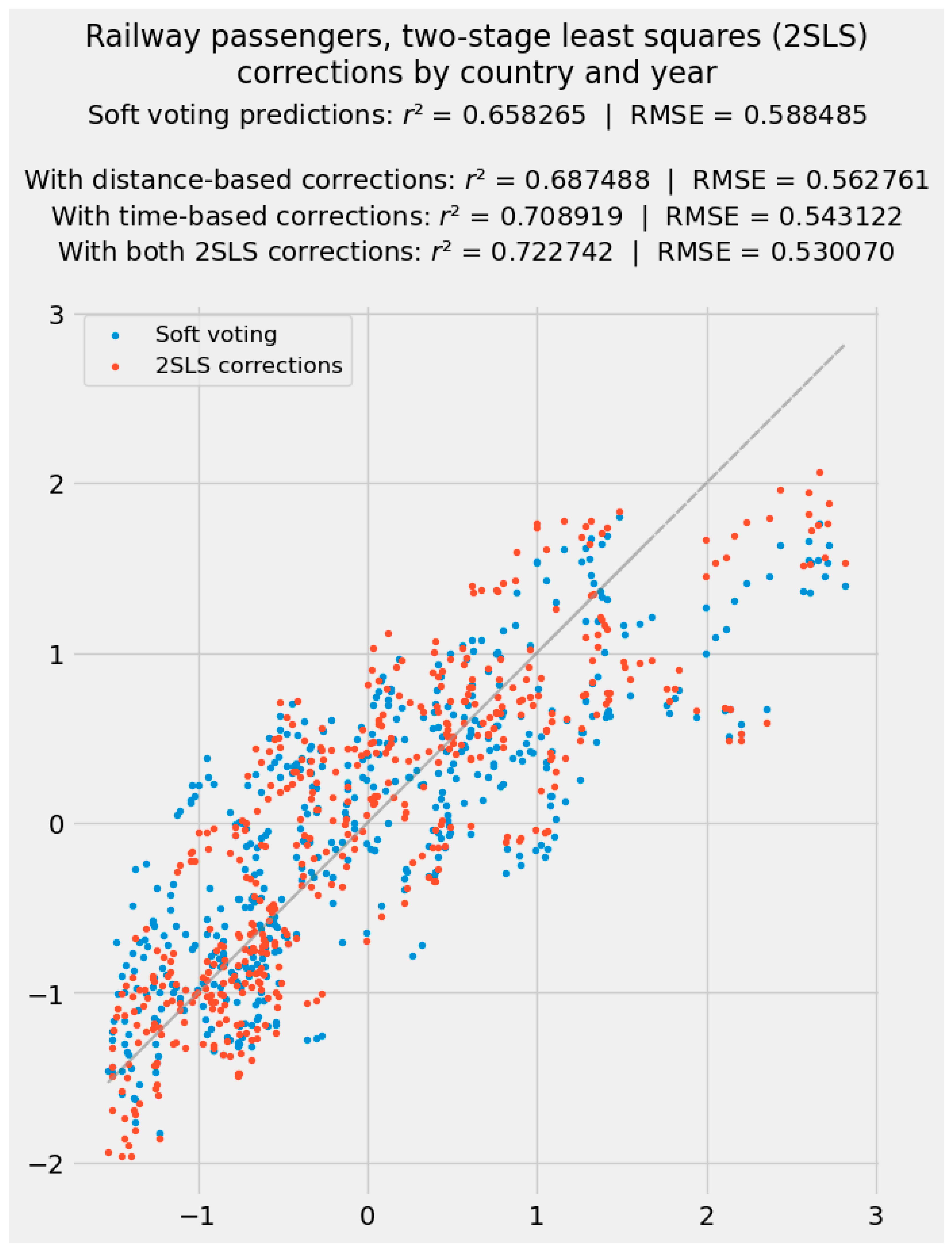
3. Results, Part 1: Two-Stage Least Squares
3.1. Geopolitical Distance: A Stylized Vector of “Carolingian Distances”
3.2. Correcting Residuals over the Course of Time
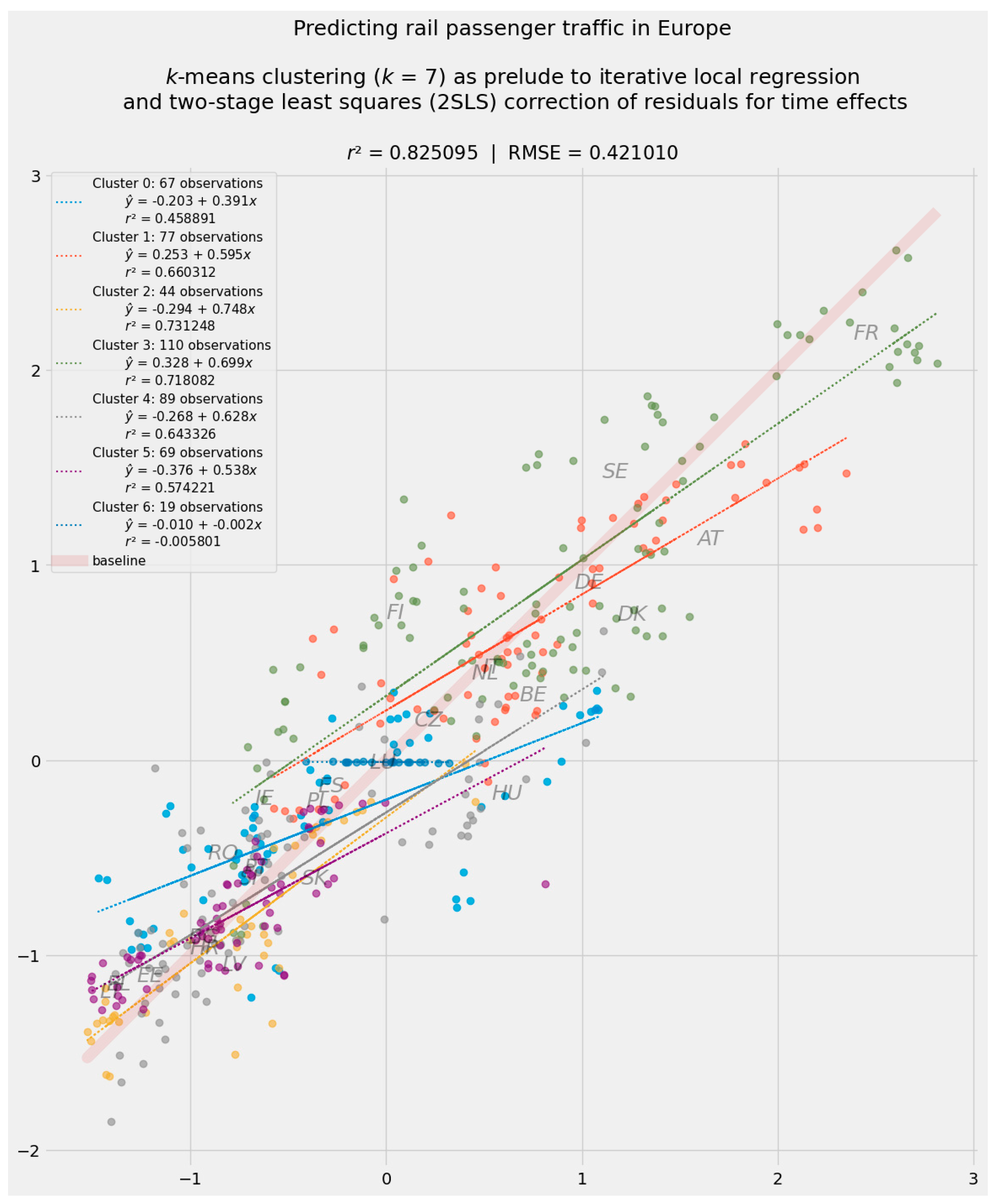
4. Results, Part 2: Clustering and Iterative Local Regression
4.1. Fixed Effects as a Form of Clustering
4.2. K-Means Clustering
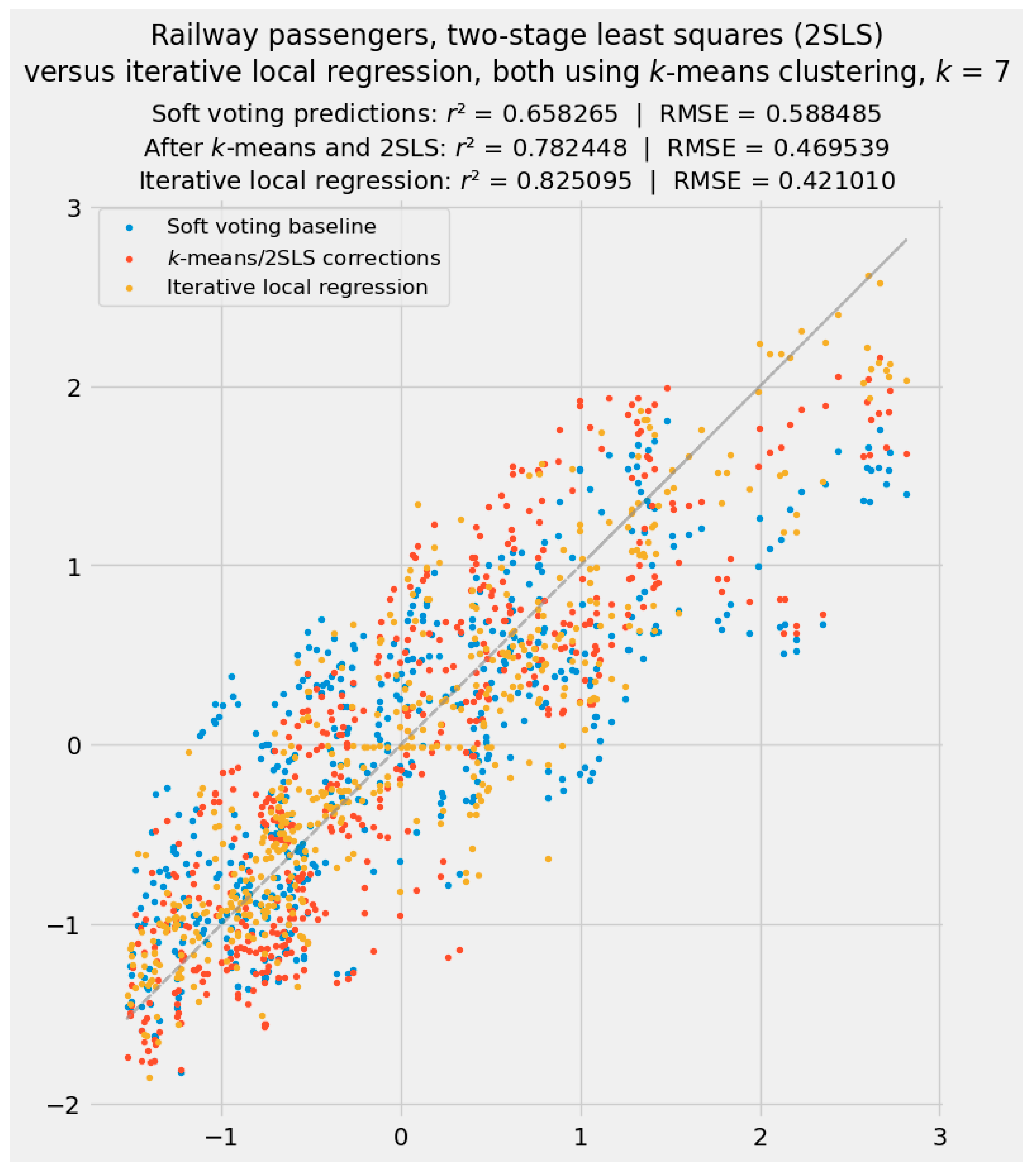
4.3. Analytical Results from Iterative Local Regression
SLS Correction of Residuals from Cluster-Based Local Regression
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2SLS | Two-stage least squares |
| GDP | Gross domestic product |
| OLS | Ordinary least squares |
| RMSE | Root mean squared error |
Appendix A
References
- Poufinas, T.; Panagopoulou, A.C.; Chen, J.M. On the economic determinants of railway passenger traffic in the European Union. Atl. Econ. J. 2025; 53, in press. [Google Scholar]
- Chen, J.M. Drift and diffusion in geospatial econometrics: Implications for panel data and time-series. Comput. Sci. Math. Forum, 2025; in press. [Google Scholar]
- Chen, J.M. A practical introduction to regularized regression for panel data. Contrib. Stat. 2025; in press. [Google Scholar]
- Dubin, R.A. Spatial autocorrelation and neighborhood quality. Reg. Sci. Urban Econ. 1992, 22, 433–452. [Google Scholar] [CrossRef]
- Maydeu-Olivares, A.; Shi, D.; Rosseel, Y. Instrumental variables two-stage least squares (2SLS) vs. maximum likelihood structural equation modeling of causal effects in linear regression models. Struct. Equ. Model. Multidiscip. J. 2019, 26, 876–892. [Google Scholar] [CrossRef]
- Inoue, A.; Solon, G. Two-sample instrumental variable estimators. Rev. Econ. Stat. 2010, 92, 557–561. [Google Scholar] [CrossRef]
- Haddock, D.D. Basing-point pricing: Competitive vs. collusive theories. Am. Econ. Rev. 1982, 72, 289–306. Available online: https://www.jstor.org/stable/1831533 (accessed on 28 May 2025).
- Thisse, J.-F.; Vives, X. Basing point pricing: Competition versus collusion. J. Indus. Econ. 1992, 40, 249–260. [Google Scholar] [CrossRef]
- Supreme Court of the United States. Federal Trade Commission v. Cement Institute. United States Rep. 1948, 333, 648–740. [Google Scholar]
- Pace, R.K.; Barry, R. Sparse spatial autoregression. Stat. Prob. Lett. 1997, 33, 291–297. [Google Scholar] [CrossRef]
- Likas, A.; Vlassis, N.; Verbeek, J.J. The global k-means clustering algorithm. Pattern Recognit. 2003, 36, 451–461. [Google Scholar] [CrossRef]
- Pham, D.T.; Dimov, S.S.; Nguyen, C.D. Selection of K in K-means clustering. J. Mech. Eng. Sci. 2005, 219, 103–119. [Google Scholar] [CrossRef]
- Hout, M.C.; Papesh, M.H.; Goldinger, S.D. Multidimensional scaling. WIREs Cogn. Sci. 2013, 4, 93–103. [Google Scholar] [CrossRef] [PubMed]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least angle regression. Annals Stat. 2004, 32, 407–499. [Google Scholar] [CrossRef]
- Wasserstein, R.L.; Schirm, A.L.; Lazar, N.A. Moving to a world beyond “p < 0.05”. Am. Stat. 2019, 73 (Suppl. 1), 1–19. [Google Scholar] [CrossRef]
- Mullainathan, S.; Spiess, J. Machine learning: An applied econometric approach. J. Econ. Persp. 2017, 31, 87–106. [Google Scholar] [CrossRef]


| Predictive Variable | OLS | Soft Voting |
|---|---|---|
| gdp_pc | 0.507549 *** 1 | 0.482761 *** |
| gdp_growth | −0.056322 | −0.040858 |
| inflation | −0.031413 | −0.013827 |
| unemployment | −0.206676 *** | −0.196214 *** |
| fertility | 0.112462 * | 0.108103 * |
| network_log | 0.612954 *** | 0.595888 *** |
| cars_pc | −0.021308 | −0.003860 |
| deaths_pc | −0.037088 | −0.011879 |
| Country | “Carolingian Distance” (Kilometers from Aachen) 2 | Carolingian Distance Expressed as a Z-Score |
|---|---|---|
| Austria | 795.36 | −0.433695 |
| Belgium | 121.51 | −1.743004 |
| Bulgaria | 1585.75 | 1.102055 |
| Croatia | 915.40 | −0.200454 |
| Czechia | 595.26 | −0.822495 |
| Denmark | 694.67 | −0.629338 |
| Estonia | 1520.40 | 0.975078 |
| Finland | 1572.19 | 1.075708 |
| France | 342.21 | −1.314178 |
| Germany | 541.48 | −0.926991 |
| Greece | 1988.79 | 1.885173 |
| Hungary | 1009.08 | −0.018431 |
| Ireland | 889.91 | −0.249981 |
| Italy | 1102.83 | 0.163728 |
| Latvia | 1360.59 | 0.664563 |
| Lithuania | 1358.86 | 0.661201 |
| Luxembourg | 129.63 | −1.727227 |
| Netherlands | 195.79 | −1.598676 |
| Poland | 1043.88 | 0.049187 |
| Portugal | 1794.42 | 1.507507 |
| Romania | 1651.30 | 1.229420 |
| Slovakia | 847.77 | −0.331861 |
| Slovenia | 813.07 | −0.399284 |
| Spain | 1377.94 | 0.698274 |
| Sweden | 1216.05 | 0.383718 |
| Predictive Variable | Correlation with Carolingian Distance |
|---|---|
| gdp_pc | −0.558713 ** 3 |
| gdp_growth | 0.077160 |
| inflation | 0.346282 + |
| unemployment | 0.534734 ** |
| fertility | −0.385699 + |
| network_log | 0.006705 |
| cars_pc | −0.367631 + |
| deaths_pc | 0.402817 * |
| passengers | −0.612838 ** |
| Variables | Cluster 0 | Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 | Cluster 5 | Cluster 6 |
|---|---|---|---|---|---|---|---|
| gdp_pc | −0.624985 | 0.275276 | −0.414271 | 0.911555 | −0.445655 | −1.015505 | 3.201688 |
| gdp_growth | 0.170321 | −0.319924 | −1.465259 | −0.222085 | 0.239041 | 1.067098 | 0.135049 |
| inflation | 0.399676 | −0.263255 | −0.310005 | −0.295721 | −0.231274 | 0.850973 | −0.174410 |
| unemployment | −0.436845 | −0.396739 | 1.805759 | −0.399750 | −0.191861 | 0.744581 | −1.012578 |
| fertility | −0.769180 | −0.540283 | −0.594548 | 1.363578 | 0.273314 | −0.967505 | 0.242712 |
| network_log | 0.010233 | 1.013735 | −0.267620 | 0.127315 | −0.547535 | −0.217838 | −2.713473 |
| cars_pc | −0.266320 | 0.988292 | −0.066136 | 0.318287 | −0.067569 | −1.284779 | 1.948569 |
| deaths_pc | 1.073907 | −0.380362 | −0.255050 | −0.803224 | −0.281161 | 1.510772 | −0.015089 |
| Variables | Cluster 0 | Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 | Cluster 5 | Cluster 6 |
|---|---|---|---|---|---|---|---|
| ℓ1 alpha | 0.022699 | 0.017015 | 0.006488 | 0.000000 | 0.002039 | 0.004957 | 0.051609 |
| r2 | 0.386987 | 0.639893 | 0.884457 | 0.723767 | 0.694480 | 0.563336 | 0.000000 |
| intercept | −0.667326 | 0.508055 | −0.728775 | 0.546850 | 0.282417 | −0.744207 | −0.013269 |
| gdp_pc | 0.000000 | 0.888764 | 0.000000 | 0.663217 | 1.349062 | 0.000000 | 0.000000 |
| gdp_growth | 0.000000 | −0.074480 | 0.000000 | −0.163557 | −0.352117 | 0.000000 | 0.000000 |
| inflation | 0.000000 | 0.000000 | 0.000000 | −0.249260 | 0.075187 | 0.029277 | 0.000000 |
| unemployment | −0.676279 | −0.190030 | −0.103394 | −0.313400 | −0.084758 | 0.082659 | 0.000000 |
| fertility | −0.346999 | 0.000000 | −0.089854 | −0.259930 | 0.000000 | 0.000000 | 0.000000 |
| network_log | 0.401915 | 0.000000 | 0.409860 | 1.126678 | 0.496841 | 0.298184 | 0.000000 |
| cars_pc | 0.000000 | −0.127164 | −0.233341 | −0.247714 | −0.184285 | 0.000000 | 0.000000 |
| deaths_pc | −0.089092 | 0.000000 | −0.284552 | 0.254671 | −0.202252 | −0.049151 | 0.000000 |
| Predictive Variable | OLS | Iterative Local Regression (Weighted Mean) |
|---|---|---|
| intercept | 0.000000 | −0.008359 |
| gdp_pc | 0.507549 *** 4 | 0.550432 |
| gdp_growth | −0.056322 | −0.115925 |
| inflation | −0.031413 | −0.039383 |
| unemployment | −0.206676 *** | −0.212224 |
| fertility | 0.112462 * | −0.117463 5 |
| network_log | 0.612954 *** | 0.491980 |
| cars_pc | −0.021308 | −0.134123 |
| deaths_pc | −0.037088 | −0.024984 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.M.; Poufinas, T.; Panagopoulou, A.C. Drift and Diffusion in Panel Data: Extracting Geopolitical and Temporal Effects in a Study of Passenger Rail Traffic. Comput. Sci. Math. Forum 2025, 11, 31. https://doi.org/10.3390/cmsf2025011031
Chen JM, Poufinas T, Panagopoulou AC. Drift and Diffusion in Panel Data: Extracting Geopolitical and Temporal Effects in a Study of Passenger Rail Traffic. Computer Sciences & Mathematics Forum. 2025; 11(1):31. https://doi.org/10.3390/cmsf2025011031
Chicago/Turabian StyleChen, James Ming, Thomas Poufinas, and Angeliki C. Panagopoulou. 2025. "Drift and Diffusion in Panel Data: Extracting Geopolitical and Temporal Effects in a Study of Passenger Rail Traffic" Computer Sciences & Mathematics Forum 11, no. 1: 31. https://doi.org/10.3390/cmsf2025011031
APA StyleChen, J. M., Poufinas, T., & Panagopoulou, A. C. (2025). Drift and Diffusion in Panel Data: Extracting Geopolitical and Temporal Effects in a Study of Passenger Rail Traffic. Computer Sciences & Mathematics Forum, 11(1), 31. https://doi.org/10.3390/cmsf2025011031





